Soft-computing approach to solve ill-posed inverse problems: application to random materials and imperfect cylindrical shells

Abstract

In this work a soft-computing approach, based on a hybrid stochastic optimization (HSO) tool, is suggested to solve numerically inverse problems. These problems are formulated and solved using optimization methods. The HSO tool combines genetic algorithms, simulated annealing and taboo list. One of the key features of the proposed approach is the possibility of identifying multiple solutions that satisfy the ‘forward’ model. The HSO tool has been applied to reconstruct the microstructural configurations of random materials. The ill-posed inverse problem associated with the reconstruction process, i.e. the identification of the microstructural configurations, can be seen as an optimization problem where a set of target correlation functions is prescribed and the reconstruction method proceeds to identify realizations of the random material that best match the prescribed set of target correlation functions. The proposed approach is highly parallelizable, flexible and scalable and it can be, in principle, adopted to solve other types of optimization problems as well.

Keywords:

• stochastic optimization
• random materials
• inverse problem
• optimization
• correlation function
• taboo list

AMS Subject Classifications:

• 68W10 Parallel algorithms
• 65C35 Stochastic particle methods
• 68N01 General
• 74N15 Analysis of microstructure
• 74A40
• Random materials and composite materials

1. Introduction

Numerical models play an increasingly important role in simulating, studying and predicting future outcomes in every field of science. The growing power of computers allows for the establishment of refined numerical models, aimed at a close representation of real characteristics observed in nature 1. These numerical models are used, for instance, to design and produce advanced materials with the desired performance characteristics, by controlling the material configuration at the microscopic level 2. This type of analyses involve the solution of an inverse problem, i.e. identify the material configurations at the microscopic level that satisfy the desired performance (the ‘forward problem’), as systematized in Figure 1.

Figure 1. Schematic representation of proposed approach to reconstruct the microstructure configurations of random materials.

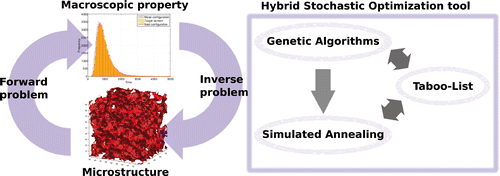
Figure 2. (a) Example of a forward problem, (b) the corresponding ill-posed inverse problem and (c) the associated optimization problem.

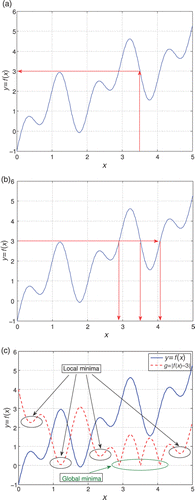
Figure 3. (a) Rastrigin's function, (b) the identification of the minima of the by means of genetic algorithms, (c) genetic algorithms and simulated annealing and (d) the proposed HSO tool.

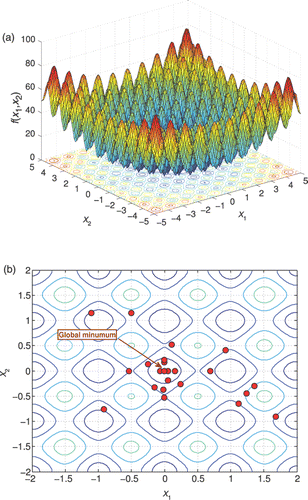
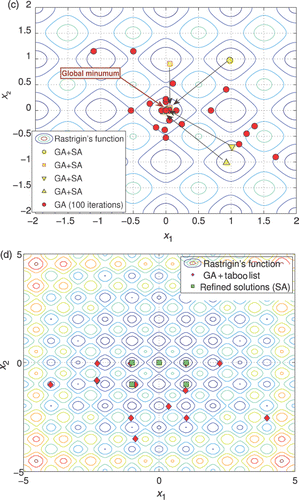
Figure 4. Examples of cross sections of the porous material: (a) the target material and (b) the reconstructed material.

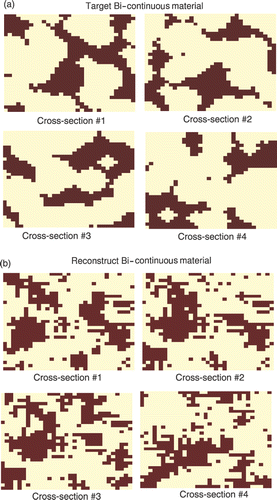
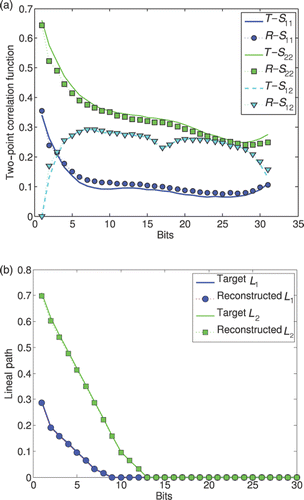
Figure 5. Correlation functions of the porous material. (a) two-point correlation functions of the target domain and the reconstructed material for the voids, , the matrix, , and voids-matrix, , respectively. (b) lineal path correlation functions of the target domain and the reconstructed material for the voids, L⁽¹⁾, and the matrix, L⁽²⁾.

From the mathematical point of view, this inverse problem can be formulated as an optimization problem in which one seeks to minimize a real function by systematically choosing values of real or integer variables within an allowed set. Unfortunately, finding the optimum, especially in the case of non-linear functions, may be computationally involved. Moreover, in most cases it is impossible to determine analytical solutions. In such cases, various heuristic methods may be useful which, however, do not always guarantee that the optimal solution can be found. Nevertheless, they can find a solution close to the best one within a reasonably brief period of time. For instance, artificial neural networks have been shown to be efficient tools to model complex relationships between inputs and outputs (see, e.g., 3,4).

The scope of this work is to present an accurate and efficient soft-computing approach to numerically solve the inverse problem associated with the reconstruction of the material microstructure of porous materials and boundary imperfections of cylindrical shells starting from limited microstructural information. The proposed approach combines three different tools: genetic algorithms, simulated annealing and taboo list. The inclusion of taboo list in the hybrid stochastic optimization (HSO) tool, originally proposed in 5, allows to identify a set of unique solutions of the inverse problem. The subsequent analysis of the samples can be performed to obtain the desired macroscopic properties providing a link between the micro- and the macro-scale.

In the next section the formulation of the inverse problem as an optimization problem is outlined. The HSO tool proposed to solve the inverse problem is presented in Section 3. In Section 4 a number of different applications demonstrate the applicability of the proposed approach.

2. Background

An inverse problem is the task that often occurs in many branches of science and mathematics where the values of some model parameter(s) must be obtained from the observed data. It can be mathematically formulated as follows: (1) where y* represents the observed data, f(·) the model and x the parameters of the model to be identified. Figure 2 shows: (a) a forward model and (b) the corresponding inverse problem, respectively.

Inverse problems are typically ill posed 6, as opposed to the well-posed problems more typical for modelling physical situations where the model parameters or material properties are known. Inverse problems are generally difficult to solve because different values of the model parameters may be consistent with the data, and discovering the values of the model parameters may require the exploration of a huge parameter space.

The ill-posed inverse problem can be formulated as an optimization problem. Instead of trying to identify the values that satisfy the forward problem, the following objective function is minimized: (2) Although the original forward model may be quite simple, the objective function associated to the inverse problem is generally characterized by many global and local minima (Figure 2(c)).

In the context of the analysis of random materials, the reconstruction of the microstructural configuration, i.e. the inverse problem, can be seen as an optimization problem where a set of target correlation functions is prescribed and the reconstruction method proceeds to identify realizations of the random material that best match the prescribed set of target correlation functions. This inverse problem is solved by minimizing an objective function that represents the distance between the correlation functions adopted to characterize the target material and the reconstructed material, respectively 5.

Let and be the k-th probabilistic descriptor for the reconstructed digitized system and the target system, respectively. The k-th probabilistic descriptor can represent any type of correlation function, e.g represents the n-point correlation function for the j-th phase 7. In the reconstruction process, the system configuration evolves towards from an initial guess. Once is evaluated at a particular time step, the objective function, denoted with the symbol E, can be calculated as (3) where the sum on i is multi-dimensional over all configurations of r. The parameter α_k is an arbitrary weight assigning the relative importance to each individual k-th correlation function that contribute to the total energy, E.

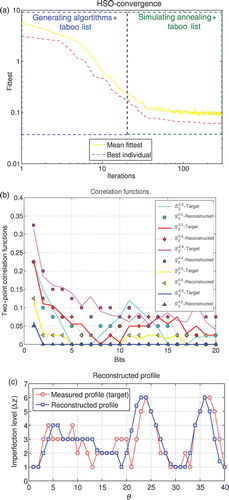
Figure 6. Diffusion times of simulated particles through the target domain, the best reconstructed porous material and the domain that corresponds to the average (‘mean’) reconstructed material.

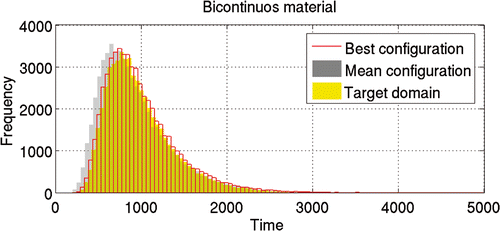
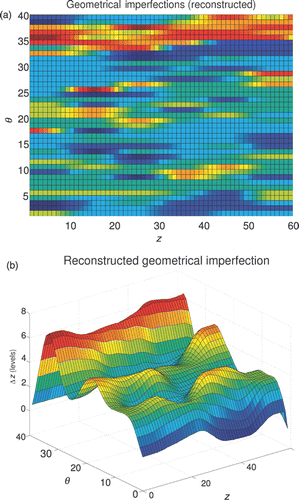
Figure 7. Geometrical imperfections field of the cylinder Z15 18: (a) measured values and (b) the correspondent digitalized values.

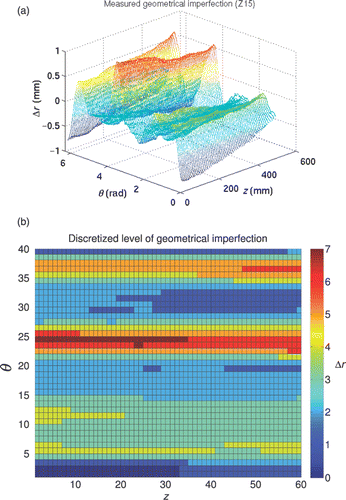
Figure 8. Reconstruction of the geometrical imperfections of a cylindrical shell by means of the HSO tool: (a) objective function; (b) target and reconstructed correlation functions and (c) target and reconstructed profile of the geometrical imperfections.

Figure 9. Reconstructed field of geometrical imperfections of a cylindrical shell: (a) bi-dimensional and (b) three-dimensional representation.

Figure 10. Buckling analysis of a cylindrical shell with geometrical imperfections reconstructed by means of the HSO tool. (a) Load-displacement (time) relationship and (b) post-buckling cylindrical shape.

3. A soft-computing approach

A number of different optimization algorithms can be adopted to find a minimum of Equation (3) and in particular stochastic optimization techniques. The latter are used because they are global search techniques, they are easily parallelizable, and most importantly, they have been shown to work appropriately in a number of different applications.

In this work, an efficient and accurate hybrid stochastic optimization tool that combines the genetic algorithms, simulated annealing and taboo list, is suggested. These three component are briefly outlined in the following; more details can be found in the specialized literature (see 8–10 among others).

The genetic algorithms are global search tools that provided a group of solutions (population) rather than a single solution. Due to the parallel nature of the stochastic search, the genetic algorithms are much more likely to locate a global peak than traditional techniques and their performance is much less sensitive to the initial conditions. Hence the genetic algorithms' convergence time is quite predictable. The genetic algorithms are very efficient methods to identify the most promising areas in the phase space. However, they are usually slower than traditional techniques in identifying the optimal solution, when a good solution close to the global optimum has been identified as shown in 5. For this reason genetic algorithms are adopted by the HSO tool to identify the most promising areas in the phase space using a limited number of iterations (i.e. population selection, evaluation and mutation).

Simulated annealing is a procedure to finding a state of minimum ‘energy’ among a set of many local minima by manipulating appropriately the phase of pixels in the digitized system, for instance, interchanging the states of two arbitrarily selected pixels of different phases. After each pixel manipulation, the value of the objective function, E ′, and the difference ΔE = E′ − E between two successive states of the system are computed. The new configuration is then accepted with probability p(ΔE) applying the Metropolis method as (4) where T is a parameter called ‘temperature’. As shown in 5, simulated annealing is a quite accurate method but its performance is very sensitive to the initial configuration. Hence, the simulated annealing technique is adopted to refine the solutions identified by means of the genetic algorithms. In fact, these solutions are already ‘good’ solutions but they can be further improved by means of simulated annealing, i.e. each individual of the final population of genetic algorithms represents the initial solution for simulated annealing optimization.

Next, taboo list is included in the HSO tool. This strategy is used in the selection procedure of the candidate solutions by genetic algorithms and by simulated annealing. Taboo list inhibits solutions characterized by certain attributes, e.g. microstructures which include undesirable configurations, and avoids the presence of equivalent solutions in the reconstruction process. Taboo list is adopted for the identification of multiple solutions and for avoiding unnecessary computations. In fact, if a candidate solution is ‘taboo’ it is immediately discharged; otherwise, it is processed and the corresponding objective function is evaluated.

4. Numerical examples

4.1. General remarks

In this section, different numerical examples are presented in order to demonstrate the applicability of the proposed approach. The first numerical example is presented in Section 4.2 for the purpose of verification of the approach. In Section 4.3 the reconstruction of a porous material is proposed. Finally, in Section 4.4 the HSO is used to generate a random field that represents the geometrical imperfections of a cylindrical shell.

4.2. Verification: Rastrigin's function

The HSO tool is used to minimize the Rastrigin's function (Figure 3a) 11. It is a typical example of non-linear multimodal function, defined as following: (5) The global minimum of the function is the vector x* = (0, 0) with R(x*) = 0.

The minimum of this function may be identified adopting traditional technique such as the genetic algorithms and simulated annealing, as shown in Figure 3(b) and (c). However, our aim is not only to identify the global minimum of Equation (5) but also to identify as many minima as possible that are close to the global one, in terms of values of R(x). For this purpose, the soft-computing technique presented in Section 3 is adopted.

The results of this identification are shown in Figure 3(d) where the genetic algorithms and the taboo list are used; first, to identify the promising solutions and then the simulated annealing and taboo list are used to refined the identified solutions. The taboo rule adopted here is the minimum distance between solutions equal to π/4, i.e. if the distance of a proposed solution, i, to another solution, j, already present in the population is lower than d ≡ ‖x_i − x_j‖< π/4 ∀j ≠ i, then the solution is marked as ‘taboo’ and hence it is immediately discharged.

4.3. Reconstruction of a porous media

Porous materials are composed by a solid phase (matrix) and a void phase (pores). In this numerical example, the target material has been generated numerically: spatially uncorrelated spheres that represent the voids, with a constant radius and centres determined by a Poisson process, are entered in the system until the desired volume fraction is reached, as suggested in 12. The porous material is discretized in 96 × 96 × 96 binary pixels, i.e. 2⁸⁸⁴⁷³⁶ configurations.

The digitized microstructure is characterized by means of the generalized indicator function, I^(j)(x) of V^(j) where each phase j = 1, … , n_j, occupies a disjoint sub-domain V^(j) ⊂ ℜ³. The indicator function defined as (6) completely describes the configuration of the phases within the medium. The indicator function represents a random field which satisfies . The microstructure samples are statistically described by the two-point correlation functions of the voids, , of the matrix, , and between phases, and, by the lineal path correlation function, L⁽¹⁾, L⁽²⁾, for the voids and the matrix, respectively. Here only statistical descriptors (i.e. correlation functions) of the two-dimensional cross sections of the digitized image of the material are used to characterize the microstructure 7 (Figure 4(a)).

Based on this set of correlation functions, the microstructure of the porous material is reconstructed, adopting the HSO tool with the taboo list formed by the collection of identified microstructures. Examples of the reconstructed cross sections of the porous material are shown in Figure 4(b). Figure 5 shows the correlation functions of the target and the reconstructed material, respectively. Although the correlation functions are reconstructed with a satisfactory agreement, the cross sections of the target material and the reconstructed material might be quite different because the correlation functions adopted to reconstruct the microstructure are not sufficient for a perfect reconstruction of the morphology of the porous media.

In this numerical example, the macroscopic quantity of interest considered is the diffusion coefficient. A Monte Carlo model 13 is used to estimate the diffusion coefficient of the porous materials. The model follows the random walk of 6 × 10⁴ particles and the time required by the particles to migrate from one surface to the opposite one is collected by appropriate counters. The distributions of the arrival times of the particles, expressed in arbitrary time units, are shown in Figure 6. A satisfactory agreement between the target and the reconstructed material is obtained due to the connectivity information embedded in the lineal path function.

The computational time required to generate a database of 100 three dimensional microstructure samples takes approximately 16 h on a Linux cluster of 32 processors (Intel® Xeon® E5345 and E5430).

4.4. Geometrical imperfections of a cylindrical shell

Thin-walled cylindrical shells are sensitive to instability phenomenon and have a tendency to respond with undesired dynamic amplitudes when being loaded by compressive membrane stresses beyond instability limits. When a state of static instability is reached, the released amount of energy during the transition to a new stable state can result in disastrous structural responses (see, e.g. 14,15). Despite their simple geometry, the limit load of cylindrical shells under axial compression is greatly influenced by geometrical imperfections, i.e. irregularities in shape. These irregularities in shape are usually modelled as random fields and represented by a Karhunen–Loève expansion (see, e.g. 16,17).

The aim of this numerical example is to reconstruct random fields of the surface imperfections of a cylindrical shell that have the same statistical characteristics of the geometric imperfections measured on the real specimens by means of the HSO tool. The reconstructed imperfections can be used, for instance, to study buckling of cylindrical shells. However, a discussion on the buckling analysis is beyond the scope of this article.

The geometrical imperfection pattern, i.e. the target material, has been obtained from DLR-ESA 18, scanning the surface of eight specimens with the help of an high-speed optical sensor. As an example, the scanned surface of the cylinder labelled Z15 is plotted in Figure 7(a). The variation of the surface of the cylinder from the nominal values of the radius, Δr, is discretized in eight different levels and interpolated to a regular grid of 40 × 60 representing the circumferential coordinate, θ, and the axial coordinate, z, respectively. Hence, the optimization space is 8²⁴⁰⁰. The digitalized random field is shown in Figure 7(b). This digitized random field can be seen as a multiphase random material. Hence, the random field is characterizable by means of the generalized indicator function, as shown in Section 4.3, where each phase, j = 1, … , 8, represents a discretized level of the geometrical imperfection. 15 two-point correlations functions along the θ direction are calculated: with i = 1, … , 8 and j = i, min(8, i + 1). Furthermore, eight more functions are used to represent the variation of the distribution of the phases (imperfection levels) along the z axis.

Based on the knowledge of these correlation functions, the geometrical imperfections of the cylindrical shell is reconstructed by means of the HSO tool with a taboo-list formed by the collection of identified geometrical imperfections. Figure 8 shows the evolution of the objective function, the comparison between (a selection of) correlation functions and an example of the reconstructed profile of the geometrical imperfection, respectively. The rendering of the reconstructed imperfection field obtained by means of the HSO tool is shown in Figure 8.

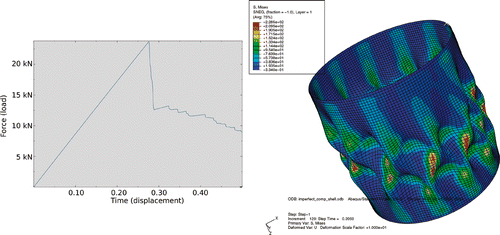
For completeness, a non-linear Finite Element analysis is carried out in order to determine the buckling load of the cylindrical shell with the geometrical imperfection described by the reconstructed field (Figure 9). For the details of the FE analysis of the cylindrical shells, it is referred to 17. Figure 10 shows the results of the buckling analysis of the cylindrical shell and the correspondent buckling load. The buckling load obtained by the simulation is 23.711 kN and it is an agreement with the range of the experimental results that are in between 21.320 kN and 25.690 kN 18. Less then 2 h are required to generate a database of 100 geometrical imperfections fields on a Linux cluster of 32 processors (Intel Xeon® E5345 and E5430).

5. Conclusions

In this work, an efficient and accurate soft-computing approach is proposed for solving the ill-posed inverse problem associated with the reconstruction of the microstructures of random materials where an unique solution does not exist, which also form the context in which this method has been developed. The proposed hybrid stochastic optimization tool takes advantage of the salient features of different methods: the efficiency of genetic algorithms, the accuracy of simulated annealing and the ‘memory’ of the taboo list method. Hence, it is possible to identify multiple solutions that satisfies the inverse problem in an efficient and accurate way.

The numerical examples presented have shown the feasibility of the current approach. In fact, the proposed method has been applied successfully for the reconstruction of the microstructure of a porous material as well as for the reconstruction of the random field that represents the geometrical imperfections of a cylindrical shell. The current procedure is easily parallelizable and can, in principle, be adopted to solve a number of inverse problems.

Acknowledgements

This project was partially supported by the Austrian Science Foundation (FWF) under the contract P19781-N13, which is gratefully acknowledged by the authors.