Immune identification of piezoelectric material constants using BEM

Abstract

This article deals with an application of the artificial immune system (AIS) to the identification problem of piezoelectric structures analysed by the boundary element method (BEM). The AIS is applied to identify material properties of piezoelectrics. The AIS is a computational adaptive system inspired by the principles, processes and mechanisms of biological immune systems. The algorithms typically use the characteristics of immune systems, such as learning and memory to simulate and solve a problem in a computational manner. The main advantage of the AIS, contrary to gradient methods of optimization, is the fact that it does not need any information about the gradient of fitness function.

Keywords:

• artificial immune system
• boundary element method
• identification
• piezoelectricity

1. Introduction

Identification of material constants using the artificial intelligence techniques is a very active field of research 1–4. The main approach in solving the identification problem is to find the material constants using the response of the structure. Several novel techniques have been recently developed.

One of the best known approaches is based on the minimization of the special functional 5. In 5, the identification problem consists in finding such values of the material constants, which give solution fields that differ the least from the measured ones known from the experiment. The fields on the boundary are known at a given number of boundary points. The identification problem of material constants is equivalent to the minimization problem of the special functional. Minimization with respect to the searched parameters can be done using many approaches.

A general approach is presented in 6. In this study, the genetic least-squares technique is applied for system identification. In 4, genetic algorithms are used for identification of material constants in anisotropic media. In 7, the authors applied the evolutionary-simplex algorithm and structural dynamic response to identify the structural physical parameters. A genetic algorithm was also applied in 3 to search for the elastic parameters of composites. The distributed evolutionary algorithm was used in 5 for optimization and defect identification in elastic structures.

In another interesting approach, the genetic or evolutionary algorithms are connected with other optimization techniques 1. In 1, the combination of topological sensitivity and genetic algorithms are used for inverse identification problems in anisotropic materials. Also, Chaparro et al. 8 proposed gradient-based, genetic and hybrid optimization algorithms for material parameters identification problem. Identification of effective elastic constants of composite plates based on a hybrid genetic algorithm was also considered in 2.

A hybrid approach based on coupling of fuzzy-neural nets and evolutionary computation in the identification of defects as voids and cracks was examined in 9.

Another approach to inverse identification problems, based on hybrid techniques, has been developed in 10, where the surrogate-model accelerated random search algorithm for global optimization was applied to inverse material identification.

The evolutionary algorithm for identification of material coefficients of human pelvic bone was used in 11. Identification of tumour region parameters using evolutionary algorithms was considered in 12 and 13.

The method presented in this article is based on the application of the artificial immune system (AIS) and the boundary element method (BEM) to the inverse identification problem in the piezoelectric material. The AIS is developed on the basis of a mechanism discovered in biological immune systems 14. Recently, Zilong et al. 15 proposed the immune evolutionary algorithm incorporating chaos optimization. An evolutionary AIS was applied to multi-objective optimization in 16.

In piezoelectric materials, mechanical and electric fields are coupled. Namely, they produce an electric field when deformed or conversely, they deform when subjected to an electric field. Piezoelectric materials are widely used as sensors and actuators in smart structures and micro-electro-mechanical systems (MEMS). In 17, the authors developed a finite element model for the identification of mechanical and piezoelectric properties through gradient optimization and experimental vibration data. In 18, the authors estimated piezoelastic and viscoelastic properties in laminated structures using the classical algorithms of nonlinear optimization combined with the sensitivities and the finite element model.

The piezoelectricity phenomenon is widely used in many devices, for example sensors, actuators, MEMS and transducers. The ceramic piezoelectrics are solids, which belong to the hexagonal symmetry class of crystals. These crystalline solids have anisotropic physical properties; therefore, in this article, a homogeneous, transversal isotropic, linear elastic and dielectric model of the piezoelectric material is chosen. For this material, the piezoelectric effect in the two-dimensional case is described by nine material constants: four elastic, three piezoelectrics and two dielectrics. In addition, the dielectric constants are 20 orders of magnitude smaller than the elastic constants. These facts, i.e. a relatively big number of the constants and lack of gradient information, make the identification problem of the piezoelectric material constants quite complicated. An analysis of piezoelectric devices requires a solution of the coupled mechanical and electrical partial differential equations. In this article, the BEM is implemented to solve the static two-dimensional problem of linear piezoelectricity. To obtain the fundamental solutions, the Stroh formalism is used. To solve both direct and inverse problems of piezoelectricity, the BEM computer code is developed and the AIS algorithm is coupled to the BEM code. Numerical examples are given and good results are obtained.

In the authors’ opinion, no application of the AIS for solving inverse identification problems in piezoelectrics modelled using the BEM can be found in the literature until now.

This article is organized as follows. In Section 2, the AIS is briefly reviewed. In Section 3, the BEM for linear piezoelectricity and the Stroh formalism are introduced and applied to obtain the fundamental solutions. The Stroh formalism is also used to investigate the influence of the polarization direction. In Section 4, the formulation of the inverse identification problem is proposed. In Section 5, the benchmark numerical examples are presented. Finally, concluding remarks are given in Section 6.

2. Artificial immune systems

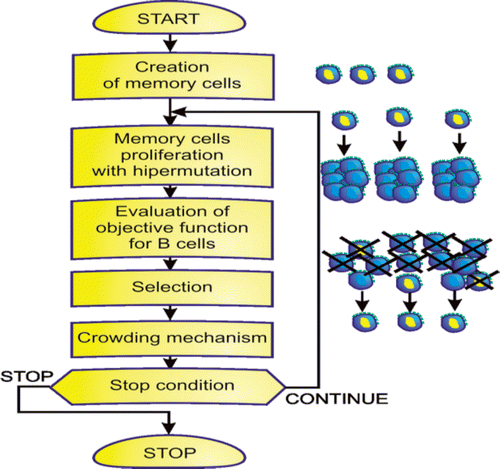
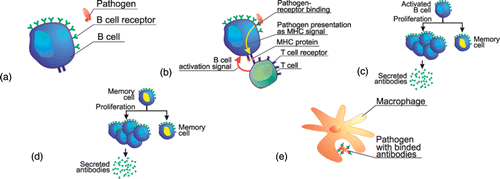
The AISs are developed on the basis of a mechanism discovered in biological immune systems 14. An immune system is a complex system which contains distributed groups of specialized cells and organs. The main purpose of the immune system is to recognize and destroy pathogens – funguses, viruses, bacteria and improper functioning cells. The lymphocytes play a very important role in the immune system. The lymphocytes are divided into several groups of cells. There are two main groups: B- and T-cells, both containing some subgroups. The B-cells contain antibodies, which can neutralize pathogens and are also used to recognize pathogens. There is a big diversity between antibodies of the B-cells, allowing recognition and neutralization of many different pathogens. The recognition of a pathogen is performed in a few steps (Figure 1). First, the B-cells or macrophages present the pathogen to a T-cell using MHC (Figure 1b), the T-cell decides if the presented antigen is a pathogen. The T-cell gives a chemical signal to B-cells to release antibodies. A part of the stimulated B-cells goes to a lymph node and proliferate (clone; Figure 1c). A part of the B-cells changes into memory cells, the rest of them secrete antibodies into the blood. The secondary response of the immunology system in the presence of known pathogens is faster because of memory cells. The memory cells created during primary response proliferate and the antibodies are secreted into the blood stream (Figure 1d). The antibodies bind onto the pathogens and neutralize them. Other cells like macrophages destroy pathogens (Figure 1e). The number of lymphocytes in the organism changes, while the presence of pathogens increases, but after attacks, a part of the lymphocytes is removed from the organism.

Figure 1. An immune system: (a) a B-cell and pathogen; (b) the recognition of pathogen using B- and T-cells; (c) the proliferation of activated B-cells; (d) the proliferation of a memory cell – secondary response and (e) pathogen absorption by a macrophage.

The AISs take only a few elements from the biological immune systems. The most frequently used are the mutation of the B-cells, proliferation, memory cells and recognition using the B- and T-cells. The presented approach is based on Wierzchoń's algorithm 26, but the mutation operator is changed. The Gaussian mutation is used instead of the nonuniform mutation in the presented approach. At the beginning of the AIS, the memory cells are created randomly. They proliferate and mutate creating B-cells. The number of clones created by each memory cell is determined by the memory cell's objective function value. The objective functions for B-cells are evaluated. The selection process exchanges some memory cells for better B-cells. The selection is performed on the basis of the geometrical distance between each memory cell and B-cells (measured by using design variables). The crowding mechanism removes similar memory cells. The similarity is also determined as the geometrical distance between memory cells. The process is iteratively repeated until a termination criterion is fulfilled. An AIS is schematically shown in Figure 2.

Figure 2. An AIS.

3. BEM for linear piezoelectricity

An analysis of piezoelectric devices requires a solution of coupled mechanical and electrical partial differential equations 19. In this article, the BEM 20 is implemented to solve the static two-dimensional problem of linear piezoelectricity.

The coupled field equations of static piezoelectricity are given by the following system of partial differential equations 21: (1)

The tensors C_ijkl, e_lij, ε_il denote elastic moduli, measured in a constant electric field, piezoelectric constants and dielectric constants, measured at constant strains, respectively; u_k is the displacement vector, φ denotes the electric potential and b_j is the body force vector per unit volume. In Equations (1), the intrinsic electric charge is neglected because piezoceramic materials are dielectrics, which possess no free electric charges 19.

To get the classical boundary value problem formulation, Equations (1) must be completed with appropriate boundary conditions, both mechanical and electric. The coupled field equations (1) with boundary conditions formulate the direct problem in linear piezoelectricity.

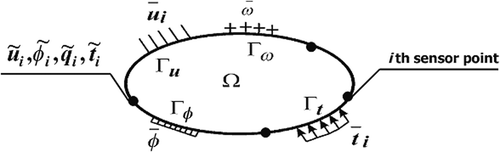
The plane boundary value problem of linear piezoelectricity can be formulated in a much more convenient form using generalized quantities 19,21. The following vectors are introduced: (2) where are the generalized displacement, traction and body force vectors, respectively. Vectors contain: displacement vector components u₁, u₃ and the electric potential φ, traction vector components t₁, t₃ and the charge flux density ω, and body force vector components b₁, b₃, respectively.

Let us assume that a piezoelectric solid occupies the simply connected domain Ω , which is an open and bounded subset of with boundary of Lipschitz-type. Here, and are disjoint nonempty open subsets of with . More formally, the mixed boundary value problem of plane linear piezoelectricity can be formulated in the following way: find the generalized displacement vector satisfying: (3) where is the elliptic operator of plane linear piezoelectricity given by (4)

The coefficients , and are the values of the elastic, piezoelectric and dielectric constants, respectively. In this study, a homogeneous, transversal isotropic, linear elastic and dielectric model of the piezoelectric material is chosen 19,21.

denotes the traction operator given by (5) where are components of the unit vector normal to ; ; are the trace operators from the domain to parts of the boundary and the prescribed generalized displacement boundary conditions . According to Borelli et al. 22, all known results on existence, uniqueness and regularity of solutions to elliptic systems are also applicable to plane piezoelectricity problem of transversal isotropic piezoelectric material.

The integral formulation of the present problem is simply the generalized Betti theorem 19: (6)

If v is the fundamental solution of the operator , i.e.: (7)

where is the Dirac distribution and is an identity matrix, then one can obtain the following boundary integral equation of the present problem 19: (8) where is the coefficient which depends on the boundary regularity. Equation (8) can be solved approximately using the BEM. The boundary Γ is divided into boundary elements. The boundary generalized displacements and tractions are approximated using shape functions. In the present method constant boundary elements are used. The discretized equation is applied to all boundary nodes, and the following system of linear algebraic equations is obtained: (9)

In Equation (11), H denotes the matrix which depends on the derivatives of the fundamental solution and G is a matrix which depends on the fundamental solution. The vectors and contain discretized values of the boundary generalized displacements and tractions. The set of equations is modified according to the boundary conditions and solved, giving the unknown boundary quantities. When boundary conditions are taken into account, the system of Equation (10) is given by (10) where and N is the number of constant boundary elements. C denotes the matrix which depends on the fundamental solution and its derivatives, F is obtained using boundary conditions and X contains the unknown values of the generalized boundary displacements and tractions.

For the material given by (4), the piezoelectric effect in the two-dimensional case is described by the nine material constants. These constants are: four elastic constants, three piezoelectric constants and two dielectric constants. In addition, the dielectric constants are 20 orders of the magnitude smaller than the elastic constants. This fact, that there are a relatively big number of the constants and a lack of gradient information, makes the identification problem of the piezoelectric material constants quite complicated.

Since ceramic piezoelectric materials are anisotropic, the fundamental solutions are rather complicated, even for the transversal isotropic model of the material. To obtain the fundamental solutions, the Stroh formalism is used 19. The Stroh formalism is a powerful and elegant analytic technique for the anisotropic elasticity, which is expanded to the linear piezoelectricity in this case. The orientation of the polarization direction is also taken into account using this formalism. The formalism requires the solution of a special eigenvalue problem with respect to the material constants of the piezoelectric material. The eigenvalues and the eigenvectors related to these constants are transformed according to the polarization direction.

4. Identification problem

The identification problem is how to find the material constants and the polarization direction using the response of the structure 21. The identification problem consists in finding those values of the material constants which give solution fields (both mechanical and electric) that differ the least from the measured ones known from the numerical experiment. The fields on the boundary (such as displacements, tractions, potential and charge flux density) are known at a given number of boundary points called sensors, see Figure 3.

Figure 3. Sensor points on the boundary.

More formally, inverse problems, especially parameter identification, are ill-posed in the sense of Hadamard. The mathematical problem of piezoelectric material constants identification presented here has the form (11) where Z is a nonlinear operator mapping from the Hilbert space X into Y. Its argument d denotes the searched parameters, , where θ denotes the polarization direction and is the noisy measurement input: (12) where m denotes data without noise and s is a level of noise.

The map Z is from the set (or subset of it) of parameters to the set of measurements , where n_p and n_m denote the number of parameters and number of measurements, respectively. The set E contains those values of parameters d for which eigenvalues of the Stroh formalism have the nonpositive imaginary part, which does not ensure the positivity of the strain energy 19.

For the BEM model, the nonlinear mapping has the form, according to (10) and (11), (13) where is a weighted sensor placement matrix. To find the searched parameters, one can formulate the minimization problem in the following way: find a vector such that (14) where the cost functional has the form (15)

The functional (15) is also called the fitness function. Ideally, the optimal value of the fitness function would be equal to zero. The fitness function values are evaluated using the BEM and the measurements are also simulated using the BEM. The noise is also added to the data. The AIS method is used to solve the identification problem 23,24. The solution of coupled field equations using BEM is needed for each cell in the immune algorithm.

To minimize the functional (15), the AIS was applied, then the second form of (15) can also be used, because the AIS does not require the gradient information, so the functional does not have to be Frechet differentiable. The bounds for searched parameters are known from the physical restriction.

Due to ill-posedness the solution of the inverse problem may depend discontinuously on the data. To construct a stable solution, regularization is necessary. The AIS generally belongs to the nonlinear iterative methods, hence the regularization can be performed by early stopping. The number of iterations at which the iterative process is ceased is the regularization parameter. In this study, an a posteriori regularization parameter choice strategy was applied, namely Morozov's discrepancy principle 25, in which the iteration process is stopped when the cost functional (residual norm) is smaller than the approximate levels of the data error.

5. Benchmark numerical examples

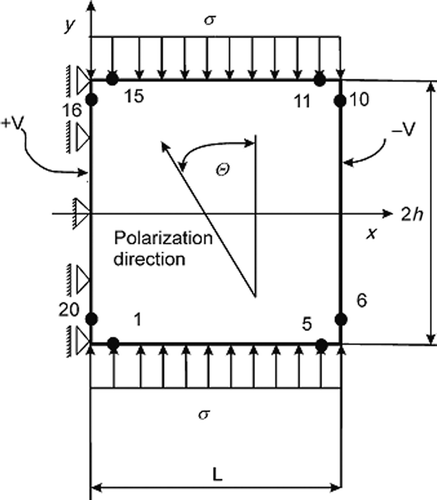
The identification of piezoelectric material constants and the polarization direction given by (9) of a plate were considered. The plate is subjected to a stress in the y-direction and an applied voltage as shown in Figure 4.

Figure 4. Geometry and boundary conditions for the considered plate.

The PZT-4 ceramic material is modelled 21. The applied voltage is V₀ = 1000 V. On the horizontal edges of the strip, the charge flux density is equal to zero. The applied stresses are equal to σ = 5 MPa. The length of the strip L = 1 mm and the height h = 0.5 mm. To discretize the boundary of the strip, 20 constant boundary elements are employed.

Ten design variables are used: nine material constants and the value of the angle θ, which describes the polarization direction. The parameters of the AIS are presented in Table 1. The constraints on B-cell receptor parameters values are presented in Table 2.

Table 1. Parameters of the AIS.

Number of memory cells	Number of clones	Crowding factor	Gaussian mutation
6	30	0.25	0.25

Table 2. The B-cell receptor parameters constraints.

Number	Constant	Minimum value	Maximum value
1	c11 (Pa)	0.2 × 10^11	0.8 × 10^11
2	c12	0.2 × 10^11	0.8 × 10^11
3	c13	0.2 × 10^11	0.8 × 10^11
4	c22	0.2 × 10^11	0.8 × 10^11
5	e13 (C m^−2)	−3.0	25.0
6	e21	−3.0	25.0
7	e22	−3.0	25.0
8	ε11 (C V^−1 m^−1)	5 × 10^−9	150 × 10^−9
9	ε22	5 × 10^−9	150 × 10^−9
10	θ (°)	0	180

The AIS is coupled to the BEM code. The measured values are simulated using the BEM. The displacements, electric potential and charge sensors are placed in every node. The displacement sensors measure x and y displacements of nodes.

In the first identification problem, all the material constants without polarization direction are searched. The exact and best found values of material constants after the first and 518th iterations (18,648 fitness function evaluations) are presented in Table 3.

Table 3. The results of the material constants identification.

Constant	Exact value	The best in first iteration	The best after 518th iteration	Error in first iteration (%)	Error after 518th iteration (%)
c11 (Pa)	0.73 × 10^11	0.71 × 10^11	0.76 × 10^11	2.7	4.1
c13	0.64 × 10^11	0.63 × 10^11	0.61 × 10^11	1.6	4.7
c33	0.21 × 10^11	0.29 × 10^11	0.20 × 10^11	38.1	4.8
c44	0.28 × 10^11	0.22 × 10^11	0.29 × 10^11	28.6	3.6
e15 (C m^−2)	−2.1	−2.93	−2.28	39.5	8.1
e31	19.1	20.4	18.0	6.8	5.8
e33	12.3	18.1	11.2	47.2	8.9
ε11 (C V^−1 m^−1)	8.13 × 10^−9	6.01 × 10^−9	8.75 × 10^−9	26.1	7.6
ε33	143 × 10^−9	126.07 × 10^−9	143.38 × 10^−9	11.9	0.3

It can be noticed that the material constants are identified with rather low accuracy, because a relatively large number of the constants makes the identification problem quite difficult.

In the second identification task, only the piezoelectric constants are searched for. The exact and best found values of piezoelectric material constants after the first and 82nd iteration (2952 fitness function evaluations) are presented in Table 4.

Table 4. The results of the piezoelectric constant identification.

Constant	Exact value	The best in first iteration	The best after 82nd iteration	Error in first iteration (%)	Error after 82nd iteration (%)
e15 (C m^−2)	−2.1	−0.910	−2.060	56.667	1.905
e31	19.1	19.240	19.101	0.733	0.005
e33	12.3	10.810	12.190	12.114	0.894

In the third identification problem, the piezoelectric constants and polarization direction are searched for. The exact and best found values are presented in Table 5 (15,984 fitness function evaluations).

Table 5. The results of the piezoelectric constants and polarization direction identifications.

Constant	Exact value	The best in first iteration	The best after 444th iteration	Error in first iteration (%)	Error after 444th iteration (%)
e15 (C m^−2)	−2.1	−0.460	−2.090	78.096	0.476
e31	19.1	11.760	19.090	38.429	0.052
e33	12.3	10.670	12.381	13.252	0.659
θ (°)	90	90.470	90.002	0.522	0.002

Table 4 indicates that the polarization direction and the piezoelectric constants are identified as very good. Of course, the accuracy of the solution depends on the boundary value problem for which the identification problem is being solved. Also, the parameters of the AIS algorithm given in Table 1 have a great influence on the quality of the results. These parameters are chosen after several trial and error heuristic tests.

In the previous examples, the measurements do not contain noise. This is an inverse crime, but noise-free data was applied in order to check the possibility of finding the global solution by the AIS. To get the more realistic problem, the next identification task was performed. The number of sensors was decreased to three: in the middle of the bottom, upper and right edge of the plate, where only the displacements and the electric potential were measured. Quantities Q_i along the boundary were perturbed using an additive normal noise, with the mean equal to zero and the standard deviation equal to , where r is the percentage of the additive noise included in the input data quantities Q_i. Only the three piezoelectric moduli were searched for, i.e. .

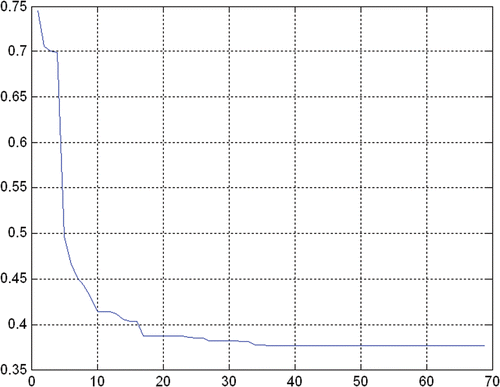
In Table 6 the results of the identification are presented. The results presented in Table 6 show that the AIS is able to give a stable and rather accurate solution for noisy data. The regularization is performed by stopping the iterative AIS process after 13, 22 and 35 iterations for r = 1%, 5% and 10% noise, respectively, according to the discrepancy principle.

Table 6. The results for noisy data.

Noise level r (%)	e15 (C m^−2)	e31	e33
1	−2.03	19.10	11.11
5	−2.24	19.64	12.05
10	−3.13	18.41	12.24

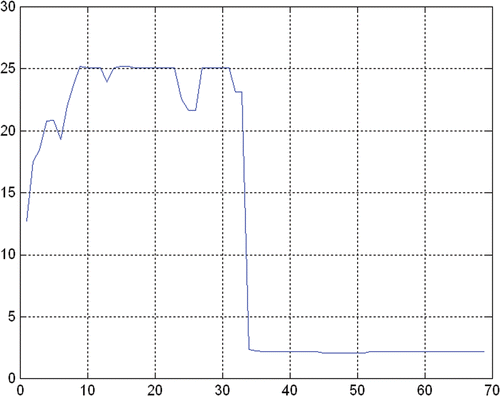
The process is convergent as shown in Figure 5, where the fitness function history is presented. In Figure 6, changes of the solution norm during optimization are presented. The solution norm also gives some information about the regularization parameter.

Figure 5. Fitness function versus the number of iterations, for r = 10%.

Figure 6. Solution norm versus the number of iterations, for r = 10%.

6. Conclusions

In this article, the formulation and application of the BEM and the AIS to identification of piezoelectrics are presented. The AIS can be easily implemented because it needs only the values of the objective function.

The AIS coupled to the BEM give an efficient computational intelligence method for identification of piezoelectric material constants and the polarization direction. To solve both direct and inverse problems of piezoelectricity, the BEM computer code is developed and the AIS is coupled to the BEM code. Numerical examples are given and good results are obtained.

Acknowledgement

This research is partially financed from the Polish science budget resources as a research project (no. 2976/B/T02/2007/33).