A new regularization method and application to dynamic load identification problems

Abstract

In this article, a new regularization method is proposed and applied to the identification of multi-source dynamic loads acting on a surface of composite laminated cylindrical shell. In general terms, regularization is the approximation of an ill-posed problem by a family of neighbouring well-posed problems. Based on the construction of a new regularization operator, corresponding regularization method is established. We propose a regularization operator, thus construct a new regularization method, and prove its regular property. The present method is applied to load identification of composite laminated cylindrical shell. The transient displacement response can be obtained by the finite element method. The multi-source dynamic loads on a surface of composite laminated cylindrical shell are successfully identified, which demonstrates the efficiency and robustness of the present method.

Keywords:

• load identification
• ill-posed problems
• regularization method
• finite element method
• composite laminated cylindrical shell

1. Introduction

In many practical engineering problems, such as structural strength analysis, health monitoring and fault diagnosis, vibration isolation, etc., the knowledge of dynamic load acting on the structure is always required and important. In common situation, the input load can be directly measured by a force transducer positioned in the load transfer path. However, there exist countless applications in which it is difficult or impossible to directly measure the dynamic load acting on a structure. For instance, when the tall building suffers wind load, it is impossible or very difficult to directly measure the dynamic load in real time. It means that the dynamic load must be recovered by the help of indirect measurements. Therefore, it is valuable to develop some inverse analysis techniques for load identification by measured response which are easily obtained.

The past decade has witnessed numerous studies of identifying the dynamic loads on a system of multiple degrees of freedom 1–7, the moving loads on a bridge 8–10 and impulsive load or multi-point load on a continuum 11–13. For instance, Liu and Sheppard 14 adopted the singular value decomposition (SVD) method to locate the small singular value affected by the noisy response. Liu and coworkers 15,16 presented an inverse procedure for identifying both concentrated and extended line load using Green's function and Heaviside step function in time domain. Pezerat and Guyader 17 studied the reconstruction of harmonic excitations acting on a rectangular plate, and Djamaa et al. 18 studied the loads on a thin cylindrical shell. Furthermore, Jiang and Hu 19 proposed an approach to reconstruct the distributed dynamic loads on an Euler beam from its steady-state response. Gunawana et al. 20 presented a two-step B-splines regularization method to identify impact force. Jacquelin et al. 21 considered a deconvolution technique to reconstruct the impact force. But we may encounter some difficulties. For instance, the model of multiple degrees of freedom and the multi-point excitation may fail to work. Moreover, direct measurement for distributed dynamic loads is not available. However, in practical engineering problems, it is necessary to reconstruct the distributed dynamic loads on a continuum. Unfortunately, they are complex inverse problems with inherent ill-posedness. Regularization methods usually control well a level of numerical accuracy to these inverse problems. For these above-mentioned studies, much attention was paid to the complicated technical problems in mathematics, especially in the ill-posedness and regularization methods. In this article, a new regularization method is proposed to solve the dynamic load identification problem of composite laminated cylindrical shell.

This article is organized as follows. In Section 2 we briefly describe the determinate forward problem for a linear elastic structure. In Section 3 we introduce the base knowledge of regularization theory for solving the dynamic load identification problem, propose a new regularization operator, and prove the regular property of its corresponding method. In Section 4, the present method is applied to the load identification of composite laminated cylindrical shell, and some conclusions are presented in Section 5.

2. Formulation of the direct problem

To illustrate the use of present methodology in determining the unknown time-dependent multi-source dynamic loads acting on composite laminated cylindrical shell, we need to know the following knowledge for a linear elastic structure.

Consider the multi-source dynamic load identification problem for a linear and time-invariant dynamic system. The response at an arbitrary receiving point in a structure can be expressed as a convolution integral of the forcing time-history and the corresponding Green's kernel in time domain 16: (1) where y(t) is the response which can be displacement, velocity, acceleration, strain, etc. G(t) is the corresponding Green's function that is the kernel of impulse response. p(t) is the desired unknown dynamic load acting on the structure.

By discretizing this convolution integral, the whole concerned time period is separated into equally spaced intervals, and Equation (2.1) is transformed into a system of algebraic equation: (2) or equivalently, where y_i, g_i and p_i are response, Green's function matrix and input force at time t = i▵t, respectively. ▵t is the discrete time interval. Since the structure without applied force is static before force is applied, y₀ and g₀ are equal to zero. All the elements in the upper triangular part of G are zeros and are not shown. The special form of Green's function matrix reflects the characteristic of the convolution integral.

To recover the time history p(t), the knowledge of y(t) and G(t) are required. In fact, the response at a receiving point and the numerical Green's function of a structure can be obtained by finite element method (FEM). However, the problem of identifying the dynamic load p(t) by y(t) and G(t) is usually ill-posed and cannot be solved by inverse matrix method. In the following section, a new regularization method will be established to solve this inverse problem.

3. Reconstruction theory of distributed dynamic loads

In general, a numerical regularization method is suggested to solve ill-posed inverse problems by minimizing the data error, the discretization error and the round-off error. The reconstructed dynamic loads are usually sensitive to the error of the input which causes large deviations for the exact solution in the inverse problems when these problems are not performed by any regularization method. So we cannot use the conventional inverse matrix method to deconvolute it. In order to obtain the efficient and numerically stable solution, regularization method is adopted.

Considering the noisy response, Equation (2.2) can be given as follows: (3) where ‘err’ is the noisy data of the response in the measurement. It is easy to check that the SVD of G is expressed as (4) where U = (u₁, u₂, … , u_m) and V = (v₁, v₂, … , v_m) are matrices with orthonormal columns, U^TU = V^TV = I_m, and S = diag(μ₁, μ₂, … , μ_m) has non-negative diagonal elements appearing in non-increasing order. Moreover, it is really interesting that this decomposition gives a formulation of the identified load (5) Through Equation (3.3), it can be found that the ill-conditioned characteristic of system (2.2) occurs to the small singular value μ_i compared with maximal singular value μ₁ in the inverse analysis. When the singular values gradually decay to zero, the noisy data of response will strongly affect the accuracy of load identification. To overcome this difficulty, the small singular value needs to be filtered. The method for solving this problem is that is multiplied by a regularization operator f_α(μ_i), thus this can make decay to zero when μ_i decays to zero, where α is the regularization parameter. Thus we can obtain a good approximate solution P_α of the identified force: (6) If we select the regularization operator as follows: (7) this regularization method is just the famous regularization method called Tikhonov regularization 22 and the smooth solution to minimize the error amplification in force identification is found: (8)

It is well known that ill-posed problems arise in several contexts and have important applications in science and engineering 22–26. In this section we propose a new regularization operator, and correspondingly establish a regularization method, and will prove its regular property in the following. Our results modify the case of Tikhonov regularization operator, and obtain a stable regularization method. First, we define q(α, μ) : R⁺ × (0, ‖K‖] → R⁺, given by (9)

In fact, we can assure that: the function q(α, μ) defined by (3.7) is a regularization operator. Moreover, (10) First of all, it is easy to check that q(α, μ) ≤ 1 and Since we have Then the first result of the assertion follows. In the following we prove the second result.

By virtue of we have Now the assertion can be proved easily.

Using the above results, we obtain that the good approximate solution P_α of the identified force can be defined by (11) where R_α : Y → X is given by

Remark 3.1

Due to prior information in actual computations of engineering problems, it is difficult or impossible to determine an appropriate value for the regularization parameter. As the errors in the measurement are unknown, L-curve method 27 is usually adopted to perform it. So we will choose the regularization parameter by L-curve method in the numerical simulations of engineering example in next section.

Remark 3.2

When identifying the unknown dynamic force by Tikhonov regularization method, all the singular values of Green's function matrix will be filtered by the same function. The bigger singular values are also revised, and this just influences the accuracy of identified dynamic force. The present method will propose a new filter function. These unusually smaller singular values are approximately truncated, and those bigger singular values are maintained. So it not only overcomes the ill-condition of Green's function matrix, but also ensures the precision of identification.

4. Application

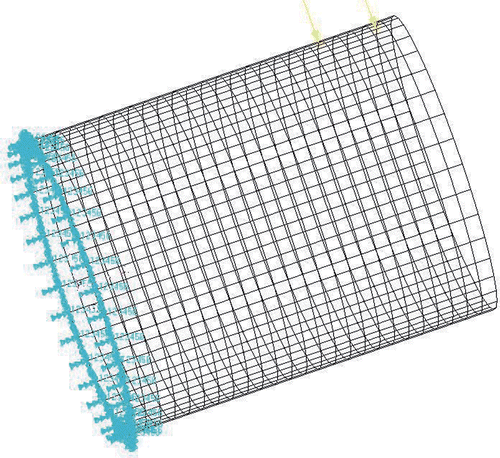
A practical engineering problem is to determine radial forces of composite laminated cylindrical shell, as shown in Figure 1. Thin-walled cylindrical shell structure has been widely used in the aerospace structures. The cylindrical shell size is 200.0 mm in middle radius, 10.0 mm in thickness and 500.0 mm in length. It consists of one carbon/epoxy layer and one glass/epoxy layer. Its stacking sequence is denoted by [C90/G + 45/G − 45]_s, where C and G stand for the carbon/epoxy and the glass/epoxy layer, respectively, and 90, +45 and −45 stand for the angle of fibre-orientation to the centre axis. The subscript of ‘s’ means that it is symmetrically stacked. The material properties of carbon/epoxy and glass/epoxy given by Takahashi and Chou 28 are listed in Table 1.

Figure 1. The FEM model of composite laminated cylindrical shell.

Table 1. The material properties of composite laminated cylindrical shell.

	Material poperties of glass/epoxy and carbon/epoxy
Material constants	E1 (GPa)	E2 (GPa)	G12 (GPa)	ν12	ν23	ρ (g cm^−3)
Glass/epoxv	38.49	9.367	3.414	0.2912	0.5071	2.66
Carbon/epoxy	142.17	9.255	4.795	0.3340	0.4862	1.90

The radial concentrated load is applied to the outside surface and the measured response is the radial displacement. One side of the shell is free, and the other side is fixed. We establish its finite element model, as shown in Figure 1. The arrow in Figure 1 denotes the point of dynamic force.

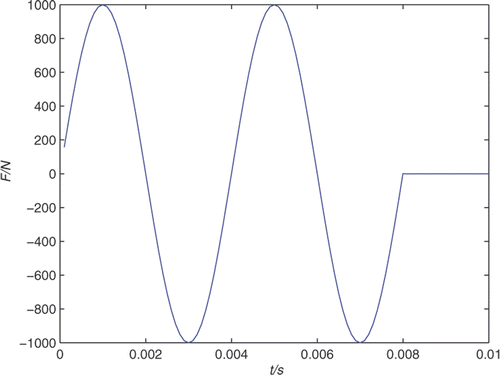
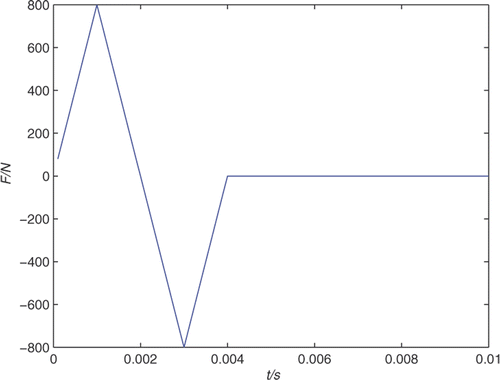
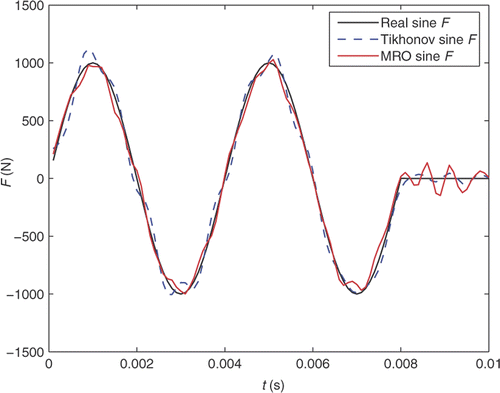
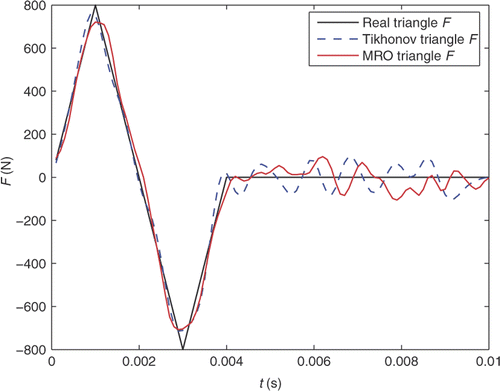
The concentrated loads are defined as follows: where t_d is the time cycle of sine force and q_i (i = 1, 2) is a constant amplitude of the force. When t_d = 0.004s, q₁ = 1000N and q₂ = 800N, the sine force and triangle force are as shown in Figures 2 and 3.

Figure 2. The radial concentrated sine load acting on the outside surface.

Figure 3. The radial concentrated triangle load acting on the outside surface.

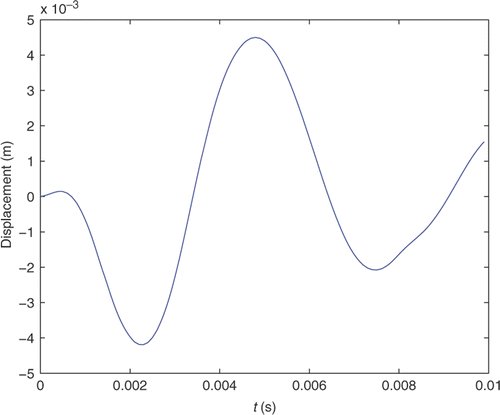
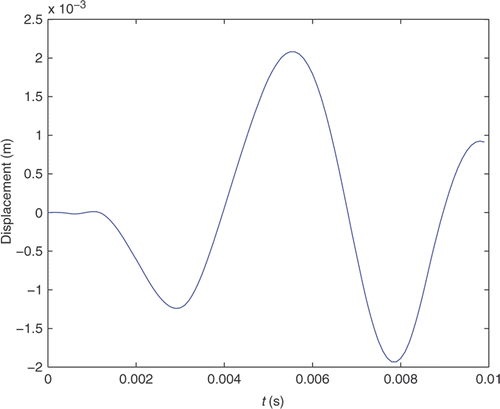
Herein, the experimental data of response is simulated by the computed numerical solution, and the corresponding radial displacement response can be obtained by FEM, as shown in Figures 4 and 5. Furthermore, a noise is directly added to the computer-generated response to simulate the noise-contaminated measurement, and the noisy response is defined as follows: where Y_cal is the computer-generated response; std(Y_cal) is the standard deviation of Y_cal; rand(−1, 1) denotes the random number between −1 and +1, l_noise is a parameter which controls the level of the noise contamination. In order to investigate the effect of measurement error on the accuracy of estimated values, we consider the case of noise level, namely 5%, and this new regularization method is suggested to determine the multi-source dynamic forces. To evaluate the effectiveness of the present method, five time points are selected, and the identified force for each point will be compared to the corresponding actual force.

Figure 4. The corresponding vertical displacement response at one point.

Figure 5. The corresponding vertical displacement response at the other point.

The results of numerical simulations are as follows. From Figures 6 and 7, it can be shown that the present method (MRO) can identify both the effective and stable loads from the measured noisy response. The other results of the identified loads at five time points are listed in Table 2. It can be found that at these time points for noise level ±5%, these deviations of identified loads by the present method are smaller than Tikhonov regularization method due to efficient identification. It can also be found that most of the deviations by Tikhonov regularization method and the present method concentrate in the range of 15.5% and 14.8%, respectively. In addition, for the identification of sine force, the maximal deviation and average deviation by the present method are 14.78% and 4.84%, respectively, obviously smaller than Tikhonov regularization method. Moreover, the maximal deviation and average deviation of the identification of triangle force by the present method are 13.2% and 5.02%, respectively, both smaller than Tikhonov regularization method. The results of numerical testing show that the present algorithm is stable and effective when recovering the loading time function, and gives satisfactory and stable results.

Figure 6. The identified sine force at 5% noise level.

Figure 7. The identified triangle force at 5% noise level.

Table 2. The identified force at five time points at 5% noise level.

			Tikhonov		Present method
	Time	Real	Identified	Error (%)	Identified	Error (%)
	point	force	force		force
Sine	0.001	1000	1081.9	8.19	968.41	3.16
Triangle	0.0006	480	521.98	5.25	482.94	0.3675
Sine	0.003	−1000	−900.95	9.91	−975.39	2.46
Triangle	0.001	800	752.84	5.90	720.69	9.91
Sine	0.0045	707.11	775.59	6.85	635.11	7.2
Triangle	0.0016	320	328.41	1.05	345.98	3.25
Sine	0.0063	−453.99	−549.44	9.55	−435.53	1.85
Triangle	0.0033	−560	−639.79	9.97	−560.21	0.03
Sine	0.0073	−891.01	−905.15	1.41	−839.22	5.18
Triangle	0.0038	−160	−176.15	2.02	−181.99	2.75
Error (%)			Maximum	Average	Maximum	Average
Sine			15.41	5.57	14.78	4.84
Triangle			13.72	5.56	13.20	5.02

5. Conclusion

A new regularization method can efficiently and stably identify the multi-source dynamic loads acting on composite laminated cylindrical shell by the noisy response. Additionally, in the numerical simulations, the present method can provide better approximation of true loads, comparing with the traditional Tikhonov regularization method. This confirms that the present method is convenient, effective and accurate for solving load identification problems in practical structural engineering.

Acknowledgements

This work is supported by the National Science Foundation of China for Distinguished Young Scholars (10725208) and a research grant from the Research Grants Council of the Hong Kong Special Administrative Region, China (Project No. CityU 113809). The authors thank the anonymous referees and the editor for carefully reading this article and suggesting many helpful comments on improving the original manuscript.