A survey of applications of the MFS to inverse problems

Abstract

The method of fundamental solutions (MFS) is a relatively new method for the numerical solution of boundary value problems and initial/boundary value problems governed by certain partial differential equations. The ease with which it can be implemented and its effectiveness have made it a very popular tool for the solution of a large variety of problems arising in science and engineering. In recent years, it has been used extensively for a particular class of such problems, namely inverse problems. In this study, in view of the growing interest in this area, we review the applications of the MFS to inverse and related problems, over the last decade.

Keywords:

• inverse problems
• MFS
• regularization

AMS Subject Classifications:

• Primary 65N21
• 65N35
• Secondary 35R30
• 35R35
• 65M32
• 65J20

1. Introduction

The method of fundamental solutions (MFS) is a meshless boundary collocation method which belongs to the family of Trefftz methods 1 (see also 2) and is applicable to certain boundary value problems and initial/boundary value problems. In particular, it is readily applicable to homogeneous boundary value problems in which a fundamental solution of the operator in the governing equation is known explicitly. Moreover, the method can also be applied, in conjunction with the method of particular solutions (MPS) to problems governed by inhomogeneous equations. Despite the fact that the applicability of the method is restricted to a certain class of equations, it has, since its introduction as a numerical method by Mathon and Johnston 3 in the late 1970s, become increasingly popular. This popularity is primarily due to the ease with which the MFS can be implemented in particular to problems in complex and irregular geometries and to three-dimensional problems. A detailed description of the method and its application to a large variety of problems may be found in the survey papers 4–7 and books 8,9.

The advantages that the MFS has over the more classical domain or boundary discretization methods and the reasons that make it so easy to implement are the following. First of all, it is meshless which means that no mesh, but a mere collection of points is required for the discretization of the problem. Secondly, it does not involve integration which could be potentially troublesome and complicated, as is the case with, for example, the boundary element method (BEM). Thirdly, it is a boundary method which means that it shares all the advantages that the BEM has over domain discretization methods such as the finite element (FEM) or finite difference (FDM) methods. Finally, it can easily deal with infinite domains by incorporating the behaviour of the solution of the problem at infinity into the fundamental solution of the governing equation. As a result, the method is ideally suited for the solution of problems in which the boundary is of major importance or requires special attention.

Inverse problems are such problems and it is for this reason that in recent years there has been a lot of activity in the application of MFS for their solution. In direct problems, one is trying to determine the solution of a boundary or initial/boundary value problem governed by a partial differential equation in a fixed domain subject to prescribed initial and boundary conditions. In contrast, in inverse problems one or more of the data describing the direct problem is missing. This means that often, in order to obtain the solution of an inverse problem, a direct FDM, FEM, BEM or MFS solver needs to be called repeatedly as part of an iterative process. Consequently, the advantages (ease of implementation, speed of computation, less storage requirements and exponential convergence properties) that the MFS possesses over the more classical domain or boundary discretization methods make it an ideal candidate for efficiently solving inverse problems in complicated geometries and in higher dimensions. Inverse problems are also more difficult to solve than direct problems since, in general, they are ill-posed as they do not fulfil the well-posedness criteria of Hadamard 10. In particular, small errors in the measured data may lead to large errors in the solution, a fact which makes inverse problems difficult to solve numerically. As will be described later, this instability is treated by using regularization methods 11–13 which also alleviate the ill-conditioning of the MFS approximation matrices.

Motivated by the rapidly growing interest in the area, our aim in this article is to review the development of the MFS for the solution of various types of inverse and related problems over the last decade. We emphasize linear elliptic and parabolic partial differential equations since for linear hyperbolic wave-type equations the applications of the MFS are rather scarce 14,15 and restricted to direct problems only. In addition, we identify areas related to inverse problems where the method could potentially be applied in the future.

A brief outline of this article is as follows. In Section 2, the formulation of the MFS for direct and inverse problems is presented. In Sections 3, 4, 5, 6 and 7, we review the applications of the MFS to Cauchy problems, source identification, boundary parameter identification, geometric inverse problems and free boundary problems, respectively. Comments, conclusions and suggestions for future applications are given in Section 8.

2. The MFS

2.1. The MFS for direct problems

Let us consider, as an example, the MFS for the solution of the direct boundary value problem in a bounded and sufficiently smooth domain Ω ⊂ ℝ^d, d = 2, 3, (1) subject to the boundary conditions (2) and (3) where the boundary of Ω is ∂Ω = Γ₁ ∪ Γ₂, Γ₁ ∩ Γ₂ = ∅, L is a second-order linear operator, ℬ₁ and ℬ₂ are boundary operators defining Dirichlet, Neumann or Robin boundary conditions and f₁, f₂ are sufficiently smooth known functions. The natural mathematical setting for the functions f_i, i = 1, 2, is in L₂(Γ_i) in the weak sense and in C^ℓ(Γ_i), ℓ ≥ 0, in the strong sense. If the change in the type of boundary conditions (2.1b) and (2.1c) generates a corner singularity at the intersection then the singular solution should be removed first and then the numerical technique be applied to the regular part of the solution.

In the MFS the solution u of problem (2.1) is approximated by the linear combination (4) where K(P, Q) is a fundamental solution associated with the operator L, and are singularities (sources) placed outside . These singularities are either preassigned or taken to be part of the unknowns of the problem along with the coefficients . In either case, the unknowns are determined so that the approximation (2.2) satisfies, in some sense, the boundary conditions (2.1b) and (2.1c) as well as possible. Usually, this is done by collocating the boundary conditions at a chosen set of boundary points . In the early applications of the MFS (see, e.g. 3,16,17), the locations of the singularities were not specified, which leads to a non-linear system of equations that can be solved using existing non-linear least-squares minimization software for such systems. This approach, however, has attracted limited attention primarily because of its high computational cost and the criticism that one often transforms a linear boundary value problem to a non-linear discrete problem. In the now more established approach in which the singularities are preassigned, collocation leads to a linear system of M equations in N unknowns which can be solved by a least-squares solver. It should be noted that in case the locations of the singularities are preassigned, they are usually located on a pseudo-boundary, preferably taken to be a circle or a curve similar to the boundary ∂Ω 18, containing . One of the major challenges in the application of the MFS is the optimal location of this pseudo-boundary 19–21. Denseness results which justify the MFS approximation (2.2) are given in 22–24 for the Laplace L = Δ, modified Helmholtz L = Δ − κ²I and Helmholtz L = Δ + κ²I operators, respectively.

As with the BEM, an obvious limitation of the MFS is that it is readily applicable only to problems for which a fundamental solution of the operator L in (2.1a) is known explicitly. As already mentioned, in the case of inhomogeneous problems where the governing equation (2.1a) is replaced by (5) where F is a known function, the method can be applied in conjunction with the MPS. In the MPS (see e.g. 25,26), a particular solution of the inhomogeneous equation is first obtained, usually by means of radial basis functions 27. If we let u^p be a particular solution of the inhomogeneous equation, then clearly (6) If we write the solution u of the inhomogeneous problem (2.3), (2.1b) and (2.1c) as (7) then u^h satisfies the homogeneous boundary value problem (8) subject to the boundary conditions (9) and (10) Problem (2.6) can be solved for u^h using the MFS, and then the solution u of the inhomogeneous problem may be recovered from (2.5).

When the operator L is of higher order, the MFS approximation (2.2) takes a different form. For example, in the case of the biharmonic equation we have the approximation (11) where K₁ and K₂ are fundamental solutions of the Laplace operator and biharmonic operator, respectively. Denseness results which justify the MFS approximation (2.7) for the biharmonic operator L = Δ² are given in 23,28.

In the case of time-dependent evolutionary problems where the governing equation (2.1a) is replaced by (12) where T > 0 is a final time of interest and an initial condition at time t = 0 is prescribed, the MFS approximation is given by 29 (13) where K is a fundamental solution of the heat equation, are space singularities placed outside and are time singularities located in the interval (−T, T). Denseness results which justify the MFS approximation (2.9) for the heat operator (2.8) are given in 30,31.

In the case we have a system of homogeneous partial differential equations instead of (2.1a) we have a vector of unknown functions to approximate. For example, when we have the Cauchy–Navier equations of elasticity, the unknown displacements are approximated by (14) where , is a fundamental solution matrix of the Cauchy–Navier system. Denseness results which justify the MFS approximation (2.10) for the Lamé and Stokes operators in solid and fluid mechanics are given in 22,32, respectively.

2.2. The MFS for inverse problems

In the application of the MFS to inverse problems we shall assume that one uses the approach in which the singularities are preassigned. In such a case we may consider two types of inverse problems.

2.2.1. Linear problems

These comprise Cauchy problems and source identification problems. Boundary parameter identification problems can also be reduced to Cauchy problems, as will be described in Section 5.1. Typically, in such problems the boundary of the problem is known and the unknowns are determined by collocating the boundary conditions on part of the boundary and in some instances collocating the solution at some interior points. This leads to a system of linear equations (15) where A is an M × N matrix, c is the N × 1 vector of the unknown coefficients c_j in the MFS approximation (2.2) and b is an M × 1 vector. The system of equations (2.11) is ill-conditioned and requires the use of a regularization method. A very popular technique is the Tikhonov regularization method 13, in which the following functional is minimized in a least-squares sense (16) where λ ≥ 0 is known as the regularization parameter. The minimization of (2.12) readily yields the explicit solution (17) where the superscript ^tr denotes the transpose of a matrix and I_N is the N × N identity matrix. When λ = 0, expressions (2.12) and (2.13) yield the well-known least-squares method solution which is unstable for ill-posed problems. One criterion for the choice of the optimal λ, which has been studied extensively, is the discrepancy principle 33. Although this criterion is mathematically rigorous, it requires a reliable estimation of the amount of noise added into the data which may not be available in practical problems. Heuristic approaches are preferable in the case when no a priori information about the noise is available, such as the L-curve criterion 34–36 and the generalized cross-validation (GCV) 37. Alternatively, instead of the Tikhonov regularization method one can use the truncated singular value decomposition method 34,35. Finally, we note that there has been some recent interest in using statistical Bayesian inference for solving inverse problems 38,39.

2.2.2. Non-linear problems

These comprise inverse geometric problems and free boundary problems in both of which part of the boundary is unknown and needs to be determined as part of the solution. In this case, the collocation of the boundary conditions, typically leads to a non-linear system of equations (18) where c is as before the N × 1 vector of unknown coefficients and x is an L × 1 vector containing the geometric parameters describing the unknown part of the boundary. In (2.14), b is an M × 1 vector and F is also an M × 1 vector of functions of c and x. Thus (2.14) is a system of M non-linear equations in N + L unknowns which can be solved using the non-linear least squares NAG 40 routine E04UNF, or the MINPACK 41 routine lmdif. The system of equations (2.14) is also ill-conditioned and often requires the use of Tikhonov's regularization. In this case, one could, for example, minimize the functional (19) where λ₁ and λ₂ are positive regularization parameters which can be chosen according to the L-surface criterion 42.

In the next sections we sequentially survey applications of the MFS for solving several inverse problems associated with various governing equations.

3. Cauchy problems

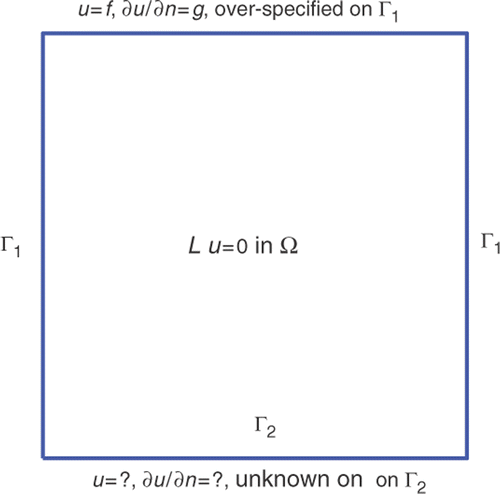
In these problems the boundary ∂Ω of the domain Ω of the problem under consideration is known. On part of the boundary Γ₁ some boundary conditions are over-specified, while on the remaining part of the boundary Γ₂ = ∂Ω\Γ₁ either no boundary conditions are given or they are under-specified. This inaccessibility may be due to hostile environments such as high temperatures/pressures. In practice, if any thermocouple or sensor were attached to such a hostile boundary it would, most likely, be destroyed or the temperature readings would be very inaccurate. In such a difficult practical situation, one could instead measure both the temperature and heat flux, i.e. Cauchy data, on the remaining friendly portion of the boundary, or even measure the internal temperature distribution with invasive thermocouples embedded within the material, and solve the resulting inverse and ill-posed problem. A sketch of a Cauchy problem is illustrated in Figure 1.

Figure 1. Sketch of a Cauchy problem.

3.1. Laplace/Poisson's equation

Consider the Laplace equation in a bounded domain Ω, namely (20) subject to the Cauchy boundary conditions (21) where f and g are given functions, while n is the outward unit normal vector on Γ₁. The goal is to determine both u and ∂u/∂n on Γ₂. Although the (local) existence and uniqueness of the solution are ensured by the Cauchy–Kowalevskaya and Holmgren unique continuation theorems, the Cauchy problem (3.1a), (3.1b) is still ill-posed since the solution does not depend continuously on the input data (3.1b), i.e. it is unstable with respect to small perturbations in the input boundary data on Γ₁. The MFS was, apparently, used for the first time for the solution of a Cauchy problem when it was applied to problem (3.1) in 43. Problem (3.1) was also studied in 44 where the authors also considered problems in irregular domains, as well as problems with singular points outside the domain Ω. The conditioning of the matrices resulting from the MFS discretization of Cauchy problems similar to (3.1) was carried out in 45. An interesting three-dimensional version of problem (3.1) was studied in 46 where the authors applied the MFS to a Cauchy problem arising in electrocardiography concerned with computing potentials on the surface of the heart from measured body surface electrocardiographic data. Further applications of the method to two- and three-dimensional Cauchy problems like (3.1) may be found in 47. The convergence of a Tikhonov-regularized MFS approximation for the Cauchy problem (3.1) with noisy data in the case that Ω is an annulus and Γ₁ is either the interior or exterior boundary circle of the annulus was proved in 48. This result generalizes the original convergence result of 49 for exact Cauchy data. In 50, the Cauchy problem for the two-dimensional Laplace equation was solved iteratively using the MFS. This method is based on the algorithm originally proposed in 51. Two relaxation procedures of the aforementioned iterative MFS algorithm were introduced in 52 in order to speed up convergence.

The MFS was used for the first time for the solution of an inhomogeneous inverse problem in 53 where the author studied, among others, problem (3.1) with equation (3.1a) replaced by the Poisson equation Δu = F. The inhomogeneous part was dealt with using the two-step MFS/MPS approach of 54. In the same paper other related inverse problems were considered including one in which the additional data is provided in the interior of the domain Ω rather than on the boundary Γ₁. In 55, the same author solved the Cauchy problem (3.1) in the presence of boundary singularities. The latter was dealt with using a singularity subtraction technique.

3.2. Helmholtz/modified Helmholtz's equation

Marin and Lesnic applied the MFS for the solution of the Cauchy problem associated with the two-dimensional Helmholtz and modified Helmholtz equations in 56. They considered a Helmholtz-type equation (22) subject to the Cauchy boundary conditions (23) In case q > 0 we have the Helmholtz equation, while when q < 0 we have the modified Helmholtz equation. As in problem (3.1), the goal is to determine the missing u and ∂u/∂n on Γ₂.

The corresponding three-dimensional Helmholtz and modified Helmholtz Cauchy problems (3.2) were investigated in 57. In 58, the authors applied the MFS with various regularization techniques for the solution of the Cauchy problems (3.1) and (3.2) for the Laplace and the Helmholtz/modified Helmholtz equations, respectively, in both two and three dimensions. Further applications of the MFS to inverse Helmholtz and modified Helmholtz Cauchy problems in two dimensions can be found in 59. In 60, two-dimensional Cauchy problems for the Helmholtz equation with boundary singularities were studied with a singularity subtraction technique. The Cauchy problem (3.2) was solved using the alternating iterative algorithm of 51 and the MFS in 61, while two relaxation procedures of this iterative MFS algorithm were introduced in 62. Cauchy problems for the Helmholtz equation were also considered in 63.

The boundary knot method (BKM), which is a boundary method very closely related to the MFS introduced by Chen and Tanaka 64,65, was also applied to the Cauchy problem (3.2) in 66. In addition, the authors also considered the inverse problem where one of the boundary conditions (3.2b) is replaced by measurements of u at some interior points. Moreover, the same authors applied the BKM in conjunction with the MPS to the inhomogeneous Helmholtz equation Δu + qu = F in 67.

3.3. Laplace–Beltrami's equation

In 68, the authors studied the steady-state heat conduction problem in a two-dimensional anisotropic medium described by (24) subject to the boundary conditions (25) where (k_ij)_i,j=1,2 is the thermal conductivity tensor whose components satisfy , and f and g are given functions. Both u and ∂u/∂n need to be recovered on Γ₂. The same Cauchy problem was investigated in 69,70 by applying the MFS in an iterative manner and also using two relaxation procedures, respectively. In the same spirit, the MFS was applied to the Cauchy problem for steady-state heat transfer in two-dimensional functionally graded materials in 71. The three-dimensional version of problem (3.3) was also considered, as well as a different inverse problem in which instead of the boundary condition ℬ₂u = g in (3.3b) the additional data is provided by a set of internal measurements of u.

3.4. Biharmonic equation

In 72, the MFS was employed for the solution of various Cauchy problems associated with the two-dimensional biharmonic equation. More precisely, the following boundary value problems were considered:

The biharmonic equation (26) needs to be solved subject to one of the following sets of boundary conditions: (27) or (28) or (29) or (30) or (31) where f_i, g_i, i = 1, 2 are given functions.

A slightly different inverse boundary value problem given by equations (3.1b) and (3.4a) together with the measurement of u on an internal, simple and closed curve was investigated with the MFS in 73.

3.5. Cauchy–Navier's equations of elasticity

In 74, the authors employed the MFS to solve the Cauchy problem in two-dimensional elasticity. In particular, they considered the Cauchy–Navier equations of elasticity for the displacements u_i, i = 1, 2 (32) subject to the Cauchy boundary conditions (33)

In (3.5a), G and ν are the shear modulus and Poisson ratio, respectively. In (3.5b), t_i, i = 1, 2 are the tractions and f_i, g_i, i = 1, 2 are given functions. In this case, the goal is to determine u_i and t_i, i = 1, 2 on Γ₂. Recently, this inverse boundary value problem was solved by combining the alternating iterative algorithm of 51 and the MFS in 75. Two relaxation procedures of this iterative MFS algorithm were proposed in 76 in order to speed-up convergence.

The three-dimensional version of the linear elasticity boundary value problem (3.5) was studied in 77.

3.6. Stokes' equations

In 78, the inverse Cauchy problem associated with the two-dimensional Stokes equations (34) where u = (u, v) is the velocity, p is the pressure and μ is the dynamic viscosity of the fluid, was investigated. Regarding the boundary conditions, the case (35) where f_i, i = 1, 2, 3 are given functions and the boundary ∂Ω = Γ₁ ∪ Γ₂ ∪ Γ₃, was examined. In this problem, one needs to determine v on Γ₂ and p on Γ₁ ∪ Γ₂.

3.7. Heat equation

In 79, the MFS was applied to the inverse heat conduction problem for the one-dimensional heat equation, namely (36) subject to the initial condition (37) and the boundary conditions (38) where f, g and h are given functions. The objective is to determine the boundary temperature u and the heat flux ∂u/∂x on the side x = 0. In a second problem considered in the same study, the authors determined u and ∂u/∂x on x = 0 with the heat flux boundary condition in (3.7c) replaced by temperature measurements at internal points. The same authors extended this approach to more general two- and three-dimensional inverse heat conduction problems in 80,81. The corresponding two-dimensional inverse heat conduction problem in an anisotropic medium was studied in 82. In this case equation (3.7a) is replaced by the equation (39) A related inverse problem, namely the so-called backward heat conduction problem in which the initial temperature (3.7b) needs to be retrieved from known temperature measurements inside the solution domain at a later time, was solved for the heat equation in one and two space dimensions using the MFS in 83–85.

4. Source identification problems

In these problems one considers inhomogeneous equations where the boundary ∂Ω of the domain Ω of the problem under consideration is known and on part of the boundary Γ₁, conditions are over specified. Typical practical applications arise in problems where one is interested in locating the sources of pollution in the environment. A sketch of a source identification problem is illustrated in Figure 2. The unknown inhomogeneous source/sink forcing term in the governing equation needs to be determined.

Figure 2. Sketch of a source identification problem.

4.1. Poisson's equation

In particular, suppose we consider the inverse boundary value problem given by the Poisson equation (40) subject to the boundary conditions (41) where f and g are given functions. The goal, in this case, is to determine the heat source function F in Ω.

Since the solution of inverse source problem (4.1) is not unique additional hypotheses on the source F are required. In 86, the source F was assumed to either satisfy the Laplace, or the homogeneous modified Helmholtz equation. In the case when F is assumed to be harmonic, problem (4.1) can be written as the biharmonic equation (42) subject to the boundary conditions (4.1b). The idea is to obtain the MFS solution u of the well-posed direct problem (4.1b), (4.2) from which one obtains F = Δu. A similar approach was applied when F is assumed to satisfy the homogeneous modified Helmholtz equation. A thorough investigation of the same problem is carried out in 87. In one approach, the same assumptions were made on F. Alternatively, the authors suggested using the MFS/MPS approach of 54 for dealing with the inhomogeneous part of equation (4.1a). Recently, the identification of heat sources in the steady-state, i.e. in the case of Poisson's equation, was investigated by employing the MFS in conjunction with radial basis functions in 88.

4.2. Helmholtz's equation

In 89, the following problem was considered for recovering the unknown source function F. Solve the Helmholtz equation (43) subject to the boundary conditions (44) for many frequencies q. Both the cases, when Γ₂ ≠ ∅ and Γ₂ = ∅, were considered and the problem was solved using the MFS/MPS approach of 54.

4.3. Heat equation

In 90, the following source identification problem for the one-dimensional heat equation is studied using the MFS. Solve the heat equation with unknown time-dependent source (45) subject to the initial condition (46) the boundary conditions (47) and the additional condition (48) where f, g₀, g₁ and h are given functions, and x₀ is a fixed known internal space location within the interval (0, 1). Here, one needs to determine the unknown source function F(t).

Another inverse problem which requires finding the spacewise dependent heat source F(x) entering the heat equation (49) subject to the initial condition (50) the Dirichlet boundary condition (51) and the additional upper base condition (52) has been investigated with the MFS in 91,92.

5. Boundary parameter identification problems

In these problems the boundary of the domain of the problem under consideration is known. Moreover, boundary conditions on part of the boundary are over-prescribed and the goal is to recover some unknown physical property coefficient (heat transfer coefficient, coefficient of corrosion or impedance) in a boundary condition specified on the remaining part of the boundary. A sketch of a boundary parameter identification problem is illustrated in Figure 3.

Figure 3. Sketch of a boundary parameter identification problem.

5.1. Laplace's/Poisson's equation

Consider the Laplace equation (53) subject to the boundary conditions (54) and the Robin convective boundary condition (55) where f, g and h are given functions. Here, the unknown heat transfer coefficient α ≥ 0 in (5.1c) needs to be recovered. This boundary parameter identification problem is closely related to the inverse Cauchy problem (3.1) of Section 3.1 which, once solved in a stable manner, yields on Γ₂ (see 93 for more details). The MFS was used for the solution of a boundary parameter identification problem very similar to (5.1) in 94. In the same study, the authors also studied the same problem for the Poisson equation using the MFS/MPS approach of 54.

5.2. Cauchy–Navier's equations of elasticity

In 95, the authors considered the Cauchy–Navier equations of elasticity for the displacements u_i, i = 1, 2 and tractions t_i, i = 1, 2, given by (3.5a) subject to the Cauchy boundary conditions (3.5b) and (56) where f_i, g_i, h_i, i = 1, 2 are given functions and the unknown 2 × 2 matrix B is to be recovered.

6. Inverse geometric problems

In these problems the location and shape of part of the boundary of the domain of the problem under consideration is unknown. On the known part of the boundary the boundary conditions are over specified, and the unknown part of the boundary is determined by the imposition of a specific boundary condition on it. These are harder than the previously mentioned types of inverse problems because the systems resulting from the MFS discretization are non-linear. The occurrence of this non-linearity may be explained as follows. 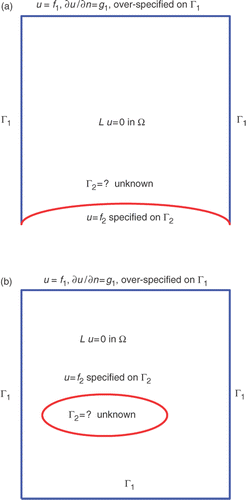In this type of problem, the location of part of the boundary is unknown, which in the MFS meshless sense means that the coordinates of some of the boundary points described in Section 2.1 are unknown as well as the coefficients of the fundamental solutions in approximation (2.2). In the determination of these unknowns by imposing the known boundary conditions, the coordinates of the boundary points describing the unknown part of the boundary appear nonlinearly in the fundamental solutions. This yields non-linear systems of equations. Inverse geometric problems can be classified into: (i) identification of an unknown part of the boundary; and (ii) identification of internal boundaries or interfaces modelling defects such as obstacles, cavities, inclusions, flaws, faults, voids and cracks. The detection of anomalies such as tumours inside or on the boundary of a body is a typical medical application. In practice, inverse geometric problems are investigated using various imaging and tomographic techniques such as electrical impedance tomography (EIT), gamma ray emission tomography (GRET), magneto-resonance imaging (MRI), etc. Sketches of inverse geometric problems are illustrated in Figure 4.

Figure 4. Sketches of inverse geometric problems: (a) Boundary identification and (b) Internal defect detection.

6.1. Laplace's equation

Consider the two-dimensional Laplace equation (57) subject to the boundary conditions (58) and (59) where f₁, f₂ and g₁ are given functions. In this problem, which models corrosion and belongs to the first category of inverse geometric problems, the (unknown) portion of the boundary Γ₂ needs to be determined (see Figure 4(a)). The uniqueness of solution and stability estimates of logarithmic type are provided in 96 and 97 in two and three dimensions, respectively. However, the problem is still ill-posed under no a priori regularity assumption on Γ₂ since its solution is unstable with respect to small perturbations in the boundary data (6.1b) on Γ₁.

Problem (6.1) was first solved by a meshless method in 98 where the authors used linear combinations of harmonic functions (not fundamental solutions) to approximate the solution. The same method was employed for the problem with Tikhonov regularization in 99. Apparently, the MFS was used for the first time in the solution of an inverse boundary determination problem in 100, where the authors solved a three-dimensional version of problem (6.1) which arises in potential corrosion damage. The two-dimensional problem (6.1) was solved independently as a Cauchy level-set problem using the MFS in 45,101. Similar problems were also considered using a regularized MFS in 102. Further, an adaptive greedy algorithm for the selection of the locations of the singularities when the MFS is applied to problem (6.1) was proposed in 103.

The detection of cavities and inclusions, which belongs to the second category of inverse geometric problems arising in EIT was investigated using the MFS in 104–107. In particular, in 105 the authors solved problem (6.1) where the domain Ω is doubly-connected and the boundary Γ₂ describes an unknown perfect conductor compactly contained in Ω, see Figure 4(b). In 106, the same problem was solved in the case of an insulator on which the Dirichlet boundary condition (6.1c) is replaced by the Neumann boundary condition (60) The similar problem of determining the location, size and shape of a body in the interior of a domain from boundary measurements, using the MFS in conjunction with the Kirsch–Kress method, was studied in 104. Finally, in 107 the following inverse conductivity problem was considered. Solve the Laplace equation (61) subject to the Cauchy boundary conditions (62) and the interface continuity conditions (63) where f₁ and g₁ are given functions, and 0 < k ≠ 1 is the constant conductivity of the unknown medium Ω₂ ⊂ Ω₁. As in problem (6.1), the unknown boundary Γ₂ is to be recovered.

6.2. Helmholtz's/modified Helmholtz's equation

The following inverse two-dimensional boundary identification problem was considered in 108. Solve the Helmholtz equation (64) subject to the Cauchy boundary conditions (65) and (66) where f₁, f₂ and g₁ are given functions, α and β are specified parameters, with either α = 0, β = 1 or α = 1, β = 0, which determine the type of boundary condition on Γ₂. This problem belongs to the first category of inverse geometric problems. The MFS was used with Tikhonov's regularization for the determination of the unknown boundary Γ₂ in several examples. Regarding the second category of inverse geometric problems, the method was also recently used for detecting a sound-soft scatterer embedded in a host acoustic homogeneous medium from scant measurements of the scattered acoustic pressure in the vicinity of the obstacle in 109.

6.3. Laplace–Beltrami's equation

In 110, the authors apply the MFS in conjunction with the Tikhonov regularization method to the numerical reconstruction of an unknown part of the boundary, Γ₂, from the Dirichlet boundary condition on Γ₂ and the Cauchy data on the remaining, accessible and known portion of the boundary, Γ₁ = ∂Ω ∖ Γ₂, in the case of two-dimensional steady-state heat conduction problems in anisotropic media governed by the Laplace–Beltrami equation (67) where 𝕂 = (k_ij)_i,j=1,2 is the thermal conductivity tensor, which is symmetric and positive definite. Moreover, the same problem was considered in 111, but for steady-state heat conduction problems associated with functionally graded materials, i.e. materials whose thermal conductivity tensor is given by . Here the constant real or purely imaginary vector β characterizes the degree of grading, and the matrix is symmetric and positive definite.

6.4. Biharmonic equation

In 112, the MFS was used for the solution of an inverse boundary determination problem associated with the two-dimensional biharmonic equation. In particular, the following problem was considered for the determination of the unknown boundary Γ₂. Solve the biharmonic equation (68) subject to the Cauchy boundary conditions (69) and (70) where f_i, g_i, i = 1, 2 and h are given functions.

6.5. Cauchy–Navier's equations of elasticity

In 113, the authors considered the Cauchy–Navier equations of elasticity for the displacements u_i, i = 1, 2 given by (3.5a) subject to the Cauchy boundary conditions (3.5b) and (71) where f_i, g_i, h_i, i = 1, 2 are given functions and the 2 × 2 prescribed matrices B_i, i = 1, 2 determine the type of boundary data given on the unknown boundary Γ₂ which is to be determined. Here the domain Ω is doubly connected with Γ₂ describing an inclusion. In 114, the unknown part of the boundary, Γ₂, of the two-dimensional domain, Ω, occupied by an isotropic linear elastic solid was reconstructed from the knowledge of either the displacement or the traction vector on Γ₂ and both the displacement and the traction vectors on the remaining, accessible and known portion of the boundary, Γ₁ = ∂Ω ∖ Γ₂.

6.6. Stokes' equations

The MFS was used in 115 for the solution of the Stokes inverse identification problem (72) (73) and (74) where f_i, g_i, i = 1, 2 are given functions. The goal is to determine the unknown boundary Γ₂ which describes an inclusion, i.e. it is enclosed by Γ₁. The vector t in (6.8b) is the stress force defined by The corresponding problem expressed in the streamfunction-pressure formulation was considered using the MFS in 116.

6.7. Heat equation

In 117, the MFS was applied to one- and two-dimensional inverse boundary determination heat conduction problems. For the one-dimensional case the authors considered the problem (75) subject to the initial condition (76) the Cauchy boundary conditions (77) and (78) where f, g₀, g₁ and h are given functions. The objective is to determine the unknown moving boundary Γ(t). Problem (6.9) was also considered independently in 118. Further, in 119,120, the authors considered problem (6.9) in a multi-layer domain with a moving boundary at the end of the last layer.

7. Free boundary problems

This class of problems does not belong to the general class of inverse problems, but is related to them. Typically, in such problems, the shape and position of part of the boundary is unknown and the boundary conditions are over specified on it. Classical free boundary problems occur in monitoring the boundary corrosion of a blast furnace in the steel industry, free-surface flows under the action of gravity, seepage problems in hydraulic structures, etc. Sketches of free boundary problems are illustrated in Figure 5 (compare with Figure 4). As with inverse geometric problems the MFS discretization leads to non-linear systems of equations. The reason for this is the fact that part of the boundary is unknown and needs to be determined as part of the solution. As explained in the beginning of Section 6, the fact that the coordinates of the points describing the unknown part of the boundary appear non-linearly in the fundamental solutions leads to non-linear systems.

Figure 5. Sketches of free boundary problems: (a) Boundary identification and (b) Internal defect detection.

7.1. Laplace's equation

Consider the Laplace equation (79) subject to the boundary condition (80) and (81) where f₁, g_I and g_II are given functions, and the goal is to determine the free boundary Γ₂.

In 121, the MFS was applied to several problems of this type, whereas in 122 it was applied to an axisymmetric free boundary problem. The MFS and a modified version of it were applied to free boundary problems arising in potential flow around deformable bodies in 123,124, respectively.

A particularly interesting class of free boundary problems which arise in electropainting, are the so-called Signorini problems. In such problems the boundary is known, but on part of the boundary two types of boundary conditions alternate and the points (curves) on which the changes occur are not known. Bogomolny 23 used the MFS in a variational formulation to solve Signorini problems associated with the Laplace equation and the Cauchy–Navier equations of elasticity in two dimensions. A simpler MFS formulation for the solution of two- and three-dimensional Signorini problems associated with the Laplace equation may be found in 125,126, respectively.

7.2. Stokes' equations

In 127, the simple layer potential MFS of 128 was applied to a Stokes flow free boundary problem, namely the so-called planar Newtonian extrudate-swell problem, given by the Stokes equations (82) with boundary conditions on the fixed part of the boundary Γ₁ of the type (83) and on the free boundary Γ₂ to be recovered we have (84)

In (7.2b), the f_i, i = 1, 2 are given functions, the 2 × 2 matrices B_i, i = 1, 2 are known and u_n = (∂u/∂n, ∂v/∂n)^tr.

In (7.2c), Ca is the capillary number and R⁻¹ the mean curvature of the free surface.

7.3. Heat equation

We consider the following one-phase Stefan problem given by the heat equation (85) subject to the initial condition (86) the boundary condition on the fixed boundary (87) and the following conditions on the free boundary (88) where f and g are given functions, and the objective is to determine the free boundary s(t). Problem (7.3), as well as the more complicated two-phase Stefan problem, were solved using the MFS in 129 for the first time for this class of free boundary problems. The solution of inverse Stefan problems using the MFS is the subject of current research 130.

8. Concluding remarks

As evidenced by its extensive use for the solution of inverse and related problems arising in science and engineering in recent years, the MFS has proved to be a powerful tool for the numerical solution of such problems. This is due to the many advantages it offers over space- and other boundary-discretization methods which make it ideally suited for the solution of inverse problems. For example, the MFS-based numerical results obtained in 75,76 using the alternating iterative algorithm of 51, in the case of Cauchy problems in simply connected domains occupied by an isotropic linear elastic material, are not only more accurate than their BEM-based counterparts obtained in 131,132, but they are also exempt from oscillations at the endpoints of the under-specified boundary. Similar conclusions have also been obtained for Cauchy problems in two-dimensional simply connected domains associated with both isotropic and anisotropic heat conduction, as well as the modified Helmholtz equation, 50,53,61,69,70.

The method does have its shortcomings, such as the optimal location of the pseudo-boundary on which the singularities are to be placed, although some progress has been reported in recent years regarding this issue.

Future research associated with the MFS to inverse problems could involve:

•	The application of the method to the most difficult class of inverse problems, namely inverse geometric problems has been somehow limited. The application, for example, to problems where multiple cavities need to be identified is still to be investigated. Also, only a few applications have been reported for inverse geometric problems governed by the Cauchy–Navier equations of elasticity.
•	Relatively little research has been carried out in the application of the MFS to three-dimensional inverse problems of all types.
•	Further applications of the method to multi-phase moving boundary problems.
•	The numerical analysis related to the application of the method has not yet been studied in detail.

Acknowledgements

The authors would like to thank the University of Cyprus for supporting this research. The authors are also grateful to Professor Graeme Fairweather and the two anonymous referees for their comments.