A computational method to estimate the unknown coefficient in a wave equation using boundary measurements

Abstract

The objective of this article is to develop a computational method, which combines an efficient high-order finite difference method for solving wave equation, auto differentiation tools and globally convergent optimization algorithms to estimate the unknown coefficient in a 1-D wave equation. The forward problem is solved by efficient and higher order finite difference methods while the gradient of the cost functional with respect to the coefficient is calculated by an adjoint code which is generated by an auto differentiation tool, such as Tangent linear and Adjoint Model Compiler. Three numerical examples are conducted to demonstrate the effectiveness, robustness and accuracy of the proposed computational method.

Keywords:

• wave equation
• acoustic coefficient
• parameter estimation
• finite difference scheme
• inverse problem

AMS Subject Classifications::

• 65M06
• 65M32
• 65N06
• 65N21
• 35L20

1. Introduction

The identification of model coefficients in an acoustic wave equation through additional boundary measurements plays a crucial role in applied mathematics, geo-science, physics and many other areas. This technique has been widely used to determine the unknown property of a medium in which the wave is propagated by measuring data on its boundary or a specified location in the domain. In the wave equation, the unknown coefficient which characterizes the property of the medium is important to the physical process but usually cannot be measured directly, or very expensive when measured, thus some mathematical method is needed to estimate it.

Let us consider the following wave equation (1) with the initial conditions (2) and the Neumann lateral boundary condition (3) and the extra boundary condition (4) where c(x) denotes the normal velocity of the wavefront, S(x, t) is the wave source/sink, ν denotes the unit outer normal from Γ = ∂Ω, g₁(x, t) and g₂(x, t) are known functions that are defined on the boundary of the physical domain. Γ₁ ⊆ Γ is a part of the boundary of the domain Ω. Throughout this article, we assume that the coefficient c(x) is independent of time, which is reasonable in cases where the property of the medium does not change rapidly.

The above wave equation has been widely used in modelling wave propagation in mediums, such as earth. Geophysicists quite often need to know the internal structure of a certain area of the earth. However, due to the high drilling cost, it is impossible to drill many wells and examine the rock samples. Fortunately, the underlying mathematical model that describes the wave propagation is well-understood, and it is much easier and more cost-effective to record the wave information on the surface of the domain of interest. Such a technique forms exactly an inverse problem of wave equation. The basic question is: is it possible to recover the coefficient from the measurements on the surface of the interested part of the earth? As one can expect, there is no simple answer for this question, as a matter of fact, the complete mathematical solution of this questions is quite complicated, and is still partially answered or even unanswered at all, especially for the cases when the multidimensional domain is considered.

Let us use the following simple but intuitive argument to illustrate the situation. Obviously, if the coefficient c(x) is known, the initial-boundary value problem (1–4) would be over-specified because of the extra boundary condition in (4), thus the solution may not exist if the compatibility of the initial and boundary conditions is violated. Now, let c(x) be an unknown function in some function space for instance L₂(Ω), then there exists the possibility that the coefficient function can be determined from the surface measurements, provided that some conditions for the initial and boundary conditions in (2–4) are satisfied. If such a solution is not unique, we can place additional regularity conditions on c(x), for instance we can restrict c(x) in H¹(Ω), or H²(Ω) or even C^∞(Ω), then there exists the possibility that the solution to the inverse problem is unique.

Another difficulty in solving an inverse problem is the instability, which means that a set of almost perfect observational data could produce a totally wrong result.

In the past decades, a great deal of work have been done and many direct and iterative methods have been reported. An early attempt was done by Gerver in 1, who studied the uniqueness and stability of the solution to the inverse problem of a wave equation from a theoretical point of view. In 2, the author studied the stability of the inverse problem in 1-D wave equation and some interesting results were reported. More work regarding the existence and uniqueness of the solution to the inverse problem of wave equation can be found in 3–7 and a complete formal statement is given in 8. As for the stability, according to Isakov, the inverse problem is stable if some smooth conditions for the domain, initial and boundary conditions are satisfied. More details regarding the well-posedness of the inverse problem can be found in 8.

In general, the analytical solution to the inverse problem is not possible even when one can prove the existence and uniqueness of the solution, thus the numerical method is the choice for most application problems. While most previous methods are iterative, there were few direct methods such as the one proposed by Lin and Ewing 9. In this method, the authors took advantage of the special property that the wave equation is still a wave equation if one considers x as time and t as space variable, thus a so-called ‘space marching’ technique was applied and a higher order finite difference algorithm was developed to solve the inverse problem. The resulted direct method is very efficient as no iterative procedure is needed. However this method can be used only for equations in which x and t can be switched. For a more general case, most of the available methods are iterative methods. Xie 10 developed an iterative method by defining a nonlinear operator equation, so solving the inverse problem is transformed to solving a nonlinear operator equation. The first-order Frechet derivative operator was derived and proved to be invertible. So Newton's or quasi-Newton's method can be used to solve the linearized operator equation. The proposed iterative numerical method is fast and efficient, and the defined inverse problem is well-posed, so regularity term is not necessary. However, the definition of the nonlinear operator equation is based on zero initial conditions and special boundary conditions. For a general initial-boundary value problem, it is difficult to define the nonlinear operator equation. Nevertheless, this method was proved to be effective, and it was then extended by Chen and Xie 11 for simultaneous determination of bulk and shear moduli and density variation in an elastic wave equation. A more general method was proposed by Ding et al. 12 who defined a multi-cost-functional method, then identify the unknown coefficient by minimizing the multi-cost-functional.

For homogeneous wave equation, i.e. S(x, t) = 0 in Equation (1), the analytical solution can be obtained for certain initial and boundary conditions. However, for the general case, the analytical solution is difficult to get, thus we should rely on the numerical methods for the forward problem when an inverse problem is solved. In the past decades, various numerical methods had been developed to solve (1–4) or similar problems 13–19. The high-order finite difference scheme proposed in 17 will be adopted in this article, and more details of the numerical methods will be provided later.

In this article, we proposed an adjoint-based iterative method to solve the inverse problem of the wave equation subject to extra non-homogeneous boundary conditions. First, the inverse problem is formulated as a PDE-constrained optimization problem, which is then solved by an adjoint-based optimization method. The cost functional is defined as the discrepancy between the extra boundary conditions and numerical solutions on the boundary based on an initial guess of the unknown coefficient. Regularity terms are included in the cost functional to enforce the smoothness of the unknown coefficient c(x). In principle, both continuous and discrete adjoint methods can be used to generate the gradient. However since in this article the wave equation is solved numerically, it is not necessary to use continuous adjoint in optimization procedure, so here we apply automatic differentiation tools, which take the numerical program for solving the forward problem as the input, to generate discrete adjoint, then use it to calculate the gradient of the cost functional with respect to the unknown coefficient. To the best of my knowledge, this is the first attempt in applying automatic differentiation to solve the inverse problem of the wave equation. The rest of this article is organized as follows. In Section 2, we formulate the inverse problem as a PDE-constrained optimization problem, then in Section 3, several finite difference numerical schemes are introduced to solve the wave equation. In Section 4 two automatic differentiation tools, Tangent linear and Adjoint Model Compiler (TAMC) and TAPENADE are briefly introduced. The optimization procedure is discussed and several optimization algorithms/packages are covered in Section 5. Three numerical examples are solved in Section 6 to illustrate the effectiveness, robustness and accuracy of the proposed method, and finally some conclusions and possible future work are discussed in Section 7.

2. Mathematical formulation of the inverse problem

We formulate the inverse problem as a PDE-constrained optimization problem. To simplify the presentation, throughout the rest of the article, we consider the following 1-D initial-boundary value problem, which is a special case of Equations (1–4): (5) (6) (7) and subject to the extra boundary conditions: (8) where c(x) is the unknown coefficient, u₀(x), u₁(x), φ₁(t), φ₂(t), ψ₁(t) and ψ₂(t) are functions that satisfy some regularity conditions. Note that in some real applications, the extra boundary conditions in Equation (8) are replaced by the following non-local integral condition: (9) which is much weaker than that given in Equation (8), where E₁ and E₂ are constants.

If the coefficient c(x) is known, the problem (5–8) is obviously over-specified because of the extra boundary conditions in (8). However, since the coefficient c(x) is unknown, a unique solution may exist and can be obtained through solving an inverse problem governed by the wave equation. Since our focus in this article is the computational aspects, we assume that the initial and boundary conditions are sufficiently smooth to guarantee a unique solution. For more details regarding the existence and uniqueness for the inverse problem, the readers are referred to 8,20.

The numerical procedure to estimate c(x) and corresponding solution u(x, t) is inherently an iterative procedure, which includes three main steps:

1.	Starting from an initial guess c0(x), the forward problem defined in Equations (5–7) is solved.
2.	The numerical results from step 1 are compared with the extra boundary conditions in Equation (8) to calculate the cost functional, then the gradient (derivative) of the cost functional with respect to c0(x) is calculated from the adjoint equation.
3.	Optimization algorithm is applied to minimize the cost functional, and the three steps are repeated till convergence is obtained.

We first define the cost functional 𝒥(c(x)) as follows: (10) If the extra measurements are also available on other grid points x_k with k ∈ K, where K is a subset of the set: {1, 2, … , N}, the cost functional can be generalized as follows: (11) where w_i, i ∈ K are prescribed positive weights satisfying ∑_i∈K w_i = 1, and ψ_i(t) are the extra measurements of u_x(x, t) prescribed at x_i for i ∈ K, ũ(c(x), x, t) is the solution of the initial-boundary value problem Equations (5–7) based on c(x), λ and μ are regularity parameters.

3. Numerical schemes

For special initial and boundary conditions, the initial-boundary value problem defined in Equations (5–7) can be solved analytically, but it becomes almost impossible when a more general initial and boundary value problem is considered. Thus, accurate and efficient numerical schemes are necessary to solve the inverse problem. In this section, several numerical schemes are introduced, as well as the method to calculate the cost functional.

To simplify the presentation, we divide the solution domain [0, L] × [0, T] into a uniform N × M grid with step sizes h = 1/(N − 1) and Δt = T/(M − 1), and the grid points (x_i, t_j) are defined as (12) (13) and the numerical solution of u(x, t) at grid point x_i and time level t_j is denoted as .

Following the spatial discretization used in 16–18, we first approximate as , where A_h is an approximation of the differential operator of order p depending on the numerical scheme used for the approximation. Based on the approximation, the original wave equation in Equation (5) is transformed to the following ODE system: (14) where C is a diagonal matrix whose diagonal entries are c(x₁), c(x₂), … , c(x_N), U = (u(x₁, t), u(x₂, t), … , u(x_N, t))^T and S = (S(x₁, t), S(x₂, t), … , S(x_N, t))^T.

Depending on the discretization of time derivative, the numerical methods for the ODE system Equation (14) can be classified into two categories: explicit and implicit schemes. The explicit scheme is efficient but only conditionally stable, so in general small time step size is required. The implicit scheme is usually unconditionally stable but a linear algebraic system needs to be solved at each time step, which makes it less efficient. In what follows, several explicit and implicit schemes will be briefly introduced.

3.1. Explicit scheme

Explicit methods are still widely used in solving time-dependent problem due to its efficiency, since the solution to a linear/nonlinear system (the system is usually in large size) is not required. Simply applying the central finite difference operator to U_tt, one can obtain the following second-order three-level scheme (15) Obviously this numerical scheme is very efficient and accurate (second order in time and p-th order in space). However, it is only conditionally stable. As a matter of fact, Δt = O(h) has to be enforced as a stability constraint. Another shortcoming of this scheme is that it works well only if the solution is smooth, otherwise it may introduce non-physical oscillations, as reported in 17. Another issue of this algorithm is that two initial conditions are required thus the initial condition given in Equation (2) cannot be used directly, and some extra effort is needed to approximate the initial condition at t = t₂. In this article, the following second-order approximation is derived and used (16)

Using Taylor's expansion, the scheme given in (15) can be improved to the following fourth-order accurate (in time) scheme (17) Similarly, two initial conditions, U¹ and U² are required for algorithm (17), thus a fourth-order approximation to U² is needed. Using Taylor's expansion and the original wave equation, we can derive the following fourth-order approximation (18)

Note that in Equation (18) the approximations to u_tt(x, 0) and u_ttt(x, 0) are obtained by using the wave equation, assuming that the solution u(x, t) is sufficiently smooth in both x and t. Here we just briefly introduce the numerical algorithm, for more details regarding the stability, accuracy and efficiency of these two numerical algorithms, the readers are referred to 15,21–23.

Due to the stability constraint Δt = O(h), it is desirable that the approximation operator A_h has the same order of accuracy as that of the time integration, thus for the numerical method in Equation (15), we should use a second-order operator A_h while for the numerical method in Equation (17) we should equip it with a fourth-order operator A_h, to maximize the performance.

3.2. Implicit scheme

The implicit numerical method is usually less efficient but more stable than the explicit method, therefore larger step size can be used for time integration. In the past several decades, many implicit numerical schemes have been developed to solve the ODE system Equation (14), such as multi-level linear method and implicit Runge-Kutta type method. In this article, we focus on two-level and three-level linear methods. The advantage of two-level method is that only one initial condition is needed thus the approximation in Equation (16) or Equation (18) is not required. The basic idea of two-level method is to re-write the original second-order ODE system as the following two first-order ODE systems by introducing an auxiliary variable V: (19) (20)

It is easy to verify that Equation (14) is equivalent to the ODE systems in Equations (19)–(20). Various two-level schemes have been developed in the past. For instance, in 19 Johnson developed the following scheme: (21) (22) where 0 ≤ α and β ≤ 1 are two parameters. If the source/sink term S in Equation (5) is independent of u, S^j+α can be calculated directly as S^j+α = (S(x₁, t_j + αΔt), S(x₂, t_j + αΔt), … , S(x_N, t_j + αΔt))^T. Otherwise, the linear interpolation S^j+α = αS^j+1 + (1 − α)S^j is used.

As reported by Kim and Lim and Johnson in 17,19, the numerical algorithm given in Equations (21)–(22) is unconditionally stable when α, β ≥ 0.5, and is second-order accurate (in time) when α = β = 0.5.

Apply the regular central finite difference operator to U_tt, we can derive a second-order accurate three-level method, which can be improved to fourth-order accuracy by applying compact finite difference technique 24–27 to approximate U_tt without increasing the size of the stencil. Let us denote the regular central finite difference operator as , which is defined as . Using Padé approximation we have the following fourth-order (in time) three-level scheme (23) which is actually a special case of the more general fourth-order three-level implicit method (θ = 1/12) proposed in 17. It is easy to see that this algorithm is unconditionally stable, thus large Δt can be used for time integration.

Note that the three-level scheme given in Equation (23) requires two initial conditions U¹ and U², so a fourth-order approximation for U² such as the one in Equation (18) is needed.

To maximize the performance, we use the second-order operator A_h for the numerical method in Equations (21)–(22) and fourth-order approximation A_h for the numerical method in Equation (23). However it is worth pointing out that an approximation operator A_h with any order of accuracy can be used since there is no stability constraint for the two methods.

3.3. Cost functional

Upon solving the initial-boundary value problem Equations (5–7) with an initial guess c⁰(x), we can calculate the cost functional 𝒥(c⁰(x)) using the extra boundary conditions given in Equation (8). We first apply Taylor's expansion to approximate u_x(c⁰(x), 0, t) and u_x(c⁰(x), L, t) using the numerical solution of the wave equation. If the wave equation is discretized in space by a second-order scheme, it is required that an approximation with at least second-order accuracy should be used to calculate u_x, while if a fourth-order scheme is used, an approximation with at least fourth-order accuracy should be used, so on and so forth, to maintain the higher order accuracy. For example, if A_h is second-order accurate, we can use the following second-order approximation (24) (25) while if A_h is fourth-order accurate, we can use the following fourth-order approximation (26) (27) where u_i's in Equations (24–27) are numerical solutions of the wave equation at (x_i, t) based on the initial guess c⁰(x). Similarly, if measurements are also available on other grid points, the cost functional can be generalized to include more grid points such as that in Equation (11). Note that if the integral boundary condition such as Equation (9) is specified, some higher order integral method for instance, Simpson's rule should be used to calculate the cost functional.

4. Discrete adjoint generated by automatic differentiation

The success of the gradient-based optimization relies on an accurate derivative of the cost functional with respect to the unknown coefficient c(x). In this section, we introduce several automatic differentiation tools that can be used to generate the discrete adjoint which will be used to calculate the gradient of the cost functional with respect to the unknown coefficient c(x). In real computation, c(x) has to be discretized on a finite grids, thus we can only estimate it on a finite number of grid points, although theoretically it can be a function in a more general space. To simplify the discussion, we assume that we estimate c(x) on the same grid as that on which the forward problem is solved.

Based on the size of C, different methods can be used to calculate the gradient. For instance, if the coefficient c(x) is a constant c on [0, L], the cost functional 𝒥 is a function of a single variable c, one can use the finite difference approximation (𝒥(c + ε) − 𝒥(c))/ε to approximate 𝒥′(c), which results in the secant method for the optimization procedure. This method, although is simple in the prospective of implementation, is impractical when the coefficient is non-constant on the domain [0, L]. For example, let C = (c₁, c₂, … , c_N), then in each iteration, to compute the gradient , one needs to calculate the partial derivative with respect to each c_i using the finite difference approximation (𝒥(c₁, … , c_i + ε, … , c_N) − 𝒥(C)/ε, which involves numerically solving the wave equation N + 1 times, and this is just the computational cost for one iteration. Further, if the unknown coefficient is time-dependent, or if the problem is solved on a very fine grid, the size of the problem will be too huge to be handled, thus the finite difference quotient approximation is impractical for the general case, and some efficient method to calculate the gradient is needed.

The adjoint method has been widely used in calculating the gradient. In principle, both continuous and discrete adjoint methods can be used to derive the gradient. Theoretically, there is no formal advantage of one method over other in any general sense, however one method may be better suited to a given application.

In the method of continuous adjoint, the adjoint equation, which is derived using methods such as calculus of variations, is numerically solved to generate the gradient. While in the method of discrete adjoint, the numerical scheme for the forward problem defined in Equations (5–7) is considered as the forward model, thus this approach actually computes the derivatives of the numerical solution, rather than approximating the derivatives of the exact solution. Obviously discrete adjoint relies on the choice of the numerical method of the forward problem.

To derive the discrete adjoint, one can either take the adjoint of the forward numerical scheme directly, or apply automatic differentiation tools, such as TAMC 29 and TAPENADE 30. Since the direct approach is time-consuming and error-prone, the automatic differentiation, which builds a new augmented program based on the program written by the user to solve the forward problem, has been widely used. Another advantage of automatic differentiation is its quick and simple implementation. Basically, there are many AD tools that can be used to generate discrete adjoints, some maybe even better than the two AD tools that will be used in this article. However due to the limits in space, it is impossible and also not necessary to compare and test all AD tools that are available, since the purpose of this article is to examine the feasibility of applying AD tools to solve the inverse problem of wave equation. Therefore, only TAMC and TAPENADE are tested and some comparisons between the two packages are presented in this article.

TAMC is a source-to-source translator that generates Fortran routines for computation of the first-order derivatives out of Fortran routines. It provides both forward and reverse modes for a given numerical program written in Fortran. Currently it supports both Fortran 77 and Fortran 90 standards. Since its development, TAMC has been widely used in many application areas, such as atmospheric modelling, oceanic modelling, aerodynamics and radiative transfer models. To the best of my knowledge, TAMC has not been used previously to solve the inverse problem of the wave equation. Simply speaking, the user provides a Fortran program fun.f that implements a function f (x) as the input for TAMC, which then conducts a source-to-source translation and returns a new Fortran program adfun.f, which implements f ′(x). The user can simply run the returned Fortran program adfun.f to generate the gradient of the function f (x).

TAPENADE is also an automatic differentiation engine which was developed at INRIA Sophia-Antipolis by the TROPICS team. It is an online source-to-source AD tool; however, it can be also installed and used locally as a set of JAVA classes. Currently it supports Fortran 77, Fortran 95 and C, and generates the derivative of a given function in forward (tangent) or reverse (adjoint) mode. So far it has been successfully used in applications such as modelling complex environmental systems, sensitivity analysis of global sea-ice model and adjoint code development in CFD.

5. Optimization algorithms

Minimizing the cost functional is a key step in the computational method, here we provide a brief introduction to the optimization algorithms that will be used to solve the PDE-constrained optimization problem. Limited memory Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) is one of the widely used quasi-Newton optimization algorithms. It is very efficient in solving the large scale optimization problem. For the considered PDE-constrained optimization problem, the domain [0, L] is divided into a grid with N grid points, so the discrete coefficient c(x) has a size of N, which in general is large. When an l-dimensional problem is considered, the size of the parameters will be N^l. The L-BFGS method, which is also called the SQN method in 31, is almost identical to the regular BFGS method in terms of implementation. The only difference is in the matrix update. In L-BFGS, only a short history of the past updates have been used, thus the requirement on storage has been reduced significantly. Let f (x) be the function being minimized, g(x) = ∇ f (x) be the gradient and x_k be the kth iteration. Define s_k = x_k+1 − x_k and y_k = g_k+1 − g_k, the L-BFGS method is implemented as follows:

•	Step 1: Set initial guess x0 and let k = 0, choose parameter m, which is the number of BFGS corrections that are to be kept. Choose a sparse symmetric and positive definite matrix H0, which approximates the inverse Hessian matrix of f (x). Choose two parameters and τ as and .
•	Step 2: Compute dk = −Hkgk and xk+1 = xk + αkdk, where αk is a parameter satisfying the Wolf conditions: and .
•	Step 3: Let , and update the matrix Hk times using the pairs and the following formula:
•	Step 4: Set k = k + 1 and go to Step 2.

A detailed description of the algorithm can be found in 31, and an implementation can be found in 32, which and can be freely downloaded. It has been shown 33 that this package is very robust and converges faster than many other popular methods such as the widely used standard conjugate gradient method for almost all test cases. For more details of the algorithm and its performance, the readers are referred to the above-mentioned papers.

For comparison, we also tested three conjugate gradient optimization algorithms: the Fletcher–Reeves method, the Polak–Ribiere method and the positive Polak–Ribiere method. Conjugate gradient method has been widely used to solve nonlinear optimization problem. Suppose f (x) is a smooth function to be minimized, and g(x) is its gradient. Let x₀ be the initial guess, g₀ = g(x₀), and x_k be the kth iteration, the conjugate gradient method is implemented as follows: where b_k is a scalar and a_k is a step length determined by means of a 1-D search. The three methods that are implemented in the package CG+ 34 are almost identical with the only difference in the formula to calculate b_k. In the Fletcher–Reeves method, b_k = ‖g_k‖²/‖g_k−1‖², in the Polak–Ribiere method, b_k = ⟨g_k, g_k − g_k−1⟩/‖g_k−1‖², while in the positive Polak–Ribiere method, b_k is calculated as b_k = max{⟨g_k, g_k − g_k−1⟩/‖g_k−1‖², 0}, thus only non-negative b_k is allowed in this method.

In principle, the user can choose any other optimization packages or implement any other optimization algorithm to solve the optimization problem, since the proposed computational method is very flexible, and a new component can be easily integrated.

6. Numerical results and discussions

In this section three numerical examples are solved. The first simple example is used to validate the numerical scheme for solving the wave equation, and the discrete adjoint generated by the automatic differentiation tools. The second example is used to illustrate the efficiency, accuracy and robustness of the proposed computational method. The third example is a wave equation with discontinuous c(x). For all examples, we assume that the exact solutions are known.

6.1. Example 1

We consider the initial-boundary value problem defined in Equations (5–8) with for which the exact solution is (28) and the coefficient is given as (29)

We first validate the numerical methods for the forward problem. The maximum errors of the numerical solutions by both second-order and fourth-order methods are listed in Table 1 and Table 2, respectively. It is clear from Table 1 that the numerical method defined in Equation (15) is second-order accurate in both time and space, as we can see that when Δt and h are reduced by a factor of 2, the maximum error is reduced by a factor of 4. Similarly, the data in Table 2 confirms that the numerical method defined in Equation (23) is fourth-order accurate in both time and space, as we can see that the maximum error is reduced by a factor of 16 when Δt and h are reduced by a factor of 2.

Table 1. Maximal error ‖u − u_exact‖_∞ between the exact solution and the numerical solution by the second-order scheme defined in Equation (15).

(h, Δt)	(1/8, 1/10)	(1/16, 1/20)	(1/32, 1/40)	(1/64, 1/80)	(1/128, 1/160)
E(h, Δt)	1.2138E−04	3.0503E−05	7.6392E−06	1.9108E−06	4.7773E−07
	–	3.9793	3.9930	3.9979	3.9997
	–	1.9925	1.9975	1.9993	1.9999

Table 2. Maximal error ‖u − u_exact‖_∞ between the exact solution and the numerical solution by the fourth-order scheme defined in Equation (23).

(h, Δt)	(1/8, 1/10)	(1/16, 1/20)	(1/32, 1/40)	(1/64, 1/80)	(1/128, 1/160)
E(h, Δt)	7.8152E−06	4.6310E−07	2.6581E−08	1.5215E−09	8.7092E−11
	–	16.8758	17.42258	17.4699	17.4702
	–	4.0769	4.1229	4.1268	4.1268

We then validate and compare the discrete adjoints generated by the two auto differentiation tools introduced in Section 4. To do this, we first calculate the finite difference quotient approximations of at nine grid points using the formula with various values of ε. The approximated derivatives are then compared with the results generated by TAMC and TAPENADE. To reduce the effect of numerical error, we use the fourth-order numerical method in Equation (23) to solve the forward problem. All finite difference approximations and auto differentiations are based on the fourth-order method. The finite difference is calculated for a constant coefficient c(x_i) = 1.2, i = 1, 2, … , N, with Δt = 1/200 and h = 1/100. The results in Table 3 show that both the auto differentiation tools generate accurate discrete adjoints, although the results generated by TAMC are much more accurate than that by TAPENADE. As one can see, when ε is reduced from 0.01 to 0.0001, the finite difference approximation (denoted as FD in the table) converges to the result generated by TAMC. Therefore in the next numerical example, we only test the computational method using the gradients generated by TAMC.

Table 3. Comparison of derivatives generated by various methods.

xi	FD (ε = 0.01)	FD (ε = 0.001)	FD (ε = 0.0001)	TAMC	TAPENADE
0.1	0.1547459996	0.1547356869	0.1547355778	0.1547355843	0.1548949188
0.2	0.2193119526	0.2192973117	0.2192971754	0.2192971651	0.2192654826
0.3	0.2851436441	0.2851247931	0.2851245907	0.2851246039	0.2849388791
0.4	0.3465546654	0.3465319277	0.3465316861	0.3465316996	0.3462826013
0.5	0.4160232908	0.4159961009	0.4159958051	0.4159958286	0.4156669989
0.6	0.4372516947	0.4372231528	0.4372228554	0.4372228672	0.4362583627
0.7	0.4669640295	0.4669334619	0.4669331458	0.4669331575	0.4659774826
0.8	0.4764092251	0.4763779912	0.4763776626	0.4763776802	0.4751535480
0.9	0.4485708252	0.4485416621	0.4485413880	0.4485413683	0.4462902136

6.2. Example 2

In this example, we solve the initial-boundary value problem defined in Equations (5–8) with (30) (31) (32) (33) for which the exact solution is u(x, t) = e^−t(x² + sin(x)) and the coefficient is given as c(x) = 1 − x²/100.

Theoretically we need to estimate the coefficient c(x) as a function defined on the whole domain [0, 1], but in real application problems, the medium property on the boundary of the domain can be easily measured, thus we can assume it is known. As a matter of fact, it can be derived from the compatibility conditions among the boundary and initial conditions. Here we derive the value of c(x) at x = 0 as the example. Assume that u(x, t) is sufficiently smooth and u_xx ≠ 0 at x = 0, otherwise from Equation (5) we have u_tt = S(x, t) at x = 0, so u(x, t) is independent of c(x) at x = 0. From the wave equation (5), we solve the coefficient as , then take the limit as (x, t) → (0, 0) on both sides and change the order of differentiation and limit if necessary, we can derive c(x) at x = 0 as (34) Similarly, we can derive c(x) at x = 1 as (35)

Remark

In all the following test cases, we assume that the medium properties at the boundary of the domain are known. Further, in the real computation, it is infeasible (also not necessary in general) to recover the function c(x) on the whole domain [0, 1], so we restrict our discussion on the grid points only. However if we have some prior information for instance the function space that c(x) belongs to, it is possible to span c(x) in that function space and recover it exactly. To simplify the discussion, here we use the same grid as that used in solving the forward problem, thus we only estimate the values of c(x) on the grid points. When the value of c(x) on a non-grid point is needed, one can use interpolation technique to get the value of c(x) on the desired location.

As a measure of the accuracy of the method, we consider the difference between the estimated and the exact coefficient c(x) in both maximal and root mean square norms, which are defined as (36) and (37) respectively, where is the estimated value for c(x_i). Here we calculate the difference for grid points from x₂ to x_N−1 because we assume that c(x₁) = c(0) and c(x_N) = c(1) are known. In all the following test cases, the initial guess is set as c⁰(x) = 1.2 + sin(24x)/3.

6.2.1. Test Case I

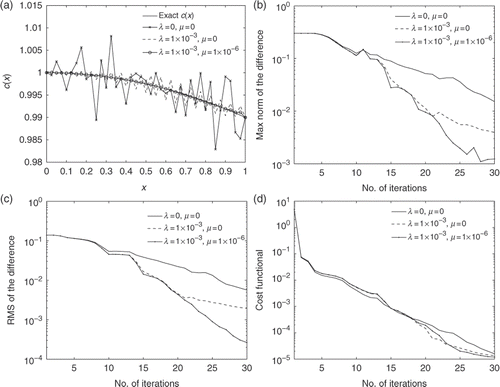
We first investigate the impact of the numerical method that is used to solve the forward problem. It is worth pointing out that regularity terms are not used in this test case, i.e. λ and μ are set to 0 for this test case. For comparison, we tested the second-order method defined in Equation (15) and the fourth-order method defined in Equation (23), and the results are shown in Figure 1.

Figure 1. Comparison of the results by the second-order and fourth-order methods for Example 2, with h = 1/40 and Δt = 1/80.

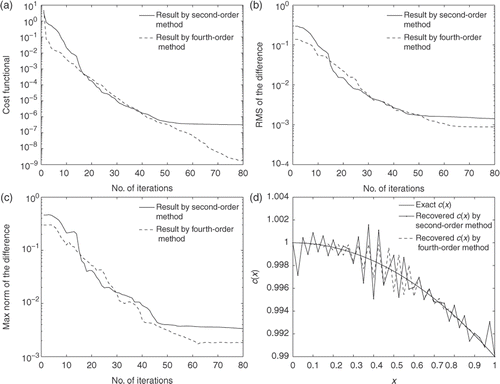
Apparently the results based on the fourth-order method are more accurate than that by the second-order method, which suggest that the higher-order method is preferred if the computational cost is not an issue. Therefore, in all of the following test cases, unless otherwise stated, the fourth-order method is used to solve the forward problem.

6.2.2. Test Case II

In this test case, we investigate the impact of regularity terms. The discrete adjoint is generated by TAMC, and the optimization package L-BFGS is used to minimize the cost functional. It is well-known that regularization is an effective approach to resolve the ill-posedness of an inverse problem; however, determining the regularity terms requires some prior information of the state variable and the unknown parameters. Such information can be obtained by limiting the admissible function space for c(x) or enforce some constraints on c(x). Here we implement this by carefully choosing the regularity parameters λ and μ in Equation (11) where the discrete norms are defined as (38) and (39) respectively.

The results show that well-selected regularity terms can significantly resolve the ill-posedness of the inverse problem; however, there is no general rule to select the two parameters λ and μ, which determine the smoothness of the solution c(x). As one can see from the cost functional, the larger λ is, the smaller ‖c′(x)‖ should be, which indicates that the solution curve is closer to a horizontal line. Similarly, the larger μ is, the smaller ‖c″(x)‖ should be, which indicates the solution curve is closer to a line. Therefore, including the two regularity terms implies that both ‖c′(x)‖ and ‖c″(x)‖ are bounded. Since the true solution for this example is known, the user can choose an optimal set of parameters to improve the performance. Normally, if we set both parameters to zeros, it is equivalent to consider the solution c(x) in L₂(Ω). If the solution is not unique (the cost functional converges to zero but the solution does not converge to c(x)), we can restrict the solution to H₁(Ω) by choosing a parameter λ > 0. If the solution is still not unique, one can choose μ > 0 to restrict the solution to H₂(Ω). In summary, the regularity terms are optional in the sense that if the user has prior information of the unknown coefficient c(x), they may be included in the cost functional. It is possible that the iteration is still convergent without the regularity terms, although it may converge slowly. To demonstrate the difference clearly, only 30 iterations were performed, so the difference is visible. The results with various values of λ and μ are shown in Figure 2.

Figure 2. Comparison of the results with various regularizers.

6.2.3. Test Case III

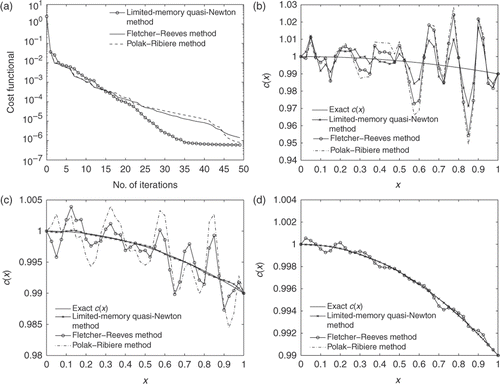
We now investigate the impact of the optimization algorithm. The optimization algorithms that have been tested are L-BFGS and three conjugate gradient methods: the Fletcher–Reeves method, the Polak–Ribiere method, and the positive Polak–Ribiere method. The numerical results show that the Polak–Ribiere method and the positive Polak–Ribiere method produce almost identical results, therefore the result by the positive Polak–Ribiere method is not included here. First, Figure 3(a) shows that when less than 20 iterations are performed, the results by the three algorithms are similar, however L-BFGS outperformed the three conjugate gradient methods when the number of iterations is between 25 and 45. To see this, we compared the estimated c(x) with the exact c(x) when 20, 35 and 50 iterations are performed in Figure 3(b), (c) and (d), respectively. The results indicate that L-BFGS produces the most accurate result, while the results by the Fletcher–Reeves method and the Polak–Ribiere method are comparable. Note that the conclusion is based on this specific example only, it is possible that the conclusion is different when a different problem is solved. Nevertheless, the purpose here is to show that the performance of the computational method relies on the choice of optimization algorithm.

Figure 3. Comparison of the results by different optimization algorithms.

Remark

The comparison is conducted among the three algorithms when the same number of iterations is used but the total number of function evaluations are different, thus the total CPU time for each case varies significantly, as shown in Table 4, which confirmed that the most efficient algorithm is L-BFGS.

Table 4. Computational cost of various algorithms.

Number of iterations	Number of function evaluations
	L-BFGS	Fletcher–Reeves	Polak–Ribiere
20	23	47	44
35	41	78	75
50	57	109	107
	CPU time (s)
	L-BFGS	Fletcher–Reeves	Polak–Ribiere
20	4.64	8.96	8.45
35	7.94	14.62	14.10
50	11.04	20.31	20.06

6.2.4. Test Case IV

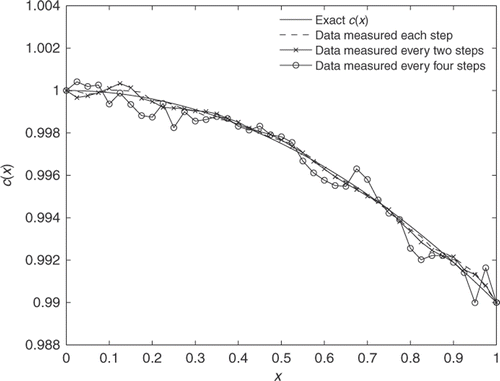
For many applications it is expensive to obtain boundary measurements, thus it is always desirable to reduce the size of boundary measurements. In general, the cost functional defined in Equation (10) involves the boundary measurements at all time steps t_j, j = 1, 2, … , M. In this test case, we examine the possibility of reducing the size of boundary measurements by taking a partial set of the full time steps. The results obtained by using boundary measurements at each time step, every two time steps and every four time steps are compared with the exact solution in Figure 4. It seems that the estimated c(x) is still very accurate when the boundary measurements are taken at every two time steps and the result is reasonably accurate if the boundary measurements are taken every four time steps. Obviously, the result will be less accurate when fewer measurements are taken. When the boundary measurements are taken every six time steps, the recovered result is unacceptable, which is not plotted.

Figure 4. Comparison of the results by using different number of boundary measurements.

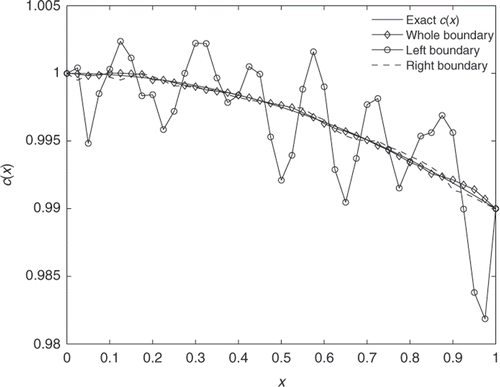
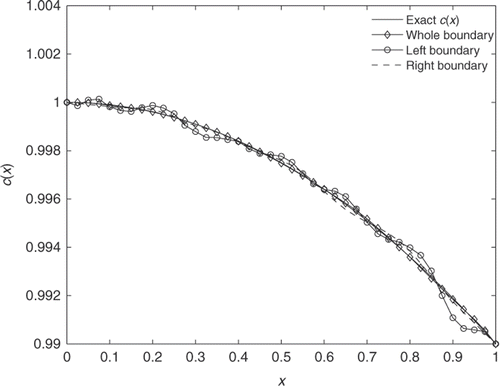
Sensitivity analysis indicates that the observational data on different locations are of different levels of importance in recovering the unknown parameters. In the 1-D wave equation, the observational data is obtained at the left- and right-end points of the domain, so we compare the result obtained by using data from both sides with the results obtained by using data from one side only. The results are presented in Figure 5 and Figure 6. It is interesting that the observational data at x = 1 are more useful in estimating the coefficient c(x) than the data at x = 0. As one can see, the estimated coefficient by using boundary measurements at x = 1 only is almost the same accuracy as that by using boundary measurements at both end points, while the result from using boundary measurements at x = 0 only is much worse. It is clear that the cost functional depends more on the boundary measurements at x = 1 than on the boundary measurements at x = 0. Thus more weights should be assigned to the boundary measurements at x = 1, and the weights of boundary measurements at x = 0 can be reduced without effecting the accuracy of the results. A further study indicates that for this specific example, the boundary measurement at x = 0 is somewhat redundant, if the current regularity terms are included. As one can see, the true solution is c(x) = 1 − x²/100, so c′(x) = −x/50, which is very close to 0 near x = 0. Therefore, if λ is large, when cost functional converges to zero, ‖c′(x)‖₂ converges to zero too, which already implies that c′(x) converges to zero at x = 0, so the boundary measurements at x = 0 make little difference. Consequently, removing the constraint from left boundary conditions from the cost functional does not change the result significantly. To verify this, we reduce λ by a factor of 10, then the numerical result shows that the boundary measurement at x = 0 is almost equally important as the boundary measurement at x = 1. Nevertheless, numerical results show that the observational data at different locations may have different impacts on the result, and can help the user to reduce the size of boundary measurements.

Figure 5. Comparison of the results by using partial and complete boundary measurements, λ = 1 × 10⁻³.

Figure 6. Comparison of the results by using partial and complete boundary measurements, λ = 1 × 10⁻⁴.

6.2.5. Test Case V

In this case, we test the stability and robustness of the computational method by perturbing the boundary measurements with noisy data. It is well-known that the boundary measurements, which are obtained from experiments or observations, usually contain some random errors. 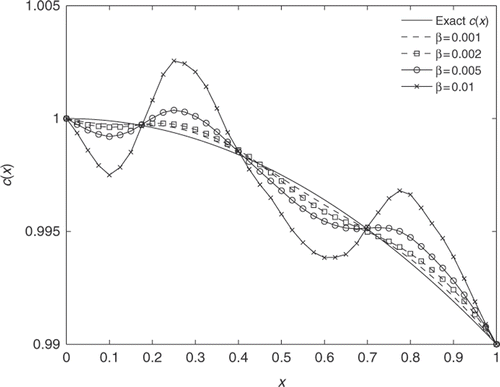We perturb the boundary conditions by adding a random noisy term to the exact boundary conditions in Equation (33) and consider the following boundary conditions: (40) where β is the perturbation level and rand is a uniform random number between −1 and 1. The results presented in Figure 7 show that the proposed method is very robust, as we can see that when β = 0.001, the recovered coefficient is almost identical to the result without perturbation, while when β = 0.002 and β = 0.005, the recovered coefficient is still reasonably accurate, however when β > 0.01, the method produces poor results and fails to recover c(x). The results with various perturbation levels are presented in Figure 7.

Figure 7. Comparison of the results by different levels of perturbations.

6.3. Example 3

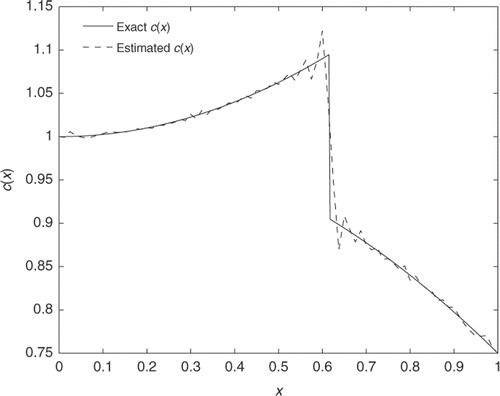
We finally consider the wave equation with discontinuous S(x, t) and c(x). To simplify the discussion, we assume that there is only one discontinuous point. The case with multiple discontinuous points can be treated similarly. We solve the initial-boundary value problem defined in Equations (5–8) with for which the exact solution is u(x, t) = x sin(x/2 + t) and the coefficient is Since c(x) has discontinuity, the regularity terms are not included in the cost functional. The numerical result, which is obtained after 50 iterations, shows that the proposed computational method is very accurate and reliable in estimating the coefficient with discontinuity, as one can see in Figure (8).

Figure 8. Numerical result for problem with non-smooth c(x), Δt = 1/80, h = 1/40.

7. Conclusions and future work

A computational method to estimate the space-dependent coefficient c(x) is developed in this article. The computational method, which combines efficient and accurate finite difference scheme for solving wave equation, auto differentiation tool and optimization algorithms, provides a fast and robust approach to estimate the unknown coefficient in the wave equation, as shown by the numerical examples. It is noted that the performance of the method depends on various factors, such as the numerical schemes for solving the forward problem, the method to generate the adjoint code and the choice of regularity parameters.

In the future, we plan to extend this computational method to more general cases such as time-dependent coefficient, wave equations defined on multi-dimensional space and elastic wave equation. In this article only discrete adjoints generated by auto differentiation tools are implemented, so it would be an interesting work to generate the continuous adjoint, which is derived from solving the corresponding adjoint equation. Another possible extension is to consider a wave equation with nonlinear source term s(u, x, t), as it is well-known that the non-linearity will bring some challenges in all aspects of the computational method.

Acknowledgements

The work of the author is supported by the Natural Sciences & Engineering Research Council of Canada (NSERC) through the project RT734491. The author thanks the anonymous referees for their suggestions and comments on the revision of this manuscript.