Shape functions associated with super-convergent mass matrix

Abstract

This article presents a novel approach in obtaining shape functions associated with super convergent element formulations with and continuity. In structural dynamics super-convergent element models are obtained by eigen-value convergence analysis, or minimizing the discretization errors leading to maximum convergence rates in their eigen-solutions. The element formulations developed by these inverse strategies are obtained without the need to define any shape functions. This article proposes a methodology to define the inverse model associated shape functions. The method employs trigonometric functions to define shape functions corresponding to the super convergent element formulations. Using the proposed strategy, the shape functions of super-convergent rod and beam elements are obtained. The presented rod and beam shape functions corresponding to the inverse formulations are just examples on how the presented methodology can be implemented.

Keywords:

• finite element modeling
• trigonometric shape functions
• beam element
• inverse method
• mass matrix

1. Introduction

In classical finite element method many admissible shape functions are considered for an element, each results a different formulation. The difference among these models is in their accuracy and the rate of convergence 1. The accuracy of finite element (FE) models may be improved by number of methods. The first and most common method is H-version in which the order of element is kept fixed while the number of elements is increased in a way that maximum size, h, of the elements approaches to a small value 2. The second method known as p-version, whereby the mesh of the model is fixed and the order of the interpolation functions, p, is progressively increased until meeting the desired degree of convergence 3.

Another strategy in obtaining accurate FE models is to employ inverse methods. Considerable efforts in FE modelling have been devoted to obtaining an element formulation that gives a small discretization error and fast convergence. Employing inverse methods was first introduced by Argyris et al. 4, Bergan et al. 5 and Simo and Rafai 6. MacNeal 7, Kim 8, Hanssan 9 and recently Fried et al. 10,11, obtained super-convergent models by eigen-value convergence analysis for rod, beam and membrane elements in a natural coordinate. The super-convergent mass matrices of elements are developed by using an inverse method, without any shape functions. The properties of these mass matrices have minimum discretization error and superior rate of frequency convergence in respect to their existing mass matrices in the literature. Stavrinidis et al. 12, Ahmadian et al. 13,14 derived super-convergent element formulations by minimizing the discretization errors for several elements in natural coordinates. The drawback in these inverse approaches is that the element model is obtained without specifying the associated shape functions required in transforming the element formulation from local to global coordinates.

To overcome this problem, Kim 8 proposed a method for obtaining shape functions of super-convergent rod element. He used a linear combination of shape functions associated with lumped and consistent mass matrices and adjusted the weighting for each function to achieve the super-convergent finite element model. It is not always possible to attain super-convergent models obtained by inverse approach using Kim's proposal 8. In the case of elements with rotational degrees of freedom such as beam 12 and bending plate elements, the super-convergent models cannot be established with a linear combination of lumped and consistent models.

In this article trigonometric series are used to establish the shape functions for super-convergent models. Trigonometric functions were used as shape functions of Timoshenko beam element 15, and vibration analysis of membranes 16. Shavezipur et al. 17 used trigonometric shape function for analysing non-uniform beams by employing refined dynamic finite element method. Christian 18 used trigonometric shape functions for investigating local buckling of stiffened composite plates. Recently Faroughi et al. 1 obtained shape functions associated with the super-convergent stiffness matrix of membrane element using hierarchical polynomials.

The trigonometric series are employed in this article to establish the shape functions for super-convergent models. The series coefficients are determined such that the obtained finite element model regenerates the super-convergent element formulation. The obtained shape functions must also be physically justifiable and satisfy general requirements of compatibility, and completeness. To demonstrate the proposed method and its efficiency the shape functions for rod and beam super-convergent models are obtained.

The rest of this article runs as follows. In section 2, the essential properties of shape functions are discussed. Theses properties are then enforced in development of shape functions for super-convergent element models. Sections 3 and 4 demonstrate the basic concept of developing shape functions for super-convergent models of rod and beam elements, followed by the concluding remarks in Section 5.

2. Essential properties of shape functions

The quality of approximation achieved by FE approach depends upon the admissible assumed shape functions. These functions are chosen from different base functions such as polynomials and trigonometric functions 16,18. In general these functions must meet certain conditions. These conditions reported in references 19,20 are as follows:

1.	Vertex modes have unit magnitude at one vertex and zero at all other vertices.
2.	Edges modes have magnitude along one edge and zero at all edges and vertices.
3.	Inter-element compatibility and degrees of continuity ().
4.	Completeness condition.
5.	Physical requirements imposed on shape functions, such as rigid body modes, element symmetry axes, etc.

The first four conditions are extensively explained in the literature. The physical requirements are related to the element geometry. The element has some rigid body modes and symmetry axes. The selected shape functions must provide element deformed shapes compatible with the rigid body requirements and these symmetry properties. These essential requirements on the shape functions and the condition regarding their integral products producing the super-convergent model are imposed on selected series to obtain the shape functions corresponding to the super-convergent models. The number of series terms is defined by the number of requirements that must be satisfied.

In the following these requirements are enforced on truncated selected series to obtain the shape functions of one dimensional rod and beam elements.

3. Rod element with trigonometric shape functions

In this section, a super-convergent model of rod is provided to demonstrate the procedures of determining its shape functions. A two-node axial vibration rod element with length L, as shown in Figure 1, is considered. Each node has one degree of freedom and the stiffness matrix, consistent and lumped mass matrices are (1) where E is module of elasticity and A the cross section area, m the mass per unit length of the rod element. The convergence rate of eigen solution using lumped and consistent mass matrices are of the same order and their errors are of order . McNeal et al. 7 and Stavrinidis et al. 12 showed a super-convergent model for rod element can be obtained by averaging of the lumped and consistent mass models (2)

Figure 1. Rod element with natural coordinate.

The mass matrix (2) produces eigen-solutions with the fourth order accuracy and the discretization errors are of order 12. In the literature there is no shape functions associated with the super-convergent model (2). Trigonometric functions may be used to produce shape functions associated with the averaged mass matrix of Equation (2). The following steps should be taken for obtaining shape functions.

The axial displacement field, u, of the rod element is defined as (3) where is the non-dimensional coordinate, and the shape functions of rod element.

The following trigonometric series are selected for the shape function associated with the non-consistent mass matrix of (2) as (4)

The element has one symmetry axis; the shape functions must represent this geometric property. By rotating the shape function about the symmetry axis of element the shape function is obtained. As a result the first term of selected series (4) is considered , (5)

The shape function is determined by using rigid body requirement (6)

The selected series (5) satisfies the first four conditions mentioned in Section 2 provided that (7)

The shape functions and are required to produce the super-convergent mass matrix of (2), i.e. (8)

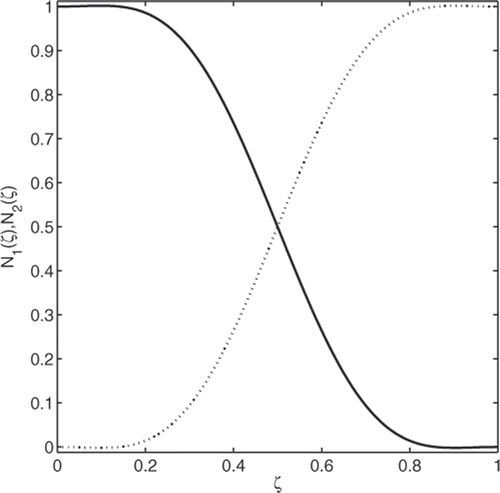
The requirements defined in Equation (8) produce one more quadratic equation and brings the total number of equations regarding the coefficients of the series defined in Equation (5) to two. There are two equations to be satisfied and it is decided to set N = 2. The series coefficients of the trigonometric function of (5) are obtained as (9)

The resulting shape functions are shown in Figure 2. As shown in Figure 2 the shape functions can regenerate the super-convergent model of rod elements. The rod example demonstrates the important steps in obtaining the shape functions of a super-convergent model. The same steps will be followed in the next section to construct trigonometric shape functions for super-convergent model of a beam element.

Figure 2. The shape functions of rod element (—), (- - -).

4. Beam element with trigonometric shape functions

In this article, a two-node transversal vibration Euler–Bernoulli beam element with length L, as shown in Figure 3, is considered. The element has two degrees of freedom at each node; v_i and v_j are the lateral displacements and the rotational displacements.

Figure 3. Beam element DOFS.

The stiffness matrix and its associated consistent mass matrix developed using Hermetical family of shape functions are 2 (10)

The eigen-solution formed using consistent mass matrix produces second order convergence rates in eigen-problem while the super-convergent model leads to a fourth order eigen solution convergence rate 13 (11)

No shape functions associated with the mass matrix (11) are reported in the literature. The steps followed to obtain shape functions of beam super-convergent model is the same as those of rod super-convergent model. First, the displacement field of the element is defined as (12) where N_i is the ith shape function. The element has two rigid body modes which establish the following requirement on the shape functions of the beam element: (13) (14)

The beam shape functions are expressed as the following trigonometric series (15) (16)

The polynomials terms are included in to satisfy the rigid body motion requirements.

The element has one symmetry axis and an applied displacement at one node while the other node is fixed produces an anti-symmetric deformation with respect to the element symmetry axis. This symmetry condition can be expressed in mathematical form as (17) (18)

The selected form for the shape functions in Equation (15) satisfies Equation (17), if the first term of selected series (15) is set to (19)

There are two more requirements that must be satisfied by series defined in Equations (16) and (19) leading to specifications of series coefficients . They are as follows.

1.	The function must be unit at node i and zero at other nodes, i.e.

(20)

This requirement produces a linear relation between the series coefficients.

1.	These functions must produce the entries of beam super-convergent model defined in Equation (11). (21)

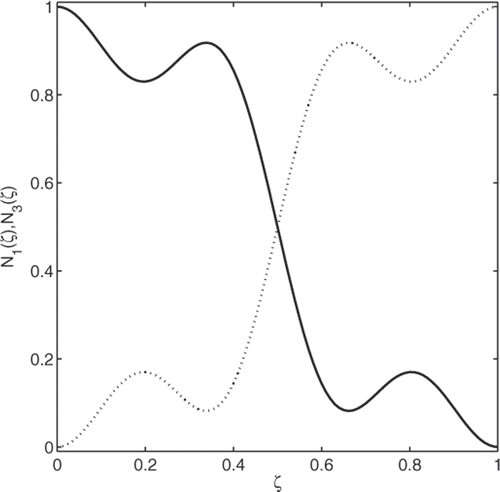
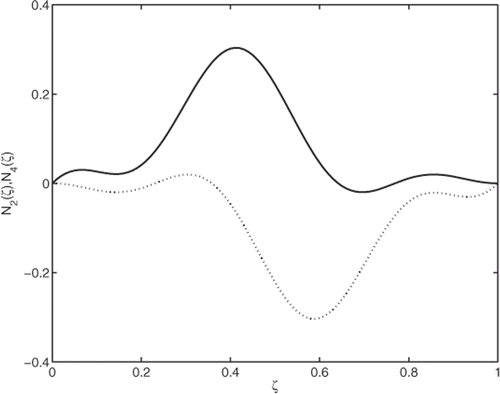
The requirements defined in Equations (20) and (21) produce 12 independent equations to be satisfied. The series coefficients of shape functions are obtained from these equations as (22)

The obtained trigonometric shape functions and of beam super-convergent model are shown in Figures 4, 5. The other two shape functions are obtained by rotation of and about the symmetry axis.

Figure 4. Shape functions of beam element  (—), (- - -).

Figure 5. Shape functions of beam element  (—), (- - -).

These two examples are just presented on how the new methodology can be implemented. The associated shape functions with super-convergent model of any other elements can be obtained using the same strategy. The requirements mentioned in Section 2 are met by each obtained shape functions. The first two requirements are related to boundary conditions. The second requirement is only applied to two and three dimensional elements. The proposed shape functions of the rod and beam elements met the first requirement due to applying Equations (7, 20), respectively. The third and fourth requirements are related to continuity and completeness of element shape functions. The new proposed trigonometric shape functions of rod and beam elements satisfy these requirements. Proposed shape functions of rod and beam elements met the geometric symmetry requirement due to applying Equations (6) and (17, 18), respectively. In order to enforce symmetry properties, only the odd trigonometric terms are used in proposed shape functions.

5. Conclusion

In this article a new method is developed to generate the shape functions associated with super-convergent model obtained by eigen-value convergence analysis, or minimizing the discretization errors. The shape functions are formed using trigonometric functions. The coefficients of the selected series are assigned such that the optimum formulation for the element in terms of its accuracy is achieved in natural coordinates and also the corresponding shape functions satisfy general requirements of compatibility and completeness. The proposed procedure is demonstrated for a super-convergent model of rod and beam elements with and continuity, respectively. Using the proposed method, shape functions can be developed for any super-convergent element formulations such as plate element and membrane element. These super-convergent membrane and plate elements are known to us but the associated shape functions are not defined which limits their applications in modelling structures.