Fast reconstruction of harmonic functions from Cauchy data using the Dirichlet-to-Neumann map and integral equations

Abstract

We propose and investigate a method for the stable determination of a harmonic function from knowledge of its value and its normal derivative on a part of the boundary of the (bounded) solution domain (Cauchy problem). We reformulate the Cauchy problem as an operator equation on the boundary using the Dirichlet-to-Neumann map. To discretize the obtained operator, we modify and employ a method denoted as Classic II given in [J. Helsing, Faster convergence and higher accuracy for the Dirichlet–Neumann map, J. Comput. Phys. 228 (2009), pp. 2578–2576, Section 3], which is based on Fredholm integral equations and Nyström discretization schemes. Then, for stability reasons, to solve the discretized integral equation we use the method of smoothing projection introduced in [J. Helsing and B.T. Johansson, Fast reconstruction of harmonic functions from Cauchy data using integral equation techniques, Inverse Probl. Sci. Eng. 18 (2010), pp. 381–399, Section 7], which makes it possible to solve the discretized operator equation in a stable way with minor computational cost and high accuracy. With this approach, for sufficiently smooth Cauchy data, the normal derivative can also be accurately computed on the part of the boundary where no data is initially given.

Keywords:

• alternating method
• Cauchy problem
• Dirichlet-to-Neumann map
• Laplace equation
• second kind boundary integral equation

AMS Subject Classifications:

• 35R25
• 65N20
• 65N35
• 31A10
• 31A05

1. Introduction

The stable reconstruction of a harmonic function from given Cauchy data is a problem of fundamental importance in many engineering applications in fluid and heat flow, such as in non-destructive testing and tomography (see, e.g. 1–5). The governing model is the Laplace equation with overspecified data given on a part (arc) of the boundary of the solution domain in the form of the solution and its normal derivative; the solution u satisfies (1) We assume here that Ω is a planar bounded Lipschitz domain in R² with Γ_C an (open) arc of the boundary Γ = ∂Ω, and define . The element ν is the outward unit normal to the boundary Γ. On the boundary part Γ_U, the solution and its normal derivative are unknown and have to be reconstructed. We assume that the given Cauchy data f_C and g_C are sufficiently smooth and compatible such that there exists a solution u. Note that uniqueness of the solution is well established (see, e.g. 6,7). It is well-known that the Cauchy problem (1) is ill-posed and thus measurement errors in the data can completely destroy the reconstructions unless regularizing methods are employed.

Reconstruction of u in (1) is a classical problem and there are therefore many different numerical methods in the literature for its solution, some are listed in 8. Kozlov and Maz'ya 9,10 proposed the alternating method, which is an iterative procedure for the reconstruction of the solution u. This method preserves the governing Laplace operator and the regularizing character is achieved by appropriate change of the boundary conditions. The alternating method has successfully been employed to several applied problems (see, e.g. 11–24. However, in most studies it has been reported that this procedure can be time-consuming and that non-accurate reconstructions of the normal derivative are obtained. There are more involved methods that can be more efficient 25,26.

Recently, in 27, the authors of this article investigated ways of implementing the alternating method to speed up convergence and minimize the computational cost. The authors took advantage of the reformulation of the alternating method in terms of an operator equation on the boundary, together with a recent integral equation method 28,29. Inspired and encouraged by those results, we reformulate the Cauchy problem as another operator equation on the boundary. In the literature, the most straightforward reformulation based on the Dirichlet-to-Neumann map seems to have been overlooked and we therefore present this reformulation in this article and shall compare the obtained results with those in 27. Note that, however, a method in this direction was given in 30, where the Cauchy problem (1) was discretized using the boundary element method, and the corresponding linear system of equations was regularized using various techniques including Tikhonov regularization. Moreover, there is also a recent investigation on an effective way to numerically implement the Dirichlet-to-Neumann map 28, making our present approach for the Cauchy problem timely. We point out that our focus is to produce a fast method that is straightforward to implement and has high accuracy. The obtained approximation could perhaps then be used as a priori information for methods given in 8,9.

To discretize the obtained operator, we modify and employ a method denoted as Classic II given in 28, Section 3]. This method was originally given to compute the Dirichlet-to-Neumann map on the boundary of a two-dimensional domain exterior to a single contour, and is based on Fredholm integral equations and Nyström discretization schemes. We outline how to adjust the method to our case. Then, for stability reasons due to the ill-posedness of the Cauchy problem (1), to solve the discretized integral equation we use the method of smoothing projection introduced in 27, Section 7], which makes it possible to solve the discretized operator equation in a stable way with minor computational cost and high accuracy.

This article is organized as follows. In Section 2, we present the reformulation of the Cauchy problem and point out some properties of the Dirichlet-to-Neumann map and its relation to the Poincaré-Steklov operator. In Section 3, geometry and parameters for the numerical investigations are presented. The numerical method for the discretization of the operator from Section 2, based on Fredholm integral equations and Nyström discretization schemes, are given in Section 4. In Section 5, we show how to numerically construct the solution and its normal derivative on Γ_U, and give some numerical results including noisy data. Conclusions are found in Section 6.

2. Reformulation of the Cauchy problem (1)

2.1. The Dirichlet-to-Neumann map

Let L²(Ω) be the standard L²-space with the standard norm. As usual, H¹(Ω) is the Sobolev space of real-valued functions in Ω with finite norm given by the relation , where .

For trace spaces, we recall that the space of traces of functions from H¹(Ω) on Γ is H^1/2(Γ). Restrictions of elements in H^1/2(Γ) to the boundary part Γ_C (Γ_U) constitute the space H^1/2(Γ_C) (H^1/2(Γ_U)).

We then recall some facts about the Dirichlet-to-Neumann map, for the proofs we refer to 31. Given f ∈ H^1/2(Γ), the Dirichlet problem (2) has a unique solution in H¹(Ω). Moreover, the normal derivative g = ∂u/∂ν of u on Γ is well-defined as an element in the dual space H^−1/2(Γ). The operator D that maps f to g is a bounded operator denoting the Dirichlet-to-Neumann map. Furthermore, (3) where is the duality pairing between the space H^1/2(Γ) and H^−1/2(Γ) induced by the scalar product in L²(Γ). For connections between the Dirichlet-to-Neumann map and the Poincaré-Steklov operator, see 32,33.

2.2. Reformulation of (1)

To reformulate problem (1), we use restrictions of the Dirichlet-to-Neumann map to the respective boundary part. First, let the operator A_CU be defined such that A_CU f_U is the normal derivative on Γ_C of the solution to (4) Similarly, let A_CC be defined such that A_CC f_C is the normal derivative on Γ_C of the solution to (5) Then the Cauchy problem (1) is equivalent to solving the following operator equation on the boundary: (6) The corresponding operator equation obtained in 27 was derived using mixed boundary value problems instead of the above ones which only have a Dirichlet condition imposed.

Note that in both these problems (4) and (5), we possibly have discontinuous Dirichlet data. Thus, suitable spaces for the data are then the corresponding L²-spaces on the respective boundary part, and the corresponding solution will then be in L²(Ω). The normal derivative on Γ_C in (4) has meaning since local regularity results for elliptic equations clearly imply that u has, locally, derivatives of second order near Γ_C due to the zero Dirichlet condition imposed on Γ_C. Similarly, since we assumed that Cauchy data in (1) is sufficiently smooth, the normal derivative on Γ_U exists in (5).

Now, it is straightforward, using the pairing (3), to obtain the following theorem.

Theorem 2.1

The adjoint operator of A_CU is defined by where u is the solution to (5).

With knowledge of the adjoint operator, we can then, for example, employ Tikhonov regularization to (6) and obtain a stable approximation f_U,λ from Alternatively, iterative methods, such as the Landweber–Fridman or conjugate gradient methods can be employed to solve (6). However, since our focus is to develop a fast method that is straightforward to implement and has high accuracy, to solve (6) we shall instead employ a recent method based on smoothing projections that was introduced in 27, Section 7].

Provided data is smooth enough, the normal derivative, g_U, also exists on Γ_U of the solution to the Cauchy problem (1). To construct it, let A_UU f_U be the normal derivative of the solution to (4) on Γ_U, and let A_UC f_C be the normal derivative of the solution to (5) on Γ_U. Then (7) Note that from Theorem 2.1, we have .

3. Configuration for the numerics

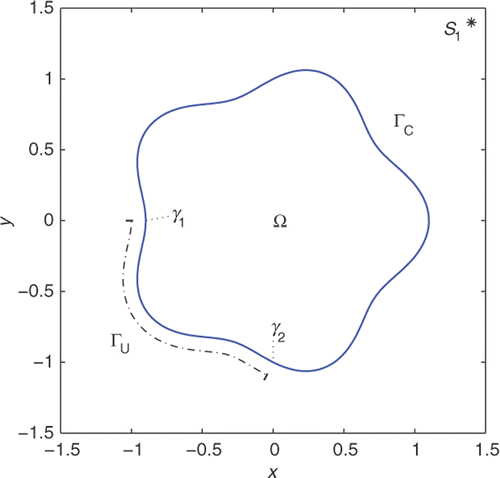
To compare results, we shall use the same configuration as in 27 and recall its definition below. We make no distinction between points in the real plane R² and points in the complex plane C, thus all points are denoted z or τ. The solution domain that we use for the numerical experiments is a bounded domain enclosed by a curve with the parameterization (Figure 1) (8) Note that this geometry is not trivial since its curvature is varying. The two arcs Γ_U and Γ_C are defined by (9) and the closure of these parts have two points in common, γ₁ = τ(π) and γ₂ = τ(−π/2). The Cauchy data is generated from the harmonic function (10) where S₁ = 1.4 + 1.4i (Figure 1).

Figure 1. The solution domain Ω with boundary Γ = Γ_U ∪ Γ_C given by (8) and (9). The arcs Γ_U and Γ_C meet at the two points γ₁ and γ₂. A total of 256 discretization points are constructed on Γ, 64 of which are located on Γ_U. A source S₁, for the generation of Cauchy data via (10), is marked by ‘*’.

All numerical experiments presented are performed in MATLAB version 7.9 and executed on an ordinary workstation equipped with an Intel Core2 Duo E8400 CPU at 3.00 GHz.

4. Discretization

We discretize problem (1) via the reformulation in Section 2.2 using a variant of an integral equation scheme originally designed for the fast and accurate computation of the Dirichlet-to-Neumann map on the boundary of a two-dimensional domain exterior to a single contour. The original scheme is denoted as Classic II in 28, Section 3], and we now briefly review the main steps of our variant of that method.

The solution u(z) is represented in terms of an unknown layer density ρ(z) on Γ via a double-layer potential. Enforcing Dirichlet boundary conditions f(z) on Γ leads to a Fredholm second kind integral equation (11) where the action of the compact integral operator k on ρ(z) is given by (12)

Once (11) is solved for ρ(z), the normal derivative of u(z) at Γ can be computed by applying a Cauchy-singular integro-differential operator K to ρ(z) (13) The action of K on ρ(z) is given by (14) where the differentiation ρ′(z) = dρ(z)/dz is along the tangent to Γ and ν(z) is the outward unit normal to Γ at z.

We discretize the operators k and K using a Nyström scheme based on the composite trapezoidal quadrature rule. We use 256 discretization points on Γ, of which the 64 first points are located on Γ_U and the remaining 192 points are located on Γ_C. The Cauchy-singular integral in (14) is to be interpreted in the principal value sense and we use the method denoted global regularization in 29 to achieve this. The Fast Fourier Transform, carried out with MATLAB's built-in functions fft and ifft, is used for differentiation. The discretization results in two square matrices k and K, both of dimension 256 × 256.

Now define the matrix A as the composition (15) where I is the identity matrix. Clearly, A is a discretization of the Dirichlet-to-Neumann map given in Section 2.1, and if we let f and g be column vectors containing the values of u(z) and ∂u(z)/∂ν at the discretization points we have (16) On partitioned form, where we have separated points on Γ_C from points on Γ_U, this relation reads (17) Thus, in order to get the discretizations of the operators A_UU, A_UC, A_CU and A_CC defined in Section 2.2, one only has to pick the appropriate blocks from the matrix A in (16) via (17). Computing all the entries of A takes about 0.03 s on the workstation mentioned in Section 3.

5. Solving for f_U and g_U

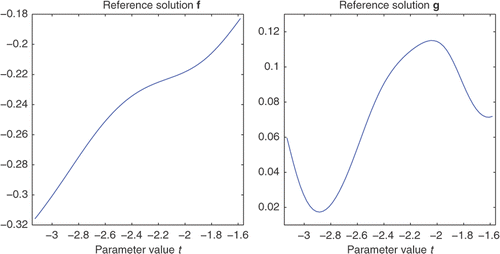
Now that we have access to the discretized operators A_UU, A_UC, A_CU, A_CC, as well as the known data f_C and g_C, it is easy to solve the discretized counterpart of (6) for f_U and subsequently use the discretized counterpart of (7) for g_U. We concentrate on the setup detailed in Section 3. The reference solutions, that is, the correct analytical values for f_U and g_U are shown in Figure 2.

Figure 2. Reference solutions f and g on Γ_U for the problem detailed in Section 3.

Rather than using (6) as it stands, we shall, for stability reasons, use the method of smoothing projections introduced in 27, Section 7]. We represent f_U in terms of n coefficients in a monomial basis on the canonical interval [−1, 1] (18) where V_n is a 64 × n Vandermonde matrix. Thus, we first solve (in the least squares sense) the 192 × n overdetermined linear system (19) for the unknown . Then we use (18) to obtain f_U. 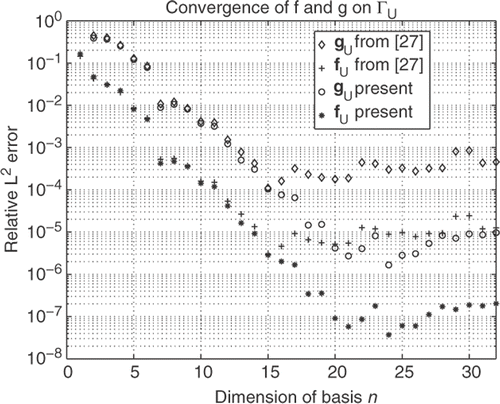Finally, we compute g_U from (20) Doing this for n = 1, 2, … , 32, takes an additional 0.01 s on the workstation mentioned in Section 3. The excellent quality of the reconstruction is shown in Figure 3. Comparing with Figure 7 in 27 shows an improvement in achievable accuracy with between one and two digits. To further illustrate this and to make it easier to compare, the results from Figure 7 in 27 are also included in Figure 3.

Figure 3. Clean (no noise) Cauchy data f_C and g_C. Convergence of the reconstructions f_U and g_U with the dimension n of the monomial basis onto which f_U is projected. Equations (18)–(20) are used (present). For comparison the corresponding results obtained with the method from 27 are included.

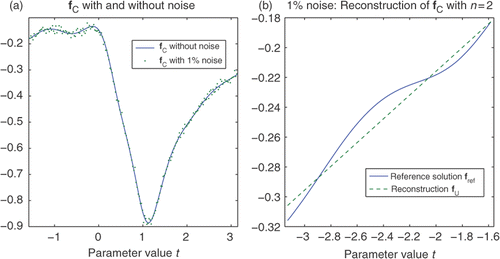
It is also of interest to add noise to the Cauchy data to verify the stability of the method. Naturally, the more noise that is added, the less accurate the reconstruction will be. Furthermore, the quality of the reconstruction varies between realizations and if a very large number of points are sampled on Γ_C, one could try filtering the Cauchy data to reduce the noise. Here, we shall ignore such issues and simply add Gaussian noise with mean zero and standard deviation to f_C. The element f_C and the corresponding noisy data are shown in Figure 4(a), no noise is added to g_C. As it turns out, a low degree basis with n = 2 for f_U most often gives the best reconstruction at this high level of noise. A typical example is shown in Figure 4(b). The reconstruction of the derivative is more inaccurate as expected.

Figure 4. (a) Given clean (no noise) data f_C in (1) and the corresponding noisy data. (b) Reconstruction of f_U via (19) and (18) for n = 2 and noisy data.

6. Conclusion

We have proposed and investigated a method for the stable reconstruction of a harmonic function from Cauchy data. The aim was to produce a fast method that is straightforward to implement and has high accuracy. To achieve this, the Cauchy problem was rewritten as an operator equation on the boundary using the Dirichlet-to-Neumann map. To discretize the obtained operator, we modified and employed a method denoted as Classic II in 28, Section 3]. This method was originally given to compute the Dirichlet-to-Neumann map on the boundary of a two-dimensional domain exterior to a single contour, and is based on Fredholm integral equations and Nyström discretization schemes. For stability reasons, to solve the discretized integral equation, we used the method of smoothing projection introduced in 27, Section 7], which makes it possible to solve the discretized operator equation in a stable way with minor computational cost and high accuracy. A numerical example was investigated in a bounded domain having a non-trivial boundary (curvature is varying). Comparing with the numerical results in 27 and using the proposed approach, we obtain a higher accuracy in the reconstructed function values and normal derivatives of between one and two digits. Stability against noise in the data was also investigated, showing that a stable solution can be obtained with increasing accuracy as the noise is decreasing. Moreover, the present approach is more efficient and faster, and also more straightforward to implement requiring a small amount of computer code.

Acknowledgements

J. Helsing was supported by the Swedish Research Council under the contract 621-2007-6234.