Iterative prescription refinement in fully discretized inverse problems of radiation therapy planning

Abstract

We formulate the method of iterative prescription refinement for inverse planning in any fully discretized model of radiation therapy. The method starts out from an ideal dose prescription and repeatedly refines it into a refined dose prescription. This is done computationally without human interaction until a prespecified stopping rule is met, at which point the refined dose vector and the accompanying beamlet intensities vector are evaluated and presented to the planner. The algorithmic regime is general enough to encompass various physical models that may use different particles (photons, protons, etc.) It is formulated for a general inversion operator thus different objective functions or approaches to the optimization problem (such as DVH, gEUD, or TCP and NTCP cost functions) may all be applied. Although not limited to this model, we demonstrate that the approach at all works on two exemplary cases from photon intensity-modulated radiation therapy.

Keywords:

• inverse problem
• iterative prescription refinment
• iterative data refinment
• radiation therapy
• fully discretized model

1. Introduction and problem definition

Radiation therapy treatment planning (RTTP) is basically an inverse problem but of a nature that sets it apart from other inverse problems in science and technology. Many inverse problems are data-inversion problems. By this we mean that there is a relation of the form Qx = b where b is a vector of measured data, which cannot be changed once the measurements have been performed, the vector x is the object that needs to be recovered, and Q is an operator that represents our knowledge of the physics of the situation that relates the measurements to the object that was measured. There are some fundamental deviations from this in the inverse problem of RTTP. First, in RTTP the right-hand side b is not fixed throughout like in a data-inversion problem but is a prescription vector that might be modified if the planner does not like to accept, for some reason, the recovered object x. This property justifies us in dubbing the inverse problem of RTTP as a prescription-inversion problem. Second, the operator Q cannot be inverted mathematically, without major compromise on its realism, therefore, a fully discretized approach must be taken and not a continuous model of the physical situation. For a discussion of this matter, see, e.g. 1,2. General review and tutorial papers on RTTP from various aspects are abound. Some of the more mathematically algorithmically oriented reviews are 3–6.

There is yet another important aspect to the prescription-inversion problem in RTTP that sets it apart from conventional data-inversion inverse problems. The inversion method itself requires information-input from the planner, which will, in turn, affect the resulting recovered object x. Let us agree, for the purpose of this article, to use the term ‘inversion method’ as an overall term that consists of the union of the following ingredients: (1) the chosen mathematical model, (2) the chosen objective (cost) function (if an optimization model is used), (3) the choice of algorithm employed and (4) the specification of all parameters necessary to run the algorithm on the chosen cost function for the chosen model. Now, if the ‘inversion method’ is applied to some prescribed right-hand side vector b and if the resulting recovered object x (e.g. beamlets intensities in intensity-modulated radiation theraphy (IMRT)) does not satisfy the planners goals then the planner is confronted with a dilemma. He can either ‘revise’ his original prescribed right-hand side vector b or insist on that b as originally prescribed. In the latter case some changes must be made to the information-input for the ‘inversion method’ itself before running it again, because otherwise (i.e. same b and no changes to the ‘inversion method’) there will be no new alternative recovered object x obtained for the planner's assessment.

Just to make the above more concrete, think – by way of example only – about an inversion method in which a weighted sum of several cost functions, associated with specific organs, has to be minimized via some optimization algorithm or package. An example of changing the information-input to the ‘inversion method’ might be changes to the coefficients (weights of importance) given in the weighted sum cost function. The difficulty is manifold: it is not simple or clear how such changes should be made, they might be done repeatedly several times, and, most importantly, they require the planner's human involvement.

Our goal in this article is propose a methodology to handle the above situation. The proposed approach and procedure are not limited to IMRT or to the specific objective function used in the examples, but is applicable to ANY fully discretized model of prescription-inversion. The mathematical background and connection with another method from medical imaging, offered here, puts the whole approach on more secure foundations (in spite of the admitted, still remaining, questions even in the math of the procedure). The case examples are presented only to demonstrate that the approach and method ‘work’ at all. More efforts might be needed in any specific area where this will be employed to fine-tune the method to reach computational advantages. To these ends we formulate a method, that we call iterative prescription refinement (IPR), for inverse planning in any model of RTTP that is fully discretized. IPR is not limited to IMRT or to a specific choice of objective functions for optimization. It is a general principle that is applicable to any fully discretized model of an inversion problem that might occur in RTTP, or even in prescription-inversion problems outside RTTP. It puts forward and identifies an approach, not considered hitherto, that replaces the currently commonly used sequence of steps in RTTP by a different one which attacks the problem from a different angle. The method should start out from an ideal dose prescription (ideal in the sense that it is most probably not deliverable) and repeatedly refines this prescription into a refined dose prescription. This is done computationally without human interaction until a prespecified stopping rule is met, at which point the refined dose vector is ready to be evaluated by the planner. The purpose is to circumvent in this way the inevitable ‘imperfections’ of the inversion operator that is employed in the solution process of the inverse problem. This will be further clarified below.

The algorithmic regime is general enough to encompass various physical models that may use different particles (photons, protons, etc.) and/or model the problem mathematically in one of several possible different ways.

1.1. The fully discretized model

We consider the following fully discretized model in RTTP which has its early roots in 1. There are J voxels in total in the cross-section. A dose vector is where d_j is dose in voxel j. (observe the ‘notational rule’ to use superscripts to count vectors and subscript to count vector components). There are N recognized organs (counting both targets and organs at risk (OARs)) in the cross-section, denoted by their voxel sets O₁, O₂, … , O_N. A dose vector d is partitioned accordingly into subvectors (1) where is a subvector of d that contains the doses in only the voxels of organ O_i.

There are T external radiation beamlets, counted by t = 1, 2, … , T, in total, and is a vector of beamlet intensities such that x_t is the intensity of beamlet t. We partition the J × T dose matrix A accordingly, so that, (2) namely A_ix = d ⁱ for all i = 1, 2, … , N. The dimensionality of the submatrix A_i is ∣ O_i∣ × T where ∣ O_i ∣ is the cardinality of O_i, i.e. the number of voxels in organ O_i. The, now classical, see, e.g. 2, inverse problem of RTTP is to find an intensities vector x that will deliver to the patient's cross-section a prescribed dose vector d, for a given patient data and for a given particle model and available treatment machine setup.

1.2. The problem

We assume that ℛ is an operator that represents some given ‘inversion method’ as an overall term that consists of the union of the following ingredients: (1) the chosen mathematical model, (2) the chosen objective (cost) function (if an optimization model is used), (3) the choice of algorithm employed and (4) the specification of all parameters necessary to run the algorithm on the chosen cost function for the chosen model, for the inverse problem of a fully discretized RTTP problem, such as, but not necessarily only, photon IMRT. By this we mean that ℛ : R^J → R^T (i.e. it maps the J-dimensional Euclidean space R^J into R^T). This operator takes a dose vector d ∈ R^J and outputs an intensity vector x = ℛ(d) that supposedly will create the dose distribution d when applied in the clinic to the treatment case whose parameters were used in the inversion with ℛ. Therefore, we call ℛ an inversion operator.

We further assume that 𝒟 : R^T → R^J is a ‘state-of-the-art’ forward dose calculation package that is available to us. It takes any intensity vector x ∈ R^T and outputs a dose vector d = 𝒟(x) that supposedly will be created by that x, when applied in the clinic to the treatment case whose parameters were used in the inversion with ℛ. Therefore, we call 𝒟 a dose operator. The difficulties associated with both the forward and inverse problems in IMRT stem from the fact that to this date there exists no, realistically adequate, closed-form analytic representation of the dose operator 𝒟. Although the interaction between radiation and tissue is measured and understood at the atomic level, the situation is so complex that, to solve the forward problem in practice, a state-of-the-art computer program (i.e. a sufficiently accurate dose calculation engine), which represents a computational approximation of the operator 𝒟, must be used.

Denote by d ^pres a vector of prescribed doses to voxels, for a given treatment case. If ℛ and 𝒟 were perfect (ideal), i.e. representing the model perfectly, applying the inversion method without any errors (numerical or others) and performing a perfect forward dose calculation, respectively, then the composition of the ideal inversion operator ℛ and the ideal dose operator 𝒟 should return the input, i.e. 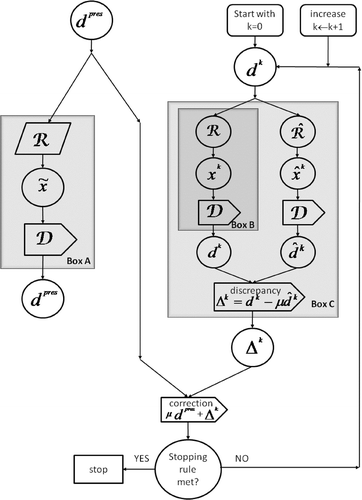(3) In this case ℛ(d ^pres) would be an intensity vector that will deposit precisely d ^pres as prescribed, see Box ‘A’ in Figure 1. Let us call such ℛ and 𝒟 ideal operators and note that if (3) holds for all d ^pres then 𝒟ℛ = ℐ, where ℐ stands for the identity operator that leaves any vector to which it is applied unchanged.

Figure 1. Outline of the IPR procedure.

In the real world we have at our disposal only approximations of the ideal operators ℛ and 𝒟, let us denote them by and and call them actual inversion and actual dose operators, respectively. So, in the real world, applying the composition of operators to a dose vector does not return the vector to which it is applied, namely, (4) meaning that the dose vector deposited by the intensity vector will differ from the prescribed dose vector d ^pres.

It is our purpose in this study to address only imperfections of the actual inversion operator (and not of the actual dose operator ). Therefore, we assume from this point onward that is an ideal dose operator which is also actual, thus available to us.

1.3. The usual approach

The usual approach to cope with the discrepancy between the prescribed dose d ^pres and the actually deliverable dose obtained from (4), consists basically of the following actions performed in the given order: (1) perform the inverse planning with the actual inversion operator (according to some given model and solution method), (2) apply the dose operator and show the resulting dose vector and its various derivatives (e.g. isodose map, dose-volume histogram (DVH), etc.) to the planner, (3) if the results do not satisfy the planner's clinical goals, change parameters in the actual inversion operator and repeat the process (i.e. go back to (1) above). For example, if represents a minimization of a linear combination of some individual cost functions for various organs, then a commonly used ‘change of parameters’ is to change the coefficients in the linear combination of individual cost functions that is being minimized. These coefficients reflect the relative importance attributed by the planner to minimizing the individual cost functions, each of which is usually related to one organ (target or OAR). Then the, so revised, actual inversion operator is applied again and the new resulting actually deliverable dose is evaluated for the case at hand, say, via observation of the DVHs. This process demands continuous and repeated involvement of the treatment planner and it is stopped only when the latter accepts a clinically acceptable treatment plan presented to him, even if it sometimes deviates from the original prescription that he gave initially.

The main difficulty with this approach seems to lie not so much in the repetitious application of the actual inversion operator . This repetitious application is a technical problem that can be addressed by hardware acceleration via more powerful computer and/or parallel computations such as on general purpose graphics processing units (GP-GPUs). The main difficulties with this approach are twofold: (i) the need to repeatedly and manually evaluate the resulting actual dose and, even more fundamentally, (ii) since the overall process is a ‘search process’ and the options for changing parameters in the actual inversion operator are numerous, it is far from clear or simple how to change the parameters each time the resulting dose distribution does not yet meet the clinical requirements.

2. The IPR method

To circumvent the difficulties mentioned above, we examine here, instead of the traditional approach, an iterative process by which the final refined dose is reached by iteratively refining and steering a given ideal dose prescription vector. Repeated applications of the operator are still used but instead of doing parameter changes inside that require manual intervention and are not always known how to perform, is used without changes and the method itself keeps reducing the discrepancy between the current refinement of the dose vector and the original ideal prescription.

2.1. The method

The method, which we call IPR, iterates on dose vectors. The procedure is outlined in Figure 1. Box ‘A’ depicts the not achievable situation of (3). If we had (i.e. if we knew and could implement) the ideal inversion operator ℛ we could have calculated the desired intensity vector This not being the case, we propose to resort to the IPR procedure depicted on the right-hand side of Figure 1. The aim is to generate a sequence of intensity vectors such that the dose vectors deposited by them get closer, or as close as possible, to d ^pres. As we show below, this aim can be achieved by the IPR procedure.

No work needs to be done to implement what is in Box ‘B’ because, by 𝒟ℛ = ℐ, its input and output are identical. The right-hand side within Box ‘C’ uses the actual inversion operator to generate from which is obtained by The discrepancy vector is then added to μd ^pres, where μ is a user-chosen relaxation parameter, to generate the next refined dose vector d ^k+1 and so on, until some predefined stopping rule applies, see the algorithm below.

Algorithm 1 Iterative Prescription Refinement

Initialization Choose d ⁰, a very reasonable choice is d ⁰ = d ^pres and choose a relaxation parameter real number μ.

Iterative step Given the current prescription dose vector iterate d ^k, k = 0, 1, 2, … ,

1.	Calculate the k-th intensity vector by applying the actual inversion operator (5)
2.	Calculate the dose vector that will be obtained from by applying the dose operator 𝒟 (6)
3.	Calculate the dose discrepancy vector Δk (7)

(4) Calculate the next prescription dose vector iterate d ^k+1 by (8)

Stopping rule Stop the process by applying some stopping rule.

2.2. Analysis of the IPR procedure

The IPR method can be mathematically identified (with appropriate nonessential changes of notations dictated by the problem at hand here) with the iterative data refinement (IDR) method of 7, see also [8, Section 10.5] and 9, pp. 90, 99]. This method has been developed in medical imaging to cope with difficulties stemming from discrepancies between idealized and actual measuring devices in models of image reconstruction from projections. It has been found useful for beam hardening correction in computerized tomography, for attenuation correction in single photon emission computed tomography (SPECT) and in image reconstruction with incomplete data, see [7, Section 2]. It was further used for magnetic resonance imaging, see 10,11. Recently it has been used for transfer function restoration in 3D electron microscopy by Sorzano et al. 12, and in positron emission tomography (PET) by Crepaldi and De Pierro 13.

Comparing IDR with the IPR outline proposed here the necessary adjustments to the IDR which yield the IPR and the identification of quantities can be observed as follows. The ‘idealized measuring device’ and the ‘actual measuring device’ that appear in the IDR scheme are of no use here because what is there the measurement vector y is here a prescription vector d that is not at all measured, but prescribed. IPR aims to overcome imperfections of the inversion operator (not of the measuring device, as in the IDR). The correspondence between quantities in each of the two procedures is given in the table.

Exploiting this homomorphism enables us to ‘translate’ some statements and thus shed light on the algorithmic behavior of IPR. This can be done in the following manner.

Definition 2

IPR associates with every 4-tuple (d ^pres, d ⁰, 𝒰, μ), where 𝒰 : R^J → R^J is an operator that maps dose vectors onto dose vectors, μ is a real number, and d ^pres and d ⁰ are vectors in R^J, a sequence generated by (9)

The quantities and notations identifications in the table show that IPR is indeed a special case of IDR, and, in particular, that our (9) coincides with (1) of 7. Specifically, focusing on the IPR process depicted in Figure 1 and described by Algorithm 1, we actually use the operator (10) thus 𝒰(d ^k) = Δ^k. Now that the connection between IPR and IDR is established, the results of the mathematical analysis of 7 are applicable. The interested reader is referred to 7 for this mathematical contents. In particular, Proposition 8 in 7 (also refer 8, Section 10.5]) translated to the IPR procedure, guarantees, generally speaking, that under the conditions set forth there, one of the following two possibilities must happen:

i.

Asymptotic convergence of the sequence of refined dose vectors d k to the prescribed dose vector d pres, as k goes to infinity, i.e. limk→∞d k = d pres, or

ii.

there exists an index k0 such that are all in a certain set (denoted Gβ in 7), and (11) where is the distance from d pres of the point in which is nearest to d pres. is the component of Gβ which contains d 0. For practical reasons (explained in 7, p. 116]) it seems that the convergence option (i) is unlikely and the most that we could hope for is (ii). The meaning is that, provided that d 0 ∈ Gβ, improvement is guaranteed by (11) all along and up to a certain iteration index k0. Not having a constructive way of finding this index ahead of time, one must rely on experiments to demonstrate that this initial improvement actually occurs. The situation (ii) is not uncommon for ill-posed problems. The phenomenon is often referred to as semi-convergence, see, e.g. 14.

3. A demonstration of IPR in photon IMRT

To illustrate the IPR method, we have generated IMRT treatment plans for two clinical head and neck cases in the following manner. We emphasize that the case examples are presented only to demonstrate that the approach and method ‘work’ at all. More details about the experimental work that leads to the following can be found in 15. Further efforts might be needed in any specific area where this will be employed to fine-tune the method to reach computational advantages. First, we have calculated the dose matrix A from a patient's CT scan using Computational Environment for Radiotherapy Research (CERR) 16 and the Voxel-based Monte Carlo (VMC)++ Monte Carlo package optimized for radiation treatment planning 17 in MATLAB on a PC with 2.66 Core 2 Duo CPU and 3.25 GB of RAM. To reduce computational time we have downsampled the original CT voxel size by a factor of 4 in the xy-plane. No downsampling in the z-direction was used. Next, we have obtained an optimal fluency map as a solution of the inversion problem . This was done in MATLAB using MOSEK 18 optimization software 19. The MOSEK Optimization Software is designed to solve large-scale mathematical optimization problems. It provides specialized solvers for linear problems, conic quadratic problems, convex quadratic problems, general convex problems and mixed integer problems. No specific regularization is used in the MOSEK package. However, it may happen that some optimization problem with regularization can be reformulated as a quadratic programming problem (see, e.g. Appendix A of Zhu et al. 20) or the problem mentioned above. The reformulated problem may then be efficiently solved using MOSEK. The resultant fluency map was converted into a 3D dose distribution using the dose matrix A. To characterize and compare different dose distributions we have calculated corresponding DVHs and isodose curves.

To demonstrate that the IPR method works we have generated two plans for each clinical case. The first plan is a standard plan, without IPR, with the prescription set to its ideal values – 100% to the target and 0% to OARs. The second plan is a realization of the proposed the IPR method with the number of model iterations set to 5. The plans were compared using DVHs and 3D dose distributions plotted in MATLAB using CERR package.

The iterative calculation has two parts here: first, for a given set of prescription, the optimization finds the corresponding solution via an iterative process and this typically takes 20–30 iterations. Second, after the above iterative calculation is done, we modify the prescription in such a way that the dose inhomogeneity in the PTV and the high doses in the sensitive structures can be reduced. After the prescription is changed, the optimization described above (inner-loop optimization) is performed again. We found that after 4–5 changes of the prescription, the final solution saturates and any further change of the prescription does not improve the quality of the treatment plan any more. Considering the inner-loop optimization, the total number of iteration for 5 sets of prescription is roughly 100–150. The computational time for 150 iterations on a PC with 3 GHz CPU is roughly 10–15 min.

In this work, the beamlet kernels for unit beamlet intensity were pre-computed by using the VMC algorithm 21 after the treatment beam configuration was determined. The total dose at a point is a sum of all the contributing beamlets weighted by appropriate intensities resulted from the optimization.

3.1. Case I

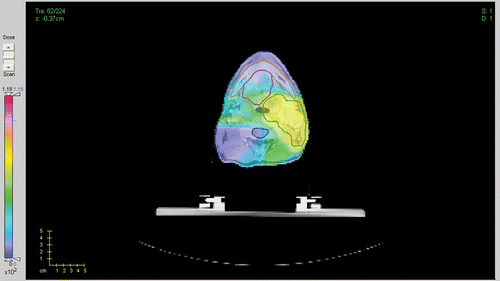
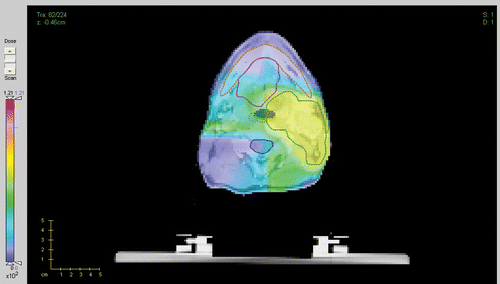
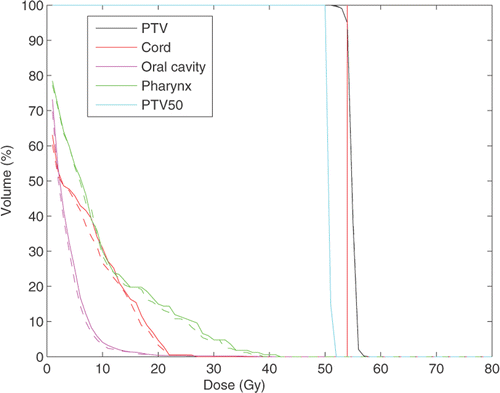
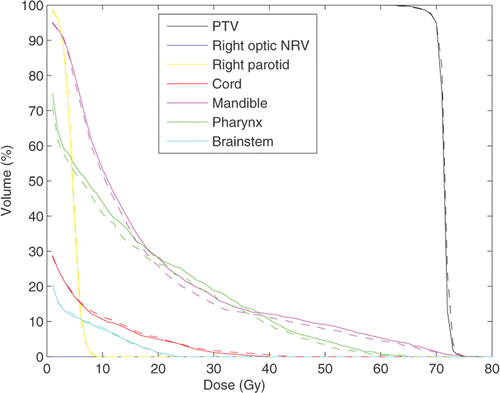
For the first clinical case we used treatment geometry with 7 beams at 0°, 40°, 80°, 90°, 120°, 180° and 270°, represented by a total of 2384 beamlets. The total number of voxels in all structures including all targets is 256 × 256 × 224. We compare treatment plans by plotting corresponding DVHs. Our figure of merit is a plan with the fixed ideal prescription. In Figure 2, we compare DVHs for the fixed and iterative prescription refinement (after 5 iterations) plans for different structures. We see that, while the target coverage is comparable for both plans, there is a reduction in the delivered dose to the mandible and pharynx for the iterative prescription plan. To run a more detailed comparison of the plans we have plotted correspondent 3D dose distributions for a fixed slice of the patient's anatomy. The resultant colour dose maps and organ outlines are depicted in Figures 3 and 4.

Figure 2. DVH comparison for the fixed ideal prescription and IPR plans. Solid lines represent the fixed prescription dose plan. Dashed lines correspond to the IPR plan. The plans are normalized such that 95% of the PTV receives 100% of the prescription dose (70 Gy). (Available in colour online.)

Figure 3. Dose map for the fixed prescription plan. Colours correspond to different doses (left slider). The PTV is outlined with the green dotted line. The cord, mandible, pharynx and oral cavity are outlined with the blue, orange, light green and purple lines. (Available in colour online.)

Figure 4. Dose map for the IPR plan. Colours correspond to different doses (left slider). The PTV is outlined with the green dotted line. The cord, mandible, pharynx and oral cavity are outlined with the blue, orange, light green and purple lines. (Available in colour online.)

3.2. Case II

For the second case we chose a slightly different beam geometry with 7 beams at 30°, 55°, 95°, 130°, 150°, 170° and 210°, represented by a total of 3490 beamlets. The total number of voxels in all structures is 169 050. As in the previous case, we compare a treatment plan generated with the IPR method to a standard fixed prescription plan. Figure 5 shows the comparison for different structures. We observe that both plans are identical in the PTV dose coverage for both the primary PTV and the secondary PTV (50 Gy). PTV stands for planning target volume, which is defined to select appropriate beam sizes and beam arrangements, taking into consideration the net effect of all the possible geometrical variations and inaccuracies in order to ensure that the prescribed dose is actually absorbed in the clinical target volume (CTV). Its size and shape depend on the CTV but also on the treatment technique used, to compensate for the effects of organ and patient movement, and inaccuracies in beam and patient setup, see 22. The cord, the pharynx and the oral cavity enjoy a slight dose reduction in the case of the IPR plan.

Figure 5. DVH comparison for the fixed ideal prescription and IPR plans. Solid lines represent the fixed prescription dose plan. Dashed lines correspond to the IPR plan. The plans are normalized such that 95% of the PTV receives 100% of the prescription dose (54 Gy). (Available in colour online.)

4. Concluding comments

The basic idea of IPR admittedly comes from the earlier works 15,23 with the current formulation (1) giving this idea a new motivation, (2) putting it on sound theoretical ground and (3) being more general then in those papers which were limited to IMRT. Any inverse problem, in RTTP or in another physics problem that can be identified as a fully discretized prescription-inversion problem can adopt and adapt the IPR methodology. Experimental work in IMRT that implemented the IPR methodology is reported in our recent 15 and in 23. The methodology of IPR is not specific to IMRT or to any specific inverse planning method within IMRT. Any inverse planning situation modelled by full-discretization can benefit from IPR. In this article we identified the algorithmic nature of IPR and validated it mathematically by showing that it is a special case of the general IDR paradigm. The mathematics of IDR itself is limited, so is our current understanding of the foundation of IPR. Therefore IPR needs to be further studied experimentally and mathematically, raising a host of questions. Is the inverse problem at hand ill-posed, e.g. is the matrix A in (2) ill-conditioned (or is the underlying continuous operator compact in some reasonable topology?) It would be interesting to see a plot of the singular values of A even for a small model problem. Even for noise-free problems possible ill-posedness must be taken into account. Otherwise, the computed solution can be corrupted by the noise necessarily introduced in the computational procedure itself. How should a stopping criterion be constructed in the IPR procedure? How should the relaxation parameter μ be chosen?

Table

IDR notations in 7	IPR notations in this article
Data vectors y^(k)	Dose vectors d ^k
Relaxation parameter μ	Relaxation parameter μ
Actual ỹ and ideal ŷ	Assumed
The product operator AS	The identity operator ℐ
The product operator BS
U = (A − μB)S

Acknowledgements

We heartily thank Dr Pavel Lougovski for his help in all phases of the work on this article. We thank three anonymous referees whose constructive comments helped us to improve an earlier version of this work. This work was partially supported by Award Number R01HL070472 from the National Heart, Lung, and Blood Institute at the National Institutes of Health (NIH), and by US Department of Army award number W81XWH-10-1-0170 and United States-Israel Binational Science Foundation (BSF) grant No. 2009012.