A modified Tikhonov regularization method for a backward heat equation

Abstract

In this article, a backward heat conduction problem is considered. A modified Tikhonov regularization method is presented and error estimates are obtained with an a priori strategy and an a posteriori choice rule to find the regularization parameter. Numerical tests show that the proposed method is effective and stable.

Keywords:

• backward heat equation
• ill-posed problem
• Tikhonov regularization method
• discrepancy principle
• error estimate

AMS Subject Classifications::

• 32D15
• 47A52

1. Introduction

The direct problem related to the heat equation is to determine the temperature distribution from the knowledge of the initial temperature and boundary conditions, which generally leads to a well-posed problem. However, it is not always possible to specify the initial temperature and boundary conditions in many practical situations. So an inverse problem is raised: we have to determine the temperature distribution from the knowledge of the final temperature and boundary conditions. This is usually referred to as the backward heat conduction problem (BHCP), which is a typical ill-posed problem 1,2. In general, no solution which satisfies the heat conduction equation, the final data and the boundary conditions, exists. Further, even if a solution exists, it will not be continuously dependent on the boundary and the final data. So it is impossible to solve the BHCP using classical numerical methods and requires special techniques to be employed. Some techniques have been developed for this problem: the quasi-reversibility method 3,4, the optimal filtering method 5, the boundary element method 6, the mollification method 7, the group preserving method 8, the operator-splitting method 9 and the Fourier regularization method 10,11.

In most of these papers, the regularization parameters are a priori. It is well-known that an ill-posed problem is usually sensitive to the regularization parameter and an a priori bound is difficult to be obtained precisely in practice. In this article, we will use the Tikhonov regularization method to solve this problem in which a modified Tikhonov functional will be used. We will show that the proposed method can be realized by fast Fourier transform (FFT) and the regularization parameters can be chosen by the discrepancy principle.

This article is organized as follows. In Section 2, we give the method to construct approximate solution. The convergence results are given in Section 3. Some numerical results are given in Section 4 to show the effectiveness of the new method.

2. Problem and method

In this article, we consider the following one-dimensional backward heat equation in an unbounded region 7,10: (1) where we want to determine the temperature distribution u(·, t) for 0 ≤ t < T from the data φ(x). In practice, the data at φ(x) is often obtained on the basis of reading of physical instrument. So only a perturbed data φ^δ(x) can be obtained. We assume that the exact and measured data satisfy (2) where δ > 0 denotes the noisy level. In addition, note that for any ill-posed problem some a priori assumption on the exact solution is needed and necessary, otherwise, the convergence of the regularization approximate solution will not be obtained or the convergence rate may be arbitrary slow 12. In this article, we will assume there holds the following a priori bound: (3)

Let denote the Fourier transform of φ ∈ L²(ℝ) defined by (4) and ‖·‖ denotes the norm in L²(ℝ) defined by (5) Applying the Fourier transform technique to problem (1) with respect to the variable x, we can get the Fourier transform of the exact solution u(x, t) 10: (6) or equivalently, the solution of problem (1) is given by (7) It is apparent that the exact data must decay faster than the rate . However, in general, the measured function φ^δ does not possess such a decay property. So cannot give a reliable approximation for u(x, t). In the following, we apply the Tikhonov regularization method to reconstruct a new function ϕ^δ from the perturbed data φ^δ. L_tϕ^δ will give a reliable approximation of u(x, t) for 0 ≤ t < T. We let ϕ^δ = ϕ^α,δ be the minimizer of the Tikhonov functional (8) where α > 0 is a regularization parameter. It can be verified that ϕ^α,δ is the solution of the following equation 12: (9) It is obvious that (10) Hence (11) So we can get (12) Then the approximation solution can be given as (13)

3. Choices of regularization parameter α and convergence results

In this section, we consider an a priori strategy and a posteriori choice rule to find the regularization parameter. Under each choice of the regularization parameter, convergence estimates can be obtained. The following lemma is needed.

Lemma 3.1

If ‖L₀φ‖ ∈ L²(ℝ), then for 0 ≤ t < T, (14)

Proof

By the Hölder inequality, (15) ▪

3.1. The a priori choice rule

We assume that we have obtained an E in (3), then we take (16) as the a priori rule. We obtain the following theorem.

Theorem 3.2

Suppose that conditions (2) and (3) hold and be defined by (13) and (16). Then for 0 ≤ t ≤ T (17)

Proof

Owing to ϕ^α,δ being the minimizer of (8), we can obtain (18) and (19) So (20) and (21) The assertion of the theorem will be obtained by (20), (21) and Lemma 3.1.▪

3.2. The a posteriori choice rule

Morozov's discrepancy principle is used as a posteriori rule in this article, i.e. choosing α₂ from the following equation: (22)

Theorem 3.3

Suppose that conditions (2) and (3) hold and be defined by (13) and (22), then for 0 ≤ t ≤ T (23)

Proof

Since ϕ^α,δ is the minimizer of (8), (24) So by (2), (3) and (22), (25) Hence (26) Moreover, (27) The assertion of the theorem will be obtained by (26), (27) and Lemma 3.1.▪

4. Numerical tests

In this section, some numerical tests are given to verify the effect of the proposed method. The tests are performed using MATLAB 7.0.

Example

If we let (28) then it is easy to see that (29) is the unique solution of (1). We give the numerical results for T = 1, 2, 3, respectively. Since Φ(x) approaches zero as |x| ≥ 12 when T ≤ 3, we do the numerical tests in x ∈ [−12, Let . The perturbed data are given by (30) where are generated by function randn(N, 1) × δ₁ in Matlab (randn(N, 1) is an N dimension vector with random entries, chosen from a normal distribution with mean zero, variance one and standard deviation one).

In the following, we present numerical results to check the efficiency of the method. Because the a priori bound E in (3) is difficult to be obtained precisely in practice, we compute the regularization solution by the formulae (13) and (22). The relative errors are measured by the weighted l²-norms defined as follows: (31) We give the values of RE_t(u) for , which are displayed in Table 1. We can see that when δ decreases from 0.1 to 0.0001, the relative errors become smaller and when t increases, the rates of convergence become larger. The comparison between the exact solution and its approximation for different t and T with δ₁ = 0.01 are shown in Figure 1. It can be seen that the numerical results become worse with the increase T and the decrease t. This accords with our theoretical results and we can conclude that the proposed numerical solutions are stable and effective.

Figure 1. Exact solution and its approximation: (a) T = 1, t = 0, δ₁ = 0.01, (b) T = 1, t = , δ₁ = 0.01, (c) T = 1, t = T, δ₁ = 0.01, (d) T = 2, t = 0, δ₁ = 0.01, (e) T = 2, t = , δ₁ = 0.01, (f) T = 2, t = T, δ₁ = 0.01, (h) T = 3, t = 0, δ₁ = 0.01, (h) T = 3, t = , δ₁ = 0.01 and (i) T = 3, t = T, δ₁ = 0.01.

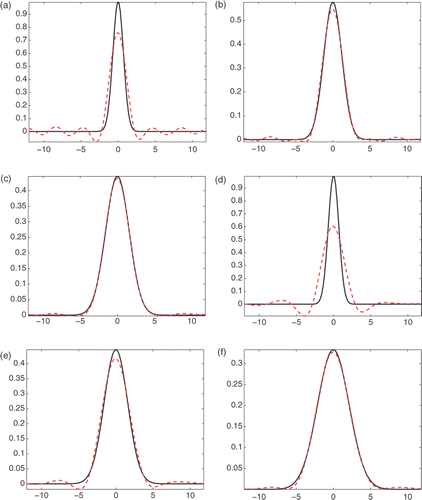
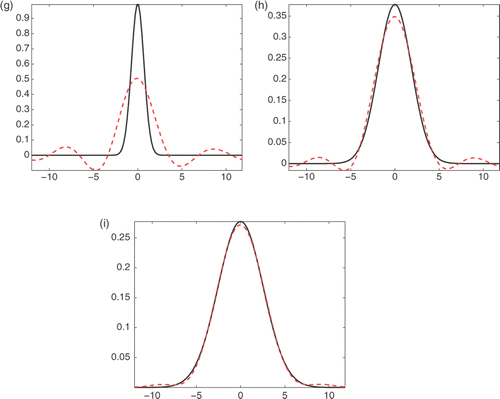
Table 1. RE_t(u) for various T and t.

δ1	T = 1			T = 2			T = 3
	t = 0	t = T/2	t = T	t = 0	t = T/2	t = T	t = 0	t = T/2	t = T
1e−1	0.4295	0.2308	0.1701	0.5984	0.2318	0.1511	0.6257	0.1979	0.1517
1e−2	0.2756	0.0586	0.0236	0.4408	0.0829	0.0270	0.5580	0.0964	0.0249
1e−3	0.1650	0.0143	0.0027	0.3114	0.0171	0.0027	0.4155	0.0244	0.0032
1e−4	0.1158	0.0046	0.0003	0.2477	0.0069	0.0003	0.3230	0.0056	0.0003

5. Conclusion

In this article, we apply a modified Tikhonov regularization to solve the BHCP. Theoretical analysis as well as experience from computations indicate that the proposed method works well. Moreover, the proposed method is readily extendable to solve some other ill-posed problems, but these investigations are deferred to future work.

Acknowledgements

The author wishes to thank the editor and the referees for their very constructive comments and suggestions, which led to the present improved version of his paper. This work is supported by the China Postdoctoral Science Foundation (No. 20100480556).