Metric-topological–evolutionary optimization

Abstract

This article shows a novel approach for optimization and inverse problems based on evolutionary computation with the aim to satisfy two opposite requirements: exploration and convergence. The proposed approach is particularly suitable for parallel computing and it gives its best both for multimodal problems and for problems in which bad initializations can occur. The proposed algorithm has been called MeTEO to point out its metric-topological and evolutionary inspiration. In fact, it is based on a hybridization of two heuristics coming from swarm intelligence: the flock-of-starlings optimization (FSO; which shows high exploration capability but a lack of convergence), the standard particle swarm optimization (which is less explorative than FSO but with a good convergence capability) and a third evolutionary heuristic: the bacterial chemotaxis algorithm (that has no collective behaviour, no exploration skill but high convergence capability). Finally, with the aim of speeding up the algorithm, a technique that we call fitness modification is proposed and implemented. Suitable tests regarding optimization benchmarks and inverse problems will be presented with the aim of pointing out the MeTEO performances compared with those of each single heuristic used for hybridization.

Keywords:

• evolutionary computation
• flock-of-starlings optimization
• particle swarm optimization
• bacterial chemotaxis algorithm
• multimodal optimization

1. Introduction

Exploration and convergence are two important requirements for the algorithms which are devoted to inverse-problems and/or optimization. In many applications, it is usual to prefer those algorithms showing better capabilities of convergence to the global optimum. On the other hand, we have to consider that: (a) many optimization problems require finding more than one single global optimum; (b) in many cases, the global optimum must be found within a solution space having very high dimensions 1. Frequently, the previous points (a) and (b) are simultaneously present. Thus, the designer of the algorithms must decide if it is better to expand the search or to privilege the convergence on a subspace. This is very hard to be decided a priori 2. In fact, the risk of being entrapped into a local minimum is higher if an algorithm does not explore a suitably large space. On the other hand, an algorithm could make an over-sampling of the space and spending long time before achieving convergence to a good solution 2. This article shows a novel approach based on evolutionary computation able to enhance exploration preserving convergence. The proposed algorithm has been called MeTEO for pointing out its metric-topological and evolutionary inspiration. In fact, it is based on a hybridization of two heuristics coming from swarm intelligence: the flock-of-starlings optimization (FSO; topological swarm), the standard particle swarm optimization (PSO; metric swarm) and a third evolutionary heuristic: the bacterial chemotaxis algorithm (BCA) that has no collective behaviour. In particular, the FSO has been first described and applied in 3,4 as a modification of the well-known PSO 5 by adding topological rules to the metric rules that are typical of the PSO. The FSO is inspired by the recent naturalistic observation about the real starling flight 5. As it is shown in 3,4, the FSO is particularly suitable for exploration and multimodal analysis. The BCA 6 is based on the emulation of the motion of a real bacterium looking for food (i.e. fitness function). It is a heuristic that shows its better performances in local search 1. The present approach uses the FSO to explore the solution space, the PSO to investigate subspaces in which the global optimum could be present and finally the BCA to refine solutions. A parallel strategy is implemented: the FSO is permanently running, and each time it finds a possible solution, the PSO is launched. After that, it is transformed in BCA, and so on. A final important computational strategy completes the present approach: the fitness function is deliberately made worse just in those suitable narrow regions in which the FSO has decided to launch PSO–BCA. This fitness modification (FM) aims to prevent FSO from coming back in an already explored subspace. MeTEO has been tested on the main optimization benchmarks currently used in the literature but also novel harder benchmarks are presented. Moreover, MeTEO has been tested also for an inverse problem regarding the identification of the parameters in the Jiles–Atherton (J–A) magnetic hysteresis model.

2. Heuristics components of MeTEO

2.1. Swarm algorithms: PSO and FSO

The PSO is one of the most used and studied among the optimization methods. It was proposed by Kennedy and Eberhart 7 in 1995, starting from the works of Reynolds 8 and Heppner and Grenander 9. It is an algorithm based on some metric rules applied for simulating the collective behaviour of swarms. The metric approach consists of describing the behaviour of a flying bird which must keep a distance from its neighbours that is forced to stay within a fixed interaction range, i.e. all birds keep alignments of velocity among all flock members. Although the metric rule allowed the simulation of a collective movement of animals, significant differences still remained compared to the behaviour of a real flock. However, on the basis of this paradigm, Kennedy and Eberhart 7 first proposed their approach by establishing a one-to-one relationship between the motion of a flock governed by metric rules during its food searching and the iterative steps of a numerical algorithm searching the solution for optimization problems. As a second step, they found that some metric rules of the paradigm were an obstacle for multi-objective optimization tasks. Thus, they modified the algorithm by removing some parts of it. For example, the matching with the velocity of the nearest neighbour was removed, and so on. These variations have altered the virtual collective movement of the swarm and the final algorithm simulates a behaviour more similar to a swarm of insects than to a flock of birds. Thus, we can say that the original PSO has been created by starting from the simulation of a flock of birds for arriving to the emulation of a swarm of generic ‘particles’. The introduction of topological rules into PSO is the hub of the algorithm called FSO. The FSO 3,4 adopts an approach based on recent naturalistic observations 5 on the collective behaviour of the European starlings (Sturnus vulgaris). The authors of paper 5 have discovered an interaction among members of the same flock which has a topological nature: it is relevant to know how many intermediate birds separate two starlings, not how far apart they are from the other. This means that the main property of the topological interaction is that each starling interacts with a fixed number of neighbours, i.e. their metric distance is not crucial. Thus, real flocks of starlings have a behaviour that can be numerically simulated by using topological rules rather than metric rules. In fact, the topological approach is able to describe the density changes that are typical of flocks of birds, whereas the metric approach is not able to do it. In real flocks, each generic k-th bird controls and follows the flights of a generic number of other members of the flock, no matter which positions are their inside the flock.

The pseudo-codes of the implemented PSO and FSO referred to a generic function, , to be minimized in the search space having dimension are recalled in Figures 1 and 2.

Figure 1. Main parameters managed by PSO and FSO.

Figure 2. Pseudo-code for PSO and FSO.

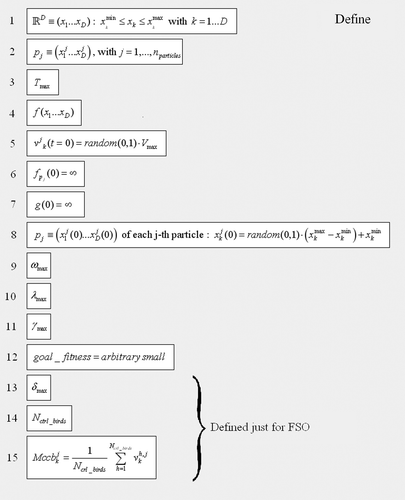
In particular in Figure 1, we have indicated in the boxes numbered from 1 to 11 that the definition of the main common parameters to be used by both the PSO and FSO algorithms. They are: the dimension of the search space, , the values of the main parameters for each j-th particle with ; the maximum number of iterations, ; the fitness function ; the maximum value of each velocity component ; the initialization of velocities (where is a function returning a random value between 0 and 1); the personal fitness ( indicates an arbitrarily large value); the global fitness ; the position of each j-th particle with ; the value of the inertial coefficient ; the maximum value of cognize coefficient, ; the maximum value of social coefficient, ; the fitness threshold . Moreover, in Figure 1, we have indicated the parameters used just for FSO (i.e. they do not appear in the PSO algorithm), by the blocks numbered from 12 to 13: the maximum value of the topological coefficient, among all topological coefficients ; the quantity ; and the number of the birds that are controlled by each other single bird within the flock. In Figure 2, the pseudo-code valid both for PSO and for PSO is reported.

However, it is evident from Figure 2 that the PSO and the FSO differ just for the expressions written in blocks #20 and #21, respectively. This apparently small difference produces huge differences in the behaviour of the two heuristics. In fact, even if the PSO shows a quite good exploration capability as well as a good degree of convergence, it has been noted that, especially when the searching space becomes larger and larger, it can be trapped into a local minimum without the possibility of escaping 1. Furthermore, for multi-modal functions, the algorithm is not comprehensive 1. In fact, it is important to note that the standard PSO has undergone many changes. In fact, many authors have derived new PSO versions and published theoretical studies on the effects produced on the algorithm by changing the values of the various parameters (e.g. , , and so on 10). Other authors have investigated the effects produced by changing some aspects of the algorithm (see e.g. 11,12,] and the references therein). It is important to note, however, that the cited papers focus their attention more on convergence rather than on exploration. On the other hand, in 3,4, it has been shown that FSO has high exploration capability, avoids entrapments into local minima and is particularly suitable for multimodal optimizations. Unfortunately, FSO shows a lack of convergence. This is the cost to be paid for obtaining a high exploration capability for the algorithm. Practically, the FSO does not stop running without user intervention. But this also is the reason that allows the FSO to operate a complete mapping of the solution space. This makes the FSO immune from the worst initializations, i.e. it can return a good solution regardless of how large is the dimension of the solution space. In fact, the FSO has the potential to find each subspace in which a minimum (local or global) lies. Although the FSO can or cannot find better solutions depending on the values assigned to the parameters appearing in Figure 1, the PSO cannot ever achieve the exploration capability of the FSO simply by means of a modification of its parameters. We can conclude these notes by saying that FSO is a very good explorer but it is not convergent, whereas PSO makes a balance between exploration and convergence, favouring (maybe too much) convergence.

2.2. The BCA

The BCA has been proposed in 6 and is an algorithm based on the emulation of the motion of a real bacterium looking for food (i.e. fitness function). A mathematical description of a 2D bacterium motion can be developed by assuming an assigned speed v and by the determination of suitable probabilistic distributions of the motion duration and of the direction shown by each individual. The 2D description can be easily extended to n-dimensional hyperspaces defining, for the virtual-bacterium path, a vector made of n positions , with , and a vector made of directions , with . 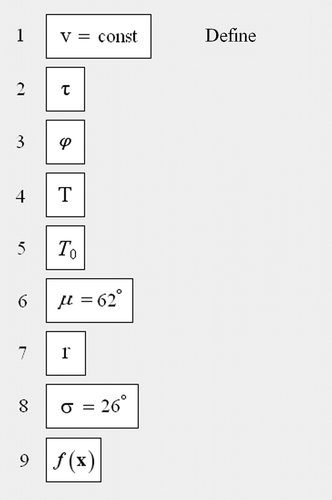Thus, the virtual bacterium motion follows the rules proposed in 6 and summarized here in Figures 3 and 4:

Figure 3. Main parameters managed by BCA.

Figure 4. Pseudo-code of BCA.

In Figure 3, we have indicated the two expectation values of a suitable exponential probability density functions with T and μ, the standard deviation with σ, the minimum mean time with T₀, the module of the difference between the new position vector, , and the old position vector, , of individuals with and the function cost to be minimized with ; the parameters T₀, τ are usually called strategy parameters. Regarding directions, the probability density function describing the turning angle between two consecutive trajectories is Gaussian.

Figure 4 shows the flow-chart of BCA pseudo-code. The path of each bacterium is composed by adding the vector to the old position of virtual bacteria, step by step, by the equation , with . Moreover, the b parameter is another strategy parameter, which is introduced to modify the dynamic of individuals’ movement. Finally, for each bacterium, is the difference between the current fitness function value (), referred to the current position (current algorithm step), and the value of that () referred to previous position (previous algorithm step).

The BCA effectiveness is strongly influenced by the choice of the parameters: T₀, τ and b. They are usually obtained empirically depending on the typology of the optimization problems. In particular, the BCA convergence becomes difficult if the T₀ value is excessively large. This is because T₀ is the shortest time interval of a single position change of the bacterium. This shortest movement should be small enough for allowing the BCA to achieve the requested accuracy. On the other hand, if the elementary bacterium movement were too small, the BCA running-time would be excessive. Furthermore, in the presence of a large gradient (i.e. the motion excitation for the bacterium), b should be chosen small enough for avoiding the risk of a removal from the attraction zone.

3. Parallel architecture, FM and the activation strategy of the different MeTEO components

3.1. Parallel architecture

MeTEO provides its best performances on a distributed architecture and the algorithm has been fully designed for parallel computation based on a Master-Slaves configuration. According to the peculiarities of each previously described single heuristic (PSO, FSO and BCA), MeTEO uses FSO just on the Master node whereas PSO and BCA on Slave ones. The FSO performs the exploration of the whole space of solutions and whenever it finds a sub-region in which there is a high probability of discovering a global minimum (briefly called ‘suspected region’), two simultaneous operations are made: (1) the current fitness is modified in such a way to prevent FSO from exploring again any found ‘suspected region’; (2) MeTEO launches the PSO algorithm on a Slave node of the cluster, being the PSO population initialized by means of the best result found by FSO at the current iteration. Let us explain these points in more detail.

3.2. FM and activation strategy of each single MeTEO components

The FM is inspired to the famous Tabu-search algorithm 13, and in particular to the Tabu list. Since the global optimum is coincident with the smallest value achievable for the fitness functions, the FM has to ensure that the new fitness function must never indicate again a ‘suspected region’ if it has been already detected by the FSO. In fact, the FM consists in adding to the past fitness function a positive Gaussian function centred into the best co-ordinates found by FSO at the current iteration. A further control is made by MeTEO on the number of iterations for which the fitness does not improve its value. In other words, if the fitness does not improve for a number of FSO iterations equal to , MeTEO assumes the coordinates of the last found global best as the centre of a ‘suspected region’ and activates a Slave node in which PSO and BCA are acting on. The metric dimension of this region is automatically set by the FM as it is next described. It is important to remark that the effect of the FM acts just on the PC-Master, i.e. it is valid just for FSO, whereas the fitness function holds the original starting expression for both PSO and BCA working on the PC-Slave. In more detail, let us show how the FM acts when the FSO finds a generic k-th ‘suspected region’. Before finding a ‘suspected region’, FSO was managing a fitness function that was fixed at the moment in which the FSO found the ‘suspected region’: with , (it is clear that the starting original fitness will be indicated with ). Let us assume to be a vector collecting the co-ordinates minimizing the value of . Then, FM operates according to the following equation: (1) where A is a suitable constant that must have opposite sign compared with and the standard deviation that defines the size of the k-th ‘suspected region’ detected by FSO. In this way, the new fitness , which will be managed by the FSO till it will find a further ‘suspected region’, will not show a minimum in , anymore, i.e. the FSO will not be attracted anymore by that region. Obviously, in the Slave node, no FM is made. Let us see now what happens in the Slave node. When a k-th ‘suspected region’ is detected, a Slave node is activated. On this node, the PSO is initialized by whereas the fitness function is always set equal to the starting one: . The PSO will be left to run for a prefixed number of iterations . When the PSO iterations are equal to , the PSO ends its task and it is substituted, on the same Slave node, by the BCA. The BCA population will be initialized by means of the best result achieved by PSO so far. The BCA plays the role of the local search. It searches the minimum until its own number of iterations is equal to a maximum number that has been set before to running MeTEO.

While the process on a Slave node is running, FSO still continues to explore the space on the Master node. Any time FSO finds a further ‘suspected region’, MeTEO again launches a further process on a different Slave node and so on. Any final result coming from Slave nodes is stored in a dedicated file that is located in a shared folder in the Master node. After delivering the found solution to the Master node, a Slave is ready to be used again for a further exploration on a new ‘suspected region’. Finally, when all processes will be ended and all PC-Slaves have completed the PSO + BCA procedures previously described, a list of all minima detected will be available in the file in which all the results coming from Slaves have been stored. At the end, from this stored list, the best minimum can be trivially identified. Finally, some remark on FSO stopping criterion must be made. A simply criterion consists of stopping MeTEO whenever the FSO performs a number of iterations that are set by the user before running MeTEO. However, this strategy could not be effective in all cases. In fact, some hard multi-modal optimizations, i.e. in those cases in which the FSO needs a higher number of iterations for detecting all the global minima, it could be convenient to alternatively use a stopping criterion based on a maximum number of ‘suspected regions’ . In other cases, it will be recommendable to use a Boolean OR logic gate. Obviously, the choice of a specific MeTEO stopping criterion depends on the user experience on the optimization problem or inverse problem to be solved.

4. Validation

MeTEO has been validated on typical optimization benchmarks, as well as on typical inverse problems, i.e. the identification of the J–A hysteresis model by the knowledge of an experimental hysteresis loop and the fit problem called ‘Amid_pro’ that is one of the 295-ODE-test examples proposed by Schittkowski 14.

4.1. Validation on optimization benchmarks

In Table 1, test results performed by MeTEO applied to an ad hoc benchmark are shown. The used benchmark is: (2)

Table 1. List of benchmarks used for tests.

Benchmark name	Type of optimization	Benchmark function
Levy	Unimodal
Schaffer	Unimodal
Giunta	Multimodal
Bird	Multimodal
Test tube older	Multimodal
Cross in Tray	Multimodal
Bukin	Multimodal

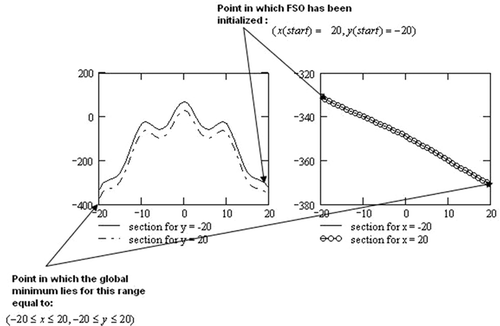
In Figure 5, the cross-sections of (2) in planes at constants x and y are shown. The benchmark (2) shows its smallest value (global minimum) in the point that is located at the border of the variable-range: . Thus, if MeTEO is initialized at the opposite corner of the variable-range: (Figure 5), it has to exit to the closest ‘attractive’ local minimum in , and to the other local minima (Figure 5) that are on the ‘hill’ that separates the starting point from the global minimum.

Figure 5. Cross-sections of (2) in planes at constants x and y.

Each single heuristics that composes MeTEO has to explore a different range within the solution space according to the different exploration capabilities it shows. Thus, for problem (2), whereas the FSO explores the whole range: , the PSOs and the BCAs explore smaller sub-regions depending on the size of the ‘suspected region’ detected by FSO.

At the end of the whole processing, MeTEO detected 14 ‘suspected regions’ for problem (2). Among them, MeTEO found the global minimum in the last detected suspected region. In more detail, in this last region, the FSO detected the smallest value equal to , then the PSO performed and finally the BCA found the best fitness equal to −363.77 in the point (−19.82, 19.58).

Taking into account that the true global-minimum co-ordinates are in (−20, 20), the good accuracy of MeTEO performance is evident. The total PC-Master processing time (FSO) has been 54.8 s. After that, the processing time of PC-Slaves working in parallel has been about 67 s (the average time taken by PSOs was 63 s whereas a time of 4 s has been necessary for BCA).

MeTEO performances have been validated also for classical optimization benchmarks (Table 1) and they are also compared with those returned by each single heuristic PSO, FSO and BCA for solving the same problems.

The MeTEO performances for each benchmark presented in Table 1 have been evaluated by averaging the results obtained on 50 different launches both for MeTEO and for each single heuristics. A multi-launch is required for the stochastic nature of the algorithms. For each different launch, both MeTEO and the other heuristics have been always initialized at the same starting point. Obviously, the starting point has been differently chosen for different benchmarks. The dimension of the search space has been intentionally made sizeable in order to make the optimization more difficult 1, and just 1000 iterations have been set both for MeTEO and for the other single heuristics.

All the simulation results are listed in Tables 2 and 3 for analyses and comparisons. In particular, Table 2 reports the number of global optima correctly detected by each algorithm. We have considered as a success the event in which the algorithm finds a minimum showing a percentage error on the true minimum smaller than a fixed threshold.

Table 2. Performance of MeTEO and its components.

Benchmark	MeTEO (number of found minima)/ (number of total minima)	FSO (number of found minima)/ (number of total minima)	PSO (number of found minima)/ (number of total minima)	BCA (number of found minima)/ (number of total minima)
Levy	1/1	1/1	1/1	0/1
Schaffer	1/1	1/1	0/1	0/1
Giunta	3/3	1/3	0/3	0/3
Bird	4/4	4/4	2/4	0/4
Test tube older	3/6	2/6	1/6	0/6
Cross in Tray	4/4	2/4	1/4	0/4
Bukin	2/5	1/5	1/5	0/5

Table 3. MeTEO performances.

Benchmark	FSO	PSO	BCA	Number of detected ‘suspected regions’
Levy	0.001128100069129	1.112549902700000 ×	1.626793947000000 ×	138
Schaffer	0.004245907810385	6.985129917416143 ×	−7.216739485161167 ×	30
Giunta				18
Bird	−1.066907387112337 ×	−1.067645235721507 ×	−1.067645142301463 ×	169
Test tube older	−10.808077079559949	−10.852437039909185	−10.852491680226905	131
Cross in Tray	−2.061780609712529	2.062611702638596	−2.062611853281188	155
Bukin	1.297356414422297	0.597342511668211	0.161506034691595	165

As it is possible to see in Table 2, for the unimodal optimization, Levy and Schaffer, the MeTEO always obtains a success like FSO, whereas both PSO and BCA fail for Schaffer function. For harder multimodal benchmarks, the power of MeTEO is more evident. In fact, whereas it finds anyway at least one global minimum, and in many cases all the global minima, FSO, PSO and BCA cannot assure the same performances.

In Table 3, the best fitness results obtained by MeTEO are listed. In particular, Table 3 shows the best performance achieved by each single MeTEO component in the best ‘suspected region’. For multimodal functions, the best results obtained for one of the global minima are indicated. Finally, in the last column of Table 3, the number of ‘suspected regions’ detected by MeTEO during the elaboration is also reported.

4.2. Validations on inverse problems

MeTEO has been tested also on an inverse problems as follows.

4.2.1. Identification of the J–A model

The Jiles–Atherton hysteresis model identification. Let us remind J–A model 15: (3) where M_an is the anhysteretic magnetization provided by the Langevin equation: (4) in which H_e is the effective magnetic field . In (3), is the irreversible magnetization component defined by (5) where .

The parameters to be identified of the J–A model are and their physical meaning is: is a form factor, the coefficient of reversibility of the movement of the walls, the saturation magnetization, and finally, represent the hysteresis losses and the interaction between the domains, respectively.

The performed test is based on the use of a given set of parameters 15 inserted into Equations (3–5) for obtaining by integration a pseudo-experimental loop. The sampled points of this pseudo-experimental loop have been used to estimate the error between that loop and that returned by MeTEO and the other single heuristics. All algorithms have been randomly initialized; the maximum number of ‘suspected regions’ has been set to 80.

The tests consist of 50 different launches as for MeTEO as well as for PSO, FSO and BCA working alone. In particular, the best result obtained by each algorithm is listed in Table 4. A further statistical analysis referred to on the 50 launches made has been reported in Table 5 by using two indicators: mean percentage error (MPE) and (determination coefficient). As it is possible to see, MeTEO shows the lowest MPE in comparison with those obtained by any single heuristic FSO or PSO or BCA working alone, as it is shown in Figure 6.

Figure 6. Comparison of the simulation results obtained by MeTEO and FSO, PSO and BCA when each one works alone.

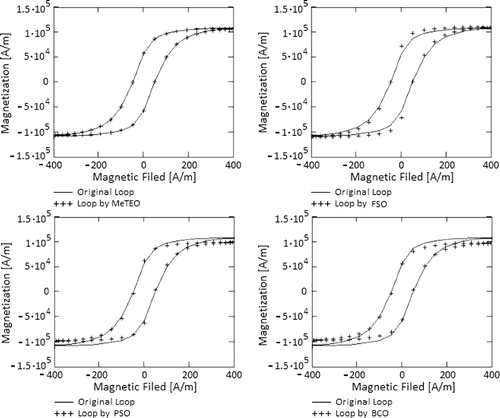
Table 4. Best results among 50 launches of MeTEO and its components for the J–A inverse problem.

Algorithm	Best parameter estimation	Percentage error on the experimental loop points
MeTEO
FSO
PSO
BCA

Table 5. Statistical analysis of MeTEO and its components for the J–A inverse problem.

	MPE
Algorithm	Mean value	Variance
MeTEO	0.53552	1.4576e−5	0.9996
FSO	1.294	0.9030e−3	0.9993
PSO	1.6388	1.6527e−3	0.9968
BCA	2.4268	2.9507e−2	0.5870

4.2.2. Amid proton replacement with protein folder inverse problem

A further classical inverse problem has been taken into consideration with the aim to validate MeTEO: the Amid proton replacement with protein folder inverse problem. In particular, we have taken into account the model called Amid_pro proposed by Schittkowski in 14 among a list of 295 fit problems. The problem under analysis is described by the following set of differential equations: (6)

The performed test is based on the use of a given set of parameters 14 inserted into Equation (6) for obtaining a pseudo-experimental data set by integration. Also, in this validation test, the performances of the used heuristics have been computed over 50 launches with random selection of guess parameters. The suspected regions have been set equal to 80. Also, for this test, we have observed that MeTEO has performed the best solution in comparison with those returned by each single heuristic working alone. All the best results obtained among the 50 different launches per heuristic are listed in Table 6 and in Figure 7 are plotted the corresponding curves obtained by integrating (6). A statistical analysis of the several heuristic performances is shown in Table 7. It is evident in this case also that MeTEO has returned the best performances also in statistical terms.

Figure 7. Comparison of the simulation results obtained by MeTEO and FSO, PSO and BCA when each one works alone on the Amid_pro inverse problem.

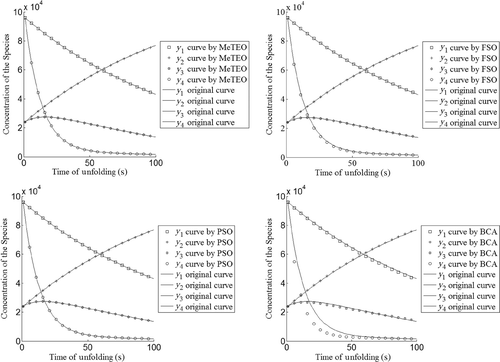
Table 6. Best results among 50 launches of MeTEO and its components for the Amid_pro inverse problem.

Algorithm	Best parameter estimation	Percentage error on the 4-dim Amid_pro
MeTEO		0.0060
FSO		0.7709
PSO		0.1628
BCA		2.0764

Table 7. Statistical analysis of MeTEO and its components for the Amid_pro inverse problem.

Algorithm	MPE
	Mean value	Variance
MeTEO	0.42562	0.1292e−4	0.9999
FSO	1.0674	0.4048e−4	0.9987
PSO	2.9633	7.9884e−3	0.9968
BCA	10.8683	5.948e−2	0.3476

5. Conclusions

A hybrid optimization algorithm called MeTEO based on evolutionary computation has been proposed. The aim of MeTEO is to build an algorithm that assures convergence without sacrificing exploration capability. For this reason, MeTEO uses three different heuristics: two coming from swarm intelligence and the last from the simulation of the behaviour of bacteria into a habitat.

Moreover, MeTEO has been designed (and implemented) on a parallel Master–Slaves computing system. All presented validation tests were applied both to optimization benchmarks and to two inverse problems indicating that MeTEO shows competitive performances compared with the results of the single-heuristic PSO, FSO and BCA when each one works alone.