CMARS: a new contribution to nonparametric regression with multivariate adaptive regression splines supported by continuous optimization

Abstract

Regression analysis is a widely used statistical method for modelling relationships between variables. Multivariate adaptive regression splines (MARS) especially is very useful for high-dimensional problems and fitting nonlinear multivariate functions. A special advantage of MARS lies in its ability to estimate contributions of some basis functions so that both additive and interactive effects of the predictors are allowed to determine the response variable. The MARS method consists of two parts: forward and backward algorithms. Through these algorithms, it seeks to achieve two objectives: a good fit to the data, but a simple model. In this article, we use a penalized residual sum of squares for MARS as a Tikhonov regularization problem, and treat this with continuous optimization technique, in particular, the framework of conic quadratic programming. We call this new approach to MARS as CMARS, and consider it as becoming an important complementary and model-based alternative to the backward stepwise algorithm. The performance of CMARS is also evaluated using different data sets with different features, and the results are discussed.

Keywords:

• Tikhonov regularization
• conic quadratic programming
• interior point methods
• nonparametric regression
• multivariate adaptive regression splines

AMS Subject Classifications::

• 62G08
• 65F22
• 90C25
• 90C90

1. Introduction

Regression modelling is extensively used to establish a relationship between some predictors and a response variable. There are various forms of regression models used for different purposes such as data description, summarization, parameter estimation for learning and control, almost in every field of engineering, and science 1. Among them, the linear regression model (LRM) is a well-known global parametric model. However, they only work well in cases where the true underlying relationship is close to the hypothesized function in the model. To overcome the disadvantages of the global parametric approach, nonparametric models are developed locally over specific subregions of the data. Then, the data is analysed for optimum number of subregions, and a simple function is optimally fit to the realization in each subregion 2. Multivariate adaptive regression splines (MARS), developed by Friedman 3, is such a nonparametric modelling approach of the form (1) where y is a response variable, x = (x₁, x₂, … , x_p)^T is a vector of predictors and ε is an additive stochastic component which is assumed to have zero mean and finite variance. While the aim of classical parametric regression is to estimate the model parameters, that of the nonparametric regression is to estimate the regression function, f.

The main ability of MARS is to construct flexible models by introducing piecewise linear regressions. Nonlinearity of the models is approximated by different regression slopes in the corresponding intervals of each predictor variable. The slope of each regression line is allowed to change from one interval to another with the condition that there is a ‘knot’ defined in between. Hence, splines are used rather than normal straight lines if there is a need. Predictors to be included in the final model along with their respective knots are found via a fast but intensive search procedure 4 in a two-stage process: forward and backward 3.

In recent years, MARS has been successfully applied to many areas of science and technology. Some interesting examples can be found in 5–12. In this study, we first employ a new approach to regression and classification from the theories of statistical learning, inverse problems and continuous optimization. Indeed, a wealth of real-life motivations give rise to the nonparametric method called classification and regression trees (CART) 13 as well as least squares estimation (LSE). We choose one of its most advanced and refined versions and modifications, called MARS, and apply it by Tikhonov regularization and conic quadratic programming (CQP) 14. For this study, having introduced linear combinations of the special basis functions (BFs) of MARS, we construct penalized residual sum of squares (PRSS) parameter estimation problem instead of a LSE problem. This estimation problem aims at accuracy and a smallest possible complexity of the model, or equivalently, in stability (robustness, well-conditionedness). Both goals are first combined in the tradeoff that is given in the form of a penalized problem, i.e., of minimizing the residual sum of squares (RSS) and complexity. In fact, we unify some discretized complexity (or energy) terms, and include them into inequality constraints, where we impose a bound on them, and obtain a CQP problem to which we can apply interior point methods 15,16 via the program package MOSEK™ 17. We call this new approach to MARS as CMARS. In fact, the ‘C’ in CMARS stands for not only ‘Conic’ but also ‘Convex’ and ‘Continuous’.

Afterwards, the implementation of CMARS algorithm developed is illustrated with a numerical example. Furthermore, we apply the two methods on several data sets with different characteristics. Then, their performances are evaluated and compared by using general (method-free) performance measures.

This article is organized as follows. MARS is described in Section 2. In Section 3, CMARS, the proposed alternative to MARS algorithm, is presented. A numerical example is given in Section 4. In Section 5, methods are applied on different data sets, and also, validated and compared. Concluding remarks and further studies are mentioned in the final section.

2. MARS method

MARS algorithm is a flexible approach to high-dimensional nonparametric regression, based on a modified recursive partitioning methodology. It uses expansions in piecewise linear, actually, truncated BFs of the form (2) where [q]₊ ≔ max {0, q} and τ is a univariate knot. Each function is piecewise linear, with a knot at the value τ, and the corresponding couple of function is called a reflected pair.

The first important advantage of using the piecewise linear BFs is their ability to operate locally. They are zero over some part of their ranges. When they are multiplied together, the result is nonzero only over the small part of the feature space where both component functions are nonzero. As a result regression surface is built up parsimoniously, using nonzero components locally only where they are needed. This is important, since one should use parameters carefully in high dimensions, as they can run out quickly. The use of other BFs, such as polynomials, would produce a nonzero product everywhere, and would not work as well. The second important advantage of using the piecewise linear BFs is related to the computation.

Let us consider the general model on the relation between the predictor and response variables given in (1). The goal is to construct reflected pairs for each predictor x_j (j = 1, 2, … , p) with p-dimensional knots τ_i = (τ_i,1, τ_i,2, … , τ_i,p)^T at x_i = (x_i,1, x_i,2, … , x_i, p)^T or just nearby each data vector (i = 1, 2, … , N) of that predictor.

After these preparations, our set of BFs becomes (3)

Thus, we can represent f (x) by a linear combination as follows: (4) Here ψ_m (m = 1, 2, … , M) are BFs from ℘ or products of two or more such functions, ψ_m is taken from a set of M linearly independent basis elements, and θ_m are the unknown coefficients for the mth BF (m = 1, 2, … , M ) or for the constant 1 (m = 0). A set of eligible knots τ_i,j is assigned separately for each predictor variable dimension and is chosen to approximately coincide with the predictor levels represented in the data. Interaction BFs are created by multiplying an existing BF with a truncated linear function involving a new variable. In this case, both the existing BF and the newly created interaction BF are used in the MARS approximation. Provided that the observations are represented by the data (i = 1, 2, … , N ), the form of the mth BF can be written as follows: (5) where K_m is the number of truncated linear functions multiplied in the mth BF, is the predictor variable corresponding to the jth truncated linear function in the mth BF, is the knot value corresponding to the variable , and is the selected sign +1 or −1.

The MARS algorithm for estimating the model function f (x) consists of two subalgorithms: the forward stepwise algorithm searches for the BF and at each step, the split that minimizes some lack-of-fit criterion, called generalized cross-validation (GCV), from all the possible splits on each BF is chosen. One can refer to Appendix B for description of GCV. The process stops when a user-specified value M_max is reached. Then, the backward stepwise algorithm starts to prevent from over-fitting by decreasing the complexity of the model without degrading the fit to the data, and to remove from the model BFs that contribute to the smallest increase in the residual squared error at each stage, producing an optimally estimated model with respect to each number of terms, called α. We note that here α expresses some complexity of estimation, and also note that M_max is reduced to M.

In this study, we do not employ the backward stepwise algorithm to estimate the function f (x). Instead, as an alternative, we use penalty terms in addition to the LSE to control the lack-of-fit from the viewpoint of the complexity of the estimation 14. We will explain the details below.

3. CMARS: an alternative to MARS

3.1. The PRSS problem

The PRSS with M_max BFs having been accumulated in the forward stepwise algorithm of the MARS approach has the following form: (6) where is the variable set associated with the mth BF, ψ_m (cf. (5)), represents the vector of variables which contribute to the mth BF, ψ_m. Furthermore, we refer to for α = (α₁, α₂)^T, |α| ≔ α₁ + α₂, where α₁, α₂ ∈ {0, 1}.

Indeed, we note that in any case where α_i = 2, the derivative vanishes, and by addressing indices r < s, we have employed Schwarz's Theorem. In order not to overload the exposition, we still accept a slight flaw in the notation since in case of |α| = 1 and K_m > 1, the integral terms become K_m times the number of pairs where r < s. By redefining λ_m by λ_m/K_m, this little deficiency could be easily corrected. The reader may choose a notation of his or her preference. Furthermore, for convenience, we use the integral symbol ‘∫’ as a dummy in the sense of , where Q^m is some appropriately large K_m-dimensional parallelpipe where the integration takes place. We will come back to this below. Finally, since all the regarded derivatives of any function ψ_m exist except on a set of measure 0 (zero), the integrals and entire optimizsation problems are well defined.

The PRSS problem bases on the tradeoff between both accuracy, that is, a small sum of error squares, and not too high a complexity. This tradeoff is established through the penalty parameters λ_m. The second goal on a small complexity encompasses two parts: (a) Firstly, the areas where the BFs contribute to an explanation of the observations, should be large. In the case of classification, this means that the classes should be big rather than small. This aim is achieved by a ‘flat’ model which is the linear combination of the BFs, together with our wish to have small residual errors; i.e. the model being ‘lifted’ from the coordinate axes towards the data points (x_i, y_i) (i = 1, 2, … , N). Here, the basic idea is to dampen the slope of the linear parts of the BFs via the parameters θ_m, while still guaranteeing a quite satisfactory goodness of data fitting. (b) Secondly, we aim at the stability of the estimation, by taking care that the curvatures of the model function with its compartments according to (4)–(5) are not so high, and hence their oscillations are not so frequent and intense. For detailed information one may refer to 18.

Motivated in this way, both first- and second-order partial derivatives of the model function f, better to say, of its additive components, enter our penalty terms in order to keep the complexity of the LSE appropriately low.

In this article, we tackle that tradeoff by penalty methods, such as regularization techniques 19, and by CQP 16.

If we consider some arrangements in 14, the objective function (6) can be expressed in the following form: (7) where denotes any of the predictor vectors and stands for the corresponding projection vectors of onto those coordinates which contribute to the mth BF, ψ_m, they are related with the ith response y_i. We recall that those coordinates are collected in the set V_m. Here, CMARS uses up all M_max basis functions provided by the forward algorithm of MARS, while MARS may eliminate some of them reducing the number of basis functions to M (≤M_max) using its backward algorithm (Section 2). The second-order derivatives of the piecewise linear functions ψ_m (m = 1, 2, … , M_max), and hence, the penalty terms related in Equation (7) vanish. Now, we can rearrange the representation of PRSS as follows: (8) where , with the point in the argument. To approximate the multi-dimensional integrals , again we use discretization forms of it. The discretizations and model approximations as presented in the following are very carefully prepared, and play an important role in order to raise our final model. The final model is linear in unknown parameters, and via the intermediate form of a Tikhonov regularization, we introduce our algorithmic approach which uses that linearity in a conic quadratic regression problem and by the use of interior point methods.

For discretizations, our data point (l = 1, 2, … , N) with are given. In a natural way, these predictor data (l = 1, 2, … , N) generate a subdivision of any sufficiently large parallelpipe Q of ℝ^N which contains each of them as elements. Let Q be a parallelpipe which encompasses all our predictor data; we represent it by where Q_j =: [a_j, b_j], (j = 1, 2, … , p) (l = 1, 2, … , N). Without loss of generality, we may assume . For all j we reorder the coordinates of the predictor data points: , where (σ = 1, 2, … , N; j = 1, 2, … , p), and is the jth component of , the predictor vector after reordering. Without loss of generality we may assume for all σ, φ = 1, 2, … , N with σ ≠ φ; i.e. (j = 1, 2, … , p).

Indeed, whenever equality is attained for some coordinate, we would obtain subparallelpipes of a lower dimension in the following integration process and its approximation, that is, zero sets. Let us denote

In order to increase the readability of the following formulas, we make a small simplification without loss of generality. In fact, let us think that the canonical projections of the data points into the p input (feature) dimensions are of the same increasing order. So we assume (j = 1, 2, … , p). Otherwise, we could just replace the index (or discrete parameter) l_σ by a j-, i.e. feature-depending one, called . Now, we can write Q as

Based on the aforementioned notation, we discretize our integrals as follows:

We note that in our case subdivision and approximation done for all needs to be done for all with the corresponding variables and lower dimensions of t^m also. For this we look at the projection of Q into related with the special coordinates of t^m and we take the subdivision of the corresponding Q^m according to the subdivision obtained for Q.

Then, we rearrange PRSS in the following form: (9) where . Let us introduce some more notation related with the sequence : (10)

By (10), we can approximate PRSS as: (11)

For a short representation, we can rewrite the approximate relation (9) as the following: (12) where is an (N × (M_max + 1))-matrix, ‖·‖₂ denotes the Euclidean norm and the numbers L_im are defined by their roots

3.2. Tikhonov regularization applied

Now, we approach our problem PRSS as a Tikhonov regularization problem 19 (see Appendix A for detailed explanation). For this purpose we consider formula (12) again, arranging it as follows: (13) where (m = 1, 2, … , M_max). But, rather than a singleton, there is a finite sequence of the tradeoff or penalty parameters such that this equation is not yet a Tikhonov regularization problem with a single parameter as such. For this reason, let us make a uniform penalization by taking the same λ for each derivative term. Then, our approximation of PRSS can be rearranged as (14) where L is a diagonal (M_max + 1) × (M_max + 1)-matrix with the first column and the other columns being the vectors L_m introduced above. Herewith, we can write L as follows:

Furthermore, θ is an ((M_max + 1) × 1)-parameter vector to be estimated through the data points. Then, our PRSS problem looks as a Tikhonov regularization problem (26) with ϕ > 0, i.e. λ = ϕ² for some ϕ ∈ ℝ 19. Our Tikhonov regularization problem treats the multiple objective functions and using a linear combination of them. This combination is a weighted linear sum of the objectives. We set a weight by the penalty parameter λ. However, coming up with meaningful combinations of weights can be challenging. In Section 4, we give more explanations on the choice of the penalty parameter, and of the parameter occurring in the CQP problem which we introduce next.

3.3. CQP problem

The Tikhonov regularization problem (14) can be expressed as a CQP problem. Indeed, based on an appropriate choice of a bound Z ∈ ℝ, we state the following optimization problem: (15)

Let us underline that this choice of Z should be the outcome of a careful learning process, with the help of model-free or model-based methods 20 (refer to Section 4 for more information). In our study, this bound is selected by a trial and error approach as an initial treatment, but in a future work more effective algorithms can be developed for handling the bound. In (15), we have the least squares objective function and the inequality constraint function which is requested to be nonnegative for feasibility. Now, we equivalently write our optimization problem as follows: (16) or equivalently again, (17)

A CQP problem is generally expressed as the following 18,21: (18)

In fact, we see that our optimization problem is such a CQP program with

In order to write the optimality condition, the dual problem and the primal dual optimal solution for this problem, and we first reformulate the problem (17) as follows: (19) where L^N+1, are the (N + 1)-and (M_max + 2)-dimensional ice-cream (or second-order, or Lorentz) cones, defined by

The dual problem to the latter primal one is given by (20)

We must note that dual problem constructed in Equation (20) is standard dual problem for convex programming in Equation (17) and so there is no duality gap. Moreover, (t, θ, χ, η, ω₁, ω₂) is a primal dual optimal solution if and only if (21)

The penalty parameter λ in the PRSS and the parametrical upper bound Z in a constraint of the CQP are related. λ can be determined via Tikhonov regularization. This regularization method utilizes an efficiency curve that comes from a plotting of the optimal solutions to problem (14) according to a large (finite) number of parameter values, as points in a coordinate scheme with two axes. At one axis, the complexity is denoted, whereas the other axis stands for the length of the residual vector (or goodness-of-fit). In this regularization method, logarithmical scales are employed such that some ‘kink’ (corner) kind of a point on the efficiency boundary, called L-curve according to its more pronounced shape, is obtained. This point is regarded to be the closest to the origin, and it is therefore often chosen, together with the corresponding penalty parameter 19. For our approach with CQP, in 22, a lot of numerical experience is presented, related with varying upper bounds by using the software package of MOSEK™. The solutions obtained at the upper bounds are expected to be the same non-dominated solutions as obtained above.

In the following section, the implementation of CMARS algorithm is explained with a numerical example. The comparison study of the MARS and CMARS methods will be presented in the next section.

4. A numerical example

The data set used for illustrating the implementation of CMARS algorithm is taken from 23, p. 71]. It contains five predictor variables (x₁, x₂, x₃, x₄, x₅) with 32 observations. Here, we write x as a generic variable in the corresponding space ℝ^l (l ∈ {1, 2, … , 5}). Later, we substitute x by t¹, t², … , or t⁵.

While implementing the CMARS algorithm, first, the MARS model is built by using the Salford MARS® v.2 24. In the construction of the model, the maximum number of BFs (M_max) and the highest degree of interactions are determined by trial and error. In this example, M_max and the highest degree of interactions are assigned to be five and two, respectively. As a result, the largest model built in the forward MARS algorithm by the software contains the following BFs: Here, ψ₁ and ψ₂ are the standard BF and mirror image (reflected) BF for the predictor variable x₂, respectively. Let us note that the knot point for ψ₁ is −0.159. BF ψ₄, on the other hand, uses the function ψ₃ to express the interaction between the predictor variables x₁ and x₄. Similarly, ψ₅ represents the interaction between the predictor variables x₄ and x₅.

From this point on, only two of the BFs are listed above, namely ψ₁, which represents the main effect of a variable, and ψ₄, which stands for an interaction effect of two predictor variables, are selected to illustrate the implementation details of our CMARS algorithm.

To prevent our optimization problem from nondifferentiability, we do not choose the knot values as data points, but as values very close to them. Actually, we could even choose the knots τ_i,j farther away from the predictor values , if any such position promises a better data fitting. For example, we select the knot value for ψ₁ as τ_16,2 = −0.159, which is different from but very close to it. Similarly, we select the knot values for ψ₄ as τ_5,1 = − 2.576 (not ), and τ_1,4 = −1.517 (not ).

Then, the first and the fourth BFs of the form (5) can be written as follows: and As a result, the large model given in (4) becomes

Next, we can write the PRSS objective function in (8) as follows: Some evaluations for the notations V_m and t^m (for m = 1 and 4) in the above equation are given as Besides, the derivatives for the BFs (for m = 1 and 4) are stated below. For the BF ψ₁(t¹), there is no interaction; so r = s = 2. The sum of indicated first- and second-order derivatives for ψ₁ is where For the BF ψ₄(t⁴), on the other hand, there is an interaction between the predictors x₁ and x₄, and r = 1 and s = 4 so r < s. Then, the sum of indicated first- and second-order derivatives of ψ₄ can be written as where

If , then the Tikhonov regularization application put the PRSS function in the form of (14) as follows: The first part of the PRSS objective function and that of the Tikhonov regularization problem are equal to each other. For illustration, the first part is expanded as follows:

When the maximum functions are computed, the RSS becomes

The multi-dimensional integral in the second part of Equation (8) takes the form of (11) by discretizing. The discretized form is denoted by L as given in Equation (14). In order to apply this discretization, first we sort the data set, and then, slightly decrease the first value of each predictor variable and slightly increase the last value of each predictor variable. Thus, adding two new observations to each of the predictor variables, we get a completely new data set totally with 34 observations. In the new data set, for example, the first data value is x_1,1 = −2.5759 and the last data value is x_32,1 = 2.4197. As a result, the first discretization value of x₁ becomes and the last discretization value becomes .

The L_m (m = 1, 4) values corresponding to BFs ψ₁ and ψ₄ are calculated as follows: and As a result, the L matrix becomes a (6 × 6)-diagonal matrix as follows: Note that the first column elements of L are all zero and the diagonal elements of this matrix are L_m (m = 1, 2, … , 5) as introduced above.

In Equation (14), is the squared norm of Lθ which is (22)

From the Equations (12) and (13), we can calculate the objective function PRSS. In order to solve this problem, we reformulate PRSS as a CQP problem by using (17) as follows: (23)

Our previous CQP problem can be rewritten as follows: (24) Here θ₃₈ = 1.9545θ₁, θ₃₉ = 0.5999θ₂, θ₄₀ = 2.0622θ₃, θ₄₁ = 1.6002θ₄, θ₄₂ = 13.1962θ₅.

As can be seen from Equation (24), our problem involves 32 linear constraints and two quadratic cones. For solving it, we transform (24) into the MOSEK™ format 17. For this transformation, we have introduced new unknown variables (θ₆, … , θ₄₂), to the linear constraints in these two quadratic cones. By default, MOSEK™ uses an interior-point optimizer to solve CQP problem. It is a well-recognized implementation of the homogeneous and self-dual algorithm, and it computes the interior point solution which is an optimal solution.

We note that our family of optimization problems, indexed by Z, can be regarded as a problem of parametric programming. Such a problem will be analysed by us in future research. Next, we compare the performance of MARS and CMARS algorithms by using the model dependent measures which are GCV (a measure for MARS performance); and ‖Lθ‖₂ (measures for CMARS performance). 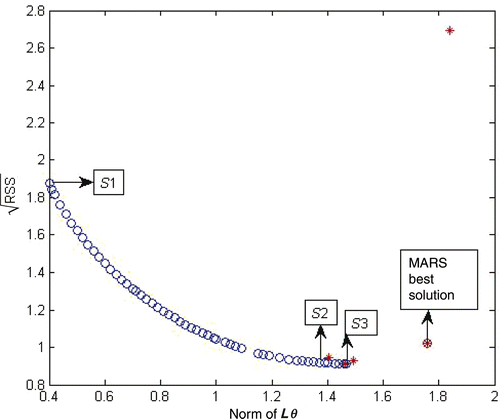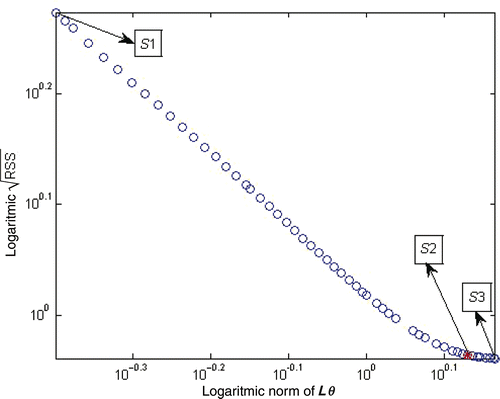For this purpose, several values of in (24) are used to obtain several corresponding CMARS solutions, each based on five BFs for this particular problem. Among them, three representative solutions of the CMARS algorithm, S1, S2 and S3, are chosen. Here, S1 and S3 are the ones that minimize the objective functions ‖Lθ‖₂ and , respectively. S2, on the other hand, is the CMARS solution that tries to minimize both of them in a balanced manner. To determine S2, a log–log scale curve of versus ‖Lθ‖₂ values of the solutions obtained by solving the CQP problem for various different Z values is plotted (Figure 1). It is a characteristic L shaped curve, the corner value of which is taken as the S2 solution.

Figure 1. The solutions obtained for different Z values for problem (24).

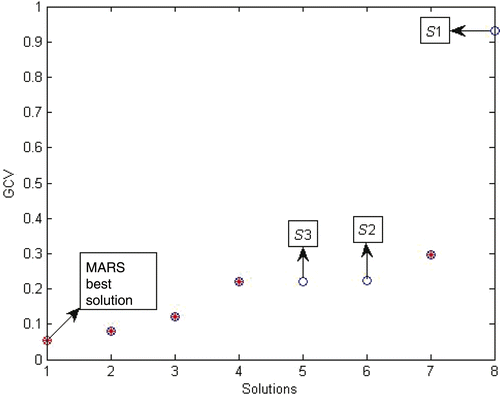
To compare the performances of the methods with respect to the CMARS performance measures, the plot of versus ‖Lθ‖₂ is made for both MARS and CMARS solutions (Figure 2). It reveals, based on our example and data, that CMARS solutions dominate MARS solutions according to these two measures.

Figure 2. Norm of Lθ versus for the solutions of methods (*: MARS solution; o: CMARS solution).

On the other hand, the plot of GCV values for different solutions of CMARS and MARS algorithms indicate that most of the MARS solutions dominate CMARS solutions with respect to GCV measure (Figure 3). As a result, we can conclude that model-dependent measures may not enable us to distinguish between the performances of the algorithms studied. For that reason, in the next section, we apply MARS and CMARS algorithms to nine data sets having different characteristics, and compare them by using general performance measures.

Figure 3. GCV values for the solutions of methods (*: MARS solution; o: CMARS solution).

This result is to be expected, since MARS and CMARS optimize for the accuracy and complexity of the models based on their own corresponding measures.

5. Numerical comparison of the methods

In this section, we compare performances of the two methods: MARS and its alternative CMARS with respect to some general measures. For this purpose, first, data sets used in this comparison are described. Then, the cross validation (CV) technique employed for validating and comparing the methods' performances is explained. Next, the measures used in the comparison are described. Afterwards, the findings of our comparison studies are presented. Moreover, performances of the two methods on noisy data are evaluated by Monte Carlo simulation technique.

5.1. Data sets

In order to more realistically compare the performance of the CMARS method with that of the MARS method, nine data sets with different sample size (n) and number of predictors (p) are selected from regression test problems residing in well-known data repositories 25,26. Then, these data sets are classified according to two important features of data: size and scale; scale here refers to the complexity in terms of the number of predictors involves in data. For both features three levels are considered: small, medium and large. Information about the data sets used in this study and their classification with respect to size and scale are presented in Table 1.

Table 1. Data sets used in the comparison.

Data Sets			Features
Number	Name	Source	n	p	Size	Scale
1	Concrete Slump Test	[25]	103	7	Small	Small
2	Uniform Sampling	[27]	160	10	Small	Medium
3	Metal Casting	[28]	92	35	Small	Large
4	PM10	[26]	500	7	Medium	Small
5	Forest Fires	[25]	517	11	Medium	Medium
6	Parkinsons Telemonitoring	[25]	578	21	Medium	Large
7	Concrete Compressive Strength	[25]	1030	8	Large	Small
8	Red Wine Quality	[25]	1599	11	Large	Medium
9	Communities and Crime	[25]	879	24	Large	Large

Before construction of the models, all data sets are preprocessed to handle missing values, inconsistencies and outliers if there are any. Besides, variables are all normalized to make them comparable. It should be noted here that the ‘Communities and Crime’ data set is reduced in both size and scale to fit it into our classification.

5.2. Validation technique

In our applications, to compare and validate the methods, we have used a 3-times replicated 3-fold CV approach 29. In this approach, the original data set is randomly divided into three sub-samples (folds). While one sub-sample is retained for testing the model, the remaining two sub-samples are used for training data (i.e. building models). This process is performed three times; each time taking a different sub-sample for testing. This procedure, in turn, is replicated two more times, with new partitions. Overall, a total of nine test results are obtained. To produce better estimates for each measure, the three results obtained from 3-folds of a replication are averaged, as well as all nine results. Note that, we have applied a stratified CV where necessary (e.g. in metal casting data).

5.3. Criteria and measures used in the comparison

In the comparison, five criteria, namely, accuracy, complexity, stability, robustness, and efficiency are used. The accuracy criterion tries to measure the predictive capability of the model developed. For this purpose, mean absolute error (MAE), multiple coefficient of determination (R²), proportion of residuals within three sigma (PWI) and predicted error sum of squares (PRESS) are selected as the measures. Note here that these are the least correlated accuracy measures among many others extensively used in the literature. Complexity, on the other hand, can be measured by the mean squared error (MSE). Furthermore, in order to measure the change in the performance of the methods on the training and testing data sets, stabilities of above measures are calculated. Formal definitions of all these measures used in the comparison are given in Appendix C. Moreover, robustness of the methods under different data features is also assessed with the help of the spread of performance measures used. For this purpose, standard deviation of the measures is utilized. Finally, the performance of the methods is also evaluated with respect to their efficiency. To measure the efficiency of methods, computational run times of the data sets are recorded, and compared.

5.4. Applications and findings

In the following, the CV approach is applied on all data sets as explained in Subsection 5.2. MARS models are built by using Salford MARS® software program 24. CMARS models, on the other hand, are constructed by running the MATLAB® code developed by the authors 30.

After the models are built, comparison measures listed in Section 5.3 are defined in Appendix C are calculated for training and testing samples as well as stabilities of the measures for all 3-folds and three replications of each dataset. Then, averages of these nine values are obtained for each measure for MARS and CMARS (Table 2).

Table 2. Averages of performance results of the models built for the data sets.

		Training		Test		Stability
Data set number	Performance Measures	MARS	CMARS	MARS	CMARS	MARS	CMARS
1	MAE	0.4852	0.4518	0.6549	0.6946	0.7399	0.6692
	MSE	0.3814	0.3520	0.6584	0.8507	0.5486	0.4734
	R^2	0.6254	0.6757	0.4121	0.3962	0.6259	0.5594
	PWI	0.9984	0.9968	1.0000	0.9970	0.9984	0.9938
	PRESS	27.9504	97.7900	27.5762	35.6460	0.6944	0.5748
2	MAE	0.0004	0.2029	0.0005	0.2093	0.7568	0.9433
	MSE	0.0000	0.0592	0.0000	0.0625	0.5113	0.9150
	R^2	1.0000	0.9982	1.0000	0.9984	1.0000	0.9997
	PWI	0.9885	1.0000	0.9852	1.0000	0.9883	1.0000
	PRESS	0.0000	6.7330	0.0002	3.9259	0.5512	0.5891
3	MAE	0.2444	0.2145	0.8039	0.7362	0.3352	0.3156
	MSE	0.1780	0.2097	4.6815	7.3187	0.0991	0.0568
	R^2	0.8558	0.8880	0.1598	0.1921	0.1907	0.2194
	PWI	0.9819	0.9819	0.9748	0.9711	0.9710	0.9743
	PRESS	10.9591	10.1713	672.5287	685.3657	0.1388	0.1267
4	MAE	0.4984	0.4888	0.6878	0.6881	0.7295	0.6616
	MSE	0.4275	0.4590	0.8773	0.9519	0.5313	0.3989
	R^2	0.5910	0.6026	0.2936	0.2923	0.5027	0.3933
	PWI	0.9964	0.9934	0.9902	0.9898	0.9927	0.9910
	PRESS	142.4560	124.8675	156.0576	172.4247	0.8128	0.7461
5	MAE	0.2106	0.2083	1.5833	1.3309	0.2566	0.2176
	MSE	0.2283	0.2797	155.7983	108.1064	0.0746	0.0781
	R^2	0.7436	0.7266	0.0115	0.0118	0.0147	0.0163
	PWI	0.9819	0.9855	0.9818	0.9851	0.9866	0.9925
	PRESS	79.1786	87.7969	30595.9500	19218.3500	0.0494	0.1199
6	MAE	0.2550	0.2421	0.3839	0.3715	0.6732	0.6560
	MSE	0.1183	0.1097	0.5961	0.3970	0.3057	0.3063
	R^2	0.8848	0.8973	0.6250	0.7109	0.7069	0.7928
	PWI	0.9899	0.9904	0.9871	0.9851	0.9924	0.9935
	PRESS	46.7619	41.8522	17092.2200	5279.0400	0.3535	0.2721
7	MAE	0.1628	0.1591	0.2437	0.2434	0.5979	0.5897
	MSE	0.0503	0.0511	0.2872	0.2891	0.2884	0.2849
	R^2	0.9525	0.9534	0.7930	0.7933	0.7439	0.7462
	PWI	0.9906	0.9898	0.9888	0.9883	0.8952	0.8943
	PRESS	33.3882	32.8392	100.8555	97.7900	0.5579	0.5464
8	MAE	0.5290	0.5081	0.6745	0.6849	0.7885	0.7467
	MSE	0.4694	0.4493	0.9931	1.1457	0.5079	0.4287
	R^2	0.5403	0.5706	0.2360	0.2059	0.4515	0.3778
	PWI	0.9929	0.9923	0.9891	0.9885	0.9962	0.9960
	PRESS	498.1073	465.5898	550.9740	629.8354	0.7948	0.6794
9	MAE	0.1968	0.1543	0.6566	0.6952	0.3053	0.2231
	MSE	0.0770	0.0556	2.1762	2.2735	0.0585	0.0275
	R^2	0.9294	0.9542	0.3244	0.2784	0.3501	0.2918
	PWI	0.9875	0.9868	0.9796	0.9818	0.9903	0.9937
	PRESS	44.2664	28.5964	766.1493	727.2282	0.0956	0.0459

In order to decide whether or not there are statistically significant differences in the performance of the models built, repeated analysis of variance (RANOVA) 31 is performed by using the statistical software SPSS™ 32, and the following hypotheses are tested for each performance measure separately: versus

Here, M stands for the expected value of a performance measure (i.e. MAE, MSE, R², PWI and PRESS) used in the comparisons. When the null hypothesis of RANOVA is rejected at α = 0.05 level of significance, Fisher's Least Significant Difference (LSD) test 32 is also performed to identify the statistically different models. Above testing procedure is applied for both training and test data sets in addition to the stabilities of the measures used in the comparisons, and the results are shown in Table 3.

Table 3. Overall performances (mean ± standard deviation) of MARS and CMARS methods.

	Training		Test		Stability
	MARS	CMARS	MARS	CMARS	MARS	CMARS
MAE	0.288* ±	0.292 ±	0.632 ±	0.628* ±	0.576 ±	0.559* ±
	0.174	0.143^**	0.427	0.345^**	0.222^**	0.251
						(p-value = 0.094)
MSE	0.215*±	0.225 ±	18.452±	13.488*±	0.325*±	0.330 ±
	0.175^**	0.186	52.056	42.145^**	0.215^**	0.274
				(p-value = 0.042)
R^2	0.790 ±	0.807* ±	0.428 ±	0.431* ±	0.509* ±	0.488 ±
	0.169	0.168^**	0.310^**	0.317	0.303^**	0.309
		(p-value = 0.000)
PWI	0.990 ±	0.991* ±	0.986 ±	0.987* ±	0.979 ±	0.981* ±
	0.006	0.006^**	0.009	0.009	0.056	0.056
						(p-value = 0.001)
PRESS	99.44 ±	91.51* ±	5551 ±	2983* ±	0.450 ±	0.410* ±
	155.10	142.90^**	11252	7578^**	0.304	0.272^**
		(p-value = 0.004)		(p-value = 0.001)		(p-value = 0.042)
Notes: * Indicates better performance with respect to mean; p-value of LSD test is recorded within the parentheses when there is a statistically significant difference in means.
^** Indicates better performance with respect to standard deviation.

5.5. Results

5.5.1. Overall performance

The mean and standard deviation values of all accuracy and complexity measures for the training and test data sets are presented in Table 3 as well as those of the stability of the measures. In any data set, greater mean indicates better performance of the associated method while smaller standard deviation indicates more robust method.

Depending on the results presented in Table 3, the following conclusions can be drawn:

•	In all training and test data, and stability comparisons, as far as differences in the means are concerned, there are no cases where MARS is statistically significantly better than CMARS.
•	CMARS performs better and is more robust than MARS in training data sets with respect to most of the comparison measures also include the complexity measure, MSE.
•	CMARS performs better and is more robust than MARS in testing data sets with respect to all measures.
•	CMARS is more stable with respect to most of the measures.
•	MARS is more robust than CMARS in stability with respect to most of the measures.

5.5.2. Performance with respect to sample size

Mean of all accuracy measures for MARS and CMARS for different sample sizes are recorded in Table 4.

Table 4. Average of accuracy measures with respect to different sample sizes.

		Training		Test		Stability
Measures	Size	MARS	CMARS	MARS	CMARS	MARS	CMARS
MAE	Small	0.243*	0.290	0.486*	0.547	0.611	0.643*
	Medium	0.321	0.313*	0.885	0.797*	0.553*	0.512
	Large	0.296	0.274*	0.525*	0.541	0.564*	0.520
MSE	Small	0.186*	0.207	1.780*	2.744	0.386	0.482*
	Medium	0.258*	0.283	52.424	36.485*	0.304*	0.261
	Large	0.199	0.185*	1.152	1.236*	0.285*	0.247
R^2	Small	0.827	0.854*	0.524	0.529*	0.606*	0.593
	Medium	0.740	0.742*	0.310	0.338*	0.408*	0.401
	Large	0.807	0.826*	0.451*	0.426	0.515*	0.472
PWI	Small	0.990	0.993*	0.987	0.989*	0.986	0.989*
	Medium	0.989	0.990*	0.986	0.987*	0.991	0.992*
	Large	0.990	0.990	0.986	0.986	0.961	0.961
PRESS	Small	12.970*	38.231	233.368*	241.646	0.461*	0.430
	Medium	89.466	84.839*	15948.076	8223.272*	0.405*	0.379
	Large	191.921	175.675*	472.660*	484.951	0.483*	0.424
Note: * Indicates better performance.

The effect of sample size on the performance of the methods can be summarized as follows:

•	MARS and CMARS performance decrease as the training/test sample size increases from small to medium; their performance increase as the training/test sample size increases from medium to large (except for PWI and PRESS). MARS and CMARS performance for small and large training samples are mostly similar (except for PRESS); they perform better in small test samples (except for MSE).
•	MARS performs better than CMARS mostly on small training samples; CMARS performs better than MARS mostly on medium to large training samples (except for MSE).
•	CMARS and MARS perform better mostly on small training/test samples.
•	CMARS performs better than MARS on large training and test samples with respect to MSE, a complexity measure.
•	CMARS and MARS are more stable on small data sets.
•	MARS is more stable than CMARS on medium to large data sets while CMARS is more stable than MARS on small data sets.

5.5.3. Performance with respect to scale

Mean of all measures for MARS and CMARS for different scales are given in Table 5.

Table 5. Average of measures for different problem scales.

		Training		Test		Stability
Measures	Size	MARS	CMARS	MARS	CMARS	MARS	CMARS
MAE	Small	0.382	0.367*	0.529*	0.542	0.689*	0.640
	Medium	0.247*	0.306	0.753	0.742*	0.601	0.636*
	Large	0.232	0.204*	0.615	0.601*	0.438*	0.398
MSE	Small	0.286*	0.287	0.608*	0.697	0.456*	0.386
	Medium	0.233*	0.263	52.264	36.438*	0.365	0.474*
	Large	0.124*	0.125	2.485*	3.330	0.154*	0.130
R^2	Small	0.723	0.744*	0.500*	0.494	0.624*	0.566
	Medium	0.761	0.765*	0.416*	0.405	0.489*	0.465
	Large	0.760	0.785*	0.340	0.370*	0.450	0.463*
PWI	Small	0.995*	0.993	0.993*	0.992	0.962*	0.960
	Medium	0.987	0.992*	0.985	0.991*	0.957	0.962*
	Large	0.986	0.986	0.981*	0.979	0.985	0.987*
PRESS	Small	67.932*	85.166	94.830*	101.954	0.688*	0.622
	Medium	192.429	186.707*	10382.308	6617.370*	0.465*	0.463
	Large	33.996	26.873*	6176.966	2230.545*	0.196*	0.148
Note: * Indicates better performance.

The effect of problem scale on the performance of both methods can be evaluated as follows:

•	MARS and CMARS perform better (or the same) as the scale changes from small to medium and medium to large with respect to the measures (except for PRESS) in training samples.
•	MARS and CMARS perform the best on large-scale training data sets (compared to others) with respect to PRESS.
•	CMARS performs better than MARS on medium or large-scale training/test data sets.
•	CMARS perform better and is more stable than MARS on medium scale with respect to MSE.
•	CMARS and MARS are more stable on small-scale data sets.
•	MARS is more stable than CMARS on small or large-scale while CMARS is more stable on the medium-scale.

5.5.4. Interactions among methods, sample size and problem scale

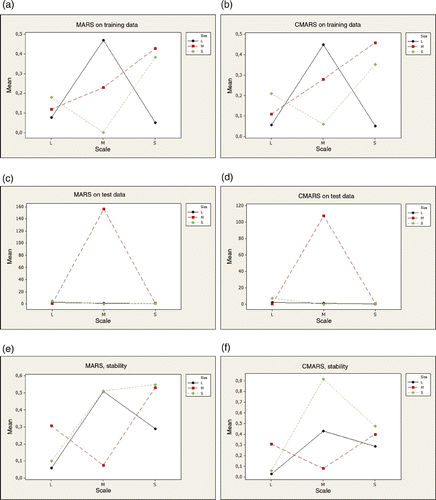
The performance of the methods studied as the sample size changes mainly depends on the problem scale in training samples with respect to MAE (p-value = 0.0), R² (p-value = 0.0), PWI (p-value = 0.0) and PRESS (p-value = 0.002). This indicates the existence of interaction among the methods, sample size and the scale of data sets. Similar dependency is also detected in test samples with respect to MAE (p-value = 0.001), MSE (p-value = 0.002), PWI (p-value = 0.002) and PRESS (p-value = 0.0). This interaction exists in stability of the measures MAE (p-value = 0.001), MSE (p-value = 0.0), R² (p-value = 0.049) and PWI (p-value = 0.0) as well. Due to the significant three-way interaction effects, a typical pattern for the best performance of the methods is hard to detect. Nevertheless, interaction plots (Figure 4) can be helpful for determining the best size-scale combination for a method in relation with a measure. To examplify, when the complexity measure, MSE, is considered, similar best performances are obtained on small/large scale and large training/test samples for MARS and CMARS methods. On the other hand, the best stability of MSE is obtained only for large scale and large samples for both methods. In general, but not a rule, we may say that better performances of MARS method are obtained for small size-small scale, and that of CMARS method for small size-medium scale data sets.

Figure 4. Interaction plots of size and scale for the complexity measure, MSE, for MARS and CMARS.

5.5.5. Performance with respect to efficiency

To compare the efficiencies of the methods, in this study, the computational run times (in seconds) for each training data sets are recorded on the computer with Intel (R) Pentium (R) CPU 3.40 GHz processor and 32-bit operating system Windows®. The maximum run time obtained for each training data sets are given in Table 6.

Table 6. Classification of run times (in seconds) of the methods with respect to size and scale.

		Scale
		Small	Medium	Large
	Small	MARS: < 2 s	MARS: < 2 s	MARS: < 2 s
		CMARS: < 21 s	CMARS: < 20 s	CMARS: < 21 s
Sample size	Medium	MARS: < 4 s	MARS: < 10 s	MARS: < 5 s
		CMARS: < 46 s	CMARS: < 35 s	CMARS: < 43 s
	Large	MARS: < 20 s	MARS: < 26 s	MARS: < 13 s
		CMARS: < 89 s	CMARS: < 140 s	CMARS: < 103 s

We can summarize Table 6 as follows:

•	Run times seem to be related to the sample size but not the problem scale particularly for small size data.
•	The least amount of run times for both methods is obtained for small size samples regardless of the scale.
•	In small size data sets, run times of CMARS method are almost ten times as much that of MARS method. As sample size increases, they reduce up to three to five times as much to that of MARS.

5.5.6. Performance on noisy data

Finally, a simulation study is carried out using MATLAB® to see the effect of noise on performance of both methods. For this purpose, a test problem is adopted from Jin et al. 33, which is originally taken from 34. In this problem, data are artificially created from the following function: (25) where the regressors, x₁ and x₂ are assumed to have uniform (−10, 10) distribution. This data set is referred to as ‘noise-free’ data. To obtain noisy data, normally distributed noise, ε, having zero mean is added to the response, f (x). Here, the variance of the noise is assumed to be 1/100 of the variance of f (x) given in (25). When −5 ≤ x₁, x₂ ≤ 5, however, the variance of the noise is assumed to be 1254.9/100 = 12.55 (see 33, p. 13]). This way we try to locally reduce the error variance. After training data sets each having 100 observations are created as described above with and without noise, MARS and CMARS methods are fitted to them, and both accuracy and complexity measures are obtained. Then, test data are created by rerunning the code with different seeds, and the same measures are calculated. Results are shown in Table 7. In addition, to measure the sensitivity of the fits to the noisy data, the performance measures are re-calculated using fitted values obtained for the noisy data, and the noise-free data points (instead of the noisy ones). These latter measures are reported under the category labelled as ‘noisy fit vs noise-free data’ in Table 7.

Table 7. Performance results of the methods on noisy data.

			Measures
	Data sets	Methods	MAE	MSE	R^2	PWI	PRESS
Noise-free data	Training	MARS	0.4318	0.3780	0.9999	0.9900	31.737
		CMARS	0.3188*	0.2670*	1.0000*	0.9900	16.127*
	Test	MARS	0.5573	0.6838*	0.9999	0.9900	58.029
		CMARS	0.5496*	0.7771	0.9999	1.0000*	47.534*
Noisy data	Training	MARS	6.2843	69.4419*	0.9869	1.0000*	6588.309
		CMARS	6.2281*	69.6126	0.9870*	0.9900	6522.154*
	Test	MARS	7.6158	102.1720	0.9895	0.9900	9630.179
		CMARS	7.3908*	97.1906*	0.9896*	1.0000*	9058.165*
Noisy fit vs noise-free data	Training	MARS	3.2556	21.3454	0.9963	1.0000*	2042.576
		CMARS	3.2156*	20.1152*	0.9966*	1.0000*	1898.328*
	Test	MARS	3.3300	21.8986	0.9991	0.9800	2070.795
		CMARS	3.0013*	15.2437*	0.9993*	1.0000*	1421.167*
Note: * Indicates better performance.

As it can be seen in the above table, CMARS method overperforms MARS on noisy data. CMARS fits to noisy data seem to provide not only a closer fit to the noisy data itself but also to noise-free ones compared to MARS. We should note here that the data set used in the comparison is small scale and small data. More analysis with different types of data are needed before generalizing this conclusion.

6. Conclusion and future research

This study provides a new contribution to the well-known MARS method which has been applied in many areas during the last decade. The MARS algorithm is modified by constructing a PRSS as a Tikhonov regularization problem. This problem is then solved by using continuous optimization, particularly, CQP. This provides us an alternative modelling technique for MARS, which is named as CMARS.

For examining the efficiency of the developed method CMARS, it is compared with MARS method by using nine data sets, each with different features. In comparisons, method-free measures, such as R² and MSE are used.

According to the results, in general, CMARS produces more accurate, robust and stable models than MARS. Besides, it results in less complex and robust models than MARS on test data sets. We should emphasize here that better performance of CMARS on test data with respect to all measures indicates the power of our method. Another important finding is that CMARS performs better than MARS mostly on medium and large training data sets, and large-scale training and test data sets. This finding indicates the success of CMARS as scale increases. In addition, CMARS is more stable on the medium scale data.

Because the performance of the methods are based on the size and the scale and type of data (i.e. training, test, stability), no pattern is detected for the best performance. However, we can say that CMARS method is more successful on medium scale, small data sets. Furthermore, our method performs better than MARS on noisy data. Having the above results of comparison study, we can say that CMARS may be a good alternative to MARS.

At this point, the only drawback of our method is not being as efficient as MARS. And, accuracy gains are small in absolute values compared to the run times; however, they are statistically significantly better only in favour of CMARS. Therefore, to improve CMARS algorithm to reduce computational run time, further research is being carried out. Within this context, an improvement for the forward part of the algorithm is being considered. Because the first part of MARS algorithm determines knot points among the data points for obtaining BFs, increasing the number of data points results in, a one-to-one manner, an increase in the number of knot points. Therefore, it gives rise to complexity. For this reason, a study is underway to determine suitable knot points for the data set by using clustering theory, supported by statistics and optimization theory 22.

On the other hand, CMARS has a disadvantage that it uses the model including the maximum number of BFs provided by the MARS algorithm. Hence, it may provide more complex models than MARS. To overcome this deficiency, insignificant model co-efficients can be detected and removed. Hence, the model size can be decreased.

By this article we intented to give a contribution to the theory, methods and applications in the fields of nonparametric regression/classification and data mining, as well as to invite future research challenges.

Acknolwedgements

This study is supported by the Turkish Scientific and Technological Research Institute (TUBITAK) under the project number 105M138. One of the authors, Fatma Yerlikaya-Özkurt, has been supported by the TUBITAK Domestic Doctoral Scholarship Program.

Appendix

A.1. Tikhonov regularization

This regularization method is used to make ill-posed 19,35 problems well-posed (regular or stable). A Tikhonov solution can be expressed quite easily in terms of SVD of the coefficient matrix X of a regarded linear system of equations Xβ = y.

There are different kinds of Tikhonov regularization represented by minimization problems including the penalized length of the solution β, and these problems can be solved using SVD 19. Here the norm (length) ‖β‖₂ of β represents the complexity of the possible solution 19. But, in many situations, it is preferred to obtain a solution which minimizes the norm of first- or second-order derivative of β. These derivatives are given by first- or second-order difference quotients of β, regarded as a function that is evaluated at the ‘points’ i and i + 1. These difference quotients approximate first- and second-order derivatives; all together they are comprised of products Lβ of β with a matrix L that represent the discrete differential operators of first- and second-order, respectively. In the original case, we aim at the norm ‖β‖₂ itself, and we have L = I (unit matrix). Herewith, we use the following optimization problem (26)

Generally, (26) comprises higher-order Tikhonov regularization problems which can be solved using generalized singular value decomposition (GSVD) 19. In our article, we apply a Tikhonov regularization problem (Section 3.2) in which we have a different type of L matrix for MARS, and we solve this problem (Section 3.3) by using CQP. In Sections 3.2 and 3.3, we explain and discuss Tikhonov regularization and CQP in detail.

GCV can be used, which shows the lack-of-fit for a MARS model is defined as (27) where 36. Here N is the number of sample observations as defined before, u is the number of linearly independent BFs, K is the number of knots selected in the forward process and d is a cost for BF optimization as well as a smoothing parameter for the procedure. Note that if the model is additive then d is taken to be two; if the model contains interaction terms then d is taken to be three 3,20.

C.1. General notation

To evaluate the performances of MARS and CMARS, several measures can be used. The performance measures that we use in our applications and their general notation are presented in the following:

yi	=	ith observed response value,
ŷi	=	ith fitted response,
	=	mean response,
N	=	number of observations,
p	=	number of terms in the model,
ei = yi − ŷi	=	is the ith ordinary residual,
hi	=	is a leverage value for the ith observation, which is the ith diagonal element of the hat matrix, H. The hat matrix is H = X (XT X)−1 XT, where X is an N × p design matrix and rank(X) = p (p ≤ N).

C.2. Accuracy measures

C.2.1. Multiple coefficient of determination (R²)

This value is a coefficient of determination. It indicates how much variation in response is explained by the model. The higher the R², the better the model fits the data. The formula is

C.2.2. Mean absolute error (MAE)

MAE measures the average magnitude of error. The smaller the MAE, the better it is. The formula is:

C.2.3. Prediction error sum of squares (PRESS)

PRESS is an assessment of a model's predictive ability. PRESS, similar to the residual sum of squares, is the sum of squares of the prediction error. In general, the smaller the PRESS value, the better the model's predictive ability is. In least squares regression, PRESS is calculated with the following formula: Many of these measures can be found in any statistic text book such as 1.

C.2.4. Proportion of residuals within some user-specified range (PWI)

PWI is the sum of indicator variables over all observations divided by the total number of observations. The indicator variables take the value of one if the absolute value of the difference between actual and predicted response is within some user-specified thresholds 37. Here, we have used three ±3σ as a threshold. Hence PWI can be considered as another measure of accurate prediction of the dependent variable.

C.3. Complexity measure

C.3.1. Mean square error (MSE)

MSE is an unbiased estimate of the error variance. It is affected by both residual sum of squares and number of terms in the model. The smaller the MSE, the better it is. The formula is

C.4. Stability

The prediction model obtained from the methods is stable when it performs just as well on both seen (training) and unseen (test) data sets. The stability can be measured by where CR_TR and CR_TE are the performance measure values for the test and the training, respectively. Closer values of this measure to one indicate higher stability 38.