Abstract
An approach based on multivariate function decomposition is presented with the aim of performing the learning optimization of multi-input-multi-output (MIMO) feed-forward neural networks (NNs). The proposed approach is mainly dedicated to all those cases in which the training set used for the learning process of MIMO NNs is sizeable and consequently the learning time and the computational cost are too large for an effective use of NNs. The basic idea of the presented approach comes from the fact that it is possible to approximate a multivariate function by means of a series containing only univariate functions. On the other hand, in many practical cases, the conversion of a MIMO NN into several multi-input-single-output (MISO) NNs is frequently adopted and investigated into state-of-the-art NNs. The proposed method introduces a further transformation, i.e. the decomposition of a MISO NN into a collection of single-input-single-output (SISO) NNs. This MISO–SISOs decomposition is performed using the previously cited series coming from the technique of the multivariate decomposition of functions. In this way, each SISO NN can be trained on each one-dimensional function returned from the cited decomposition, i.e. using limited data. Moreover, the present approach is easy to be implemented on a parallel architecture. In conclusion, the presented approach allows us to treat a MIMO NN as a collection of SISO NNs. Experimental results will be shown with the aim of proving that the proposed method is effective for a strong reduction of learning time by preserving anyway the accuracy.
1. Introduction
Applications of multi-input-multi-output (MIMO) neural networks (NNs) are quite frequent in many scientific fields Citation1,Citation2. In these applications, MIMO NNs with m input neurons and n output neurons are directly applied. The drawback of this direct approach is the high computational cost to be paid when the training patterns and the number of neurons are quite large. Thus, with the aim of reducing the processing time due to the learning process, many authors try to simplify the problem using a collection of n multi-input-single-output (MISO) NNs by means of a multiplexing approach Citation3–6. On the other hand, the learning process and the design of the NNs would be quite simplified if it were possible to operate a further decomposition of each single MISO NN to a collection of single-input-single-output (SISO) NNs. This last operation is not at all an easy task, unfortunately. In this article, we propose a method to decompose a MISO NN into several SISO NNs. Although several attempts to decompose NNs are already present in literature Citation7–9, the method proposed here is based on a novel iterative Singular Value Decomposition (SVD) based function decomposition which approximates a multivariate function by a series of univariate functions. The set of univariate functions is used to learn single SISO NNs. The experimental results show that the total learning time required for the training of all SISO NNs is strongly reduced compared with the direct application of MISO NNs. Finally, due to the particular structure of the resulting series, a further speed-up is possible by parallelizing the learning of each SISO NN on separate computers by a simple PC cluster.
2. SVD-based approximations of bivariate functions
The proposed method is based on the extension to multivariate functions of the method proposed in reference Citation10 valid for bivariate functions. In fact, in reference Citation10, how to efficiently approximate a continuous over a rectangular domain by a finite series of univariate functions using a SVD-based method is shown. In this article, we will show how to decompose a function,
, with
.
Let us recall the method Citation10 valid for a bivariate function. As it is known, any rectangular m × n matrix M can be written by SVD as:
(1)
where S is a rectangular diagonal matrix having its non-zero diagonal entries equal to the singular values
, with
and
, written in descending order, i.e.
, whereas
and
, i.e. U and V are orthogonal.
Equation (1) returns the expression:
(2)
where
and
are orthonormal vectors coincident with the column vectors of the matrices U and
, respectively. Usually, an approximate version of (1) or (2) is used. It happens when the smallest singular values are neglected, i.e.
with
, whereas
is forced to be 0, for
. Using this approximation, we have:
(3)
i.e. now
. But if we select
in such a way, the following inequality is verified
(4)
with
and we can obtain that
if
. Thus, by fixing
, we fix the accuracy of the approximation (3).
It is interesting to note that we can assume that the M entries are coming from the sampling of a bivariate function , i.e. we have
with
and
. Similarly, we can assume that the columns of the matrices U and
are coming from the sampling of unknown univariate functions, i.e.
and
.
Under these assumptions, we can write (2) as follows:
(5)
Obviously, an approximation of the (5) can also be provided. In this case, by applying (3) after having obtained with a fixed accuracy
from (4), we can write:
(6)
The several unknown univariate functions appearing in (5) and (6) can be estimated by suitable curve-fitting techniques (e.g. using NNs), obtaining approximate univariate known functions , and
. Finally, we can write that:
(7)
this is the way to interpolate a bivariate function by means of simply univariate functions.
3. Analytical SVD-based approximations of multivariate functions
In this section, we present a novel approach that is the extension to multivariate functions of the decomposition (7) valid for bivariate function approximation. By means of the proposed decomposition, we will able to manage univariate function (SISO) for approximating a multivariate function (MISO). This fact is fundamental for the aim of this article, i.e. to improve the NNs training in MIMO cases. As will be demonstrated soon, using the SVD-based multivariate function decomposition presented here, we will have the possibility to achieve two fundamental goals for NNs, when they are used as universal interpolators: (1) strong reduction of the size of training set necessary to achieve a fixed accuracy and (2) parallelization of the training of feed-forward NNs with a strong reduction of learning time. Thus, let us start by considering a trivariate function that has been sampled in several points indicated by
and
with
,
and
. It is evident that the function becomes bivariate if we consider its projection on the generic plane
. Thus, we can use (5) in the following form:
(8)
Where the sth values are the singular values referred to the projection on the plane
. Then, they can be thought as the numerical result of a sampling along the
axis of a unknown function that we simply call
. It is also evident that
and
can be seen as the numerical results of a sampling along the axes
,
and
of the unknown bivariate functions that we simply call
,
. Then, Equation (5) is applicable to them, obtaining:
(9)
(10)
where the meaning of the new appearing symbols is easy to identify by comparison with those appearing in Equation (5). Then, the final trivariate function decomposition can be obtained as follows:
(11)
Similarly, as it has been observed that Equation (7) is an approximation of Equation (5), it will be possible to write an approximation of Equation (11):
(12)
The several unknown univariate functions appearing in (11) can be now estimated by suitable curve-fitting techniques (e.g. using NNs), obtaining approximate univariate known functions ,
,
and
; the values
and
are simply singular values, instead.
For extension, let us consider a tetra-variate function . In this case, we can consider (11) as the decomposition of the trivariate function obtained by projection of the assigned tetra-variate function on the generic hyper-plane
, where
is the lth constant value among all the values obtainable by sampling with
. On the other hand, each trivariate projected function on the plane
can be further projected on a
developing a procedure that is similar to that we previously have followed for bivarite and/or trivariate functions. Obviously, for multivariate functions, we have just to operate a recursive multi-projection on suitable hyper-planes.
4. Algorithmical SVD-based approximations of Multivariate functions
From the previous argumentations, with the aim to convert the described mathematical procedure into a numerical algorithm, it is convenient to define a decomposition operator (i.e. a subroutine) . In such a way, we indicate the decomposition of the function,
, with
with
. When it is applied,
generates
new multivariate functions (children functions):
,
and
with
and
,
and
, whose dimensions are
and
, respectively, i.e. two and one degrees smaller than the dimension of x. Thus, it will be immediate to write the recursive approach as follows:
(13)
Obviously, according to (5), for a bivariate function decomposition we have:
(14)
whereas, for non-decomposable functions, i.e. univariate functions
, and constant functions, we have:
(15)
(16)
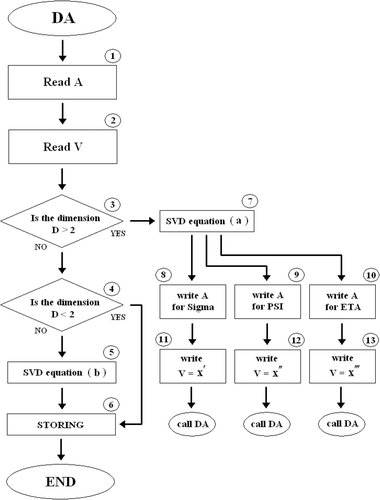
The algorithm is recursive and requires several checks on the data and processing flow. We will try to give its general description by taking advantage of the flowchart shown in .
The first instructions in blocks 1 and 2 of the flowchart of are referred to the load of the input array A containing the values returned by the unknown multivariate function to be approximated and their corresponding coordinates appearing in the vector V. We indicate the number of independent variables with D. If , block 3 activates the block 7 which operates as in (13). Otherwise, if
, block 3 activates block 4. In its turn, if
, block 4 activates block 5 that evaluates the expression (14); otherwise, block 4 activates block 6 in which the expressions (15) and (16) are performed and finally the algorithm is ended. In fact, when
, we have that the function to be decomposed is bivariate, whereas when
, the function is simply univariate or a constant.
By summarizing:
| 1. | if D < 2, the following sequence is followed: START – block 1 – block 2 – block 3 – block 4 – block 6 – END; | ||||||||||||||||||||||
| 2. | if D = 2: START – block 1 – block 2 – block 3 – block 4 – block 5 – block 6 – END; | ||||||||||||||||||||||
| 3. | if D > 2, after having applied (13), three independent sub-path are activated, any single path is referred to one of the children functions:
| ||||||||||||||||||||||
It is worth noting that since the three paths c.1, c.2 and c.3 are independent, they lend themselves to be run in parallel. Finally, it is still worth noting that at the end of the three c's paths there is the block START. It is for indicating that the algorithm is calling itself, i.e. it is recursive. In fact, the blocks 8, 9, 10, 11, 12 e 13 create new input data arrays to be fed to block 1 and to block 2 referred to a further decomposition of the new generations of children functions. Obviously, at each new recursive call, the dimension D will be smaller than that referred to the previous call. This means that after a suitable number of calls, we will have the condition and the recursive algorithm converges to its end.
5. Application to the optimization of NNs and parallel training: validation tests
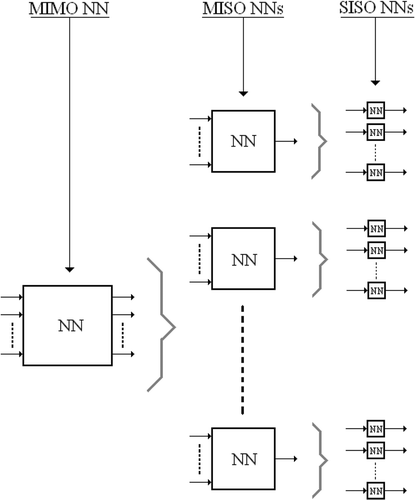
The recursive algorithm that performs the SVD-based approximations of multivariate functions described in the previous section is suitable to be adopted for the optimization of the training of feed-forward NNs for MIMO problems. Although MIMO problems can be directly managed by a MIMO NN, the training becomes harder and harder with the growing of the complexity of the problem that can be estimated as a function of number of input and output variables and the size of the set of data that are necessary for a correct NN learning. Thus, the idea is to decompose the problem in such a way to have to manage a collection of SISO NNs that are always more simple to train. This simplification is mainly due to the strong reduction of the size of the training data (it is obvious that now we have also just one input and one output). The proposed NN optimization is schematized in in which the transformation of a MIMO NN in a collection of SISO NNs is shown. The MIMO NN is first transformed in the same way in which many authors have already tried to simplify the MIMO problem using a collection of MISO NNs by means of a multiplexing approach Citation6. Further transformation is really the core of the present approach. In fact, using SVD-based approximations of multivariate functions, each MISO NN can be further decomposed in a collection of SISO NNs. Simply, each SISO NN has the task of interpolating each univariate function coming from the SVD-based approximations.
It can be useful to make an example about the SVD-based NN training. Since the core of the proposed method consists of the decomposition of a MISO problem in a collection of SISO problems, let us consider an array of data, A (see ), obtained by sampling the following trivariate MISO test-function.
(17)
A direct MISO feed-forward back-propagation NN approach (3-input, 1-output) has requested the use of a 3-input, 1-output NN with two hidden layers. The implemented training strategy uses the early stopping (es) method for avoiding the overtraining. The es controls the sign of the derivative of the MSE estimated on a further suitable set of patterns (it will be next indicated ‘es-MSE’) different from that used for the training. The role of es is to stop the training when the derivative of the es-MSE becomes positive. Finally, with the aim of evaluating the effectiveness of the NNs to perform accurate solutions on original out-of-training data, we have interrogated the trained NNs by means of 100 random new test patterns. Then, we have evaluated the MSE obtained at the end of the whole learning process both using standard MISO application and SVD-based decomposition. These last MSE values will be next indicated with ‘MSE (test set)’. For case (17), the number of training patterns was quite large: (50 samples for dimension). This allows us to obtain a fitting with a very small MSE (test set) less than
. The relative learning time was obtained as 35 h using a dual core processor, 2.71 GHz. On the contrary, through the previous SVD-based decomposition, the same MSE (test set) of the MISO approach has been obtained with 77 SISO feed-forward back-propagation NNs (one-input one-hidden with 10 hidden neurons, and one-output) trained on just 50 samples per dimension. In this case, the whole learning process has required just 110 min (time that is comprehensive of the SVD decomposition). From the previous test-example, it emerges that the SVD-based NN training is strongly competitive for MISO problems. However, a further fundamental advantage of the proposed approach emerges. In fact, the training of each SISO NN can be performed by parallel computing being each SISO NN independent from each other (see ). In fact, if we consider a cluster of 20 nodes (PC) for the MIMO problem (5), we obtain that each NN can be trained in parallel on a single stand-alone computer. The processing time necessary for the learning process in this last case was reduced to just 6 min. This value highlights the computational power of the proposed approach when it is compared with the 35 h that were necessary for the training of the MISO NN. On the other hand, it is much harder to parallelize the standard algorithms that are directly used to train a MISO NN. Let us now consider the following test-function:
(18)
It is important to remark that for problem (18) the direct MISO NN approach does not produce a valid solution in 35 h, whereas the SVD-based SISO NN approach returns good performances with acceptable elaboration time (comprehensive of the SVD decomposition). The advantage of parallelization in terms of elaboration time is also evident.
Finally, let us consider a harder 5-variate problem:
(19)
The obtained results are summarized in .
The discussion previously made for (18) can also be used for (19). Moreover, it is important to remark that for (18) the array of data have been made by 50 samples per dimension, whereas for (19) the sampling was 15 samples per dimension. The smaller number of samples for case (19) than (18) is justified by the necessity to hold allocation of memory down for the MISO NN ( patterns). On the contrary, in the less complex case (18), it was possible to allocate
patterns without problems for the MISO NN. This opportunity has been exploited for demonstrate that the proposed SISO decomposition can reach very large accuracy (MSE (test set) = 0.05) even if just
patterns are used. The more complex case (19) has been instead presented to demonstrate how the obtained MSE values can be still low, even if we use a lower number of patterns due to problems of memory allocation.
Then, even if the number of SISO NNs for problem (19) is larger than that for problem (18), the total processing time (comprehensive of the SVD decomposition) is smaller for (19) than for (18). The observed decrease in processing time from the less complex case (18) to the more complex case (19) is not paradoxical because, in the case (19), the lower number of training patterns than in (18) allows a lower training time for each NN. Obviously, as consequence, the reduced number of patterns produces a higher value of es-MSE in case (19) than in (18). Thus, the lower response time due to ‘early stopping’ has caused a further training-time decrease for each singular SISO NN although we have used a much larger number of NNs for case (19). These higher values of es-MSEs have naturally caused a higher value on the MSE (test set) for case (19) than for case (18) (see 1 and ). Finally, further remarks about the effectiveness of the parallelization must be made. In fact, if we consider the ratio between the number of the NNs elaborated for cases (19) and (18), we obtain 27394/77 = 355.76, which means that for the higher complexity of the case (19), we have to manage a much larger number of NNs. But the ratio between the number of training patterns for cases (19) and (18) is just 15/50 = 0.3. This means that the effectiveness of the parallelization cannot be measured simply by the ratio between the computation time with/without parallelization: 110/6 = 18.3 for case (18) and 54/5 = 10.8. In fact, in this way, we could reach a false conclusion that for higher number of inputs, the effectiveness of the parallelization dramatically decreases. But we must consider that for a growing number of inputs, the complexity of the problem always requires a price to pay to ensure a solution with acceptable accuracy. Thus, for the 5-input case (19), we have paid a higher value of MSE (test set) (that is however an acceptable low value) than for 3-input case (18). However, we still get a great advantage since the processing time was reduced from 54 min to 5 min. Last, but not least, it is also evident that the effectiveness of the parallelization strongly depends on the number of cluster nodes (note that the previous cases (18) and (19) have been elaborated using always 20 PCs.). Anyway, the validation examples (18) and (19) have shown that classical MISO NNs (i.e. networks that are not SISO decomposed) have never found acceptable solution (see and ). This justifies the fact that, apart from parallelization, the proposed method based on MISO decomposition can be very attractive because it allows us to achieve acceptable solutions also in such cases where a conventional approach fails. This capability is due to the fact that the training of a SISO NN is much simpler than that of a MISO NN. It is clear that under the same conditions, the parallelization will reduce the computation time anyway, depending on the number of cluster nodes. Thus, the possibility that the proposed method seems to be parallelized is surely a further benefit.
Table 1. Results for (18).
Table 2. Results for (19).
6. Conclusions
An algorithm able to perform the SVD-based approximation of multivariate functions can be very effective when the training set used for the learning process of a MISO NN becomes sizeable. In fact, in many cases, a direct MISO approach returns a solution only if one accepts paying a high computational cost due to the duration of the training process that can be very long. In many cases, no solution can be even available due to the complexity of the MISO function. The SVD-based decomposition, instead, returns a good solution in any case. Moreover, the approach allows the parallelization of the NN training with a strong reduction of the processing times. Thus, since in a wide range of problems, a MIMO NN is decomposable in a multiplex of several MISO NNs, the proposed method allows passing from a MIMO NN to a collection of SISO NNs. The performances of the proposed approach in our experiments show that the presented method is effective to reduce the processing time and, at the same time, to preserve the accuracy of the solutions. In addition to these facts, it is worth noticing that the proposed approach is able to provide acceptable solutions also in such cases in which the conventional use of MIMO (and/or MISO) NN fails.
References
- Lim, KH, Seng, KP, Ang, LM, and Chin, SW, 2009. Lyapunov theory-based multilayered neural network, IEEE Trans. Circuits Syst. Express Briefs 56 (4) (2009), pp. 305–309.
- Yalcin, B, and Ohnishi, K, 2009. Infinite-mode networks for motion control, IEEE Trans Ind. Electron. 56 (8) (2009), pp. 2933–2944.
- Jianyo, L, Yongchun, L, Jianpeng, B, Xiaoyun, S, and Aihua, L, 2009. Flaw Identification Based on Layered Multi-subnet Neural Networks. Tianjin, China: Proceedings of Second International Conference on Intelligent Networks and Intelligent Systems; 2009. pp. 118–128.
- Sun, A, Zhang, A, and Wang, Y, 2006. Largescale Artificial Neural Network Owning Function Subnet. Luoyang, China: Proceedings of 2006 IEEE International Conference on Mechatronics and Automation; 2006. pp. 2465–2470.
- Haikun, W, Weiming, D, and Sixin, X, 2000. Designing Neural Networks Based on Structure Decomposition. Hefei, P.R. China: Proceedings of the 3rd World Congress on Intelligent Control and Automation; 2000. pp. 821–825.
- Kabir, H, Wang, Y, Yu, M, and Zhang, QJ, 2010. High-dimensional neural-network technique and applications to microwave filter modeling, IEEE Trans. Microwave Theory Tech. 58 (1) (2010), pp. 145–156.
- Fiori, S, 2003. Singular value decomposition learning on double Stiefel manifold, Int. J. Neural Syst. 13 (2) (2003), pp. 1–16.
- Huynh, HTrung, and Won, Y, 2009. Training Single Hidden Layer Feedforward Neural Networks by Singular Value Decomposition. Seoul, Korea: Proceedings of 2009 Fourth International Conference on Computer Sciences and Convergence Information Technology; 2009. pp. 1300–1304.
- Rohani, K, Chen, MS, and Manry, MT, 1992. Neural subnet design by direct polynomial mapping, IEEE Trans. Neural Networks 3 (6) (1992), pp. 1024–1026.
- Bizzarri, F, Parodi, M, and Storace, M, , SVD-Based Approximations of Bivariate Functions, IEEE International Symposium on Circuits and Systems (ISCAS 2005), 23–26 May 2005, Vol. 5, pp. 4915–4918.