Inverse source problem in a 2D linear evolution transport equation: detection of pollution source

Abstract

This article deals with the identification of a time-dependent source spatially supported at an interior point of a 2D bounded domain. This source occurs in the right-hand side of an evolution linear advection-dispersion-reaction equation. We address the problem of localizing the source position and recovering the history of its time-dependent intensity function. We prove the identifiability of the sought source from recording the state on the outflow boundary of the controlled domain. Then, assuming the source intensity function vanishes before reaching the final control time, we establish a quasi-explicit identification method based on some exact boundary controllability results that enable to determine the elements defining the sought source using the records of the state on the outflow boundary and of its flux on the inflow boundary. Some numerical experiments on a variant of the surface water biological oxygen demand pollution model are presented.

Keywords:

• inverse source problem
• exact boundary controllability
• optimization
• advection-dispersion-reaction equation
• surface water pollution

1. Introduction

In the last few decades, we have started to see inverse problems be involved in several areas of science and engineering: in medicine, the inverse problem of electrocardiography, for example, is employed to restore the heart activity from a given set of body surface potentials 1. In seismology, inverse source problems are used to determine the hypocenter of an earthquake 2 as well as to study the dynamic problem of seismology, which is one of the most topical problems of geophysical 3. Here, one motivation for our study concerns an environmental application that consists of the identification of pollution sources in surface water: in a river, for example, the presence of organic matter which could have origin such as city sewages, industrial wastes etc., usually drops to too low the level of the dissolved oxygen in the water. Since the lack of dissolved oxygen constitutes a serious threat to human health and to the diversity of the aquatic life, identifying pollution sources could play a crucial role in preventing worse consequences regarding the perishing of many aquatic species as well as in alerting downstream drinking water stations about the presence of an accidental pollution occurring in the upstream part of the river.

In this article, we are interested in the inverse source problem that consists of localizing a sought pollution source spatially supported at an interior point of a 2D bounded domain and recovering the history of its time-dependent intensity function using some boundary records related to the biological oxygen demand (BOD) concentration. This concentration represents the amount of dissolved oxygen required by the micro-organism living in the water to decompose the introduced organic substances 4,5. Therefore, the more organic material there is, the higher the BOD concentration. This article is organized as follows. Section 2 is devoted to stating the problem, assumptions and proving a technical lemma for later use. In Section 3, we prove the identifiability of the sought source from recording the BOD concentration on the outflow boundary of the controlled domain. In Section 4, we establish an identification method that uses the records of the BOD concentration on the outflow boundary and of its flux on the inflow boundary to determine the elements defining the sought source. Section 5 is reserved for deriving the identification results in the case of a rectangular domain. Some numerical experiments on a variant of the surface water BOD pollution model are presented in Section 6.

2. Governing equations and problem statement

We consider a portion of a river represented by a bounded and connected open set Ω of IR² with a Lipschitz boundary ∂Ω = Γ_N ∪ Γ_D. Here, Γ_D denotes the inflow boundary of the domain Ω whereas Γ_N = Γ_L ∪ Γ_out with Γ_L representing the lateral solid boundaries and Γ_out the outflow boundary of Ω. The BOD concentration, denoted here by u, is governed by the following two-dimensional linear advection-dispersion-reaction equation 6,7: (1) where T is the final control time, F represents the pollution source and P is the linear parabolic partial differential operator defined as follows: (2) where V is the flow velocity, R is the reaction coefficient and D denotes the diffusion tensor. Here, V satisfies the so-called dry lateral solid boundary conditions which means that along Γ_L, the normal component of the velocity field V vanishes: (3) where ν is the unit vector normal and exterior to the boundary ∂Ω. In the remainder, we assume some available mean flow velocity data: V = (V₁, V₂)^⊤. Then, according to 8,9, the diffusion tensor D is defined by the 2 × 2 symmetric matrix where the entries D₁, D₀ and D₂ are given by (4) with and D_L, D_T are the longitudinal and transverse diffusion coefficients. As in the most cases of interest we have D_LD_T ≠ 0 and since det(D) = D_LD_T, we assume in the remainder that the matrix D is invertible. To the evolution equation (1), one has to append initial and boundary conditions. For the initial condition, we could use without loss of generality no pollution occurring at the initial control time and thus a null initial BOD concentration. As far as the boundary conditions are concerned, an homogeneous Dirichlet condition on the inflow boundary seems to be reasonable since the convective transport generally dominates the diffusion process. However, other physical considerations suggest the use of a rather Neumann homogeneous condition on the remaining part of the border. Therefore, we employ the following homogeneous conditions: (5) Note that due to the linearity of the operator P and according to the superposition principle, the use of a non-zero initial condition and/or inhomogeneous boundary conditions do not affect the results established in this article.

In this study, we are interested in the inverse source problem that consists of the identification of the source F involved in (1) using some boundary records related to the state u. The main difficulty in such kind of inverse problem is the no identifiability of the source F in its general form. To illustrate this difficulty, we introduce the following common counterexample 10: let f ∈ 𝒟(Ω) be an infinitely differentiable function with compact support in Ω and g = −Δf. Then, v(x, y, t) = tf (x, y) satisfies (6) without having necessarily f + tg null. Therefore, same boundary records may lead to identification of different sources. In the literature, to overcome this difficulty, authors generally assume some available a priori information on the source F: for example, time-independent sources F(x, t) = f (x) are treated by Cannon 11 using spectral theory, then by Engl et al. 12 using the approximated controllability of the heat equation. The results of this last article are generalized by Yamamoto 13,14 to sources of the form F(x, t) = α(t) f (x) where f ∈ L² and the time-dependent function α ∈ C¹[0, T] is assumed to be known and satisfying the condition α(0) ≠ 0. Furthermore, Hettlich and Rundell 15 addressed the 2D inverse source problem for the heat equation with sources of the form F(x, t) = χ_𝒟(x) where 𝒟 is a subset of a disk. They proved the identifiability of 𝒟 from recording the flux at two different points of the boundary. El Badia and Hamdi 16,17 studied the case of a 1D time-dependent point source F(x, t) = λ(t)δ(x − S) where the source position S and the time-dependent intensity function λ are both unknown. They proved the identifiability of the sought source from recording the state and its flux at two interior points framing the source region. Those results have been recently improved by Hamdi 18,19 to requiring only the record of the state at the two observation points, then extended to the 2D stationary problem in 20. Finally, the case where the source depends on the state F(x, t) = G(u(x, t)) was considered by DuChateau and Rundell 21 and Cannon and DuChateau 22.

In this article, we consider a 2D time-dependent point source F defined as follows: (7) where δ denotes the Dirac mass, S = (S_x, S_y) is an interior point to the domain Ω that represents the source position and λ is its time-dependent intensity function which is assumed to be in L²(0, T). In 23, it was shown for a similar problem that using a source F as introduced in (7) implies that (1–5) admits a unique solution u which belongs to (8) Since the source position S is assumed to be interior to the domain Ω, the state u is smooth enough on the boundary ∂Ω to define the following boundary observation operator: (9) where ∑_out ≔ Γ_out × (0, T). This is the so-called direct problem.

The inverse problem with which we are concerned here is that: given Φ the record of D∇u · ν on ∑_D and f the record of u on ∑_out, find the elements S_x, S_y and the time-dependent intensity function λ defining the sought source F as introduced in (7) such that (10) As far as the regularity of the state u at a particular instance t ∈ (0, T) is concerned, the authors in 10,24 proved for a similar problem that the assumption (11) implies that we have (12) Let us introduce the new variable w defined from the state u as follows: (13) where α and β are two real numbers. Then, since det(D) = D_LD_T ≠ 0, we choose the coefficients α and β such that (14) which, in view of (4), leads to (15) Therefore, by changing the variable u to w, the problem (1–5) with the source F introduced in (7) is rewritten as (16) where ∑_L ≔ Γ_L × (0, T) and ρ is the real number defined by (17) In addition, for later use we need to prove the following lemma.

Lemma 2.1

Assume (11) holds and let T^* be such that T⁰ < T^* < T. The elements defining the source F introduced in (7) are subject to (18) where and the coefficients θ₁, θ₂ are such that (19) where w is the solution to (16) and for i = 1, 2. Here, and .

Proof

Assuming (11) holds, let T^* be such that T⁰ < T^* < T and v₁, v₂ be the two functions defined in as follows: (20) where α and β are the two real numbers derived in (15). Then, using (14) we find (21) Therefore, in view of (3) and (17), v_i introduced in (20) satisfies for i = 1, 2 the following adjoint system: (22)

Multiplying the first equation in (16) by v_i and integrating by parts over using Green's formula gives the following for i = 1, 2: (23) where . By substituting the function v_i in (23) with its value given in (20), we obtain the following system: (24) Then, using the two equations in (24), we find the results announced in (18)–(19).▪

3. Identifiability

Here, we prove the identifiability of the time-dependent point source F introduced in (7) from recording the state u on the outflow boundary ∑_out. This theorem is inspired by the results derived in 10.

Theorem 3.1

The time-dependent point source F introduced in (7) is uniquely determined by the record f of the state u on the boundary ∑_out = Γ_out × (0, T).

Proof

Let u_i be the solution to the problem (1–5) with the time-dependent point source and f_i be the record of u_i on ∑_out for i = 1, 2. If f₁ = f₂, then the variable ū = u₂ − u₁ satisfies a system similar to the problem (1–5) where the right-hand side of Equation (1) is F₂ − F₁ and the boundary condition (25)

Let 𝒟 be an open disk of IR² such that (𝒟 ∩ ∂Ω) ⊂ Γ_out and for i = 1, 2. Therefore, the open 𝒪₁ = (𝒟 ∩ Ω) is a subset of Ω∖{Sⁱ}. Besides, the condition (25) enables to extend ū by zero in 𝒪₂ × (0, T) where . Then, ū satisfies (26) which implies, according to the Mizohata unique continuation theorem 25,26, that ū = 0 in 𝒪₁ × (0, T). Furthermore, with this the last result ū satisfies the same system than (26) in (Ω∖{Sⁱ}) × (0, T) and {𝒪}₁ × (0, T). Therefore, a second application of the Mizohata unique continuation theorem leads to the conclusion that ū = 0 in (Ω∖{Sⁱ}) × (0, T). Then, since ū ∈ L²(Ω × (0, T)), it follows that ū = 0 in Ω × (0, T). That implies F₂ = F₁, which is equivalent to having λ₂ = λ₁ and S² = S¹.▪

4. Identification

In this section, we establish an identification method that determines the elements defining the sought time-dependent point source F introduced in (7). This method not only requires the record f of the state u on the outflow boundary but also the record of its flux Φ on the inflow boundary. We proceed in two steps: the first step consists of proving a result that expresses S_x in terms of S_y. Then, the second step describes the recovery of the time-dependent intensity function λ once the source position S is fully known. We end this section by giving an algorithm that details the identification procedure.

4.1. Step 1: link between the source parameters

A link between the source parameters is given by the following theorem.

Theorem 4.1

Assume that (11) holds and let T^* be such that T⁰ < T^* < T. Then, given the records {Φ, f } introduced in (10), the elements defining the source F are subject to (27) where and P₁, P₂ are the following coefficients: (28)

Proof

According to (14), the variable w introduced in (13) satisfies (29) Since u = 0 on ∑_D, it then follows from (29) that D∇w · ν = e^{αx + βy}D∇u · ν on ∑_D. Therefore, using (13) and the records {Φ, f } introduced in (10), the proof of Theorem 4.1 is an immediate consequence of Lemma 2.1.▪

Remark 4.2

Note that for β = 0, which is according to (15) the case when V₂ = 0 (unidirectional velocity field), the computation of S_x using (27)–(28) does not require the knowledge of S_y. In practice, this remark can be very useful especially in the case of an accidental pollution source where the knowledge of S_x could lead to deduce S_y without any need of an additional computation.

However, as the state u is subject to only the knowledge of its value on ∑_out and of its flux D∇u · ν on ∑_D, the determination of the parameters S_x, S_y and using (27)–(28) is not so far possible since the coefficients P₁ and P₂ involve the unknown data u(·, T^*).

To determine the two integrals in (28) involving the unknown data u(·, T^*), we introduce for a given fixed T^* in (T⁰, T) the following two exact boundary controllability problems: for i = 1, 2 find a boundary control ψ_i such that the solution to (30) (31)

Moreover, using s = T + T^* − t, and we obtain the two equivalent problems: for i = 1, 2, find such that the solution to (32) (33)

Then, we prove the following proposition.

Proposition 4.3

Assume that (11) holds, T^* ∈ (T⁰, T) and for i = 1, 2 there exists ψ_i in solution to the exact boundary controllability problem (30)–(31). Then, given the records {Φ, f } introduced in (10), we have (34) where is the solution to (32) with the boundary control and .

Proof

In view of (11) and (12), the variable w introduced in (13) satisfies in a system similar to (16) where the right-hand side of the first equation is zero and the initial condition is w(·, T^*) ∈ L²(Ω). Therefore, multiplying the first equation of this system by , the solution to (32) and integrating by parts over using Green's formula gives (35) Then, using the initial condition in (35) and as established in (29) that D∇w · ν = e^{αx + βy}D∇u · ν on , we obtain in view of (13) and by employing the records {Φ, f } the results announced in (34).▪

4.1.1. Determination of the HUM boundary control ψ_i

As far as solving the exact boundary controllability problem (30)–(31) is concerned, we use the Hilbert uniqueness method (HUM) introduced by Lions 27,28 to determine the so-called HUM boundary control ψ_i. To this end, we introduce the adjoint problem (36) where T^* ∈ (T⁰, T) and z⁰ ∈ H¹(Ω). We start by establishing a necessary and sufficient condition on ψ_i to be a solution to the exact boundary controllability problem (30)–(31).

Theorem 4.4

The solution ϕ_i ∈ L²(T^*, T; H²(Ω)) to the problem (30) with a boundary control satisfies (31) if and only if (37) for all z ∈ L²(T^*, T; H²(Ω)) solution to the adjoint problem (36) with z⁰ ∈ H¹(Ω).

Proof

In view of (30), (36) and using Green's formula, we find (38) Therefore, since ϕ_i(·, T^*) = 0 in Ω, the necessary condition is an immediate consequence of (38). Furthermore, by subtracting (37) from (38), we obtain (39) which implies that in Ω.▪

To determine the HUM boundary control ψ_i for i = 1, 2, we introduce the function J_i defined for all z solution to the adjoint problem (36) with z(·, T) = z⁰ ∈ H¹(Ω) as follows: (40) Note that, as established in 29, one proves that the function J_i introduced in (40) is strictly convex and coercive. That implies the existence and the unicity of its minimizer. In the remainder, for i = 1, 2 we denote by the minimizer of the function J_i. Then, according to the first-order optimality condition, we have the following for all z⁰ in H¹(Ω): (41) where z_i and z are the solutions to the adjoint problem (36), respectively, with and z(·, T) = z⁰. We define the HUM boundary control ψ_i as follows 29,30: ψ_i = −D∇z_i · ν. Therefore, in view of (41), it is clear that ψ_i fulfils (37), and thus it is a solution to the exact boundary controllability problem (30)–(31).

Consequently, to determine the HUM boundary control ψ_i, we need to compute the minimizer of the function J_i. To this end, we introduce the following two operators 29,30: such that, to a given z⁰, associates G_T(z⁰) = −D∇z · ν where z is the solution to the adjoint problem (36) with the initial data z(·, T) = z⁰. The second operator is such that, to a given boundary control ψ, , the solution to the problem (30) taken at the final time T. Hence, according to (38), we find (42) which implies that G_T and are two adjoint operators. Then, in view of (41), we obtain (43) for all z⁰ in H¹(Ω). Therefore, the minimizer of J_i can be determined from solving (44)

Inner product method: To determine the minimizer , the inner product method 29 uses a matrix A as a representation to the controllability operator introduced in (44). The entries of this matrix A are defined by following proposition.

Proposition 4.5

Let (e_k)_k≥0 be a complete orthonormal family of L²(Ω). If e_k ∈ H¹(Ω) for all k ≥ 0, then the entries of the matrix A are given for all l ≥ 0 and k ≥ 0 as follows: (45) where z_k and z_l are the solutions to (36) with the initial data z_k(·, T) = e_k and z_l(·, T) = e_l.

Proof

Let (e_k)_k≥0 be a complete orthonormal family of L²(Ω). Then, for all two elements X, Y of L²(Ω), we have and . Therefore, AX = Y leads to That implies . Since for all k ≥ 0 the function e_k is in H¹(Ω), using the controllability operator introduced in (44) and in view of (42) we find for all l ≥ 0 and k ≥ 0. This is the result announced in (45).▪

Therefore, using the inner product method, we can determine for i = 1, 2 the minimizer of the function J_i introduced in (40) from solving the following linear system: (46) where A is the matrix defined in Proposition 4.5, the kth component of the vector θⁱ is and of the vector bⁱ is . As far as the complete orthonormal family (e_k)_k≥0 is concerned, one could use the normalized eigenfunctions that solve the following eigenvalue problem: (47) That implies the solution z_k to the adjoint problem (36) with the initial data z_k(·, T) = e_k is given by , which in view of (45) leads to find (48) for all l ≥ 0 and k ≥ 0.

4.2. Step 2: recovery of the time-dependent intensity function λ

Here, we assume the source position S = (S_x, S_y) to be fully known and focus on recovering the history of the time-dependent intensity function λ. Let Δt > 0 be a given time step and assume there exists an integer N⁰ > 0 such that N⁰Δt = T⁰. We denote by t_m, for m = 1,‥,N⁰, the regularly distributed discrete times t_m = mΔt and by ϕ_m+1 the solution to the problem (30) in Q_m+1 ≔ Ω × (0, t_m+1) with the initial data ϕ_m+1(·, 0) = 0 and the time-independent boundary control ψ = e^−αx−βy on . Then, using s = t_m+1 − t, the function satisfies the following system: (49) where . Multiplying the first equation in (16) by and integrating by parts over Q_m+1 using Green's formula gives (50) Therefore, to recover the time-dependent intensity function λ, we proceed as follows: using the trapezoidal rule, we find the following for 1 ≤ m ≤ N⁰: (51) where λ_m = λ(t_m). In (51), we used λ(t₀) = 0. Besides, using the records {Φ, f } given in (10) and in view of (50), we introduce the following notations: for m = 1, … , N⁰: (52) Here, and according to (29), we used D∇w · ν = e^{αx + βy}D∇u · ν on . Then, with reference to (50) and by employing (51)–(52) we obtain the following recursive formula: (53) Furthermore, to compute for k = 1, … , m we multiply the first equation in (54) by and integrate by parts over Q_m+1 using Green's formula. That leads to (55) Moreover, in view of (11)–(12) and using the orthonormal basis (e_j)_j made by the normalized eigenfunctions of the system introduced in (47), we express ξ_k the solution to (54) as follows: (56) where ℋ is the Heaviside function and μ_j is the eigenvalue associated to e_j.

4.3. Identification procedure

According to the two previous steps, we see that given S_y, one can determine the sought S_x using (27) of step 1 and the time-dependent intensity function λ by employing the recursive formula derived in (53) of step 2. Therefore, starting from some initial guess , we use the following minimization problem to identify S_y and thus S_x and λ: (57) where ℓ is the width of Ω. We detail the identification procedure in the following algorithm:

Begin

Data: the records Φ and f

1.	For i = 1 to 2 do • Compute the minimizer of the function Ji introduced in (40). • Set the HUM boundary control ψi = −D∇zi . ν where zi is the solution to the adjoint problem (36) with the initial data . • Compute ϕi, the solution to (30) with the boundary control ψi.
2.	Initialization of .
3.	Compute the associated from (27) and , for m = 1, … , N0, using (53).
4.	Determine un the solution to (1–5) with the source .
5.	Test: if is small enough, go to End Otherwise, correct and go to 3.

End

5. Identification of F in a rectangular domain

Here, we apply the identification method established in the previous section to the case where the controlled portion of the river is a rectangular domain: Ω = (0, L) × (0, ℓ) and the mean velocity vector V is perpendicular to the inflow boundary, i.e. V₂ = 0. In such situation, the longitudinal and transverse diffusion directions coincide with the x and y cartesian axes. And thus, according to (4), the diffusion tensor D is represented by the 2 × 2 diagonal matrix of entries D₁ = D_L and D₂ = D_T. Therefore, using the dimensional analysis method 31, the solution to the system (58) can be expressed as follows: (59) where ℋ is the Heaviside function and ⋆_(t) denotes the convolution product with respect to the variable t. Furthermore, using ū such that (60) implies that the solution to the problem (1–5) with the source F introduced in (7) is u = û + u₀. Besides, using the separation of variables method, we determine the normalized eigenfunctions solutions to the eigenvalue problem introduced in (47) for Ω = (0, L) × (0, ℓ) and V₂ = 0 as follows: for all n ≥ 0 and m ≥ 0 (61) and the associated eigenvalues μ_nm are such that (62) Let M and N be two sufficiently large integers. For simplicity, we employ the following notations: for n = 0, … , N − 1; m = 0, … , M − 1 and p = 0, … , N − 1; q = 0, … , M − 1 (63) Then, since the unit normal vector exterior to the inflow boundary Γ_D is ν = (−1, 0)^⊤, we find according to (48) that for l = 0, … , NM − 1 and k = 0, … , NM − 1 (64) As according to (61) we have c_nm = c_pm for all integers n, m and p, the square symmetric matrix A of order NM is defined for l = 0, … , NM − 1 and k = 0, … , NM − 1 as follows: (65)

We use the expansions of ϕ_i(·, T) and of the minimizer of the function J_i introduced in (40) in the complete orthonormal family (e_k)_k≥0: and . Then, in view of the linear system (46) and for each 0 ≤ m ≤ M − 1, we determine the N components for n = 0, … , N − 1 from solving (66) and the vector b^i,m is such that for p = 0, … , N − 1. As far as the linear system introduced in (66) is concerned, we prove the following result.

Proposition 5.1

For all m = 0, … , M − 1, the real N × N matrix A^m involved in the linear system introduced in (66) is symmetric and positive definite.

Proof

According to (66), we have for all p = 0, … , N − 1 and n = 0, … , N − 1 (67) Therefore, for all vector x^⊤ = (x₀, … , x_N−1) of IR^N we have (68) Furthermore, since D₁ ≠ 0, it follows from (68) that (69) As for all m = 0, … , M − 1 the sequence (μ_pm)_p is strictly increasing, then the second equation in (69) implies that x_p = 0 for all p = 0, … , N − 1.▪

Once the NM components are determined from solving the linear system (66) for m = 0, … , M − 1, the solution z_i to the adjoint problem (36) with the initial data where is then given by (70) Hence, for i = 1, 2 and in view of (70) the HUM boundary control ψ_i = −D∇z_i · ν solution to the exact boundary controllability problem introduced in (30)–(31) for Ω = (0, L) × (0, ℓ) and V₂ = 0 is defined on as follows: where γ(t) = (D₁π/l^1/2L^3/2)e^−ρ(T−t).

6. Numerical experiments

We carry out numerical experiments in the case of a rectangular domain: Ω = (0, L) × (0, ℓ) where the inflow boundary Γ_D coincides with the y-coordinate axis and the lower lateral boundary coincides with the x-coordinate axis. Furthermore, we assume the mean velocity vector V to be perpendicular to the inflow boundary Γ_D, i.e. V₂ = 0. That implies, as mentioned in Section 4, β = 0 and the diffusion tensor is represented by the 2 × 2 diagonal matrix D with entries D₁ = D_L and D₂ = D_T.

For numerical computation, we reduce the domain Q_T = Ω × (0, T) to the unit cube Q = (0, 1)³ using the following undimensioned variables: (71) Then, to determine ϕ the solution to the problem (30) with a boundary control ψ, we compute φ(x₁, x₂, x₃) = ϕ(x₁L, x₂ℓ, x₃T) solution to (72) where . Given three positive integers N_x, N_y and N_T, we discretize the problem (72) using the steps Δx₁ = 1/N_x, Δx₂ = 1/N_y, Δx₃ = 1/N_T and the five-point finite difference method with the Crank–Nicolson scheme. For numerical experiments, we take L = 1000 m, ℓ = 50 m, V₁ = 0.5 ms⁻¹, D_L = 30 m² s⁻¹ and D_T = 10 m² s⁻¹. We suppose controlling the rectangular domain Ω = (0, L) × (0, ℓ) for T = 14400 s (4 h). To generate the records {Φ, f }, we use (59)–(60) with a source located at S = (S_x, S_y) and loading the following time-dependent intensity: (73) where c₁ = 1.2, c₂ = 0.4, c₃ = 0.6 and v₁ = 10⁻⁶, v₂ = 5 × 10⁻⁵, v₃ = 10⁻⁶. The coefficients τ_i are such that τ₁ = 4.5 × 10³, τ₂ = 6.5 × 10³, τ₃ = 9 × 10³. We use N_x = 10, N_y = 5 and N_T = 210. That means, we employ four sensors on each of the inflow and the outflow boundaries. Those sensors are recording the evolution of D∇u · ν and of u with a time step Δt = T/N_T. Here, we used N⁰ = N* = 180 which implies that T⁰ = T^* = N⁰Δt and equivalent to say that T⁰ = T^* = (6/7)T. As far as the computation of the boundary control ψ_i is concerned, we employed N = M = 5.

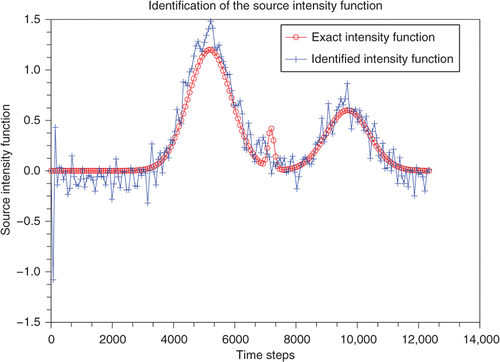
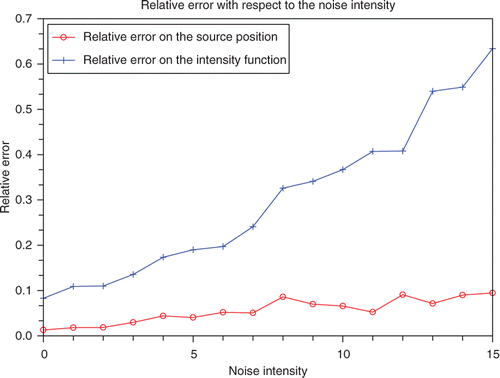
As mentioned in Remark 4.2, for β = 0, which is the case in our numerical experiments since we are using V₂ = 0, the determination of the x-coordinate S_x from (27) does not require the knowledge of S_y. Then, we carry out numerical experiments with S_y assumed to be known and focus on studying numerically how does the introduction of a Gaussian noise on the used records {Φ, f } affect the identification results of S_x using (27) in step 1 and of the time-dependent intensity function λ from (53) in step 2. In the sequel, we start by presenting for some introduced Gaussian noise the identified x-coordinate of the source position, denoted here by , and the two curves representing the used intensity function introduced in (73) and the computed λ using the recursive formula derived in (53). 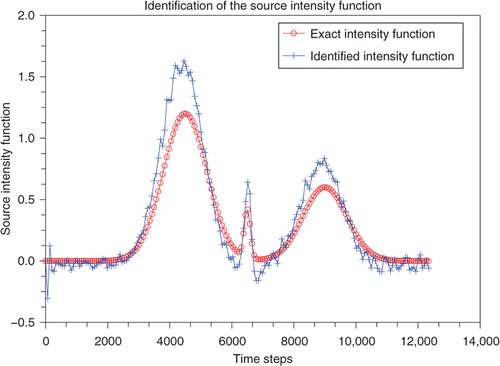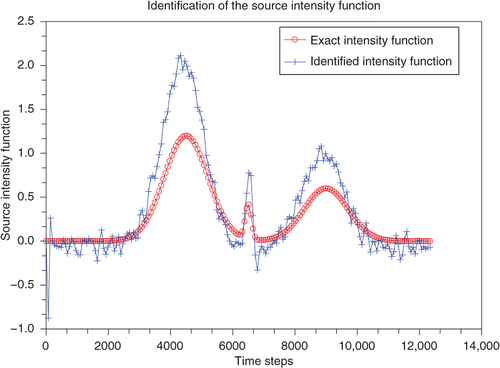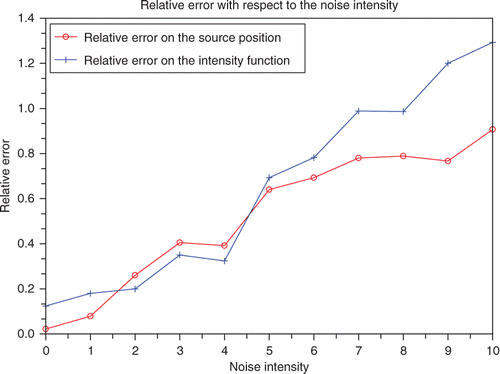We also compute for each introduced Gaussian noise the following relative errors: (74) where the vectors with λ is the function introduced in (73) and identified from (53). Then, we draw the relative errors computed from (74) with respect to the intensity of the introduced Gaussian noise. We carry out numerical tests for two different source locations: S₁ = (200, 1) and S₂ = (600, 49). We start by presenting the numerical experiments corresponding to the first location S₁. Then, we give those related to the second location S₂.

The numerical experiments presented above seem to be saying that the established identification method enables us to identify the elements defining the sought time-dependent point source F. However, those numerical results corresponding to the source S₁ = (200, 1) which is located rather in the upstream part of the river seem to be relatively sensitive with respect to the introduction of a high intensity of Gaussian noise on the used measures. In fact, the accuracy in Figures 1 and 2 starts to deteriorate when the intensity of the introduced Gaussian noise becomes relatively high. This tendency is confirmed by Figure 3. The deterioration of the accuracy in this case may be explained by the following: since the convective transport usually dominates the diffusion process, then the main information on the source activity seems to be the data recorded on the outflow boundary. Therefore, the bigger the distance separating the source position and the outflow boundary, the more sensitive the data recorded on this boundary.

Figure 1. Graph of location S₁: Noise 3%, , ErrorLam = 35.01%.

Figure 2. Graph of location S₁: Noise 5%, , ErrorLam =69.3%.

Figure 3. Graph of location S₁: relative errors with respect to the introduced Gaussian noise.

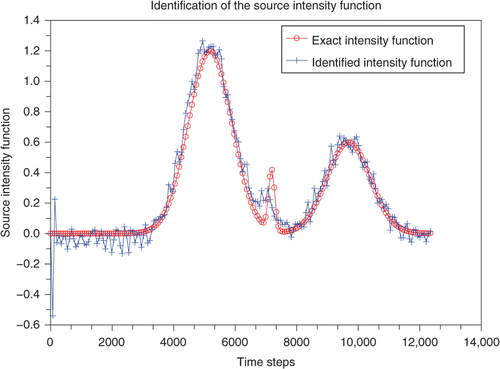
In Figures 4–6 we present the numerical experiments associated to the second source location S₂ = (600, 49).

The analysis of the numerical experiments corresponding to the second source location to be S₂ seems to be confirming our intuition for the numerical results associated to the upstream source location S₁. Indeed, we remark that even with a higher intensity of the introduced Gaussian noise on the used measures, the results in Figures 4 and 5 are more accurate than those presented in Figures 1 and 2. Moreover, comparing to those presented in Figure 3, the behaviour of the relative errors on the source location and on the intensity function given in Figure 6 confirms our expectation that for the downstream source location S₂ the identified results will be more accurate and also stable with respect to the introduction of a Gaussian noise on the used measures. This expectation comes from the fact that in the case of a downstream location, the quality of the signal observed on the outflow boundary could be much better than the one corresponding to a rather upstream source location.

Figure 4. Graph of location S₂: Noise 5%, , ErrorLam =19.01%.

Figure 5. Graph of location S₂: Noise 10%, , ErrorLam =36.7%.

Figure 6. Graph of location S₂: relative errors with respect to the introduced Gaussian noise.

7. Conclusion

In this article, we studied the inverse source problem that consists of localizing a time-dependent source spatially supported at an interior point of a 2D bounded domain and recovering the history with respect to the time of its intensity function. This source occurs in the right-hand side of an evolution linear advection-dispersion-reaction equation. We proved the identifiability of the sought source from recording the state on the outflow boundary. Then, we established an identification method based on some exact boundary controllability results. This method requires the records of the state on the outflow boundary and of its flux on the inflow boundary of the controlled domain. Some numerical experiments in the case where the controlled domain is rectangular and the mean velocity vector is perpendicular to the inflow boundary are presented. The analysis of those numerical experiments shows that the proposed identification method is accurate and relatively stable with respect to the introduction of a Gaussian noise on the used records.