Thermal characterization of materials using Karhunen–Loève decomposition techniques – Part I. Orthotropic materials

Abstract

A new method for reliable thermal characterization of orthotropic, homogeneous materials is proposed. It is based on the use of Karhunen–Loève Decomposition (KLD) techniques in association with infrared thermography experiments or any other kind of experimental device providing dense data in the spatial coordinate. Main problem addressed in this paper is how to deal efficiently with large amount of rather noised experimental data. It is proven that orthogonal properties of KLD eigenfunctions and states allow achieving simple estimates of thermal diffusivities which depend only on the first and the second KLD eigenelements. This means that the 2D KLD approximation of the temperature field provides information enough for estimation purposes. As a result, a significant amplification of the signal/noise ratios is reached. Moreover, we prove that spatially uncorrelated noise has no effect on KLD eigenfunctions, the noise being entirely reported on states (time-dependent projection coefficients). This is particularly interesting because thermal diffusivities estimation involves spatial derivatives of the eigenfunctions calculation. Consequently, the proposed method results in an attractive combination of parsimony and robustness to noise. Indeed, because it does not require analytical solutions of the associated heat conduction problem, the method could be extended to application involving heterogeneous materials. The second part of the paper deals with this extension.

Keywords:

• thermal characterization
• infrared thermography
• Karhunen–Loève decomposition
• singular values decomposition

Nomenclature

	=	Biot number
	=	Covariance
	=	Approximation error
	=	Vector of approximation errors
	=	Effective heat transfer coefficient
	=	Signal/noise ratio
	=	Temperature field
	=	Vector of temperature
	=	Time
	=	Variance
	=	Eigenfunctions of
	=	Matrix of eigenfunctions
	=	Energy function
	=	Energy matrix
	=	Coordinates
	=	States
	=	Vector of states

	=	Thermal diffusivity
	=	Thermal loss coefficient
	=	Noise field
	=	Noise vector
	=	Thermal capacity
	=	Eigenvalues of
	=	Noise energy

	=	Expectation
	=	Unitarily invariant norm
	=	Scalar product
·	=	Time derivative
∼	=	Noisy variable
	=	Mean value
	=	Estimated value

KLD	=	Karhunen-Loéve Decomposition
PCA	=	Principal components analysis
SVD	=	Singular values decomposition

1. Introduction

Infrared thermography is widely used to measure the thermal diffusivity of materials. An experiment usually consists in applying a heat flux on the front face of a sample by, i.e. a laser beam (point like, line or other motifs) and detecting the sample thermal response on either its front or its rear face. The laser beam intensity can be Dirac-like, modulated, pseudo-random, etc. The thermal behaviour of the sample is observed using an infrared camera with a focal plane array of infrared detectors. The development of infrared video cameras with fast data acquisition (thousands of images/s) and high lateral resolution (tens of micrometres) provides powerful tools for fast materials testing. Counterpart is the huge amount of noisy data to be treated. To overcome such a difficulty, experimental conditions are usually chosen, so that simple analytical solutions of the heat conduction problem concerned by exist. For instance, the diffusivity of homogeneous materials can be easily retrieved by the so-called slope method when exciting a thin but large enough sample placed in a vacuum chamber by a point-like or a line-like intensity modulated laser beam (see, i.e. 1 and references within). Otherwise (i.e. heterogeneous materials, other lighting motifs), the estimation process (heat conduction model inversion) becomes a tricky task: computing time and memory resources required when using standard approaches, i.e. diffusivity estimation by minimization of a chosen residuals norm defined over the whole spatial domain, are generally huge while results are very sensitive to noise when using point-by-point least squares estimation approaches 2,3. In such a sense, mathematical tools allowing significant reduction of the data set dimension, as well as noise control and parsimonious estimations, could be an interesting alternative to deal efficiently with data provided by infrared cameras and for extending materials characterization based on infrared thermography to thermal problems with unknown analytical solutions.

Proper orthogonal decomposition techniques are widely used for multivariate data reduction in many areas of application. Reduction starts by choosing an appropriate orthogonal basis providing some few dominant components (referred as dominant directions, eigenfunctions or modes). A low-dimensional approximate description of the whole set of data is thus obtained by projecting the initial high-dimensional set on the dominant eigenfunctions. The choice of the basis makes the main difference among methods. When dealing with regular signals, the basis coming from spectral decomposition of the energy matrix (or covariance matrix) of the multivariate data is the one leading to the best results. This means that it provides the lowest dimension for a given approximation precision or, alternatively, the best precision for a given dimension. Such a method has been developed about 100 years ago by Pearson 4 as a tool for graphical data analysis and re-developed several times since them in different areas of application 5–7, so that it goes under many names as Principal Components Analysis (PCA), Karhunen–Loève decomposition (KLD), Singular Value Decomposition (SVD), etc. PCA/KLD/SVD is a very common tool today in image processing and signal processing problems for compression and noise reduction 8. It is also widely used for signals classification, data clustering and information retrieval problems 9–11. Powerful model reduction techniques based on PCA/KLD/SVD have been also proposed for low-dimensional description of problems described by partial differential equations, mostly in the field of turbulent flows 12,13. In thermal analysis, SVD-based methods have been developed for efficient reduction of linear and non-linear heat transfer problems 14–18, as well as for solving heat transfer inverse problems dealing with unknown heat sources 19–21. For a fairly comprehensive introduction to PCA/KLD/SVD, we recommend the books by Jolliffe 22 and Deprettere 8. For more details on the mathematics and computation, good references are 23–26.

A method for reliable and parsimonious thermal characterization of materials based on the use of KLD techniques in association with infrared thermography is proposed in this paper. First part of the paper focuses on homogeneous materials while the second one is devoted to heterogeneous materials. The KLD of infinite-dimensional and finite-dimensional problems is defined in section 2, part I. Functions and signal considered are, respectively, space-time dependent functions and multivariate time series. In the framework of thermal analysis, functions represent the thermal field while multivariate time series are data coming from thermal field sampling. The property of KLD to provide the closest -dimensional approximation for an infinite-dimensional problem or the closest rank- approximation for a rank- () matrix is recalled too. In section 3, measurement noise propagation through KLD is analysed. We prove that spatially uncorrelated noise has no effect on eigenfunctions, the noise being entirely reported on states (time dependent projection coefficients). This is particularly interesting because estimating thermal diffusivities involves calculation of spatial derivatives of the eigenfunctions. The ability of KLD to amplify signal/noise ratio when truncated is also studied and formal expressions for evaluating this effect are proposed. This is a key point for understanding the robustness to noise of the method proposed for diffusivities estimation. The KLD-based method for estimating thermal diffusivity of homogeneous materials is described in section 4. Orthogonal properties of eigenfunctions and states are intensively used for achieving simple estimates of thermal diffusivities which only depend on the first and the second KLD eigenelements. Numerical examples in last section illustrate the powerfulness of the proposed method.

2. The Karhunen–Loève decomposition (KLD)

Let be a space-time dependent function in a bounded region , with and representing point coordinates and time respectively. It is assumed that this function verify so that it belongs to the infinite-dimensional Hilbert space associated to . Sampling on leads to the continuous in time -dimensional vector (), whose components represent temperature values at the different sampling points. In the following, we will assume that sampling is done, so that provides a good enough approximation of .

2.1. KLD of infinite-dimensional problems

Let us define the energy function associated to as follows: (1) It can be easily proven that (symmetry property). Indeed, is a compact, positive operator on . The well-known spectral theorem states that if is compact and self-adjoint, then there is a complete orthonormal set in (Hilbert basis) consisting of the eigenfunctions of , noted as in the following. Moreover, because is positive, its spectrum consists of 0 (zero) together with a countable infinite set of real and positive eigenvalues: . The problem defining eigenvalues and eigenfunctions of is (2) with orthogonal condition: (3)

Hilbert–Schmidt theorem allows writing (see, e.g. 27): (4) Besides, all functions belonging to can be projected in a unique manner on the eigenfunctions set because is a complete set in (Hilbert basis). Since for , it follows that (5) where decomposition coefficients (states in the following) are given by (6)

Taking into account Equations (4) and (5), it can be easily proven that states are orthogonal, they verify: (7) Equation (5) gives the so-called Karhunen–Loève decomposition of , also named singular value decomposition. The squared root of the eigenvalues are the singular values of . The term in Equation (5) is referred as mth principal component of .

As already mentioned in the introduction, KLD provides the most efficient way of capturing the dominant components of an infinite-dimensional process with only a finite number of modes, often surprisingly few. A -dimensional linear approximation of is achieved when truncating the expansion series given by Equation (5) to its first terms: (8)

The approximation error is (9)

Taking into account orthogonal properties of eigenfunctions and states , it can be easily proven that (10)

As , the approximation error tends to zero: . Indeed, Allahverdiev theorem (cf. 27) for compact operators, say , states that all -dimensional approximations of verify: , where is the (r + i)th singular value of and represents unitarily invariant norms of the approximation error. The same theorem states that the minimum value is achieved by truncation of the Schmidt development of (Equation 7) to its first terms (those associated to the largest singular values). It follows that all -dimensional linear approximations of verify: . Consequently, Equation (8) provides the best -dimensional linear approximation of with regard to unitarily invariant norms of the approximation error.

2.2. KLD of finite-dimensional problems

Let us now define the energy matrix associated to T(t) () as follows: (11) The meaning of this matrix is close to that of the covariance matrix of T(t) signals. Diagonal terms represent the energy (close to the variance) of T(t) components, while non-diagonal terms measure the dynamic likeness among signals. It can be easily demonstrated that () is a symmetric, definite positive matrix. Accordingly, spectral decomposition of leads to a -dimensional set of orthonormal eigenvectors, with , and associated eigenvalues verifying . The energy matrix can hence be written as (12) Moreover, is a complete orthonormal set in . Consequently, elements of T(t) can be represented as linear combinations of the eigenvectors: (13)

Using matrix writing, equations above become: (14) with . From Equations (11), (12) and (14), it can be easily proven that states are orthogonal: (15) Equation (14) is the Karhunen–Loève decomposition (or singular values decomposition) of T(t). It must be noticed that for an appropriate sampling, the elements of and the eigenvectors () can be considered as good numerical approximations of and , respectively.

In matrix algebra, Fan 28 and Mirsky 29 demonstrated that all rank- approximations for a rank- () matrix, say , verify (16)

Indeed, the closest rank- approximation is provided by , where and . It follows that (17) with , provides the best -dimensional approximation of in the sense of unitarily invariant norms of the approximation error. As previously, it can be easily proven that (18)

3. Noise propagation through KLD and filtering effects

Some key elements for understanding the robustness to noise of the method we are proposing are here provided. First, we prove that spatially uncorrelated noise has no effect on eigenfunctions, the noise being entirely reported on states. This is particularly interesting because estimating thermal diffusivities involves calculation of spatial second-order derivatives of the eigenfunctions (see section 4.3). Next, we prove that KLD truncation (-dimensional approach of ) acts as a signal/noise ratio amplifier. This effect is as much important as is small. The interest of this property is evidenced in section 4.3, where it is shown that the information required for diffusivity estimation can be reduced to the two first KLD eigenelements.

3.1. Noise propagation through KLD

Let us first consider infinite-dimensional problems with noise-corrupted observations (19)

Noise is assumed to be independent of as well as spatially uncorrelated: (20) (21)

Accordingly, the energy function associated to the observations can be written as (22)

Reporting Equation (4) into Equation (22) yields (23) which proves that eigenfunctions are not corrupted by noise. As already mentioned, this property has great interest because estimating thermal diffusivities involves calculation of spatial second-order derivatives of the eigenfunctions (see section 4.3).

From Equation (23), it follows (24)

Noise-corrupted states are hence given by (25) where represents the orthogonal projection of the noise on eigenfunction . Comparing Equations (23) and (24), it follows that (26)

For finite-dimensional problems, similar results are achieved starting from noise-corrupted observations given by (27)

Energy matrix associated to the observations is (28) with . Consequently, the KLD of is (29) with and . As before, it can be easily proven that (30)

3.2. Signal/noise amplification effects

Consider the observations given by Equation (25), with noise verifying properties described by Equations (26) and (27). The energy of the observed thermal response at point is (31)

The signal/noise ratio is hence (32)

Consider now the -dimensional approximation of given by (33)

The energy of at point and the corresponding signal/noise ratio are (34)

Comparing signal/noise ratios and leads to (35) The first term into brackets in the equation above tends to 1 because eigenvalues verify and eigenfunctions are . Indeed, first eigenvalue is usually largely dominant (). Hence we can write: (36)

This equation shows that the signal/noise ratio is improved when truncating the KLD of the observations. This effect is as much important as is small. In section 4.3, we prove that the information required for thermal diffusivities estimation reduces to eigenfunctions and , and to the associated states and . In other words, we prove that the 2D KLD approximation of the temperature field provides information enough for estimation purposes. It is hence expected, as shown in section 5.3, to reach significant signal/noise ratio amplification when using the diffusivity estimates proposed in section 4.3.

4. Thermal characterization of homogeneous materials using KLD

The method we are proposing for thermal characterization of homogeneous materials is here described. It is based on the use of KLD techniques in association with infrared thermography. The problem is stated in section 4.1. It includes the equations governing the thermal behaviour of the material's sample as well as a short description of the experimental framework. We remind readers that the proposed method does not require analytical solutions (contrary to, i.e. “slope method”), so that few constraints regarding samples illumination (spatial and time patterns) come. It is, however, restricted to infrared thermography based on thin samples; that is, to experimental situations where 2D heat transfer can be assumed. In sections 4.2 and 4.3., orthogonal properties of KLD eigenfunctions and states are intensively used for getting simple diffusivities estimates. It is shown that the information required for thermal diffusivities estimation reduces to eigenfunctions and , and to the associated states and . In other words, we prove that the 2D KLD approximation of the temperature field provides information enough for estimation purposes. As shown later, this leads to an exciting combination of parsimony and robustness to noise.

4.1. Problem statement

Let us consider the following heat conduction problem in a rectangular plate . Energy equation at inner points () is (37)

Boundary conditions are assumed to be adiabatic (38)

Initial condition is . represents the excess of temperature with regard to the plate surroundings, which are assumed to remain at constant temperature during the experiment. Rectangular domain and Cartesian coordinates have been intentionally chosen to be in accordance with infrared camera images (small square pixels covering a rectangular or a square area). Parameters and represent, respectively, the thermal diffusivities in the and directions. Parameter is defined as , where represents the effective heat transfer coefficient between the plate and its surrounding, is the thermal capacity of the material and is the thickness of the plate. Last one is assumed to be small enough for the thermal gradient in the thickness direction to be negligible and 2D modelling in the plane (Equations (37) and (38)) to be valid. The Biot number (;  = thermal conductivity) has hence to be small, let say less than 0.1.

To be fully in line with the model above, experiments must be carried out on thin samples (plates) located in an environment at constant and uniform temperature. Starting from a plate in thermal equilibrium with its environment, the initial condition can be established using, i.e. a laser beam with almost arbitrary spatial and time patterns. Thermal relaxation of the plate is thus observed using an infrared camera. At each sampling time, a plate temperature-map is recorded and stored: . The dimension of vector is equal to the number of pixel of the infrared image. Measurements noise is assumed to be spatially uncorrelated: . This is not true for all infrared cameras, but it has been successfully tested for CEDIP-ORION ones 30. We suppose that the lateral resolution of the camera is high enough for to be a good approximation of . Indeed, the plate dimensions are as large as required to warrant the border is not reached by thermal sollicitation. Thermal characterization consists in determining the values of parameters and from the recorded temperature data.

4.2. Fundamental equations and properties

Let us consider again the KLD of the theoretical thermal field: (39)

We remind that eigenfunctions and states verify orthogonal properties: (40)

Introducing Equation (39) into Equation (37) leads to (41)

Multiplying this equation by , integrating over and taking into account eigenfunctions orthogonal property, we obtain: (42)

Equation above is now multiplied by and integrated over time. Taken into account states orthogonal property, this leads to (43)

In a similar way, from Equations (38) and (40), it can be easily proven that (44)

As demonstrated in Appendix 1, the following identity is verified for all (i,k) (45)

Taking into account Equations (43) and (45), it follows: (46)

Accordingly, Equation (43) for (i,k) indexes and Equation (43) for are identical equations. Indeed, we can write: (47) (48)

Adding equations above leads to (49)

Consequently, we can write (50)

where is the experiment end-time.

Another interesting equation comes from integration of Equation (37) over . For adiabatic boundary conditions, this leads to the lumped model (51)

Hence (52)

4.3. Estimation method

For free-noise space-time continuous observations, parameters , and can be calculated from any three arbitrarily chosen Equations (50). On the contrary, for noise-corrupted observations, it is convenient to cast the parameters , and estimation problem into a least squares problem.

Taking into account the efficiency of the spatial-mean operator for noise reduction, the best estimate of parameter is achieved applying the linear least squares method to Equation (52). This leads to (53) with and .

On the contrary, the estimation of parameters and must be based on Equations (50). It is evidence that at least two of these equations are required because the problem involves two unknown parameters. However, keeping all of them will be a wrong strategy because there are terms in the KLD of which are not significant compared to the noise. As shown in section 3.1, signal/noise rate for states is . On the other hand, eigenvalues usually decrease quickly, so that (see Table 1). Hence, the Equations (50) that will be preferred for diffusivities estimation are those involving the states with largest eigenvalues, namely and . As demonstrated in the previous paragraph, Equation (50) with and Equation (50) with are equivalent. However, for no perfectly uncorrelated noise (see section 5), eigenfunctions from KLD of will be slightly corrupted by noise, with degradation increasing with decreasing eigenvalues. Consequently, Equation (50) with will be preferred to Equation (50) with to limit noise amplification effects due to second-order space derivatives. We can hence write (54) with (55) and , .

Table 1. Eigenvalues of the energy matrix of free-noise data () and their contribution to the total energy of the whole set of temperature data.

	1	2	3	4	5	6	7
Eigenvalues	2322.1	297.6	25.35	2.56	0.2936	0.0304	0.0048
Contribution to E (%)	87.69	11.24	0.9575	0.0967	0.0111	0.0011	0.0002

The solution of Equation (54), in the least squares sense, leads to (56)

As proven in Appendix 2, the expectation and the variance of the observers are (57) and (58)

Equation (57) shows that provides a biased approximation of that could lead to biased estimations of parameters and . The necessary condition for the bias becomes negligible is . In such a case, the mean value and the variance of the observers can be approached by (59) (60)

Besides, the covariance of the observers and is (see Appendix 2): (61)

Provided that (almost unbiased observers), the statistical properties of the diffusivities estimation defined by Equation (56) are hence as follows: (62) represents the covariance matrix of the observers, whose diagonal and out-of-diagonal terms are, respectively, given by Equations (60) and (61).

In the experimental framework of infrared thermography with high lateral resolution, can be often considered as a good approximation of . Hence, KLD of provides appropriate approximations of eigenfunctions and states . Using previous notation for finite-dimensional problems, with eigenvectors , the elements of the sensitivity matrix become: (63) where is the numerical approximation of .

For isotropic materials (), the estimate of the diffusivity can be easily obtained by addition of the columns of the matrix .

It must be noticed that the thermal capacity of the sample should be obtained by some other independent method in case the thermal conductivity and/or the effective heat transfer coefficient are to be known.

5. Numerical example

A numerical example is used here for illustrating the appropriateness of our developments. The problem is described in section 5.1. Main KLD eigenelements are analysed in section 5.2. Section 5.3 illustrates the signal/noise amplification effects reached by KLD truncation. Last section is devoted to thermal parameters estimation using different scenarios for noise amplitude and spatial resolution. The robustness to noise of the KLD-based method and its validity for rather low spatial resolutions are evidenced.

5.1. Experiments generation

Let us consider an orthotropic, homogeneous plate (, and ) exchanging heat by convection/radiation with an environment at constant temperature, say at 0°C. As in actual experiments, the plate is assumed to be in thermal equilibrium with the environment at the beginning of the experiment. Thus, a heat flux is applied on the centre of the plate during a short time using either a laser or a lamp with a mask: (64) represents the laser/lamp spot, which is assumed to be circular with diameter . Reference axes are chosen, so that the equation governing the thermal evolution of inner points () is (65) with . At points on the plate boundaries (), adiabatic conditions are assumed. Thermal diffusivity values are and , while (, ). Assuming , Biot number is about 0.001, so that we can consider that Equation (65) applies.

The finite volume method has been applied on an equally spaced (, pixel size: ) grid for discretization of Equation (65). This leads to the state-space model: (66) where and represent numerical approximations of and , respectively. Temperature data are thus generated by time integration of the equation above. The experiment we are going to analyse has been generated using the following parameters: , , , (final time) and (sampling time). It must be noticed that only data for , those describing the thermal relaxation of the temperature field established by the applied heat flux, are being used for estimation purposes. In the following, we note and (initial temperature field).

To emulate experiments with low spatial resolution, temperature data produced before have been averaged as done by infrared cameras. Data with -spatial resolution (pixel size: , ) and data with -spatial resolution (pixel size: , ) are being considered in the following. The initial temperature field established on the plate is represented in Figure 1(a) (lowest resolution), whereas Figure 1(b) describes the thermal relaxation of the plate. It includes the time behaviour of the temperature at each pixel, (), from to with (2000 sampling times).

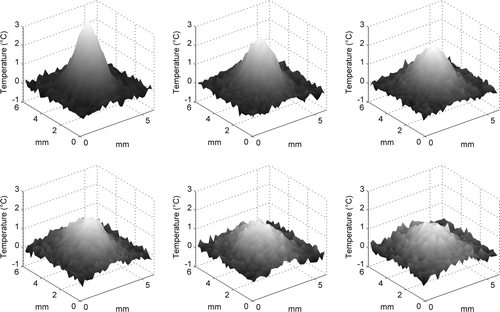
Figure 1. Simulated temperature data: (a) initial temperature field on the plate (free-noise data); (b) temperature time behaviour, one curve by volume of control (free-noise data); (c) initial temperature field on the plate (±0.5°C noisy data); (d) temperature time behaviour, one curve by volume of control (±0.5°C noisy data).

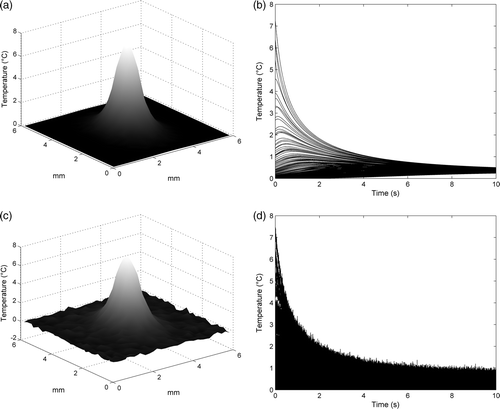
For estimation purposes, the plate thermal behaviour is corrupted by additive noise: (, , ), with . Four different values of noise amplitude have been considered: (very bad quality data), (bad quality data), (medium quality data) and (good quality data). The quality of each set of data can be appreciated through the following index evaluating the signal/noise ratio: (67) were and represent the elements of vectors and . The value of SN is very high for temperature data with noise amplitude equal to () and it is high for data with noise amplitude equal to (). On the contrary, SN is low and very low, respectively, for temperature data with noise amplitude equal to () and (). In the last case, the variance of the noise is globally greater than that of the signals ().

Figure 1(c) represents the temperature field of the plate at time for noise amplitude equal to and -spatial resolution, while Figure 1(d) includes the time behaviour of the temperature at each pixel. The temperature map on the plate at different times is depicted in Figure 2.

Figure 2. Temperature field on the testing plate at different times (±0.5°C noisy data).

5.2. Main eigenelements analysis

KLD of the set of free-noise signals (lowest resolution) has been carried out as described in section 2.2: . Table 1 includes eigenvalues as well as the corresponding contribution of the total energy of signals: . It can be noticed that most part of the signals energy is captured by the four first KLD components. Eigenfunctions associated to the two first singular values are depicted in Figure 3(a) and (c), while the time evolution of the corresponding states is represented in Figure 4(a).

Figure 3. Eigenfunctions associated to the largest eigenvalues: (a) first eigenfunction calculated from free-noise data, ; (b) differences (±0.5°C noisy data); (c) second eigenfunction calculated from free-noise data, ; (d) differences (±0.5°C noisy data).

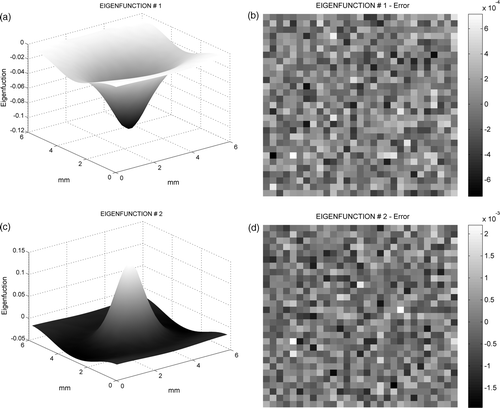
Figure 4. States associated to the largest eigenvalues: (a) for free-noise data, and ; (b) for ±0.5°C noisy data, and .

KLD of noise-corrupted data has been also carried out: . Results achieved for noise amplitude equal to (worst case) are here presented and discussed. Eigenvalues () as well as relative errors are reported in Table 2. Last row of this table includes calculated signal/noise ratio for states (). As expected, relative error increases and signal/noise ratio reduces as the state energy decreases. It can be seen that for signal/noise ratios start to be less than one. This means that useful information in signals with is completely bogged down in noise. On the contrary, signal/noise ratios for the two first states, those which are required for parameters estimation, are very high (>1000). Figure 4(b) shows the time behaviour of and .

Table 2. Eigenvalues of the energy matrix of noise-corrupted data (), relative errors () and signal/noise ratios ().

	1	2	3	4	5	6	7
Eigenvalues	2322.1	297.6	25.35	2.56	0.2936	0.0304	0.0048
Relative error (%)	0.018	0.102	1.392	2.372	5.270	440.95	3274.1
Signal/noise	9775.4	1232.3	110.9	9.451	0.665	0.0465	0.0074

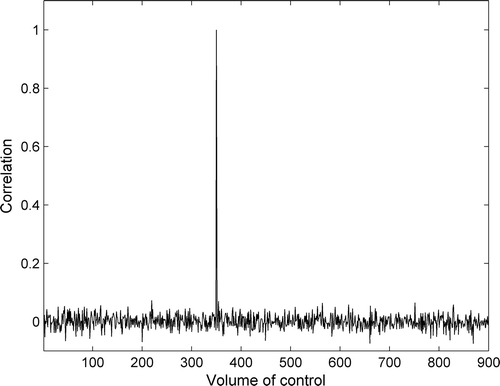
The maps in Figure 3(b) and (d) represent the difference between the eigenfunctions (first and second ones) coming from KLD of and those from KLD of . These differences are due to a not strictly diagonal matrix. Figure 5 shows the statistical correlation of an arbitrary element of , say , with elements . It can be seen that correlation is almost zero, but no zero. This means that noise energy matrix is diagonal dominant, but not strictly diagonal. As for states, the differences between the eigenfunctions coming from KLD of and those from KLD of are greater for eigenfunctions associated to lower eigenvalues.

Figure 5. One row of the added noise correlation matrix.

5.3. Signal/noise amplification analysis

As shown in section 4.3, data required for parameters estimation purposes are the two first KLD eigenfunctions, , and the corresponding states, and . In other words, for estimation purposes primary data reduce to (68) with . This results in an interesting effect with regard to measurements noise that we analyse here.

As explained in section 3.2, the signal/noise ratio for the primary signal at any point on the plate is (69) while for the associated 2D approximation it becomes (70)

After spatial sampling, equations above become (): (71) where and represent the ith component of the temperature vector and the ith element of the noise vector , respectively, and is the (i,m) element of matrix .

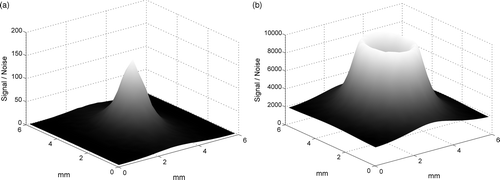
Calculated signal/noise ratios for the primary signals (lowest resolution) are depicted in Figure 6(a), while Figure 6(b) represents signal/noise ratios for the associated 2D approximation . In the first case, signal/noise values range from 0 to 120; while in the second one, they range from 2000 to 10,000. A huge amplification of the signal/noise ratio is achieved when reducing primary signals to their 2D KLD approximation. This explains the robustness to noise of the method we are proposing for diffusivities estimation.

Figure 6. Signal/noise ratio field: (a) for primary data in ; (b) for the 2D KLD approximation .

5.4. Thermal properties estimation

The estimation of the parameters , and has been carried out by the method described in section 4.3. Step by step this means:

–	Calculation of the KLD of : (), with . This involves calculation and spectral decomposition of the energy matrix: , with . Thus, calculation of the states: . It must be noticed that the number of the KLD components required for estimations is very low (two for orthotropic materials). Hence, algorithms allowing calculation of only the largest eigenvalues and associated eigenvectors of can be used.
–	Estimation of the parameter by applying the linear least squares method to equation , where represent the mean value of at time and .
–	Estimation of and using Equation (56). This involves calculation of vector and matrix (Equation (55)). The elements of are approached as descried by Equation (57).

Results achieved are summarized in Table 3. It includes the estimated values of the parameters , and as well as the corresponding 95% confidence intervals (in brackets). The quality of the results will be discussed in terms of bias and uncertainty of parameters and : (72)

Table 3. Estimated values for thermal parameters. True values are , and .

Resolution	Noise amplitude
100 µm	±0.02	0.0152	0.1516	0.3028
		(±3.10 × 10^−6)	(±1.52 × 10^−4)	(±3.45 × 10^−4)
	±0.10	0.0152)	0.1519	0.3015
		(±1.67 × 10^−5	(±7.82 × 10^−4)	(±0.0017)
200 µm	± 0.02	0.0152	0.1516	0.3027
		(±7.53 × 10^−6)	(±3.65 × 10^−4)	(±8.25 × 10^−4)
	±0.10	0.0152	0.1517	0.3022)
		(±4.17 × 10^−5)	(±0.0015)	(±0.0037
	±0.50	0.0152)	0.1553	0.2883
		(±1.74 × 10^−4	(±0.0072)	(±0.0164)
	±1.00	0.0152	0.1726	0.2370
		(±4.29 × 10^−4)	(±0.0498)	(±0.0982)

First, it is remarked that there is no significant difference in terms of bias between the estimations carried out on data with -spatial resolution and those coming from -spatial resolution data. However, the uncertainty of the estimations is slightly increased when the resolution is lowered. The proposed method can hence be used with simple infrared cameras providing low spatial resolution. As already explained, the necessary condition for the method works is that temperature maps provide a good enough finite-dimensional approximation of the thermal field.

Second, it is observed that (as expected) the quality of the estimations reduces when increasing the noise amplitude of the temperature data. Results are excellent for noise amplitude up to ±0.1°C (medium quality data). They are quite good for noise amplitude equal to ±0.5°C (bad quality data, ), with bias less than 5% and uncertainty lower than ±5%. On the contrary, estimations of poor quality (bias >10%, uncertainty >30%) are obtained when using highly noised temperature data, with noise amplitude equal to ±1°C and .

6. Parametric analysis

More extreme situations concerning the values of the thermal parameters are here considered to explore the limits of the proposed method. The quality of the estimations for much higher heat transfer coefficients, much higher thermal diffusivities, markedly different thermal diffusivities and closer thermal diffusivities, will be analysed. Medium and bad quality temperature with, respectively, noise amplitude equal to ±0.1 and ±0.5°C will be used. Indeed, only low spatial resolution data (pixel size: ) will be considered. The numerical experiments are generated as explained in section 5.1. The experiment analysed in section 5 will be referred as “reference case” in the following. Thermal parameters of the “reference case” are denoted as , and .

6.1. Higher heat transfer coefficient

The effective heat transfer coefficient has been assumed to be in the reference case. This is a quite likely value in the framework of infrared thermography experiments for thermal characterization of materials. A much higher value of the effective heat transfer coefficient is now considered, . Assuming and as before, we have now . The other parameters of the problem (geometry, diffusivities, thermal excitation, end time and sampling time) remain unchanged. The results of the estimations carried out with this new experiment are reported in Table 4. Compared with results in Table 3 (reference case), a degradation of the diffusivities estimations is observed. The results achieved remain of quite good quality in terms of bias but the uncertainty is significantly increased and become unacceptable (>90%) for temperature data with noise amplitude equal to ±0.5°C. This degradation of the results could be explained by the fact that increasing the value of the effective heat transfer coefficient (and only this parameter), the maximum temperature reached by the plate decreases and, consequently, signal/noise reduces if the noise amplitude remains unchanged. Index SN (see Equation (67)) is now (instead of ) for noise amplitude equal to ±0.1°C and (instead of ) for ±0.5°C.

Table 4. Effect of higher value. Estimated values for thermal parameters. True values are , and .

Parameters variations	Noise amplitude	Signal/ noise
	±0.10	54.1	0.1515	0.1508	0.3036
			(±1.23 × 10^−4)	(±0.0096)	(±0.0178)
	±0.50	2.2	0.1517	0.1420	0.3009
			(±6.28 × 10^−4)	(±0.1543)	(±0.2833)
	±0.10	114.1	0.1515	0.1515	0.3025
			(±7.43 × 10^−5)	(±0.0056)	(±0.0103)
	±0.50	4.6	0.1516	0.1491	0.2968
			(±3.82 × 10^−4)	(±0.0414)	(±0.0742)

The numerical experiment has been repeated using a larger laser/lamp spot ( instead of ) to improve the signal/noise ratio of the data. As shown in Table 4 (last two rows), signal/noise is now higher than in the reference case: (noise amplitude: ±0.1°C) and (noise amplitude: ±0.5°C). As expected, estimation results have been improved. The bias in parameters and is now lower than in the reference case but uncertainties remain higher even though acceptable (i.e. ∼20% for noise amplitude equal to ±0.5°C against to ∼5% in the reference case).

Accordingly, increasing the effective heat transfer coefficient requires using temperature data of higher quality for the performances of the estimation method to be similar.

6.2. Much higher diffusivity values

In the reference case, a poorly diffusive material has been considered: and . Much higher diffusivity values up to ∼10⁻⁴m²s⁻¹ will be taken into account now. Three different experiments have been generated with (as in the reference case) and , and . As in actual experiments, the geometry of the plate has been adapted to ensure that the thermal perturbations do not reach the borders of the plate, so that adiabatic boundary conditions can be assumed. For diffusivity value (), the plate dimension becomes ( for , for , and for ). Doing so we also warrant that signal/noise of the new sets of temperature data is similar to that of the reference case (see Table 5, third column). The spatial resolution of the simulated experiments is also scaled by . Pixels size is for , for , and for ). The other parameters of the problem remain unchanged.

Table 5. Effect of higher diffusivity values. Estimated values for thermal parameters. True values are , and .

Parameters variations	Noise amplitude	Signal/ noise
Reference case
	±0.10	60.0	0.0152	0.1517	0.3022
			(±4.17 × 10^−5)	(±0.0015)	(±0.0037)
	±0.50	2.4	0.0152	0.1553	0.2883
			(±1.74 × 10^−4)	(±0.0072)	(±0.0164)
	±0.10	60.1	0.0152	1.5174	3.0219
			(±3.92 × 10^−5)	(±0.0153)	(±0.0368)
	±0.50	2.4	0.0151	1.5498	2.8935
			(±2.05 × 10^−4)	(±0.0748)	(±0.1659)
	±0.10	60.0	0.0151	15.1665	30.2375
			(±4.40 × 10^−5)	(±0.1463)	(±0.3574)
	±0.50	2.4	0.0152	15.4351	29.0441
			(±1.70 × 10^−4)	(±0.7345)	(±1.6408)
	±0.10	60.2	0.0152	151.8400	302.0224
			(±3.86 × 10^−5)	(±1.4071)	(±3.5206)
	±0.50	2.4	0.0151	154.7727	289.4940
			(±2.0244 × 10^−4)	(±8.0158)	(±17.6240)

The results achieved when applying the estimation method proposed in this paper are reported in Table 5. Compared to the reference case, no degradation of the results has been observed. As in the reference case, worst results correspond to the estimation of parameter . The bias in this parameter ranges from 0.27% (noise amplitude equal to ±0.1°C) to 4.8% (noise amplitude = ±0.5°C) whereas uncertainty ranges from 0.93% (noise amplitude equal to ±0.1°C) to 5.8% (noise amplitude = ±0.5°C).

The proposed method is hence applicable for a wide range of thermal diffusivity values.

6.3. Markedly different diffusivity values

Diffusivities verify in the reference case. Markedly different diffusivity values have been tested here: and with . As in the previous section, the dimension of the plate and the spatial resolution have been scaled by , with . The other parameters of the problem remain unchanged. As explained in section 5.1, simulations have been carried out with an equally spaced () grid and resulting temperature data have been averaged to reach lower spatial resolution.

Achieved estimation results are reported in Table 6. Compared to the reference case, the bias in parameters and has been significantly reduced. It ranges from 0.033 to 1.1%. Regarding uncertainties, the estimation of the parameter has been improved (0.43–2.6% instead of 1–5%) probably due to the fact that the signal/noise of the temperature data is now higher. The uncertainty in parameter is comparable to that of the reference case, when . On the contrary, it is significantly increased when (1.12% for noise amplitude equal to ±0.1°C and 13.2% for ±0.5°C). This behaviour is the consequence of the spatial grid that has been used. As in infrared camera experiments, the grid is formed by squared pixels whose size has been adapted to the largest diffusivity value, namely . Hence, when the diffusivities start to be highly different, i.e. , the pixel size becomes unsuitable for estimations. Just reducing the pixels size is not a solution to this problem because the dimension of the plate is reduced as well (the number of pixels of the camera sensor is fix, so that increasing the observed surface reduces the spatial resolution and inversely) and becomes unsuitable for estimations (too low thermal gradient in the direction). Because of the limitations of the experimental device, two distinct experiments will be hence required for high-quality estimations of both parameters and : one where the plate dimension and the spatial resolution are adapted to value and one where these parameters are scaled taking into account value (as in the example).

Table 6. Effect of markedly different diffusivities. Estimated values for thermal parameters. True values are , and .

Parameters variations	Noise amplitude	Signal/ noise
Reference case
	±0.10	60.0	0.0152	0.1513	0.3034
			(±3.72 × 10^−5)	(±0.0029)	(±0.0081)
	±0.50	2.4	0.0151	0.1459	0.3115
			(±2.15 × 10^−4)	(±0.0126)	(±0.0346)
	±0.10	155.3	0.0152	0.1517	1.5138
			(±4.31 × 10^−5)	(±0.0010)	(±0.0066)
	±0.50	6.2	0. 0152	0.1532	1.5007
			(±2.01 × 10^−4)	(±0.0061)	(±0.0392)
	±0.10	161.5	0.0152	0.1517	15.1470
			(±3.97 × 10^−5)	(±0.0017)	(±0.0375)
	±0.50	6.5	0.0152	0.1524	15.1094
			(±1.95 × 10^−4)	(±0.0201)	(±0.4091)

6.4. Closer diffusivity values

A situation with rather close diffusivity values is now tested: with . The other parameters of the problem remain unchanged. Temperature data are generated as explained in section 5.1. Final spatial resolution is and two noise scenarios have been considered: noise amplitude equal to ±0.1 and ±0.5°C. Signal/noise ratios of the new sets of temperature data are comparable to those of the reference case (see Table 7, third column).

Table 7. Effect of closer diffusivities. Estimated values for thermal parameters. True values are , and .

Parameters variations	Noise amplitude	Signal/ noise
Reference case
	±0.10	60.0	0.0152	0.1513	0.3034
			(±3.72 × 10^−5)	(±0.0029)	(±0.0081)
	±0.50	2.4	0.0151	0.1459	0.3115
			(±2.15 × 10^−4)	(±0.0126)	(±0.0346)
	±0.10	80.8	0.0151	0.1484	0.1700
			(±3.78 × 10^−5)	(±0.0371)	(±0.0403)
	±0.50	3.2	0.0152	0.0871	0.2337
			(±1.88 × 10^−4)	(±0.1798)	(±0.1958)
	±0.10	459.0	0.0152	0.1516	0.1665
			(±1.24 × 10^−5)	(±0.0068)	(±0.0074)
	±0.50	18.0	0.0152	0.1515	0.1660
			(±6.52 × 10^−5)	(±0.0246)	(±0.0268)

We first remind that the bias and the uncertainty of the estimated diffusivities in the reference case range, respectively, from 0.12 to 4.8% and from 1 to 5.4%. Lowest values correspond to the data with lowest noise amplitude (±0.1°C). Results coming from new temperature data sets () are reported in Table 7. For noise amplitude equal to ±0.1°C, the bias of the estimated diffusivities are 4.4% () and 2% () whereas uncertainties are about 24% (too high). When noise amplitude increases (±0.5°C), the results achieved become unacceptable, with bias around 40% and uncertainty about 115%. This was expected because the thermal diffusivities difference (10%) is of the same order of magnitude than the uncertainty of estimated diffusivities in the reference case (5.4%). To improve the results, the quality of the temperature data has to be improved too. Two more experiments have been generated with and noise amplitude equal to ±0.1 and ±0.5°C, but using this time a larger laser/lamp spot ( instead of ) to increase the signal/noise ratio of the temperature data (see Table 7). As shown in Table 7 (last row), estimation results are highly improved. The bias becomes negligible (ranging from 0.01 to 0.5%) and the uncertainty is significantly reduced with values around 4.5% for noise amplitude equal to ±0.1°C and values about 16% for noise equal to ±0.5°C.

For estimating close thermal diffusivities, temperature data has to be of rather high quality in terms of noise.

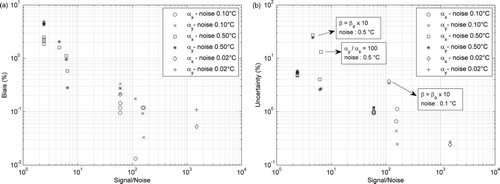
6.5. Overview

The bias and the uncertainty of the whole set of estimations carried out (except those in section 6.4, ) are depicted in Figure 7. It includes a wide span of representative parameter values (,, ) and provides an appropriate summary of the performances of the estimation method we have proposed. The upper limit of the bias seems to be entirely controlled by the signal/noise ratio of the temperature data. If we except rather extreme situations, as experiments with very high effective transfer coefficient (i.e. ) or experiments reaching the limits of the experimental device (, with high noise amplitude), the upper limit of the uncertainty of the estimations is also controlled by the signal/noise ratio of the temperature data. The method leads to bias less than 1% and uncertainties less than 4% for signal/noise ratios (see Equation (67)) higher than 6.

Figure 7. Overview of the results: (a) bias in parameters and as a function of the signal/noise ratio of the temperature data (SN index, Equation (67)); (b) uncertainty in parameters and against the signal/noise ratio of the temperature data.

7. Conclusion

A new method for reliable thermal characterization of homogeneous materials has been proposed. It is based on the use of KLD techniques in association with infrared thermography experiments carried out on thin samples. Orthogonal properties of KLD eigenfunctions and states allow achieving simple estimates of thermal diffusivities which depend only on the first and the second KLD eigenelements. As a result, the proposed method is an attractive combination of parsimony and robustness to noise. The last feature comes from the ability of KLD to amplify signal/noise ratios when truncated, as well as from free-noise KLD eigenfunctions when spatially uncorrelated measurement noise applies. Numerical tests carried out cover a wide range of representative parameter values and situations, and the results achieved are conclusive. However, they must be completed with actual experiments.

Compared to the existing methods for thermal characterization of homogeneous materials using infrared thermography, the proposed method has two main advantages. First one is robustness to noise, which allows reliable estimations even when using quite poor quality data. Second one is that the method applies even when no analytical solutions of the heat conduction problem exist. This implies that constraints regarding samples illumination (spatial and time patterns) are significantly reduced. Indeed, because no analytical solutions are required, the method could be extended to applications involving temperature-dependent parameters or heterogeneous materials. The second part of the paper deals with the extension of the method for thermal characterization of multi-phase materials with arbitrary microstructure.

Let us consider Equation (43) for . For simplifying writing but without loss of generality, we suppose . Hence, we can write:

Taking into account second Green theorem, the difference of equations above can be written as

As eigenfunctions verify Equation (44), it yields:

Let us consider the observer : with and

As already mentioned, the noise is assumed to be spatially uncorrelated. Indeed, we consider to be stationary and white. Hence where represents the expectation operator and is the variance of the added noise. Taking into account the statistical properties of , as well as the orthonormality of eigenfunctions, it follows: We suppose that the statistical moments of higher order of the variables can be neglected. Besides, we assume that is an unbiased estimation of parameter , so that . We note the variance of . As already proven, eigenvalues and verify where represents the energy of the added noise .

From equations above, it can be easily proven that where represents the covariance between the observers and .