Size distribution of nanoparticles by dynamic light scattering. Comparison of Bayesian and Tikhonov inversion methods

Abstract

The diameter distribution of nanometric particles is estimated from multiangle dynamic light scattering (MDLS) measurements by solving an ill-conditioned nonlinear inverse problem through Tikhonov and Bayesian methods. For both methods, the data inputs are the angle-dependent average diameters of the particle size distribution (PSD), which are in turn calculated from the measured autocorrelation functions of the light intensity scattered by a dilute sample of particles. The performances of both methods were tested on the basis of: (i) two simulated polymer latexes that involved PSDs of different shapes, widths and diameter ranges; and (ii) two real polystyrene latexes obtained by mixing two well-characterized standards of narrow PSDs (of known nominal diameters and standard deviations). For PSDs exhibiting highly asymmetric modes, or modes of quite different relative concentrations, the Bayesian method produced PSD estimates better than those obtained through Tikhonov regularization.

Keywords:

• dynamic light scattering
• inverse problem
• Bayesian method
• Tikhonov regularization method
• particle size distribution

Nomenclature

=

Table B – burn-in period (in the Metropolis-Hasting sampling method) CI – Mie scattering coefficient c1, c2 – cognitive and social accelerations in a PSO algorithm nm DLS average particle diameter nm mean diameter of a Gaussian PSD nm geometric mean diameter of a log-normal PSD Di nm i-th particle diameter (in the diameter axis of a discrete PSD) Dmin nm minimum diameter (in the diameter axis of a discrete PSD) Dmax nm maximum diameter (in the diameter axis of a discrete PSD) nm (R × 1) vector containing the DLS average particle diameters (at all θr's) d1, d2 nm nominal diameters of each mode (in latexes L1 and L2) fj – (j = a, b, 1, 2, L1, L2) discrete number-PSD f – (N × 1) vector containing the ordinates of a discrete number-PSD Fj – (j = 1, 2, L1, L2) discrete weight-PSD G – best position reached by the entire ‘particle’ population in a PSO algorithm – baseline of – second-order autocorrelation function of the scattered light (at θr) – first-order autocorrelation function of the electric field (at θr) – normalized second-order autocorrelation function of the scattered light (at θr) H – (N × N) matrix corresponding to the second-derivative operator Jf – performance index for PSD estimates [Equation (19)] K1, K2 – constants in Equations (8)–(10) k – iteration number in Equation (6a) kB (= 1.38 × 10^–23) Boltzmann constant M – number of points of the autocorrelation functions N – number of points of the PSD nm – refractive index of the non-absorbing medium np – refractive index of the particles Q – jumping distribution R – number of measurement angles R1, R2 – random numbers in the range (0, 1) [Equation (6a)] T K absolute temperature Vi – velocity of the i-th ‘particle’ in a PSO algorithm w – inertia function in a PSO algorithm Xi – i-th ‘particle’ in a PSO algorithm x1, x2 – number-fractions for the modes of latex L2 α – regularization parameter β – instrumental parameter for DLS measurements [Equation (2)] Γ0 nm/s DLS constant [Equation (4)] γ – smoothing parameter [Equation (9)] ΔD nm diameter interval (in the diameter axis of a discrete PSD) ε – Gaussian random sequence (mean = 0; variance = 1) [Equation (18)] η medium viscosity θr ° detection angle in MDLS λ nm in vacuo laser wavelength π – probability density σL – standard deviation of a log-normal distribution σG nm standard deviation of a Gaussian distribution τ nm decay constant of a decreasing exponential function τj s discrete time delay of

=

Table ^ estimated value ∼ contaminated with noise * convolution product ^T transposed vector

1. Introduction

The particle size distribution (PSD) is an important physical characteristic of several particulate systems, such as aerosols, emulsions, suspensions, dispersions and powders. The PSD can strongly influence the rheological behaviour and the stability of heterogeneous fluids, the coagulation or film formation processes of latexes, the magnetic and optical properties of dispersions, the taste and texture of foods, the coverage properties of paints, the burning rate of fuels and explosives, the quality properties of inks and toners, etc. 1.

Dynamic light scattering (DLS) 2, elastic light scattering 3 and turbidity 4 are fast and reliable optical techniques frequently used for determining average diameters of dilute systems that contain particles in the sub-micrometric range. When the PSD is estimated from light scattering and/or turbidity measurements, then the estimation procedure consists in inverting the mathematical model that describes the light extinction (scattering + absorption) suffered by light rays traversing a highly dilute sample of the particulate system. Typically, the Mie theory 5 is used for describing the light extinction under single scattering regime (i.e. in the absence of multiple scattering). The estimation procedure normally involves the solution of a linear ill-conditioned inverse problem (ICIP). Unfortunately, optical measurements contain a relatively small amount of information on the PSD; and for this reason only low-resolution PSDs can be estimated. The combination of two or more independent sets of measurements allows increasing the information content and can improve the quality of the PSD estimate. Previous works have combined turbidity and elastic light scattering measurements 6, DLS measurements taken at several angles (or multi-angle DLS measurements) 7,8 and turbidity and multi-angle DLS measurements 8. In some cases, the combination of independent measurements can lead to the necessity of solving a non-linear ICIP.

Classical approaches for solving linear and non-linear ICIPs are based on Tikhonov regularization techniques 9,10, which have been applied to estimate PSDs 1,2,6,7. On the other hand, statistical methods based on Bayesian inference 11,12 have scarcely been applied to sizing nanoparticles. For example, a Bayesian method was applied to solve the linear ICIP of estimating the PSD of ferrofluids from magnetization measurements, for particle diameters lower than 20 nm 13,14. Bayesian methods have also been used for solving other linear and non-linear ICIPs 12,15, but as far as the authors are aware, no application of Bayesian inference to the estimation of PSDs from optical techniques has yet been published.

In what follows, we will restrict our analysis to the case of DLS. In a DLS experiment, a dilute sample is irradiated with a monochromatic laser light, and the light scattered at different angles fluctuates due to the Brownian particle motion. In single-angle DLS, a digital correlator calculates the (discrete) second-order autocorrelation function of the fluctuating scattered light collected at a given angle, , where τ_j (j = 1, 2, … , M) represents the time delay. In multi-angle DLS (MDLS), a set of R measurements is obtained by collecting at the R different . From such measurements, R angle-dependent average particle diameters, , can be estimated through the cumulants method 16. Therefore, can be considered as a set of R indirect measurements of the average diameters.

Typically, the discrete number-PSD is denoted by f (D_i), where the ordinates of f (D_i) represent the number-fractions of particles contained in the diameter intervals [D_i, D_i+1], with i = 1, … , N. All the D_i values are spaced at regular intervals ΔD along the diameter range [D_min, D_max]; thus, D_i = D_min + (i – 1) ΔD, with ΔD = (D_max – D_min)/(N – 1). It can be proven that f (D_i) is theoretically related to the (noise-free) average diameters through the following non-linear expression 1,7: (1) where is the light scattered at the angle by a particle of diameter D_i, and can be calculated by the Mie scattering theory 5. Then, the estimation of the PSD f (D_i) from the indirect measurements consists in inverting the non-linear Equation (1) for known values of the coefficients.

The ill-conditioning characteristic of the inverse problem can be evidenced in Figure 1. Two quite different PSDs (f_a: bimodal, and f_b: unimodal) were defined (Figure 1a). To simulate the MDLS measurements, the following procedure is used. Each (noise-free) is related to its corresponding (first-order and normalized) autocorrelation function of the electric field, , through 7: (2) where is the measured baseline, β (<1) is an instrumental parameter and M is the number of points of each autocorrelation function. At each , is related to f (D_i) as follows 7: (3) with (4) where are normalization factors that insure  = 1 7 and adopt different values at different , λ is the in vacuo wavelength of the incident laser light, n_m is the refractive index of the non-absorbing medium (pure water), k_B is the Boltzmann constant, T is the absolute temperature and η is the medium viscosity at T.

Figure 1. The ill-conditioned problem. (a) Two arbitrary PSDs. (b) Mie coefficients corresponding to nanometric particles (at 5 angles). (c) Normalized autocorrelation measurements. (d) Derived DLS average diameters.

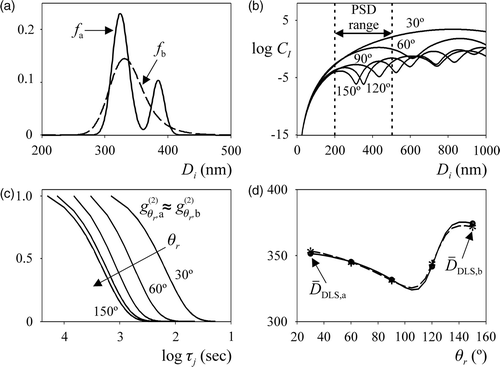
The coefficients C_I in Equations (1) and (3) also depend on the particle refractive index (n_p), λ, and the laser light polarization, and can be calculated on the basis of the Mie scattering theory 5. For λ = 632.8 nm, n_p = 1.5729, and a vertically polarized laser, the C_I coefficients are represented at five different angles (30°, 60°, 90°, 120° and 150°) in Figure 1(b). For D_i < 100 nm, all C_I coefficients are practically independent of (i.e. the light is scattered according to the Rayleigh regime 5), and therefore no additional information on the PSD could be extracted by measuring at several angles. The noise-free autocorrelation measurements were calculated from Equations (2) to (4), and then normalized according to (see Figure 1(c)). At any selected angle, the measurements corresponding to both PSDs are practically overlapped. The application of the cumulants method 16 on the produces the average diameters and indicated in Figure 1(d), where the symbols correspond to the five selected angles, and the curves represent the theoretical continuous measurements at all angles. Note that both PSDs practically produce the same derived average diameters. As a consequence, the involved inverse problem is ill-conditioned. Although normalized autocorrelations and (Figure 1c) are almost identical, their original exhibit small differences that cause the differences between and (Figure 1d).

In this work, a Tikhonov regularization technique and a Bayesian method are used for estimating PSDs of particulate systems on the basis of the average DLS diameters derived from MDLS measurements of highly diluted samples that ensure a single scattering regime. The performances of both inversion strategies are compared on the basis of simulated and experimental examples that involve PSDs of different shapes, widths and diameter ranges. Figure 2 summarizes the utilized calculation paths. In simulated examples, the PSD is assumed to be known, Equations (2) to (4) are used to calculate the noise-free measurements , and a random noise ε is then added to obtain the noisy measurements . In experimental examples, the DLS equipment directly produces . In all examples, the cumulants method 16 is applied to estimate the indirect measurements, . Finally, both inversion methods are used to estimate the PSDs by solving the nonlinear ICIP of Equation (1). Sections 2 and 3 explain the inversion methods. Sections 4 and 5 show some simulated and experimental examples that were used to assess and compare the two inversion strategies. Finally, some conclusions are given in section 6.

Figure 2. PSD estimation from MDLS measurements: schematic data treatment paths.

2. Estimation of the PSD through a Tikhonov Regularization Method

Let us call and the vectors containing the ordinates of the (unknown) PSD and the measured average diameters, respectively. For solving the non-linear ICIP, a Tikhonov regularization method (stated as an optimization problem) is proposed as follows 10: (5) where (R × 1) contains the average diameters corresponding to the estimated PSD, , which are directly calculated by injecting into Equation (1), W (R × R) is the covariance matrix of the measurement errors, α is a regularization parameter, H (N × N) is a regularization matrix and represents the 2-norm of a vector. We will assume that the measurement errors are uncorrelated and normally distributed with mean zero and standard deviation σ_r (r = 1, … , R), then W = diag(σ₁², … , σ_R²). Concerning the penalty term in Equation (5), the parameter α will be calculated through the L-curve method 17; and the matrix H will be implemented as a discrete second derivative operator to ensure high smoothness in the estimated PSD, as normally expected in practical applications.

As a first attempt to solve Equation (5), a sequential quadratic programming algorithm was applied on several simulated examples; but the PSD estimates resulted highly dependent of the chosen initial guess, thus revealing the existence of local minima. Therefore, a more effective optimization algorithm able to find the global minimum was required. Particle swarm optimization (PSO) algorithms proved to be powerful tools for solving linear and nonlinear optimization problems, in continuous as well as in discrete domains 18. Here, a PSO algorithm in the form of a linearly decreasing inertia weight PSO (LDW-PSO) is used 19.

In a PSO algorithm, the search is performed by using a large population of ‘particles’. (To avoid confusions, the term ‘particle’ corresponding to the PSO algorithm is here indicated between apostrophes.) Then, in the context of a PSO algorithm, a ‘particle’ corresponds to an individual; i.e. each ‘particle’ is a candidate PSD to represent the sought solution to the optimization problem.

During the execution of a PSO algorithm, each ‘particle’ continuously moves through the search space until some relatively stable state is reached 18. A PSO algorithm combines an ‘exclusively social model’ (which suggests that individuals ignore their own experience and adjust their knowledge according to the success of other individuals in the neighborhood), with an ‘exclusively cognitive model’ (which treats individuals as isolated beings). A ‘particle’ changes its position according to these two models.

The i-th ‘particle’ X_i is a point in a N-dimensional space, i.e. X_i = (x_i,1, … , x_i,N). The best position reached by X_i corresponds to the minimum value of the cost function [Equation (5)], and is represented by P_i = (p_i,1, … , p_i,N). The best position reached by the entire ‘particle’ population is represented by G = (g₁, … , g_N). The position change rate (or velocity) of X_i is represented by V_i = (v_i,1, … , v_i,N). The ‘particles’ are manipulated according to the following model: (6) (7) where k stands for the iteration number, c₁ and c₂ are two positive constants, R₁ and R₂ are two random numbers in the range (0, 1) 19 and w is the inertial weight 19. Equation (6a) is used to calculate the updated ‘particle’ velocity, v_i,j(k + 1), according to (i) its previous velocity, v_i,j(k), (ii) its current location distance to its best historical position, [p_i,j – x_i,j (k)], and (iii) its current location distance to the best position found within the group, [g_j – x_i,j (k)]. Then, the ‘particle’ moves from its old position, x_i,j (k), to its new position, x_i,j (k + 1), according to Equation (6b). This process is iteratively repeated until reaching the algorithm convergence, which is assumed to occur when G does not exhibit significant changes.

3. Estimation of the PSD Through a Bayesian Inference Method

Let us consider f and as random vectors. Then, the Bayes theorem can be stated as 11 (8) where is the posterior probability density, i.e. the conditional probability of f given the measurements , ; is the prior probability density, i.e. a statistical model for the information about the unknown parameters prior to the measurements; is the likelihood function, which gives the relative probability density of different measurements outcomes corresponding to a fixed f and is the marginal probability density of the measurements, which plays the role of a normalizing constant.

Since the random measurement noise is assumed independent, additive and Gaussian, then the likelihood function can be stated as 11,13,15: (9) where K₁ is a known constant that depends on the covariance matrix of the measurement errors, W.

The prior probability density function should include all a priori information available on the PSD. In practice, the PSD is generally accepted to be a smooth non-negative function; and among several possible smoothness conditions, we here particularly adopt that the PSD exhibit bounded second derivatives. Then, the maximum entropy principle 13 enables us to write: (10) where K₂ is a constant (strictly unnecessary for implementing the estimation procedure), and γ is a smoothing parameter that can also be obtained by the L-curve method 17. By substituting Equations (8) and (9) into Equation (7), we obtain: (11) In a statistical sense, the most likely solution of the estimation problem is the so-called maximum a posteriori (MAP), i.e. that f which maximizes Equation (10). Maximization of can be obtained by minimizing the exponent of Equation (10), i.e. (12) The minimization of the quadratic problem in Equation (11) is similar to the Tikhonov regularization of Equation (5). As a consequence, the MAP solution will coincide with the Tikhonov estimate. In this context, the Tikhonov inversion method may be considered as a particular case of a (more general) Bayesian inference method.

An alternative PSD estimate can be obtained by evaluating the mean of instead of its maximum, i.e. (13) It is important to note that if were a Gaussian distribution, then the maximum of Equation (10) would coincide with its mean, and therefore the PSD estimates obtained through Equations (11) and (12) would become identical. However, since is not a Gaussian distribution [see Equation (10)], then the solutions obtained through Equations (11) and (12) will be different.

Unfortunately, the PSD estimation through Equation (12) would require solving high-dimension integrations for evaluating in Equation (10), and the numerical procedure would be extremely time-consuming. To overcome such problem, a Markov Chain Monte Carlo (MCMC) method is usually proposed for sampling Equation (10), and inference on can be obtained from inference on the samples. Here a MCMC method implemented in the form of the Metropolis–Hasting algorithm 11,15 was used for sampling . The reason for using the Metropolis–Hasting algorithm is due to its simplicity for drawing samples from .

3.1. Metropolis–Hasting algorithm

The Metropolis–Hasting algorithm is used to draw a sequence of samples from . The algorithm can be summarized in the following steps 11,15:

1.	Start with any initial distribution f1 that satisfies . Set k = 1.
2.	Use the current f k to obtain a new candidate f*, from some jumping distribution q(f k, f*), which is the probability of returning f* given f k.
3.	Given the candidates f k and f*, calculate the acceptance factor: (14)
4.	Choose a random value U from a uniform distribution on (0,1). If U ≤ ξ, set f k+1 = f*; otherwise, f k+1 = f k.
5.	Set k = k + 1 and return to step 2 to generate the sequence {f1, … , f k}.

After a total number of K iterations, the iterative procedure generates a Markov chain {f¹, … , f^K}, provided that the transition probabilities from f^k to f^k+1 depend only on f^k and not on {f¹, … , f^k-1}. After a sufficiently large burn-in period (of B iterations), the chain approaches an stationary state, and samples from the set {f^B+1, … , f^K} are samples from . More details concerning MCMC and the Metropolis–Hasting algorithm can be consulted in 11,15.

Once the Markov chain is obtained, the estimated PSD, , can be calculated from Equation (12), i.e. (15) In what follows, we will refer to ‘Tikhonov inversion’ (TI) as the classical inversion method carried out to solve Equation (5), which also produces the MAP solution of Equation (10). Also, we will refer to ‘mean-based Bayesian inference’ (m-BI) as the method for solving the estimation problem through Equation (14).

4. Simulated Examples

The proposed inversion methods were first tested through simulated examples, because in these cases the solutions are a priori known, and therefore the performance of the algorithms can be adequately evaluated and compared. Two PSDs corresponding to hypothetical polystyrene (PS) latexes with spherical particles of diameters in the range 200–550 nm were considered. In all cases, the discrete diameters were spaced at regular intervals of ΔD = 1 nm. Both PSDs exhibited different shapes, widths and diameter ranges; and were selected to evaluate the ability of the proposed methods to deal with different kind of PSDs. All testing cases were defined on the basis of discrete number-PSDs, f (D_i).

The first PSD, f₁(D_i), was an asymmetric exponentially modified Gaussian (EMG), obtained by convoluting a Gaussian (of mean diameter  = 340 nm, and standard deviation σ_G = 10 nm), with a decreasing exponential function (of decay constant τ = 20 nm), i.e. (16) where ‘*’ represents the convolution product.

The second PSD, f₂(D_i), was the weighted sum of two normal-logarithmic distributions, as follows: (17) were each mode is obtained through (18) with the following parameters: { = 350 nm, σ_L,1 = 0.05}, for f_2,1(D_i), and { = 450 nm, σ_L,2 = 0.05}, for f_2,2(D_i). Therefore, f₂(D_i) is a bimodal PSD with asymmetric modes.

The light source was a vertically polarized He–Ne laser of wavelength λ = 632.8 nm. At such wavelength, the refractive indexes are n_p = 1.5729, for the PS particles, and n_m = 1.3319, for the dispersion medium (pure water). Measurement angles were selected to vary from 30° to 140°, at regular intervals of 10°. The above-detailed optical parameters were used to evaluate C_I(θ_r,D_i) 5, and are required to simulate the noise-free measurements through Equations (2) to (4). In addition, each was contaminated with additive and uncorrelated noises (similar to those observed in typical experiments), to obtain the noisy measurements , i.e. (19) where ε is a Gaussian random sequence of mean zero and variance one. From , the noisy first-order autocorrelation function of the electric field, , was calculated through Equation (2), and the noisy derived measurements were obtained through the cumulants method 16.

From the (r  =  1, … , R), the TI and m-BI methods were applied for estimating f₁ and f₂. In all estimation procedures, a diameter axis in the range 100–1100 nm, with N = 101 points regularly spaced each 10 nm, was selected. In order to estimate W, hundreds of simulations were implemented on many PSDs, for different noise realizations in Equation (18). For each PSD, the standard deviation of the resulting , σ_r, were calculated at each angle θ_r. Independently of the PSD, it was observed that σ_r are adequately approximated through: σ_r  =  0.0025 mean{}. This expression is particularly appropriate in experimental cases where only a few measurements can be carried out at each angle, which would avoid a reasonable estimation of σ_r. Then, the covariance matrix was built as W = diag(σ₁², … , σ_R²).

For solving the ICIP through the TI method, a LDW-PSO algorithm with 25 ‘particles’ was implemented. The usual parameters c₁ = c₂ = 2 were directly adopted from literature 19. The PSO algorithm was initialized by assigning to each ‘particle’ a random PSD of components sampled from a uniform distribution. Both simulated PSDs were used as testing examples, for adjusting the inertia function as well as the criterion for stopping the algorithm. The inertia function was selected as a linear function that decreased from w = 0.5 (for the first iteration) to w = 0.1 (for the iteration 10,000). After several runs, 10,000 iterations were adopted as a reliable criterion for stopping the optimization procedure.

For solving the ICIP through the m-BI method, the Metropolis–Hasting algorithm was initialized with positive random values (f¹) selected from a uniform distribution. A Gaussian jumping distribution [q(f^k, f*)] with zero mean and standard deviation of 0.001 was utilized. From q(f^k, f*) a new sample f* is derived from f^k by modifying the i-th component of f^k, where i is randomly selected from a uniform distribution. Again, both simulated PSDs were used as testing examples. The Markov chain length was adopted after many trial-and-error simulations. First, it was observed that short chain lengths produced noisy and non-repetitive estimates. Then, the chain length was gradually increased and more repetitive PSD estimates were obtained. Very long chain lengths (e.g. >1,000,000) importantly increased the computing time but did not produce meaningful changes in the PSD estimates. Therefore, a Markov chain length of 500,000 was finally selected as a trade-off between a reasonable PSD estimate and an excessive computing time. Moreover, with a Markov chain length of 500,000, a reasonable repeatability for different MCMC realizations was verified in each example. For the simulated PSDs, the evolution of revealed that the Markov chain reaches equilibrium in a burn-in period B = 15,000 states.

The regularization parameter, α, was selected according to the L-curve method 17, as follows: (1) Equation (5) was solved for a large set of α values, (2) for each α, the corresponding PSD estimate was used to evaluate the two terms of Equation (5): T₁ =  and T₂ = , (3) a cubic spline was used to fit T₁ vs. T₂, which produced an L-shaped curve when plotted in a log–log scale, (4) the final α was chosen as that value corresponding to the maximum curvature point of the L-curve. In spite of the non-linearity of Equation (5), the characteristics of the L-curve method 17 were reproduced. A similar procedure should be implemented for selecting the smoothness parameter, γ, from Equation (11). However, Equations (5) and (11) are equivalents, and therefore γ  =  α was directly selected in each example.

To evaluate the quality of the estimations, the following performance indexes were defined: (20) (21) where were obtained by injecting each estimated PSD, , into Equation (1). The index evaluates the ability of each inversion method to estimate the ‘true’ PSD, , and the index quantifies the errors in the recuperation of the noisy measurements, , from the estimated PSD. Note that in a real measurement, it would be impossible to calculate because is unknown; however, this criterion was adopted for the simulated examples to investigate the limitations of the proposed methodology.

Each example was simulated 25 times to investigate the effect of the artificial random noise ε added to the measurements [Equation (18)] on the final results. For each example, Table 1 shows the final average performance indexes [, ] and their corresponding standard deviations [, ]. The maximum and minimum values of and [, , , ] are also indicated. In the case of the bimodal PSD, f₂, the results corresponding to and are indicated for each mode. In all cases, the m-BI method produced better PSD estimates as suggested by the lower values of , and . In addition, the lower values of produced by the m-BI method indicate a more reduced sensitivity of the PSD estimates to the measurement noise, when compared to the results obtained from the TI method. In contrast, the TI method produced better recuperations of the measurements, as indicated by the smaller values of , and . These results can be justified by the fact that the m-BI method does not aim at minimizing the measurement errors, and therefore larger values of are obtained.

Table 1. Simulated examples.

	m-BI	TI	m-BI	TI
10^1×  (–)	1.56	2.14	0.87/2.62	1.19/9.91
10^1×  (–)	0.32	0.34	0.24/0.64	0.37/2.03
10^1×  (–)	2.41	2.86	1.47/4.16	1.98/12.89
10^1×  (–)	1.00	1.60	0.47/1.35	0.65/5.15
10^3×  (–)	1.86	1.31	1.81	1.34
10^3×  (–)	0.45	0.49	0.33	0.44
10^3×  (–)	3.37	3.03	2.56	2.28
10^3×  (–)	1.25	0.71	1.27	0.62
Note: Performance indexes corresponding to 25 simulations of each analysed example.

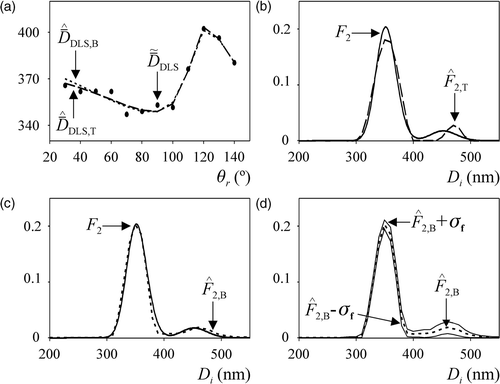
Figures 3 and 4 present the results corresponding to a particular realization of the examples 1 and 2, respectively. From the simulated measurements indicated in Figures 3(a) and 4(a), the proposed inversion methods produced the PSD estimates of Figures 3(b, c) and 4(b, c). In all figures, the ordinates are F_j(D_i) = f_j(D_i) D_i³ [instead of f_j(D_i)] to highlight the estimation errors at large diameters. Note that F_j(D_i) represents a weight-PSD; i.e. the ordinates of F_j(D_i) represent the weight-fractions corresponding to the discrete diameters. The estimated mean diameters, , are shown in Figures 3(a) and 4(a). In all figures, subscripts T and B added to the estimated variables stand for TI and m-BI, respectively.

Figure 3. Simulated example for the PSD f₁. (a) Average diameters i) calculated from the ‘noisy’ MDLS measurements (dots), and ii) simulated with the estimated PSDs. (b, c) The simulated PSD and its estimates from the TI method (b) and m-BI method (c). (d) Estimated PSD obtained from the m-BI method and the standard deviations calculated from the samples obtained through the Metropolis–Hasting algorithm.

Figure 4. Simulated example for the PSD f₂. (Legends as in Figure 3).

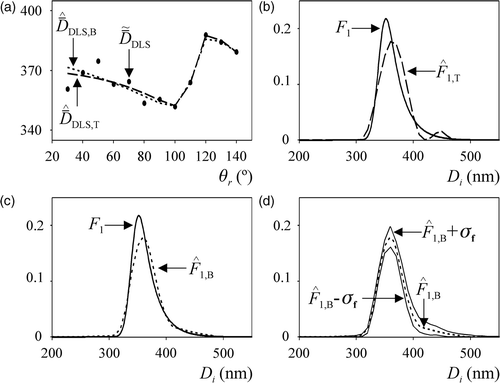
Figures 3(b) show that the Tikhonov regularization produced an erroneous mode around 450 nm, when estimating f₁. Such a spurious mode is due to the presence of measurement noises. Complete compensation of the erroneous mode was impossible even after applying a stronger regularization. On the other hand, m-BI technique seems to be less influenced by measurement noises, and produced an acceptable unimodal estimate (Figure 3c). In addition, while the TI method was unable to acceptably estimate the asymmetry in f₁, the m-BI method produced an accurate estimate. In the case of the bimodal PSD, f₂, both methods predicted the two modes, but the m-BI technique produced an estimate closer to the true PSD. In Figure 4, the mode corresponding to larger diameters was estimated through the TI method as a narrower mode of higher mean diameter (Figure 4b). In contrast, the m-BI approach produced a wider estimate that almost coincides with the true PSD (Figure 4c).

A statistical analysis of the set {f^B+1, … , f^K} was conducted to get information on the precision of the PSD estimate obtained on the basis of the m-BI method. Figures 3(d) and 4(d) show the estimates of f₁ and f₂, and the confidence bands defined by their corresponding standard deviations, σ_f, calculated from the Markov chains. Uncertainties resulted larger at the asymmetric zone of the unimodal PSD f₁, and for the mode of higher diameters of the bimodal PSD f₂.

Even though not shown, for unimodal PSDs with small asymmetries, for relatively broad PSDs, for bimodal PSDs with modes of similar concentrations, and/or for PSDs of higher diameters, both inversion methods produce accurate and similar estimates. In contrast, for PSDs with particles of small sizes (<150 nm), both inversion methods predict unreal spike distributions. These deteriorated predictions are quite reasonable because the shape of PSDs with particles of small diameters slightly contributes to modify the average diameters measured at the different angles, and therefore the measurements have low information content on the true PSD. All predicted spikes can be eliminated by increasing the regularization parameters, but excessively broad PSDs will be produced.

5. Experimental Examples

TI and m-BI inversion methods were also applied to evaluate experimental examples. Two latexes (L₁ and L₂) of bimodal PSDs were obtained by mixing two narrow and unimodal standards of PS (from Polysciences), of nominal diameters 300 and 1000 nm. The number fraction of the secondary mode (with particles of 1000 nm) was gravimetrically determined, yielding: x_L1,2 ≈ 1.05% for latex L₁, and x_L2,2 ≈ 2.10% for latex L₂.

MDLS measurements were carried out at 30°C and nine detection angles: [30° 40° 50° 60° 70° 80° 90° 110° 130°], with a general-purpose laser light-scattering photometer (Brookhaven Instruments, Inc.) fitted with a vertically polarized He–Ne laser (λ = 632.8 nm), and a digital correlator (model BI-2000 AT). The total measurement times ranged from 200 to 500 s. All latexes were well diluted in distilled, filtered and deionized water, yielding mean intensities lower than 200,000 counts/s at each detection angle, as recommended for avoiding multiple scattering 7.

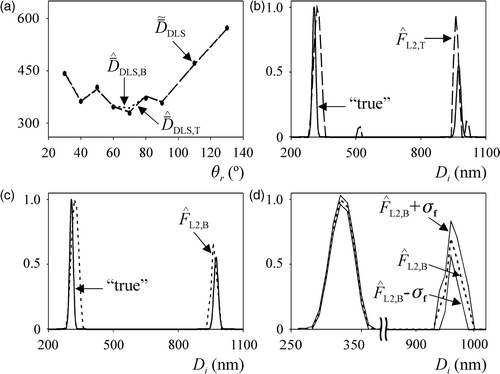
The average diameters, , were calculated by applying the quadratic cumulants method 16 onto the measured ; and are indicated by dots in Figures 5(a) and 6(a). These values were fed into the proposed inversion methods for estimating the PSDs indicated in Figures 5(b, c) and 6(b, c). In both experimental examples, the same discrete diameter axis adopted for the simulated examples was utilized. The components of the W, σ_r, were estimated from the expression described in the previous section, but simplified to the present case where only a single DLS measurement was available at each angle: σ_r = 0.0025 . The regularization parameter α was selected through the L-curve method. As in the case of the simulated examples, γ  =  α was adopted. Since the experimental data involved diameter and measurement vectors of dimensions close to those of the simulated examples, then the Markov chain length and the burn-in period were kept unchanged (i.e. 500,000 and 15,000, respectively). These last values were also checked to be appropriate after several PSD estimations with higher and lower values.

Figure 5. Experimental example for latex L₁. (a) Average diameters i) calculated through the cumulants method 16 (dots), and ii) simulated with the estimated PSDs. (b, c) Comparison of the ‘true’ PSD with its estimates from the TI method (b) and m-BI method (c). (d) Estimated PSD obtained from the m-BI method and the standard deviations calculated from the samples obtained through the Metropolis–Hasting algorithm.

Figure 6. Experimental example for latex L₂. (Legends as in Figure 5).

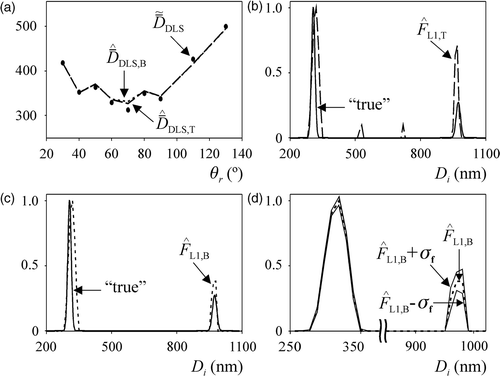
For evaluating the performance of the numeric inversion methods, ‘true’ PSDs must be adopted for latexes L₁ and L₂. These PSDs were defined on the basis of the nominal diameter and the standard deviation of each standard, which were reported by the manufacturer after characterization through disk centrifuge (DC) 1. The reported mean diameters and standard deviations were  = 306 nm and σ_PS1 = 8 nm, for the first standard; and  = 974 nm and σ_PS2 = 10 nm, for the second standard. Then, the ‘true’ PSDs were represented by bimodal distributions, with Gaussian modes centred at the diameters and , with standard deviations σ_PS1 and σ_PS2, and with number fractions x_L1,1 = 98.95% and x_L1,2 = 1.05%, respectively, for the first and second mode of latex L₁; and x_L2,1 = 97.90% and x_L2,2 =  2.10%, respectively, for the first and second mode of latex L₂.

Table 2 shows the nominal diameters, number fractions and performance indexes calculated for the ‘true’ and the estimated PSDs. Note that J_f is discriminated for each main mode of L₁ and L₂.

Table 2. Experimental examples.

	‘true’,			‘true’,
		m-BI	TI		m-BI	TI
(nm)	306	315	315	306	320	320
(nm)	974	971	965	974	965	963
(%)	98.95	99.00	97.40	97.90	98.10	96.80
(%)	1.05	1.00	1.50	2.10	1.90	2.20
10^1× Jf (–)	–	7.7/7.4	7.7/20.7	–	9.8/8.6	9.5/14.6
10^3× JD (–)	–	8.0	7.4	–	4.5	3.5

From Table 2 and Figures 5 and 6, the m-BI method produced better PSD estimates, except for the smallest mode of L₂, where the TI method showed a slightly better performance. Although the TI method produced acceptable estimation of the main modes of L₁ and L₂, it also estimated erroneous intermediate modes. On the other hand, the m-BI method produced bimodal PSDs that practically coincided with the ‘true’ PSDs, and it was able to adequately estimate the average diameter and number fraction of each mode of L₁ and L₂.

Figures 5(d) and 6(d) show the confidence bands for the PSD estimates obtained through the m-BI method. In both figures, the abscissa axes were conveniently expanded for a better visualization of the high diameter modes, where larger uncertainties were again observed.

6. Conclusions

A Tikhonov regularization technique and a mean-based Bayesian inference method were analysed as feasible numerical tools for solving the non-linear and ill-conditioned inverse problem that arises when the PSD of nanometric particles is estimated from MDLS measurements. The algorithms were implemented and fairly compared on the basis of simulated and experimental examples corresponding to PSDs of polystyrene latexes.

In general, the m-BI method produced improved PSDs with respect to the TI technique. The m-BI approach seems to be more efficient to deal with noisy measurements, without predicting the spurious intermediate modes observed with the TI methods. This can be justified by analysing the J_D index. In fact, the TI method tends to overweight the measurement noises and therefore yields lower J_D indexes than the m-BI method. Major differences between m-BI and TI predictions were observed for (i) highly asymmetric unimodal PSDs; and (ii) bimodal PSDs including modes of highly different concentrations. In case (i), the TI method normally predicts a spurious mode; and in case (ii), the m-BI method produces a better estimation of the low concentration mode.

All data processing was made in a standard PC with a Pentium(R) Dual-Core (2 GHz) processor and a RAM memory of 3 GB. Once the regularization parameter was chosen, the m-BI method required around 90 s to complete the 500,000 Markov chains plus the 15,000 burn-in periods; while the TI method required around 30 s to reach the optimum of Equation (5). Although the TI method reached the solution three times faster than the m-BI method, this advantage becomes almost negligible when it is compared to the global time required to obtain a PSD estimate. In fact, such a typical global time may reach 2–3 h, involving the sample preparation, the room conditioning, the equipment stabilization, the measurements at several angles (normally 200–500 s per angle), and the data processing. Thus, the advantages of m-BI method rely on its improved ability for estimating an accurate PSD in a global computing time similar to that of the TI method.

Acknowledgements

The authors are grateful for the financial support received from CONICET, MinCyT, Universidad Nacional del Litoral, Universidad Tecnológica Nacional (Argentina) and CNPq - Project 490.556/207-8 of the Program PROSUL (Brazil).