Estimating thermal and radiative properties of insulating materials

Abstract

In many practical situations, it is impossible to measure directly the characteristics, such as thermal and radiative properties, of analysed materials. The only way which can often be used to overcome these difficulties is indirect measurements. This type of measurement is usually formulated as the solution of inverse heat transfer problems. The experimental methods of identification of the mathematical models of heat transfer based on solving the inverse problems are one of the modern effective solving manners. The main purpose of this article is to estimate thermal and radiative properties of advanced materials (thermal conductivity , heat capacity and emissivity ) using the approach based on inverse methods. New metrology under development is the combination of accurate enough measurements, which can be experimentally observable under real conditions, and accurate data processing, which are based on the solutions of inverse heat transfer problems. In this article, the development of methods for estimating thermal and radiation characteristics is carried out for thermally stable, high-temperature insulating materials. Such problems are of great practical importance in the study of properties of materials used as non-destructive surface coating in objects of space engineering, power engineering, etc.

Keywords:

• thermal conductivity
• heat capacity
• emissivity
• parametric identification
• iterative regularization

1. Introduction

For a long time, when developing new prototypes of technology, much attention was paid to structural composite materials, an industry where we observe obvious achievements. Similar interest is attached to composite materials with other functional roles: acoustical, optical, electromagnetic and thermo-technical. Among functional materials of thermal engineering, the role of the most interesting materials with extreme properties – superinsulators and super thermo-conductive composites are increasing (for example: high-dense composite materials as carbon–carbon, carbon–ceramics and carbon–glass (‘Gravimol’); high-porous heat insulators made from fibres as TZMK, FRCI or micro spheres, light aerogels with density from 3 to 200 mg sm⁻³, foam plastics and polyurethane foams, etc.). Such materials find broad application in different structures, including those operating in the conditions of extreme temperatures; for example, in perspective flight vehicles; thermal and nuclear power; ferrous and non-ferrous metallurgy; chemical industry; engine manufacturing; the production of manufacturing structures; cryogenic engineering; etc.

The modern approaches to the design of structures assume broad application of mathematical and physical simulation methods. But mathematical simulation is impossible if there is no true information available on the characteristics (properties) of objects analysed. In the majority of cases in practice, the direct measurement of materials’ thermal properties, especially complex composition, is impossible. There is only one way which permits to overcome these complexities – the indirect measurement. Mathematically, such an approach is usually formulated as a solution of the inverse problem: through direct measurements of system's state (temperature, pressure, etc.), define the properties of a system analysed, for example, the thermal and radiative properties. Violation of cause-and-effect relations in the statement of these problems results in their ill-posedness in mathematical sense (i.e. the absence of existence and/or uniqueness and/or stability of the solution). Hence to solve such problems, we develop special methods that are usually called regularization methods.

In estimating properties of modern structural, thermoprotective and thermoinsulating materials – as temperature dependent – the most effective are the methods based on solution of the coefficient inverse heat conduction problems. The most promising direction in further development of research methods for non-destructive composite materials using the procedure of inverse problems is the simultaneous determination of a combination of material's thermal and radiative properties (thermal conductivity , heat capacity and integral emissivity ). Such problems are of great practical importance in the study of properties of composite materials used as non-destructive surface coating in objects of space technology, power engineering, etc. 1–7. The mathematical model of heat transfer in the specimen is (1) (2) (3) (4) where

In models (1)–(4), the coefficients , and are unknown. The experimental equipment and the method described below could be applied for estimating the three characteristics of the material; the availability of a few specimens of the material allows us to provide uniqueness of the solution. This article is concerned with modification of the approach, presented in Nenarokomov and Alifanov 8 (further it will be called approach A). The main difference from approach A is the interpretation of input data of the experiment in another way, namely, the heat flux from the metallic heater was considered in Nenarokomov and Alifanov 8 as Stefan–Boltzmann irradiation with known (measured by thermocouple) temperature of the heater and a priori known (theoretically) emissivity of the heater .

At this article, the emissivity of the heater is considered as additional (forth) estimating functions. Therefore, the accuracy of the inverse problems, considered below, will not depend on the a priori information about the radiation properties of the heater's material.

The data processing of the single experiment is not enough to provide the conditions of uniqueness of the inverse problem solving by simultaneous estimation of thermal conduction, heat capacity and emissivity of the testing material. To solve this problem, the data of several N (in partial three) similar experiments with equal material specimen and different heating regimes were processed simultaneously.

The results of temperature measurements inside the specimen are assigned as necessary additional information to solve an inverse problem (5)

In the inverse problems (1)–(5), first of all, it is necessary to indicate a temperature range of the unknown functions, which is general for all experiments and for which the inverse problem analysis has a unique solution. For T_min, the minimum value of initial temperature is used. Of much greater importance is a correct sampling of value, T_max. Proceeding from the necessity to provide uniqueness of solution, it seems possible to sample, for T_max, a minimum among maximum temperature values gained on the thermocouple positioned on the heated surface at every testing specimen. The same should be done for the heater temperature range .

2. Inverse problem algorithm

Suppose then that the unknown characteristics are given in their parametric form. With this purpose, introduce in the interval , three uniform difference grids with the number of nodes .

Then, in case of cubic B-splines, as approximation functions for unknown characteristics, the unknown function is presented as (6)

Also, the unknown functions on grids (6) using the cubic B-splines also can be presented as (7) where , k = 1, N₁, , k = 1, N₂ and , k = 1, N₃ are parameters.

Let us introduce in the interval uniform difference grids with the number of nodes and approximate the unknown function on grids (8) using the cubic B-splines (8) where , is a parameter.

As a result of approximation, the inverse problem is reduced to the search of a vector of unknown parameters , , with dimensions . Writing down a mean-square error of the design and experimental temperature values in points of thermal sensors positioning than the residual functional will depend on four functions (9) where is determined from a solution of the boundary-value problem Equations (1–4) for nth experiment using the approximations of Equation (7). It is assumed here that the conditions of uniqueness of the inverse problem solving are satisfied. To simplify the notation of equations, index n will be excluded.

In processing the results of real experiments and tests, there are always errors, depending on a number of reasons. First of all, the errors in the experimentally measured data are both random and systematic by nature. Random errors in input data are stipulated by a spread of thermal and electrical characteristics in thermal sensors and other measuring devices, by inaccuracy of their calibration, etc.; as a rule, these errors show a large enough value. Systematic errors in the input data f are usually connected with inaccuracy in determining the coordinates of thermal sensors, with temperature pattern distortion in the specimen by thermal sensors, with displacement of the very specimen during filming or X-ray survey, etc. That is why, the term f_m is always known with some error.

The second group of errors are the errors of finite-difference approximation of differential operator in the initial problem and round-off errors in the computer.

Besides, there are errors due to uncertainties in the a priori assigned characteristics of a mathematical model, Equations (1–4), which are determined either through calculations or from a solution of the corresponding inverse problems.

Due to mathematical ill-posedness of the problem in defining the heat transfer characteristics, the availability of errors in the input information leads to a solution, which can have nothing in common with an unknown one. To overcome this circumstance, it was suggested to make use of the regularized properties of gradient methods of optimization, which permit to quickly begin an iterative process from a distant estimate of characteristics to be determined, and it slows down abruptly while approaching the functional minimum. As the number of iterations increases, the solution of the inverse problem can start oscillating, gradually losing its smooth nature. A necessity occurs to stop the iterative process, falling short of solution oscillations. An important task here is to sample a stop criterion for the iterative process. By principle of generalized discrepancy, such criterion can be a constraint on the value of minimized functional .

A successive approximation method stated here, according to general definition of Tikhonov's regularizing operators, gives rise to a regularizing set of operators in which a regularization variable is the number of the last iteration. For linear ill-posed problems, the iterative regularization method has received a rigorous mathematical substantiation and practical verification through data of mathematical modelling. Applicable to non-linear problems, there are at present no complete theoretical results on the substation of stability of iterative algorithms. However, the results of computational experiments already made in solving the inverse heat transfer problems of different types prove the high efficiency of the iterative regularization method and the possibility to analyse a wide range of non-linear problems.

So, proceeding from the principle of iterative regularization 8–10, the unknown vector can be determined through minimization of functional Equation (9) by gradient methods of the first order prior to a fulfilment of the condition (10) where is an integral error of temperature measurements , and the measurement variance.

To construct an iterative algorithm of the inverse problem solving, a conjugate gradient method was used. The successive approximation process is constructed as follows:

1.	a priori, an initial approximation of the unknown parameter vector is set; and
2.	a value of the unknown vector at the next iteration is calculated. (11) where is the value of the functional gradient at the current iteration.

The greatest difficulties in realizing the gradient methods are connected with calculation of the minimized functional gradient. In this approach, the methods of calculus of variations are used. Here, an analytic expression for the minimized functional gradient can be obtained. (12) (13) (14) (15) where is the solution of a boundary-value problem adjoint to a linearized form of the initial problem (Equations (1–4)). (16) (17) (18) (19) (20)

3. Experimental verification

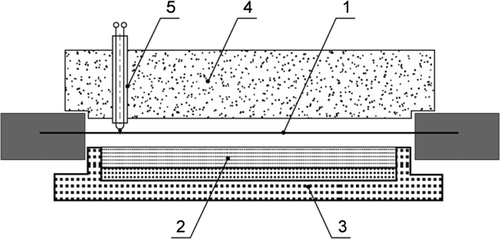
As an example, the results of data processing on experimental study of material specimens are used, which involves the thermo-vacuum facility developed in MAI, the Department of Space System Engineering (Figure 1). The test facility consists of a horizontally set cylindrical vacuum chamber with a water-cooling system.

Figure 1. Test stand: 1, vacuum chamber; 2, experimental module; and 3, heater iterative process.

A heating element consists of a molybdenum foil with dimensions 80 × 70 × 0.05 mm³ (Figure 2). The tested specimen is located on a thermo-insulating base made of thermal insulation material, so that its heating surface is parallel to heater's plane and at certain distance from it (3–5 mm). A ceramic plate is put over the heater, which reduces the heat withdrawal from it in the direction opposite to the test specimen improving its heating uniformity. Control of the specimen heating regime is performed by the temperature of the exposed surface in accordance with a preset regime. Control over the heating regime was maintained in the experiment using the results of three trial starts with specimens from test materials, the structure of which being similar to the structure used in tests. In making the trial starts, a criterion for choosing a suitable heating regime is based on the coincidence of specimen's external surface temperature measured with the preset temperature.

Figure 2. Experimental module: 1, heater; 2, test specimen; 3, insulating basement; 4, insulating cover; and 5, control thermocouple.

An example as to how to apply the approach suggested is presented below. Given are the results of data processing of specimen experimental investigations with modern composite materials. The investigations were carried out on a set of pairs of specially manufactured specimens (the first in the pair for simultaneous estimation of material's heat capacity and thermal conductivity and the second for determining boundary conditions).

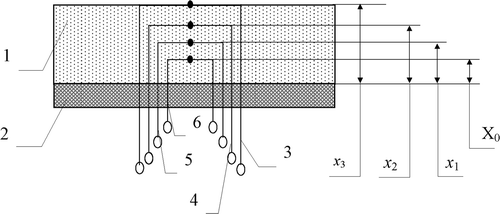
The models of test materials are the square plates of 50 × 50 × 15 mm³ (Figure 3) with four thermocouples installed in the specimen. Installation of thermal sensors in the specimens was chosen from a solution of the problem of optimal experiment design. The coordinates of thermocouple positioning in the first set of specimens, for estimating the material's thermal characteristics, had the following values: (for a boundary condition of the first kind, sensor readings on the internal surface were used), , and (positioned on the exposed surface). The second set of specimens, for defining the emissivity, has the thermocouples at points , , and .

Figure 3. Test specimen: 1, test materials; 2, metallic basement; and 3–6, thermocouples.

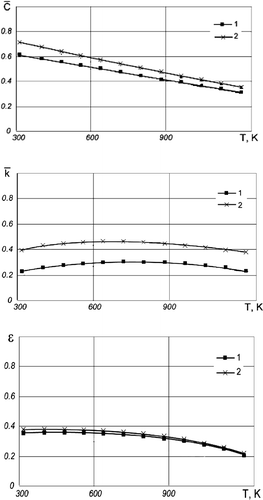
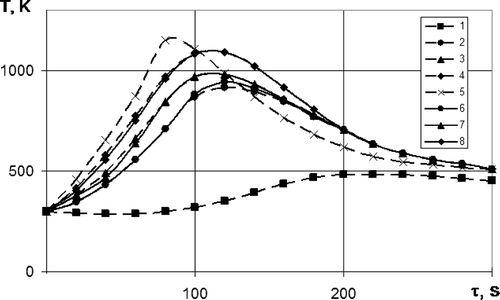
The number of approximation parameters N1, N2, N3 and N4 for every characteristic was assumed to be five. During specimen heating, a theoretically preset time dependence of surface temperature (Figure 4) was provided. The measurement errors were estimated as 5%. A comparison of experimentally measured and calculated (with the help of thermal characteristics obtained from a solution of the inverse problem) temperature values in points of thermocouple positioning is shown in Figure 4 (only for one specimen). The results are in agreement, which shows the robustness of the inverse problem algorithm.

Figure 4. Measured and calculated temperatures: 1, measured temperature used as Dirichlet boundary condition (internal thermocouple, position 6 in Figure 2); 2, measured temperature (internal thermocouple, position 5 in Figure 2); 3, measured temperatures (internal thermocouple, position 4 in Figure 2); 4, measured temperatures (thermocouple on exposed surface, position 3 in Figure 2); 5, measured temperature of the heater; and 6–8, calculated temperatures at the points of thermocouple installations.

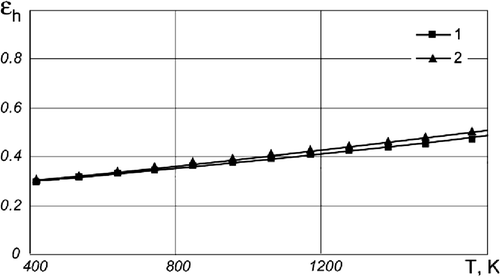
The results of the inverse problem solving – the composite material's thermal characteristics and emissivity – are given in Figures 5 and 6 (the results for two sets by three experiments in vacuum and air conditions). The accuracy of the results of the inverse heat conduction problem was verified using different (quite distinct from each other) initial approximations for an iterative process. The results show a reasonable agreement.

Figure 5. Results of estimating: (a) heat capacity; (b) thermal conductivity; and (c) emissivity. 1, vacuum and 2, air.

Figure 6. Estimated emissivity of the heater foil: 1, vacuum and 2, air.

4. Conclusions

This article seeks to describe the algorithm developed to process the data of unsteady-state thermal experiments. The algorithm is suggested for determining these unknown on the surface of a slab as a solution of the non-linear inverse heat conduction problem in an extreme formulation.

The following main factors have an influence on the accuracy of the inverse heat conduction problem (in sequence of significance): the errors in coordinates of thermal sensor positions; the errors in values of different characteristics; and the errors in estimating the residual level. It was shown that in the cases considered, the accuracy of the inverse problem solution is compatible with the errors of the simulated ‘experimental measurements’. Next step in the development of the proposed approach is to consider an estimating interface conductance between periodically contacting surface of specimen and heater foil using the approach similar to Orlande and Ozisik 11.

Acknowledgements

This study was done with the financial support provided by the Russian Basic Research Foundation (grant no. 11-08-00952а).