Retrieving of the initial moisture field in porous material based on temperature measurements during drying

Abstract

In this article, a simultaneous initial inverse problem and parameter estimation inverse problem in context of the vacuum paper drying process is presented. In this problem an evaporation constant and initial distribution of the water content are retrieved indirectly based on the temperature measurements at selected sampling points during vacuum phase of the process. As such, a problem is ill-posed and two different Tikhonov-type regularization techniques are proposed. The L-curve method was used to establish the value of the regularization parameter for both techniques. Results obtained with both regularization techniques are compared.

Keywords:

• vacuum paper drying
• initial inverse problem
• parameter estimation inverse problem
• Tikhonov regularization
• L-curve method

AMS Subject Classifications::

• 65M32
• 65Z05
• 76S05
• 76T30

1. Introduction

Crepe paper, due to its superior insulating properties, is very widely used in the electrical industry, e.g. in the production of electrical transformers or bushings. However, the insulating properties of paper strongly depend on the moisture content and rapidly deteriorate if it is higher than 3%. Practically, at the manufacturing stage it is desirable to keep the moisture content within the paper below around 0.5%. So low water content in the paper can be achieved by utilizing the special drying technologies. In the electrical industry vacuum drying technology is the most commonly used for proper preparation of the insulation crepe paper 1. In this technology dried material is placed in the hermetic vacuum chamber, then it is heated up to some prescribed temperature and further air is evacuated (reaching deep vacuum), which causes rapid water evaporation. This heating-vacuum procedure is periodically applied for a given number of times. This technology is very efficient and allows one to obtain very low water content in the dried material, which is crucial for electrical appliance production. However, it is very difficult to control this process as the only pieces of information that are available are pressure and temperature of the air in the vacuum chamber. Therefore, a mathematical model was developed, which allows us to predict the course of the process including distributions of temperature, water content and velocity within the paper and vacuum chamber 2,3. In addition, this model can be successfully applied for optimal design of the process. The model was validated experimentally 3,4. Gathered experimental data was employed in inverse procedure to retrieve its important model parameters 5. Together with those model parameters, an initial water content distribution within the paper being dried should also be reconstructed. To overcome the problem of ill-posedness of the analysed coupled initial and parameter estimation inverse problem, some regularization methods have to be considered.

Application of inverse approach to drying process is not new problem. For instance, in the literature numerous works by Kanevce, Kanevce and Dulikravich can be found. Kanevce et al. 6,7 considered inverse concepts to 1D Luikov diffusion transient problem of drying the thin body. Additionally, in 7 they took into account the shrinkage effect. The same authors also proposed the methodology of simultaneous estimation of thermophysical properties and heat and mass transfer coefficients of a drying body (e.g. 8–10).

A few different regularization techniques are commonly used for the solution of ill-posed inverse problems, i.e. truncated singular value decomposition (TSVD), Tikhonov regularization or iterative regularization 11. In the TSVD, high-frequency oscillation due to errors in the input data are filtered out by the truncation of lowest singular values of the considered linear operator (for further reference, see 11,12). Traditionally, in the Tikhonov method the solution is obtained by minimizing the smoothing functional 13–16: (1) where L is the operator representing the considered model, x stands for the regularized solution vector, d is the input data and Γ corresponds to the stabilizing operator. The stabilizing operator can be considered as an identity operator, first or second derivative, leading to the zeroth-, first- or second-order smoothing, respectively. Depending on the specific problem, other stabilizing operators are also allowed 17. The group of iterative regularization techniques is represented by methods like steepest descent method, Landweber iteration, conjugate gradient method or Levenberg–Marquardt method 11,17,18. In these methods solution is obtained by the iterative improvement of the initial guess until stopping criteria is met. Also some hybrid methods were reported in the literature, e.g. Alifanov proposed the procedure in which the Tikhonov functional was minimized with steepest descent method 19.

As mentioned above, in this article the coupled initial and parameter estimation inverse problem is considered, which arises in the technology of the vacuum drying in electrical industry. In this problem a parameter of the water evaporation model as well as the initial water distribution is being reconstructed. This problem is poorly conditioned. Hence, a hybrid regularization algorithm was proposed in which the Tikhonow-like smoothing functional is minimized through the Levenberg–Marquardt technique. Two different stabilizing terms in the smoothing functional are considered. The first one puts constraint on the solution with respect to the value of the evaporation constant. The second one regularizes the solution with respect to the total water mass evaporated during the process. Results obtained with different values of the regularization parameter are presented.

2. Vacuum drying experiment

To investigate experimentally the vacuum drying process of the paper, a special experimental rig was build. It allowed us to carry out the single heating phase followed by the vacuum phase. Experimental data gathered during this experiment were used to validate the mathematical model of the process as well as to reconstruct the unknown evaporation constant and the water content distribution within the paper after heating phase and before vacuum phase.

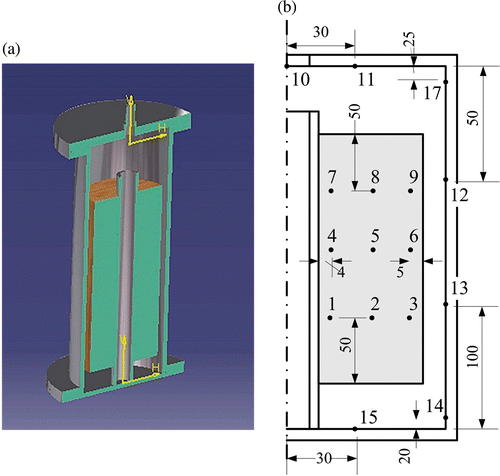
The picture of the experimental stand is presented in Figure 1. The main part of the stand is the vacuum chamber in which paper roll wrapped around the aluminium conductor is placed (cf. Figure 1a). The chamber was connected with the airtight hose to the vacuum pump. Inside the vacuum chamber, a number of thermocouples were placed. Some of them were positioned at the chamber walls to be able to determine boundary conditions for the mathematical model of the process. Remaining thermocouples are placed inside the paper roll to record the changes in temperature field. Exact locations of all thermocouples are presented in Figure 1(b).

Figure 1. The experimental stand for the paper vacuum drying experiment: (a) cross-section of the vacuum chamber, (b) position of thermocouples inside the chamber and paper roll.

The heating phase of the experiment took about 5 h and then the vacuum phase of the experiment lasted for 600 s. During the vacuum phase, the pressure was gradually decreased by the vacuum pump until it reached about 1 kPa, details of the experiment are given in 3,4. The first 50 s of the vacuum phase are employed in the inverse procedure to determine the unknown evaporation parameter (C_mt in Equation (11)) and distribution of the water content inside the paper roll at the beginning of this phase. The remaining temperature recordings from the heating and vacuum phase of the experiment were used to validate the mathematical model of the process as well as the inverse procedure itself. After the experiment, the paper was weighted to find out the amount of water removed from the paper during the experiment. The initial amount of water in the paper was also measured.

3. Mathematical model of the vacuum paper drying process

Mathematical model of the vacuum paper drying comprises the main phenomena that take place at the paper and inside the vacuum chamber. In the model, paper is treated as a porous medium which is in thermodynamic equilibrium with a surrounding humid air. Hence, one energy equation, common for both phases, is solved. Water inside the paper is treated as one phase regardless of its state. Its distribution is governed by the lumped diffusion equation, containing the effective diffusion coefficient D_eff. This coefficient depends on the water content and temperature and was determined experimentally 4.

Taking the above assumptions, the main governing equations of the model are as follows:

•	continuity equation for humid air (2) where ϱa is the density of air (kg m−3), wa is the air velocity vector (m s−1) and is the water vapour mass source/sink due to water evaporation/condensation (kg s m−3).
•	diffusion equations for air constituents Humid air is treated as a mixture of three components: water vapour, oxygen and nitrogen. For two of them, namely water vapour and oxygen, diffusion equations read as (3) (4) where Yi is the mass fraction of the i-th constituent (dimensionless), Da,i is the diffusion coefficient of i-th constituent in humid air (in m2 s−1). Mass fraction of the nitrogen is obtained by summing up all fractions to one.
•	momentum equation for humid air (5) where p is the pressure shared by all the phases (Pa), τ is the stress tensor (Pa), g is the gravitational acceleration (m s−2) and S is the momentum source term due to the flow through the porous media (kg m−2 s−2). It is calculated using the following formula 20,21: (6) where D is the viscous resistance tensor (in 1 m−2) and C is the inertial resistance tensor (in 1 m−1).
•	turbulence model equations – the standard k − ϵ model was adopted: (7) (8) where k is the turbulence kinetic energy (m2 s−2), ϵ refers to the turbulence dissipation rate (m2 s−3) and Gk stands for the generation of the turbulence kinetic energy due to the mean velocity gradients (kg s−3 m−1). Model parameters were Cϵ1 = 1.44 (dimensionless) and Cϵ2 = 1.92 (dimensionless).
•	water diffusion equation within paper (porous material) (9) where γ is the porosity of the porous material (dimensionless), ϱs is the density of the paper, X is the water content in the dry material (dimensionless) and Deff is the water effective diffusion coefficient within the porous material (m2 s−1) 22,23.
•	energy equation for the system consisted of the humid air and the porous material (10) where e is the specific internal energy of the material (J kg−1), subscript a stands for air and s for solid, is the latent heat of evaporation (J kg−1) (or heat of moisture adsorption in solid), keff is the effective heat conduction coefficient (W m−1 K−1) accounting for both axial and radial directions. The volumetric heat source (in W m−3) accounts for radiative heat transfer through participating media. Details on determining both latter quantities can be found in 3.
•	interphase mass transfer – the modified Hertz–Knudsen equation 24,25 (11) where pv is the vapour pressure (Pa) and T is the temperature of the porous material (K) (temperature of water – dry paper composition), peq is the vapour equilibrium pressure at the porous material surface (Pa), R refers to the universal gas constant () and Cmt stands for the evaporation constant (1 m−1).

This model was implemented in the Fluent 6.3, a commercial computational fluid dynamics (CFD) software 21,26. It is solved in each iteration of the proposed inverse algorithm to calculate the temperature and water content distribution inside the vacuum chamber and paper.

4. Formulation of the inverse problem

As already mentioned, one of the main aims of the proposed inverse procedure is to determine the value of the evaporation constant C_mt that appears in Equation (11), which would be appropriate for the vacuum drying process. Since the direct measurement of the water content inside the paper during the drying process is not possible, it was proposed to calculate the evaporation constant indirectly by measuring temperature histories during the vacuum phase of the process. However, it appeared that together with the evaporation constant, the water content distribution at the beginning of this process phase also has to be reconstructed 5. This was done by the minimization of the functional that represents a sum of the squares of deviations between temperatures measured during the experiment and those predicted by the mathematical model discussed in Section 3, i.e. (12) where T* is the vector of temperatures measured at all nine sampling points inside the paper during the first 50 s of the vacuum phase of the experiment. T(P) stands for the vector of temperatures predicted by the mathematical model described in Section 3 in the same time instances and at the sampling points. is the temperature measurements covariance matrix 16,17. Vector P stores evaporation constant C_mt (see Equation (11)) as well as information on the initial water content distribution: (13) where X_0,i is the water content at the i-th sampling point at the beginning of the vacuum phase of the experiment (cf. Figure 1). These values are further used to approximate the whole initial water content distribution with the second-order polynomial: (14) where ϕ(x) =  [y², xy, x², y, x, 1]^T reads the base functions vector, x and y are the radial and axial coordinates, respectively, at any point (axisymmetry is assumed in the model). α = [α₅, α₄, α₃, α₂, α₁, α₀]^T refers to the vector of the approximation coefficients. Values of these coefficients are determined utilizing values of the water content at all nine sampling points and by solving Equation (14) in the least squares sense: (15) where x* is the 9 × 2 matrix of sampling points coordinates (Figure 1b).

Application of the Levenberg–Marquardt procedure to the least squares functional (12) leads to the following formula for updating of the unknown parameters 17: (16) where Z(P) is the sensitivity coefficient matrix, μ is the damping parameter while Ω is the diagonal matrix. To some extent, it is arbitrary how Ω matrix is determined but the most commonly it is just a main diagonal of the matrix Z^T(P^k)Z(P^k). Sensitivity coefficients were calculated by the central difference scheme just for the initial set of sought parameters. The main reason for this simplification was a very long computation time to obtain the solution of the direct problem.

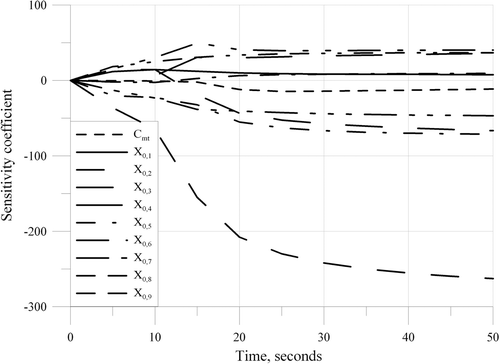
The inverse problem described by Equations (12–15) is badly conditioned as the evaporation rate strongly depends on the evaporation constant value as well as on the local values of the water content (see Equation (11)). It can also be deduced from the plots of the sensitivity coefficient values. In Figure 2 time histories of the values of the sensitivity coefficients at exemplary point no. 1 are shown. It can be seen that the sensitivity coefficient for X_0,2 has the largest value. For all remaining parameters, sensitivity coefficient values are considerably smaller. Moreover, it should be noted that at some time instances their plots are almost parallel. It means that they have similar influence on the temperature field as a function of time. To overcome these problems, two regularization approaches of the Tikhonov type were proposed.

Figure 2. Values of the sensitivity coefficients for all sought parameters at point no. 1 inside the paper roll.

4.1. Parameter regularization approach

In the first regularization approach, the functional (12) was supplemented with the regularization term that measures the deviation of the sought value of the evaporation constant C_mt from the assumed value : (17) where λ is the regularization parameter. The evaporation constant value may be assumed based on a previous observation or an experience. Depending on the reliability of such predictions, larger or smaller value of the standard deviation can be prescribed. In the case of ill-posed problems, the above regularization approach results in searching the solution which minimizes both temperature deviations and distance to the assumed solution. The above-mentioned approach can be generalized for all parameters which are sought in the inverse procedure as follows: (18) where P* refers to the vector of assumed values of the parameters which are to be estimated with inverse procedure, is the covariance matrix of the assumed values of parameters and λ is the regularization matrix. The regularization matrix has all off-diagonal elements equal zero. The elements on the main diagonal are either zero or equal to the regularization parameter, depending on whether the solution is regularized or not with respect to a given parameter.

Application of the Levenberg–Marquardt algorithm to the functional (18) leads to the following formulae for updated values of sought parameters: (19) As seen above, an extra regularization term in the functional (18) resulted in an extra term on the main diagonal of the matrix on the left-hand side of Equation (19). Changing the value of the regularization parameter, one can influence the diagonal dominance of the left-hand side matrix. This can affect both the conditioning of the problem as well as the convergence of the iterative procedure.

4.2. Initial distribution regularization approach

In the second regularization approach, the functional (12) was complemented with the regularization term that enforces minimization of the deviation between the total amount of the water predicted by the mathematical model and an assumed value of that quantity: (20) where m_w is the total amount of water in paper after heating and before vacuum phase predicted by the numerical model whilst represents the assumed amount of the water at this time instance. This value can be assumed based on previous experience or on the total amount of water removed during heating and vacuum phase. Quantity is the standard deviation of this assumed value.

Before the Levenberg–Marquardt algorithm can be applied to the functional (20), the total amount of the water in the paper predicted by the mathematical model needs to be expressed in terms of the unknown values of the water content at all nine sampling points. Having the approximation of the initial water content distribution in paper in the form of (14), the total amount of the water in the paper can be calculated by integration over the whole paper volume V_s: (21) Marking of the integral of the vector of the base functions over the paper volume as Φ (22) and employing Equation (15), one can rearrange Equation (21) to obtain formulae for the total water content in terms of the water content values at the sampling points: (23) Defining a block vector Θ in the form of (24) Equation (23) can be rewritten in the short form as (25) Introducing Equation (25) into the functional (20) and applying the Levenberg–Marquardt algorithm one, can obtain the following equation for updating the unknown set of parameters P: (26)

As seen above, an additional regularizing term appeared on the left-hand side of Equation (26). It is easier to estimate reasonably the total amount of the water in the paper, which is necessary for the presented regularization method than the parameter values themselves as in the previously described method. Hence, this approach seems to be superior to the direct parameter regularization.

5. Results

In Tables 1 and 2 the values of the unknown parameters obtained with both the described regularization approaches are presented. It can be seen that for the parameter regularization (Section 4.1) the obtained values do not differ significantly for different values of the regularization parameter. The situation is slightly different for the water mass regularization approach (Table 2). It can be noticed that the values of the parameters obtained with regularization (non-zero value of the regularization parameter) differ perceptibly from the value obtained without regularization. But the solutions with different values of the regularization parameter also differ considerably for some cases, e.g. see value X_0,5 of the water content at the sampling point no. 5. The Tikhonov regularization can be interpreted as putting some extra constraint on the solution. From this point of view, the direct parameter regularization as in Section 4.1 has stronger influence on the solution than indirect regularization described in Section 4.2. However, in the considered problem, it is easier to estimate reliably the information on the water mass which is needed for the regularization procedure than the values of the parameters themselves.

Table 1. Results of the parameter regularization approach for different values of the regularization parameter (see Equation (19)).

Regularization parameter	0.0	1.0	10.0	100.0	1000.0
Cmt	0.27994	0.30547	0.30087	0.30032	0.30000
X0,1	0.03657	0.03626	0.03620	0.03614	0.03589
X0,2	0.05539	0.05481	0.05537	0.05676	0.05809
X0,3	0.04636	0.04569	0.04544	0.04417	0.04309
X0,4	0.02760	0.02746	0.02763	0.02885	0.02971
X0,5	0.04872	0.04778	0.04730	0.04510	0.04298
X0,6	0.04659	0.04646	0.04690	0.04807	0.04921
X0,7	0.03410	0.03389	0.03354	0.03287	0.03204
X0,8	0.05156	0.05116	0.05147	0.05225	0.05305
X0,9	0.04050	0.03985	0.04006	0.04003	0.04004
Water mass	0.021342	0.021113	0.021182	0.021172	0.021198

Table 2. Results of the initial distribution regularization (or water mass regularization) approach for different values of the regularization parameter (see Equation (26)).

Regularization parameter	0.0	1.0	10.0	100.0	1000.0
Cmt	0.27994	0.05140	0.09330	0.07719	0.05639
X0,1	0.03657	0.05346	0.04443	0.04580	0.05008
X0,2	0.05539	0.11372	0.07251	0.07542	0.08327
X0,3	0.04636	0.08622	0.06140	0.06407	0.07194
X0,4	0.02760	0.03661	0.03260	0.03340	0.03560
X0,5	0.04872	0.10209	0.06617	0.06887	0.07562
X0,6	0.04659	0.06392	0.05438	0.05575	0.05940
X0,7	0.03410	0.04945	0.04086	0.04197	0.04521
X0,8	0.05156	0.08884	0.06531	0.06770	0.07432
X0,9	0.04050	0.06665	0.05264	0.05492	0.06157
Water mass	0.021342	0.035950	0.027164	0.028148	0.031264

The second important element which may influence the solution is the fact that in the Levenberg–Marquardt procedure the sensitivity matrix with respect to unknown parameters is evaluated only once at the beginning of the procedure. As the Levenberg–Marguardt algorithm is actually the directional search algorithm, calculating the sensitivity matrix only once limits the set of accessible search directions. Hence, we may never reach the problem solution. But on the other hand, the sensitivity matrix reflects the influence of the given parameters on the solution and this influence will not vary significantly if we are close to the optimum (solution). Therefore, if the starting point is not far from the solution, keeping the sensitivity matrix constant through the whole procedure should not introduce a big error. Nevertheless, this simplifying assumption will be verified in the nearest future.

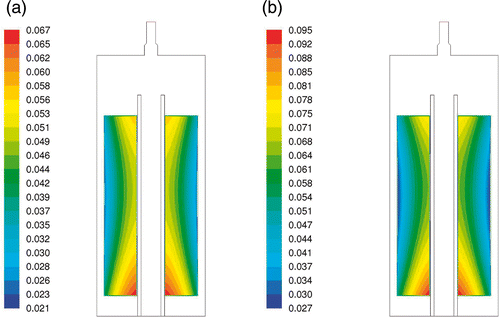
In Figure 3(a) and (b), initial water distribution obtained by both methods is demonstrated. It can be noticed that the water content is considerably smaller in the external layers of the paper. This seems to be a reasonable result as these layers of the paper were exposed to the hot chamber walls and were partly dried out during the heating phase of the experiment. The local water content values as well as the total amount of the water for the first regularization approach are slightly smaller than for the second approach. Nevertheless, in both cases the physical constraint, that the mass of the water has to be smaller than the water mass at the beginning of the whole experiment (in our experiment it was equal to 0.0335 kg), is fulfilled.

Figure 3. The water content distribution in the paper obtained from inverse procedure for: (a) parameter regularization approach, (b) water mass regularization approach.

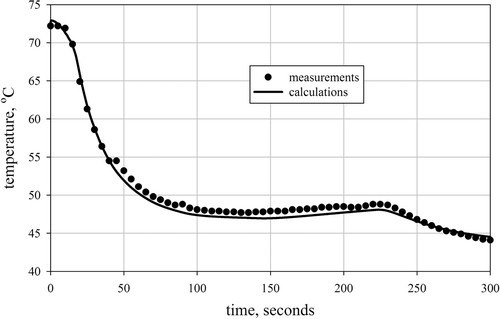
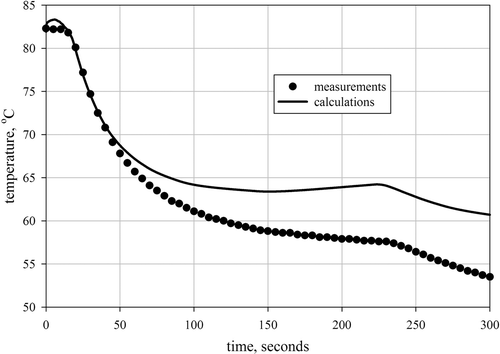
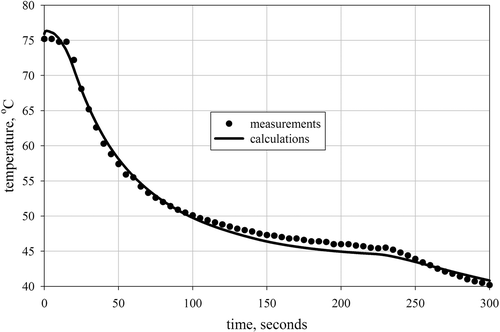
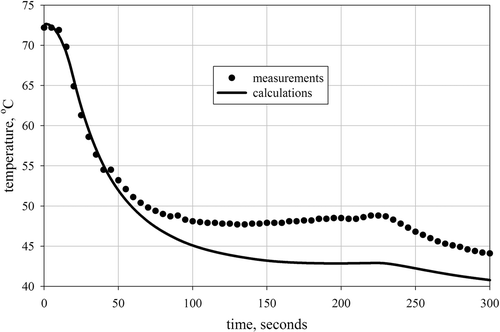
In Figures 4–7 the time histories of the temperatures obtained from the model for estimated parameters and measured during the experiment are shown. These figures show the best (Figures 4 and 6) and the worst (Figures 5 and 7) fitting obtained for parameter and mass regularizations, respectively. It can be seen that for optimized parameters the numerical model produces temperature values which represent the experimental data reasonably well.

Figure 4. Time history of temperature values at point no. 9.

Figure 5. Time history of temperature values at point no. 1.

Figure 6. Time history of temperature values at point no. 8.

Figure 7. Time history of temperature values at point no. 1.

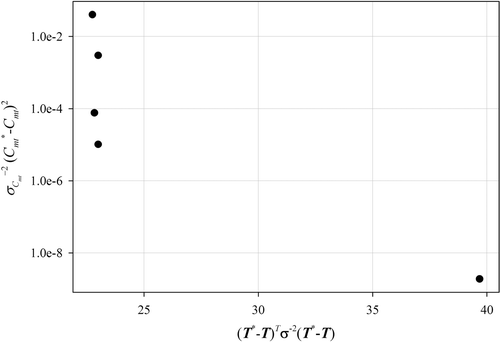
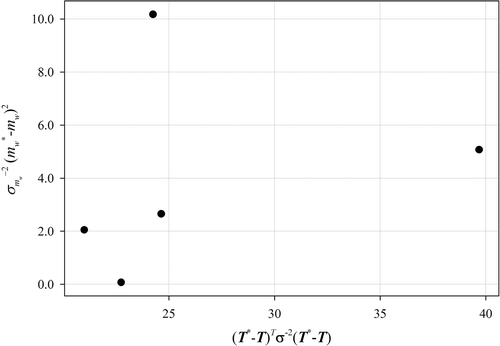
Finally, the obtained results that are gathered in Tables 3 and 4, were used to construct the so-called L-curves. The L-curves allow one to choose the optimal value of the regularization parameter 12. The optimal value of the regularization parameter is the one for which the bend of the curve is observed. For the parameter regularization approach is it clearly visible (Figure 8). Unfortunately, this approach has failed for the mass regularization method (cf. Figure 9). This is most likely due to the reasons discussed above.

Figure 8. The L-curve for the parameter regularization approach.

Figure 9. The L-curve for the mass regularization approach.

Table 3. Values of both terms of the objective function (18) and the value of the function itself for parameter regularization approach for different values of the regularization parameter.

λ			Δ
0.0	22.74	0.07202	22.74
1.0	24.25	10.18	34.43
10.0	20.99	2.053	41.53
100.0	24.64	2.656	290.2
1000.0	39.68	5.075	5114.8

Table 4. Values of both terms of the objective function (20) and the value of the function itself for water mass regularization approach for different values of the regularization parameter.

λ			Δ
0.0	22.74	0.4025·10^−1	22.74
1.0	22.99	0.2988·10^−2	23.00
10.0	22.83	0.7606·10^−7	22.83
100.0	22.99	0.1019·10^−7	22.99
1000.0	39.68	0.1891·10^−10	39.68

6. Conclusions

It was already proved in the previous works 5 that using local temperature measurements it is possible to estimate simultaneously the drying kinetics parameters and initial moisture field. It has been demonstrated, however, that due to a substantial amount of information to be retrieved, to obtain solution with high accuracy, some regularization technique is recommended. In this work, rough information on the evaporation constant and the total amount of water mass in the paper was used to regularize the solution procedure. This greatly improved the solution convergence as well as more reliable results are obtained. In this article the L-curve technique was also used in order to obtain the optimal value of the regularization parameter. This methodology worked well for the parameter estimation approach whilst for the mass regularization approach it was not possible to infer the optimal value of the regularization parameter from the L-curve plot. This was most likely caused by utilizing the sensitivity matrix calculated at the beginning of the procedure throughout the whole Levenberg–Marquardt algorithm. Such a conclusion will be verified further in the nearest future.

Acknowledgements

This work has been partially supported by RECENT 7FP project, grant no. 245819.