On finite element analysis of an inverse problem in elasticity

Abstract

This investigation concerns an inverse problem modelled by the finite element method. For a given mesh and set of physical properties, even though a well-posed direct problem possesses a unique solution in classical linear elasticity, variational arguments establish that a corresponding inverse problem may not. Furthermore, even when the inverse problem admits a unique solution when modelled ‘exactly’ using the classical linear theory of elasticity, an unfortunate mesh choice may cause the finite element model of the inverse problem to fail to do so. The current investigation introduces a simple matrix nonsingularity criterion assuring that the finite element model possesses a unique solution. An apparently new and readily computed numerical test is introduced to verify satisfaction of the criterion. Examples are given illustrating the effectiveness of the criterion and its application to mesh design.

Keywords:

• finite element modelling
• inverse modelling
• matrix nonsingularity condition
• mesh modification

1. Introduction

1.1. Direct and inverse problems

In a linearly elastic body which has known physical properties and which is experiencing small strains under static loads, the finite element equation may be written as (1) Here the vector denotes the displacement degrees of freedom at internal nodes, while the vector and the vector the displacement degrees of freedom at two different sets of boundary nodes. It is assumed that external forces are applied only to boundary nodes, with the force vector and the force vector referred to the two sets. The purpose of using multiple sets will be evident in the subsequent discussion of inverse problems. All matrices and vectors are real.

The system has n degrees of freedom in which . It is assumed that Equation (1) reflects degrees of freedom remaining after any simple constraints on the body have been applied. Here, in a simple constraint, a displacement degree of freedom is specified and the corresponding reaction force is an unknown. This contrasts with complex (overspecified) constraints appearing in the current inverse problem in which both the displacement and force are prescribed for a degree of freedom.

In finite element models of static problems in the linear theory of elasticity, the stiffness matrix K is symmetric and positive definite, written K > 0. In the direct problem, which is considered ‘well posed', the force vectors are prescribed, and the corresponding displacement vectors are unknowns to be determined (after simple constraints have been enforced). Accordingly, at each boundary degree of freedom, only one quantity (the force) is specified. Positive definiteness of K implies that the solution of the direct problem exists and is unique (cf. Section 1.2).

In contrast, in the particular type of inverse problem studied here 1, the first node set is ‘overspecified' in that displacements and tractions are simultaneously specified at the nodes (i.e. exhibit complex constraints). Correspondingly, the second node set is ‘underspecified' in that neither displacements nor tractions are specified at the nodes. In fact, both are unknowns to be determined by solving this type of inverse problem, assuming the solution exists and is unique. However, as shown subsequently and in Section 1.2, there is no assurance that a unique solution exists for the inverse problem even when it does in the direct problem. Conditions for determining the existence and uniqueness of a solution are in fact the goal of the current investigation.

Alternative types of inverse problems are described in Kleiber 2 and Gladwell 3. For example, tractions and displacements may be overspecified on the whole boundary, with mechanical properties of the medium serving as the unknowns to be estimated. There may be holes, cracks or other defects whose location, orientation and/or severity the analyst seeks to characterize using the overspecified boundary conditions. An optimization scheme may be attempted in which a sequence of direct problems is solved, with the defect property estimates modified in each step to minimize the total potential energy.

The case under study in the foregoing paragraphs is therefore seen to be a specific type of inverse problem.

1.2. Variational principles in the direct and inverse problems

This section presents a simple variational argument under which the solution of the inverse problem satisfies a saddle point condition rather than a minimum condition, and discusses the implications for the finite element model.

Consider an elastic body with domain V and surface S. Let e denote the strain vector and the corresponding positive definite symmetric tangent modulus tensor. The surface has two segments

In the direct problem, the traction vector is prescribed on but the displacement vector is unknown, while on the displacement vector is prescribed and the traction vector is unknown. The Principle of Virtual Work, applied to the direct problem, implicitly defines a potential through the equilibrium equation in which (2)

The second variation gives (3) from which it is evident that the solution satisfies a minimum principle. Furthermore, since finite element interpolation models represent a subset of the full function space in the variational principle, it follows that the potential energy of the finite element model will exceed the ‘exact' potential energy at equilibrium, and will therefore also be positive.

In the inverse problem, the Principle of Virtual Work implicitly determines a new potential through the equilibrium relation in which (4)

The second variation gives (5)

There is no reason for to be positive at equilibrium, and in fact the potential energy achieves a saddle point. Given this fact, there is no assurance that the potential energy of the finite element model exceeds that of the exact model, and in fact may well be less than the exact value!

To illustrate this interpretation, suppose global interpolation models are used such that : here are ‘shape functions' while and are nodal displacements and tractions. The equilibrium relation is (6)

Note that H is neither symmetric nor positive definite. The second variation for the inverse problem now gives (7) and there is simply no reason to expect it is positive at the equilibrium solution.

2. Condition for existence of a unique solution to the current inverse problem

2.1. On nonexistence of a unique solution in an inverse problem

We first employ an example to demonstrate that in inverse problems a unique solution may not exist even though the corresponding direct problem does possess a unique solution. Consider the following problem.

Let be two symmetric positive definite matrices and a singular matrix. Next introduce the matrix given by (8)

Of course, under the stated conditions

Direct problem: Letting be a known vector, positive definiteness of implies that there exists a unique solution for the unknown vector satisfying .

Inverse problem: Now suppose that the right hand side contains the vector in which is known but is unknown. Also suppose that the left hand side now contains the vector in which is known but is unknown. We are now confronted with the inverse problem (9)

The upper block row implies that (10) But K₁₂ and hence are singular, so that either there is no unique solution for or there are many solutions. The second block row does not mitigate this difficulty, since it introduces the additional unknown vector Otherwise stated, there does not exist a unique solution to this inverse problem in this example, although a unique solution for the direct problem certainly exists.

To repeat, in direct problems in quasi-static elasticity, the exact solution satisfies the Principle of Minimum Potential Energy. A finite element model based on this Principle has greater potential energy than in the exact problem, and hence is ‘stiffer'. It follows that the finite element model possesses a solution whenever the direct problem does. However, as shown in Section 1.2, the inverse problem of interest here satisfies a stationary principle rather than a minimum problem. Consequently, there is no assurance that a finite element model will possess a solution even when the exact problem does. Furthermore, we will see via an example that the existence or nonexistence of the solution is affected by the mesh, in which event it should be possible to modify the mesh to avoid singularity.

2.2. Sufficient condition for existence and uniqueness

A sufficient condition is presented for the existence and uniqueness of the solution to a finite element model of the inverse problem of interest. However, as will be demonstrated in a subsequent section, it is quite possible that the stiffness matrix in one mesh will not satisfy the sufficient condition, while the stiffness matrix in another mesh for the same physical problem will do so.

From the third row in Equation (1), we have (11) and, recalling that , (12)

Upon substitution, the upper two rows provide the equations (13) (14)

Positive definiteness of implies that its principal minors are positive definite, and so and (15)

Now suppose that are known, while are unknown, thereby introducing an inverse problem of the type of interest here. Equations (7) and (8) are now rewritten as (16) (17) Equation (10) immediately furnishes (18)

For the solution of the inverse problem expressed by Equations (13) and (14) to exist and be unique it is necessary and sufficient that be nonsingular. Note that the existence of a unique solution to the inverse problem is unaffected by the actual values of . Also it is not necessary to solve simultaneously for , as appears to be sometimes supposed. Indeed, once u_u is obtained by solving Equation (18), f_u is immediately found from Equation (17) as (19)

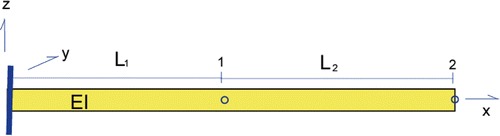
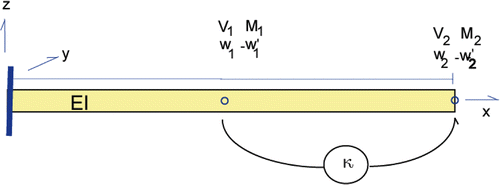
2.3. Example: two element model of a cantilevered beam

Figure 1 depicts a beam modelled by two elements. The elastic modulus E and the bending moment of area I are the same in the two elements, but their lengths differ. The (unclamped) nodes are denoted as 1 and 2. The vertical (z) displacement and slope are denoted by , the shear force by and the bending moment by

Figure 1. Inverse problem for a two element beam.

The finite element equation for the two element beam configuration is given by (20)

Four distinct inverse problems are now considered.

Case i

are prescribed

The solution exists and is unique if is nonsingular. In fact it is, with determinant equalling .

Case ii

are prescribed.

The matrix of interest is and has the nonvanishing determinant .

Case iii

The matrix arises which is nonsingular with determinant equalling 72/

Case iv

are prescribed.

The matrix is nonsingular, with determinant equalling .

We will later add an control system to Case iv, which produces an singular matrix for a specific ratio of the element lengths.

3. Computational test for nonsingularity of

3.1. Alternate form of matrix

We now introduce a simple numerical test for determining whether is nonsingular. Of course, it is necessary that since otherwise this matrix is not square and hence is singular. It is first demonstrated that nonsingularity is equivalent to requiring that the matrix be nonsingular. In particular, note that is singular if and only if there exists a vector satisfying (21)

Of course But, from the bottom row, and hence in the singular case. Substitution into the top row and some manipulations furnish (22) as anticipated.

It follows that is singular whenever is singular, and is nonsingular whenever is nonsingular. The numerical test presented next is intended to determine whether is in fact nonsingular.

3.2. Method for verifying the existence and uniqueness of the inverse solution

We give a general presentation of a numerical test for the nonsingularity of an real matrix A. The test exploits the independence of the rows of a nonsingular matrix. A search in the current investigation has not detected this method in existing literature. Instead, the literature on tests for nonsingularity identifies two major methods which stand in contrast to the method being introduced. The first involves a determinant search, while the more favoured method is based on Singular Value Decomposition. Of course, the latter is very effective and otherwise plays a major role in inverse problems owing to its relative insensitivity to errors 4. Its numerical implementation typically depends on using orthogonal transformations to convert the matrix to triangular or bidiagonal form, and is not selective in that it produces all singular values and not just the minimum value 5.

More importantly, as will be seen, the major advantage of the current test is that it indicates how entries of the untransformed stiffness matrix can be modified to avoid singularity in the inverse problem of interest. Since the entries of the untransformed stiffness matrix have a clear correspondence with the nodal degrees of freedom, the current test provides guidance on mesh modifications to avoid singularity. Its implementation mostly requires simple additions and multiplications.

To introduce the current test, the matrix A is written in the form (23) in which the ith row of the matrix A is written as the row vector . We now construct a set of orthonormal base vectors e_i as follows. The n base vectors e_j are given by (24)

If the matrix is nonsingular, the nth row vector cannot be a linear combination of the foregoing n − 1 row vectors. Furthermore, the jth row vector exists in the j-dimensional subspace spanned by orthonormal base vectors For the moment suppose instead that the matrix is singular with rank deficiency unity, and that is a linear combination of the foregoing row vectors and hence exists in an n − 1 dimensional subspace spanned by the orthonornal base vectors . But, if simultaneously (i) lies in the n − 1 dimensional subspace and (ii) is orthogonal to the base vectors of the subspace, it must equal the null vector:

More generally, if the matrix is singular, then at least one row vector is a linear combination of the foregoing row vectors , and exists in the corresponding dimensional subspace. The vector likewise is orthogonal to the base vectors of the space it lies in, and hence

Accordingly, the condition for the matrix A to be nonsingular is (25)

Conversely, if any of the vectors vanish, is singular.

Of course, the test is Equation (25) can just as easily be formulated using the columns of as the vectors . In practice, owing to numerical error, it is wise to establish a tolerance on the magnitudes of the vectors . In particular, the matrix will be deemed to be nonsingular if the magnitudes of all of the vectors are greater than a ‘judiciously chosen’ minimum value

An eigenvalue interpretation of the test becomes evident if Equation (24) is written in the alternate form (26)

It is evident that vanishes if and only if the matrix possesses an eigenvalue equal to unity, with a_k serving as the corresponding eigenvector.

3.3. Examples

Simple examples are now introduced to illustrate the application and performance of the nonsingularity test expressed in Equation (25).

Example 1

We first consider the matrix (27)

Following the operations in Equation (24), the vectors of interest are found to be (28)

In fact, this matrix is nonsingular if and becomes singular when But also note that, in the current test, 0 if and , consistent with Equation (25).

Example 2

Now consider (29)

We first seek to determine whether the current test correctly identifies values of ε₁ and ε₂ for which is singular. We first check . (30)

It is evident that is singular if The current procedure furnishes that but Assume for the moment that such that (31)

Note that does not appear in . Note that is not affected by the magnitude of .

We now determine the third base vector. (32) The test in Equation (25) indicates that the matrix is singular regardless of ε₂. That this result is correct is easily seen by recognizing that the second column in is proportional to the first column regardless of ε₂ (or ε₁).

Recapitulating, the solution of the current inverse problem exists and is unique if is nonsingular. Further this matrix can be shown to be nonsingular if n₂ = n₁ and the numerical test in Equation (25) is satisfied.

4. Mesh dependence of the existence of a unique solution: mesh modification

It is quite possible that a unique solution exists in an inverse problem when treated ‘exactly' in the theory of elasticity, but that a finite element model fails Equation (21) even though it produces an accurate solution in the corresponding direct problem. Such a situation may reflect mesh dependence, and if so it may be remedied by altering the mesh details. An obvious example of mesh dependence arises when An example in which is now presented.

4.1. Example of mesh dependence: actively controlled two element beam

We now revisit Case iv in the two element beam problem, but modify it to include a feedback control system which senses the displacement w₁ and generates a negative additional shear force on the last node (Figure 2). The quantity κ is called the gain. As in Case iv, the slope and the moment are both known at the first (unclamped) node, while the displacement and the shear force (without the control system contribution) are known at the second node. Of course, these conditions give rise to an inverse problem of the type of interest here. Ignoring inertial forces, the modified beam equation is now (33) in which the subscript k refers to known (prescribed) quantities.

Figure 2. Two element model of actively controlled beam.

Equation (33) is now rewritten to incorporate the gain in the stiffness matrix. (34)

The inverse problem now reduces to the solution of the following equation. (35)

Finally, although it will prove to be an unfortunate choice of L₁ and L₂, suppose that the location of the first node is chosen such that . We now apply the nonsingularity test to Equation (25). Manipulation furnishes (36) (37)

For the sake of visualization, Equation (37) is rewritten as (38)

Clearly, vanishes whenever: (i) is an eigenvalue of and (ii) r is the corresponding eigenvector. The following two equations are now satisfied simultaneously. (39)

Straightforward manipulation serves to verify that the two equations are the same and are equivalent to (40)

The matrix arising in the inverse problem is singular if , which is precisely how were selected. That this result is correct is easily verified by evaluating the determinant of the matrix from Equation (35).

The nonexistence of a unique solution for the current mesh may be obviated by altering the mesh as follows. We introduce an increment , set the length of the first element to , and set the length of the second element to . The total length of the beam is unchanged, but now the sensor is located at . Using Equation (35), we construct the residual as follows. (41)

As expected, the residual vanishes as the mesh perturbation parameter vanishes, in conformity with the singular character of the example. But, for nonzero values of , the test matrix arising in the inverse problem is nonsingular. Clearly, the larger the value of the greater the deviation of the determinant from zero.

5. Conclusion

Solution of finite element models in a type of inverse problem has been investigated. Variational methods have been employed to establish that, in contrast to the corresponding direct problem, the inverse problem satisfies a stationary rather than a minimum principle, with the consequence that a finite element model may fail to possess a solution even when the ‘exact' problem does. Further, the failure of the finite element model may be a consequence of the mesh chosen, as is demonstrated in an example. A matrix criterion for existence and uniqueness of solution has been formulated and applied to a simple inverse problem in a beam. By exploiting the linear independence of the rows of a nonsingular matrix and using Gram–Schmidt orthogonalization, a simple and tractable numerical test for the criterion has been developed and illustrated with examples. In particular, an example has been provided in which the existence of a unique solution depends on the mesh, and in which the test has served to identify mesh variations obviating singularity.