Block-sparse compressed sensing: non-convex model and iterative re-weighted algorithm

Abstract

Compressed sensing is a new sampling technique which can exactly reconstruct sparse signal from a few measurements. In this article, we consider the block-sparse compressed sensing with special structure assumption about the signal. A novel non-convex model is proposed to reconstruct the block-sparse signals. In addition, the conditions of the proposed model for recovering the block-sparse noise or noise-free signals are presented. The experimental results demonstrate that the proposed non-convex method surpasses the convex method (the mixed -norm optimization) and some algorithms without considering the block-sparse structure (the - and -norm optimization).

Keywords:

• block-sparse compressed sensing
• non-convex model
• block-sparse recovery
• iterative re-weighted algorithm

1. Introduction

The traditional signal acquisition must follow the Nyquist–Shannon sampling theorem. Based on this theorem, the sample rate is at least twice of the signal bandwidth for exact reconstruction. In many recent applications, the Nyquist rate may result in high storage and transmission pressure. In addition, the traditional signal acquisition model does not consider the signal structure known as the prior information. A breakthrough in data acquisition, namely compressed sensing, was brought by Donoho 1 and Candès et al. 2,3, which has been widely applied in magnetic resonance imaging 4 and radar imaging 5. Compressed sensing assumes that the original signal is sparse or approximately sparse under some bases. Without loss of generality, we assume that the original signal is sparse under the canonical basis. Then, the -sparse signal means that there are no more than nonzero entries in the signal. Let be the -sparse signal. The task of compressed sensing is to recover from the measurements calculated as (1)

Here, is the measurement matrix with more columns than rows. Obviously, Equation (1) is underdetermined. However, the theory of compressed sensing indicates that the sparse or compressible signal can be exactly reconstructed from a few measurements through the following optimization problem: (2) where denotes the -norm counting the number of nonzero entries. However, the problem (2) is a combinatorial optimization problem. Solving it directly is general NP-hard. Therefore, some sub-optimization strategies are proposed to approximate the exact solution.

Popular sub-optimization strategies include greedy algorithms (such as the orthogonal matching pursuit 6), and relaxation methods (such as convex and non-convex relaxation methods 7–9). The representative convex method is the -optimization problem which is called basis pursuit (BP) 7 (3) where is the -norm of the vector . In the noise case, the problem (3) can be modified as the basis pursuit denoising (BPDN) 7 (4) where is a tradeoff parameter. The non-convex relaxation method has been studied in 8,9, i.e. the following non-convex optimization problem: (5) where . In 8, the experimental results show that the non-convex problem (5) can reconstruct the sparse signal from fewer measurements than the convex method acquiring. The restricted isometry property (RIP) 3 plays a crucial role in the theory of compressed sensing. The previous results show that if the measurement matrix has the RIP with a certain parameters, the convex and non-convex optimization methods can recover the sparse signal exactly.

The existed analysis of compressed sensing does not consider the special inherent structures of signals. This article considers a variation of the compressed sensing problem named the block-sparse compressed sensing. In block-sparse compressed sensing, the block structure of sparse signal is investigated, i.e. the nonzero entries of the signal occur in clusters. Various practical signals exhibit the block structure, such as DNA microarrays 10, multiband signal 11 and magnetoencephalography (MEG) 12. The framework of block-sparse compressed sensing was introduced and studied first in refs 13–15. The mixed -norm optimization is developed to recover the block-sparse signal in 13, which is a convex method. In this article, we propose a novel non-convex model termed as the mixed -norm optimization for block-sparse signal recovery, which can greatly improve the performance of the mixed -norm optimization.

The remainder of this article is organized as follows. In Section 2, we briefly review the block-sparse compressed sensing. In Section 3, the mixed -norm optimization problem is proposed, and the stability and uniqueness of the proposed model is investigated. In Section 4, the re-weighted -algorithm is used to solve mixed -norm optimization problem, and some numerical experiments are reported. Finally, Section 5 concludes this article.

2. Block-sparse compressed sensing and RIP

In this section, we briefly review block sparsity and the block-sparse compressed sensing.

In the block-sparse compressed sensing, the signal is the concatenation of some blocks. Without loss of generality, we assume that there are n blocks with the block size in x. Then, the signal x can be rewritten as (6) where , . Then, the signal x is called K-block-sparse if no more than K blocks over are nonzero. In 13, a convex optimization problem termed as the mixed -norm optimization is proposed to reconstruct the block-sparse signal, i.e. the following model: (7) where . In noisy measurements case, the measurements can be calculated as (8) where is unknown noise. In this article, we assume , and the standard deviation denotes the noise level. In this noise case, the block-sparse signal can be reconstructed via the following optimization problem: (9)

To investigate the theory of compressed sensing, Candès and Tao 3 introduce the RIP. The matrix is said to have the RIP with parameter , if the inequality (10) holds for every K-sparse signal x. Many random matrices have been proven to have the RIP with overwhelming probability, such as Gaussian, Bernoulli and partial Fourier matrices 16. To study the mixed -norm optimization problems (7) and (9), Eldar and Mishali 13 introduce the block RIP (B-RIP) which is the block-sparse version of RIP. The matrix has the B-RIP with parameter , if the inequality (11) holds for every K-block-sparse signal x, where is the B-RIP constant over . In 13 Eldar and Mishali show that the Gaussian random matrix has the B-RIP with high probability.

3. Non-convex recovery model

In this section, the motivation of proposed non-convex method is stated first. Then, the theoretical results about the uniqueness and robust of the proposed non-convex model to recover the block-sparse noised and noise-free signals are studied. At last, an iterative re-weighted algorithm is presented to solve the non-convex method.

3.1. Motivation

In 13, Eldar and Mishali claim that the block-sparse signal x can be exactly reconstructed from the measurements by the following optimization problem: (12) where By introducing auxiliary variables and , the objective function of problem (12) can be equivalently transformed as . It is most accurate to measure the sparsity by the -norm. Unfortunately, the -norm optimization problem is combinatorial optimization, which cannot be solved directly. An effective relaxation strategy of the -norm to measure the sparsity is -norm, i.e. . 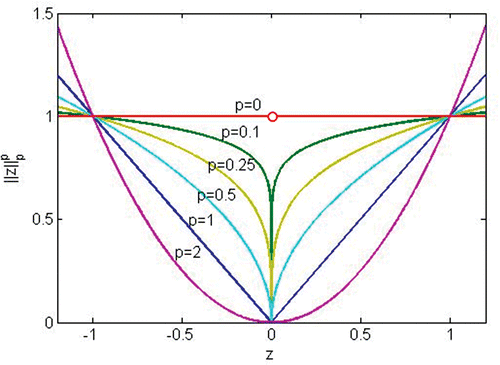Figure 1 illustrates the one-dimensional trend of for varying p. Some previous results have demonstrated that the -norm can approximate the -norm effectively 3,13. However, with , the -norm tends to the -norm. Obviously, the non-convex -norm can give more powerful sparsity measure than the -norm. Therefore, we focus on non-convex method in our work. Corresponding to the block-sparse signal x, we study the following non-convex method termed as the mixed -norm optimization: (13) where

Figure 1. The one-dimensional trend of for varying p.

3.2. Exact recovery

In this section, we show that the proposed non-convex model (13) can recover the block-sparse signal x exactly in the noise-free case with a certain condition of the measurement matrix .

Theorem 1

Let be the measurements of the K-block-sparse signal x. If the measurement matrix has the B-RIP with the condition (14) where , then x is the unique solution of the problem (13).

3.3. Robust recovery

This section considers the noise case. Assume x be an arbitrary signal, and the measurements are computed with noise, i.e. (15) where is the Gaussian noise. In this case, the optimization problem (13) must be modified as (16)

The following Theorems 2 and 3 state the robustness of the proposed non-convex model. In addition, we prove that the reconstruction error of problem (16) is the linear function of the noise energy .

First, the case of the block-sparse signal with noise is studied.

Theorem 2

Let be the noisy measurements of the K-block-sparse signal x. If the measurement matrix has the B-RIP and the below inequality (17) holds, where . Assume be the solution of the problem (16). Then, where

Afterwards, let x and be an arbitrary signal and the K-block-sparse approximation of x, respectively. Assume T₀ be the index set corresponding to the first K largest blocks in terms of -norm. Then, we have the following theory for general case.

Theorem 3

Let be the noisy measurements of any signal x. If the condition (17) holds, then the solution of problem (16) obeys where

Proof

Following the method of proof stated in 9, let be the difference between the true signal and the reconstructed signal. The set can be divided as , where is the indices set which is make up of blocks, chosen such that the -norm of over is largest, and the -norm of over is the second largest, and so on. So, we can decompose h as .

Based on the B-RIP and the triangle inequality of , we obtain the lower bound of as follows: (18)

Next, we will give the bounds of and .

For all , holds. Following this inequality, we have

Thus, we obtain

Due to ,

Therefore,

Applying the Holder inequality, the is bounded as the -norm, i.e.

Thus, we have (19)

Combining (18) and (19), the following inequality holds where

Furthermore, has the upper bound as

Then, we have . That is, the upper bound of is (20)

By the condition of (17), we know that . Hence, the inequality (20) holds.

Let be the th largest block of in -norm. The below inequality can be obtained easily. For , the is bounded as

Finally, we have

▪

Remark 1

Theorems 1 and 2 are the special cases of Theorem 3. When the original signal x is a K-block-sparse signal, then yields Theorem 2. Furthermore, Theorem 1 is the K-block-sparse signal and noise-free case of Theorem 3.

3.4. The iterative re-weighted -algorithm

In this section, we propose the re-weighted -algorithm for solving the -norm optimization deriving from the re-weighted -algorithm 17. Due to the main steps of the iterative re-weighted -algorithm are summarized in Algorithm 1.

Algorithm 1

The iterative re-weighted -algorithm

	Input: , , , , Num.
	For i=1: Num
	While , do
	(1) Solve the weighted -norm optimization

(2) Update the weights

End while

	End for
	Output: The block-sparse signal x.

The weighted -norm optimization can be equivalently transformed to a second-order cone programming (SOCP):

Furthermore, the ‘cvx’ software packages (the code is available at http://cvxr.com/cvx/) can be used to solve the above SOCP.

4. Experiments

In this section, some numerical experiments are presented to evaluate the performance of the mixed -norm optimization. First, the experimental settings are presented. Then, the performance of the mixed -norm optimization is compared with three popular methods, including the mixed -norm optimization, -norm optimization and the -norm optimization.

4.1. Experimental settings

Three numerical experiments are performed to assess the capacity of the mixed -norm optimization: (a) the noise-free case; (b) the noise case; (c) the large scale problem. Therefore, in this section, we describe the experiments setting, including the generation of the experiment data and the parameters setting.

We assume that the synthetic signal has n blocks. Then, the synthetic block-sparse signals are generated as follows: (1) the K blocks are selected from these n blocks randomly; (2) the entries restricted to these K blocks are generated from a standard Gaussian distribution and the entries out of the selected K blocks are set to zero. In our experiments, the Gaussian random matrix is used as the measurement matrix. For different experiment cases, we set the parameters of the re-weighted -algorithm listed in Table 1. In addition, the parameters for other tested algorithms are set according to refs 7,8,13. The relative error and probability of exact reconstruction are used as the evaluation indices. The relative error between the reconstructed signal and the original signal x is calculated as

Table 1. The parameters of the re-weighted -algorithm for three different experiments.

	Noise-free case	Noise case	Large scale
Num	5	3	3

The signal is said to be exactly reconstructed, if the relative error between the reconstructed signal and the original signal x obeys .

4.2. Experimental results

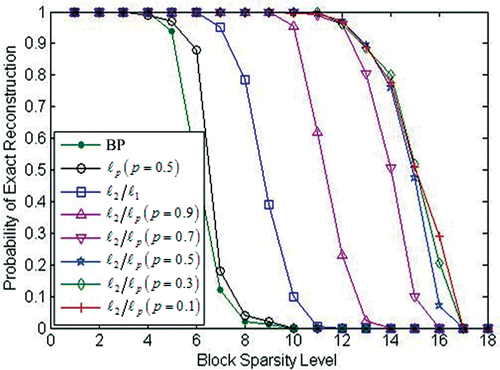
Firstly, we consider the noise-free case. The dimension of signal is , and the block size is . The comparison experiments about recovering the block-sparse signal from the measurements are performed. The active blocks vary from 1 to 18. For each block-sparsity level, the tested algorithms are all repeated 500 times. The probability of exact reconstruction is used to valuate the performance of the algorithms. The proposed method is compared with the mixed -norm optimization, BP and the -method. The exact reconstruction performances are presented in Figure 2. The horizontal axis of Figure 2 denotes the block-sparsity level K, and the vertical axis is the probability of exact reconstruction. When the block-sparse level is greater than 6, the BP, and mixed -norm optimization methods cannot recover the signal exactly, but the proposed method can recover the signal exactly up to 9-block-sparse level. In addition, when the block-sparse level is greater than 11, the BP, and mixed -norm optimization methods cannot recover the signal, but the proposed non-convex method can also recover the signal exactly with high probability. Therefore, from Figure 2, it can be seen that the proposed non-convex method is more accurate and effective than other three methods. Especially, the capacity of the mixed -norm optimization is improved with the decreasing p.

Figure 2. The exact reconstruction performance of four algorithms in noise-free case.

Secondly, the case of noisy measurements is studied. The dimension of the simulation signal is , and the block number is . The relative error is used to valuate the performance of the test algorithms from measurements. The noise is assumed as i.i.d. Gaussian with zero mean and standard deviation . The experimental results about three block-sparsity levels and four noise levels are listed in Table 2. The best results are labeled in bold. The experimental results indicate that the mixed -norm optimization provides lower relative error than the , BPDN and the mixed -norm methods in the presence of noise. Especially, for the less block sparse and , when the noise level is small, the performance of mixed -norm optimization is more efficient with a little smaller p. However, if the noise level is large, the reconstruction capacity decreases with small p. For block-sparsity level , when p is around 0.5, the mixed -norm optimization have better reconstruction performance. Especially, comparing with the convex method (the mixed -norm optimization), the proposed method generates smaller reconstruction error. These experimental results demonstrate that the proposed method is more robust than the mixed -norm optimization in the case of noisy measurements.

Table 2. The comparison results (, ; average of 20 runs).

							BPDN
0.001	1.18e−4	9.11e−5	9.11e−5	9.12e−5	9.15e−5	9.70e−5	4.40e−3	1.61e−2
0.01	1.30e−3	9.52e−4	9.50e−4	9.49e−4	9.51e−4	1.00e−3	6.00e−3	1.87e−2
0.05	6.20e−3	6.40e−3	5.70e−3	5.00e−3	4.90e−3	5.20e−3	1.47e−2	2.29e−2
0.1	1.24e−2	1.36e−2	1.23e−2	1.13e−2	1.02e−2	1.04e−2	2.61e−2	2.30e−2
0.001	1.48e−4	8.80e−5	8.80e−5	8.81e−5	8.87e−5	9.87e−5	2.14e−1	1.46e−2
0.01	1.40e−3	8.77e−4	8.75e−4	8.72e−4	8.74e−4	9.62e−4	1.93e−1	2.12e−2
0.05	7.30e−3	6.00e−3	5.30e−3	4.70e−3	4.61e−3	5.00e−3	2.22e−1	2.89e−2
0.1	1.43e−2	1.26e−2	1.18e−2	1.07e−2	9.70e−3	1.02e−2	1.96e−1	3.05e−2
0.001	8.90e−3	9.03e−5	9.02e−5	9.02e−5	9.08e−5	1.08e−4	4.06e−1	4.71e−2
0.01	5.80e−3	9.16e−4	9.14e−4	9.13e−4	9.19e−4	1.10e−3	3.74e−1	1.10e−1
0.05	1.72e−2	6.00e−3	5.40e−3	4.70e−3	4.60e−3	5.40e−3	3.87e−1	1.24e−1
0.1	3.18e−2	1.25e−2	1.17e−2	1.06e−2	9.90e−3	1.12e−2	3.93e−1	1.54e−1

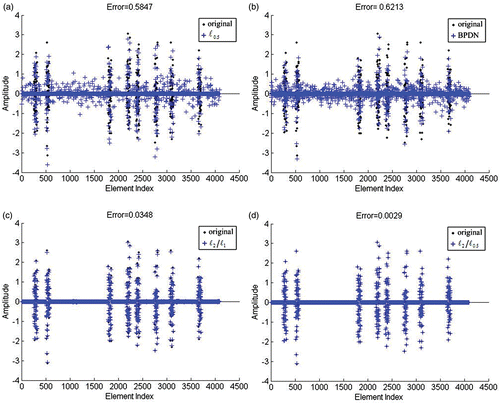
Lastly, the large-scale problem is studied. The length of the block-sparse signal is set to , the number of blocks is 64, and the block-sparsity level is fixed as . Figure 3 illustrates the original true signal and the reconstructed signal of different algorithms from measurements with the noise level . The black diamond is the original true signal and the blue cross is the reconstructed signal. Figure 3(a)–(d) shows the results of , BPDN, and , respectively. The relative errors are listed simultaneously. Obviously, the mixed -norm optimization generates the lowest relative error, which shows the effectiveness of proposed non-convex method for large scale block-sparse signal recovery.

Figure 3. The simulation results of the large scale problem: (a) the original signal and the reconstructed signal by , (b) the original signal and the reconstructed signal by BPDN, (c) the original signal and the reconstructed signal by and (d) the original signal and the reconstructed signal by .

5. Conclusion

In this article, we propose a non-convex model for block-sparse signals recovery termed as the mixed -norm optimization. Based on the B-RIP, we prove that this non-convex method can recover the block-sparse signals effectively in noise-free and noise cases. The re-weighted -algorithm is developed to solve the proposed non-convex optimization problem. The experimental results show that the performance of the mixed -norm optimization surpasses the mixed -norm optimization and some reconstruction algorithms without considering the block structure. Our future works will focus on the applications of block-sparse compressed sensing including the DNA microarrays, multiband signals and MEG.

Acknowledgements

This article is supported by the National Natural Science Foundation of China (no. 61172161), the Fundamental Research Funds for the Central Universities, Hunan University, the Scholarship Award for Excellent Doctoral Student granted by Chinese Ministry of Education, the Independent Research Funds of the State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body (Hunan University, no. 71165002) and the Hunan Provincial Innovation Foundation For Postgraduate (no. CX2011B131).