Application of the linear sampling method to identify cracks with impedance boundary conditions

Abstract

We use the linear sampling method (LSM) to identify a crack with impedance boundary conditions from far-field measurements at a fixed frequency. This article extends the work of Cakoni–Colton [F. Cakoni and D. Colton, The linear sampling method for cracks, Inverse Probl. 19 (2003), pp. 279–295] where LSM has been used to reconstruct a crack with impedance boundary conditions on one side of the crack and a Dirichlet boundary condition on the other one. In addition, we present two methods to also reconstruct the impedance parameters whence the geometry is known. The first one is based on the interpretation of the indicator function produced by the LSM, while the second one is a natural approach based on the integral representation of the far-field in terms of densities on the crack geometry. The performance of the different reconstruction methods is illustrated through numerical examples in a 2D setting of the scattering problem.

1. Introduction

We are concerned in this work with the inverse scattering problem from a crack with impedance boundary conditions. More precisely we shall investigate the application of the linear sampling method (LSM) to retrieve the geometry of the crack from multi-static far-field data at a given frequency. This inverse problem has its application in non-destructive testing of dielectrics (e.g. to monitor the quality of wood, composite materials, thin coatings, etc.) where one is interested in identifying infinitely thin inclusions or crack-type faults using electromagnetic or acoustic waves.

As compared to previous works on this type of problem and on employed methods 1–5, the originality of the present one relies on considering the case of impedance boundary conditions on both sides of the crack. This induces more technical difficulties in the justification of the method and raises new questions for the numerical algorithm. For instance, the numerical procedure proposed in 1 works only if a Dirichlet boundary condition is verified on one side of the crack. In that case the use of monopoles as test functions for the far-field equation is sufficient to obtain good reconstructions of the geometry. This is no longer the case if the impedance boundary conditions hold on both sides of the crack and the impedance values are small. In those cases the use of dipoles is important. The main difficulty then relies on the choice of the orientation of the dipole (or equivalent probing ‘small’ crack). On the basis of the theoretical justification of the LSM we propose a minimization procedure that enforces the correct choice of this orientation.

Prior to considering the inverse problem, we propose a study of the forward problem using an integral equation approach. This part is then used in deriving the theory associated with LSM and also in designing a numerical method to solve the direct problem and generate the synthetic data needed for the inverse scheme. The theoretical developments of this first part are inspired by 1. We also quote the work of 6 for the study of the direct problem using an integral equation approach in Hölder spaces and the work of 7 for the study of the inverse problem using a different sampling method.

After having reconstructed the geometry of the crack, it would be useful to obtain more information about the crack for example by determining the impedance values. To do so, we shall apply two approaches. The first one is a natural approach based on the expression of the far-field pattern and on the scattering problem. First, the measurement of the far-field pattern is used to find the values of the jump of the scattered wave and its normal derivative on the crack. These values are then used to retrieve the Cauchy data associated with the total field on each part of the crack and an estimate of the impedance values. This kind of approach is similar to the one used in 2 for planar cracks where Fourier expansion is used to evaluate the total field on the crack. The second approach is based on an interpretation of the solution of the far-field equation in terms of associated scattered field and on the reconstructed crack. This approach is similar to the one used in 8 for an obstacle with an impedance boundary condition.

For an overview of recent works on the impedance parameters identification we refer to 7,9 and the references therein). We also quote that the extension of the first part of the current work to the factorization method 10 will be the subject of a forthcoming paper.

This article is organized as follows. In Section 2, the direct problem is introduced along with a study of the uniqueness and existence of the solution using an integral equation method. In Section 3, we introduce the inverse problem and we describe our formulation of the LSM along with the mathematical justifications. Then, we propose and test different sampling schemes for different shapes of the cracks and different values of the impedances. Lastly, we develop in Section 4 two different approaches to determine the unknown impedance values.

2. The direct scattering problem for a crack with impedance boundary conditions

Let σ ⊂ ℝ^m, m = 2 or 3, be a smooth non-intersecting m − 1 manifold. For further considerations, we assume that σ can be extended to an arbitrary smooth boundary ∂Ω enclosing a bounded domain Ω in ℝ^m. The normal vector ν on σ coincides with the outward normal vector to ∂Ω.

Impedance type boundary conditions on σ lead to the following problem (1) (2) where the wave number κ is positive and λ^± ∈ L^∞(σ) are the given (complex-valued) impedance functions with non-negative imaginary part. Notice that and for x ∈ σ. The total field u = uⁱ + u^s is decomposed into the given incident plane wave uⁱ(x, d) = e^iκd·x with unitary direction d and the unknown scattered field u^s which is required to satisfy the Sommerfeld radiation condition (3) uniformly in all directions .

The ‘free space fundamental solution’ to the Helmholtz equation is given by (4) with x ≠ y and being the Hankel function of the first kind of order zero.

In order to formulate the scattering problem more precisely we need to define the trace spaces on σ. If , H^1/2(∂Ω) and H^−1/2(∂Ω) denote the usual Sobolev spaces we define the following spaces 11: Now we denote by H^−1/2(σ) and the dual spaces of and H^1/2(σ) respectively. Let us also introduce the boundary integral operators defined for regular densities ψ and ϕ by and the corresponding operators defined on σ. These restricted operators have the following mapping properties 11

Using the notation (5) the problem (1)–(3) is a special case of the following problem:

Impedance crack problem (ICP): Given g^± ∈ H^−1/2(σ) such that and (λ^±) ∈ L^∞(σ) with Im(λ^±) ≥ 0 and (λ⁺ + λ⁻)⁻¹ ∈ L^∞(σ), find satisfying the Sommerfeld radiation condition (3) and (6) (7)

The aim of this section is to prove the existence of the solution of the (ICP), since the following uniqueness result can be found in 2,6:

Theorem 2.1

The (ICP) has at most one solution.

To prove the existence of the solution of the (ICP), we use a boundary integral equations approach (see 2 for a sound soft crack and a sound hard crack, 1 for a partially coated crack and 6 for a 2D impedance crack when λ⁺ = λ⁻ is Hölder continuous).

We define and , the jump of u^s and ∂_νu^s respectively, across the crack σ.

Lemma 2.2

Assume that (λ⁺ + λ⁻)⁻¹ ∈ L^∞(σ) and g^± ∈ H^−1/2(σ) such that . The scattered field u^s is solution of the (ICP) if and only if (8) where the matrix operator is given by (9)

Proof

If u^s is a solution of the (ICP) then and (see Lemma 2.2 in 1). Using the Green representation formula, the following relation holds for (see theorem 2.24 in 2): (10) where Φ is the fundamental solution to the Helmholtz equation given by (4).

Next by making use of the jump relations of the single and double layer potentials across ∂Ω 11, we obtain from (10) (11) (12) Moreover, from the boundary condition (7) and using (5), we have (13) (14) Finally, by combining the relations (11)–(14), we show that ([u^s], [∂_νu^s])^T solves the system of Equations (8). Conversely, assume that ([u^s], [∂_νu^s])^T satisfies (8)–(9), so (15) and (16) The potential u^s, defined by (10), belongs to and satisfies the Helmholtz equation in and the Sommerfeld radiation condition. It remains to show that u^s satisfies the boundary condition (7). To this end, we first inject (12) into (15) and (11) into (16). We obtain (17) (18) Multiplying (18) by λ^± and adding the results to (17), we obtain that Therefore, the field u^s given by (10) is a solution of the (ICP).▪

Lemma 2.3

The operator A_σ given by (9) has a trivial kernel.

Proof

Let satisfying .

Define the potential This potential belongs to and satisfies the Helmholtz equation in and the Sommerfeld radiation condition. Moreover, using the jump relations of the single and double layer potentials across σ, we get Hence, (19) Therefore, as in the proof of Lemma 2.2, we show that satisfies and the Sommerfeld radiation condition. Then, from the uniqueness of the solution of this system, we have v = 0 and we conclude, by (19), that α = β = 0.▪

Lemma 2.4

Assume that (λ⁺ + λ⁻)⁻¹ ∈ L^∞(σ). The operator given by (9) has a bounded inverse.

Proof

Let and be the extension by zero to ∂Ω of and , respectively.

Let A_∂Ω be the operator defined on H^1/2(∂Ω) × H^−1/2(∂Ω) → H^1/2(∂Ω) × H^−1/2(∂Ω) by (20) where such that and . A can be decomposed as A = A_c,Ω + A_0,Ω, where (21) and (22) We denote by T_0,∂Ω the boundary integral operator corresponding to the Laplace operator, defined as T_∂Ω by replacing the kernel Φ(x, y) by (23) The operator −T_0,∂Ω is coercive on ∂Ω. Consequently, we can directly deduce that A_0,∂Ω is invertible.

We now prove that the operator A_c,∂Ω is compact. In fact, T_c,∂Ω ≔ T_∂Ω − T_0,∂Ω is a compact operator since it has a continuous kernel.

Since the injection from to is compact and , the operators and are also compact from to .

On the other hand, is a compact operator from to . The operator S_∂Ω is continuous from to . Thus is compact from to . The operator K_∂Ω is continuous from to , which implies that is compact from to . We conclude that A_c,∂Ω: H^1/2(∂Ω) × H^−1/2(∂Ω) → H^−1/2(∂Ω) × H^−1/2(∂Ω) is a compact operator.

Let us prove now the same properties for A_σ. A decomposition of A_σ can be given as A_0,σ + A_c,σ where A_0,σ and A_c,σ are, respectively, defined by and (24) We can observe that A_c,σ is the restriction of A_c,∂Ω to on σ. Then, we can directly deduce the compactness of this operator. The coercivity of A_0,σ is deduced from the coercivity of −T_0,σ. In fact, we have for all for some α > 0. Therefore which leads to the coercivity of the operator −T_0,σ on σ. Consequently, the operator A_0,σ is invertible. In fact, let and such that This is equivalent to Consequently Therefore the invertibility of A_σ,0 is equivalent to the invertibility of T_0,σ.

Finally, A_σ is a Fredholm operator with index zero and since A_σ is injective (see Lemma 2.3) we conclude that it has a bounded inverse.▪

As a consequence of these lemmas, we have the following result

Theorem 2.5

The (ICP) has a unique solution given by (25) where ([u^s], [∂_νu^s]) is the unique solution of the system of integral equations (8).

A detailed discussion about the numerical implementation of the (ICP) using a Galerkin method can be found in 12.

We recall that the solution of the (ICP) has the asymptotic behaviour of an outgoing spherical wave 13 (26) where u^∞ is the far-field pattern of the scattered wave, , and r = |x|.

3. The inverse problem

3.1. Settings and theoretical results motivating the LSM

In this section, we adapt the LSM for scattering by a partially coated crack 1 to the following inverse problem. We shall keep the same hypothesis on λ^± as in Section 2.

Inverse scattering by an impedance crack (IIC): Given the far-field pattern u^∞(·, ·) on 𝕊^m−1 × 𝕊^m−1 of the solution to (ICP), reconstruct the crack σ.

To solve the (IIC) by the LSM method, we first define the far-field operator (27) and consider the far-field equation (28) where is given by (29) (30) Notice that is the far-field pattern of the potential Φ_L defined by (31) with densities and , for any smooth non-intersecting open arc L ∈ ℝ^m−1.

We will characterize the crack σ by the behaviour of an approximate solution g_L of the far-field equation (28).

To prove the existence of an approximate solution of (28), we factorize the operator F as F = Bℋ where maps the boundary data (g⁺, g⁺ − g⁻) to the far-field pattern of the solution of (ICP) and ℋ is the trace operator defined by where v_g is the Herglotz wave function of kernel g ∈ L²(𝕊^m−1), (32) We will show that the traces of the solution of the (ICP) on both sides of σ can be approximated by the appropriate traces of the Herglotz wave function v_g.

Lemma 3.1

The operator ℋ is injective and has a dense range.

Proof

Let g ∈ L²(𝕊^m−1) be an element of the kernel of ℋ. Then, Since by assumption (λ⁺ + λ⁻) ≠ 0 then v_g = 0 and ∂_νv_g = 0 on σ₀ ⊂ σ. From the unique continuation principle it implies that v_g = 0 in ℝ^m and therefore g = 0 which proves that ℋ is one to one.

The main idea of the proof of the second part of the lemma is to show that ℋ*, the adjoint operator of ℋ, is injective.

To this end, we first determine the expression of ℋ*. Let g ∈ L²(𝕊^m−1) and , then satisfies where .

By changing the order of integration and using (32),

Therefore, for d ∈ 𝕊^m−1, the operator ℋ* is given by We observe that ℋ* is the far-field pattern of the potential for . This function is well defined in since α and β can be extended by zero to functions in H^1/2(σ). Moreover, satisfies the Helmholtz equation and the Sommerfeld radiation condition.

Therefore, if ℋ*(α, β) = 0, the far-field pattern of V is zero and from Rellich's lemma and the unique continuation principle we conclude that V = 0 in . Then, by the jump relations of the layer potentials, we have [V] = −γα and . This implies that Thus, since by assumption (λ⁺ + λ⁻)⁻¹ ∈ L^∞(σ), α = β = 0. We conclude that the operator ℋ* is injective and using Lemma 2.10 in 11 the operator ℋ has a dense range.▪

In the next step, we provide some properties of the operator B. We need to introduce the operators given by (33) and defined by (34)

Lemma 3.2

The operator M has a bounded inverse and B = γℱM⁻¹.

Proof

For a given , the function is the far-field pattern of the potential The function satisfies the Helmholtz equation in and the Sommerfeld radiation condition. In addition, following the proof of Lemma 2.3, we show that ϕ = [P], ψ = −[∂_νP] and where is given by (34). This operator is related to the matrix A_σ defined by (9). More precisely, with defined by (35) Since (λ⁺ + λ⁻)⁻¹ ∈ L^∞(σ), 𝒞 is an invertible operator and by Lemma 2.4, exists and is bounded.▪

Lemma 3.3

The operator is injective and has a dense range in L²(𝕊^m−1).

Proof

The injectivity of ℱ can be proved in the same way as in Lemma 3.1, by replacing the potential V by P.

Proceeding again as in the proof of Lemma 3.1, let g ∈ L²(𝕊^m−1) and , Therefore, ℱ*(g) = γ(∂_νv_g, v_g)_|σ.

Now, if ℱ*(g) = 0 then v_g = ∂_νv_g = 0 on σ.

Thus, as in Lemma 3.1, g = 0 which proves the density of the range of ℱ.▪

Summarizing the previous results, the operator F defined by (27) is factorized as F = ℱM⁻¹ℋ. Hence, the range of F is included in the range of ℱ. Therefore, thanks to the following lemma, there exists an approximated solution of Equation (28).

Lemma 3.4

For any smooth non-intersecting arc L and functions , such that (α_L, β_L) ≠ (0, 0), the function given by (29) belongs to R(ℱ), the range of ℱ, if and only if L ⊂ σ.

Proof

First assume that L ⊂ σ. Since , it follows from (33) that .

Now let L ⊄ σ and assume, on the contrary, that . Hence, there exists and such that

Thus is the far-field pattern of the potential Since by definition is also the far-field pattern of the potential Φ_L given by (31) then using Rellich's lemma and the unique continuation principle, the potentials Φ_L and P coincide in .

Let and B_ε a small neighbourhood of x₀ with B_ε ∩ σ = ∅. Then, P is analytic in B_ε while Φ_L or its normal derivative is not continuous across L which is a contradiction. This proves that .▪

Theorem 3.5

We assume that L is a non-intersecting smooth open arc. The following is true:

1.	If L ⊂ σ; there exists a sequence (gn)n∈ℕ on L2(𝕊m−1) such that where .
2.	Otherwise, for any sequence (gn)n∈ℕ ⊂ L2(𝕊m−1) that satisfies we have

Proof

•

If L ⊂ σ, it is easy to find a bounded solution of the far-field equation (28). In fact, we have and . Thus, and there exists a unique such that Therefore by Lemma 3.2 there exists a unique such that  Moreover by Lemma 3.1 the range of ℋ is dense on H−1/2(σ) × H−1/2(σ). Hence there exists (αn, βn)n∈ℕ ⊂ R(ℋ) such that . Using the continuity of ℋ, we show the existence of a sequence (gn)n∈ℕ ⊂ L2(𝕊m−1) verifying which proves that

•

Let L ⊄ σ and let us assume that . Therefore, (36) Let (αn, βn) ∈ R(ℋ). Since ℋ is injective there exists a sequence (gn)n∈ℕ ⊂ L2(𝕊m−1) such that ℋ(gn) = (αn, βn). From (36), the sequence (αn, βn) is bounded in . Therefore, we can extract a subsequence that we still denote (αn, βn) which weakly converges to (α, β).

 The integral operator ℱ is compact since it has a regular kernel and M⁻¹ is a bounded operator, so that the operator ℱM⁻¹ is also compact. Consequently, and by the uniqueness of the limit, we have We deduce that and L ⊂ σ which is a contradiction.▪

For the purpose of the numerical experiments, we cannot give a crack characterization by using the norm of v_g as suggested in Theorem 3.5 since this norm depends on the impedance values and on the crack σ. However, similar to the case of obstacles with non-empty interior 14, we expect that has the same behaviour as in the sense that has smaller values when L ⊂ σ, where g_L denotes a nearby solution of the far-field equation. The latter heuristic argument can be for instance justified by the fact that, at the discrete level, the Herglotz operator ℋ is invertible. Our indicator function will be then based on .

3.2. Numerical schemes and results

3.1.1. Numerical scheme

The numerical experiments are conducted in a 2D setting of the problem. We consider n equally distant observation points of the far-field on the unit circle 𝕊¹. (37) where w_j is the arc length between two adjacent points. Let L be a small segment of centre z and with normal ν. Then (38) The discrete equation to solve is then (39) using a classical Tikhonov regularization and the Morozov principle to fix the regularization parameter. The sampling procedure will consist then in varying z and ν in (38). According to Theorem 3 we expect ‖g‖ (where g is a solution to (39)) to be large except when z ∈ σ and ν is the normal to σ at z.

We shall consider two types of solutions: the first one denoted by g_z corresponds to α(z) = 1 and β(z) = 0, the second one denoted by g_z,ν corresponds to α(z) = 0 and β(z) = 1.

Remark 1

One can guess from the theoretical section (end of the proof of Lemma 3.4) that for a crack with Neumann boundary conditions (corresponds with vanishing impedances), Lemma 3.4 (and therefore Theorem 3.5) is not verified if α_L = 0. The same is true if the impedances are infinite (Dirichlet boundary conditions) and β_L = 0. From the numerical point of view, this suggests that g_z,ν plays a more important role for small values of the impedances than for larger ones. The numerical reconstructions below will confirm this observation.

First criterion: Since a priori knowledge on the correct orientation of the normal ν is not known a priori, a natural approach would be to consider the use of two independent normals for instance ν₁ = (0, 1)^T and ν₂ = (1, 0)^T. At each sampling point z we then compute (40) This criterion would provide good reconstructions in the case of obstacles with non-empty interior. However, as we shall observe later, for the case of cracks it may not be efficient if ν₁ or ν₂ does not coincide with the exact normal to σ at z (see the numerical tests in Section 3.1.2).

Second criterion: Let us define the normal ν as Therefore, by linearity of Equation (39) Based on the theoretical justification, the normal ν to σ at z ∈ σ corresponds with the value ζ that minimizes (41) The proposed criterion will be the determination on each point z of (42) where g_z,ν corresponds with ζ that minimizes (41).

3.1.2. Numerical tests

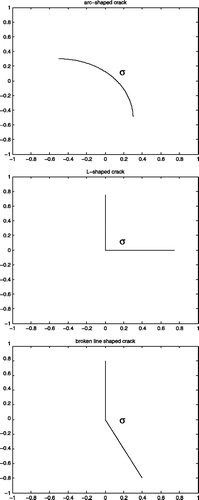
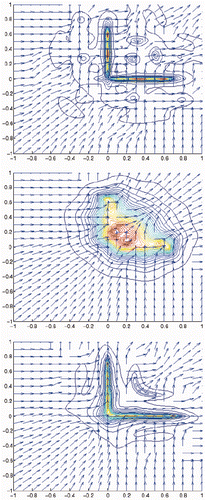
The efficiency of our approach is tested using both criteria for several ranges of the impedance values and for different shapes, namely arc-shaped cracks, L-shaped cracks and angular cracks (Figure 1). We present in the following figures the isovalues of the right-hand side of (40) and (42). The location of the crack would correspond with the red isovalues in the figures.

Figure 1. Exact geometry of the cracks.

In all the numerical tests, we use 100 observation points of the far-field pattern and the same number of incident plane waves. The wavelength is equal to 1 and the synthetic data is corrupted with 1% random noise. The minimization of (41) is simply done by taking the min value of (41) evaluated on 50 equidistant values of ζ. The reconstructions computational time is of order of seconds on a MacBook Pro laptop.

Both criteria give a good reconstruction of the crack for the case of large impedances (Figures 2–4).

Figure 2. Reconstruction of an L-shaped crack (Figure 1, middle) with vertices (0.75, 0), (0, 0), (0, 0.75) for λ^± = 0.01(1 + i) (top), λ^± = 5(1 + i) (middle), λ^± = 1000(1 + i) (bottom).

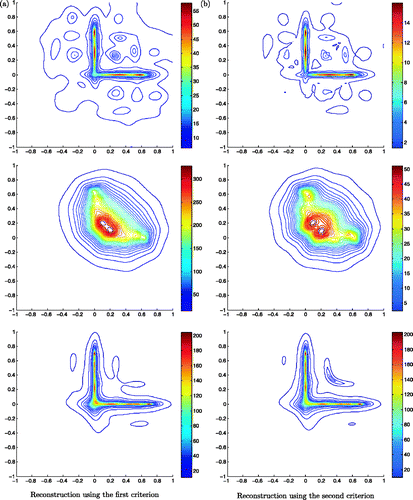
In the case of small impedances, using the first criterion, the result is not satisfactory for all geometries. This is due to the fact that for large impedances we are close to the Dirichlet case, hence the dominant term in (40) is whereas for small impedances we are close to the Neumann case where the dominant term is the one that contains the normal derivatives. Figure 2(a) shows that if ν₁ or ν₂ coincides with the exact normal to the crack we have a good reconstruction otherwise only the part of the crack for which the normal coincides with ν₁ or ν₂ is correctly reconstructed (Figures 3a and 4a). Hence having a good approximation of ν is very important for the precision of the result. This problem is fixed by the use of the second criterion as demonstrated by the reconstruction shown in Figures 2(b), 3(b) and 4(b).

Figure 3. Reconstruction of an arc-shaped crack (Figure 1, top) with centre (−0.5, −0.5), radius 0.8 and angle varying from 0 to π/2 for λ^± = 0.01(1 + i) (top), λ^± = 5(1 + i) (middle), λ^± = 1000(1 + i) (bottom).

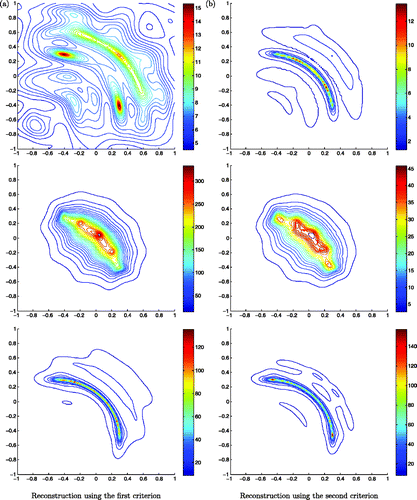
Figure 4. Reconstruction of two segments with endpoints (0, 0.8), (0, 0) and (0, 0), (0.4, −0.8) (Figure 1, bottom) for λ^± = 0.01(1 + i) (top), λ^± = 5(1 + i) (middle), λ^± = 1000(1 + i) (bottom).

We also observe that the quality of the results deteriorates when the impedance values are intermediate between high and small magnitudes.

To illustrate the correlation between the reconstruction of the normals (i.e. the ν that minimizes (41)) and the precision of the crack reconstruction, we represent these vectors in Figure 5. We observe that the best crack reconstructions for intermediate values of the impedances correspond with the cases where the normals at the crack are close to the exact ones. For large values of the impedances, the reconstruction of the normal is not correct but has negligible influence on the crack reconstruction (see Remark 1).

Figure 5. Reconstruction of the normals in the case of L-shape (Figure 1, middle) for λ^± = 0.01(1 + i) (top), λ^± = 5(1 + i) (middle), λ^± = 1000(1 + i) (bottom).

4. Determination of the impedance values

After determining the geometry of the crack, a second step would be to get estimates on the impedances values on both sides of the crack. To do so, we develop and compare two different approaches: a so-called natural approach and an approach based on the LSM formalism.

4.1. A natural approach

This approach is based on the expression of the far-field pattern. We recall that By knowing the crack σ, we can deduce ([u], [∂_νu]) on σ by inverting the operator defined by This is an ill-posed problem since ℱ is a compact operator. Consequently a regularization is needed. We shall use a Tikhonov regularization by solving where ζ is a regularization parameter chosen by using the Morozov criterion. 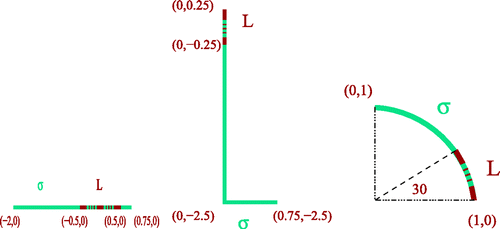From the integral representation of the scattered solution one deduces Finally, by considering the boundary conditions on σ, In the case of constant impedance values we prefer using the formula (43) which would be less sensitive to pointwise small values of u_±. This approach is tested for different shapes, namely a segment, an arc and a broken line (Figure 6). The results are presented in Tables 1–4.

Figure 6. The exact crack σ is represented in blue and L ⊂ σ in red.

Table 1. Reconstruction of the average of λ^± given by (43) on σ = [−0.5, 0.5] × {0} for n equidistant directions of plane waves starting from θ = 0 with the wavelength λ = 1.

		n
2	i	4	2.01 + i0.06	−0.02 + i1.23
2	i	100	1.99 + i0.06	−0.06 + i1.18
5(1 + i)	5(1 + i)	4	4.57 + i5.04	4.67 + i4.96
5(1 + i)	5(1 + i)	100	4.68 + i5.19	4.77 + i5.22
0.5 + i	0.2 + i0.4	4	0.46 + i1.15	0.17 + i0.54
0.5 + i	0.2 + i0.4	100	0.44 + i1.13	0.15 + i0.51

In Tables 1 and 2, we fix the geometry and provide different estimates of the average of n reconstructed impedance values where n is the number of the different directions of uⁱ for segment and arc-shaped cracks, respectively. Both tables show in general good estimates of the impedance values. One also observes that for the case of arc-shaped cracks, when the imaginary part is relatively high, the accuracy of reconstructed values deteriorates. Since this is not the case of segment, we think that the loss of accuracy is due to the non-convexity of the geometry.

Table 2. Reconstruction of the average of λ^± given by (43) on the arc σ centred at (0, 0) with aperture for n equidistant directions of plane waves starting from θ = 0 till θ = 2π with the wavelength λ=1.

		n
2	i	4	2.07 + i1.50	0.37 + i0.82
2	i	100	2.06 + i0.038	0.22 + i1.01
5(1 + i)	5(1 + i)	4	5.53 + i2.18	7.69 + i5.07
5(1 + i)	5(1 + i)	100	5.08 + i2.30	7.07 + i5.01
0.5 + i	0.2 + i0.4	4	0.46 + i0.99	0.15 + i0.41
0.5 + i	0.2 + i0.4	100	0.47 + i1.08	0.18 + i0.41

We next test whether the reconstructed impedance is sensitive to errors on the cracks geometries. To do so, we introduce a small perturbation on the geometry of the crack by shifting its vertical position with ϵ. The results shown in Tables 3 and 4 below indicate that a stable approximation is obtained only for kϵ small enough.

Table 3. Reconstruction of the average of λ^± given by (43) on a perturbed geometry where the exact crack is σ=[−0.5, 0.5]×{0} for 100 equidistant directions of plane waves starting from θ=0 till θ=2π and a wavelength λ=1.

		ε
2	i	0.1	10.10 − i0.38	9.24 + i1.18
2	i	0.01	2.03 + i0.04	−0.02 + i1.21
5(1 + i)	5(1 + i)	0.1	25.96 + i3.54	12.39 + i2.28
5(1 + i)	5(1 + i)	0.01	4.33 + i5.39	5.24 + i4.97
0.5 + i	0.2 + i0.4	0.1	12.28 + i0.18	7.92 + i0.80
0.5 + i	0.2 + i0.4	0.01	0.56 + i1.05	0.20 + i0.55

4.2. An approach inspired by the LSM algorithm

According to the proof of the main lemma of the LSM (see Theorem 3.5), if L ⊂ σ then Φ_L is an approximation of the scattered wave associated to an incident Herglotz wave with the kernel g_L solution of the LSM equation (28). Hence we have the following relations: (44) We recall that where . Hence to estimate the value of the impedance over the small crack L, the following formula can be used, which can be directly deduced from (44) for constant impedance values over L. (45) The main advantage of this procedure as compared to the previous one is that a complete knowledge of σ is not required to obtain an approximation of λ^± on L. This is particularly attractive for cases where the reconstructed geometry is good only in some parts of the crack. This has been observed for instance for complex geometries with impedances having ‘intermediate’ values.

Before investigating the cases where L is a part of σ let us consider similar configurations as for the previous approach. Namely we take L = σ = [−0.5, 0.5] × {0}. Since (α, β) should be in , we can choose β as a constant function and α as a function that vanishes on the vertices of σ given by The results of Table 5 show that a good reconstruction of the impedance values is obtained when using this criterion. The accuracy of the results seems to be not very sensitive to the values of β for the adopted choice of test functions.

Table 4. Reconstruction of λ^± given by (43) on a perturbed geometry where the exact crack is σ=[−0.5, 0.5] × {0} for 100 equidistant directions of plane waves starting from θ = 0 till θ = 2π and a wavelength λ = 4.

		ε
2	i	0.1	1.99 + i0.06	1.65 + i0.90
2	i	0.01	2.01 + i0.04	−0.02 + i1.07
5(1 + i)	5(1 + i)	0.1	1.06 + i4.11	5.48 + i2.97
5(1 + i)	5(1 + i)	0.01	4.15 + i5.20	4.67 + i4.73
0.5 + i	0.2 + i0.4	0.1	0.38 + i0.80	0.68 + i0.52
0.5 + i	0.2 + i0.4	0.01	0.45 + i1.03	0.22 + i0.42

Table 5. Reconstruction of the average of λ^± using formula (45) on L = σ = [−0.5, 0.5]×{0}.

		β
2	i	1	2.03	0.01 + i0.95
2	i	5	2.01	i
5(1 + i)	5(1 + i)	6	5.02 + i4.97	4.88 + i4.99
0.5 + i	0.2 + i0.4	1	0.53 + i1.01	0.19 + i0.38
0.5 + i	0.2 + i0.4	6	0.50 + i1.01	0.20 + i0.40

As done in the first approach we test also the sensitivity of this approach to small perturbations of the exact geometry (Tables 6 and 7). We qualitatively observe similar behaviour as in the first approach, namely kϵ should be small enough to ensure a good accuracy. However, we can state that the second method seems to be more sensitive to error in the geometry than the first one.

Table 6. Reconstruction of λ^± using formula (45) on the perturbed geometry where the exact crack is σ = [−0.5, 0.5]×{0} for the wavelength λ = 1 and β = 6.

		ε
2	i	0.1	6.72 − i1.14	−5.14 + i2.08
2	i	0.01	2.37	−0.42 + i1.06
5(1 + i)	5(1 + i)	0.1	7.95 + i4.63	−3.10 + i0.51
5(1 + i)	5(1 + i)	0.01	5.11 + i4.92	3.66 + i4.50
0.5 + i	0.2 + i0.4	0.1	4.96 + 0.7i 5	−4.44 + i0.22
0.5 + i	0.2 + i0.4	0.01	0.88 + i0.96	−0.20 + i0.39

Table 7. Reconstruction of λ^± using formula (45) on the perturbed geometry where the exact crack is σ = [−0.5, 0.5]×{0}, β = 6 and the wavelength λ = 4.

		ε
2	i	0.1	2.12 − i0.08	0.44 + i1.05
2	i	0.01	2.01 − i0.02	0.03 + i1.03
5(1 + i)	5(1 + i)	0.1	−0.33 + i8.64	4.38 + i1.95
5(1 + i)	5(1 + i)	0.01	4.41 + i5.27	5.28 + i4.08
0.5 + 1i	0.2 + i0.4	0.1	0.49 + i0.96	0.15 + i0.46
0.5 + i	0.2 + i0.4	0.01	0.48 + i0.96	0.20 + i0.43

We now consider the cases where L is only a part of σ. We test this issue for three different geometries given in Figure 6.

In the first experiment, we assume that L = [−0.5, 0.5] × {0} is a part of the exact crack σ = [−2, 0.75] × {0}. Table 8 shows that a good estimate of the impedance is also obtained in this case.

Table 8. Reconstruction of the average of λ^± using formula (45) when L = [−0.5, 0.5] × {0} is a part of the exact crack σ = [−2, 0.75] × {0} (see Figure 6, left).

		β
2	i	6	2.03 + i0.01	0.10 + i1.02
5(1 + i)	5(1 + i)	6	5.12 + i4.967	5.33 + i4.57
0.5 + 1i	0.2 + i0.4	6	0.52 + i1.02	0.22 + i0.43

In the following test, we show that even for a complex shape as the L-shaped crack we can get good reconstructions. In Table 9, σ is an L-shaped crack with vertices (0, 0.25), (0, −2.5), (0.75, −2.5) and L = {0} × [−0.25, 0.25] for a constant β and

Table 9. Reconstruction of the average of λ^± using (45) on L = {0}×[−0.25, 0.25] which is a part of the exact L-shaped crack σ in Figure 6 for the wavelength λ = 1.

		β
2	2	6	2.13 − i0.01	2.12
2	2 + i	2	2.58 − i0.04	2.34 + i0.98
5(1 + i)	5(1 + i)	1	5.81 + i3.92	5.38 + i4.38
0.5 + i	0.2 + i0.4	6	0.54 + i1.05	0.23 + i0.43
0.5 + i	0.2 + i0.4	1	1.09 + i1.03	0.34 + i0.39

Finally, let L be a part of the arc shown in Figure 6 (right). The results in Table 10 show that a good approximation of the exact values of the impedance is obtained on the known part of the exact crack.

Table 10. Reconstruction of the average of λ^± on L using formula (45) where L is the arc centred at (0, 0) with aperture which is a part of the exact crack σ (see Figure 6, right) for the wavelength λ=1.

		β
2	i	10	2.21 − i0.07	−0.05 + i0.98
5(1 + i)	5(1 + i)	10	5.72 + i4.86	5.20 + i4.69
0.5 + i	0.2 + i0.4	10	0.59 + i1.13	0.19 + i0.36

Acknowledgements

This work is supported by the Ministère de l'Enseignement Supérieur, de la Recherche Scientifique et de la Technologie (MESRST, TUNISIA) under the LAB-STI-02 program and the Franco-Tunisian INRIA-DGRSRT 08/I10 scientific program.