Abstract
In this article we discuss the determination of the aerosol particle size distribution function using the particle spectrum extinction equation. This is an ill-posed integral equation of the first kind, since we are often faced with limited or insufficient observations in remote sensing and the observations are contaminated. To overcome the ill-posed nature, using the a priori information, we study the inflection point regularization method and develop a conjugate gradient projection method for solving the corresponding optimization problem. In our work, regularization parameter can be considered as the number of inflection points and their position. The algorithms for constructing an approximate solution are described. Error estimates are also presented. Our numerical tests for both the synthetic problem and practical problem are given to show the efficiency and feasibility of the proposed algorithm.
1. Introduction
It is well known that the characteristics of the aerosol particle size, which can be represented as a size distribution function in the mathematical formalism, say n(r), plays an important role in climate modelling. So, the determination of a particle size distribution function becomes a basic task in the aerosol research Citation1,Citation2. Since Angström Citation3 first suggested the relationship between the size of atmospheric aerosol particles and the wavelength dependence of the extinction coefficient, the size distribution began to be retrieved by extinction measurements.
For the sun-photometer, if the aerosols can be considered as globular particles, then the attenuation of the aerosols can be written as the integral equation of the first kind:
(1)
where τaero is the measured aerosol optical thickness (AOT); r is the particle radius; n(r) is the columnar aerosol size distribution (i.e. the number of particles per unit area per unit radius interval in a vertical column through the atmosphere); η is the complex refractive index of the aerosol particles; λ is the wavelength and Qext(r, λ, η) is the extinction efficiency factor from Mie's theory Citation4. Since AOT can be obtained from the measurements of the solar flux density with sun-photometers, one can retrieve the size distribution by the inversion of AOT measurements through the above equation. This type of method is called extinction spectrometry, which is not only the earliest method applying remote sensing to determine atmospheric aerosol size characteristics, but also the most mature method thus far.
In practice, the sun-photometer CE 318, which we used to obtain observation data can be modelled numerically by the operator equation of the first kind, can only supply four aerosol modelled Citation5, i.e. only four observations are obtained, which are insufficient for the retrieval of the particle size distribution function n(r) by solving Equation (1). Therefore, numerical difficulty occurs. To overcome the oscillations in recovering of the particle size distribution function n(r), various techniques have been developed, e.g. direct regularization methods and iterative methods Citation4,Citation6,Citation7. In this article, we introduce some a priori constraints to the solution. We first assume that the particle size distribution is always nonnegative and piecewise-convex, and then we study the inflection point regularization method and develop the conjugate gradient projection method for solving the corresponding optimization problem.
2. Mathematical formulation
To begin with this section, we describe some assumptions for our analysis:
(C1) The particle size radius interval of interest is ℛ ≜ [rmin, rmax](=[0.1, 2] µm) (the reason can be found in Citation8). | |||||
(C2) This aerosol particle size distribution function consists of the multiplication of two functions h(r) and f(r) : n(r) = h(r)f(r), where h(r) is a rapidly varying function of r, while f(r) is more slowly varying. | |||||
Since most measurements of the continental aerosol particle size distribution reveal that these functions follow a Junge distribution Citation9, h(r) = r−(ν+1), where ν is a shaping constant with typical values in the range 2.0–4.0. Therefore it is reasonable to use h(r) of Junge type as the weighting factor to f(r). In this article, we set ν = 2.5.
Definition 2.1
Integral operator K from the parameter space ℱ (C(ℛ) or ℒ2(ℛ)) to the observation space 𝒯 (C(ℛ) or ℒ2(ℛ)) is called the scattering operator of aerosol if for every particle the size distribution function n(r) ∈ ℱ satisfies:
where the kernel Qext is the extinction efficiency factor from the Mie's theory.
In spherical coordinate system, if we denote z = 2πr/λ, the extinction efficiency factor can be written by
where an = an(z, η) and bn = bn(z, η) are the scattering coefficients from Mie's theory. If we assume that a boundary condition is homogeneous, then scattering coefficients can be written by Citation2
where
,
, Jn+1/2(z) and Nn+1/2(z) are Bessel functions and Neumann functions of order n + 1/2. For a given rapidly varying function h(r), to simplify the problem, we can define a new operator A, which is also a mapping of ℱ to 𝒯:
Then, using the equality Kn = τaero, whose right-hand side is interpreted as the measured AOT and is always positive, we can obtain some properties for the operator K (and A):
Theorem 2.2
The scattering operator of aerosol K (or A) is a linear, continuous, bounded and injective operator. In addition, for any aerosol particle size distribution function n(r) (or slowly varying function f(r)): (Kn)(λ) > 0 (or (Af)(λ) > 0) for all λ > 0.
Remark 1
Obviously, operators K and A have the same property. Below we only discuss the property of the operator A, which is also called the scattering operator of aerosol, because all properties obtained for operator A are obviously correct for operator K.
For the attenuation problem, let us rewrite Equation (1) in the form of the operator equation:
(2)
It is well known that for an operator Equation (2), in which A(λ, r) is a continuous function, the problem is ill-posed. Actually, from another point of view for the aerosol particle size distribution function retrieval problem, the ill-posedness arises because: (1) the model operator is compact; (2) the observations contain noise and (3) the number of observations is insufficient. These ill-posedness characteristics produce a kind of jump in the solution space; i.e. instead of being centred on the true solution, the results may spread over the whole parameter space.
Remark 2
Regularization is a necessary way to tackle the ill-posed nature of the inversion process. In this article, an a priori information is that the solution is a nonnegative piecewise-convex function. As proposed by us, the inflection point regularization method bases on the variational regularization method because this method is easy to add the a priori information. In our work, the regularization parameter can be considered as the number of inflection points and their positions.
3. Approximate solution and its error estimation
Usually, instead of the exact data we are given an approximate admissible data {Ah, τδ} such that: the perturbed right-hand side τδ ∈ 𝒯 and Ah is a operator of ℱ to 𝒯, which has the same properties as the operator A described in Theorem 2.2. Here the admissible data {Ah, τδ} are described by two methods:
(M1) ‖Ah − A‖ℱ→𝒯⩽h, | |||||
(M2) ∣ Ah(λ, r) − A(λ, r) ∣⩽h(λ, r), | |||||
Suppose that, the exact solution belongs to the set of bounded piecewise-convex functions
(⊆ℱ). Titarenko and Yagola Citation10 proved that the set of bounded picecewise-convex functions
on some bounded segment ℛ is a compact set in ℒp(ℛ)(1 < p < ∞). According to Tikhonov et al. Citation11, the approximate solution fη for Equation (2) can be accepted as any element in the set:
(3)
But this set is not a convex set. In practise, if we can define
, the approximate solution can be accepted as any element in the convex set:
(4)
where ϑ ≡ ϑ(η) → 0 as η → 0. In both cases, by Ivanov's theorems Citation11,Citation12, we can prove that
in ℱ as η → 0, where
is the accurate solution. If errors of the right-hand side and the kernel of the scattering operator of aerosol were given by (M2), similar as Citation11,Citation13,Citation14, then we have the following theorem.
Theorem 3.1
Let C2 = (rmax − rmin)maxr∈ℛ f(r) and . The approximate solution
can be accepted as any element in the set:
(5)
i.e. ϵ → 0 (or
) as
for every fixed point r.
We now address the question about error estimation of the approximate solution. Let be any set of sets
,
and
. If we fix any approximate solution
of our problem (2), which has perturbed operator and right-hand side, we can write error estimation by:
. Obviously, we have the inequality:
. In practice, fixed approximate solution may be selected as any element in the set
. Thus, in principle, we can find the error estimate before solutions of the problem if we calculate the diameter of set
, i.e.
. Of course, we can estimate an optimal a priori error by
.
However, an error estimator of approximate solution can be considered as the error in the domain of definition at every point. In this case, for every point r ∈ ℛ, the error function can be written as: ,
and
.
Therefore, for all approximate solutions we have inequalities:
and for all r ∈ ℛ:
, where σ = 0, 1, 2. Moreover, for every fixed point r, Δσ, Δσ → 0 as η → 0. So Δσ and Δσ are error estimates.
4. Finite-dimensional approximation
In this section, we discuss the finite-dimensional approximation for Equation (2). To simplify, we divide the solution domain [rmin, rmax] × [λmin, λmax] into a uniform grid with step sizes hr and hλ. Sets of grid points are denoted as and
. The values of functions f(r), τ(λ), A(λ, r) and Ah(λ, r) at grid point rn and λm are denoted by f(rn) = fn, τ(λm) = τm, A(λm, rn) = Amn and Ah(λm, rn) = amn. Instead of the exact right-hand side
, the exact kernel of the operator A(λ, r) and their discrete value at grid point
, Amn, we are given vectors
,
and matrixes [amn]MN, [hmn]MN such that:
, and
. The finite-dimensional approximation of the set
and
will be denoted as
and
. Obviously,
is a closed convex and bounded polyhedron in
. The element of
is denoted as
. Moreover, the discretization of the discrepancy functional
can be obtained by (using the trapezoidal rule):
(6)
Thus, for finding a unique element of the set
we can solve a minimization problem
. In the end, instead of the finite-dimensional approximate solution
, we use a piecewise-linear function fN(r) such that:
, where
.
Remark 1
For the set (4) error estimation of the operator and the right-hand side can be found by the formula: and
. In addition, when we solve the minimization problem
, we can ignore the restriction ‖Ahf − τδ‖𝒯⩽ϑ, which will not influence our result. Thus, we have
In fact, for some special compact set, we have a more effective method to find an approximate solution Citation15. First of all, we assume that there exist functions ,
and
such that
for all r ∈ ℛ. Notice that the aerosol particle size distribution function f(r) is always nonnegative and using the properties of operators A and Ah, which are described in Theorem 2.2, we have inequalities
where the operator H is defined by Hf = ∫ℛh(λ, r)f(r)dr. Using decomposition functions
and
by
, and integrating the above inequalities, we can obtain
(7)
where
and
. For some special compact set (the set of monotonic functions, the set of concave functions, etc.), we can construct the formula of
and
, then the approximate solution can be accepted for any element in the set
(8)
where the matrix Ĝ and the vector ĝ are defined by inequalities (7).
It is easy to get the embedding: . Below, for simplicity, we only discuss the minimization problems
and
.
In the end of this section, we discuss the error estimator of the approximate solution. Instead of the a priori error estimator, here we use an a posteriori error estimator, which can be calculate by Δ3(η) ≜ ‖ f u − f l‖ℱ and Δ3(η, r) ≜ f u(r) − f l(r), where f l(r) is the lower solution and f u(r) is the upper one. The method of construction of f l(r) and f u(r) will be discussed in Section 5.1.3.
Remark 2
We do not use functions and
as the lower and the upper solutions because we have only the approximate discrete solution
, whose components are not the basic functions for
and
.
5. Inflection points method
In this section, we discuss how to find a quasi-solution of the operator Equation (2), i.e. how to solve the minimization problem: . The existence of a quasi-solution of this minimization problem can be obtained by the Weierstrass theorem Citation16.
Definition 5.1
Let denote the vector of inflection points of the slowly varying function f(r). The pair
will be called a regularization parameter of the inflection point method, where P is the number of inflection point, and vector
denotes their position. (In fact, it is their quasi-position, because it is possible that an inflection point may not be any point of grid point. In this case, instead of this inflection point, we use the grid point, which is the closest of the inflection point, i.e.
for every
)
Remark 1
If we a priori know the value of the regularization parameter (in fact, in this case our problem can already be considered as a well-posed problem), we can obtain some restrictions by this a priori information. Using these restrictions, we can solve the above minimization problem easily. In this article, in order to a posteriori determine the regularization parameter, we use a modified discrepancy principle, which are described below.
5.1. In the case of P = 1
Suppose that our solution has only one inflection point and denote the set of these functions by . But, we do not know the form of the function before the inflection point (convex or concave). Therefore, we have two cases. Now denote our set of approximate solutions by:
, where
and
.
5.1.1. Step 1: Given position of inflection point
Let r* be the inflection point and k be its position, i.e. . Then our matrix of restrictions can be written as
and
. Using the conjugate gradient projection method Citation13,Citation14 by this restriction, we can compute minimizer of the optimization problem:
.
In order to find the solution of problem , we must get the restriction matrix Ĝ, i.e. find functions
and
. First of all, we discuss the case in the set
. Since we know the position of this inflection point, we denote
Notice that, functions
and
belong to the set of convex functions. Contrarily, functions
and
belong to the set of concave functions. First of all, we discuss the function
. Using the definition of the convex-up function, we can obtain three inequalities in [rn, rn+1]:
,
, and
. Evidently, when
the function
can be designed as the piecewise-linear function, which is connected by points (rn, fn), i.e. (see ):
(9)
For r
r*, the function
can be designed as
where γ1 = 1, γk−1 = 0 and γn = −( fn−1 − 2fn + fn+1)/(fn−1 − fn − fn+1 + fn+2) as
. Similarly,
can be defined by formula (9) and
can be defined as
.
Figure 1. Functions (−○−) and
(−▵−), which were constructed by N-dimensional discrete approximate solution fN(r).
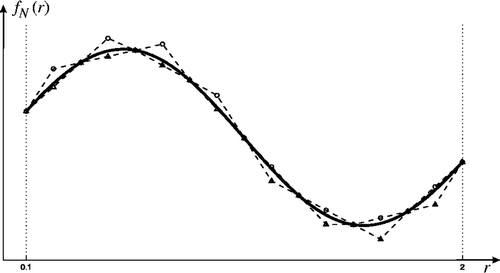
Similarly, we can also get the formula for and
in the case of
. Finally, we can get a more accurate approximate solution by solving the optimization problem
.
5.1.2. Step 2: Search for a position of an inflection point
Here, we use the enumeration method. It means that we assume every grid point (with the exception of initial point and end point) to be its inflection point. Then, at every inflection point we can construct the corresponding matrix of restrictions. After calculating all discrepancy functionals, we choose their minimum. We consider that the inflection point corresponding to the minimum discrepancy functional is a real inflection point. Notice that in the one-dimensional case we need to solve N linear programming for finding the inflection point.
5.1.3. Step 3: Construct a lower solution f l(r) and an upper solution f u(r)
Similarly, we denote the lower and upper solutions as
Denote the component of
and
as
and
. Then according to convexity of the function
and boundedness
,
, and
,
, we know that in the interval [rn, rn+1], the function f(r) is greater (less) than the straight line, which was connected by points
and
(connected by points
and
). Thus for any r ∈ [rn, rn+1], we have
as
and
as
. Now, we discuss how to construct functions
and
. At first, we discuss a function
().
Figure 2. The upper solution f u(r) and the lower solution f l(r), which are constructed by discrete functions and
(○, ▵). Right and left tangent lines of function f l(r) are denoted by - - -.
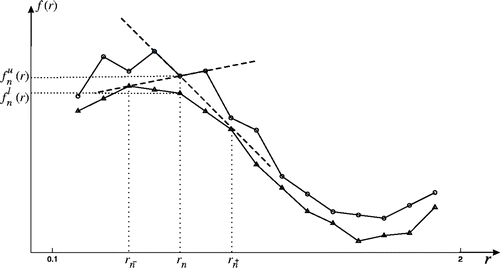
Definition 5.2
For any convex function and any index
, there exists a so-called right tangent index n+ such that: for a straight line, which connects by grid points (rn, fn) and
, we have two requirements: (1) in the interval [rmin, rmax], the function
is located under the given line; (2) the given line does not pass the grid point
. This given line will be called the right tangent of the function
.
Remark 2
| 1. | Similarly, for any | ||||
| 2. | In fact, the right and left tangent lines of function | ||||
Obviously, in [rmin, rn] all functions are less than the right tangent line of the function
, which connects by grid points
; and in [rn, rmax], they are less than the left tangent line. Thus,
can be defined as:
where
,
as
, and λ1 = 1, λk−1 = 0,
.
Remark 3
In practice, for simplicity, instead of the parameter λn we can use a constant. For example: λ1 = 1, λk−1 = 0, and λn ≡ 0.5 for .
Similarly, the function can be defined as
where
,
as
, and λk = 1, λN−1 = 0,
as
.
5.1.4. Step 4: Calculate the error estimation of the approximate solution
After constructing lower and upper functions f l(r) and f u(r), we can estimate an error of the approximate solution by two methods:
| 1. | maximum estimation of an error in space 𝒞:
| ||||
| 2. | the estimation of an error of the function: Δ3(η, r) = f u(r) − f l(r), i.e. for | ||||
5.2. In the case of P > 1
In this section, we assume that our solution has P inflection points. Similarly, we denote: , where
for
(i.e. before the first inflection point, our solution is a convex function) and
.
5.2.1. Step 1: Given position of inflection points
Let be inflection points and
be their position, i.e.
for every
. Then the matrix of restrictions can be written as
and
. Similarly, using the conjugate gradient projection method by this restriction, we can solve the well-posed optimization problem:
.
Of course, similar to the case of P = 1, we can get a more accurate approximate solution by solving the problem . However, if P is a large number, the process of construction of functions
and
is very complicated.
5.2.2. Step 2: Search the number of inflection points and their positions
It is well-known that the enumeration method is typically used when the problem size is limited, or when the simplicity of implementation is more important than speed. Therefore, it is an inefficient method for our case because its cost is proportional to the number of candidate solutions, which tends to grow very quickly as the size of the problem increases. Here, in order to answer our question, we use the language of computability theory Citation17. In fact, if we are given the largest number of inflection points P, we can prove that our problem belongs to class P. However, it is not difficult to prove that if we do not know the largest number of P, our problem already belongs to class NP-completeness. Thus, we know that for our problem there is no effective algorithm, because up to now for NP-complete problems no polynomial-time algorithms are known for solving them Citation18.
In this article, we develop a new algorithm, which is based on the enumeration method and with using some a priori information. Above all, we assume that the number of inflection points does not exceed more than a given constant P. We define this constant by P = ⌊q1 · N⌋, where q1 is the proportion of all grid points and ⌊ · ⌋ is the floor function. For numerical experiments, we choose q1 = 10%. Moreover, to suppose that the distance between two inflection points is not less than a given constant K, i.e. |kp+1 − kp|⩾K for . This constant depends on the total distance of domain of definition of our solution and the number of inflection points. For example, we can define: K = ⌊q2⌊N/p⌋⌋, where p⩽P is the number of inflection points and q2 is the proportion of the average grid points ⌊N/p⌋. For numerical experiments, we choose p = 50% and p = P. In the end of this section, we give a subalgorithm for locating the position of two inflection points:
| 1. | Locate the first inflection point for | ||||
| 2. | Locate the second inflection point for | ||||
| 3. | For every pair of inflection points (k1, k2), get solution and calculate their generalized discrepancy; | ||||
| 4. | Compare the value of generalized discrepancy and obtain the optimal solution. | ||||
6. Numerical experiments
6.1. Synthetic simulation
To verify the feasibility of our method, we test it by computer simulations. The simulation consists of two steps. First, a simulated extinction signal (input signal) is generated by computer according to Equation (2) for a given particle number size distribution nexact(r) (input distribution) and for a given complex refractive index η. Then, the input signal is processed through our algorithm, and the retrieved distribution is compared with input one.
In our example, the size distribution function nexact(r) is given by n(r) = 4.0887 × r−3.5 × (sin(3 × 10−12× r) + 1). If we set h(r) = r−3.5 and obtain the slowly varying function: f(r) = 4.0887× (sin(3× 10−12 × r) + 1). In addition, the complex refractive index η is assumed to be 1.45−0.00i. The number of discretization nodes is (N, M) = (50, 4). For numerical experiments, we set the error of the scattering operator of aerosol hmn = ϱ × maxm,namn and the error of the right-hand side , where ϱ is mainly the standard normal random noise N(0, 1). The initial approximate solution f 0(r) = 0. By our method we can obtain the approximate solution (the right side of ) and the regularization parameter (the number of inflection points and their position): α = (P, k) = (1, 24). To compare with our method, we use the least square method (LSM) on the bounded set (left side of ), variational regularization methods with different a posteriori parameter choices (generalized principle of smoothing functional (GPSF) Citation12, pseudo-optimal choice of parameter (POCP) Citation19 and generalized discrepancy principle (GDP)) and total variation (TV) with the seminorm ∫ℛ|∇f |dr (parameter is chosen by GDP) (). The relative errors for every method are showed in . The results show that the slowly varying functions of Gaussian type are well reconstructed. Our computer simulation indicates that our method does not affect too much by variation of the complex refractive index and noise. Therefore, our method is stable for retrieving aerosol particle size distribution functions.
Figure 3. The relation between the slowly varying function f(r) (unit of measurement: m−2µm−1) and the particle radius r (unit of measurement: µm). Exact solution (—); Estimator solution (−○−). The left graph: least square method. The right graph: inflection point method.
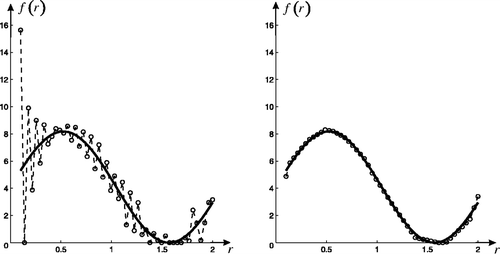
Figure 4. The relation between the slowly varying function f(r) (m−2µm−1) and the particle radius r (µm) for variational regularization methods with different methods of selecting regularization parameters Λ. Here: — exact solution; −•− GPSF; ·☆· TV; −▵− GDP; ·○· POCP.
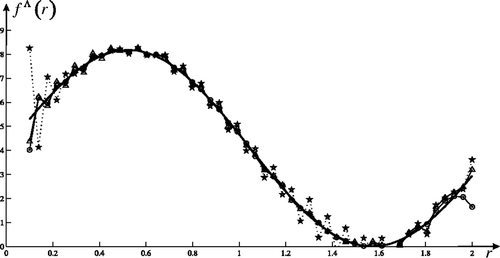
Table 1. Relative error for different methods.
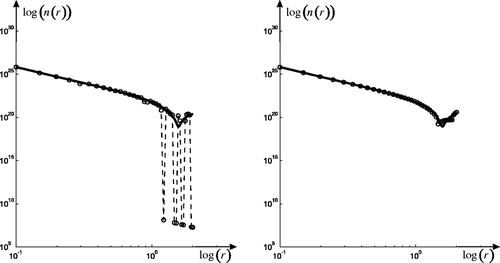
Moreover, by our method, we can get the upper and lower solutions f u(r), f l(r) (). If the slowly varying function f(r) uses time h(r), we can obtain the number of particle size distribution function nexact(r). In order to watch the results properly, we use the log–log scale ().
Figure 5. The lower (−▵−) and upper (−○−) solutions for the slowly varying function f(r). Here the exact solution denotes by the full line (—).
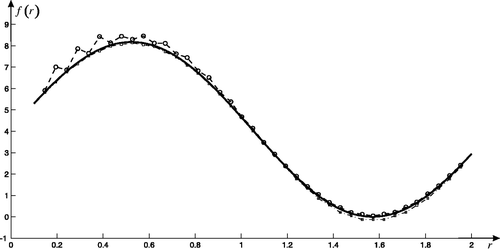
Figure 6. The relation between the atmospheric aerosol particle size distribution function n(r) and the particle radius r in log-log scale, i.e. the relation between log (n) and log (r). The left graph: GDP. The right graph: inflection point method.
Now we give anther example. The size distribution function nexact(r) is given by n(r) = 4.0887 × r−3.5 × (sin(4.6 × 10−12 · r) + 1). Similarly, we can obtain the approximate solution (the right side of ) and the regularization parameter: . The relative errors for different methods are showed in . The number of particle size distribution function nexact(r) is represented in in log–log scale.
Figure 7. Retrieval of slowly varying function f(r) in the case of P = 2. The left graph: LSM. The right graph: inflection point method.
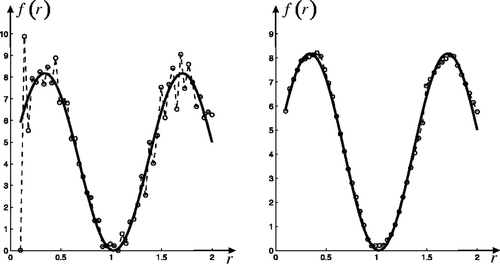
Figure 8. Retrieval of atmospheric aerosol particle size distribution function n(r) in the log–log scale for P = 2. The left graph: GDP. The right graph: inflection point method.
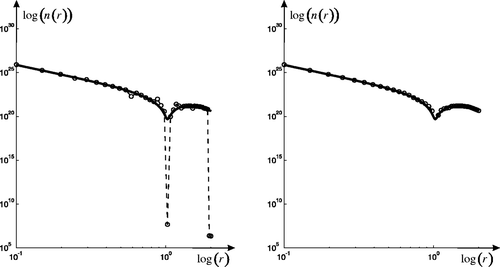
Table 2. Relative error for different methods in two-dimensional case.
6.2. Work with experimental data
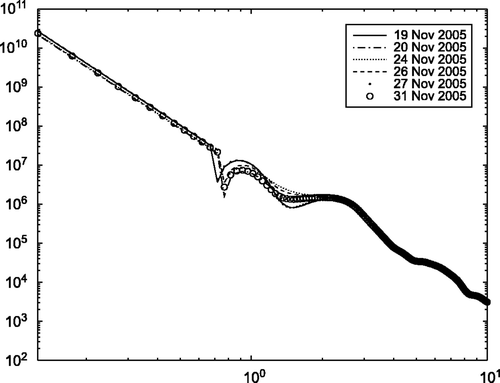
In this subsection, we choose the ground measured data by the sun-photometer CE 318 to test the feasibility of our method. We have performed successive in situ experiments using CE 318 from October 17 to October 31 in the year 2005. A complex refractive index value of η = 1.500 − 0.095i was used to perform the inversion Citation5. By our method, the retrieval results of the number of size distribution function n(r) are plotted in for the chosen data in the afternoon.
7. Conclusion
The results showed that the inflection points method is an efficient and feasible algorithm for solving this kind of ill-posed problem (recovering aerosol particle size distribution function). To compare with standard smooth regularization methods, the inflection points method yields more accurate retrieval results for recovering the aerosol particle size distribution function in our problem; and in the same accuracy, the inflection points method maintains the global shape.
Acknowledgements
The work was partially supported by RFBR grant 11-01-00040-a and 12-01-91153-NSFC-a.
References
- Twomey, S, 1977. Atmospheric Aerosols. Amsterdam: Elsevier; 1977.
- Bohren, GF, and Huffman, DR, 1983. Absorption and Scattering of Light by Small Particles. New York: John Wiley and Sons; 1983.
- Angström, AA, 1929. Atmospheric transmission of sun radiation and on dust in the air, Geogr. Ann. 11 (1929), pp. 156–166.
- Wang, YF, Fan, SF, Feng, X, Yan, GJ, and Guan, YN, 2006. Regularized inversion method for retrieval of aerosol particle size distribution function in W1,2 space, Appl. Optics 45 (2006), pp. 7456–7467.
- Wang, YF, 2007. Computational Methods for Inverse Problems and Their Applications. Beijing: Higher Education Press; 2007.
- Wang, YF, 2008. An efficient gradient method for maximum entropy regularizing retrieval of atmospheric aerosol particle size distribution function, J. Aerosol Sci. 39 (2008), pp. 305–322.
- Wang, YF, Fan, SF, and Feng, X, 2007. Retrieval of the aerosol particle size distribution function by incorporating a priori information, J. Aerosol Sci. 38 (2007), pp. 885–901.
- Wang, YF, Yagola, AG, and Yang, CC, 2011. Optimization and Regularization for Computational Inverse Problems and Applications. New York: Springer; 2011.
- Junge, CE, 1955. The size distribution and aging of natural aerosols as determined from electrical and optical data on the atmosphere, J.Meteor. 12 (1955), pp. 13–25.
- Titarenko, VN, and Yagola, AG, 2008. Error estimation for ill-posed problems on piecewise convex functions and sourcewise represented sets, Inverse Ill-Posed Probl. 14 (2008), pp. 1–14.
- Tikhonov, AN, Leonov, AS, and Yagola, AG, 1998. Nonlinear Ill-posed Problems. London: Chapman and Hall; 1998.
- Ivanov, VK, Vasin, VV, and Tanana, VP, 2002. Theory of Linear Ill-Posed Problems and Its Applications.. Utrecht: VSP; 2002.
- Beilina, L, and Klibanov, MV, 2012. Aprpoximate Global Convergence and Adaptivity for Coefficient Inverse Problems. New York: Springer; 2012.
- Tikhonov, AN, Goncharsky, AV, Stepanov, VV, and Yagola, AG, 1995. Numerical Methods for the Solution of Ill-posed Problems. Dordrecht: Kluwer Academic; 1995.
- Nikolaeva, NN, and Yagola, AG, 2003. Error estimation of the reconstruction of symmetry velocity profile using Abel type integral equation. International Symposium on Inverse Problems in Engineering 2003, 18–21 February 2003, Abstracts. Nagano City, Japan: ISIP 2003; 2003. pp. 82–83.
- Vasilev, FP, 1980. Numerical Methods for Solving Extremal Problems, [in Russian]. Nauka, Moscow. 1980.
- Cook, Stephen, 2000. The P versus NP Problem. Paris: Clay Mathematics Institute; 2000.
- Garey, MR, and Johnson, DS, 1979. Computers and Intractability, a Guide to the Theory of NP-Completeness. San Francisco, CA: W.H. Freeman; 1979.
- Leonov, AS, 1995. Pseudo-optimal choice of parameter in the regularization method, Zh. Vychisl. Mat. Mat. Fiz. 35 (7) (1995), pp. 1034–1049.
- Yagola, AG, Leonov, AS, and Titarenko, VN, 2002. Data errors and an error estimation for Ill-posed Problems, Inverse Probl. Eng. 10 (2) (2002), pp. 117–129.
- Thomas, HC, Charles, EL, Ronald, LR, and Clifford, S, 2001. Introduction to Algorithms. Cambridge, MA: MIT Press; 2001. pp. 979–983.