Numerical solution of a 2D inverse heat conduction problem

Abstract

We consider a two-dimensional (2D) inverse heat conduction problem which is severely ill-posed, i.e. the solution (if it exists) does not depend continuously on the data. For obtaining a stable approximate solution, we propose an iterative regularization method from a new point of view. On the one hand, we give and prove some order optimal convergence results in the L²-norm and H^r-norm under both a priori and a posteriori stopping rules, on the other hand, we discuss the numerical aspect of the proposed method. Three numerical examples illustrate the behaviour of the regularization method.

Keywords:

• ill-posed problem
• inverse heat conduction
• Cauchy problem
• regularization
• iteration method

1. Introduction

Inverse heat conduction problem (IHCP) is a class of important inverse problems in several engineering contexts and many industrial applications 1. These applications 2 include the determination of thermal constants in some freezing and quenching processes, the estimation of surface heat transfer measurements taken within the skin of a re-entry space vehicle, the motion of a projectile over a gun barrel surface, the determination of aerodynamic heating in wind tunnels and rocket nozzles, and infrared computerized tomography.

The difficulty of the IHCP is its ill-posedness, i.e. arbitrarily ‘small’ differences in the data can induce arbitrarily ‘large’ errors in the computed surface temperature history solutions. Thus, it is impossible to solve the IHCP using classical numerical methods and requires special techniques, e.g. regularization strategies, to be employed 3,4.

Theoretical concepts and computational implementation related to the IHCP for one-dimensional models have been well discussed by many authors, and a number of solution methods have been proposed 5,6. However, the difficulties of the two-dimensional IHCP are more pronounced and few results are available. See, e.g. the articles by Bass and Ott 7, Baumeister and Reinhardt 8, Imber 9, Tu and Beck 10, Yoshimura and Ikuta 11 and Zabaras and Liu 12. The analytical solution which is applicable to 2D conduction systems for geometries of arbitrary shape was introduced by Imber 9 for the first time. However, he required the exact data. Most of the literature related to the numerical treatment of the 2D IHCP is based on different ways of combining finite elements realizations with Beck method 13. An elaborated and comprehensive exposition of the method was presented later by Baumeister and Reinhardt 8, and by Zabaras and Liu 12. A historical perspective can be found in 5.

This article, mainly motivated by papers 2,6,14,15, introduces an iteration regularization method for a 2D IHCP (the model can be found in Section 3) from a new point of view. As far as the 2D IHCP to be concerned, the references 2,6,15 gave the a priori choice of regularization parameter, and this article studies both a priori and a posteriori choices. Considering the iteration method, we make an important extension from the 1D IHCP 14 to 2D IHCP.

We give and prove the order optimal convergence results, in the sense of Tautenhahn 16, under both a priori and a posteriori stopping rules. Our estimates show that the constructed regularization solution is continuously dependent on the data and is an approximation of the exact solution of the two-dimensional IHCP in the presence of noisy data.

We also discuss the numerical implementation of the proposed method. Three numerical examples are given to illustrate the advantage and limitation of our method.

In the following, we give the primary preparation in Section 2. In Section 3, we describe the 2D IHCP and simply analyse its ill-posedness. Section 4 gives the iterative regularization method. Section 5 is some estimates, including the L²-estimate, H^r-estimate and H^r-estimate with a posteriori stopping rules. Section 6 is the numerical aspect of the proposed method. At last, we give a concluding remark in Section 7.

2. Primary preparation

We introduce the Sobolev space H^s(ℝ²) with s ≥ 0 17 according to H⁰ = L²(ℝ²), H^s = {f(y, t) ∈ L²(ℝ²) : ‖f‖_s < ∞} where (1) with the Fourier transform of f(y, t): (2) We shall denote ‖·‖ ≔ ‖·‖₀.

Let and q_k(λ) = 1 − λp_k(λ) = (1 − λ)^k with 0 ≤ λ ≤ 1, we have the following elementary results 14, p. 4] (3) (4) where (5)

Let E > 0 be a constant, δ > 0 small enough. Hereafter, we assume that δ < E, s ≥ r. We define the elliptic domain Ω_m ⊂ ℝ² as (6) Denote (7) (8) We have the following elementary results 6, p. 1066] (9) (10)

3. Formulated problem

Suppose that one wishes to determine the temperature in a slab where only one side of the slab can be measured. To determine the temperature in the remaining section of the slab one wants to solve a problem of the following type 2,5,13,15 (11) (12) with corresponding measured data function g^δ(y, t), (13) (14) (15) We wish to determine the temperature u(x, y, t) for 0 ≤ x < L from temperature measurements g^δ(y, t) at x = L. For simplifying the theoretical analysis, we have required the homogeneity of the conditions (3.1d) and (3.1e), while this is not necessary in numerical computation (one can refer to the reference 18).

Note that, although we seek to recover u only for 0 ≤ x < L, the problem specification includes the heat equation for x > L together with the boundedness at infinity. Since we can obtain u for x > L, we may think of u_x as also known at x = L. Therefore, naturally (3.1) is a Cauchy problem with the appropriate Cauchy data [u, u_x] given on the line x = L (cf. 8). The boundedness at infinity (3.1c) may be viewed as replacing the specification of u_x. Another way, if setting x = L − x′, one can get the Cauchy data [u, u_x] at the x = 0 through a simple transform. Please refer to 2,6.

In order to use the Fourier transform techniques, we extend the functions u(x, · , ·), g(· , ·), g^δ(· , ·) to be whole real (y, t) plane by defining them to be zero everywhere in {(y, t), y < 0, t < 0}, and consider them to be in . Taking Fourier transform to Equation (3.1a) with respect to y and t, one can easily get the solution of problem (3.1) 15 (16) or equivalently (17) where denotes the principal value of the square root, (18) Consequently, we can simply write the solution (3.2a) as (19) where and hereafter .

Now, we can also write the problem (3.1) as (20) where (21)

Since is unbounded with respect to variables ξ and τ for fixed 0 ≤ x < L, and we require , we see from (3.2) that the exact data function must decay rapidly as |ξ|, |τ| → ∞. Small errors in high-frequency components can blow up and completely destroy the solution for 0 ≤ x < L. But in practice, instead of the exact data g in problem (3.1), we only have the (physical) observed noisy data g^δ. Since we cannot expect the noisy data g^δ to have the same decay in frequency as the exact data g, the solution will not, in general, be in L²(ℝ²). So our problem is severely ill-posed and unstable. Consequently, it is impossible to solve the problem (3.1) using classical numerical methods and it requires regularization techniques 3,4.

4. Iteration method

In order to obtain a stable approximation of solution of problem (3.1), we propose the following iteration method (22) where λ = e^−La, and is the characteristic function of the domain Ω_m.

If setting the initial , we can get (23) where .

Remark 4.1

Formula (4.2) can be further rewritten as (24) which shares the similar idea with the Landweber iteration. Please refer to 3,4 for the classical theory on the Landweber iteration.

Remark 4.2

In formula (4.3), if directly setting λ = 1 (the possibility of setting will be discussed in Remark 5.2), we arrive at the Fourier method 6.

In this sense, our method (4.1) is an interesting combination of Landweber method and Fourier method. From Section 6, we shall know, from the viewpoint of numerical computation, that the proposed method (4.1) has the advantage of both Landweber method and Fourier method, and has the better numerical result than each of them.

Remark 4.3

If we understand the characteristic function according to in (4.3), the spectral cut-off technique plays the role of idea of modifying ‘kernel’ 6. If we understand according to , the cut-off technique plays the role of mollifying the measured data.

5. Error estimate

In this section we shall give some error estimates to show that the constructed regularization solution is stable and is a valid approximation of the exact solution. In the following we discuss the L²-estimate and H^r-estimate under the a priori choice of stopping iteration step k. We also consider the H^r-estimate under the a posteriori choice of stopping iteration step k.

5.1. L²-estimate

Let the noisy data g^δ satisfy ‖g^δ − g‖ ≤ δ, where δ > 0 is small enough. Define f(y, t) = u(0, y, t) and assume the a priori bound ‖f‖ ≤ E, where E > 0 is a constant. We replace the value m by in (2.6), when setting the parameter s = r = 0. Denote the iteration step , where [η] with square bracket denotes the largest integer less than or equal to η. Note that the problem (3.1) can be considered as two kinds of situations: 0 < x < L and x = 0 6,15. In this subsection, we discuss the L²-estimate of problem (3.1) for the case 0 < x < L under the a priori choice of stopping iteration step k. Actually, if assuming the additional smoothness, we can also obtain the convergence for the case x = 0 (see, e.g. 6, Theorem 3.2). The following two subsections devote the H^r-estimate for 0 ≤ x < L under both the a priori and a posteriori choices of stopping iteration step k.

Theorem 5.1

Let u(x, y, t) be the solution of problem (3.1) with the exact data g(y, t). Assume that whose Fourier transform is given by (4.1), is a regularization approximation of u(x, y, t) under the initial iteration . Let the noisy data g^δ satisfy ‖g^δ − g‖ ≤ δ, the a priori bound ‖f‖ ≤ E, the iteration step . Then, we have the error estimate for 0 < x < L (25) where .

Proof

Using the Parseval equality and triangle inequality, we have (26)

For the first term on the right-hand side of (5.2), using the formula (4.2), we get (27) consequently, note that inequality (2.3) with μ = 1, inequality (2.10) with , and ‖g^δ − g‖ ≤ δ, we have (28)

For the second term on the right-hand side of (5.2), note that (3.4), , we have (29) where we have also used formula (2.4) with v = 1, formula (2.10) (which leads to (ξ, τ) ∈ ℝ²∖Ω_m ⇒ a > m) with , and the a priori bound ‖f‖ ≤ E.

Now combining (5.2) and (5.4) with (5.5), we arrive at the statement of our theorem.▪

Theorem 5.1 shows that the iterative regularization solution (4.2) is a stable approximation of the exact solution (3.2) in the sense of L²-norm for fixed x ∈ (0, L). In the theory of inverse heat conduction problem, one can also obtain continuous dependence on the data at the ‘zero-point’ x = 0 through assuming additional smoothness and using a stronger norm. Please refer to 6, Theorem 3.2]. It is not difficult to verify that this can also be done, but we do not pursue this here.

5.2. H^r-estimate

Note that the error estimate in Theorem 5.1 only solves our problem for 0 < x < L and does not give any useful information on the continuous dependence of the solution at x = 0. This is common in the theory of ill-posed problems, if we do not have additional conditions on the smoothness of the solution at this boundary. To retain the continuous dependence of the solution at x = 0, instead of ‖f‖ ≤ E, we introduce the a priori assumption (30) where ‖f‖_s is defined according to (2.1).

Theorem 5.2

Let u(x, y, t) be the solution of problem (3.1) with the exact data g(y, t). Assume that whose Fourier transform is given by (4.1), is a regularization approximation of u(x, y, t) under the initial iteration . Let the noisy data g^δ satisfy ‖g^δ − g‖_r ≤ δ, the a priori bound ‖f‖_s ≤ E, the parameter s ≥ r ≥ 0, , the iteration step . Then we have the error estimate for 0 ≤ x < L (31)

Proof

Note that we cannot use the Parseval equality in the H^r-norm. However, we can still prove our theorem.

Using the triangle inequality, we get (32)

For the first term on the right-hand side of (5.8), following the process of (5.3), and note that ‖g^δ − g‖_r ≤ δ and , we have (33)

For the second term on the right-hand side of (5.8), following the process of (5.5), and note that ‖f‖_s ≤ E and the formula (2.9), we have (34)

Now, combining (5.8) and (5.9) with (5.10), we arrive at the statement of the theorem.▪

Remark 5.1

When s = r = 0, the estimate (5.7) is just the result of Theorem 5.1. However, if s > r ≥ 0, the estimate (5.7) is attractive. On the one hand, we obtained the convergence rate at x = 0, which is not included in Theorem 5.1, on the other hand, our result is optimal in the sense of Tautenhahn 16.

Remark 5.2

In Theorem 5.2, we choose . If the noise level δ is quite small, the stopping iteration step will be large according to formula (4.1). However, if we choose λ in (4.1) by λ = e^−La/n, n > 1, the iterative step can be greatly reduced to and the convergence rate in (5.7) is not changed. We note that the bound of error estimate may expand if the n becomes large. Thus an appropriate selection of n can greatly reduces the iterative steps for a certain noise δ and still gets a nice approximate solution. For the details one can also refer to 14, Remark 1] in which the authors considered a 1D sideways parabolic equation. We can also note that, if n → ∞, the parameter λ → 1, our iteration method (4.1) will become the Fourier method 6.

Remark 5.3

In our application ‖f‖_s is usually not known, therefore we have no exact a priori bound E and cannot choose the parameter m according to (2.6) and the iteration step . However, if selecting , and , we can also obtain the convergence rate (35) where the constant C = ‖f‖_s(1 + O(1)) depends on ‖f‖_s, L, r and s.

5.3. H^r-estimate with a posteriori stopping rule

This section is devoted to a posteriori choice of the iteration step k. We shall consider a discrepancy principle of Morozov. When discussing the a posteriori choice of regularization parameter, it is natural to assume that The requirement δ < ‖g^δ‖_r makes sense in the mean that, if the noisy data is less than the error level δ, the zero solution would be an acceptable approximation to the exact solution [3,4, Sections 2.5 and 2.6].

From (3.5) and (3.6), the problem (3.1) can be written as K(x)u(x, y, t) = g(y, t) and in the frequency domain we have . We shall set our stopping rule according to (36) where k* ≔ k*(δ, g^δ) is the stopping iteration step. That is to say, we stop our iteration when the left inequality of (5.12) is satisfied for the first time, i.e. 0 ≤ k ≤ k* − 1. The parameter γ is a fixed constant given in the following lemma.

Lemma 5.3

Assume that γ > θ is fixed, where the parameter , s ≥ r ≥ 0. Let g^δ be the perturbation data with ‖g^δ − g‖_r ≤ δ and ‖g^δ‖_r > γδ. Then the discrepancy principle (5.12) determines a stopping step k*(δ, g^δ) for our iteration method (4.1) under the initial iteration .

Proof

When k = 0, the right inequality of (5.12) obviously holds. We shall prove that the left inequality also holds with gradually increased k.

In the frequency domain, we have from (3.6) and (4.2) that (37) Furthermore, (38)

In Ω_m, we can estimate (39) where we have also used the formula (2.4).

In ℝ²∖Ω_m, we can estimate (40) where we have also used the formulae (2.9) and (2.10).

From above discussion, we have (41) Consequently, (42) where

Since and γ > θ, there exists some k₀ such that Let k* be the smallest integer satisfied above inequality. Consequently, we know that

Now, we can claim the following theorem.

Theorem 5.4

Let u(x, y, t) be the solution of problem (3.1) with the exact data g(y, t). Assume that whose Fourier transform is given by (4.1), is a regularization approximation of u(x, y, t) under the initial iteration . Let the noisy data g^δ satisfy ‖g^δ − g‖_r ≤ δ and ‖g^δ‖_r > γδ, the a priori bound ‖f‖_s ≤ E, the parameter with s ≥ r ≥ 0, the stop iteration step k* be chosen according to the stopping rule (5.12). Then we have the error estimate (43)

Proof

Using the triangle inequality, we have (44) Following the process of (5.9), one can easily get (45) For the second term on the right-hand side of (5.20), we have (46) Now, following the process of (5.10), one can easily get (47) As for (ξ, τ) ∈ Ω_m, we have (48) Moreover, for , we have (49) For the second term in (5.24), we have, if 0 ≤ x < L/2, (50) and if L/2 ≤ x < L, (51) Now combining (5.20)–(5.27), we arrived at the statement of our theorem.

6. Numerical aspect

In this section, we present several numerical examples intended to illustrate the behaviour of the proposed method. The tests were performed using MATLAB 7.0.

The numerical examples were constructed in the following ways. First, we selected the exact solution f(y, t) = u(0, y, t) of system (3.1) at x = 0, and computed the function u(L, y, t) = g(y, t) by solving a well-posed problem. Then, we added a normally distributed perturbation to the data function giving vectors g^δ. Finally, we solved the system (3.1) by the iterative method (4.1) (without loss of generality, we set the initial vector ).

Our numerical procedure for the proposed method was based on the 2D discrete Fourier transform (DFT) and computed with a fast Fourier transform (FFT) algorithm. In using the DFT, it is assumed that the sequence to be transformed is periodic. In our application it is not natural to presuppose that the data vectors are periodic. Thus, we shall make the data vector periodic before computation. Please refer to 19 for the process of periodization for the 1D case. Through a simple extension from 1D to 2D, one can obtain the periodization of 2D case. Please also see Figure 1.

Figure 1. (a) a data without extension; (b) the periodic data after extension.

Out of necessity the data function g(y, t) must be sampled over a finite domain, which, without loss of generality, we assume to be [0, 8] × [0, 8]. The data function is sampled equidistantly with the points 41 × 81. We also choose different points, e.g. 60 × 100, 161 × 321, … , to test our problem. The results are similar.

We obtain the noisy data g^δ through adding a random noise to g(y, t), i.e. (52) where ‘randn(·)’ is a Matlab function and .

In the following tests, we choose the parameter L = 0.5. We shall consider three kinds of examples: the smooth, the continuous but not smooth and the discontinuous.

Example 1

We consider a function which is smooth: (53)

We take the variance of the perturbations ϵ = 10⁻² in (6.1). To illustrate the advantage of the proposed method, we firstly display the separate effect of the parameters k, m, respectively, and then show their cooperative effect. The computed l² errors between u and at x = 0 are given in Tables 1–3.

Table 1: The l² error between u and with different k at x = 0, ϵ = 10⁻².

k	1	3	5	7	9	11	13
	0.0812	0.0245	0.0131	0.0161	0.0214	0.0260	0.0292

Table 2: The l² error between u and with different m at x = 0, ϵ = 10⁻².

m	1	3	5	7	9	11
	0.1048	0.0170	0.0160	0.0403	0.1041	0.1284

Table 3: The l² error between u and with different k, m at x = 0, ϵ = 10⁻².

	k = 3	k = 5	k = 7	k = 9	k = 11	k = 13	k = 15
m = 3	0.0278	0.0191	0.0176	0.0171	0.0170	0.0170	0.0171
m = 5	0.0239	0.0121	0.0090	0.0105	0.0119	0.0128	0.0130
m = 7	0.0244	0.0120	0.0113	0.0147	0.0174	0.0175	0.0195
m = 9	0.0243	0.0113	0.0126	0.0173	0.0186	0.0219	0.0261
m = 11	0.0246	0.0133	0.0148	0.0188	0.0221	0.0272	0.0275

Table 1 shows the change of the l² errors between u(0, y, t) and with different iterative numbers k for big enough parameter m. In this mean, one can understand the formula (4.2) as (54) which shares the similar idea of Landweber method 4, p. 43]. From Table 1 we know that, (i) the iterative number k plays the role of regularization parameter and (ii) the iterative method works well for problem (3.1) and the computed result is better when k = 5.

Table 2 illustrates the change of the l² errors between u(0, y, t) and with different parameters m for big enough k. In this mean, one can understand the formula (4.2) as (55) which is Fourier truncation method 6. The authors did not discuss the numerical aspect in the reference. From Table 2 we also know that, (i) the parameter m plays the role of regularization parameter, and (ii) the Fourier truncation method works well for problem (3.1) and the computed result is better when m = 5.

We give the l² errors between u and at x = 0 for different k and m in Table 3, from which we know that the proposed iterative method (4.3) is better than the (6.3), and is better than the Fourier truncation method (6.4). Especially the l² error is rather small and satisfactory when m = 5, k = 7.

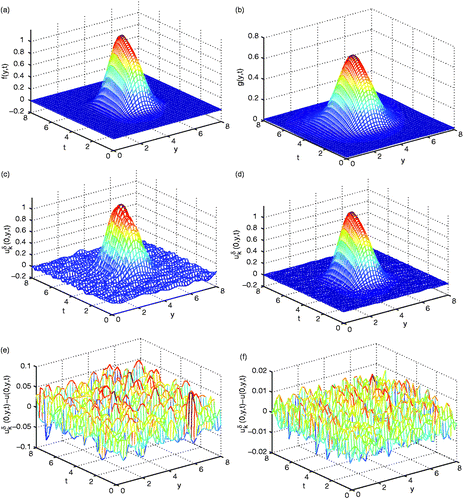
Moreover, we give the Figure 2 to show the computed effectiveness. The variances of perturbations ϵ = 10⁻², 10⁻³ are taken into account in (6.1). From these figures we know that the numerical results are satisfactory. Especially, the smaller the variance ϵ, the better the result is.

Figure 2. Example 1, (a) the exact data f(y, t) = u(0, y, t); (b) the computed function g(y, t) = u(0.5, y, t); (c) the computed with ϵ = 10⁻², m = 5, k = 7; (d) the computed with ϵ = 10⁻³, m = 7, k = 11; (e) the error between in (c) and u(0, y, t) in (a); (f) the error between in (d) and u(0, y, t) in (a).

Example 2

We consider a function which is continuous but not smooth: (56)

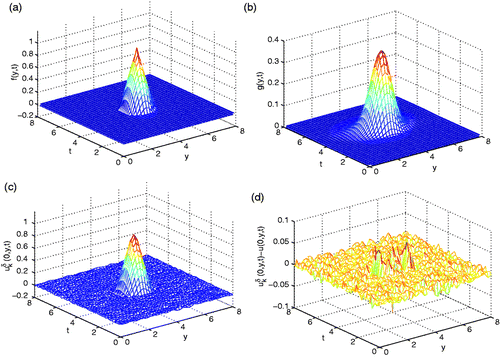
The numerical results are given in Figure 3, which shows that the computed result is good although it is not better than example 1.

Figure 3. Example 2, (a) the exact data f(y, t) = u(0, y, t); (b) the computed function g(y, t) = u(0.5, y, t); (c) the computed with ϵ = 10⁻³, m = 9, k = 15; (d) the error between in (c) and u(0, y, t) in (a).

Example 3

We consider a function that is discontinuous: (57)

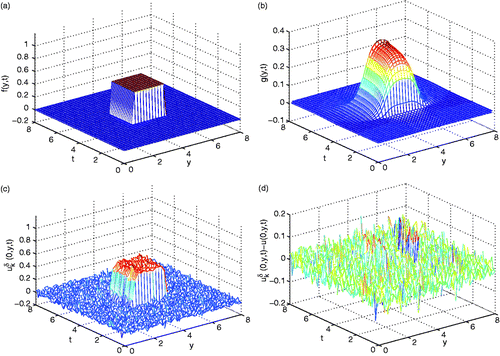
This example is challenging since it is discontinuous. However, Figure 4 shows that the computed result is also acceptable.

Figure 4. Example 3, (a) the exact data f(y, t) = u(0, y, t); (b) the computed function g(y, t) = u(0.5, y, t); (c) the computed with ϵ = 10⁻³, m = 18, k = 49; (d) the error between in (c) and u(0, y, t) in (a).

These tests illustrate that not only is the proposed method effective for the smooth example, but also it works well for the continuous and discontinuous examples.

7. Concluding remarks

Since the IHCP is of importance in some engineering texts and many industrial applications, many researchers have been involved in this topic. The 1D problems have been well investigated. However, there are so many works which are needed to investigate for the 2D problems, although many researchers have reported its difficulties.

In this article, we successfully extend an iterative regularization method from the 1D IHCP 14 to a 2D IHCP. The method can be considered as an interesting combination of Landweber iteration and Fourier method. Consequently, the method includes the advantages of both Landweber iteration and Fourier method. We gave and proved the order optimal convergence results in L²-norm and H^r-norm under the a priori stopping rule of the iteration step. We also considered the order optimal convergence results in H^r-norm after studying the a posteriori stopping rule of the iteration step using the discrepancy principle of Morozov.

The numerical experiments show that the proposed method has a better numerical result than both Landweber method and Fourier truncation method. Three numerical examples illustrate how to implement the method. Some tables and figures demonstrate that the method is effective for the 2D IHCP.

Acknowledgements

The authors (particularly the first author) are deeply indebted to the anonymous referees for their very careful reading and valuable comments and suggestions which immensely improved the previous version of our manuscript, especially corrected the proof of Lemma 5.3 and improved the convergent rate of the error estimate in Theorem 5.4. The first author is partly supported by the Natural Science Foundation of China (NSF) (Nos. 11001126 and 10971096) and a Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions. The second author is partly supported by the NSF of China (No. 11126187) and the Fundamental Research Funds for the Central Universities (No. K50511700002),