An evolution of the back and forth nudging for geophysical data assimilation: application to Burgers equation and comparisons

Abstract

We study in this article an improvement to the back and forth nudging (BFN) method for geophysical data assimilation. In meteorology or oceanography, the theoretical equations are usually diffusive free, but diffusion is added into the model equations in order to stabilize the numerical integrations and to take into consideration some subscale phenomena. We propose to change the sign of the diffusion in the backward nudging model, which is physically consistent and stabilizes the backward integration. We apply this method to a Burgers equation, study the convergence properties and report the results of numerical experiments. We compare the quality of the estimated initial condition with two other data assimilation techniques that are close from the algorithmic point of view: a variational method, and the quasi-inverse linear method.

Keywords:

• data assimilation
• back and forth nudging
• Burgers equation
• inverse diffusion

AMS Subject Classifications::

• 35L03
• 35Q86
• 65M32
• 86-08
• 86Axx

1. Introduction

Data assimilation is the ensemble of techniques combining via numerical methods the mathematical information provided by the equations and the physical information given by the observations, in order to retrieve the state of a system. It makes it possible to answer a wide range of questions such as: optimal identification of the initial state of a system, and then reliable numerical forecasts; systematic identification of error sources in the models; optimization of observation networks; extrapolation, using a numerical model, of the values of non-observed variables. Thus, data assimilation is increasingly used in the community of geophysical sciences, in relation with mathematicians. The identification of the state, or of the initial condition, of a geophysical system (e.g. atmosphere or oceans) is a typical inverse problem, as the goal is to retrieve the system state from sparse and noisy observations.

There are two main classes of data assimilation methods, the first based on estimation theory (sequential assimilation) and Kalman filters, and the other based on an optimal control theory (variational assimilation) 1,2. The most sophisticated variational method, currently used in many centres of operational forecast, is the four-dimensional variational (4D-VAR) algorithm 3. It consists of assimilating all the available information (contained both in the model and the observations) during the work (or assimilation) period. The problem of identifying the state of a system at a given time can then be written as the minimization of a criterion measuring the difference between the forecasts of the model and the observations of the system in the given time window. A disadvantage of the 4D-VAR algorithm is its quite difficult implementation, because it requires both the adjoint of the physical model and a powerful minimization algorithm. The spearhead of sequential methods, which are also operational (but more marginally than 4D-VAR), are Kalman-based filters. The Kalman filter is designed to provide, for each time step, the optimal estimate (of variance of minimal error) of the system state by using only the estimates of the state and the last observations. It alternates propagation steps (with the physical model) and correction steps (using the observations) of the state and of its error statistics.

Nudging can be seen as a degenerate, oversimplified form of the Kalman filter. It consists of applying a Newtonian recall of the state value towards its direct observation. The standard nudging algorithm, which initially appeared in meteorology 4, is the first data assimilation method used in an operational way in oceanography 5–7, and it has also been applied to a mesoscale model of the atmosphere with synoptic-scale data 8. Some recent studies have shown that it is possible to determine in a systematic way the optimal weighting coefficients of the recall force to the observations, and then nudging is equivalent to the Kalman filter, or in a variational form, to 4D-VAR 9–11. One of the main disadvantages of the sequential data assimilation methods is that they cannot, at a given time, take into account the future observations. They do not improve the estimation of the initial condition of the system.

A simple idea, allowing at the same time the improvement of the estimation of the initial condition and the assimilation of future observations, consists of applying a second time the nudging method, but on the backward (in time) model, using the estimation of the final state (obtained by the forward assimilation) as a new initial guess. Thus, at the end of this process, one obtains a new estimation of the system state at the initial time. Auroux and Blum 12 proposed an original approach of backward and forward nudging (or back and forth nudging (BFN)), which consists of initially solving the forward equations with a nudging term, and then using the final state thus obtained as an initial condition to solve the same equations in a backward direction with a feedback term (with the opposite sign compared with the feedback term of forward nudging). This process is then repeated in an iterative way until convergence of the initial state is achieved.

The presence of diffusion (or other irreversible phenomena) in the model equation generally makes the backward problems ill-posed (the Laplace equation, or heat equation, is a very good example) 13. However, it is possible to stabilize backward integrations, thanks to the nudging corrective term, and BFN algorithm has been shown to be competitive with the 4D-VAR method 12,14.

In this article, we propose to study an evolution of BFN algorithm, in which the diffusion contained in the model equation is treated apart from the rest of the physical terms. In an oceanographic or meteorological framework, the theoretical equations are usually diffusive free (e.g. Euler's equation for meteorological processes), and diffusion is added into the model equations in an artificial way, with two different goals: stabilize the numerical integration of the equations and take into consideration some subscale phenomena. In such situations, when considering the backward integrations, it is physically consistent to consider the backward theoretical model (i.e. diffusive free), in which the diffusion is then added in a similar way to the direct numerical model. In other words, all the physical processes are reversed in time (advection, Coriolis force, etc.) except the diffusion one.

In Section 2, we briefly recall the standard BFN algorithm and we present its evolution in the case of diffusive equations. Then we apply this new algorithm to Burgers equation, and compare it with the standard BFN algorithm. Finally, we report the results of numerical experiments in Section 3, including comparisons between the standard BFN algorithm, its evolution to diffusive models and the 4D-VAR algorithm or the quasi-inverse method.

2. BFN algorithms and application to Burgers equation

2.1. BFN algorithm

We first briefly recall the BFN algorithm 12. We assume that the model equations have been discretized in space, and the time continuous model then satisfies a dynamical equation of the form: (1) with an initial condition X(0) = x₀. Let Y_obs(t) be the observations of the system, and H the observation operator allowing us to compare the observations Y_obs(t) with the corresponding quantity H(X(t)) deduced from the state vector. The BFN algorithm is an iterative algorithm, made of forward and backward integrations of the model equation with a feedback term to the observations. At iteration k, the equations are: (2) for k ≥ 1, and with . K and K′ are the nudging gain operators (or matrices) for the forward and backward integrations, respectively. Note that the feedback term has an opposite sign in the backward integration, as it is solved backwards in time.

2.2. Application to the Burgers equation

We consider the following Burgers' equation over a one-dimensional cyclic domain: (3) with a given initial condition u(x, 0). This equation can be seen as a very simple meteorological model, as it can be derived from a one-dimensional projection of a 3D atmospheric model on a circle of latitude. The notations are the following: x represents the distance, e.g. around the 45°N constant-latitude circle, ν ≥ 0 is the diffusion coefficient and u is the streamfunction. After renormalization, we can consider this equation on a cyclic space domain [0; L[, or on an interval [0; L], and on the time period [0; T]. In the following, we will consider both the viscous Burgers equation (Equation (3) with ν > 0) and the non-viscous Burgers equation (when ν = 0).

2.2.1. BFN algorithm

If we apply the standard BFN algorithm to Equation (3), we obtain the following equations: (4) for k ≥ 1, ũ₀(x, 0) = u₀(x, 0), and where K (resp. K′) is the forward (resp. backward) nudging gain and H is the observation operator.

If K and K′ are proportional, and if the forward and backward trajectories u_k and ũ_k converge towards the same limit trajectory u_∞, then it is clear by making linear combinations of Equations in (4) such that u_∞ satisfies the model Equation (3), and perfectly matches the observations: H(u_∞) = u_obs. But it seems from numerical experiments that forward and backward trajectories do not converge towards exactly the same limit, except for some linear transport equations. However, this remark gives a formal idea of the way the BFN algorithm satisfies both the model equations and the fitting to the observations.

2.2.2. BFN2 algorithm

We now present the new version of the BFN algorithm. The non-viscous Burgers equation is known to create shocks in finite time, and oscillations in numerical experiments for many discretization schemes. Inviscid hyperbolic equations are not easy to solve numerically, and a numerical scheme is often either diffusive or unstable. For this reason, it can be interesting to add a small diffusion term in order to stabilize the numerical integration. Reversing time in the non-viscous Burgers equation simply consists in reversing the advection. But, then, it is also natural to add a small diffusion term into the backward equation in order to stabilize it. We refer the reader to 15 for a discussion about the physical role of such a term (mainly for modelling subscale phenomena), and the possibility to change its sign in the backward model.

Then, BFN2 algorithm is simply the application of the nudging to this situation: (5) The only difference with Equation (4) is the sign of the diffusion term in the backward model. The physical part of the model (i.e. the advection) is kept unchanged, while both diffusion and nudging have an opposite sign (in comparison with the forward equation), in order to stabilize the numerical integration and to have a feedback to the observations.

The main advantage of this new algorithm is that both forward and backward equations are mathematically well-posed in the presence of diffusion, whereas the backward equation in the standard BFN algorithm might be ill-posed. The solution of the backward equation might indeed not depend continuously on the forward solution. Note also that if ν = 0, both algorithms are equivalent, and the non-viscous Burgers equation is then reversible (at least as long as there is no shock) 13.

If K = K′ and if the forward and backward trajectories u_k and ũ_k converge towards the same limit trajectory u_∞, then, by adding the two equations of (5), u_∞ satisfies the model Equation (3) without viscosity. Moreover, the limit trajectory is also a solution of the following equation: (6) which is a well-known denoising equation in signal processing. It shows that the solution converges towards the observations regularized by the diffusion operator 16.

This formal statement is true for very simple linear transport equations (at least with constant transport parameters) (see, e.g. 15), but it has not been proven yet for the Burgers equation, and it might be false. But it gives a formal idea about how the BFN2 algorithm works, and about a possible link between the solution at convergence and the observations.

3. Numerical experiments

3.1. Discretization and numerical parameters

The direct Equation (3) has been discretized in time and space in the following way: (7) with 0 < j < J and 0 ≤ n < N. represents the discrete solution at a time step n, and at a grid point j: , with x_j = j × dx and tⁿ = n × dt. J and N are the number of grid points (in space) and the number of timesteps, respectively, and then and .

Note that the diffusion is treated implicitly, in order to ensure the numerical stability of the scheme. The nonlinear term is explicit in order to simplify the numerical integration. The discretization has been numerically validated on an analytical solution of Burgers' equation.

The nudging term is treated explicitly, and in order to get the discrete nudging equation, one simply has to add the following term to Equation (7) (8) at observation locations and observation times (see below for details about the observation operator). For the backward nudging equation, we only change the sign of some of the terms (if the backward equation is written in a forward way, then the sign of both nonlinear transport and diffusion terms have to be changed), and keep the other terms unchanged. The diffusion is still treated implicitly, the nonlinear term is treated explicitly, still with a Lax–Friedrichs scheme and the nudging term is also treated explicitly. But then, numerical instability might come from the anti-diffusion term (diffusion term with the wrong sign), and if there was no other term in the model, there would not exist any stable discretization of this equation, as it is intrinsically unstable (the discretization scheme does not have any role in this issue). The nudging term helps in controlling the numerical scheme, but the theoretical stability has not been studied yet, because of the nonlinear term. Note that the BFN2 does not have this issue, as the diffusion has the good sign in the backward integration, and any positive nudging coefficient leads to stable systems, just like the Lax–Friedrich scheme for a standard Burgers equation 17.

The boundary conditions are , ∀0 ≤ n ≤ N, and the initial condition is , ∀0 < j < J.

In all the following numerical experiments, we will consider twin experiments: a reference initial condition is set: (9) Then the direct model (3) is solved, and some data are extracted from the corresponding trajectory u_true. These data are then noised for some experiments (and not for some others), and provided as observations to the data assimilation algorithms.

We assume that some observations u_obs of the solution u are available every n_t time steps and every n_x grid points. We can then easily define an observation operator H, from the model space to the observation space, as an extraction of one out of every n_x values of the variable u. This operator is clearly linear, and allows us to compare a model solution with the observations. Note that there is no apparent difficulty in considering more complex or nonlinear observation operators. Both forward and backward nudging equations handle nonlinearities. However, in order to get the correction (or innovation) term back to the state space, one may consider the adjoint (i.e. linearized and transposed) observation operator.

For all the algorithms, we will study the error on the identification of the initial condition. As we only work with simulated data (extracted from a reference trajectory), it is easy to compare the identified solution with the true state, by considering the relative RMS error: (10)

As all the algorithms we consider in this article aim at identifying the initial condition of the system, Equation (10) is clearly the main criterion of efficiency of the schemes. Then, for forecast, we use the direct model initialized with the identified initial states, and then we can compare the quality of the forecasts (both pre-forecasts, i.e. during the assimilation window, and forecasts themselves, after the end of the assimilation window).

The stopping criterion used for the convergence of the algorithm is the following: (11) In the following experiments, we will detail the number of iterations needed to achieve the convergence of the algorithm (i.e. for which the difference between two consecutive iterates is relatively small).

All algorithms are initialized with the background state, which is set to 0.

3.2. Burgers equation in the absence of shock

We first consider the (viscous) Burgers equation in the absence of shock. Either there is some diffusion, or the time window is short enough to prevent a shock.

In the following numerical experiments, the length of the time window is T = 1 and the length of the space domain is L = 2π. The number of time steps is J = 200 and the time step is dt = 0.005. The number of grid points in the space discretization is N = 314 and the space step is dx = 0.02. The values of the diffusion coefficient ν and the nudging parameters K and K′ will be given for each experiment.

3.2.1. Full and unnoisy observations

We assume that there is no diffusion for the generation of the observations: ν = 0 in (3). Then, data are extracted at every grid point and time step and no noise is added. This is a fully idealized situation, in which we have full and unnoisy observations.

We can study in this situation the convergence of BFN and BFN2 algorithms, with or without diffusion in the models. As we have seen, the two algorithms are equivalent if ν = 0, so that there are three different cases.

First, we set ν = 0 in BFN algorithm (4) (or equivalently in (5)), assuming that the model used for data assimilation is exactly the model used for generating the observations.

But we can also assume that there is a small diffusion term in the model used for data assimilation, and we can apply both BFN and BFN2 algorithms to this situation. We can then consider both (4) and (5), with ν = 0.001.

Table 1 shows the corresponding results, for the three schemes (BFN without diffusion, and BFN and BFN2 with diffusion) in the case of full and unnoisy observations. For each simulation, Table 1 gives the values of the nudging parameters K and K′, the number of iterations needed to achieve convergence, and the relative root mean square (RMS) error at convergence.

Table 1. Comparison between the BFN and BFN2 algorithms in the case of full and unnoisy observations on Burgers equation without shock.

	K	K′	No. iterations	Relative RMS (in %)
BFN with ν = 0	1	2	4	0.22
BFN with ν = 0.001	2	4	3	0.29
BFN2 with ν = 0.001	0.4	0.8	7	0.58

In these experiments, the nudging coefficients K and K′ are the minimal values that ensure the convergence of the algorithm. Indeed, if they are too small, the presence of diffusion in the model makes the backward integration unstable. For the BFN algorithm in the case of the Burgers equation, generally K′ is taken as being twice the value of K in order to ensure a stable backward integration. Unsurprisingly, the BFN2 algorithm needs smaller coefficients to converge than the standard BFN algorithm (and even K′ could be set equal to K). This is due to the fact that both forward and backward equations are stable in the BFN2 algorithm, even with a null nudging coefficient, whereas in the BFN algorithm, the nudging term is required for the stabilization of the backward integration. However, as the BFN somehow needs larger backward nudging coefficients K′ (usually twice the value of K), we still consider K′ = 2K for BFN2 in order to make a fair comparison between BFN and BFN2 schemes. With smaller nudging coefficients, the BFN2 algorithm may need some more iterations to converge, as the feedback to the observations is smaller, but K′ = K is a good choice for BFN2, as the forward and backward equations are now totally consistent. All the three experiments lead to a small relative error (less than 1%).

Figure 1 shows the evolution of the relative RMS error along the iterations versus time for BFN algorithm with no viscosity and BFN2 algorithm with ν = 0.001. The parameters are the same as in the first and third experiments of Table 1. We can see from these figures the asymptotic (and exponential) decrease of the error during both forward and backward integrations, for both algorithms. The rate of decay of the error is smaller in the case of the BFN2 algorithm, but this is due to smaller nudging coefficients.

Figure 1. Evolution of the relative RMS error along the iterations versus time for full unnoisy observations; (a) BFN with ν = 0, K = 1 and K′ = 2; (b) BFN2 with ν = 0.001, K = 0.4 and K′ = 0.8.

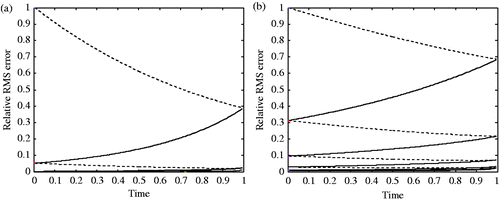
We now use the same nudging coefficients for all three experiments, in order to compare the efficiency of the algorithms with similar parameters. Table 2 gives similar results as Table 1, with K = 2 and K′ = 4 (in order to ensure the convergence of all schemes). For similar nudging coefficients (i.e. for a similar feedback to the observations), the solution identified by the BFN2 algorithm is better than by BFN algorithm (with diffusion), and similar to the diffusion-free experiment.

Table 2. Comparison between the BFN and BFN2 algorithms in the case of full and unnoisy observations on Burgers equation without shock, with the same nudging coefficients for all experiments.

	K	K′	No. iterations	Relative RMS (in %)
BFN with ν = 0	2	4	3	0.11
BFN with ν = 0.001	2	4	3	0.29
BFN2 with ν = 0.001	2	4	3	0.11

3.2.2. Sparse and noisy observations

We now consider sparse and noisy observations. We assume that the observations are available every n_x grid points in space, and every n_t time steps. Moreover, some white Gaussian noise is added to the data, the relative noise level being 15%. As in most geophysical data assimilation experiments, the observations are interpolated in space, but not in time. More precisely, nothing is done in time, and the feedback term is added only at the time steps for which observations are available. In space, each observation is spread over the neighbouring grid points. The influence of an observation decreases with the distance to the observation point. This ensures that the feedback will not produce shocks in the solution.

Tables 3 and 4 show the results of the three algorithms (BFN without diffusion, and BFN and BFN2 with a small diffusion coefficient) in the case of sparse (in time and space) observations, with or without noise. In Table 3, the nudging coefficients have been set to the minimal value ensuring the convergence of the algorithm, whereas in Table 4, all schemes use the same nudging coefficients. We can see in Table 3 that BFN2 converges towards a slightly better solution in the case of sparse and noisy observations. But the main point is that it needs smaller nudging coefficients, compared to the BFN scheme, and then one can keep a reasonable equilibrium between the physical model and the feedback to the observations. This latter point is still due to the fact that the backward integration is intrinsically stable, thanks to the diffusion operator.

Table 3. Comparison between the BFN and BFN2 algorithms in the case of discrete (and noisy) observations on Burgers equation without shock.

		nx = 4	nx = 10	nx = 10
		nt = 4	nt = 10	nt = 10
		Unnoisy	Unnoisy	Noisy (15%)
BFN with ν = 0	No. iterations	2	2	2
	Relative RMS (%)	0.11	0.15	7.70
	K	15	43	52
	K′	30	86	104
BFN with ν = 0.001	No. iterations	3	3	3
	Relative RMS (%)	0.15	0.34	8.62
	K	17	45	55
	K′	34	90	110
BFN2 with ν = 0.001	No. iterations	6	4	3
	Relative RMS (%)	0.48	0.34	7.28
	K	2	10	18
	K′	4	20	36

Table 4. Comparison between the BFN and BFN2 algorithms in the case of discrete (and noisy) observations on Burgers equation without shock, with the same nudging coefficients for all experiments.

		nx = 4	nx = 10	nx = 10
		nt = 4	nt = 10	nt = 10
		Unnoisy	Unnoisy	Noisy (15%)
BFN with ν = 0	No. iterations	2	2	2
	Relative RMS (%)	0.06	0.09	7.54
	K	17	45	55
	K′	34	90	110
BFN with ν = 0.001	No. iterations	3	3	3
	Relative RMS (%)	0.15	0.34	8.62
	K	17	45	55
	K′	34	90	110
BFN2 with ν = 0.001	No. iterations	2	2	2
	Relative RMS (%)	0.05	0.06	7.99
	K	17	45	55
	K′	34	90	110

Considering smaller nudging coefficients is interesting: from the numerical point of view, large nudging coefficients may lead to instability, as a large correction around observation locations may not be consistent with other grid points, leading to gravity waves, or spikes in the trajectory, before the solution returns to a more physical state. From a more physical point of view, we can assume that the model is not wrong at all, and then it is better to correct it with a small term than a large one. Note that the nudging coefficient should be small compared to the physical terms of the model, but not compared to the diffusion term, which was added for numerical reasons. We can also see in Tables 3 and 4 that all methods still have a good behaviour in the case of sparse observations. In this case, the nudging term is not very large, as its influence is restricted to the observation locations and times. In the case of sparse observations, the nudging term is much smaller than the physical terms.

Note that it is possible to increase the diffusion in the BFN2 algorithm. This operator indeed smoothes the noisy observations, and for instance, with ν = 0.01, the relative RMS error produced by the BFN2 algorithm is 6.05% in the case of noisy and sparse observations (to be compared with 7.28% in Table 3 when ν = 0.001).

The BFN2 algorithm has two advantages: first, the diffusion has a smoothing effect on the noisy observations; and the well-posedness of the backward integration allows us to consider smaller nudging coefficients, which is physically and numerically interesting. Finally, note in Table 3 that BFN with diffusion is the worst case. This is due to the fact that the backward integration is unstable (backward diffusion operator), even if it is stabilized by the nudging feedback.

3.3. Burgers equation with shock

We now study the interesting case, with the presence of shocks in Burgers equation. We increase the length of the assimilation window in order to let the shock appear. We now consider T = 10, and the time step is now dt = 0.02. The diffusion coefficient is ν = 0.02. It allows us to stabilize the numerical integration of the direct model during the creation of a shock.

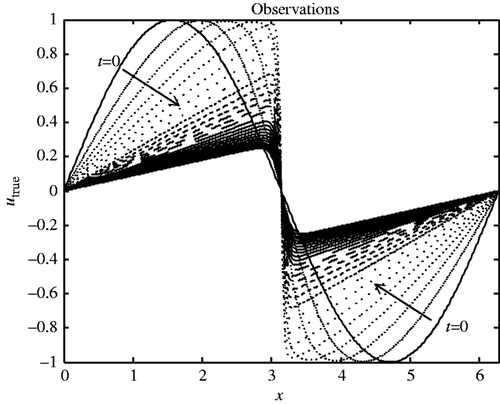
Figure 2 shows the evolution in time of the solution u_true (represented as a function of the space variable x). At the initial time, it is a sine function, while at time T = 10, it has a Z shape with the explosion of the derivative near x = π. The arrows represent the time evolution of the solution.

Figure 2. Evolution in time (arrows) of the reference solution u_true (as a function of the space variable x).

Increasing the length of the assimilation window will oblige us to consider larger nudging coefficients, in order to stabilize the backward model during a longer time. As there is some diffusion in the direct model, we will consider only two different approaches: BFN and BFN2 algorithms, with the same diffusion as in the direct model. Recall that the only difference between these two algorithms is the sign of the diffusion in the backward nudging equation.

3.3.1. Full and unnoisy observations

Table 5 gives the relative RMS error of the solution identified by BFN and BFN2 algorithms, with the same diffusion coefficient as in the direct model used for generating the observations (ν = 0.02).

Table 5. Comparison between the BFN and BFN2 algorithms in the case of full and unnoisy observations on Burgers equation with shock.

	K	K′	No. iterations	Relative RMS (in %)
BFN with ν = 0.02	100	200	2	0.22
BFN2 with ν = 0.02	5	10	2	0.47
	100	200	2	0.10

The first interesting point is that the BFN algorithm requires huge nudging coefficients to converge (i.e. to stabilize the backward integration), because of the unstable diffusion operator in the backward model. The values of K and K′ (of the order of 100) are not physically acceptable, and the BFN algorithm mainly fits the observations, and does not take into account the model.

The BFN2 is much more interesting, as the backward integration is intrinsically stable (thanks to the opposite diffusion operator in comparison with the standard BFN), and then much smaller nudging coefficients can be used. As shown in Table 5, one can use this algorithm to precisely estimate the initial condition, while keeping the equilibrium between the model and the observations (relatively small nudging coefficients).

Also note that for the same nudging coefficients as the BFN algorithm, the BFN2 algorithm gives better results, even if the algorithm mainly uses the unnoisy observations and almost no more the model itself.

3.3.2. Sparse and noisy observations

We now consider sparse and noisy observations, as in the previous section (the Burgers equation without shock).

Table 6 shows the relative RMS error of the BFN2 algorithm in the case of sparse (and noisy) observations. It was not possible to make the standard BFN algorithm converge in these situations, as the assimilation window is too long and the backward model is unstable.

Table 6. Results obtained with the BFN2 algorithm in the case of discrete (and noisy) observations on Burgers equation with shock.

		nx = 4	nx = 10	nx = 10
		nt = 4	nt = 10	nt = 10
		Unnoisy	Unnoisy	Noisy (15%)
BFN2 with ν = 0.02	No. iterations	3	3	3
	Relative RMS (%)	1.13	1.22	6.97
	K	8	20	20
	K′	16	40	40

The BFN2 algorithm still converges in a few iterations, and the identification of the initial condition is very good: less than 7% of the relative error in the case of sparse and noisy observations, and nearly 1% with sparse (but unnoisy) observations.

It shows that first, BFN2 is much less sensitive to the number of observations than the standard BFN algorithm. It is indeed due to the fact that in the new algorithm, with the reversed diffusion operator, both forward and backward equations are intrinsically stable. And then, in the absence of observations, the solution is not corrected by the feedback term but it does not diverge, as in the standard BFN algorithm.

The second interesting point is that the diffusion operator smoothes the data, both in forward and backward modes in the BFN2, instead of only in forward modes in BFN (and even there is an anti-diffusion operator in the backward mode), and then the BFN2 algorithm is less sensitive to the presence of observation noise. The solution at convergence is then more accurate and less noisy with BFN2.

We can conclude that on small time windows, both algorithms are roughly equivalent, but on longer assimilation windows, using an opposite diffusion operator in the backward integration makes the algorithm much more efficient, robust to noise and to sparsity of the observations.

4. Comparison with other data assimilation schemes

We now compare the BFN2 algorithm with other standard data assimilation schemes. The first one that we consider is the common variational data assimilation, known as 4D-VAR 3. In this case, we will call it VAR, as the original problem is only 1D, and then the assimilation scheme would be a 1 + 1D (one dimension in space and one in time). We will also compare the BFN2 algorithm with the quasi-inverse linear (QIL) method developed by Kalnay et al. 18,19. Indeed, the QIL uses a reversed (or opposite) diffusion operator in the backward model.

4.1. Comparison with the VAR algorithm

In this section, we compare the BFN2 algorithm with the standard variational data assimilation, VAR. The VAR algorithm is one of the most used data assimilation schemes, as it gives very precise results. But its numerical implementation is very expensive as it requires the adjoint model and an efficient optimization scheme.

It is based on the minimization of a cost function measuring the quadratic distance between the observations and the corresponding quantities computed by the numerical model 3. More precisely, we consider the following cost function: (12) where H is the observation operator. In our experiments, H is either the identity matrix in the case of full observations, or an extraction of one every n_x values of the solution u in space. If the observations are discrete in time, then the integral in time is discretized as a sum over the observation time steps.

For a given initial condition u₀, one solves the direct model (3) (with the diffusion term) in order to compute the trajectory u(x,t), and then the cost function J measures the distance between this solution and the observations. The goal is to minimize J and to find the best initial condition.

As the dimension of the control space is rather small, and as we initialize the minimization with the background state (as in BFN and BFN2 algorithms), there is no need for a regularization term (e.g. a feedback to the background state) to ensure an efficient minimization process. Then, as we only consider the minimization of the distance to the observations, and as we added white and uncorrelated noise to the observations, the covariance matrix of observation error R is proportional to the identity matrix, and then there is no need to incorporate it in Equation (12). If one includes the background term in the cost function, then the results will be slightly degraded, as the background state is wrong and the background covariance matrix may not be well known.

One can obtain the gradient of the cost function by simply solving once the adjoint model, backwards in time. In order to have the exact gradient of the cost function, we take the adjoint of the discrete direct model (7). From the value of the cost function and of its gradient, an optimization algorithm deduces the next estimation of the initial condition, and this process is repeated iteratively.

The VAR and BFN2 algorithms can first be compared from a methodological point of view. They both indeed consist of iterations, alternating forward and backward integrations. But we can already see that the BFN2 algorithm is cheaper, as the backward model is simply the nonlinear direct model, but solved backwards in time, and with an opposite diffusion term, whereas in the VAR algorithm, the model solved backwards in time is the adjoint model. The numerical adjoint model can be difficult to compute in realistic models, as one has to first linearize the direct model. Moreover, the VAR algorithm needs an efficient optimization algorithm in order to minimize the cost function.

The numerical comparison between these two algorithms is performed as follows. We consider a long assimilation window: T = 10. The time step is dt = 0.02. The space step is dx = 0.02 and the diffusion coefficient in the direct model (3) is ν = 0.02.

In all the following, both BFN2 and VAR algorithms are run until convergence, and we give for each experiment the number of iterations to convergence.

4.1.1. Full and unnoisy observations

We first compare BFN2 and VAR algorithms in the case of full and unnoisy observations.

Table 7 shows a comparison between the BFN2 and VAR algorithms in the case of full and unnoisy observations. The first point is that BFN2 converges much faster than VAR. But the identification of the initial condition is better with VAR, as it has recovered the initial condition with less than 0.1% relative error. The best result obtained with BFN2 is shown at the end, with larger nudging coefficients (note that in this case, BFN2 is nearly equivalent to simply replacing the solution by the observations). But for standard nudging coefficients, the identification is still good, with less than 0.5% error in two iterations (which is nearly the cost of one iteration of VAR, as the adjoint requires a little more computing time than the backward nudging integration).

Table 7. Comparison between the BFN2 and VAR algorithms in the case of full and unnoisy observations on Burgers equation with shock.

	No. iterations	Relative RMS (in %)
VAR	27	0.039
BFN2 with K = 5, K′ = 10	2	0.47
BFN2 with K = 20, K′ = 40	2	0.18

4.1.2. Discrete and noisy observations

We now study the more realistic case in which the observations are not always available, and may be noisy.

Table 8 shows a comparison between the BFN2 and VAR algorithms in the case of sparse (and noisy) observations. We still see that BFN2 converges much faster than VAR, as it only needs two iterations to converge. Then, the point is that when the observations become sparse, and possibly noisy, the results of BFN2 are much less degraded than for the VAR method. Indeed, even with sparse and noisy observations, the relative error is 3.5% with BFN2 (a few times more than in the case of full unnoisy observations), whereas the identified solution by the VAR method has more than 10% of relative error, to be compared with less than 0.1% in the perfect case.

Table 8. Comparison between the BFN2 and VAR algorithms in the case of sparse and noisy observations on Burgers equation with shock.

		nx = 4	nx = 10	nx = 10
		nt = 4	nt = 10	nt = 10
		Unnoisy	Unnoisy	Noisy (15%)
VAR	No. iterations	18	20	15
	Relative RMS (%)	0.49	1.64	10.74
BFN2	No. iterations	2	2	2
	Relative RMS (%)	0.34	0.69	3.50
		(K = 30, K′ = 60)	(K = 40, K′ = 80)	(K = 10, K′ = 20)

We can deduce that the BFN2 method is much less sensitive to the presence of noise or to the sparsity of the observations than the VAR algorithm. Indeed, nudging can be seen as a degenerated Kalman filter, and at each iteration of BFN2, the observations are filtered twice (in both forward and in backward modes), and also smoothed thanks to the diffusion term. Both filtering and smoothing explain why this scheme is not very sensitive to the observation noise.

4.1.3. Forecast

As the usual aim of data assimilation is to provide reliable forecasts of the evolution of the system, we will now study the quality of the forecasts corresponding to the identified solutions. We simply run the direct model (3) (without any nudging term), initialized with the identified solutions by BFN2 and VAR algorithms, and we study the forecast error as a function of time, after the end of the assimilation window. All the following figures show the pre-forecast error from time 0 to 10, and then forecasts after time 10 (end of the assimilation window).

We will not consider the case of full and un-noisy observations in this experiment, as it is not very realistic, and the identification error is very small, leading to extremely good forecasts. So we directly compare the algorithms in the case of sparse and unnoisy observations. Figure 3 shows the forecast error for BFN2 and VAR algorithms. The end of the assimilation window (T = 10) is represented by a dashed line. The experiment is the same as the first column of Table 8: sparse observations with n_x = 4 and n_t = 4, without noise. At convergence (after 2 iterations of BFN2 and 18 of VAR), the errors are, respectively, 0.34 and 0.49%.

Figure 3. Forecast error (difference between the reference trajectory and the solutions of the direct model initialized with the identified solutions) for BFN2 (full line) and VAR (dashed line) algorithms, with sparse and unnoisy observations (n_x = 4 = n_t).

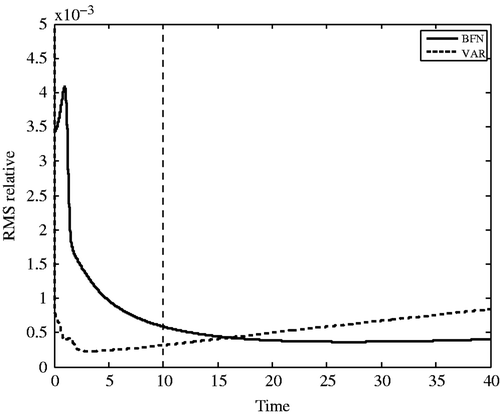
The first noticeable point is that both forecast errors present a sharp decrease in the very first time steps, even if the BFN2 forecast trajectory first increases. This is due to the non-physical solution identified by BFN2: the initial condition is the result of a backward integration of a different model than the direct reference model (as the sign of the diffusion is changed). Moreover, the feedback is done with sparse observations, which induces corrections at some grid points (at which some observations are available) and not (or less) at the other points. After a short time, the solution is smoothed by the model, and then the error decreases. Note that it is better to consider smaller nudging coefficients, leading to a worse identification, but the initial condition is then less perturbed by the feedback, and then the error decreases faster in the first iterations.

After some time (near t = 3 for VAR and t = 27 for BFN2), the error increases slowly. It means that after being on stable modes of the model (which make the error decrease), the solutions are now driven by the unstable modes of the model (and the error increases then). The forecast trajectories are relatively similar after the end of the assimilation window, the solution of BFN2 being slightly better after some time.

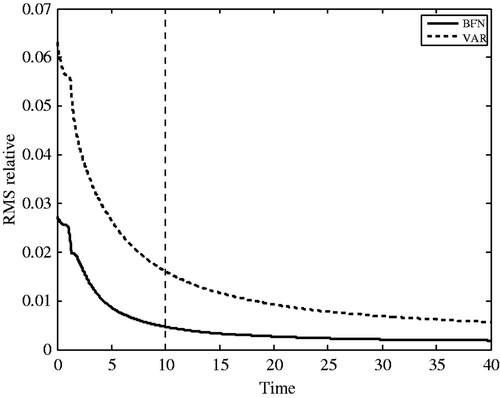
We now study the comparison in the case of full but noisy observations, with a noise level of 10%. The number of iterations needed to achieve the convergence is, respectively, 2 for BFN2 (with K = 1 and K′ = 2) and 15 for VAR, and the corresponding relative RMS error on the initial condition is 2.73% for BFN2 and 6.32% for VAR.

Figure 4 shows the evolution of the relative RMS error of the forecast for both BFN2 and VAR identified solutions. Both algorithms identify quite precisely the initial condition and are able to filter the observation noise (10%). The behaviour of the two forecast trajectories is very similar, but we can note that BFN2 gives better results than VAR. This is due to the diffusion operator, that smoothes the solution (and the observations through the feedback term) in both forward and backward integrations. The error on the BFN2 forecast is smaller than 0.5% all over the forecast period (from t = 10 to t = 40), and even of the order of 0.1% at the end of the forecast.

Figure 4. Forecast error (difference between the reference trajectory and the solutions of the direct model initialized with the identified solutions) for BFN2 (full line) and VAR (dashed line) algorithms, with full and noisy observations (10% noise).

We finally compare the two algorithms in the case of spare (n_x = 4 = n_t) and noisy (15%) observations. The results are presented in Figure 5. As already observed in previous experiments on the standard BFN, the identification of the initial condition with BFN2 can be worse than VAR 14. But then the error sharply decreases, and at the end of the assimilation window, the forecast error is smaller than 1% whereas it is three times larger for VAR. But at the end of the forecast period, both solutions are very close.

Figure 5. Forecast error (difference between the reference trajectory and the solutions of the direct model initialized with the identified solutions) for BFN2 (full line) and VAR (dashed line) algorithms, with sparse (n_x = 4 = n_t) and noisy observations (15% noise).

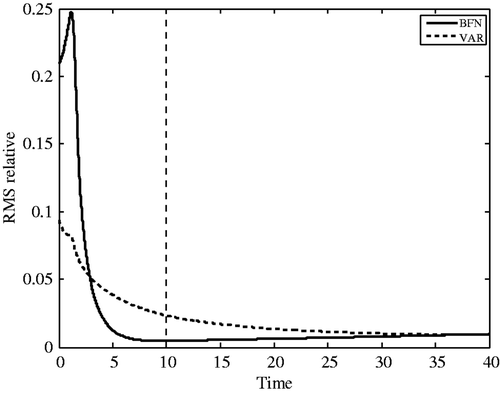
The conclusion of this comparison is that sometimes, BFN2 does not identify very precisely the initial condition, but even in these situations, the quality of the forecast is better (or much better) than with the VAR algorithm. Note that the choice of the nudging coefficients allows one to choose between the quality of the initial condition and the quality of the forecasts. Indeed, as we have seen before, by increasing the nudging feedback, it is possible to reduce the RMS error on the initial condition, but it usually leads to worse forecasts.

Also, the computing time is much smaller with BFN2, as it needs 2 or 3 iterations to converge, to be compared with 15 to 20 for VAR.

4.2. Comparison with QIL algorithm

4.2.1. QIL applied to Burgers equation

The quasi-inverse (and then QIL) method has been introduced in 18. In recent works, Kalnay et al. applied the QIL algorithm to Burgers equation 19. Similar to VAR and BFN2, QIL is initialized with a background estimate of the initial condition. Assuming that there is only a final observation on the assimilation windows (which is equivalent to splitting the assimilation window in smaller windows corresponding to the observation times), the algorithm consists in computing the innovation vector, difference between the final observation and the forecast corresponding to the initial condition.

Let ℳ_t be the resolvent of the system between the initial time 0 and time t. From an initial condition X₀, one can deduce the corresponding solution at time t: (13) We assume that there is only a final observation Y_obs(T) at time T, of the whole system state. In practice, this can be the result of an interpolation of all observations available on the assimilation window, propagated to time T. Then the forecast error (or innovation vector) at time T is Y_obs(T) − X(T).

From the forecast error at final time, the QIL algorithm uses an approximation of the inverse of the tangent linear model to back-propagate the error to the initial time. Let ℒ_t be the resolvent of the tangent linear model. For a small perturbation δX₀ of the initial condition, we have (14) and a first-order approximation of the perturbation can be given by (15) where is the quasi-inverse of the tangent linear model. We will give an explicit definition of the quasi-inverse in the following for the Burgers equation. From the forecast error at time T, QIL deduces an increment on the initial condition by back-propagation: (16) The estimation of the initial condition is updated by this increment. The process is then repeated iteratively.

If we apply this algorithm to Burgers equation, we first need to initialize the algorithm: u(x, 0) = u₀. From the direct model (3), one deduces the corresponding final state u(x,T), and then the final perturbation û(T) ≔ u_obs(T) − u(T).

The tangent linear model for the Burgers equation, linearized in the neighbourhood of the trajectory u, is: (17)

Then in this case, the QIL is nothing but the tangent linear model, solved backwards in time, with an inverse diffusion operator: (18) We refer the reader to 19 for more details about the quasi-inverse method, in which the sign of the diffusion terms is changed to avoid computational blowup.

The backward resolution of this model, initialized with û(T) as a final condition, gives an estimation of the initial perturbation û(0). Then the initial condition is updated and becomes u(0) + û(0).

As for the BFN2 (and VAR) algorithm, note that this is also an iterative algorithm, each iteration consisting of two model integrations, one forward and one backward. The cost of each iteration is somehow similar to BFN2, even if the numerical cost of the tangent linear model is larger than the backwards (nonlinear) model. Also note that one needs to linearize the model and compute the tangent linear model for QIL algorithm 18,19.

4.2.2. Numerical comparison

In order to make a fair comparison, we consider only a final observation of the system state at time T (fully observed in space), and we compare BFN2 and QIL algorithms. As QIL uses only one final observation, the final time is set small enough to make the algorithm converge, and then no shock appears in the trajectory. We can then consider a small diffusion coefficient in the model (3): ν = 0.001.

Table 9 shows the results of a comparison between these two algorithms, with a single full unnoisy observation at the final time, for various final times T. We can see that QIL is powerful on very small windows (smaller than 0.3) and with a small diffusion coefficient, whereas BFN2 is much more efficient on longer assimilation windows, or also when the diffusion is increased. Similar results have been obtained with noisy observations.

Table 9. Comparison between the BFN2 and QIL algorithms in the case of a single full unnoisy observation at final time, on Burgers' equation without shock.

Algorithm		T = 0.1	T = 0.3	T = 0.5
QIL	No. iterations	4	6	11
	Relative RMS (%)	0.0074	0.096	0.56
BFN2	No. iterations	3	5	6
	Relative RMS (%)	0.042	0.11	0.20

Note that BFN2 uses here only one observation at the final time, while it has been designed to use all the available observations on the assimilation window. QIL can be adapted to various observations spread over the time window, but the number of iterations and the complexity of the scheme drastically increases.

5. Conclusion

We compared three assimilation schemes on a Burgers equation: a standard variational method (VAR), the QIL method and the new BFN (BFN2) scheme. The main algorithmic difference between these schemes is the backward equation (adjoint model, backward tangent linear model with reversed diffusion and backward nonlinear model with reversed diffusion respectively). BFN2 consists in changing the sign of the diffusion operator in the backward equation, leading to an intrinsically stable model, even in the presence of shocks.

From the numerical experiments, we can deduce that for this model, the best scheme is BFN2: it converges in a few iterations, it is not very sensitive to the sparsity of the observations or to the observation noise, and it is also robust to the length of the assimilation window.

Sometimes, it does not produce the best estimation of the initial condition, but the forecast is better compared to other schemes. Also, thanks to its efficiency (and the very small number of iterations needed to achieve convergence), it can be used as a fast preconditioner for other data assimilation schemes.

Some preliminary experiments on a full primitive ocean model show that this new scheme is also powerful in more realistic configurations.

Acknowledgements

The authors would like to thank the referees for their suggestions. This work was partially supported by CNRS/INSU through the LEFE/ASSIM BFN program.