A numerical solution to the well resistivity-sounding problem in the axisymmetric case

Abstract

A mathematical model of the well resistivity-sounding problem is investigated. The model leads to an inverse problem of identification of the unknown coefficient (conductivity) in an elliptic equation in R² inside a cylinder. The forward problem is formulated as a mixed BVP in axisymmetric cylindrical coordinates. Measured data along the axis of the well are assumed to be available. Owing to the ill-conditioned nature of the inverse problem, a logarithmic transformation is applied to the unknown coefficient, and the inverse problem is studied as a minimization problem for the residual functional. For the radial electrical-sounding case, an effective numerical method is proposed for interpreting the data of a well sounding. The method is implemented for realistic conductivity distributions, with both noise-free and noisy data.

Keywords:

• inverse problem
• resistivity data interpretation
• well survey
• numerical simulation

AMS Subject Classifications::

• 34A55
• 35R30
• 65L08

1. Introduction

The theory of coefficient inverse problems is one of the most active areas of applied mathematics, with many practical applications. One of the most well-known applications is the electrical impedance tomography used in medicine, geophysics and defectoscopy. A review of the literature in this field of research can be found in 1. Kaufman and Dashevrky 2 provide an introduction to the basic principles and techniques of well electromagnetic sounding. Different electromagnetic sounding tools are considered by various authors. For instance, in 3,4 the problem was formulated for an inductive logging tool. In the present work, we consider the problem of well sounding using the resistivity method. The original formulation of Langer 5 is regarded as the classical statement of the resistivity-sounding problem. The Langer model assumes a vertical electrical sounding where the electrical properties of the medium depend only on the depth, and a source electrode is placed on the surface of the medium. Tikhonov 6 also studied this model, and strictly proved the uniqueness of the solution to the inverse problem. This problem is a classical example of a coefficient inverse problem that is exponentially ill-posed 7. The general principles of the solution of problems of this kind, including quasisolution and regularization methods, are described in 8,9. The first complete statement of the coefficient inverse problem (CIP) for an elliptic equation and elliptic system of equations is presented in 10,11.

The first successful attempt at a numerical solution of the problem posed in 5,6 is briefly described in the unfinished research of Alekseev et al. 12. These authors employed a regularization method, then smoothed the solution for each iteration step and obtained some examples of recovery of the unknown coefficient. In 13 we solved the problem numerically for various assumed conductivity distributions. Unlike Alekseev et al. 12, we do not use regularization of a residual functional, or a smoothing procedure. Instead, we use a two-stage procedure to recover the unknown coefficient 13, leading to a successful numerical solution of the considered inverse problem. In the first step, we recover a logarithmic derivative, p(z), of an unknown conductivity σ(z). In the second step, the function σ(z) is found using an analytical formula. The properties of the corresponding residual functional have been analysed in 14,15 and established that the functional gradient is Lipschitz and satisfies a unilateral convexity condition. In this article, we also consider the problem of resistivity-sounding using a direct current.

The novel aspect of this article is the application of the method of Mukanova and Orunkhanov 13 to the well logging problem when the electrical properties of the medium depend only on the distance to the polar axis and do not depend on the depth. In addition, whereas the previous papers 5,6,12–15) consider the case where the source electrode is placed on the surface of the vertical layered media, we assume that the current source is placed inside a well and that the surrounding media are cylindrically layered. We express the problem in cylindrical coordinates (r, ϕ, z) and use a statement of the forward problem described in 16. This statement differs from the classical treatment of 5,6 in both the boundary conditions and the geometry of the physical domain.

Well logging has been studied extensively in the Oil and Gas industry since the 1940s 17–22. Archie 17 demonstrated for the first time how the electrical log can be used to provide qualitative indications of the presence of oil and gas reservoirs. In 18, the spontaneous potential well logging inverse problem is formulated as a variational problem for an elliptic equation, in which the resistivity of the objective layer appears as a coefficient. The existence of solutions to the model is then proven, and sufficient conditions to ensure the uniqueness of the solution are obtained. The numerical solutions to the direct problem have been considered by many authors for different well logging tools (see, for instance, 19–22 and references therein).

This article is organized as follows. In Section 2, the problem is stated and the residual functional is constructed. In Section 3, the formula for the gradient of the functional is derived. The results of computational experiments with a specific noise model are presented in Section 4.

2. Statement of the problem

Assume that the conductivity of the medium in a well is a known constant, σ_w =const, and let r_w be the radius of the well. Suppose that the well is surrounded by a penetration zone, r_w ≤ r ≤ r_e, in which the conductivity of the medium changes continuously in the radial direction. Outside the penetration zone, the environment has another known and constant conductivity, σ_e =const for r > r_e.

For convenience, we introduce a number of dimensionless variables. Let the well radius r_w be the unit of length, and let the unit of conductivity be σ_w. Let the current source be placed at the origin, with current amplitude I. We take(1) to be the unit of electric potential. Then the dimensionless conductivity function can be written aswhere r₁ = r_e/r_w and σ_∞ = σ_e/σ_w. The commonly used mathematical model of the resistivity sounding is the equation for the electric field potential. In the cylindrically symmetric case, it can be expressed as(2) for as(3) for 1 < r < r₁, −∞ < z < ∞, and {0 < r < 1} ∪ {r > r₁}, −∞ < z < ∞. Here, the function U(r, z) is the dimensionless field potential and should vanish at infinity. Additional boundary conditions should express the continuity of the potential U(r, z) and the current density σ(r)∂U/∂r at the boundaries r = 1 and r = r₁. We will derive these boundary conditions later.

Let W(r, s) be the Fourier transform of the electric potential U(r, z) with respect to z:(4) Then(5) We introduce the notation(6) where σ(r) ∈ C²[1, r₁], 0 < σ₁ ≤ σ(r) ≤ σ₂ < ∞, is a conductivity function. Then, the transformed governing equation is the following ordinary differential equation with parameter s:(7)

Boundary conditions for Equation (7) were first derived in 16. As this reference is not readily available to most readers, we outline the proof here.

In the region where the conductivity function is constant, i.e. for r ∈ (0, 1) and r ∈ (r₁, ∞), the function W(r, s) is a solution of the modified Bessel equationwhose general solution can be expressed in terms of modified Bessel functions of the first and second kind of order zero:(8) We first construct the solution inside the well. Suppose that the solution is just the potential of a point source in a small region around the origin and can in general be expressed in the form(9) where the function Φ(r, z) is bounded, vanishes as z → ∞, and has a well-defined Fourier transform (with respect to z). From the formulathat holds for Bessel functions and Equation (8), we find that inside the well, the function W(r, s) can be written as(10) We next derive the boundary conditions at r = 1. The continuity conditions for the potential and current can be expressed in terms of the function W(r, s) as(11) and

Eliminating A(s) from the previous two expressions, we obtain the following formula:(12) From the properties of the Bessel functions, we have(13)

Now, we obtain boundary condition at the boundary r = r₁. By the condition that W(r, s) vanishes at positive infinity for r > r1, the coefficient A(s) in Equation (8) must vanish, and we havefor r > r₁. The continuity conditions at r = r₁ can be written asandBy eliminating B(s), we obtain(14)

From Equations (13) and (14), with an obvious change in notation, we obtain(15) (16) where the functions(17) are defined in terms of the modified Bessel functions K₁, K₀ and I₀. Equations (7), (15) and (16) comprise the forward problem, where the conductivity function is known. In the statement of the inverse problem, we suppose that the electrical properties of the medium outside the well are unknown but that we have an additional information: we assume that the potential can be measured on the axis of the well.

We now proceed to describe our model of the measured data. Let(18) be the Fourier transform of the function Φ(0, z) in Equation (9).

Using Equations (9) and (18), we express the measured potential on the well axis as(19)

Then, the function ψ(s) can be evaluated using the inverse Fourier transform:(20) By Equation (11), the solution to Equation (7) on the well boundary is given by(21)

The inverse problem is formulated as follows:

Find the function σ(r) ≡ a(r)/r using the solution of the BVP stated in Equations (7), (15) and (16), satisfying the additional condition (21), where the function ϕ(s) is given.

We have thus reduced the inverse problem to Equations (7), (15)–(16) and (21), which coincide with the solution in 13 except our different boundary conditions. We can therefore apply the same numerical method used in 13.

3. The gradient of the residual functional

As in 13, we introduce the logarithmic derivative of the coefficient in Equation (7):(22)

Let(23)

be the residual functional, where 0 ≤ s1 < s2 < ∞. We construct a quasisolution to Equations (7), (16) and (21) by minimizing the functional (23) with respect to the function p(r) 9.

However, we cannot apply the method of 13 directly because we need the formula for the gradient of the functional (23). We presently derive the formula for the gradient and then apply the gradient method to find the minimizer of the functional. We express Equation (7) in terms of variations:(24)

Multiplying both sides of Equation (24) by W and using the identitieswe obtain

Integrating this equation over the range (1, r₁), we obtain(25)

Multiplying (7) by δW, we have s²aWδW = a′W′δW′ + aW″δW. Substituting this expression into (25) and integrating, we obtain(26)

Using the boundary conditions (15) and (16) and the equality δa(1) = 0, we have(27)

As a(1) = 1 in dimensionless variables,(28)

It follows from the definition (22) that(29)

Substituting the last expression into (28) and changing the integration order, we obtain(30)

Multiplying (7) by W and integrating over the range (t, r₁), we have(31)

Using (31), expression (30) reduces to(32)

Varying expression (23) and using (32), we obtain

Finally, we obtain the gradient formula(33)

This last expression is similar to the one given in 13–15. The difference is in the weighting coefficient l⁻¹(s). Equation (7) and the coefficient restrictions are the same as in 13–15. Only the boundary conditions are different. We can therefore expect that the theoretical conclusions obtained in 14,15 are also correct for the case considered here. However, this consideration is beyond the scope of this article.

4. Computational experiments and their interpretation

4.1. The solution to the direct problem and synthetic data generation

To generate synthetic data ϕ(s), we provide the function σ(r) and solve Equations (7), (15)–(16) with a(r) = rσ(r). We therefore need to define the range of s values. We first performed a series of numerical experiments with different ranges of s ∈ [s1, s2]. When we use a range with s1 < 0.5, we encounter numerical instabilities, while large values of s2 require more grid points for s and are more computationally expensive. Our numerical experiments have demonstrated that the interval s ∈ [s1, s2], with s1 = 0.8, s2 = 5 is admissible for most of the considered σ(r). To test our solution of the inverse problem, we recover the function σ(r) as if it were unknown. In all cases, we use the value r₁ = 3 and solve the problem on the interval r ∈ [1, 3].

We solve the forward problem, Equations (7), (15)–(16), using the finite difference method (FDM) on a uniform grid, r_i = 1 + hi, h = (r₁ − 1)/N_r, i = 0, … , N_r.

The values of a(r) = rσ(r) correspond to the points r_i+1/2. Equation (5) is approximated by the finite difference scheme(34) and the boundary conditions are approximated by the expressions(35)

Equation (22) is replaced with its finite-difference analogue(36)

4.2. A gradient method algorithm

We solve the inverse problem using the following iterative algorithm 23:

i.	Specify the value of ϵ used in the termination criterion (see below); choose an initial guess p(0)(r) = ln(rσ(0)(r))′.
ii.	Find the new values of p and q using the conjugate gradient method formulas:(37) where the coefficient βn is computed asand the value αn is defined by the conditions(38) Let ζ be the tolerance of the parameter αn and one of the minima of J[p(n) − αnq(n)]; we assign a value to ζ before we perform step (ii).
iii.	Repeat step (ii) until the following termination criterion is satisfied:(39) Here, is the norm of the additive noise defined below.

4.3. Noise simulation

To assess the efficiency of our algorithm, we add stochastic noise to our input synthetic data. In practice, we cannot measure the potential function in the vicinity of the source point and must therefore extrapolate the potential using the function 1/z near the source electrode. This process produces an error in the value of σ(1) = σ_w of the conductivity inside the well. It has been shown in 13 that this noise can be simulated by adding a constant δ₁ to the transformed output data. The influence of this kind of noise has been studied in detail in 13. There is an additional noise contribution from measurements of the potential function. We assume that this noise can be represented as a linear combination of harmonics with random amplitude:(40)

Here, z_max is the maximum coordinate where the potential can be measured, and coefficients a_k, k = 1, … , m are assumed to be random variables uniformly distributed on the interval [−δ, +δ]. The noise model therefore depends on three parameters: the number of random variables, m; the scale length, L and the maximum amplitude of the random data, δ. The number m depends on a measurement and is limited by some frequency filter. To choose admissible noise parameters, we calculate the function W(1, s) for a sufficiently wide range of the parameters and compute the potential u(z) numerically, using Equations (20) and (21):(41)

We tried different values of s_min and s_max and found the values s_min = 0.05, s_max = 10 to be admissible to calculate the improper integral in (41). The function W(1, s) was evaluated on a logarithmic grid with 256 points.

We then added the noise given by (40) to the function u(z). We specify the noise level through the parameter(42)

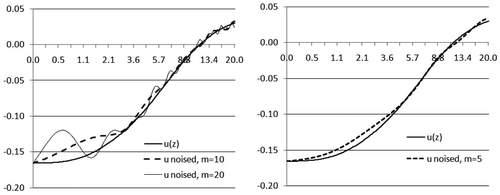
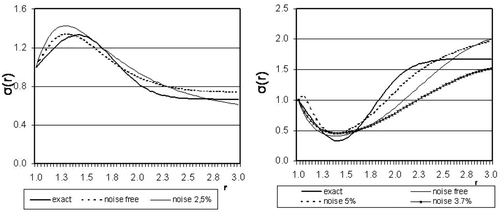
Graphs of the noisy potential are shown in Figure 1 for various values of the noise parameters. The preliminary measurements are pre-processed; therefore, cases like those presented in the left-hand panel of Figure 1 are unlikely to occur in practice. A more realistic noisy potential function is presented in the right-hand panel of Figure 1 with m = 5, L = 1, δ ∼ 0.001 and z_max = 5.

Figure 1. The noise-free and noisy potential functions with different m, δ = 0.03 and z_max = 5.

In our numerical simulations, we first compute the noise-free function ϕ(s) = W(1, s) and then we analytically calculate the Fourier transform of the noise, χ(z). By Equations (20) and (21), we have:(43)

Here, the range s_min, s_max of the parameter s is taken to be the same as in Equation (41). The function ω(s) is used to set the termination criterion for noisy data in Equation (39).

4.4. Numerical results

In all of the numerical tests described below, we take r₁ = 3, s₁ = 0.8, s₂ = 5 and noise parameters m = 5, L = 1, and z_max = 5. We set the tolerance ζ on α_n, defined by Equation (38), equal to 10⁻⁸.

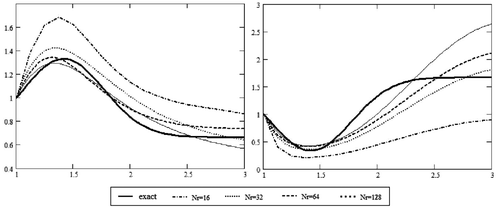
We have first tested the algorithm for different numbers of grid points, N_r = 16, 32, 64, 128, with the results shown in Figure 2. One can see that a finer grid gives superior results. All the results in Figure 2 were obtained with ‖∇J‖ ≤= 1.5 × 10⁻⁵, and corresponding values of the residual depend on the grid point numbers and vary from 5 × 10⁻⁵ to 3 × 10⁻⁸. We also varied the number of grid points in s, N_s = 32, 64, 128, with results similar to those shown in Figure 2

Figure 2. Influence of grid point numbers on the solution to the inverse problem.

Most of our numerical simulations were performed with N_r.s = 64 grid points in both r and s. Our simulations show that the termination criterion ϵ ∼ 5 × 10⁻⁵ is admissible with this number of grid points. Our numerical experiments suggest initialising the iterations with a very small α_n ∼ 10⁻⁵ and then setting the value of α_max automatically in subsequent iterations using the empirical condition: max|∇J| × α_max = 1.

We generate synthetic data σ_synth(r), r ∈ [1, 3], according to the equation:

We can explore various forms of σ(r) by varying the parameters A₁, A₂, c₀, c₁, and ϑ.

Our computations show that the conditions under which the solution can be obtained numerically are similar to those described in 13. In particular, we recover the conductivity function with satisfactory quality for contrast ratio a_max/a_min up to 10 and for simple distributions of σ(r). The results of our numerical reconstruction with noisy and noise-free data for a few forms of σ(r) are shown in Figures 3–5 The relative errors δ ≔ ‖σ_exact − σ_recov‖/‖σ_exact‖ in C-norm and the corresponding number of iterations are given in Table 1. In all cases, we stop the iteration process when criterion (39) is satisfied. In most of the cases we considered, the residual functional and its gradient decline too slowly when ϵ < 5 × 10⁻⁵, and the number of iterations therefore increases sharply. However, the increased number of iterations does not yield significant improvement of the solution.

Figure 3. Data interpretation for the monotone conductivity function with a contrast ratio equal to 10.

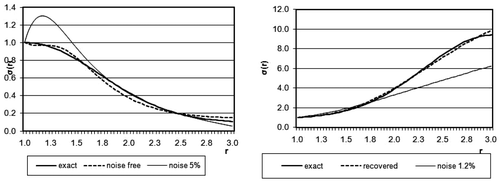
Table 1. Relative errors δ in C-norm and corresponding iterations number.

Case	Noise- free data	Noisy data γ = 1.25%	Noisy data γ = 2.5%	Noisy data γ = 3.7%	Noisy data γ = 5%
1. σ(r) is increasing (Figure 3, right);	0.11;	0.36;	0.43;
A1 = 10, A2 = 0, c1 = 2, ϑ = 1	9602	10621	13,517
2. σ(r) is decreasing (Figure 3, left);	0.04;	0.10;	0.19;	0.22;	0.63;
A1 = 10, A2 = 0, c1 = 0, ϑ = 1	2581	4041	1006	222	217
3. σ(r) has maximum (Figure 4, left);	0.04;	0.15;	0.18;	0.9;	–
A1 = 1, A2 = 0, c1 = 0.4, ϑ = 0.5	10001	12560	4000	8005
4. σ(r) has minimum (Figure 4, right);	0.28;	0.64;	0.14;	0.36;	0.18;
A1 = −0.8, A2 = 0, c1 = 0.4, ϑ = 0.5	13501	26000	37,000	3601	22503
σ(r) has minimum; 1 ≤ r ≤ 1.5	0.07	0.08	0.07	0.07	0.11
A1 = −0.8, A2 = 0, c1 = 0.4, ϑ = 0.5
Note: The last line corresponds to the same case as line 4, but relative error is calculated for 1 ≤ r ≤ 1.5 only.

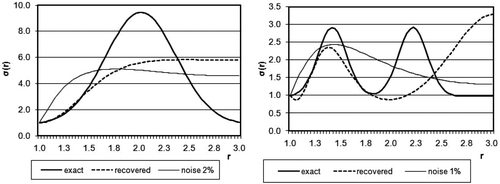
The number of iterations required before the termination criterion is satisfied depends on σ(r). In most cases, it varies from 200 to 15,000. More acceptable results are obtained for the cases where σ(r) is monotonic. Figure 3 shows the results for noise- free and noisy data with contrast ratio equal to 10. When σ(r) is decreasing, the quality of the reconstruction remains fairly high up to a noise level of 5%. However, when σ(r) is increasing, we only obtain satisfactory results up to a noise level of 1.2%. The case where σ(r) has a local maximum near the well zone is also favourable; the results for this case are presented in the left-hand panel of Figure 4. In this case, acceptable results are obtained for contrast ratios above 2.5 and noise levels up to 2.5%.

Figure 4. Data interpretation for a conductivity function maximum and minimum near the well zone, at the distance equal to 0.4.

The most unfavourable case occurs when the conductivity has a local minimum near the well zone. The reason for this is an ‘overshadowing’ effect. The zone with low conductivity is located in a valley between two zones with higher conductivity, so that very little current reaches the distant areas. The impact of the distant areas in the output data on the well boundary is negligible, and the residual functional is therefore insensitive to variations in the conductivity of these areas. As shown in table 1, line 4, a large number of iterations is required to reach the termination criterion because of this effect, and it also produces high relative errors. However, in the nearest zone, for 1 ≤ r ≤ 1.5, the quality of the reconstruction is high enough (see, for instance, the last line of Table 1). The cases with distant local extremums of the function σ(r) are also unfavourable, as are cases with two or more extremums. The results are shown in Figure 4 (right) and Figure 5. In these cases, the reconstruction quality was admissible as long as the distance to the well boundary was less than 0.5, i.e. for r ≤ 1.5. The influence of the distance on the quality of the reconstructed conductivity function can be seen in Figures 4 and 5. These figures show the deterioration in quality at large distances.

Figure 5. Data interpreation for a conductivity function having distant maximum and for a wavy conductivity distrbution with different noise level.

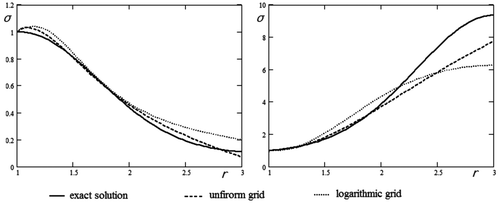
We attempted to improve the quality of the recovered data with a logarithmic grid for the solution of the direct problem (7)–(16). We applied the transformation of variables q = ln(1 + r) and then proceeded to solve the problem numerically. However, we did not achieve any significant improvement of the numerical solution using this technique. The results obtained using a uniform and a logarithmic grid are compared in Figure 6.

Figure 6. The comparison between solutions on uniform and logarithmic grids.

5. Conclusions

We have reduced a mathematical model of a cylindrical well resistivity-sounding to one of a vertical electrical sounding (VES); the only differences are in the boundary conditions and the weighting coefficients in the gradient of the residual functional. We have applied a numerical method, which is successful in VES, to the interpretation of well resistivity-sounding data. The method has been implemented numerically for some realistic conductivity distributions. Our numerical results with noise-free and noisy data demonstrate that in some simple cases, the unknown coefficient can be accurately reconstructed near the well. However, the results obtained for the cylindrically symmetric case turn out to be significantly worse than those for a vertical layered media model, and require further improvement.

Acknowledgements

The author is grateful to professor Alemdar Hasanoglu (Hasanov) for giving attention to this work and for valuable suggestions. The author would like to thank to the referees whose comments and suggestions substantially aided this article.