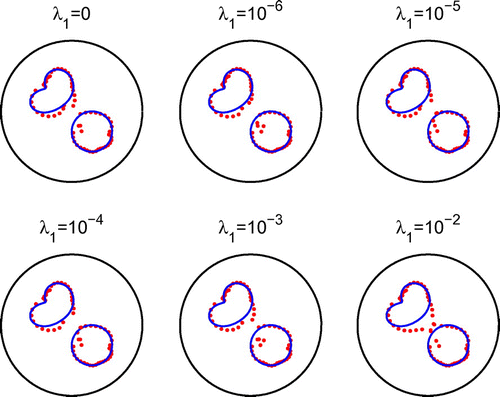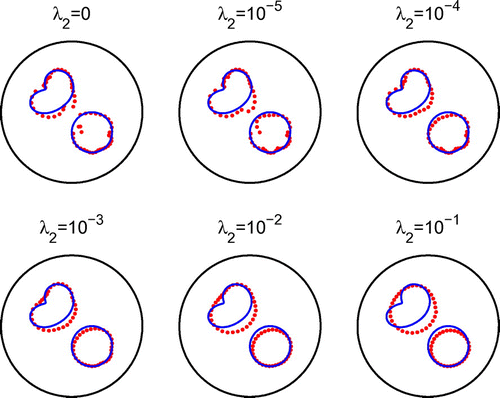Regularized collocation Trefftz method for void detection in two-dimensional steady-state heat conduction problems

Abstract

We propose the use of the collocation Trefftz method for the solution of inverse geometric problems and, in particular, the determination of the boundary of a void. As was the case in the solution of such problems using the method of fundamental solutions, the algorithm for imaging the interior of the medium also makes use of radial polar parametrization of the unknown void shape in two dimensions. The centre of this radial polar parametrization is considered to be unknown. The feasibility of this new method is illustrated by several numerical examples highlighting its advantages and shortcomings.

Keywords:

• void detection
• inverse problem
• Trefftz method
• collocation

AMS Subject Classifications:

• Primary 65N35
• Secondary 65N21
• 65N38

Introduction

Numerous practical problems in engineering and sciences are characterized by the fact that one or more of the following conditions are partially or entirely unknown: the geometry of the domain of interest, the complete boundary and initial conditions, the material properties and the external sources acting in the solution domain. These problems are known as inverse problems and they are, in general, ill posed,[1] in the sense that the existence, uniqueness and stability of their solutions are not always guaranteed, and hence more difficult to solve. An important class of inverse problems is represented by the so-called inverse geometric problems whose main feature is the lack of knowledge of part of the boundary. In particular, we focus herein on the numerical reconstruction of an internal boundary (i.e. cavity or rigid inclusion) in steady-state isotropic heat conduction (Laplace’s equation) from the knowledge of the temperature and normal heat flux (i.e. Cauchy data) on the outer boundary.

The uniqueness of solution of the inverse geometric steady-state heat conduction problem related to the determination of rigid inclusions or cavities from Cauchy data prescribed on the outer boundary of the solution domain for media with constant conductivity was proved in [2, 3], respectively. The numerical reconstruction of voids in heat conduction problems has been tackled by numerous authors and various approaches have been proposed for the solution of this inverse geometric problem, see e.g. [4–16]. Das and Mitra [6] developed an iterative algorithm to determine the location and shape of a flaw in steady-state heat conduction (i.e. Laplace’s equation). Kassab and Pollard [10, 11] proposed a linear boundary element method (BEM), an anchored grid pattern method and a Newton–Raphson method with a Broyden update for the numerical reconstruction of an unknown cavity for the same inverse geometric heat conduction problem. The conjugate gradient method (CGM) for the numerical solution of inverse design problems in estimating the optimal locations and shapes of the internal cooling passages for turbine blades based on the desired outer surface temperature distribution was considered in [17]. Gallego and Suarez [7] proposed an approach based on a boundary integral equation for the variation of the potential and flux to retrieve numerically an assumed flaw in the case of a two-dimensional isotropic solid subject to thermal loads. An iterative algorithm based on a real-coded genetic algorithm (GA) and the BEM for detecting cavities in problems governed by the two-dimensional Laplace equation was developed in [14], while [5] proposed a simplification of the CGM for the reconstruction of voids in two-dimensional steady-state isotropic heat conduction which consists of prescribing the values of the step size for the optimal searches to be constant values depending upon the resolution of the identification. An iterative algorithm using thermographic techniques based on the superposition of clusters of sources/sinks with the BEM [12] was employed for the detection of subsurface cavities and flaws. Mera [15] used kriging approximation models to speed-up the optimization process via GAs for detecting the size and location of subsurface cavities associated with the two-dimensional Laplace’s equation, whilst Tan et al. [18] solved a geometry identification problem in two-dimensional isotropic heat conduction by employing the least-squares collocation meshless method and CGM. Kazemzadeh-Parsi and Daneshmand [13] approached the cavity detection problem for the two-dimensional Laplace equation via the smoothed fixed grid finite element method in conjunction with the CGM. Yan and Ma [16] considered the reconstruction of a cavity in the case of the Laplace equation from the knowledge of the measurements on the exterior boundary and employed the domain derivative of the associated operator and a regularized Newton method for the solution of the corresponding ill-posed and nonlinear problem. Recently, Karageorghis and Lesnic [8] proposed a method of fundamental solution (MFS)-based reconstruction of a cavity for the two-dimensional stationary heat conduction equation in isotropic media, whereas Borman et al. [4] and Karageorghis and Lesnic [9] employed the same approach for the detection of inclusions.

Trefftz methods [19] have been used extensively for the solution of elliptic boundary value problems, see, for example [20–22], and also [23]. Surveys on Trefftz and related methods may be found in [23–26]. In this work, we investigate the performance of the collocation Trefftz method (CTM) for the solution of inverse geometric problems, in particular for void detection problems. The CTM is a boundary meshless method and such methods have, in recent years, become increasingly popular for the solution of inverse problems in general because of the ease with which they can be implemented for boundary value problems in complex geometries and in three dimensions. The MFS in particular has been used extensively for the solution of inverse problems.[27] Trefftz methods have been used for the solution of inverse Cauchy linear problems.[28–34] In the case of inverse geometric problems, the CTM has been recently used by Fan and his co-workers.[35–37] In particular, [37] deals entirely with boundary identification problems for Laplace’s equation, while in [35] an internal void problem is solved in the case of the Helmholtz equation. The ideas developed in this work are close to the ones developed in [36], see also [38], where two internal void detection problems are solved in the case of the Laplace equation. However, our proposed algorithm differs from the one in [36] as follows:

1. In contrast to the algorithm of [36] for void detection inverse problems, we consider problems in which the centre(s) of the void(s) to be reconstructed is (are) unknown. The coordinates of the centre(s) are merely taken as additional unknowns in the algorithm.

2. By changing and augmenting the Trefftz basis, the algorithm is capable of locating multiple inclusion with unknown centres.

3. Instead of using a scalar homotopy algorithm, we use the state-of-the-art MATLAB optimization toolbox routine lsqnonlin. This routine allows for the imposition of simple bounds on the variable which, to a great extent, eliminates physically unrealistic solutions.

4. The stability of the proposed algorithm is achieved using two regularization parameters which can be determined by the use of the L-curve criterion. The method is shown to accurately reconstruct smooth or piecewise smooth, convex or concave, single or multiple cavities and rigid inclusions.

5. We are not using the so-called modified CTM of [39, 40] which takes into account the characteristic shapes of the domains involved. This is because the size of at least one of the domains in unknown and needs to be determined as part of the solution. Efforts to normalize one set of unknowns produced little or no difference to our results.

In comparison to the MFS, the CTM does not require selecting a fictitious boundary curve on which source points need to be positioned. However, a disadvantage of the CTM with respect to the MFS is the poor conditioning of the discretization matrices [40, 41] and we aim to also address this issue in the application of the CTM to void detection problems. In fact, the connection between the CTM and the MFS has recently been pointed out in [42] where it is shown that for the Laplace equation in a bounded, simply-connected domain the CTM is retrieved as a degenerate situation of the MFS with the source points placed at infinity. The corresponding result in annular and exterior domains may be found in [43, 44], respectively.

Mathematical formulation

In this section, we formulate the direct and inverse problems related to a void such as a rigid inclusion or a cavity in the case of steady-state heat conduction (Laplace’s equation). The direct problem given by the Laplace equation(2.1) $$\begin{array}{c}\hfill \mathrm{\Delta }u=0\text{in}\mathrm{\Omega },\end{array}$$(2.1) subject to the Dirichlet boundary condition(2.2) $$\begin{array}{c}\hfill u=f\text{on}\mathit{\partial }{\mathrm{\Omega }}_2,\end{array}$$(2.2) and the homogeneous boundary condition(2.3) $$\begin{array}{c}\hfill \mathit{\alpha }u+(1-\mathit{\alpha }){\mathit{\partial }}_{n}u=0\text{on}\mathit{\partial }{\mathrm{\Omega }}_1,\text{where}\mathit{\alpha }\in \{0,1\},\end{array}$$(2.3) has a unique weak solution $u\in {\mathcal{H}}^1(\mathrm{\Omega })$ if $f\in {\mathcal{H}}^{1/2}(\mathit{\partial }{\mathrm{\Omega }}_2)$, and a unique classical solution $u\in {\mathcal{C}}^2(\mathrm{\Omega })\cap \mathcal{C}(\overline{\mathrm{\Omega }})$, provided $f$ is sufficiently smooth. In the above, $\mathrm{\Omega }={\mathrm{\Omega }}_2\setminus {\mathrm{\Omega }}_1$, where ${\overline{\mathrm{\Omega }}}_1\subset {\mathrm{\Omega }}_2$, is a bounded annular domain with boundary $\mathit{\partial }\mathrm{\Omega }=\mathit{\partial }{\mathrm{\Omega }}_1\cup \mathit{\partial }{\mathrm{\Omega }}_2$ and we assume that $\mathrm{\Omega }$ is connected. Equation (2.1c), covers both Dirichlet ($\mathit{\alpha }=1$), i.e. a rigid inclusion, and Neumann ($\mathit{\alpha }=0$), i.e. a cavity, boundary conditions on $\mathit{\partial }{\mathrm{\Omega }}_1$.

The inverse problem we are concerned with consists of determining not only the function $u$, but also the void ${\mathrm{\Omega }}_1$ so that $u$ satisfies the Laplace equation (2.1a), given the Dirichlet data $f\not\equiv \text{constant}$ in (2.1b), the homogeneous boundary condition (2.1c) and the Neumann current flux measurement(2.4) $$\begin{array}{c}\hfill g:={\mathit{\partial }}_{n}u\text{on}\mathit{\partial }{\mathrm{\Omega }}_2.\end{array}$$(2.4) In (2.1c) and (2.1d), the vector $\mathit{n}$ denotes the outward unit normal to the annular domain $\mathrm{\Omega }$. When $\mathit{\alpha }=0$, for (2.1a), (2.1c) and (2.1d) to be consistent, we require(2.5) $$\begin{array}{c}\hfill {\int }_{\mathit{\partial }{\mathrm{\Omega }}_2}g(s)\mathit{ds}=0.\end{array}$$(2.5) In contrast to the direct (forward) boundary value problem (2.1a)–(2.1c), the inverse problem (2.1a)–(2.1d) is non-linear and ill posed. Although the solution is unique, [2], it is unstable with respect to small errors in the input Cauchy data (2.1b) and (2.1d).

Collocation Trefftz method

In the CTM for the doubly-connected two-dimensional annular domain $\mathrm{\Omega }$, we seek an approximation to the solution of Laplace’s equation (2.1a) as a linear combination of T-complete functions in the form [40, 45, 46].(3.1) $$\begin{array}{cc}\hfill u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };\mathit{x})& ={\mathit{\alpha }}_0+{\mathit{\gamma }}_0\log |z|+\sum _{k=1}^N{\mathit{\alpha }}_k\mathfrak{R}\left\{z^k\right\}+\sum _{k=1}^N{\mathit{\beta }}_k\mathfrak{I}\left\{z^k\right\}\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\gamma }}_k\mathfrak{R}\left\{z^{-k}\right\}+\sum _{k=1}^N{\mathit{\delta }}_k\mathfrak{I}\left\{z^{-k}\right\},\mathit{x}=(x,y)\in \overline{\mathrm{\Omega }},\hfill \end{array}$$(3.1) where the T-complete system is given by(3.2) $$\begin{array}{c}\hfill \{1,\log |z|,\mathfrak{R}(z^n),\mathfrak{I}(z^k),\mathfrak{R}(z^{-k}),\mathfrak{I}(z^{-k});z=x+iy,k\in {\mathbb{N}}^{\ast }\},\end{array}$$(3.2) where $\mathfrak{R}$ and $\mathfrak{I}$ denote the real and imaginary part of a complex number, respectively. In (3.1(3.1) $$\begin{array}{cc}\hfill u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };\mathit{x})& ={\mathit{\alpha }}_0+{\mathit{\gamma }}_0\log |z|+\sum _{k=1}^N{\mathit{\alpha }}_k\mathfrak{R}\left\{z^k\right\}+\sum _{k=1}^N{\mathit{\beta }}_k\mathfrak{I}\left\{z^k\right\}\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\gamma }}_k\mathfrak{R}\left\{z^{-k}\right\}+\sum _{k=1}^N{\mathit{\delta }}_k\mathfrak{I}\left\{z^{-k}\right\},\mathit{x}=(x,y)\in \overline{\mathrm{\Omega }},\hfill \end{array}$$(3.1) ), there are $4N+2$ unknowns, namely the coefficients $\mathit{\alpha }={[{\mathit{\alpha }}_0,{\mathit{\alpha }}_1,\dots ,{\mathit{\alpha }}_N]}^T$, $\mathit{\beta }={[{\mathit{\beta }}_1,{\mathit{\beta }}_2,\dots ,{\mathit{\beta }}_N]}^T$, $\mathit{\gamma }={[{\mathit{\gamma }}_0,{\mathit{\gamma }}_1,\dots ,{\mathit{\gamma }}_N]}^T$, $\mathit{\delta }={[{\mathit{\delta }}_1,{\mathit{\delta }}_2,\dots ,{\mathit{\delta }}_N]}^T$. We point out that the use of complex variable notation in (3.1(3.1) $$\begin{array}{cc}\hfill u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };\mathit{x})& ={\mathit{\alpha }}_0+{\mathit{\gamma }}_0\log |z|+\sum _{k=1}^N{\mathit{\alpha }}_k\mathfrak{R}\left\{z^k\right\}+\sum _{k=1}^N{\mathit{\beta }}_k\mathfrak{I}\left\{z^k\right\}\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\gamma }}_k\mathfrak{R}\left\{z^{-k}\right\}+\sum _{k=1}^N{\mathit{\delta }}_k\mathfrak{I}\left\{z^{-k}\right\},\mathit{x}=(x,y)\in \overline{\mathrm{\Omega }},\hfill \end{array}$$(3.1) ) is only for convenience and brevity and does not pose a restriction to two-dimensions only. Once could easily use the T-complete system (3.2(3.2) $$\begin{array}{c}\hfill \{1,\log |z|,\mathfrak{R}(z^n),\mathfrak{I}(z^k),\mathfrak{R}(z^{-k}),\mathfrak{I}(z^{-k});z=x+iy,k\in {\mathbb{N}}^{\ast }\},\end{array}$$(3.2) ) expressed in polar coordinates as [47](3.3) $$\begin{array}{c}\hfill \begin{array}{c}\{1,\log (r),r^k\cos (k\mathit{\theta }),r^k\sin (k\mathit{\theta }),r^{-k}\cos (k\mathit{\theta }),r^{-k}\sin (k\mathit{\theta });\hfill \\ x=r\cos (\mathit{\theta }),y=r\sin (\mathit{\theta }),k\in {\mathbb{N}}^{\ast }\},\hfill \end{array}\end{array}$$(3.3) Then, the extension to three-dimensions requires the use of spherical coordinates and Legendre polynomials, as described in [20, p.32].

Without loss of generality, we shall assume that the (known) fixed exterior boundary $\mathit{\partial }{\mathrm{\Omega }}_2$ is a circle of radius $R$. As a result, the outer boundary collocation points are chosen as(3.4) $$\begin{array}{c}\hfill {\mathit{x}}_{M_1+\ell }=R(\cos {\stackrel{\sim }{\mathit{\vartheta }}}_{\ell },\sin {\stackrel{\sim }{\mathit{\vartheta }}}_{\ell }),\ell =\overline{1,M_2},\end{array}$$(3.4) where ${\stackrel{\sim }{\mathit{\vartheta }}}_{\ell }=\frac{2\mathit{\pi }(\ell -1)}{M_2},\ell =\overline{1,M_2}$.

We further assume that the unknown boundary $\mathit{\partial }{\mathrm{\Omega }}_1$ is a smooth, star-like curve with respect to the centre which has unknown coordinates $(X,Y)$. This means that its equation in polar coordinates can be written as(3.5) $$\begin{array}{c}\hfill x=X+r(\mathit{\vartheta })\cos \mathit{\vartheta },y=Y+r(\mathit{\vartheta })\sin \mathit{\vartheta },\mathit{\vartheta }\in [0,2\mathit{\pi }),\end{array}$$(3.5) where $r$ is a smooth $2\mathit{\pi }-$periodic function. The constraint that ${\mathrm{\Omega }}_1\subset {\mathrm{\Omega }}_2$ then recasts as(3.6) $$\begin{array}{c}\hfill {(X+r(\mathit{\vartheta })\cos \mathit{\vartheta })}^2+{(Y+r(\mathit{\vartheta })\sin \mathit{\vartheta })}^2<R^2,\mathit{\vartheta }\in [0,2\mathit{\pi }).\end{array}$$(3.6) The discretized form of (3.5(3.5) $$\begin{array}{c}\hfill x=X+r(\mathit{\vartheta })\cos \mathit{\vartheta },y=Y+r(\mathit{\vartheta })\sin \mathit{\vartheta },\mathit{\vartheta }\in [0,2\mathit{\pi }),\end{array}$$(3.5) ) for $\mathit{\partial }{\mathrm{\Omega }}_1$ becomes(3.7) $$\begin{array}{c}\hfill r_k=r({\mathit{\vartheta }}_k),k=\overline{1,M_1}\end{array}$$(3.7) and we choose the inner boundary collocation points as(3.8) $$\begin{array}{c}\hfill {\mathit{x}}_k=(X,Y)+r_k(\cos {\mathit{\vartheta }}_k,\sin {\mathit{\vartheta }}_k),\end{array}$$(3.8) where ${\mathit{\vartheta }}_k=\frac{2\mathit{\pi }(k-1)}{M_1},k=\overline{1,M_1}$.

Since the centre is not known and therefore not necessarily the origin, the basis (3.2(3.2) $$\begin{array}{c}\hfill \{1,\log |z|,\mathfrak{R}(z^n),\mathfrak{I}(z^k),\mathfrak{R}(z^{-k}),\mathfrak{I}(z^{-k});z=x+iy,k\in {\mathbb{N}}^{\ast }\},\end{array}$$(3.2) ) needs to be modified to(3.9) $$\begin{array}{c}\hfill \{1,\log |z-z_0|,\mathfrak{R}(z^n),\mathfrak{I}(z^n),\mathfrak{R}({(z-z_0)}^{-n}),\mathfrak{I}({(z-z_0)}^{-n});z=x+iy,n\in \mathbb{N}\},\end{array}$$(3.9) where $z_0=X+\mathit{iY}$. For example, this is suggested by function theoretic results concerning the expansion of functions that are analytic in multiply-connected domains [48, p.244], see also [49]. Therefore, the CTM approximation becomes(3.10) $$\begin{array}{cc}\hfill & u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };\mathit{x})={\mathit{\alpha }}_0+{\mathit{\gamma }}_0\log |z-z_0|+\sum _{k=1}^N{\mathit{\alpha }}_k\mathfrak{R}\left\{z^k\right\}+\sum _{k=1}^N{\mathit{\beta }}_k\mathfrak{I}\left\{z^k\right\}\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\gamma }}_k\mathfrak{R}\left\{{(z-z_0)}^{-k}\right\}+\sum _{k=1}^N{\mathit{\delta }}_k\mathfrak{I}\left\{{(z-z_0)}^{-k}\right\},\mathit{x}=(x,y)\in \overline{\mathrm{\Omega }}.\hfill \end{array}$$(3.10) In the cases where $R>1$, we tried to scale the terms in the first and second series in (3.10(3.10) $$\begin{array}{cc}\hfill & u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };\mathit{x})={\mathit{\alpha }}_0+{\mathit{\gamma }}_0\log |z-z_0|+\sum _{k=1}^N{\mathit{\alpha }}_k\mathfrak{R}\left\{z^k\right\}+\sum _{k=1}^N{\mathit{\beta }}_k\mathfrak{I}\left\{z^k\right\}\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\gamma }}_k\mathfrak{R}\left\{{(z-z_0)}^{-k}\right\}+\sum _{k=1}^N{\mathit{\delta }}_k\mathfrak{I}\left\{{(z-z_0)}^{-k}\right\},\mathit{x}=(x,y)\in \overline{\mathrm{\Omega }}.\hfill \end{array}$$(3.10) ) through division with $R^k$ as suggested by Liu [39, 40]. This produced little or no improvement to our results. This may be because the corresponding multiplication of each of the terms in the third and fourth series in (3.10(3.10) $$\begin{array}{cc}\hfill & u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };\mathit{x})={\mathit{\alpha }}_0+{\mathit{\gamma }}_0\log |z-z_0|+\sum _{k=1}^N{\mathit{\alpha }}_k\mathfrak{R}\left\{z^k\right\}+\sum _{k=1}^N{\mathit{\beta }}_k\mathfrak{I}\left\{z^k\right\}\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\gamma }}_k\mathfrak{R}\left\{{(z-z_0)}^{-k}\right\}+\sum _{k=1}^N{\mathit{\delta }}_k\mathfrak{I}\left\{{(z-z_0)}^{-k}\right\},\mathit{x}=(x,y)\in \overline{\mathrm{\Omega }}.\hfill \end{array}$$(3.10) ) by $R_c^k$, where $R_c$ is the characteristic length of $\mathit{\partial }{\mathrm{\Omega }}_1$, as suggested in [40] is not possible as its size is unknown.

Implementational details

The current flux data (2.1d) come from practical measurements which are inherently contaminated with errors due to noise, and we therefore replace $g$ by the noisy data $g^{\mathit{\epsilon }}$ defined as(4.1) $$\begin{array}{c}\hfill g^{\mathit{\epsilon }}({\mathit{x}}_j)=(1+{\mathit{\rho }}_{j}p)g({\mathit{x}}_j),j=\overline{M_1+1,M_1+M_2},\end{array}$$(4.1) where $p$ represents the percentage of noise and ${\mathit{\rho }}_j$ is a pseudo-random noisy variable drawn from a uniform distribution in $[-1,1]$ using the MATLAB command -1+2*rand(1,$M_2$). It is also reported that in our numerical experiments we observed that the effect of noise added to the Dirichlet boundary data (2.1b) was similar to that of perturbing the Neumann data. As a result in the numerical results section, we only present results for the noisy Neumann data (4.1(4.1) $$\begin{array}{c}\hfill g^{\mathit{\epsilon }}({\mathit{x}}_j)=(1+{\mathit{\rho }}_{j}p)g({\mathit{x}}_j),j=\overline{M_1+1,M_1+M_2},\end{array}$$(4.1) ).

The coefficients ${\left(a_k\right)}_{k=\overline{0,N}},{\left(b_k\right)}_{k=\overline{0,N}},{\left(c_k\right)}_{k=\overline{1,N}}$ and ${\left(d_k\right)}_{k=\overline{1,N}}$ in (3.1(3.1) $$\begin{array}{cc}\hfill u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };\mathit{x})& ={\mathit{\alpha }}_0+{\mathit{\gamma }}_0\log |z|+\sum _{k=1}^N{\mathit{\alpha }}_k\mathfrak{R}\left\{z^k\right\}+\sum _{k=1}^N{\mathit{\beta }}_k\mathfrak{I}\left\{z^k\right\}\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\gamma }}_k\mathfrak{R}\left\{z^{-k}\right\}+\sum _{k=1}^N{\mathit{\delta }}_k\mathfrak{I}\left\{z^{-k}\right\},\mathit{x}=(x,y)\in \overline{\mathrm{\Omega }},\hfill \end{array}$$(3.1) ), the radii ${\left(r_k\right)}_{k=\overline{1,M_1}}$ in (3.7(3.7) $$\begin{array}{c}\hfill r_k=r({\mathit{\vartheta }}_k),k=\overline{1,M_1}\end{array}$$(3.7) ), and the coordinates of the centre $\mathit{C}=(X,Y)$ are determined by imposing the boundary conditions (2.1b), (2.1c) and (2.1d) in a least-squares sense. This leads to the minimization of the functional(4.2) $$\begin{array}{cc}\hfill S(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta },\mathit{r},\mathit{C})& :=\sum _{j=M_1+1}^{M_1+M_2}{[u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)-f({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=M_1+1}^{M_1+M_2}{[{\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)-g^{\mathit{\epsilon }}({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=1}^{M_1}{[\mathit{\alpha }{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)+(1-\mathit{\alpha }){\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1(|\mathit{\alpha }{|}^2+|\mathit{\beta }{|}^2+|\mathit{\gamma }{|}^2+|\mathit{\delta }{|}^2)+{\mathit{\lambda }}_2\sum _{\ell =2}^{M_1}{(r_{\ell }-r_{\ell -1})}^2,\hfill \end{array}$$(4.2) where ${\mathit{\lambda }}_1,{\mathit{\lambda }}_2\ge 0$ are regularization parameters to be prescribed. The term multiplying ${\mathit{\lambda }}_1$ regularizes the ill-conditioning of the CTM, whilst the term multiplying ${\mathit{\lambda }}_2$ regularizes the ill-posedness of the inverse shape problem. The last term in (4.2(4.2) $$\begin{array}{cc}\hfill S(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta },\mathit{r},\mathit{C})& :=\sum _{j=M_1+1}^{M_1+M_2}{[u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)-f({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=M_1+1}^{M_1+M_2}{[{\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)-g^{\mathit{\epsilon }}({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=1}^{M_1}{[\mathit{\alpha }{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)+(1-\mathit{\alpha }){\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1(|\mathit{\alpha }{|}^2+|\mathit{\beta }{|}^2+|\mathit{\gamma }{|}^2+|\mathit{\delta }{|}^2)+{\mathit{\lambda }}_2\sum _{\ell =2}^{M_1}{(r_{\ell }-r_{\ell -1})}^2,\hfill \end{array}$$(4.2) ) imposes that the void has a smooth $C^1\text{-}$boundary, as required by the theory establishing the uniqueness of solution. If a non-smooth geometry, such as a square for example, is present then, the corners of the square can be slightly smoothed giving rise to a rounded square shape.[50, 51] Alternatively, one could replace the discretized $L^2$-norm of $r^{\prime }$ given in the last term of (4.2), by the discretized $L^1$-norm of $r$.

In (4.2(4.2) $$\begin{array}{cc}\hfill S(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta },\mathit{r},\mathit{C})& :=\sum _{j=M_1+1}^{M_1+M_2}{[u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)-f({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=M_1+1}^{M_1+M_2}{[{\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)-g^{\mathit{\epsilon }}({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=1}^{M_1}{[\mathit{\alpha }{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)+(1-\mathit{\alpha }){\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1(|\mathit{\alpha }{|}^2+|\mathit{\beta }{|}^2+|\mathit{\gamma }{|}^2+|\mathit{\delta }{|}^2)+{\mathit{\lambda }}_2\sum _{\ell =2}^{M_1}{(r_{\ell }-r_{\ell -1})}^2,\hfill \end{array}$$(4.2) ), the outward normal vector $\mathit{n}$ is defined as follows:(4.3) $$\begin{array}{c}\hfill \mathit{n}=\{\begin{array}{ccc}\cos \mathit{\vartheta }\mathit{i}+\sin \mathit{\vartheta }\mathit{j},\hfill & \text{if}\hfill & \mathit{x}\in \mathit{\partial }{\mathrm{\Omega }}_2,\hfill \\ \frac{1}{\sqrt{r^2(\mathit{\vartheta })+{r^{\prime }}^2(\mathit{\vartheta })}}[-(r^{\prime }(\mathit{\vartheta })\sin \mathit{\vartheta }+r(\mathit{\vartheta })\cos \mathit{\vartheta })\mathit{i}\hfill \\ +(r^{\prime }(\mathit{\vartheta })\cos \mathit{\vartheta }-r(\mathit{\vartheta })\sin \mathit{\vartheta })\mathit{j}],\hfill & \text{if}\hfill & \mathit{x}\in \mathit{\partial }{\mathrm{\Omega }}_1,\hfill \end{array}\end{array}$$(4.3) where $\mathit{i}=(1,0)$ and $\mathit{j}=(0,1)$. As a result, from (3.10(3.10) $$\begin{array}{cc}\hfill & u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };\mathit{x})={\mathit{\alpha }}_0+{\mathit{\gamma }}_0\log |z-z_0|+\sum _{k=1}^N{\mathit{\alpha }}_k\mathfrak{R}\left\{z^k\right\}+\sum _{k=1}^N{\mathit{\beta }}_k\mathfrak{I}\left\{z^k\right\}\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\gamma }}_k\mathfrak{R}\left\{{(z-z_0)}^{-k}\right\}+\sum _{k=1}^N{\mathit{\delta }}_k\mathfrak{I}\left\{{(z-z_0)}^{-k}\right\},\mathit{x}=(x,y)\in \overline{\mathrm{\Omega }}.\hfill \end{array}$$(3.10) ) the normal derivative ${\mathit{\partial }}_n{u}_N$ is evaluated as(4.4) $$\begin{array}{cc}\hfill & {\mathit{\partial }}_n{u}_N=\mathit{n}·\nabla u_N\hfill \\ \hfill & =\mathit{n}·({\mathit{\gamma }}_0\frac{\mathfrak{R}\{z-z_0\}}{|z-z_0{|}^2}+\sum _{k=1}^N{\mathit{\alpha }}_k\mathfrak{R}\left\{k{z}^{k-1}\right\}+\sum _{k=1}^N{\mathit{\beta }}_k\mathfrak{I}\left\{k{z}^{k-1}\right\}\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\gamma }}_k\mathfrak{R}\{-k{(z-z_0)}^{-k-1}\}+\sum _{k=1}^N{\mathit{\delta }}_k\mathfrak{I}\{-k{(z-z_0)}^{-k-1}\},\hfill \\ \hfill & {\mathit{\gamma }}_0\frac{\mathfrak{I}\{z-z_0\}}{|z-z_0{|}^2}+\sum _{k=1}^N{\mathit{\alpha }}_k\mathfrak{R}\left\{ik{z}^{k-1}\right\}+\sum _{k=1}^N{\mathit{\beta }}_k\mathfrak{I}\left\{ik{z}^{k-1}\right\}\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\gamma }}_k\mathfrak{R}\{-ki{(z-z_0)}^{-k-1}\}+\sum _{k=1}^N{\mathit{\delta }}_k\mathfrak{I}\{-ki{(z-z_0)}^{-k-1}\}).\hfill \end{array}$$(4.4) In (4.3(4.3) $$\begin{array}{c}\hfill \mathit{n}=\{\begin{array}{ccc}\cos \mathit{\vartheta }\mathit{i}+\sin \mathit{\vartheta }\mathit{j},\hfill & \text{if}\hfill & \mathit{x}\in \mathit{\partial }{\mathrm{\Omega }}_2,\hfill \\ \frac{1}{\sqrt{r^2(\mathit{\vartheta })+{r^{\prime }}^2(\mathit{\vartheta })}}[-(r^{\prime }(\mathit{\vartheta })\sin \mathit{\vartheta }+r(\mathit{\vartheta })\cos \mathit{\vartheta })\mathit{i}\hfill \\ +(r^{\prime }(\mathit{\vartheta })\cos \mathit{\vartheta }-r(\mathit{\vartheta })\sin \mathit{\vartheta })\mathit{j}],\hfill & \text{if}\hfill & \mathit{x}\in \mathit{\partial }{\mathrm{\Omega }}_1,\hfill \end{array}\end{array}$$(4.3) ), we use the central finite-difference approximation(4.5) $$\begin{array}{c}\hfill r^{\prime }({\mathit{\vartheta }}_i)\approx \frac{r_{i+1}-r_{i-1}}{4\mathit{\pi }/M_1},i=\overline{1,M_1},\end{array}$$(4.5) with the convention that $r_{N+1}=r_1,r_0=r_{M_1}$.

Since the total number of unknowns is $4N+2+M_1+2$ and the number of boundary condition collocation equations is $M_1+2M_2$ we need to take $M_2\ge 2N+2$.

Non-linear minimization

The minimization of functional (4.2(4.2) $$\begin{array}{cc}\hfill S(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta },\mathit{r},\mathit{C})& :=\sum _{j=M_1+1}^{M_1+M_2}{[u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)-f({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=M_1+1}^{M_1+M_2}{[{\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)-g^{\mathit{\epsilon }}({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=1}^{M_1}{[\mathit{\alpha }{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)+(1-\mathit{\alpha }){\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1(|\mathit{\alpha }{|}^2+|\mathit{\beta }{|}^2+|\mathit{\gamma }{|}^2+|\mathit{\delta }{|}^2)+{\mathit{\lambda }}_2\sum _{\ell =2}^{M_1}{(r_{\ell }-r_{\ell -1})}^2,\hfill \end{array}$$(4.2) ) is carried out using the MATLAB optimization toolbox routine lsqnonlin which solves non-linear least squares problems. This routine by default uses the so-called trust-region-reflective algorithm based on the interior-reflective Newton method.[52, 53] In addition, lsqnonlin does not require the user to provide the gradient and, in addition, it offers the option of imposing lower and upper bounds on the elements of the vector of unknowns. Further details regarding the application of lsqnonlin to inverse geometric problems may be found in [27].

Numerical examples

In Examples 1–5 for a single void we take the initial guess ${\mathit{r}}^0=\mathit{0}.3$, ${\mathit{\alpha }}^0={\mathit{\beta }}^0={\mathit{\gamma }}^0={\mathit{\delta }}^0=\mathit{0}$. Other reasonable initial guesses for the radial function of the void produced similar numerical results showing that the nonlinear optimization routine is robust. Further, in Examples 1–3 the centre $\mathit{C}$ is known and fixed at the origin $\mathit{0}$, whilst in Examples 4 and 5 the centre is unknown and we take the initial guess ${\mathit{C}}^0=\mathit{0}$.

All numerical simulations were performed on a Hewlett-Packard Compaq 8200 Elite PC (Intel Core i5-2400, [email protected], 4GB RAM, 32 bit).

Example 1

We first consider an example from the literature for which the exact solution is known.[4] Here we examine the case of a circular rigid inclusion where $\mathit{\alpha }=1$. In particular, we consider(5.1) $$\begin{array}{c}\hfill \begin{array}{cc}{\mathrm{\Omega }}_1\hfill & =\{(x,y)\in {\mathbb{R}}^2:x^2+y^2<R_0^2<1\},\hfill \\ {\mathrm{\Omega }}_2\hfill & =\{(x,y)\in {\mathbb{R}}^2:x^2+y^2<R^2=1\}\hfill \end{array}\end{array}$$(5.1) and(5.2) $$\begin{array}{c}\hfill u(x,y)=\log \frac{\sqrt{x^2+y^2}}{R_0}.\end{array}$$(5.2) For any $0<R_0<1$, the function $u$ satisfies problem (2.1a)–(2.1d), with(5.3) $$\begin{array}{c}\hfill f(x,y)=-\log R_0,g(x,y)=1,(x,y)\in \mathit{\partial }{\mathrm{\Omega }}_2.\end{array}$$(5.3) In the inverse problem of Example 1, we consider retrieving a circle of radius $R_0=0.5$.

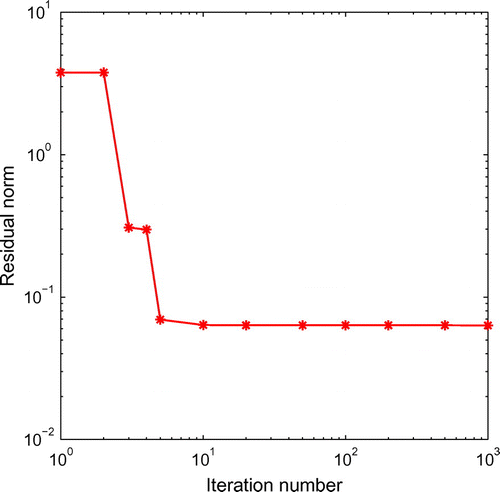
Fig. 1 Example 1: Results after 20 iterations for various numbers of degrees of freedom, no noise and no regularization.

Fig. 2 Example 1: Residual norm vs. iterations number with $M_1=M_2=48$, $N=16$, for noise $p=10\%$.

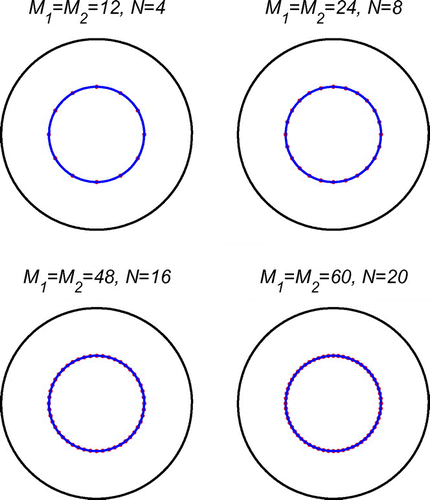
In Figure 1, we present the reconstructed curves for various numbers of degrees of freedom obtained in 20 iterations, no noise and no regularization. From this figure, it can be seen that very accurate and convergent numerical results are obtained. Although not illustrated, it is reported that the unregularized objective function (4.2(4.2) $$\begin{array}{cc}\hfill S(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta },\mathit{r},\mathit{C})& :=\sum _{j=M_1+1}^{M_1+M_2}{[u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)-f({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=M_1+1}^{M_1+M_2}{[{\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)-g^{\mathit{\epsilon }}({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=1}^{M_1}{[\mathit{\alpha }{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)+(1-\mathit{\alpha }){\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1(|\mathit{\alpha }{|}^2+|\mathit{\beta }{|}^2+|\mathit{\gamma }{|}^2+|\mathit{\delta }{|}^2)+{\mathit{\lambda }}_2\sum _{\ell =2}^{M_1}{(r_{\ell }-r_{\ell -1})}^2,\hfill \end{array}$$(4.2) ) with ${\mathit{\lambda }}_1={\mathit{\lambda }}_2=0$ decreased rapidly to a very low value of O$({10}^{-15})$. We do however present in Figure 2 the evolution of this residual norm contained in the first three terms of (4.2(4.2) $$\begin{array}{cc}\hfill S(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta },\mathit{r},\mathit{C})& :=\sum _{j=M_1+1}^{M_1+M_2}{[u_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)-f({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=M_1+1}^{M_1+M_2}{[{\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)-g^{\mathit{\epsilon }}({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=1}^{M_1}{[\mathit{\alpha }{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)+(1-\mathit{\alpha }){\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta };{\mathit{x}}_j)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1(|\mathit{\alpha }{|}^2+|\mathit{\beta }{|}^2+|\mathit{\gamma }{|}^2+|\mathit{\delta }{|}^2)+{\mathit{\lambda }}_2\sum _{\ell =2}^{M_1}{(r_{\ell }-r_{\ell -1})}^2,\hfill \end{array}$$(4.2) ), as a function of the number of iterations, for $p=10\%$ noise and $M_1=M_2=48$, $N=16$. 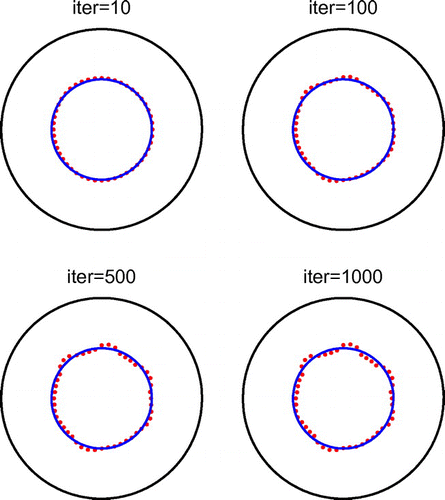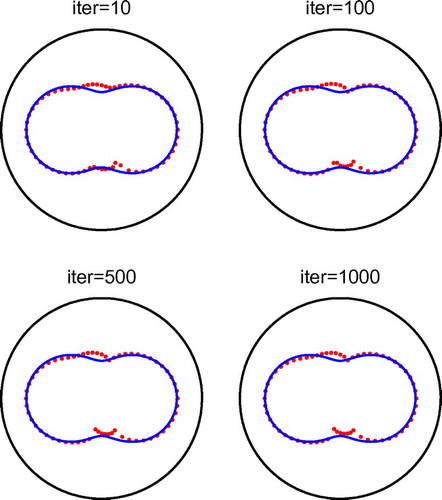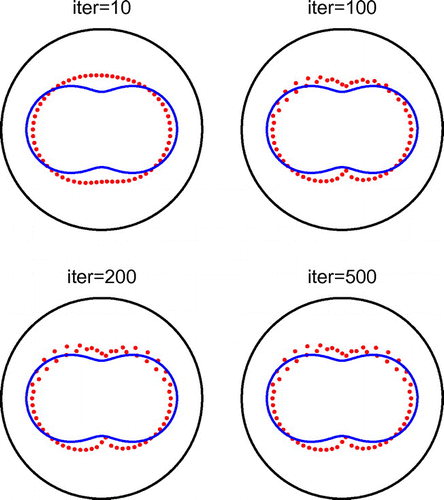The required CPU time for 1000 iterations was 388 seconds. From this figure, it can be seen that the residual norm rapidly reaches in about 10 iterations a stationary plateau which maintains horizontally, as the number of iterations increases (up to 1000). In Figure 3 we present the corresponding reconstructed curves for various numbers of iterations. From this figure, it can be seen that as the number of iterations increases instabilities start to manifest if no regularization is included.

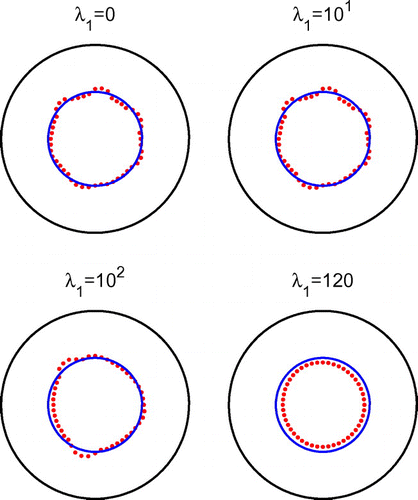
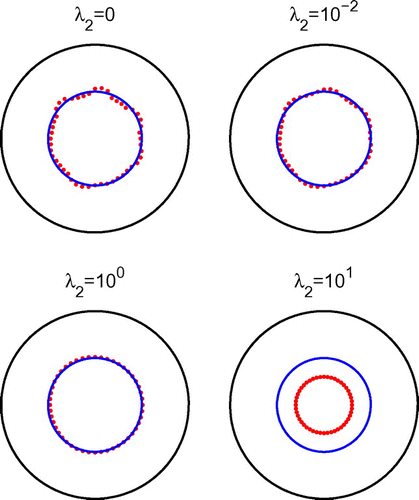
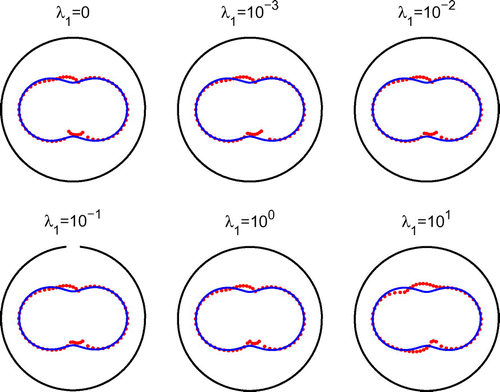
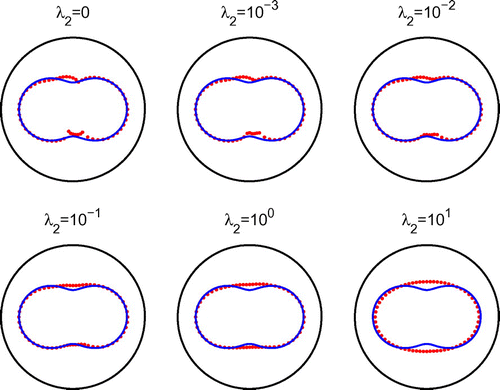
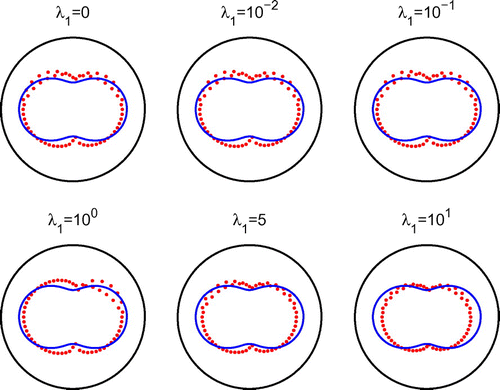
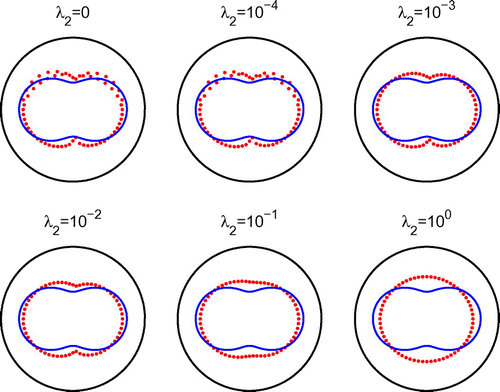
In Figure 4, we present the reconstructed curves with $p=10\%$, after 1000 iterations and various regularization parameters ${\mathit{\lambda }}_1$ with ${\mathit{\lambda }}_2=0$. The corresponding curves for various regularization parameters ${\mathit{\lambda }}_2$ with ${\mathit{\lambda }}_1=0$ are presented in Figure 5. In some instances, in this and subsequent examples, the use of regularization leads the iterative process to converge in fewer than the prescribed maximum number of iterations. Overall from Figures 4 and 5, it can be seen that regularization with either ${\mathit{\lambda }}_1=120$ or ${\mathit{\lambda }}_2=1$, respectively, does smooth out the slight oscillations recorded in the results of Figure 3 obtained after 1000 iterations with no regularization.

Fig. 3 Example 1: Results for noise $p=10\%$, no regularization and various numbers of iterations.

Fig. 4 Example 1: Results after 1000 iterations for noise $p=10\%$ and regularization with ${\mathit{\lambda }}_1$.

Fig. 5 Example 1: Results after 1000 iterations for noise $p=10\%$ and regularization with ${\mathit{\lambda }}_2$.

 

Example 2

In this example, we consider a more complicated peanut-shaped rigid inclusion whose boundary $\mathit{\partial }{\mathrm{\Omega }}_1$ is described by the radial parametrization(5.4) $$\begin{array}{c}\hfill r(\mathit{\vartheta })=\frac{3}{4}\sqrt{{\cos }^2(\mathit{\vartheta })+0.25{\sin }^2(\mathit{\vartheta })},\mathit{\vartheta }\in [0,2\mathit{\pi }),\end{array}$$(5.4) in the case of $\mathit{\alpha }=1$, which was considered in [54]. The Dirichlet data (2.1b) on $\mathit{\partial }{\mathrm{\Omega }}_2$ are taken as [54](5.5) $$\begin{array}{c}\hfill u(1,\mathit{\vartheta })=f(\mathit{\vartheta })={\mathrm{e}}^{-{\cos }^2(\mathit{\vartheta })},\mathit{\vartheta }\in [0,2\mathit{\pi }).\end{array}$$(5.5) Since in this case no analytical solution is available, the Neumann data (2.1d) is simulated by solving the direct well-posed problem (2.1a), (2.1c) and (5.5(5.5) $$\begin{array}{c}\hfill u(1,\mathit{\vartheta })=f(\mathit{\vartheta })={\mathrm{e}}^{-{\cos }^2(\mathit{\vartheta })},\mathit{\vartheta }\in [0,2\mathit{\pi }).\end{array}$$(5.5) ), when $\mathit{\partial }{\mathrm{\Omega }}_1$ is given by (5.4(5.4) $$\begin{array}{c}\hfill r(\mathit{\vartheta })=\frac{3}{4}\sqrt{{\cos }^2(\mathit{\vartheta })+0.25{\sin }^2(\mathit{\vartheta })},\mathit{\vartheta }\in [0,2\mathit{\pi }),\end{array}$$(5.4) ), using the direct CTM with $M_1=M_2=100,N=30$. In order to avoid committing an inverse crime, the inverse solver is applied using $M_1=M_2=64,N=6$.

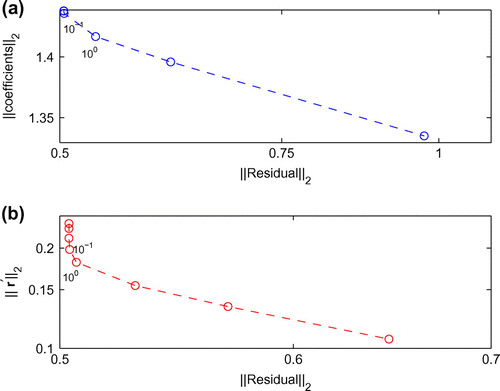
In Figure 6, we present typical examples of reconstructed curves with noise $p=10\%$ with no regularization for different numbers of iterations. In Figures 7 and 8, we present the corresponding reconstructed curves after 1000 iterations and various regularization parameters ${\mathit{\lambda }}_1$ with ${\mathit{\lambda }}_2=0$, and ${\mathit{\lambda }}_2$ with ${\mathit{\lambda }}_1=0$, respectively. The L-curves [55, 56] obtained with regularization in ${\mathit{\lambda }}_1$ or ${\mathit{\lambda }}_2$ for noise $p=10\%$ and 1000 iterations are presented in Figures 9(a) and (b), respectively. From Figure 6, it can be seen that the numerically retrieved shapes are stable and in reasonable agreement with the exact shape (5.4(5.4) $$\begin{array}{c}\hfill r(\mathit{\vartheta })=\frac{3}{4}\sqrt{{\cos }^2(\mathit{\vartheta })+0.25{\sin }^2(\mathit{\vartheta })},\mathit{\vartheta }\in [0,2\mathit{\pi }),\end{array}$$(5.4) ). This is somewhat surprising since no regularization has been imposed, but it may be that oscillations will start to appear only after a larger number of iterations than 1000. Furthermore, Figure 7 shows that regularization with ${\mathit{\lambda }}_1$ produces almost no improvement and, in fact, Figure 9(a)illustrates that an L-curve could not be obtained in this case. On the other hand, Figure 8 shows that regularization with ${\mathit{\lambda }}_2$ between ${10}^{-2}$ to 1 does produce smoother and more stable and accurate solutions with the choice of the regularization parameter given by the corner of the L-curve illustrated in Figure 9(b).

Fig. 6 Example 2: Results for noise $p=10\%$, no regularization and various numbers of iterations.

Fig. 7 Example 2: Results after 1000 iterations for noise $p=10\%$ and regularization with ${\mathit{\lambda }}_1$.

Fig. 8 Example 2: Results after 1000 iterations for noise $p=10\%$ and regularization with ${\mathit{\lambda }}_1$.

Fig. 9 Example 2: L-curves obtained with regularization in (a) ${\mathit{\lambda }}_1$ and (b) ${\mathit{\lambda }}_2$ for noise $p=10\%$.

 

Example 3

In this example, we again consider the peanut-shaped cavity whose boundary $\mathit{\partial }{\mathrm{\Omega }}_1$ is described by the radial parametrization (5.4(5.4) $$\begin{array}{c}\hfill r(\mathit{\vartheta })=\frac{3}{4}\sqrt{{\cos }^2(\mathit{\vartheta })+0.25{\sin }^2(\mathit{\vartheta })},\mathit{\vartheta }\in [0,2\mathit{\pi }),\end{array}$$(5.4) ), this time in the case of $\mathit{\alpha }=0$, which was studied in [54, 57]. As in Example 2, the Dirichlet data (2.1b) on $\mathit{\partial }{\mathrm{\Omega }}_2$ are given by (5.5(5.5) $$\begin{array}{c}\hfill u(1,\mathit{\vartheta })=f(\mathit{\vartheta })={\mathrm{e}}^{-{\cos }^2(\mathit{\vartheta })},\mathit{\vartheta }\in [0,2\mathit{\pi }).\end{array}$$(5.5) ). The Neumann data (2.1d) are simulated by solving the direct problem using the direct CTM with, $M_1=M_2=100,N=28$. In order to avoid committing an inverse crime, the inverse solver is applied using $M_1=M_2=64,N=5$.

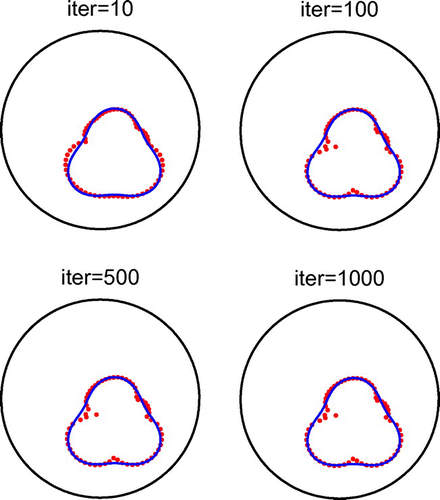
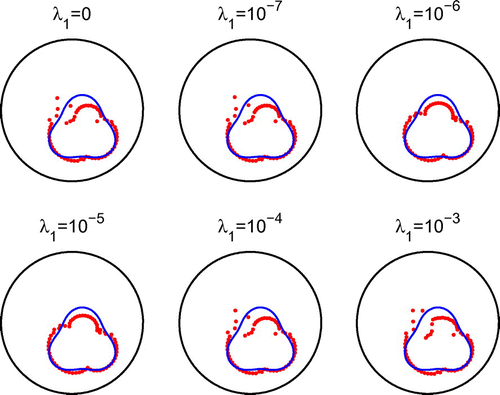
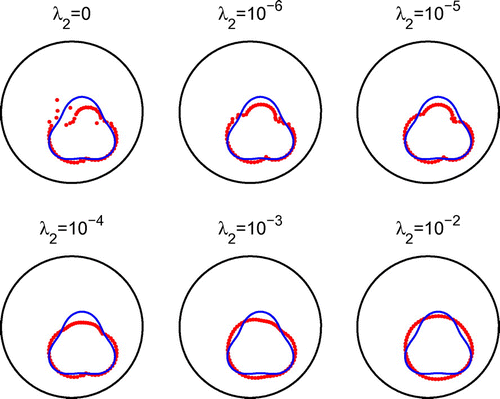
In Figure 10, we present typical examples of reconstructed curves with noise level of $p=5\%$ with no regularization for different numbers of iterations. In Figures 11 and 12, we present the corresponding reconstructed curves after 500 iterations and various regularization parameters ${\mathit{\lambda }}_1$ with ${\mathit{\lambda }}_2=0$, and ${\mathit{\lambda }}_2$ with ${\mathit{\lambda }}_1=0$, respectively. When ${\mathit{\lambda }}_2\ne 0$, it was observed that in some cases the iterative process converged in fewer than the prescribed 500 iterations. From Figures 10–12, the same conclusions as those drawn from Figures 6–8 are obtained, although the reconstructions of the cavity in Example 3 are slightly less accurate than the reconstructions of the rigid inclusion in Example 2.

Fig. 10 Example 3: Results for noise $p=5\%$ and no regularization.

Fig. 11 Example 3: Results for noise $p=5\%$ and regularization with ${\mathit{\lambda }}_1$.

Fig. 12 Example 3: Results for noise $p=5\%$ and regularization with ${\mathit{\lambda }}_2$.

 

Example 4

We consider a rigid inclusion ${\mathrm{\Omega }}_1$, i.e. $\mathit{\alpha }=1$, described by $X=0.5,Y=-1$, $R=3.5$ and the radial parametrization(5.6) $$\begin{array}{c}\hfill r(\mathit{\vartheta })=1.52-0.24\sin (3\mathit{\vartheta }),\mathit{\vartheta }\in [0,2\mathit{\pi }).\end{array}$$(5.6) This example, which was considered in [58] for the Stokes equations in slow viscous flow and in [27], is more difficult than the previous examples because of the fact that we now consider the centre of the cavity as unknown. The Neumann data (2.1d) are simulated by solving the direct problem using the MFS with 400 sources and 400 collocation points. The inverse CTM solver is applied using $M_1=M_2=64,N=6$. The starting position of the centre in the iterative process was taken to be the origin.

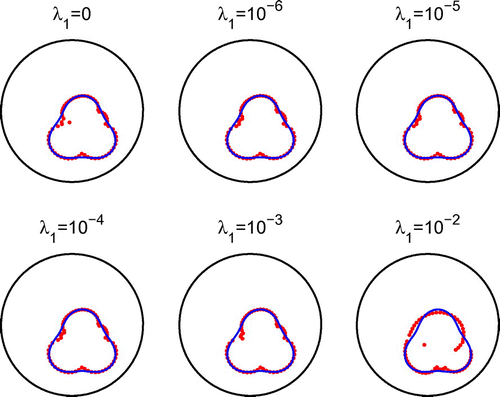
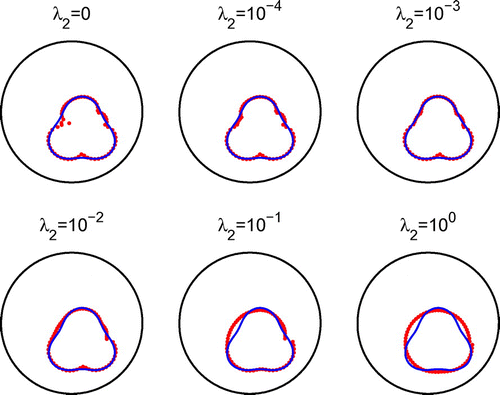
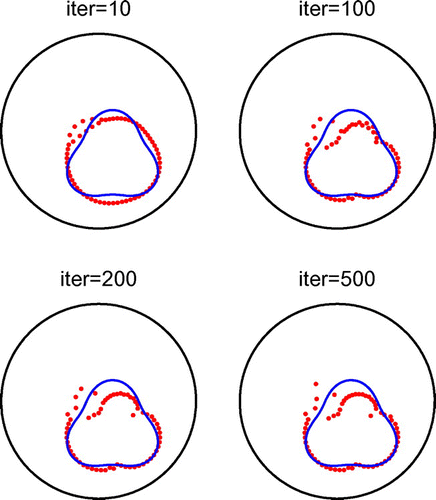
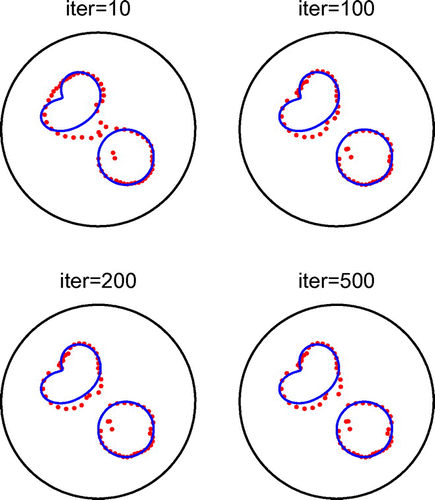
In Figure 13, we present typical examples of reconstructed curves with noise level of $p=5\%$ with no regularization for different numbers of iterations. In Figures 14 and 15, we present the corresponding reconstructed curves after 1000 iterations and various regularization parameters ${\mathit{\lambda }}_1$ with ${\mathit{\lambda }}_2=0$, and ${\mathit{\lambda }}_2$ with ${\mathit{\lambda }}_1=0$, respectively. From Figures 13–15, the same conclusions as those drawn from Figures 16–18 for Example 2 and Figures 10–12 for Example 3 are obtained. This shows that the reconstruction method also performs well when the centre of the star-shaped void is unknown.

Fig. 13 Example 4: Results for noise $p=5\%$, no regularization and various numbers of iterations.

Fig. 14 Example 4: Results after 1000 iterations for noise $p=5\%$ and regularization with ${\mathit{\lambda }}_1$.

Fig. 15 Example 4: Results after 1000 iterations for noise $p=5\%$ and regularization with ${\mathit{\lambda }}_2$.

 

Example 5

We finally consider the same obstacle as in Example 4, given by (5.6(5.6) $$\begin{array}{c}\hfill r(\mathit{\vartheta })=1.52-0.24\sin (3\mathit{\vartheta }),\mathit{\vartheta }\in [0,2\mathit{\pi }).\end{array}$$(5.6) ) but in the case of $\mathit{\alpha }=0$, i.e. ${\mathrm{\Omega }}_1$ is a cavity. The numerical details are the same as in Example 4.

In Figure 16, we present the results obtained for different numbers of iterations, with $p=5\%$ noise and no regularization. In Figures 17 and 18, we present the corresponding reconstructed curves after 500 iterations and various regularization parameters ${\mathit{\lambda }}_1$ with ${\mathit{\lambda }}_2=0$, and ${\mathit{\lambda }}_2$ with ${\mathit{\lambda }}_1=0$, respectively. From Figures 16 and 17, it can be seen that the numerically obtained shapes with ${\mathit{\lambda }}_1={\mathit{\lambda }}_2=0$, or ${\mathit{\lambda }}_2=0$, ${\mathit{\lambda }}_1>0$, are unstable, whilst from Figure 18 it can be observed that regularization with ${\mathit{\lambda }}_2$ between ${10}^{-4}$ and ${10}^{-2}$ produces smoother stable reconstructions.

We close this section by some discussion on the number of basis functions used in the CTM compared to that used in the MFS. The number of basis functions in (3.2(3.2) $$\begin{array}{c}\hfill \{1,\log |z|,\mathfrak{R}(z^n),\mathfrak{I}(z^k),\mathfrak{R}(z^{-k}),\mathfrak{I}(z^{-k});z=x+iy,k\in {\mathbb{N}}^{\ast }\},\end{array}$$(3.2) ) is $4N_{\mathit{CTM}}+2$, whilst in an MFS implementation [4, 8] the corresponding number of non-singular fundamental solutions is $2N_{\mathit{MFS}}$. Compared to the the $N_{\mathit{MFS}}$, due to the higher ill-conditioning $N_{\mathit{CTM}}$ cannot be increased too much and there is also a trade-off between the number of basis functions, the number of iterations and the amount of noise. Both meshless CTM and MFS follow the uncertainty principle/relation, e.g. for exact data, the higher ill-conditioning the better the accuracy [59]. However, this issue becomes not so important and somewhat computationally irrelevant for noisy data which, for ill-posed problems, will be amplified and thus produce unstable unrealistic solutions if no regularization is employed.

Fig. 16 Example 5: Results for noise $p=5\%$, no regularization and various numbers of iterations.

Fig. 17 Example 5: Results after 500 iterations for noise $p=5\%$ and regularization with ${\mathit{\lambda }}_1$.

Fig. 18 Example 5: Results after 500 iterations for noise $p=5\%$ and regularization with ${\mathit{\lambda }}_2$.

 

Extension to multiple voids

The CTM analysis performed so far showed the successful implementation of this method for the identification of a single void. In this section, we extend the analysis to multiple voids which may contain both cavities and rigid inclusions. For the sake of clarity, we describe the formulation for the case of two voids. Therefore, we consider the inverse problem(6.1) $$\begin{array}{c}\hfill \mathrm{\Delta }u=0\text{in}\mathrm{\Omega },\end{array}$$(6.1) subject to the boundary conditions(6.2) $$\begin{array}{c}\hfill u=f\text{and}{\mathit{\partial }}_{n}u=g\text{on}\mathit{\partial }{\mathrm{\Omega }}_2,\end{array}$$(6.2) and the homogeneous boundary conditions(6.3) $$\begin{array}{c}\hfill {\mathit{\alpha }}_{1}u+(1-{\mathit{\alpha }}_1){\mathit{\partial }}_{n}u=0\text{on}\mathit{\partial }{\mathrm{\Omega }}_1^a,\text{where}{\mathit{\alpha }}_1\in \{0,1\},\end{array}$$(6.3) and(6.4) $$\begin{array}{c}\hfill {\mathit{\alpha }}_{2}u+(1-{\mathit{\alpha }}_2){\mathit{\partial }}_{n}u=0\text{on}\mathit{\partial }{\mathrm{\Omega }}_1^b,\text{where}{\mathit{\alpha }}_2\in \{0,1\}.\end{array}$$(6.4) Here ${\mathrm{\Omega }}_1^a$ and ${\mathrm{\Omega }}_1^b$ are two disjoint voids, such that ${\mathrm{\Omega }}_1^a\cup {\mathrm{\Omega }}_1^b={\mathrm{\Omega }}_1$ and $\overline{{\mathrm{\Omega }}_1^a}\cap \overline{{\mathrm{\Omega }}_1^b}=\varnothing$. The outer boundary collocation points are chosen as(6.5) $$\begin{array}{c}\hfill {\mathit{x}}_{M_1+M_2+\ell }=R(\cos {\stackrel{\sim }{\mathit{\vartheta }}}_{\ell },\sin {\stackrel{\sim }{\mathit{\vartheta }}}_{\ell }),\ell =\overline{1,M_3},\end{array}$$(6.5) where ${\stackrel{\sim }{\mathit{\vartheta }}}_{\ell }=\frac{2\mathit{\pi }(\ell -1)}{M_3},\ell =\overline{1,M_3}$.

We further assume that the unknown boundaries $\mathit{\partial }{\mathrm{\Omega }}_1^a$ and $\mathit{\partial }{\mathrm{\Omega }}_1^b$ are a smooth, star-like curves with respect to their centres which have unknown coordinates $(X^a,Y^a)$ and $(X^b,Y^b)$, respectively. This means that their equations in polar coordinates can be written as(6.6) $$\begin{array}{c}\hfill x=X^a+r^a(\mathit{\vartheta })\cos \mathit{\vartheta },y=Y^a+r^a(\mathit{\vartheta })\sin \mathit{\vartheta },\\ \hfill x=X^b+r^b(\mathit{\vartheta })\cos \mathit{\vartheta },y=Y^b+r^b(\mathit{\vartheta })\sin \mathit{\vartheta },\mathit{\vartheta }\in [0,2\mathit{\pi }),\end{array}$$(6.6) where $r^a$ and $r^b$ are smooth $2\mathit{\pi }-$periodic functions.

The discretized forms of (6.3(6.3) $$\begin{array}{c}\hfill {\mathit{\alpha }}_{1}u+(1-{\mathit{\alpha }}_1){\mathit{\partial }}_{n}u=0\text{on}\mathit{\partial }{\mathrm{\Omega }}_1^a,\text{where}{\mathit{\alpha }}_1\in \{0,1\},\end{array}$$(6.3) ) and (6.4(6.4) $$\begin{array}{c}\hfill {\mathit{\alpha }}_{2}u+(1-{\mathit{\alpha }}_2){\mathit{\partial }}_{n}u=0\text{on}\mathit{\partial }{\mathrm{\Omega }}_1^b,\text{where}{\mathit{\alpha }}_2\in \{0,1\}.\end{array}$$(6.4) ) for $\mathit{\partial }{\mathrm{\Omega }}_1^a$ and $\mathit{\partial }{\mathrm{\Omega }}_1^b$ become(6.7) $$\begin{array}{c}\hfill r_k^a=r^a({\mathit{\vartheta }}_k),k=\overline{1,M_1}\text{and}{r}_{\ell }^b=r^b({\mathit{\vartheta }}_{\ell })\ell =\overline{1,M_2}.\end{array}$$(6.7) We choose the inner boundary collocation points as(6.8) $$\begin{array}{cc}\hfill {\mathit{x}}_k& =(X^a,Y^a)+r_k^a(\cos {\mathit{\vartheta }}_k,\sin {\mathit{\vartheta }}_k),k=\overline{1,M_1},\hfill \\ \hfill {\mathit{x}}_k& =(X^b,Y^a)+r_k^b(\cos {\mathit{\vartheta }}_k,\sin {\mathit{\vartheta }}_k),k=\overline{M_1+1,M_1+M_2}.\hfill \end{array}$$(6.8) Since we have more than one void and their centres are not at the origin, the basis (3.2(3.2) $$\begin{array}{c}\hfill \{1,\log |z|,\mathfrak{R}(z^n),\mathfrak{I}(z^k),\mathfrak{R}(z^{-k}),\mathfrak{I}(z^{-k});z=x+iy,k\in {\mathbb{N}}^{\ast }\},\end{array}$$(3.2) ) needs to be modified as in the doubly-connected domain, to (see [48])(6.9) $$\begin{array}{c}\hfill \{1,\log |z-z^a|,\log |z-z^b|,\mathfrak{R}(z^n),\mathfrak{I}(z^n),\mathfrak{R}({(z-z^a)}^{-n}),\mathfrak{I}({(z-z^a)}^{-n}),\\ \hfill \mathfrak{R}({(z-z^b)}^{-n}),\mathfrak{I}({(z-z^b)}^{-n});z=x+iy,n\in \mathbb{N}\},\end{array}$$(6.9) where $z^a=X^a+{\mathit{iY}}^a,z^b=X^b+{\mathit{iY}}^b$ and therefore the TCM approximation becomes(6.10) $$\begin{array}{c}\hfill \begin{array}{cc}{u}_N(\mathit{\alpha },\mathit{\beta },{\mathit{\gamma }}^a,{\mathit{\gamma }}^b,{\mathit{\delta }}^a,{\mathit{\delta }}^b;\mathit{x})\hfill & ={\mathit{\alpha }}_0+{\mathit{\gamma }}_0^a\log |z-z^a|+{\mathit{\gamma }}_0^b\log |z-z^b|\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\alpha }}_k\mathfrak{R}\left\{z^k\right\}+\sum _{k=1}^N{\mathit{\beta }}_k\mathfrak{I}\left\{z^k\right\}\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\gamma }}_k^a\mathfrak{R}\left\{{(z-z^a)}^{-k}\right\}+\sum _{k=1}^N{\mathit{\delta }}_k^a\mathfrak{I}\left\{{(z-z^a)}^{-k}\right\}\hfill \\ \hfill & +\sum _{k=1}^N{\mathit{\gamma }}_k^b\mathfrak{R}\left\{{(z-z^b)}^{-k}\right\}+\sum _{k=1}^N{\mathit{\delta }}_k^b\mathfrak{I}\left\{{(z-z^b)}^{-k}\right\},\hfill \end{array}\end{array}$$(6.10) for $\mathit{x}=(x,y)\in \overline{\mathrm{\Omega }}$.

The coefficients ${\left({\mathit{\alpha }}_k\right)}_{k=\overline{0,N}},{\left({\mathit{\beta }}_k\right)}_{k=\overline{1,N}},{\left({\mathit{\gamma }}_k^{\ell }\right)}_{k=\overline{0,N},\ell =a,b},{\left({\mathit{\delta }}_k^{\ell }\right)}_{k=\overline{1,N},\ell =a,b}$ in (6.9(6.9) $$\begin{array}{c}\hfill \{1,\log |z-z^a|,\log |z-z^b|,\mathfrak{R}(z^n),\mathfrak{I}(z^n),\mathfrak{R}({(z-z^a)}^{-n}),\mathfrak{I}({(z-z^a)}^{-n}),\\ \hfill \mathfrak{R}({(z-z^b)}^{-n}),\mathfrak{I}({(z-z^b)}^{-n});z=x+iy,n\in \mathbb{N}\},\end{array}$$(6.9) ), the radii ${\left(r_k^a\right)}_{k=\overline{1,M_1}},{\left(r_k^b\right)}_{k=\overline{1,M_2}}$ in (6.5(6.5) $$\begin{array}{c}\hfill {\mathit{x}}_{M_1+M_2+\ell }=R(\cos {\stackrel{\sim }{\mathit{\vartheta }}}_{\ell },\sin {\stackrel{\sim }{\mathit{\vartheta }}}_{\ell }),\ell =\overline{1,M_3},\end{array}$$(6.5) ), and the coordinates of the centres $(X^a,Y^a),(X^b,Y^b)$ can be determined by imposing the boundary conditions in a least-squares sense. This leads to the minimization of the functional(6.11) $$\begin{array}{cc}\hfill & S(\mathit{\alpha },\mathit{\beta },{\mathit{\gamma }}^a,{\mathit{\gamma }}^b,{\mathit{\delta }}^a,{\mathit{\delta }}^b,{\mathit{r}}^a,{\mathit{r}}^b,\mathit{C})\hfill \\ \hfill & :=\sum _{j=M_1+M_2+1}^{M_1+M_2+M_3}{[u_N(\mathit{\alpha },\mathit{\beta },{\mathit{\gamma }}^a,{\mathit{\gamma }}^b,{\mathit{\delta }}^a,{\mathit{\delta }}^b;{\mathit{x}}_j)-f({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=M_1+M_2+1}^{M_1+M_2+M_3}{[{\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },{\mathit{\gamma }}^a,{\mathit{\gamma }}^b,{\mathit{\delta }}^a,{\mathit{\delta }}^b;{\mathit{x}}_j)-g^{\mathit{\epsilon }}({\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=1}^{M_1}{[{\mathit{\alpha }}_1{u}_N(\mathit{\alpha },\mathit{\beta },{\mathit{\gamma }}^a,{\mathit{\gamma }}^b,{\mathit{\delta }}^a,{\mathit{\delta }}^b;{\mathit{x}}_j)+(1-{\mathit{\alpha }}_1){\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },{\mathit{\gamma }}^a,{\mathit{\gamma }}^b,{\mathit{\delta }}^a,{\mathit{\delta }}^b;{\mathit{x}}_j)]}^2\hfill \\ \hfill & +\sum _{j=M_1+1}^{M_1+M_2}{[{\mathit{\alpha }}_2{u}_N(\mathit{\alpha },\mathit{\beta },{\mathit{\gamma }}^a,{\mathit{\gamma }}^b,{\mathit{\delta }}^a,{\mathit{\delta }}^b;{\mathit{x}}_j)+(1-{\mathit{\alpha }}_2){\mathit{\partial }}_n{u}_N(\mathit{\alpha },\mathit{\beta },{\mathit{\gamma }}^a,{\mathit{\gamma }}^b,{\mathit{\delta }}^a,{\mathit{\delta }}^b;{\mathit{x}}_j)]}^2\hfill \\ \hfill & \begin{array}{c}+{\mathit{\lambda }}_1(|\mathit{\alpha }{|}^2+|\mathit{\beta }{|}^2+|{\mathit{\gamma }}^a{|}^2+|{\mathit{\gamma }}^b{|}^2+|{\mathit{\delta }}^a{|}^2+|{\mathit{\delta }}^b{|}^2)+{\mathit{\lambda }}_2^a\sum _{\ell =2}^{M_1}{(r_{\ell }^a-r_{\ell -1}^a)}^2\hfill \\ +{\mathit{\lambda }}_2^b\sum _{\ell =2}^{M_2}{(r_{\ell }^b-r_{\ell -1}^b)}^2,\hfill \end{array}\hfill \end{array}$$(6.11) where ${\mathit{\lambda }}_1,{\mathit{\lambda }}_2^a,{\mathit{\lambda }}_2^b\ge 0$ are regularization parameters to be prescribed, ${\mathit{r}}^a={[r_1^a,r_2^a,\dots ,r_N^a]}^T$, ${\mathit{r}}^b={[r_1^b,r_2^b,\dots ,r_N^b]}^T$, and $\mathit{C}={[X^a,Y^a,X^b,Y^b]}^T$. The number of unknowns is $6N+3+M_1+M_2+4$ and the number of boundary collocation equations $M_1+M_2+2M_3$, and thus we need to take $2M_3\ge 6N+7$.

Fig. 19 Example 6: Results for noise $p=5\%$, no regularization and various numbers of iterations.

Fig. 20 Example 6: Results after 500 iterations for noise $p=5\%$ and regularization with ${\mathit{\lambda }}_1$.

Fig. 21 Example 6: Results after 500 iterations for noise $p=5\%$ and regularization with ${\mathit{\lambda }}_2$.

 

Example 6

We consider the case when two rigid inclusions (${\mathit{\alpha }}_1={\mathit{\alpha }}_2=1$) ${\mathrm{\Omega }}_1^a$ and ${\mathrm{\Omega }}_1^b$ are present. The domain ${\mathrm{\Omega }}_1^a$ is a disk of radius 1, with centre ${\mathit{C}}^a=(X^a,Y^a)=(1,-1)$, while the domain ${\mathrm{\Omega }}_1^b$ is described by the radial parametrization(6.12) $$\begin{array}{c}\hfill r(\mathit{\vartheta })=\frac{1+0.8\cos (\mathit{\vartheta })+0.2\sin (2\mathit{\vartheta })}{1+0.7\cos (\mathit{\vartheta })},\mathit{\vartheta }\in [0,2\mathit{\pi }),\end{array}$$(6.12) and has centre ${\mathit{C}}^b=(X^b,Y^b)=(-1,1)$. In this example which was also examined in [57] we take $R=3.5$. The Neumann data (2.1d) are simulated by solving the direct problem using the MFS with 600 singularities and 600 collocation points. The inverse TCM solver is applied using $M_1=M_2=32,M_3=64,N=6$. We also take the initial guesses ${({\mathit{r}}^a)}^0={({\mathit{r}}^b)}^0=\mathit{0}.3$, ${\mathit{\alpha }}^0={\mathit{\beta }}^0={({\mathit{\gamma }}^a)}^0={({\mathit{\gamma }}^b)}^0={({\mathit{\delta }}^a)}^0={({\mathit{\delta }}^b)}^0=\mathit{0}$, ${({\mathit{C}}^a)}^0=(0.5,-0.5)$ and ${({\mathit{C}}^b)}^0=(-0.5,0.5)$.

In Figure 19, we present the results obtained for different numbers of iterations, no regularization, and $p=5\%$ noise. In Figures 20 and 21, we present the corresponding reconstructed curves after 500 iterations, and various levels of regularization ${\mathit{\lambda }}_1$ with ${\mathit{\lambda }}_2={\mathit{\lambda }}_2^a={\mathit{\lambda }}_2^b=0$, and ${\mathit{\lambda }}_1=0$ with ${\mathit{\lambda }}_2={\mathit{\lambda }}_2^a={\mathit{\lambda }}_2^b$, respectively. Overall, Figures 19–21 illustrate that the CTM can successfully retrieve voids having two connected components.

Conclusions

We have applied the CTM combined with a non-linear least-squares minimization for the solution of several inverse geometric problems including the detection of voids such as rigid inclusions and cavities. The centre of the assumed star-shaped void may or may not be known. For several test examples involving various shapes, the method performed well, producing accurate and stable reconstructions with relatively few terms in the approximating expansion of the solution. In some of the cases where cavities were considered ill-conditioning was observed. This is due to the inherent ill-conditioning of the CTM. Regularization appears to alleviate to a great extent the ill-posedness of this problem. The reconstruction of multiple voids is also possible with the proposed method.

Extensions of the present approach could include applications to inverse geometric problems governed by the Helmholtz and biharmonic equations, as well as applications to three-dimensional inverse geometric problems by using the appropriate bases listed in [20, p.32–33].

Acknowledgments

The authors wish to thank Professor Nick Papamichael for many enlightening discussions and are also grateful to the University of Cyprus for supporting this research. L. Marin also acknowledges the financial support received from the Romanian National Authority for Scientific Research, CNCS–UEFISCDI, project number PN–II–ID–PCE–2011–3–0521.