Two-step shape optimization methodology for designing free-form shells

Abstract

In this paper, a two-step free-form shape optimization methodology is presented for designing the optimal shapes of shell structures concerning stiffness maximization problem subject to a volume constraint. With this methodology, the optimization design problem of a shell structure is divided into two steps which consist a surface optimization step and a boundary optimization step. The shape sensitivities, called shape gradient function, are theoretically derived for both steps using the Lagrange multiplier method and the formula of the material derivative. The optimal shape is determined by applying the derived each shape gradient function on a design surface or boundaries to the $H^1$ gradient method. By the two-step free-form optimization, a smooth optimal shell with free-form surface and boundaries can be obtained to be a weight reduced form with high stiffness. Several calculated examples are presented to verify the validity and practical utility of the proposed methodology.

Keywords:

• two-step shape optimization
• curvature distribution
• boundary shape
• shell structures
• parameter-free

Introduction

In shape optimization of the free-form shell structures, the geometrical representation can be based on parametric method and parameter-free method (or node-based method).[1]

The parametric method needs shape parametrization in advance, and basis vectors and parametric surface such as Bezier surface and non-uniform rational B-spline (NURBS) are often used for the description of free-form shells.[2] This method is effective to the reduction of the design variables and most of the optimization methods proposed in previous studies are parametric methods.[3–7] However, the parametrization needs knowledge and experience, and with complication of the forms, parameter selection is troublesome for the designers. Moreover, the obtained shape by the parametric method is strongly influenced by the selected parameters, especially for the basis vector method.

In the node-based method, nodal coordinates are taken as design variables. Due to the result is not restricted to the parametrization, this method gives more freedom to the optimization process and the obtained optimal shape is near a result of natural choice. The node-based method has needed to overcome problems such as the large number of design variables and the jagged boundaries which were pointed out in one of the earliest works on shape optimization by Braibant and Fleury [8]. Bletzinger et al. used the adjoint variable method in the sensitivity analysis to solve the large-scale design variables problem, and the use of minimal surface and filtering technique has been proposed as a solution to the jagged boundary problem.[9] Scherer et al. proposed a fictitious energy approach to constrain the shape change as a new regularization technique.[10] Shimoda et al. have previously proposed a parameter-free optimization method for free-form shells based on the traction method, which is a type of gradient method in a Hilbert space.[11]

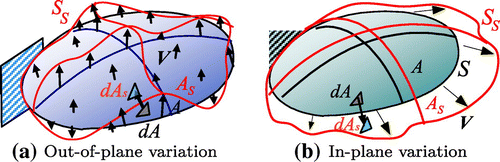
In this method, the adjoint variable method is also employed and the use of force for varying the surface reduces the objective functional while maintaining boundary smoothness.[12–14] In the shape optimization of the free-form shells performed by Shimoda et al., two kinds of shape variations was considered as design variables. One is out-of-plane shape variation, which varies the shape of a shell in the normal direction to the surface. The optimal surface shape can be obtained by optimization of the out-of-plane shape variation. Comparing to the initial shape, the optimized surface shape can substantially improve the structural characteristics.[12, 13] The other is in-plane shape variation, which changes a shell in the tangential direction to the surface. The optimal boundary shape can be obtained by optimizing the in-plane shape variation while maintaining the curvature distribution of the surface. The boundary shape optimization is effective to determine the detailed form of a shell, to find a weight saving form and to improve the structural characteristics, especially when performed in the final designing stage.[14]

For designing free-form shells with both light weight and high mechanical performance, this paper presents a new shape optimization methodology for designing optimal surface and boundary shapes of shell structures by combining the out-of-plane and in-plane free-form optimization method with two-step, which is a parameter-free method without any shape parametrization. In the first step, a shape is varied in the normal direction to the surface in order to determine the optimal curvature distribution. In the second step, the optimal boundary shape is determined while maintaining the optimal curvature distribution of the surface determined in the first step. As an application of this methodology, the mean compliance minimization problem of shell structures is dealt with in this paper. The problem is formulated as a distributed-parameter shape optimization problem, and a shape sensitivity, called a shape gradient function, is theoretically derived for both steps using the Lagrange multiplier method and the formula of the material derivative. Each shape gradient function on a design surface or boundaries is used as a distributed external force in each step to determine the optimal shape, which is the $H^1$ gradient method modified by one of the authors for shell design problem from the original one.[12–14] With this approach, the jagged-shape problem [8] caused by parameter-free method is resolved, and a smooth optimal shell with free-form surface and boundaries can be obtained. Several calculated examples are presented to demonstrate the effectiveness and practical utility of the proposed methodology.

Modelling and governing equation of shell structure

As shown in Figure 1(a) and Equations (1)–(3), consider a shell having an initial bounded domain $\mathrm{\Omega }\subset {\mathbb{R}}^{\mathbb{3}}$ ( boundary of $\mathit{\partial }\mathrm{\Omega }$ ), mid-area $A$ (boundary of $\mathit{\partial }A$ ), side surface $S$ and plate thickness $h$. It is assumed for simplicity that a shell structure occupying a bounded domain is a set of piecewise flat surfaces as shown in Figure 1(b).

Fig. 1 Shell geometry assembled by infinitesimal flat surfaces.

(1) $$\begin{array}{cc}\hfill & \mathrm{\Omega }=\{(x_1,x_2,x_3)\in {\mathbb{R}}^{\mathbb{3}}|(x_1,x_2)\in A\subset {\mathbb{R}}^{\mathbb{2}},x_3\in (-h/2,h/2)\},\hfill \end{array}$$(1) (2) $$\begin{array}{cc}\hfill & \mathrm{\Omega }=A\times (-h/2,h/2),\hfill \end{array}$$(2) (3) $$\begin{array}{cc}\hfill & S=\mathit{\partial }A\times (-h/2,h/2).\hfill \end{array}$$(3) It is assumed that the mapping of the local coordinate system $(x_1,x_2,0)$ which gives the position of the mid-area of the plate, to the global coordinate system $(X_1,X_2,X_3)$, i.e. $\mathrm{\Phi }:(x_1,x_2,0)\in {\mathbb{R}}^{\mathbb{3}}\mapsto (X_1,X_2,X_3)\in {\mathbb{R}}^{\mathbb{3}}$ , is piecewise smooth. Various finite elements have been developed for conducting a finite element analysis (FEA) of shell structures. While linear quadrilateral or triangular shell elements are often used to discretize shell structures, planar triangular shell elements were used in this work. The Mindlin–Reissner plate theory is applied concerning plate bending, and coupling of the membrane stiffness and bending stiffness is ignored. Using the sign convention in Figure 1(c), the displacement expressed by the local coordinates $\mathbf{u}=\{u_i{\}}_{i=1,2,3}$ is considered by dividing it into the displacement in the in-plane direction $\{u_{\mathit{\alpha }}{\}}_{\mathit{\alpha }=1,2}$ and the displacement in the out-of-plane direction. In this paper, the subscripts of the Greek letters are expressed as $\mathit{\alpha }=1,2$, and the tensor subscript notation with respect to $\mathit{\alpha }=1,2$ uses Einstein’s summation convention and a partial differential notation for the spatial coordinates ${(·)}_{,i}=\mathit{\partial }(·)/\mathit{\partial }x{}_i$. The Mindlin–Reissner plate theory [15] posits that(4) $$\begin{array}{cc}\hfill & {\mathit{\sigma }}_{33}=0,\hfill \end{array}$$(4) (5) $$\begin{array}{cc}\hfill & u_{\mathit{\alpha }}(x_1,x_2,x_3)\equiv u_{0\mathit{\alpha }}(x_1,x_2)-x_3{\mathit{\theta }}_{\mathit{\alpha }}(x_1,x_2),\hfill \end{array}$$(5) (6) $$\begin{array}{cc}\hfill & u_3(x_1,x_2,x_3)\equiv w(x_1,x_2),\hfill \end{array}$$(6) where Equation (4) indicates a plane stress condition. $\{u_{0\mathit{\alpha }}{\}}_{\mathit{\alpha }=1,2}$, $w$ and $\{{\mathit{\theta }}_{\mathit{\alpha }}{\}}_{\mathit{\alpha }=1,2}$ express the in-plane displacement, out-of-plane displacement and rotational angle of the mid-area of the plate, respectively. Then, the weak form equation in terms of $({\mathit{u}}_{\mathbf{0}}$,$w$,$\mathit{\theta })\in U$ can be expressed as Equation (7) by substituting Equations (4)–(6) into the variational equation (i.e. weak form) of the three-dimensional linear elastic theory, eliminating ${\mathit{\epsilon }}_{33}$ and considering the relationship ${\int }_{\mathrm{\Omega }}(·)d\mathrm{\Omega }={\int }_A{\int }_{-h/2}^{h/2}(·)\mathit{dzdA}$ .

As shown in Figure 1(b), forces acting relative to the local coordinate system $(x_1,x_2)$ on the domain $\mathit{\text{A}}$ and the boundary $\mathit{\partial }{\mathit{\text{A}}}_g(\subset \mathit{\partial }\mathit{\text{A}})$ are defined as follows: an out-of-plane load $q$ per unit area, an in-plane load $\mathbf{f}=\{f_{\mathit{\alpha }}{\}}_{\mathit{\alpha }=1,2}$, and an out-of-plane moment $\mathbf{m}=\{m_{\mathit{\alpha }}{\}}_{\mathit{\alpha }=1,2}$ per unit area, an in-plane load $\mathbf{N}=\{N_{\mathit{\alpha }}{\}}_{\mathit{\alpha }=1,2}$ per unit length, a shearing force $\mathit{Q}$ per unit length and a bending moment $\mathbf{M}=\{M_{\mathit{\alpha }}{\}}_{\mathit{\alpha }=1,2}$ per unit length.(7) $$\begin{array}{c}\hfill a(({\mathit{u}}_{\mathbf{0}},w,\mathit{\theta }),({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }}))=l({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }}),({\mathit{u}}_0,w,\mathit{\theta })\in U,\forall ({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }})\in U,\end{array}$$(7) where $(\overline{5\mathit{mu}})$ expresses a variation. In addition, the bilinear form $a(·,·)$ and the linear form $l(·)$ are defined respectively in Equations (8) and (9).(8) $$\begin{array}{cc}\hfill a& (({\mathit{u}}_{\mathbf{0}},w,\mathit{\theta }),({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }}))\hfill \\ \hfill & ={\int }_{\mathrm{\Omega }}\{C_{\mathit{\alpha }\mathit{\beta }\mathit{\gamma }\mathit{\delta }}(u_{0\mathit{\alpha },\mathit{\beta }}-x_3{\mathit{\theta }}_{\mathit{\alpha },\mathit{\beta }})({\overline{u}}_{0\mathit{\gamma },\mathit{\delta }}-x_3{\overline{\mathit{\theta }}}_{\mathit{\gamma },\mathit{\delta }})+C_{\mathit{\alpha }\mathit{\beta }}^S(w_{,\mathit{\alpha }}-{\mathit{\theta }}_{\mathit{\alpha }})({\overline{w}}_{,\mathit{\beta }}-{\overline{\mathit{\theta }}}_{\mathit{\beta }})\}d\mathrm{\Omega }\hfill \\ \hfill & ={\int }_A\{c_{\mathit{\alpha }\mathit{\beta }\mathit{\gamma }\mathit{\delta }}^B{\mathit{\theta }}_{(\mathit{\gamma },\mathit{\delta })}{\overline{\mathit{\theta }}}_{(\mathit{\alpha },\mathit{\beta })}+c_{\mathit{\alpha }\mathit{\beta }\mathit{\gamma }\mathit{\delta }}^M{u}_{0\mathit{\gamma },\mathit{\delta }}{\overline{u}}_{0\mathit{\alpha },\mathit{\beta }}+{\mathit{kc}}_{\mathit{\alpha }\mathit{\beta }}^S{\mathit{\gamma }}_{\mathit{\alpha }}{\overline{\mathit{\gamma }}}_{\mathit{\beta }}\}\mathit{dA},\hfill \\ \hfill & l({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }})={\int }_A(f_{\mathit{\alpha }}{\overline{u}}_{0\mathit{\alpha }}-m_{\mathit{\alpha }}{\overline{\mathit{\theta }}}_{\mathit{\alpha }}+q\overline{w})dA+{\int }_{\mathit{\partial }{A}_g}(N_{\mathit{\alpha }}{\overline{u}}_{0\mathit{\alpha }}\mathit{ds}-M_{\mathit{\alpha }}{\overline{\mathit{\theta }}}_{\mathit{\alpha }}+Q\overline{w})\mathit{ds},\hfill \end{array}$$(8) where $\{C_{\mathit{\alpha }\mathit{\beta }\mathit{\gamma }\mathit{\delta }}{\}}_{\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta }=1,2}$ and $\{C_{\mathit{\alpha }\mathit{\beta }}^S{\}}_{\mathit{\alpha },\mathit{\beta }=1,2}$ express an elastic tensor including bending and membrane components, and an elastic tensor with respect to the shearing component, respectively. $\{c_{\mathit{\alpha }\mathit{\beta }\mathit{\gamma }\mathit{\delta }}^B{\}}_{\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta }=1,2}$, $\{c_{\mathit{\alpha }\mathit{\beta }}^S{\}}_{\mathit{\alpha },\mathit{\beta }=1,2}$ and $\{c_{\mathit{\alpha }\mathit{\beta }\mathit{\gamma }\mathit{\delta }}^M{\}}_{\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta }=1,2}$ express an elastic tensor with respect to bending, shearing and membrane stress, respectively. In addition, $\{{\mathit{\theta }}_{(\mathit{\alpha },\mathit{\beta })}{\}}_{\mathit{\alpha },\mathit{\beta }=1,2}$ and $\{{\mathit{\gamma }}_{\mathit{\alpha }}{\}}_{\mathit{\alpha }=1,2}$, respectively express the curvatures and the transverse shear strains which are defined by the following equations. The constant $k$ denotes a shear correction factor, which is used as $k=5/6$ in the Reissner theory.[16](9) $$\begin{array}{cc}\hfill & {\mathit{\theta }}_{(\mathit{\alpha },\mathit{\beta })}\equiv \frac{1}{2}({\mathit{\theta }}_{\mathit{\alpha },\mathit{\beta }}+{\mathit{\theta }}_{\mathit{\beta },\mathit{\alpha }}),\hfill \end{array}$$(9) (10) $$\begin{array}{cc}\hfill & {\mathit{\gamma }}_{\mathit{\alpha }}\equiv w_{,\mathit{\alpha }}-{\mathit{\theta }}_{\mathit{\alpha }}.\hfill \end{array}$$(10) It will be noted that $\mathit{\text{U}}$ in Equation (7) is given by the following equation.(11) $$\begin{array}{cc}\hfill U& =\{(u_{01},u_{02},w,{\mathit{\theta }}_1,{\mathit{\theta }}_2)\in {(H^1(A))}^5\hfill \\ \hfill & |\mathrm{s}\mathit{atisfy}\mathit{the}\mathit{given}\mathit{Dirichlet}\mathit{condition}\mathit{on}\mathit{each}\mathit{subboundary}\},\hfill \end{array}$$(11) where $H^1$ is the Sobolev space of order 1.

Surface and boundary optimization problem of shell

Domain variation

The shape variation directions that determine the shape of a shell structure can be classified as out-of-plane variation in the normal direction to the surface and in-plane variation in the tangential direction to the surface as shown in Figure 2. Consider that a linear elastic shell structure having an initial domain $\mathrm{\Omega }$, mid-area $A$, boundary $\mathit{\partial }A$ and side surface $S$ undergoes domain variation $\mathit{V}$ (design velocity field) in the out-of-plane direction and/or in the in-plane direction such that its domain, mid-area, boundary and side surface become ${\mathrm{\Omega }}_s,A_s,\mathit{\partial }{A}_s,$and $S_s$, respectively. It is assumed that the plate thickness $h$ remains constant under the domain variation. The domain variation at this time can be expressed by a mapping from $A$ to $A_s$, which is denoted as $T_s:X\in A\mapsto X_s(X)\in A_s,0\le s\le \mathit{\epsilon }$ ($\mathit{\epsilon }$ is a small integer) given by $X_s=T_s(X),A_s=T_s(A)$.[17] The subscript s expresses the iteration history of the domain variation. Assuming a shape constraint is acting on the variation in the domain, the infinitesimal variation of the domain can be expressed by

Fig. 2 Shape variation of shell by $\mathit{V}$.

(12) $$\begin{array}{c}\hfill T_{s+\mathrm{\Delta }s}(X)=T_s(X)+\mathrm{\Delta }s\mathit{V},\end{array}$$(12) where the design velocity field $\mathit{V}(X_s)=\mathit{\partial }{T}_s(X)/\mathit{\partial }s$. The free-form optimization method explained later is a method for determining the optimal domain variation $\mathit{V}$ of shell structures.

Compliance minimization problem

Let us consider a free-form optimization problem for maximizing the stiffness of a shell structure. Letting the state equation in Equation (7) and the volume be the constraint conditions and the compliance be the objective functional to be minimized, a distributed-parameter shape optimization problem for finding the optimal design velocity field $\mathit{V}$, or $A_s(=A+\mathrm{\Delta }s\mathit{V})$ can be formulated as shown below:(13) $$\begin{array}{cc}\hfill \text{Given}& A,\hfill \end{array}$$(13) (14) $$\begin{array}{cc}\hfill \text{find}& A_s(\text{or}\mathit{V}),\hfill \end{array}$$(14) (15) $$\begin{array}{cc}\hfill \text{minimize}& ({\mathit{u}}_{\mathbf{0}},w,\mathit{\theta }),\hfill \end{array}$$(15) (16) $$\begin{array}{cc}\hfill \text{subject}\text{to}& \text{Equation}\text{(7)}\text{and}M(={\int }_A\mathit{hdA})\le \hat{M},\hfill \end{array}$$(16) where $M$ and $\hat{M}$ denote the volume and its constraint value, respectively. Letting $({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }})$ and $\mathrm{\Lambda }$ denote the Lagrange multipliers for the state equation and volume constraints, respectively, the Lagrange functional $L$ associated with this problem can be expressed as(17) $$\begin{array}{cc}\hfill L& (A,({\mathit{u}}_{\mathbf{0}},w,\mathit{\theta }),({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }}),\mathrm{\Lambda })\hfill \\ \hfill & =l({\mathit{u}}_{\mathbf{0}},w,\mathit{\theta })+l({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }})-a(({\mathit{u}}_{\mathbf{0}},w,\mathit{\theta }),({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }}))+\mathrm{\Lambda }(M-\hat{M}).\hfill \end{array}$$(17) For the sake of simplicity, it is assumed that the sub-boundaries acted on by the non-zero external forces $\mathit{N}$, $\mathit{Q}$ and $\mathit{M}$ do not vary (i.e. $\mathit{V}=0$) that the forces acting on the shell surface $\mathit{f},\mathit{m}$ and $\mathit{q}$ do not vary with regard to the space and the iteration history $s$ (i.e. $\stackrel{·}{f}=\stackrel{·}{m}=\stackrel{·}{q}=0$). Then, the material derivative $\stackrel{·}{L}$ of the Lagrange functional can be derived as shown in Equation (19) below using the formula of material derivative.[17](18) $$\begin{array}{cc}\hfill \stackrel{·}{L}=& l({\mathit{u}}_{\mathbf{0}}^{\mathbf{\prime }},w^{\prime },{\mathit{\theta }}^{\prime })+l({\overline{{\mathit{u}}^{\mathbf{\prime }}}}_0,{\overline{w}}^{\prime },\overline{{\mathit{\theta }}^{\prime }})\hfill \\ \hfill & -a(({\mathit{u}}_{\mathbf{0}}^{\mathbf{\prime }},w^{\prime },{\mathit{\theta }}^{\prime }),({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }}))-a(({\mathit{u}}_{\mathbf{0}},w,\mathit{\theta }),({\overline{\mathit{u}}}_0^{\prime },{\overline{w}}^{\prime },\overline{{\mathit{\theta }}^{\prime }}))\hfill \\ \hfill & {\mathrm{\Lambda }}^{\prime }(M-\hat{M})+{〈G_A{\mathit{n}}_{\mathit{A}},\mathit{V}〉}_A+{〈G_{\mathit{\partial }A}{\mathit{n}}_{\mathbf{\partial }\mathit{A}},\mathit{V}〉}_{\mathit{\partial }A},\mathit{V}\in C_{\mathrm{\Theta },}\hfill \end{array}$$(18) where,(19) $$\begin{array}{cc}\hfill {〈G_A{\mathit{n}}_{\mathit{A}},\mathit{V}〉}_A& \equiv {\int }_A{G}_A{\mathit{n}}_{\mathit{A}}·\mathit{V}={\int }_A[-\{C_{\mathit{\alpha }\mathit{\beta }\mathit{\gamma }\mathit{\delta }}(u_{0\mathit{\alpha },\mathit{\beta }}+\frac{h}{2}{\mathit{\theta }}_{\mathit{\alpha },\mathit{\beta }})({\overline{u}}_{0\mathit{\gamma },\mathit{\delta }}+\frac{h}{2}{\overline{\mathit{\theta }}}_{\mathit{\gamma },\mathit{\delta }})\hfill \\ \hfill & -C_{\mathit{\alpha }\mathit{\beta }\mathit{\gamma }\mathit{\delta }}(u_{0\mathit{\alpha },\mathit{\beta }}-\frac{h}{2}{\mathit{\theta }}_{\mathit{\alpha },\mathit{\beta }})({\overline{u}}_{0\mathit{\gamma },\mathit{\delta }}-\frac{h}{2}{\overline{\mathit{\theta }}}_{\mathit{\gamma },\mathit{\delta }})\}+\mathit{hH}\mathrm{\Lambda }+H{f}_{\mathit{\alpha }}(u_{0\mathit{\alpha }}+{\overline{u}}_{0\mathit{\alpha }})\hfill \\ \hfill & -H{m}_{\mathit{\alpha }}({\mathit{\theta }}_{\mathit{\alpha }}+{\overline{\mathit{\theta }}}_{\mathit{\alpha }})+\mathit{Hq}(w+\overline{w})]{\mathit{n}}_{\mathit{A}}\mathit{V}\mathit{dA},\hfill \\ \hfill {〈G_{\mathit{\partial }A}{\mathit{n}}_{\mathbf{\partial }\mathit{A}},\mathit{V}〉}_{\mathit{\partial }A}& \equiv {\int }_{\mathit{\partial }A}{G}_{\mathit{\partial }A}{\mathit{n}}_{\mathbf{\partial }\mathit{A}}·\mathit{V}\mathit{dS}={\int }_{\mathit{\partial }A}[-c_{\mathit{\alpha }\mathit{\beta }\mathit{\gamma }\mathit{\delta }}^B{\mathit{\theta }}_{(\mathit{\alpha },\mathit{\beta })}{\overline{\mathit{\theta }}}_{(\mathit{\gamma },\mathit{\delta })}\hfill \\ \hfill & +{\mathit{kc}}_{\mathit{\alpha }\mathit{\beta }}^S({\mathit{\theta }}_{\mathit{\beta }}-w_{,\mathit{\beta }})({\overline{\mathit{\theta }}}_{\mathit{\alpha }}-{\overline{w}}_{,\mathit{\alpha }})+c_{\mathit{\alpha }\mathit{\beta }\mathit{\gamma }\mathit{\delta }}^M{u}_{0\mathit{\alpha },\mathit{\beta }}{\overline{u}}_{0\mathit{\gamma },\mathit{\delta }}+\mathrm{\Lambda }]{\mathit{n}}_{\mathbf{\partial }\mathit{A}}\mathit{V}\mathit{dS}.\hfill \end{array}$$(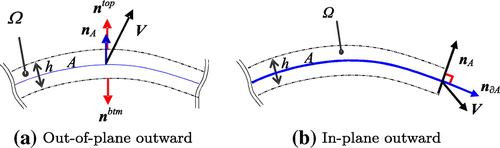19) As shown in Figure 3(a), the notation ${\mathit{n}}_{\mathit{A}}$ in Equation (20) is defined as an out-of-plane outward unit normal vector (i.e. in the normal direction to the surface) on the surface $A$ for the out-of-plane shape variation, and the relationship $(V·{\mathit{n}}_A){\mathit{n}}_A=(V·{\mathit{n}}^{\mathit{top}}){\mathit{n}}^{\mathit{top}}=-(V·{\mathit{n}}^{\mathit{btm}}){\mathit{n}}^{\mathit{btm}}$ for the out-of-plane shape variation is assumed by using the notations ${\mathit{n}}^{\mathit{top}}$ and ${\mathit{n}}^{\mathit{btm}}$, unit normal vectors that make the outward top and bottom surfaces of the shell positive. The notation ${\mathit{n}}_{\mathbf{\partial }\mathit{A}}$ in Equation (21), as shown in Figure 3(b), is defined as an in-plane outward unit normal vector (i.e. in the tangential direction to the surface: ${\mathit{n}}_{\mathit{\partial }A}·{\mathit{n}}_A=0$) on the boundary $\mathit{\partial }A$ for the in-plane shape variation. The notation $H$ denotes twice the mean curvature of the surface. Additionally, $C_{\mathrm{\Theta }}$ expresses the admissible function space that satisfies the constraints of domain variation. The notation ${(·)}^{\prime }$ and $\stackrel{·}{(·)}$ are the shape derivative and the material derivative with respect to the domain variation, respectively.[17]

Fig. 3 Definition of the notation $\mathit{n}$ in Equations (20) and (21).

When the optimality conditions with respect to the state variable $({\mathit{u}}_{\mathbf{0}},w,\mathit{\theta })$, the adjoint variable $({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }})$ and $\mathrm{\Lambda }$ are satisfied, Equation (19) becomes(20) $$\begin{array}{c}\hfill \stackrel{·}{L}\equiv 〈G\mathit{n},\mathit{V}〉,\mathit{V}\in C_{\mathrm{\Theta }}.\end{array}$$(20) The shape gradient functions, which are the sensitivity functions used to determine the optimal shape, are calculated in Equations (23) and (24) by considering the self-adjoint relationship $({\mathit{u}}_{\mathbf{0}},w,\mathit{\theta })=({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }})$.

Free-form optimization method for obtaining optimal surface and boundary of shell structures

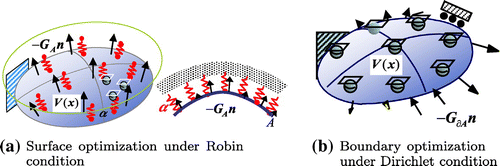
The free-form optimization method described here is based on the traction method (or the $H^1$ gradient method,[11]) which is a gradient method in a Hilbert space. The original traction method was proposed by Azegami in 1994.[18, 19] We have been modifying the original method for shell optimization.[12–14] It is a node-based shape optimization method that can treat all nodes as design variables and does not require any design variable parametrization. This approach makes it possible to obtain the optimal free-form surface and boundary shapes of shell structures. As shown in Figure 4(a), the Robin boundary conditions (spring constant $\mathit{\alpha }>0$) [20] are defined in the case of surface optimization, while the Dirichlet conditions (as shown in Figure 4(b)) or the Robin conditions are defined for a pseudo-elastic shell in the case of boundary optimization with this method. In the case of surface optimization, a distributed force proportional to the shape gradient function $-G_A$ is applied in the normal direction to the surface and a distributed force proportional to the shape gradient function $-G_{\mathit{\partial }A}$ is applied in the tangential direction to the surface in the case of boundary optimization. The analysis for shape variation is called a velocity analysis. The shape gradient function is not applied directly to the shape variation but rather is replaced by a force. This makes it possible both to reduce the objective functional and to maintain the smoothness, i.e. mesh regularity, which is the most distinctive feature of this method.

Fig. 4 Free-form optimization method.

Considering the design velocity $\mathit{V}={\{V_i\}}_{i=1,2,3}$ as a combination of the in-plane velocity ${\{{\mathit{V}}_{0_{\mathit{\alpha }}}\}}_{\mathit{\alpha }=1,2}$ and the out-of-plane velocity $V_3$, the governing equation of the velocity analysis for $\mathit{V}=(V_{0_1},V_{0_2},V_3)$ in the boundary optimization with the Dirichlet conditions is expressed as Equation (25). Moreover, when the free boundary shape is found using Equation (25), an additional constraint is put on variation in the normal direction, as it is assumed that the initial curvature of the shell surface will be maintained.(21) $$\begin{array}{cc}\hfill a(({\mathit{V}}_{0_{\mathit{\alpha }}},V_3,\mathit{\theta }),({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }}))& =-{〈G_{\mathit{\partial }A}\mathit{n},({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }})〉}_{\mathit{\partial }A},\hfill \\ \hfill & ({\mathit{V}}_{0_{\mathit{\alpha }}},V_3,\mathit{\theta })\in C_{\mathrm{\Theta }},\forall ({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }})\in C_{\mathrm{\Theta }},\hfill \end{array}$$(21) where $C_{\mathrm{\Theta }}$ is expressed as(22) $$\begin{array}{cc}\hfill C_{\mathrm{\Theta }}& =\{(V_{0_1},V_{0_2},V_3,{\mathit{\theta }}_1,{\mathit{\theta }}_2)\in {(H^1(A))}^5\hfill \\ \hfill & |\mathrm{s}\mathit{atisfy}\mathit{the}\mathit{constrains}\mathit{of}\mathit{shape}\mathit{variation}\mathit{on}S\mathrm{a}\mathit{nd}{V}_3=0\mathrm{o}nA\}.\hfill \end{array}$$(22) The governing equation of the velocity analysis for the surface optimization with the Robin conditions is expressed as Equation (27).

Fig. 5 Schematic of the two-step free-form optimization methodology.

(23) $$\begin{array}{cc}\hfill a(({\mathit{V}}_{0_{\mathit{\alpha }}},V_3,\mathit{\theta }),& ({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }}))+\mathit{\alpha }〈(\mathit{V}·\mathit{n})\mathit{n},({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }})〉=-{〈G_A\mathit{n}({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }})〉}_A,\hfill \\ \hfill & ({\mathit{V}}_{0_{\mathit{\alpha }}},V_3,\mathit{\theta })\in C_{\mathrm{\Theta }},\forall ({\overline{\mathit{u}}}_0,\overline{w},\overline{\mathit{\theta }})\in C_{\mathrm{\Theta }},\hfill \end{array}$$(23) where $C_{\mathrm{\Theta }}$ is expressed as(24) $$\begin{array}{cc}\hfill C_{\mathrm{\Theta }}& =\{(V_{0_1},V_{0_2},V_3,{\mathit{\theta }}_1,{\mathit{\theta }}_2)\in {(H^1(A))}^5\hfill \\ \hfill & |\mathrm{s}\mathit{atisfy}\mathit{Dirichlet}\mathit{condition}\mathit{for}\mathit{shape}\mathit{variation}\mathit{on}S\}.\hfill \end{array}$$(24) The stiffness tensor in the governing Equations (25) and (27) serves as a smoother (or filter [9, 10]) for maintaining mesh smoothness, and its positive definitiveness is the necessary condition for minimizing the objective functional.

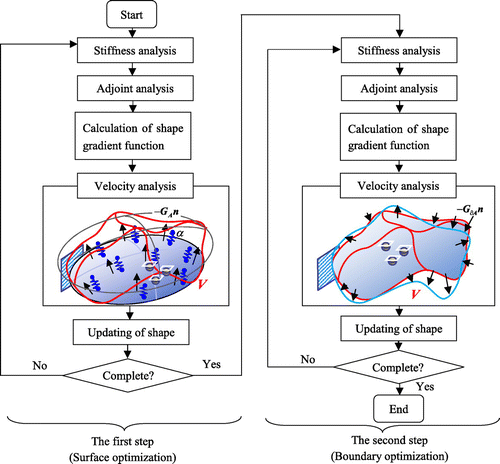
The general process by this two-step optimization methodology is schematized in Figure 5. In each step, firstly, the stiffness analysis and the adjoint analysis (not necessary in this study) were done by a standard commercial FEM code and outputs of the analyses were utilized to calculate the shape gradient function. After that, a distributed force proportional to the shape gradient function $-G_A$ or $-G_{\mathit{\partial }A}$ was applied to determine the design velocity field $\mathit{V}$ of each iteration, and the shape is updated iteratively using the design velocity field $\mathit{V}$. This process was repeated until the optimal shape of each step was obtained.

By this process, the optimal surface shape was determined to enhance the stiffness in the first step, and the boundary shape optimization was performed subsequently in the second step, which contributes to reduce the part of low load transmission to achieve a minimum weight. Then, a weight reduced form with high stiffness can be obtained.

Results of numerical calculation

In order to confirm the validity and practical utility of the developed two-step optimization methodology for designing the optimal free-form of shell structures, square plate, $L-$shaped bracket and spherical shell design problem were given below as fundamental design examples. In each design example, the linear static analysis was performed by the MSC NASTRAN finite element code, in which linear triangular shell elements with one integration point through the element thickness were employed to describe more detailed and smooth surface shapes of shells. Moreover, the element quality in the mesh of the model was inspected by the MSC Nastran throughout the optimization process, which will be discontinued when severely distorted element is found.

Fig. 6 Boundary conditions of square-plate design problem.

Fig. 7 Obtained shape of square plate problem.

Fig. 8 Iteration histories of step 1 and step 2.

Fig. 9 Comparison of strain energy components.

In all design problems, the volume constraint of the first step was set as $105\%$ of the initial shape and that of the second step was set as $70\%$ of the optimized shape by the first step, the earth spring constant $\mathit{\alpha }=20000$, which was equivalent to $1.2D$ ($D$: bending rigidity).[13]

Square-plate design problem

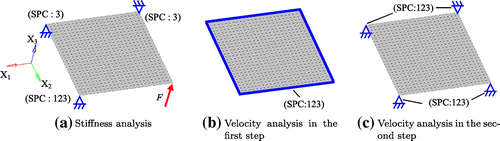
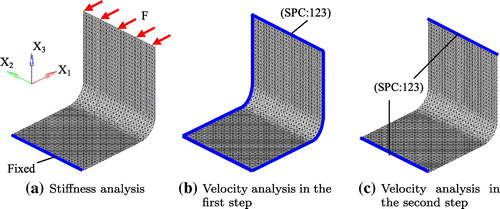
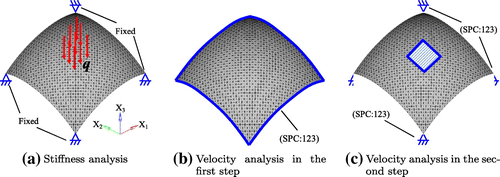
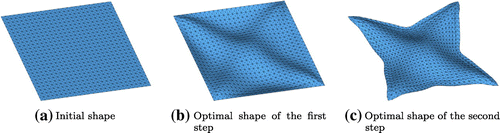
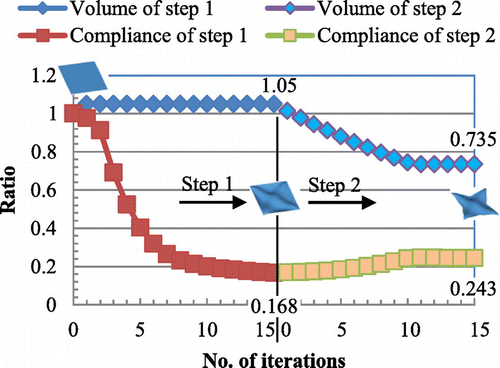
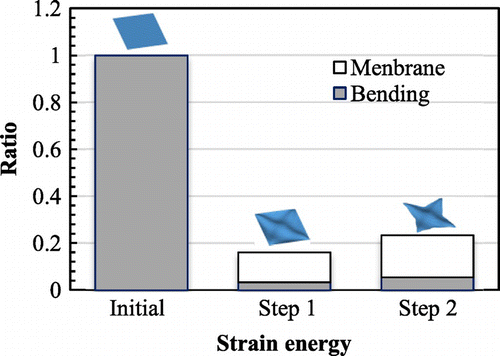
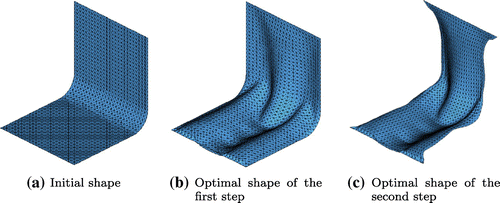
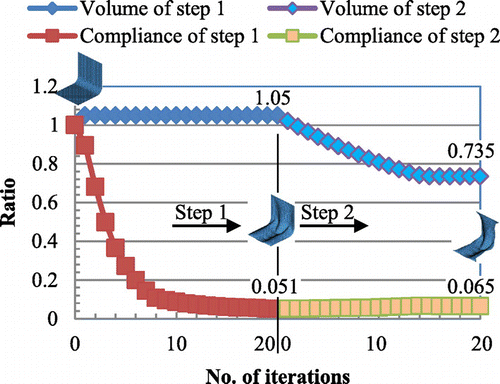
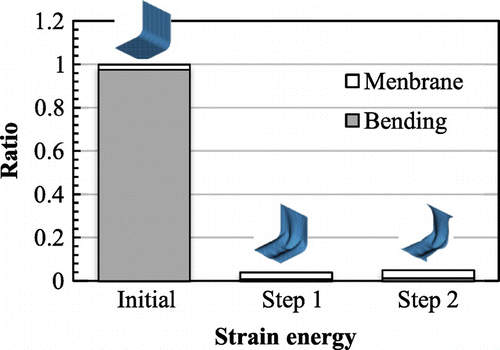
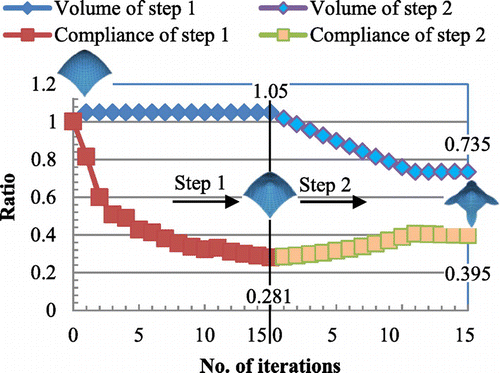
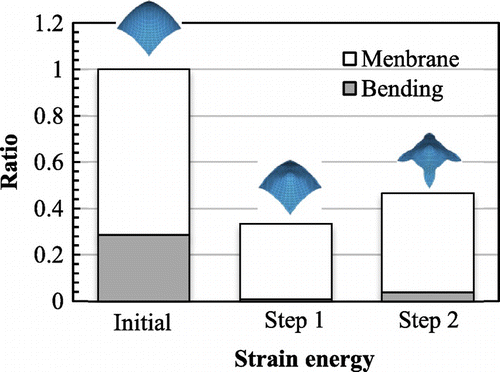
A stiffness design problem of a square plate under torsion was considered as the first application example of the two-step free-form optimization methodology. Initial shape and boundary conditions of the stiffness analysis for this problem are shown in Figure 6(a). The ‘SPC’ in Figure 6(a) expresses the single-point constraint, and 1, 2 and 3 express the $X,Y$ and $Z$ translational degrees of freedom, respectively. The constraint conditions of the velocity analysis in the first and second steps are shown in Figure 6(b) and (c) respectively. The constraint conditions of the velocity analysis can be freely defined according to the practical design requirements. But, in accordance with the assumption in the derivation of the shape gradient functions as mentioned in Section 3.2, the loading and constraint points in the stiffness analysis were constrained in each step of the velocity analysis. Moreover, all boundaries were pin-constrained (SPC:123) in the first step to maintain the basic outline of the initial shape. Figure 7(a) shows the initial shape and Figure 7(b) and (c) shows the optimized shape obtained by the first step and the second step respectively. Iteration convergence of the compliance and the volume are shown in Figure 8 and the values were normalized to those of the initial form. To investigate variation of the load-carrying performance of membrane and bending, a comparison of the ratio of strain energy is made between the initial form and the optimal forms obtained by each step, and the result is shown in Figure 9, where the values are normalized to the total strain energy of the initial form.

As a result of the surface optimization performed in the first step, the optimal curvature distribution shown in Figure 7(b) was obtained and an X-type bead was created on the surface of the plate. Accordingly, the compliance was approximately $83\%$ decreased from the value of the twisted plate with the initial shape while satisfying the given volume constraint. It means that stiffness of the square plate under torsion was substantially increased by the obtained optimal curvature distribution. In the comparison result of the ratio of the strain energy shown in Figure 9, the strain energy of the initial form was completely dominated by the bending component, and that of the plate with the optimal surface was almost dominated by the membrane component as being expected, while the total strain energy was reduced substantially.

Then, by the boundary optimization performed in the second step, the optimal boundary shape was determined while maintaining the optimal curvature distribution of the surface determined in the first step. As shown in Figure 7(c), large shape variation occurred for obtaining the sufficient load path from the clamped four corners to the load points. In spite of large reduction of the volume (from $105$ to $73.5\%$), the compliance increased only about $7.5\%$. After surface and boundary shape was optimized in stages by the first and the second steps, the compliance of the twisted plate was decreased by about $76\%$ from the initial shape, while the volume was decreased by $26.5\%$. It is obvious that both stiffened and lightweight forms can be obtained simultaneously by the two-step free-form optimization methodology.

L-shaped bracket design problem

A $L-$shaped bracket under bending, as shown in Figure 10, was optimized as the second application example by the optimization methodology. The boundary condition of the stiffness analysis is shown in Figure 10(a). In the stiffness analysis, a uniformly distributed force was applied to the upper edge and the lower edge was fixed completely. The constraint conditions for the velocity analysis are shown in Figure 10(b) and (c), in which all boundaries were pin-supported in the first step and the two edges were pin-supported in the second step. Figure 11 shows (a) the initial shape, (b) optimized shape obtained from the first optimization step and (c) final optimized shape by the two-step optimization. The iteration convergence histories of the compliance and the volume in each step are shown in Figure 12 and the comparison of the ratio of strain energy between the initial form and the two optimal forms is shown in Figure 13.

Fig. 10 Boundary conditions of $L$-shaped bracket design problem.

Fig. 11 Obtained shape of $L-$shaped bracket problem.

Fig. 12 Iteration histories of step 1 and step 2.

Fig. 13 Comparison of strain energy components.

By the surface optimization performed in the first step, the optimal curvature distribution shown in Figure 11(b) was obtained and the compliance, as shown in Figure 12, was reduced by approximately $95\%$ while satisfying the given volume constraint ($105\%$ of the initial form). With respect to the ratio of bending and membrane strain energy components, it is clear from Figure 13 that the strain energy of the initial form was dominated almost entirely by the bending component and that of the form with optimized surface was almost dominated by the bending component, while the total strain energy was reduced drastically. Subsequently to the first step, the boundary optimization was performed in the second step and the optimal boundary shape shown in Figure 11(c) was determined, while maintaining the optimal curvature distribution of the surface determined in the first step. As shown in Figure 12, the compliance increased slightly around $1.4\%$ in the second step, while the volume decreased drastically from $105\%$ to $73.5\%$. Due to the two-step optimization, not only the compliance of the $L-$shaped bracket with final optimal form was decreased by $93.5\%$, but the volume decreased by $26.5$ from the initial form.

Spherical shell design problem

The third application example is a spherical shell design problem. Figure 14(a) shows the boundary conditions of stiffness analysis, in which a uniformly distributed force was applied to the centre of the spherical shell and the four support points were fixed . The constraint conditions for the velocity analysis are shown in Figure 14(b) and (c). All boundaries were pin-supported in the first step, and the four support points and the loading points were pin-supported in the second step. Figure 15 shows (a) the initial shape, (b) optimized shape obtained from the first optimization step and (c) final optimized shape by the two-step optimization. The iteration convergence histories of the compliance and the volume in each step are shown in Figure 16 and the comparison of the ratio of strain energy between the initial form and the two optimal forms is shown in Figure 17.

Fig. 14 Boundary conditions of Spherical Shell design problem.

Fig. 15 Obtained shape of Spherical Shell design problem.

Fig. 16 Iteration histories of step 1 and step 2.

Fig. 17 Comparison of strain energy components.

As shown in Figure 15(b) and (c), smooth optimal surface and boundaries were obtained by the optimization methodology. It was confirmed that, as shown in Figure 16, the compliance of the final shape was about 72 $\%$ decreased while the volume $26.5\%$ decreased, and as shown in Figure 16, the strain energy of the final form was almost dominated by the membrane component.

Conclusions

In this paper, we have proposed the two-step free-form shape optimization methodology for designing the optimal shapes of shell structures with the aiming of stiffness maximization subject to volume constraints. In this methodology, the optimization design problem of a shell structure was divided into two steps, which are a surface optimization step and a boundary optimization step. The shape sensitivity, called shape gradient function, was theoretically derived for both steps using the Lagrange multiplier method and the formula of the material derivative. The optimal shape was determined by applying the derived each shape gradient function on a design surface or boundaries to the $H^1$ gradient method. It was confirmed by foundational and practical examples that, by the two-step free-form optimization methodology, a smooth optimal shell with free-form surface and boundaries can be easily obtained and the obtained final optimal shapes were not only weight reduced but also high stiffness. In addition to the stiffness design problem, the strength, vibration, buckling and their combined design problems will be considered in the future work.

Acknowledgments

This research was supported by grants-in-aid from the DAIKO FOUNDATION in Nagoya, Japan.