A modification of the semi-analytic inversion method: determination of the yield stress and a comparison with the parametrization algorithm

Abstract

In this study, an effective modification of the semi-analytic inversion method is presented. The semi-analytic inversion method is developed to solve an inverse coefficient problem arising in materials science instead of the parametrization method as a different and stronger method. The inverse coefficient problem is related to reconstruction of the unknown coefficient $g=g({\mathit{\xi }}^2)$, ${\mathit{\xi }}^2:=|\nabla u{|}^2$, from the nonlinear equation $-\nabla .(g(|\nabla u{|}^2)\nabla u)=2\mathit{\phi }$, $x\in \mathrm{\Omega }\subset {\mathbb{R}}^{\mathbb{2}}$. The semi-analytic inversion method has some advantages. The first distinguishable feature of this method is that it uses only a few measured output data to determine the whole unknown curve, whereas the parametrization algorithm uses many measured output data for the determination of only some part of the unknown curve. The second distinguishable feature of this method is its well-posedness. In the semi-analytic inversion method, the algorithm for determination of the yield stress, which is one of the main unknowns of the inverse problem, is very complicated. That is why we need to modify this algorithm. The demonstrated numerical results for different engineering materials also show that the modified semi-analytic inversion method allows us to determine the elastoplastic parameters of a kind of engineering materials with high accuracy, even various noise levels.

Keywords:

• yield stress
• semi-analytic inversion method
• torque
• plasticity function
• measured output data
• power-law material

Nomenclature

Symbols

1. plasticity function

2. modulus of rigidity

3. approximate function of $g$

4. strain hardening exponent

5. approximate value of $\mathit{\kappa }$

6. Poisson coefficient

7. Prandtl stress function

8. Young’s modulus

9. angle of twist per unit length

10. angle step

11. cross-section

12. theoretical value of torque

13. piecewise uniform mesh

14. experimental value of torque

15. yield stress

16. approximate value of the yield stress

17. noise level

18. shear compliance

19. absolute error

20. relative error

 

Introduction

The problems that involve determination of the unknown coefficients in partial differential equations from some additional conditions (also called measured output data) are well known in mathematical literature as the inverse coefficient problems. These additional conditions may be given on the boundary of the domain, at the final time or on the whole domain i.e., non-local condition. The inverse problems require defining related to direct problems. As it is known, a direct problem aims to find a solution that satisfies given an ordinary and partial differential equation and related to initial and boundary conditions. In some problems, the main ordinary and partial differential equation and the initial and boundary conditions are not sufficient to obtain the solution, but, instead some additional conditions are required. Such problems are called the inverse problems. A problem is said to be well-posed or properly posed in the sense of Hadamard if it has the following three properties: there exists a solution of the problem (existence), there is at most one solution of the problem (uniqueness) and the solution depends continuously on the data (stability). If at least one of these properties does not hold, then the equation is called ill-posed or improperly posed. In this context, another definition of the inverse problems can be given as follows: If one of two problems which are inverse to each other is ill-posed, we call it the inverse problem and the other one the direct problem. Inverse problems are often ill-posed.

Among the inverse problems, the inverse coefficient problems are quite interesting and receive much attention in mathematical literature, especially, the torsion problems in linear elasticity. However, the inverse problems in torsional deformation are less well known and have received relatively little attention in mathematical literature as well as in engineering literature. The quasi-static mathematical model of torsional creep within $J_2$- deformation theory of the plasticity is given in [1]. In this model, one seeks the solution $u(x),x\in \mathrm{\Omega }\subset {\mathbb{R}}^{\mathbb{2}}$, of the following nonlinear boundary value problem:(1) $$\begin{array}{c}\hfill \{\begin{array}{c}-\nabla .(g(|\nabla u{|}^2)\nabla u)=2\mathit{\phi },x\in \mathrm{\Omega }\subset {\mathbb{R}}^{\mathbb{2}},\hfill \\ u(x)=0,x\in \mathit{\partial }\mathrm{\Omega },\hfill \end{array}\end{array}$$(1) where $\mathrm{\Omega }:=(0,a)\times (0,b)$, $a,b>0$ is the cross-section of a bar, $\mathit{\phi }$ is the angle of twist per unit length, $g=g({\mathit{\xi }}^2)$, ${\mathit{\xi }}^2=|\nabla u{|}^2$ is the plasticity function and $u(x)$ is the Prandtl stress function. The non-linear boundary value problem (1) represents an elastoplastic torsion of a strain hardening bar. According to $J_2$- deformation theory, the plasticity function satisfies the following conditions [2–4]:(2) $$\begin{array}{c}\hfill \{\begin{array}{c}0<c_0\le g({\mathit{\xi }}^2)\le c_1,\forall {\mathit{\xi }}^2\in [{{\mathit{\xi }}_{\ast }}^2,{{\mathit{\xi }}^{\ast }}^2],{{\mathit{\xi }}_{\ast }}^2>0,\hfill \\ g^{\prime }({\mathit{\xi }}^2)\le 0,\hfill \\ g({\mathit{\xi }}^2)+2{\mathit{\xi }}^2{g}^{\prime }({\mathit{\xi }}^2)\ge {\mathit{\gamma }}_0>0,\hfill \\ \exists {\mathit{\xi }}_0^2\in ({{\mathit{\xi }}_{\ast }}^2,{{\mathit{\xi }}^{\ast }}^2)g({\mathit{\xi }}^2)=g_0,\forall {\mathit{\xi }}^2\in [{{\mathit{\xi }}_{\ast }}^2,{{\mathit{\xi }}_{\ast }}^2].\hfill \end{array}\end{array}$$(2) Now we define the parameters in (2). First, we define ${\mathit{\xi }}_0^2={\mathrm{m}\mathit{ax}}_{x\in \mathrm{\Omega }}|\nabla u(x){|}^2$. In materials science, it corresponds to the yield stress which is the maximum stress or force per unit area within a material that can arise before the onset of permanent deformation. When stresses up to the yield stress are removed, the material resumes its original size and shape. In other words, there is a temporary shape change that is self-reversing after the force is removed, so that the object returns to its original shape. This kind of deformation is called pure elastic deformation. On the other hand, irreversible deformations are permanent even after stresses have been removed. One type of irreversible deformation is pure plastic deformation. For such materials, the yield stress marks the end of the elastic behaviour and the beginning of the plastic behaviour. For any angle $\mathit{\phi }>0$, all points of the bar have non-zero strain intensity which means the conditon ${{\mathit{\xi }}_{\ast }}^2>0$ in (2) makes sense. Furthermore, $g_0=1/G$ is the shear compliance, $G=E/(2(1+\mathit{\nu }))$ is the modulus of rigidity, $E>0$ is the Young’s modulus, $\mathit{\nu }\in (0,0.5)$ is the Poisson coefficient, and $c_0$, $c_1$, ${\mathit{\gamma }}_0$ are some positive constants. The Poisson coefficient for some materials such as aluminum, bronze, copper, ice, magnesium, molybdenum, monel metal and nickel silver are 0.334, 0.34, 0355, 0.33, 0.35, 0.307, 0.315, 0.322 respectively. Since the Poisson coefficient of the aforementioned materials are around 0.3, it is assumed to be 0.3 throughout this paper. We note that changing of this value affect numerical calculations but does not affect the applicability of the algorithm.

The mechanical properties of a material describe how it will react to physical forces. Mechanical properties occur as a result of the physical properties inherent to each material, and are determined through a series of standardized mechanical tests. Mechanical properties are also used to help classify and identify material. The most common properties considered are strength, ductility, hardness, elastic shear modulus, yield stress and strain hardening exponent. There are many studies to determine these properties in literature. For example in [5], the authors are proposed a polycrystalline approach in order to model the elastic-plastic behavior of an austenitic-ferritic stainless steel. This study concerns the prediction of the mechanical behaviour of an austenitic-ferritic stainless steel whose microstructural heterogeneity is strongly marked. In [6], the authors investigate the mechanical behaviour of a mortar and five polymer modified mortars (PMMs) with different polymer contents. The mechanical characterization of the materials is based on compression and three-point bending tests. The determination of material parameters used in internal variable constitutive models is studied in [7]. In order to determine the best-suited material parameter set, two optimization approaches are used: a gradient-based method and a continuous evolutionary algorithm method. Both methods are used to determine the 12 material parameters needed for an AA1050-O aluminium alloy. Also the authors compare these two methods, in terms of the cost function and the convergence rate, in the case of an AA1050-O aluminium alloy. An application of inverse approach to experimental indentation data in order to determine combined hardening models parameters is given in [8]. The authors show that the inverse analysis applied to experimental cyclic indentation curves can give a quite good approximation of the monotonic stress–strain curve and the beginning of cyclic tensile test. Also it is indicated that the model used in the paper is not sufficient to take into account all phenomenons coming in the steels behaviour under cyclic indentation. Experimental applications of two different approaches for interpretation of instrumented indentation experiments are proposed in [9]. The first approach is the application of methodology developed for spherical indentation based on models. The second approach is the application of inverse algorithm based on the minimization between experiments and simulated data. Also it is shown that inverse approach leads to a good prediction of the elastic modulus for metals with a face-centred cubic crystal structure. An inverse analysis approach is used to identify the modified Cam-Clay parameters from a pressuremeter curve in [10]. The numerical process implemented in this study is based on the interaction of two numerical tools; an optimization code (SiDoLo) and a general finite element code (CESAR-LCPC). In [11], the authors investigate the mechanical behaviour of a fluoro-elastomer. Several tension and compression cyclic loading and relaxation tests have been performed to examine the non-linear stress–strain behaviour, the loading rate-dependent response, and hysteresis phenomena during cyclic tests of this material. A hybrid algorithm which combines a genetic algorithm and a gradient-based algorithm is used for the identification of material parameters in [12]. In [13], a simple theory model is proposed, which included three steps: dimensionless analysis, finite element modelling and data fitting, to characterize the elastic-plastic properties of thin film materials on elastic-plastic substrates. A new method to evaluate the in-plane anisotropic plastic properties of engineering steels by single spherical indentation is proposed in [14]. This new method deals with materials that obey the work hardening law and have in-plane anisotropy of the yield stress in orthogonal directions. Various approaches are proposed to determine the material properties of power-law materials, based on dimensionless analysis and the concept of a representative strain in [15]. In this work, non-linear optimization algorithms are developed and integrated with finite element (FE) analysis to determine and improve the accuracy of the elastic-plastic mechanical properties of a power-law material without the concept of dimensionless analysis and a representative strain. The optimization approach shows that a unique set of four key material properties of a given material (Young’s modulus, Poisson’s ratio, yield stress and work hardening exponent) can be determined from the loading–unloading indentation curve of only a single indentation curve, without the need for using results from two or more indentations. In this study, we modify the inversion method which is developed for determination of the the elastic shear modulus, the yield stress and the strain hardening exponent of a wide class of engineering materials. This determination problem arises in an inverse coefficient problem for the non-linear boundary value problem (1). We define the inverse coefficient problem. For this aim, let $u=u(x)$ be the solution of the non-linear boundary value problem (1). Then the theoretical value of the torque is defined as follows [1, 16]:(3) $$\begin{array}{c}\hfill T(\mathit{\phi })=2{\int }_{\mathrm{\Omega }}u(x;g;\mathit{\phi })\mathit{dx}.\end{array}$$(3) The inverse coefficient problem consists of determining the plasticity function $g=g({\mathit{\xi }}^2)$ in (1), from the experimentally given values $\mathcal{T}(\mathit{\phi })$ of the torque. For this purpose, two numerical methods have been developed in the literature: The parametrization method [17] and the semi-analytic inversion method (also called the fast algorithm).[18] We refer the readers to the next sections for details of these methods. Here, a new modification of the semi-analytic inversion method is given, especially for determination of the yield stress.

The remainder of this paper comprises four sections: In Section 2, the parametrization and the fast algorithms are explained. In Section 3, a new algorithm to determine the yield stress is derived and adapted to the original semi-analytic inversion method. Numerical examples are presented in Section 4. The final section of the paper contains discussions and comments on the forthcoming studies.

Parametrization of the unknown curve $g({\mathit{\xi }}^2)$ and the fast algorithm

For many engineering materials, the plasticity function $g({\mathit{\xi }}^2)$ has the following form [18–20]:(4) $$\begin{array}{c}\hfill g({\mathit{\xi }}^2)=\{\begin{array}{c}1/G,{\mathit{\xi }}^2\le {\mathit{\xi }}_0^2,\hfill \\ 1/G{({\mathit{\xi }}^2/{\mathit{\xi }}_0^2)}^{0.5(\mathit{\kappa }-1)},{\mathit{\xi }}_0^2<{\mathit{\xi }}^2,\mathit{\kappa }\in [0,1],\hfill \end{array}\end{array}$$(4) which corresponds to the Ramberg-Osgood curve ${\mathit{\sigma }}_i={\mathit{\sigma }}_0{(e_i/e_0)}^{\mathit{\kappa }}$. Within the range of $J_2$- deformation theory, the plasticity function (4) describes the elastoplastic properties of wide class of engineering materials, where $\mathit{\kappa }\in [0,1]$ is the strain hardening exponent. The value $\mathit{\kappa }=1$ and $\mathit{\kappa }=0$ correspond to pure elastic and pure plastic cases, respectively. Evidently, this function satisfies all conditions (2). We want to draw attention to the representation $g({\mathit{\xi }}^2)$ of the plasticity function. Since the relationship between the intensities of shear stress and shear strain is given by the equation $S=g({\mathit{\xi }}^2)\mathit{\xi }$, we use the notation $g({\mathit{\xi }}^2)$ instead of $g(\mathit{\xi })$ for the plasticity function.

The parametrization algorithm consists of discretization of the unknown curve (4), in the following form [21]:(5) $$\begin{array}{c}\hfill g_h({\mathit{\xi }}^2)=\{\begin{array}{c}{\mathit{\beta }}_0=1/G,{\mathit{\xi }}^2\in (0,{\mathit{\xi }}_0^2],\hfill \\ {\mathit{\beta }}_0-{\mathit{\beta }}_1({\mathit{\xi }}^2-{\mathit{\xi }}_0^2),{\mathit{\xi }}^2\in ({\mathit{\xi }}_0^2,{\mathit{\xi }}_1^2],\hfill \\ {\mathit{\beta }}_0-\sum _{m=1}^{M-1}{\mathit{\beta }}_m({\mathit{\xi }}_m^2-{\mathit{\xi }}_{m-1}^2)-{\mathit{\beta }}_M({\mathit{\xi }}^2-{\mathit{\xi }}_{M-1}^2),{\mathit{\xi }}^2\in ({\mathit{\xi }}_{M-1}^2,{\mathit{\xi }}_M^2].\hfill \end{array}\end{array}$$(5) The parametrization algorithm focuses on the unknown parameters ${\mathit{\beta }}_m$ appearing in (5). At each $m$th state, the algorithm aims to find the parameters ${\mathit{\beta }}_m$, using the measured output data ${\mathcal{T}}_m$ that corresponds to the angle ${\mathit{\phi }}_m$. For convenience of the readers, we give the parametrization algorithm. For this purpose, assume that $({\mathit{\phi }}_0,{\mathcal{T}}_0)$ is a given measured output data for the pure elastic case. Then the parametrization algorithm is presented as follows:

The parametrization algorithm:

1. Choose iterations ${\mathit{\beta }}_0^{(1)}$, ${\mathit{\beta }}_0^{(2)}$ so that the following conditions hold:$$\begin{array}{c}\hfill T_h\left[{\mathit{\beta }}_0^{(1)}\right]>{\mathcal{T}}_0>T_h\left[{\mathit{\beta }}_0^{(2)}\right].\end{array}$$

2. Use next iteration ${\mathit{\beta }}_0^{(3)}=({\mathit{\beta }}_0^{(1)}+{\mathit{\beta }}_0^{(2)})/2$, and calculate the theoretical value of the torque $T_h\left[{\mathit{\beta }}_0^{(3)}\right]$.

3. Determine the next iteration by using (14) as follows: if $T_h\left[{\mathit{\beta }}_0^{(3)}\right]<{\mathcal{T}}_0$, then ${\mathit{\beta }}_0^{(4)}=({\mathit{\beta }}_0^{(3)}+{\mathit{\beta }}_0^{(2)})/2$, if $T_h\left[{\mathit{\beta }}_0^{(3)}\right]>{\mathcal{T}}_0$, then ${\mathit{\beta }}_0^{(4)}=({\mathit{\beta }}_0^{(3)}+{\mathit{\beta }}_0^{(1)})/2$.

4. Calculate $|T_h[G^{(3)}]-{\mathcal{T}}_0|$.

5. If $|T_h[{\mathit{\beta }}_0^{(3)}]-{\mathcal{T}}_0|<{\mathit{\epsilon }}_T$, then ${\mathit{\beta }}_0={\mathit{\beta }}_0^{(3)}$. Otherwise, continue the steps (P2)–(P4).

6. Repeat the process until the following stopping condition$$\begin{array}{c}\hfill |T_h[{\mathit{\beta }}_0^{(n)}]-{\mathcal{T}}_0|<{\mathit{\epsilon }}_T\mathrm{i}s\mathit{fulfilled}.\end{array}$$

For each the pure plastic torsion case, for the determination of the unknown parameters ${\mathit{\beta }}_m$, a similar algorithm can be used (one just needs to write ${\mathit{\beta }}_m^{(n)}$ instead of ${\mathit{\beta }}_0^{(n)}$ in the parametrization algorithm). Although the parametrization algorithm is used for numerical solution of some class of inverse coefficients problems, it has some disadvantages. The first one is that the application of this algorithm requires lots of measured output data. This is of course undesirable since getting these data needs time and costs. The second is the ill-posedness of the algorithm. This situation is illustrated in [21] and a regularization method is offered.

For all these reasons a new method i.e., the semi-analytic inversion method is introduced in [18]. The semi-analytic inversion method is based on the determination of the three main unknowns of (4), namely the elastic shear modulus $G>0$, the yield stress ${\mathit{\xi }}_0^2$ and the strain hardening exponent $\mathit{\kappa }\in [0,1]$. The first distinguishable feature of this algorithm is that it uses only a few values of the data $({\mathit{\phi }}_i,{\mathcal{T}}_i)$. Furthermore, the new method determines whole of the unknown curve by using these a few data. The second distinguishable feature of this algorithm is its well-posedness. But, in the semi-analytic inversion method the algorithm that is used for determination of the yield stress is complicated and it needs many parameters to be determined before applying it. According to this algorithm, the yield stress is found using the following steps:

Algorithm for determination of the yield stress:

1. Choose the iteration ${\mathit{\phi }}_0^{(1)}$ such that ${\mathit{\phi }}_0^{(1)}>{\mathit{\phi }}_0$.

2. Use the synthetic output data $T_0^{(1)}={\mathit{\delta }}_1{\mathcal{T}}_0$, ${\mathit{\delta }}_1={\mathit{\phi }}_0/{\mathit{\phi }}_0^{(1)}$ and apply the parametrization algorithm to find ${\mathit{\beta }}_0^{(1)}=1/G^{(1)}$.

3. Calculate the relative error $\mathit{\delta }{G}^{(1)}=|(G_h-G^{(1)})/G_h|$.

   1. If $\mathit{\delta }{G}^{(1)}<{\mathit{\epsilon }}_G$, use the next iteration ${\mathit{\phi }}_0^{(2)}>{\mathit{\phi }}_0^{(1)}$.

   2. If $\mathit{\delta }{G}^{(1)}>{\mathit{\epsilon }}_G$, use the next iteration ${\mathit{\phi }}_0^{(2)}=0.5[{\mathit{\phi }}_0^{(1)}+{\mathit{\phi }}_0]$.

4. Use the synthetic output data $T_0^{(2)}={\mathit{\delta }}_2{\mathcal{T}}_0$, ${\mathit{\delta }}_2={\mathit{\phi }}_0/{\mathit{\phi }}_0^{(2)}$ and apply YS2 and YS3 for the new output data.

Repeat the process YS1–YS5 until the following conditions$$\begin{array}{c}\hfill \mathit{\delta }{G}^{(n)}<{\mathit{\epsilon }}_G,\mathit{\delta }{G}^{(n+1)}>{\mathit{\epsilon }}_G,\mathit{\delta }{\mathit{\xi }}_0^{(n)}:=\frac{|{{\mathit{\xi }}_0^2}^{(n)}-{{\mathit{\xi }}_0^2}^{(n+1)}|}{0.5[{{\mathit{\xi }}_0^2}^{(n)}+{{\mathit{\xi }}_0^2}^{(n+1)}]}<{\mathit{\epsilon }}_{\mathit{\xi }}\mathrm{a}\mathit{re}\mathit{fulfilled}.\end{array}$$Finally, the value ${\mathit{\xi }}_{0h}^2:=0.5[{{\mathit{\xi }}_0^2}^{(n)}+{{\mathit{\xi }}_0^2}^{(n+1)}]$ is assumed to be an approximate value of the yield stress ${\mathit{\xi }}_0^2$. Note that choosing the parameters ${\mathit{\phi }}_0^{(1)},{\mathit{\phi }}_0^{(2)},\dots$, ${\mathit{\epsilon }}_G$, ${\mathit{\epsilon }}_{\mathit{\xi }}$, $\mathit{\delta }G$ are very sensitive and affect the iteration number and consequently the precision of the solution provided by the algorithm. Also in each step the error $\mathit{\delta }{G}^{(n)}$ needs to be calculated. Thus, this algorithm contains many parameters to be determined before applying it. Therefore, we need a new algorithm which reduces the number of the required parameters to determine the yield stress to minimum. According to semi-analytic inversion method, the other two main parameters of the unknown function (4) are found as follows: The modulus of rigidity is determined by applying the parametrization algorithm just once for the measured output data $({\mathit{\phi }}_0,{\mathcal{T}}_0)$. Having found approximate value of the modulus of rigidity and the yield stress, the strain hardening exponent is determined by formula (7), (see below). This formula is due to the explicit form of the plasticity function given by (4). Although both the parametrization and the semi-analytic inversion methods are used for the functions in the form (4), some similar algorithms may be developed for another type of functions that satisfy all condition (2).

The rest of the paper is devoted to establish the new algorithm to find the yield stress and comparison of the numerical results with the parametrization algorithm. We note that the other steps of the semi-analytic inversion method remain the same.

Determination of the yield stress by a new algorithm

In this section, we develope a new algorithm for determination of the yield stress. For this purpose, let $({\mathit{\phi }}_1,{\mathcal{T}}_1)$ and $({\mathit{\phi }}_2,{\mathcal{T}}_2)$ be given measured output data for the pure elastic and the pure plastic cases respectively. By applying the parametrization algorithm for the pair $({\mathit{\phi }}_1,{\mathcal{T}}_1)$, the elastic shear modulus $G>0$ can be found. The approximate value of the elastic shear modulus is denoted by $G_h>0$. For the present, we assume that the approximate value of the yield stress is known and denoted by ${\mathit{\xi }}_{0h}^2$. 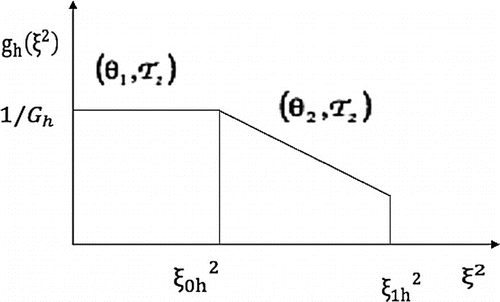By using the parametrization algorithm one more time, the following function can be constructed (see Figure 2):(6) $$\begin{array}{c}\hfill g({\mathit{\xi }}^2)=\{\begin{array}{c}{\mathit{\beta }}_0=1/G_h,{\mathit{\xi }}^2\in (0,{\mathit{\xi }}_{0h}^2],\hfill \\ {\mathit{\beta }}_0-{\mathit{\beta }}_1({\mathit{\xi }}^2-{\mathit{\xi }}_{0h}^2),{\mathit{\xi }}^2\in ({\mathit{\xi }}_{0h}^2,{\mathit{\xi }}_{1h}^2],\hfill \end{array}\end{array}$$(6) where ${\mathit{\xi }}_{1h}^2={\mathrm{m}\mathit{ax}}_{\mathrm{\Omega }}|\nabla u{|}^2$ and it can be found by solving the nonlinear direct problem for the input data (6) and $\mathit{\phi }={\mathit{\phi }}_1$. We use a finite difference scheme to solve the nonlinear direct problem with these inputs and refer the readers to the next section for details.

Since the point $({\mathit{\xi }}_{1h}^2,g({\mathit{\xi }}_{1h}^2))$ needs to be on the plasticity curve $g=g({\mathit{\xi }}^2)$, from the explicit form (4) of the plasticity function, we obtain the following equation$$\begin{array}{c}\hfill g({\mathit{\xi }}_{1h}^2)=1/G_h{({\mathit{\xi }}_{1h}^2/{\mathit{\xi }}_{0h}^2)}^{0.5({\mathit{\kappa }}_h-1)},{\mathit{\xi }}_{1h}^2>{\mathit{\xi }}_{0h}^2,\end{array}$$for the determination of the approximate value ${\mathit{\kappa }}_h$ of the unknown strain hardening exponent $\mathit{\kappa }\in [0,1]$. This equation implies $\ln (g({\mathit{\xi }}_{1h}^2)·G_h)=0.5({\mathit{\kappa }}_h-1)\ln ({\mathit{\xi }}_{1h}^2/{\mathit{\xi }}_{0h}^2)$. Hence, the following formula is obtained to get approximate value of the strain hardening exponent $\mathit{\kappa }$ [17]:(7) $$\begin{array}{c}\hfill {\mathit{\kappa }}_h=1+\frac{\ln (g({\mathit{\xi }}_{1h}^2)·G_h)}{\ln ({\mathit{\xi }}_{1h}^2/{\mathit{\xi }}_{0h}^2)}.\end{array}$$(7) The denominator of the above fraction shows that the value ${\mathit{\xi }}_{1h}^2$ can not be chosen very close to ${\mathit{\xi }}_{0h}^2$. This means the angle step $\mathrm{\Delta }\mathit{\phi }:={\mathit{\phi }}_2-{\mathit{\phi }}_1$ needs to be chosen large enough. This assertion is also confirmed by the computational experiments below. The main difference between the new method and the semi-analytic inversion method becomes more visible in the determination process of the yield stress. In addition to the pair $({\mathit{\phi }}_2,{\mathcal{T}}_2)$, the pair $({\mathit{\phi }}_3,{\mathcal{T}}_3)$ also is given in pure plastic case as an additional condition. In this procedure, we will often use the formula (7). This procedure consists of the following two algorithms (also see Figure 1):

Fig. 1 The schematical illustration of the Algorithms 1 and 2.

Fig. 2 The function $g({\mathit{\xi }}^2)$ defined by (6).

Algorithm 1:

1. Apply the parametrization algorithm for $({\mathit{\phi }}_1,{\mathcal{T}}_1)$ and find $G_h$.

2. Solve linear direct problem $\mathit{\phi }={\mathit{\phi }}_1$ and $G=G_h$. Then find ${\mathit{\xi }}_{0h}^2$ = ${\mathrm{m}\mathit{ax}}_{\mathrm{\Omega }}|\nabla u{|}^2$.

3. Suppose ${\mathit{\xi }}_0^2={\mathit{\xi }}_{0h}^2$ and apply the formula (7) for the pairs $({\mathit{\phi }}_1,{\mathcal{T}}_1)$ and $({\mathit{\phi }}_3,{\mathcal{T}}_3)$. Then find the value of ${\mathit{\kappa }}_h$.

4. Solve the nonlinear direct problem (1) for the found values of ${\mathit{\kappa }}_h,{\mathit{\xi }}_0^2,G_h,{\mathit{\phi }}_3$. Then find the value of $\stackrel{\sim }{{\mathcal{T}}_3}$.

5. Apply (A1.1)–(A1.4) for $({\mathit{\phi }}_2,{\mathcal{T}}_2)$ and $({\mathit{\phi }}_3,{\mathcal{T}}_3)$ (equivalently apply (A1.1)–(A1.4) by assuming ${\mathit{\phi }}_1={\mathit{\phi }}_2,{\mathcal{T}}_1={\mathcal{T}}_2$). Then find $\stackrel{\sim }{\stackrel{\sim }{{\mathcal{T}}_3}}$.

After getting $\stackrel{\sim }{{\mathcal{T}}_3}$ and $\stackrel{\sim }{\stackrel{\sim }{{\mathcal{T}}_3}}$, we check whether a relation such as $\stackrel{\sim }{{\mathcal{T}}_3}<{\mathcal{T}}_3<\stackrel{\sim }{\stackrel{\sim }{{\mathcal{T}}_3}}$ (or $\stackrel{\sim }{{\mathcal{T}}_3}>{\mathcal{T}}_3>\stackrel{\sim }{\stackrel{\sim }{{\mathcal{T}}_3}}$) is satisfied. Then we can find the approximate value of the yield stress ${\mathit{\xi }}_0^2$ by using Algorithm 2. If such a relation does not exist, we can not apply it. This situation appears to be a disadvantage of the new Algorithm. But later we will see that this situation does not occur in the real world. Although Algorithm 2 is valid for the former case ($\stackrel{\sim }{{\mathcal{T}}_3}<{\mathcal{T}}_3<\stackrel{\sim }{\stackrel{\sim }{{\mathcal{T}}_3}}$), a similar algorithm can be constructed for the latter case ($\stackrel{\sim }{{\mathcal{T}}_3}>{\mathcal{T}}_3>\stackrel{\sim }{\stackrel{\sim }{{\mathcal{T}}_3}}$).

Algorithm 2:

1. ${\mathit{\phi }}_0^1=\frac{{\mathit{\phi }}_1+{\mathit{\phi }}_2}{2}$.

2. Solve the direct problem for $\mathit{\phi }={\mathit{\phi }}_0^1$ and find corresponding torque $\hat{\mathcal{T}}$. Apply (A1.1)–(A1.4) for the pairs $<({\mathit{\phi }}_1,{\mathcal{T}}_1)$, $({\mathit{\phi }}_0^1,{\mathcal{T}}_0^1)>$ and $<({\mathit{\phi }}_0^1,{\mathcal{T}}_0^1)$, $({\mathit{\phi }}_2,{\mathcal{T}}_2)>$. Then find $\stackrel{\sim }{{\mathcal{T}}_3},\stackrel{\sim }{\stackrel{\sim }{{\mathcal{T}}_3}}$.

3. If $|\stackrel{\sim }{{\mathcal{T}}_3}-\hat{\mathcal{T}}|<\mathit{ϵ}$ then solve the direct problem for ${\mathit{\phi }}_0^1$, calculate ${\mathit{\xi }}_0^2={\mathrm{m}\mathit{ax}}_{\mathrm{\Omega }}|\nabla u{|}^2$ and get ${\mathit{\xi }}_{0h}^2$ by ${\mathit{\xi }}_{0h}^2={\mathit{\xi }}_0^2$.

4. If $\stackrel{\sim }{{\mathcal{T}}_3}-\hat{\mathcal{T}}>0$ then apply (A2.1)–(A2.3) for $({\mathit{\phi }}_1,{\mathit{\phi }}_0^1)$.

5. If $\stackrel{\sim }{{\mathcal{T}}_3}-\hat{\mathcal{T}}<0$ then apply (A2.1)–(A2.3) for $({\mathit{\phi }}_0^1,{\mathit{\phi }}_2)$.

Note that Algorithm 2 also involves Algorithm 1. Though there is no mathematical reason, we give a physical explanation why the relation $\stackrel{\sim }{{\mathcal{T}}_3}<{\mathcal{T}}_3<\stackrel{\sim }{\stackrel{\sim }{{\mathcal{T}}_3}}$ should hold. Since ${\mathit{\phi }}_2>{\mathit{\phi }}_1$ and we treat $({\mathit{\phi }}_2,{\mathcal{T}}_2)$ as if it is given in the pure plastic case, the solution of the direct problem in the pure elastic case gives ${\mathit{\xi }}_{{(0h)}_1}^2<{\mathit{\xi }}_0^2<{\mathit{\xi }}_{{(0h)}_2}^2$ (see step 2 in Figure 1) which means $\stackrel{\sim }{{\mathcal{T}}_3}<{\mathcal{T}}_3<\stackrel{\sim }{\stackrel{\sim }{{\mathcal{T}}_3}}$ holds. We denote ${\mathit{\xi }}_0^2$ by ${\mathit{\xi }}_{{(0h)}_1}^1$ and ${\mathit{\xi }}_{{(0h)}_2}^2$ for ${\mathit{\phi }}_1$ and ${\mathit{\phi }}_2$, respectively. The main idea of these two algorithms is to decide the interval that includes the real angle that exactly corresponds to the yield stress. After finding this angle approximately, we can determine the approximate value of the yield stress as it is explained in the Algorithm 2. The new fast algorithm differs from the original one while in finding the yield stress. The other steps remain the same. However, this modification is very useful and very effective. Because there is no parameter to choose in the algorithms except $\mathit{ϵ}>0$ which appears in the Algorithm 2. This is very important simplification for the nature of inverse problems since each choice of these parameters restricts us in the solution process. For example, in [21] the influence of the stopping parameter $\mathit{ϵ}>0$ on identifiability is shown to be very large, i.e. even very small changes of the parameter $\mathit{ϵ}>0$ lead to large deviations in the solution of the inverse problem.

Numerical examples with noise free and noise data

In many physical and engineering applications, two types of materials are encountered, i.e. stiff and soft materials with the parameters $(E=210\mathit{GPa},{\mathit{\xi }}_0^2=0.027)$ and $(E=110\mathit{GPa},{\mathit{\xi }}_0^2=0.020)$, respectively. In all numerical examples, $\mathit{\kappa }=0.2$ is used. Noise free synthetic data for these types of materials are generated by solving the direct problem (1) and precise values of torque are found by calculating the integral (3) numerically. For the numerical solution of the nonlinear problem (1), the following finite difference scheme is used [22](8) $$\begin{array}{cc}\hfill & -\frac{h_2}{h_1}[{\stackrel{\sim }{g}}_{i+1/2,j}\frac{v_{i+1,j}-v_{i,j}}{h_1}-{\stackrel{\sim }{g}}_{i-1/2,j}\frac{v_{i,j}-v_{i-1,j}}{h_1}]\hfill \\ \hfill & -\frac{h_1}{h_2}[{\stackrel{\sim }{g}}_{i,j+1/2}\frac{v_{i,j+1}-v_{i,j}}{h_2}-{\stackrel{\sim }{g}}_{i,j-1/2}\frac{v_{i,j}-v_{i,j-1}}{h_2}]=2\mathit{\phi },\hfill \end{array}$$(8) where $(x_{1,i},x_{2,j})\in w_h$, $w_h:=\{(x_{1,i},x_{2,j}):x_{1,i}={\mathit{ih}}_1/(N_1-1),x_{2,j}={\mathit{jh}}_2/(N_2-1),$$i=\overline{2,N_1-1},j=\overline{2,N_2-1}\}$ is the piecewise uniform mesh with mesh steps $h_m=l_m/(N_m-1)$, $m=1,2$, $l_1=a,l_2=b$; $v_{i,j}:=u^{(n)}(x_{1,i},x_{2,j})$ are the nodal values of the function ($n$th iteration). The coefficients ${\stackrel{\sim }{g}}_{p,q}$ are defined as follows:$$\begin{array}{c}\hfill {\stackrel{\sim }{g}}_{i\pm 1/2,j}:=g\left(\right|\nabla u^{(n-1)}(x_{1,i\pm 1/2},x_{2,j}){|}^2),{\stackrel{\sim }{g}}_{i,j\pm 1/2}:=g(|\nabla u^{(n-1)}(x_{1,i},x_{2,j\pm 1/2}){|}^2).\end{array}$$The approximation error of this scheme on uniform mesh is $O(h^2)$ where $h^2=h_1^2+h_2^2$. Table 1 shows the computational results for the stiff and the soft materials. In this table, $m=1$ and $m=2,3,4,5$ correspond to the pure elastic and the pure plastic cases, respectively.

Table 1 Synthetic noise free data for the stiff and the soft materials .

$E=210$ Gpa	$m=1$	$m=2$	$m=3$	$m=4$	$m=5$
${\mathit{\phi }}_m\times {10}^3$	2.2	3.3	3.6	3.7	3.85
${\mathit{\xi }}_m^2\times {10}^2$	1.3	4.0	6.6	7.9	10.0
${\mathcal{T}}_m\times {10}^2$	2.48	3.75	4.21	4.41	4.7
$E=110$ Gpa	$m=1$	$m=2$	$m=3$	$m=4$	$m=5$
${\mathit{\phi }}_m\times {10}^3$	4.4	5.58	5.97	6.28	6.6
${\mathit{\xi }}_m^2\times {10}^2$	1.4	3.6	5.2	7.1	9.8
${\mathcal{T}}_m\times {10}^2$	2.59	3.35	3.68	4.0	4.39

 

The solution process of the inverse problem for the stiff material by the modified semi-analytic inversion method is presented below step by step. First by applying parametri-zation algorithm for the pair $({\mathit{\phi }}_1,{\mathcal{T}}_1)$, the approximate value of $G$ is found to be $G_h=80.50$. The linear direct problem is solved for $G_h=80.50$ and ${\mathit{\xi }}_0^2$ is found to be ${\mathit{\xi }}_0^2=0.013$. For the pairs $({\mathit{\phi }}_1,{\mathcal{T}}_1)$ and $({\mathit{\phi }}_3,{\mathcal{T}}_3)$, the function $g({\mathit{\xi }}^2)$ defined by (6) is obtained as follows:(9) $$\begin{array}{c}\hfill g({\mathit{\xi }}^2)=\{\begin{array}{c}0.0124,{\mathit{\xi }}^2\le 0.013,\hfill \\ 0.0124-0.1110({\mathit{\xi }}^2-0.013),{\mathit{\xi }}^2>0.013.\hfill \end{array}\end{array}$$(9) The linear direct problem is solved with the input data (9) and ${\mathit{\xi }}_{1h}^2$ is found to be ${\mathit{\xi }}_{1h}^2=0.067$. By using formula (7), ${\mathit{\kappa }}_h$ and $\stackrel{\sim }{{\mathcal{T}}_3}$ are found to be 0.2275 and 0.0388, respectively. For the pairs $({\mathit{\phi }}_2,{\mathcal{T}}_2)$ and $({\mathit{\phi }}_3,{\mathcal{T}}_3)$, ${\mathit{\kappa }}_h$ and $\stackrel{\sim }{\stackrel{\sim }{{\mathcal{T}}_3}}$ are found to be 0.2346 and 0.0463, respectively. Consequently, we have the relation $\stackrel{\sim }{{\mathcal{T}}_3}<{\mathcal{T}}_3<\stackrel{\sim }{\stackrel{\sim }{{\mathcal{T}}_3}}$. Then, by applying Algorithm 2, after three iterations, ${\mathit{\xi }}_{0h}^2$ is found to be ${\mathit{\xi }}_{0h}^2=0.0252$. By repeating the similar steps, ${\mathit{\xi }}_{0h}^2$ is found to be ${\mathit{\xi }}_{0h}^2=0.0185$ for the soft material. These values will be accepted as the approximate value of the yield stress for the stiff and the soft materials, respectively. In the semi-analytic inversion method, the yield stress for the stiff and the soft materials are found to be $0.026$ and $0.019$. These approximate values seem more precise than the approximate values found by the modified semi-analytic inversion method. But the semi-analytic inversion method finds these values by choosing the parameters, appearing in the algorithm, very small. This means that we need more time since the algorithm requires many iterations.

Fig. 3 The reconstructed curve $g_h({\mathit{\xi }}^2)$ for different values of angle steps for the stiff (left figure) and the soft (right figure) materials, (noise free data).

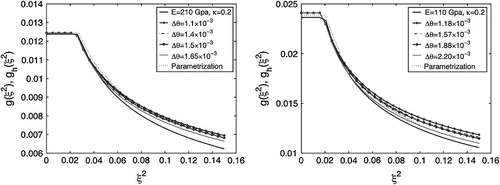
To compare these obtained results, the parametrization algorithm is also applied for the determination of the plasticity function $g({\mathit{\xi }}^2)$. The reconstructed plasticity function is plotted in the Figure 3 by the dotted line. It is obvious from the figure that the optimal angle steps $\mathrm{\Delta }\mathit{\phi }$ are $1.65\times {10}^{-3}$ and $2.20\times {10}^{-3}$ for the stiff and the soft materials respectively. We note that a smaller angle step is found for the stiff material. This result depends on the experiments given in Table 1. Thus, it may not be always true that smaller angle step is needed for the stiff material. However there are some relations between the parameters of engineering materials. For instance, in the pure elastic case an increase of the parameter $G>0$ implies an increase of the rigidity of a material, and as a result, leads to decrease of the torque for a fixed angle of twist $\mathit{\phi }$ (see [17, 18, 21] for details). Tables 2 and 3 show the approximate values of $\mathit{\kappa }$ for each given pair $(\mathit{\phi },\mathcal{T})$. Table 4 shows that the absolute and the relative errors defined by ${\mathit{ϵ}}_g=\parallel g-g_h{\parallel }_{\infty }$ and $\mathit{\delta }g=\parallel (g-g_h)/g{\parallel }_{\infty }$, respectively, for noise free inverse problem where $g_h$ is the approximate solution.

Table 2 The approximate values of $\mathit{\kappa }$ corresponding to each plastic case for the stiff material.

$(\mathit{\phi }\times {10}^3,\mathcal{T}\times {10}^2)$	$\mathrm{\Delta }\mathit{\phi }\times {10}^3$	$g_h({\mathit{\xi }}^2)$	${\mathit{\xi }}_{1h}^2$	$g_h({\mathit{\xi }}_{1h}^2)$	${\mathit{\kappa }}_h$
$(3.30,3.75)$	$1.1$	$0.0124-0.1385({\mathit{\xi }}^2-0.0252)$	0.030	0.0117	0.35
$(3.60,4.21)$	$1.4$	$0.0124-0.0900({\mathit{\xi }}^2-0.0252)$	0.058	0.0094	0.34
$(3.70,4.41)$	$1.5$	$0.0124-0.0800({\mathit{\xi }}^2-0.0252)$	0.070	0.0088	0.33
$(3.85,4.71)$	$1.65$	$0.0124-0.0670({\mathit{\xi }}^2-0.0252)$	0.092	0.0073	0.30

In practice, the torque $\mathcal{T}$ can be given with some measurement error $\mathit{\gamma }$, i.e. with noise data ${\mathcal{T}}_{\mathit{\gamma }}=\mathcal{T}+\mathit{\gamma }\mathcal{T}$. Three types of noise levels with $\mathit{\gamma }=+0.03$, $\mathit{\gamma }=-0.05$ and $\mathit{\gamma }=\pm 0.07$ are used in computational experiments. The results are presented in Figure 4. Table 5 shows the absolute and the relative errors for three different levels of the inverse problem. By comparing the numerical results in the case of noise, we can conclude that the relative error $\mathit{\delta }g$ corresponding to the modified semi-analytic inversion method is less than the relative error corresponding to the parametrization algorithm. Note that the results obtained for the soft material are almost the same in terms of accuracy, absolute and relative errors.

Table 3 The approximate values of $\mathit{\kappa }$ corresponding to each plastic case for the soft material.

$(\mathit{\phi }\times {10}^3,\mathcal{T}\times {10}^2)$	$\mathrm{\Delta }\mathit{\phi }\times {10}^3$	$g_h({\mathit{\xi }}^2)$	${\mathit{\xi }}_{1h}^2$	$g_h({\mathit{\xi }}_{1h}^2)$	${\mathit{\kappa }}_h$
$(5.58,3.35)$	$1.18$	$0.0238-0.2900({\mathit{\xi }}^2-0.0185)$	0.033	0.0196	0.33
$(5.97,3.68)$	$1.57$	$0.0238-0.2230({\mathit{\xi }}^2-0.0185)$	0.048	0.0172	0.31
$(6.28,4.00)$	$1.88$	$0.0238-0.1800({\mathit{\xi }}^2-0.0185)$	0.066	0.0153	0.30
$(6.60,4.39)$	$2.20$	$0.0238-0.1390({\mathit{\xi }}^2-0.0185)$	0.095	0.0130	0.27

Table 4 The absolute and relative errors for the noise free inverse problem.

$E=210$ Gpa	Paramet.	Fast alg.
${\mathit{ϵ}}_g$	$4.4\times {10}^{-4}$	$1.7\times {10}^{-4}$
${\mathit{\delta }}_g$	$6.0\times {10}^{-2}$	$1.5\times {10}^{-2}$
$E=110$ Gpa	Paramet.	Fast alg.
${\mathit{ϵ}}_g$	$4.6\times {10}^{-4}$	$4.3\times {10}^{-4}$
${\mathit{\delta }}_g$	$4.2\times {10}^{-2}$	$1.9\times {10}^{-2}$

Finally, we want to emphasize that this study will constitute a background for future applications, i.e. in solving some kinds of inverse problems that arise physics and materials science numerically.

Fig. 4 The reconstructed curve $g_h({\mathit{\xi }}^2)$ for $\mathrm{\Delta }\mathit{\phi }=1.65\times {10}^{-3}$ for the stiff material (left figure ) and the reconstructed curve $g_h({\mathit{\xi }}^2)$ for $\mathrm{\Delta }\mathit{\phi }=2.20\times {10}^{-3}$ for the soft material (right figure), (noise data).

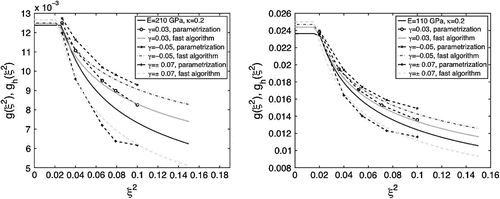
Table 5 The absolute and relative errors for the noise inverse problem.

$\mathit{\gamma }$ (For stiff)	${\mathit{ϵ}}_g$ (Paramet.)	${\mathit{ϵ}}_g$ (Fast alg.)	${\mathit{\delta }}_g$ (Paramet.)	${\mathit{\delta }}_g$ (Fast alg.)
$+0.03$	$9.3\times {10}^{-4}$	$8.5\times {10}^{-4}$	$1.3\times {10}^{-1}$	$1.0\times {10}^{-1}$
$-0.05$	$2.0\times {10}^{-3}$	$1.0\times {10}^{-3}$	$2.7\times {10}^{-1}$	$1.9\times {10}^{-1}$
$\pm 0.07$	$2.2\times {10}^{-3}$	$1.3\times {10}^{-3}$	$2.8\times {10}^{-1}$	$2.1\times {10}^{-1}$
$\mathit{\gamma }$ (For soft)	${\mathit{ϵ}}_g$ (Paramet.)	${\mathit{ϵ}}_g$ (Fast alg.)	${\mathit{\delta }}_g$ (Paramet.)	${\mathit{\delta }}_g$ (Fast alg.)
$+0.03$	$1.2\times {10}^{-3}$	$1.0\times {10}^{-3}$	$9.3\times {10}^{-2}$	$8.6\times {10}^{-2}$
$-0.05$	$2.5\times {10}^{-3}$	$2.3\times {10}^{-3}$	$2.0\times {10}^{-1}$	$1.7\times {10}^{-1}$
$\pm 0.07$	$2.6\times {10}^{-3}$	$2.4\times {10}^{-3}$	$2.2\times {10}^{-1}$	$1.9\times {10}^{-1}$

 

Concluding remarks

A new method is given for determination of the yield stress for power hardening engineering materials. It may be viewed as a very effective modification to the semi-analytic inversion method. The modification is just related to determination of yield stress and does not affect well-posedness of the semi-analytic inversion method. Thus, the modified semi-analytic inversion method is also well-posed. One of the advantages of this method is that it does not require complicated calculations and many parameters. Since each choice of these parameters affect the numerical calculations (some of them cause ill-posedness of the method), the new method solves this problem using a minimum number of parameters. The presented numerical examples show that the modified semi-analytic inversion method allows us to determine the plasticity function with high accuracy, even for acceptable noise levels. The authors of this paper consider to apply the presented method to different problems in physical and mechanical science such as the bending problem of a plate in upcoming studies. In addition, whether the presented analyses can be exploited for non-dimensional parameters in fluid mechanics, such as Reynolds number, Mach number, Froude number, Weber number and Strouhal number is also an interesting problem. Such non-dimensional parameters are used for geometric scaling, and for developing dynamic similitude in experimental processes. Furthermore, the authors consider to study applicability of both the parametrization and semi-analytic inversion methods if there is no assumption about the plastic response of the material.

Acknowledgments

The research has been partially supported by the Scientific and Technological Research Council of Turkey (TUBITAK), also by Zirve University Research Fund. The authors thank the reviewers for their very careful reading and for pointing out several mistakes as well as for their useful comments and suggestions.