A vector regularization method to solve linear inverse problems

Abstract

The linear inverse problem is discretized to be an n-dimensional ill-posed linear equations system $\mathbf{B}\mathbf{x}=\mathbf{b}$. In the present paper, an invariant manifold defined in terms of the square norm of a residual vector $\mathbf{r}:=\mathbf{B}\mathbf{x}-\mathbf{b}$ is used to derive an iterative algorithm with a fast descent direction $\mathbf{A}\mathbf{r}$, which is close to, but not exactly equal to, the best descent direction ${\mathbf{B}}^{-1}\mathbf{r}$. The matrix $\mathbf{A}$ is obtained by using a vector regularization method together with a matrix conjugate gradient method to find the right inversion of $\mathbf{B}$: $\mathbf{B}\mathbf{A}={\mathbf{I}}_n$. The vector regularization iterative algorithm is proven to be Lyapunov stable, and the direct inversion method with solution expressed by $\mathbf{x}=\mathbf{A}\mathbf{b}$ converges fast. The accuracy and efficiency of them are verified through the numerical tests of linear inverse problems under a large random noise.

Keywords:

• linear inverse problems
• vector regularization method
• invariant manifold
• vector regularization iterative algorithm
• direct inversion method

Introduction

It is known that an iterative method for solving the system of algebraic equations can be derived from the discretization of a certain ordinary differential equations (ODEs) system.[1, 2] In particular, the descent methods can be interpreted as the discretizations of gradient flows.[3] Indeed, it has a long time history that continuous algorithms have been investigated in many literature, for example, Gavurin [4], Alber [5] and Hirsch and Smale [6]. Chu [7] has developed a systematic approach to the continuous realization of several iterative algorithms in numerical linear algebra. The Lyapunov methods used in the analysis of iterative methods have been made by Ortega and Rheinboldt [8], and Bhaya and Kaszkurewicz [1, 9, 10].

The author and his co-workers have developed several methods to solve ill-posed system of linear equations: the fictitious time integration method as a filter,[11] a modified polynomial expansion method, [12] the Laplacian preconditioners and postconditioners,[13] a vector regularization method,[14] a relaxed steepest descent method,[15, 16] an optimal iterative algorithm with an optimal descent vector,[17] an adaptive Tikhonov regularization method,[18] the best vector iterative method,[19] the globally optimal vector iterative method,[20] the optimally scaled vector regularization method,[21] an optimally generalized Tikhonov regularization method,[22] as well as an optimal tri-vector iterative algorithm.[23] As a continuation of these works, in this paper, we propose a more simple and robust method to solve(1) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(1) where $\mathbf{x}\in R^n$ is an unknown vector determined from a given coefficient matrix $\mathbf{B}\in R^{n\times n}$, which might be unsymmetric, and the input $\mathbf{b}\in R^n$ which might be polluted by random noise. Many linear-type inverse problems can be discretized into the above form.

A measure of the ill-posedness of Equation (1(1) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(1) ) is the condition number of $\mathbf{B}$:(2) $$\begin{array}{c}\hfill \text{Cond}(\mathbf{B})=\parallel \mathbf{B}{\parallel }_F\parallel {\mathbf{B}}^{-1}{\parallel }_F,\end{array}$$(2) where $\parallel \mathbf{B}{\parallel }_F$ is the Frobenius norm of $\mathbf{B}$.

For every matrix norm $\parallel •\parallel$, we have $\mathit{\rho }(\mathbf{B})\le \parallel \mathbf{B}\parallel$, where $\mathit{\rho }(\mathbf{B})$ is a radius of the spectrum of $\mathbf{B}$. The Householder theorem states that for every $\mathit{ϵ}>0$ and every matrix $\mathbf{B}$, there exists a matrix norm $\parallel \mathbf{B}\parallel$ depending on $\mathbf{B}$ and $\mathit{ϵ}$ such that $\parallel \mathbf{B}\parallel \le \mathit{\rho }(\mathbf{B})+\mathit{ϵ}$. So far, the spectral condition number $\mathit{\rho }(\mathbf{B})\mathit{\rho }({\mathbf{B}}^{-1})$ can be used as an estimation of the condition number of $\mathbf{B}$ by(3) $$\begin{array}{c}\hfill \text{Cond}(\mathbf{B})=\frac{\underset{\mathit{\sigma }(\mathbf{B})}{\max }|\mathit{\lambda }|}{\underset{\mathit{\sigma }(\mathbf{B})}{\min }|\mathit{\lambda }|},\end{array}$$(3) where $\mathit{\sigma }(\mathbf{B})$ is the collection of all the eigenvalues of $\mathbf{B}$. If the Frobenius norm in Equation (2(2) $$\begin{array}{c}\hfill \text{Cond}(\mathbf{B})=\parallel \mathbf{B}{\parallel }_F\parallel {\mathbf{B}}^{-1}{\parallel }_F,\end{array}$$(2) ) is replaced by the operator norm, then Equations (2(2) $$\begin{array}{c}\hfill \text{Cond}(\mathbf{B})=\parallel \mathbf{B}{\parallel }_F\parallel {\mathbf{B}}^{-1}{\parallel }_F,\end{array}$$(2) ) and (3(3) $$\begin{array}{c}\hfill \text{Cond}(\mathbf{B})=\frac{\underset{\mathit{\sigma }(\mathbf{B})}{\max }|\mathit{\lambda }|}{\underset{\mathit{\sigma }(\mathbf{B})}{\min }|\mathit{\lambda }|},\end{array}$$(3) ) lead to the same condition number. Turning back to the Frobenius norm, we have(4) $$\begin{array}{c}\hfill \parallel \mathbf{B}{\parallel }_F\le \sqrt{n}\underset{\mathit{\sigma }(\mathbf{B})}{\max }|\mathit{\lambda }|.\end{array}$$(4) In particular, for the symmetric case $\mathit{\rho }(\mathbf{B})\mathit{\rho }({\mathbf{B}}^{-1})=\parallel \mathbf{B}{\parallel }_2\parallel {\mathbf{B}}^{-1}{\parallel }_2$. Roughly speaking, the numerical solution of Equation (1(1) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(1) ) may lose the accuracy of k decimal points when $\text{Cond}(\mathbf{B})={10}^k$.

Instead of Equation (1(1) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(1) ), we can solve a normal linear system:(5) $$\begin{array}{c}\hfill \mathbf{C}\mathbf{x}={\mathbf{b}}_1,\end{array}$$(5) where(6) $$\begin{array}{cc}\hfill & {\mathbf{b}}_1={\mathbf{B}}^{\text{T}}\mathbf{b},\hfill \\ \hfill & \mathbf{C}={\mathbf{B}}^{\text{T}}\mathbf{B}>\mathbf{0}.\hfill \end{array}$$(6) We consider an iterative method for solving Equation (5(5) $$\begin{array}{c}\hfill \mathbf{C}\mathbf{x}={\mathbf{b}}_1,\end{array}$$(5) ) and define for any vector ${\mathbf{x}}_k$ the steepest descent vector(7) $$\begin{array}{c}\hfill {\mathbf{R}}_k:=\mathbf{C}{\mathbf{x}}_k-{\mathbf{b}}_1.\end{array}$$(7) Ascher et al. [24], and also Liu and Chang [25] have viewed the gradient descent method:(8) $$\begin{array}{c}\hfill {\mathbf{x}}_{k+1}={\mathbf{x}}_k-{\mathit{\alpha }}_k{\mathbf{R}}_k,\end{array}$$(8) as a forward Euler scheme of the following system of ODEs:(9) $$\begin{array}{c}\hfill \stackrel{·}{\mathbf{x}}={\mathbf{b}}_1-\mathbf{C}\mathbf{x}.\end{array}$$(9) The absolute stability bound(10) $$\begin{array}{c}\hfill {\mathit{\alpha }}_k\le \frac{2}{\underset{\mathit{\sigma }(\mathbf{C})}{\max }\mathit{\lambda }}\end{array}$$(10) must be obeyed if a uniform stepsize is employed.

Specifically, Equation (8(8) $$\begin{array}{c}\hfill {\mathbf{x}}_{k+1}={\mathbf{x}}_k-{\mathit{\alpha }}_k{\mathbf{R}}_k,\end{array}$$(8) ) presents a steepest descent method (SDM), if(11) $$\begin{array}{c}\hfill {\mathit{\alpha }}_k=\frac{\parallel {\mathbf{R}}_k{\parallel }^2}{{\mathbf{R}}_k^{\text{T}}\mathbf{C}{\mathbf{R}}_k}.\end{array}$$(11) When $\parallel {\mathbf{R}}_k\parallel$ is small, the calculated ${\mathbf{R}}_k$ may deviate from the real steepest descent direction to a great extent due to a round-off error of computing machine, which usually leads to the numerical instability of SDM. An improvement of SDM is the conjugate gradient method (CGM), which enhances the search direction of the minimum of a quadratic functional by imposing an orthogonality to the residual vector at each iterative step. The algorithm of CGM for solving Equation (5(5) $$\begin{array}{c}\hfill \mathbf{C}\mathbf{x}={\mathbf{b}}_1,\end{array}$$(5) ) is summarized as follows.

1. Give an initial ${\mathbf{x}}_0$, compute ${\mathbf{R}}_0=\mathbf{C}{\mathbf{x}}_0-{\mathbf{b}}_1$ and then set ${\mathbf{p}}_0={\mathbf{R}}_0$.

2. For $k=0,1,2,\dots$, we repeat the following iterations:(12) $$\begin{array}{cc}\hfill & {\mathit{\eta }}_k=\frac{\parallel {\mathbf{R}}_k{\parallel }^2}{{\mathbf{p}}_k^{\text{T}}\mathbf{C}{\mathbf{p}}_k},\hfill \\ \hfill & {\mathbf{x}}_{k+1}={\mathbf{x}}_k-{\mathit{\eta }}_k{\mathbf{p}}_k,\hfill \\ \hfill & {\mathbf{R}}_{k+1}=\mathbf{C}{\mathbf{x}}_{k+1}-{\mathbf{b}}_1,\hfill \\ \hfill & {\mathit{\alpha }}_{k+1}=\frac{\parallel {\mathbf{R}}_{k+1}{\parallel }^2}{\parallel {\mathbf{R}}_k{\parallel }^2},\hfill \\ \hfill & {\mathbf{p}}_{k+1}={\mathit{\alpha }}_{k+1}{\mathbf{p}}_k+{\mathbf{R}}_{k+1}.\hfill \end{array}$$(12)

If ${\mathbf{x}}_{k+1}$ converges according to a given stopping criterion $\parallel {\mathbf{R}}_{k+1}\parallel <\mathit{\epsilon }$, then stop; otherwise, go to step (ii).

Even if the CGM works very well for most linear systems, the CGM does lose some of its luster for some linear inverse problems. The gradient descent methods enjoy a fictitious time integration method with different stepsizes. This is particularly useful for image deblurring. The concept of optimal descent vector was first developed by Liu and Atluri [26] for solving non-linear algebraic equations. In this paper, we explore the concept of best descent vector [19] and use it as a guidance to develop a new method to solve linear algebraic equations.

The remaining parts of this paper are arranged as follows. The vector regularization method for inverting non-singular matrix is introduced in Section 2. In Section 3, we start from an invariant manifold to derive a non-linear ODEs system for the numerical solution of Equation (1(1) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(1) ) with the descent direction to be $\mathbf{u}=\mathbf{A}\mathbf{r}$, where $\mathbf{A}$ is solved from the vector regularization method as a right inversion of the coefficient matrix $\mathbf{B}$ given in Equation (1(1) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(1) ). Then, a Lyapunov stable dynamics on the invariant manifold is constructed in Section 4, resulting in a vector regularization iterative algorithm (VRIA). The linear inverse problems are solved in Section 5 to display some advantages of the VRIA and the direct inversion method (DIM). Finally, the conclusions are drawn in Section 6.

A vector regularization method

The vector regularization method for inverting non-singular matrices was first developed by Liu et al. [14]. Recently, Liu [21] has developed a systematic method to determine the vector regularization parameter.

Let us begin with the following matrix equation:(13) $$\begin{array}{c}\hfill {\mathbf{V}}^{\text{T}}{\mathbf{U}}^{\text{T}}={\mathbf{I}}_m,\text{i.e.}{(\mathbf{U}\mathbf{V})}^{\text{T}}={\mathbf{I}}_m,\end{array}$$(13) if $\mathbf{U}$ is the inversion of a given non-singular $m\times m$ matrix $\mathbf{V}$, where ${\mathbf{I}}_m$ is the $m\times m$ identity matrix. Numerically, we can say that the above $\mathbf{U}$ is a left inversion of $\mathbf{V}$ due to $\mathbf{U}\mathbf{V}={\mathbf{I}}_m$. Then, multiplying the above equation by $\mathbf{V}$ from the left side we have(14) $$\begin{array}{c}\hfill \mathbf{D}{\mathbf{U}}^{\text{T}}=\mathbf{V},\mathbf{D}:=\mathbf{V}{\mathbf{V}}^{\text{T}},\end{array}$$(14) from which we can solve for ${\mathbf{U}}^{\text{T}}:=\mathbf{C}$ by the following matrix conjugate gradient method (MCGM):

1. Assume an initial ${\mathbf{C}}_0$.

2. Calculate ${\mathbf{R}}_0=\mathbf{V}-\mathbf{D}{\mathbf{C}}_0$ and ${\mathbf{P}}_1={\mathbf{R}}_0$.

3. For $k=1,2,\dots$, we repeat the following iterations:(15) $$\begin{array}{cc}\hfill & {\mathit{\alpha }}_k=\frac{\parallel {\mathbf{R}}_{k-1}{\parallel }^2}{{\mathbf{P}}_k·(\mathbf{D}{\mathbf{P}}_k)},\hfill \\ \hfill & {\mathbf{C}}_k={\mathbf{C}}_{k-1}+{\mathit{\alpha }}_k{\mathbf{P}}_k,\hfill \\ \hfill & {\mathbf{R}}_k=\mathbf{V}-\mathbf{D}{\mathbf{C}}_k,\hfill \\ \hfill & {\mathit{\eta }}_k=\frac{\parallel {\mathbf{R}}_k{\parallel }^2}{\parallel {\mathbf{R}}_{k-1}{\parallel }^2},\hfill \\ \hfill & {\mathbf{P}}_{k+1}={\mathbf{R}}_k+{\mathit{\eta }}_k{\mathbf{P}}_k.\hfill \end{array}$$(15) If ${\mathbf{C}}_k$ converges according to a given stopping criterion:(16) $$\begin{array}{c}\hfill \parallel {\mathbf{R}}_k\parallel <{\mathit{\epsilon }}_2,\end{array}$$(16) then stop; otherwise, go to step (iii). In the above, the capital boldfaced letters denote $m\times m$ matrices, the norm $\parallel {\mathbf{R}}_k\parallel$ is the Frobenius norm (similar to the Euclidean norm for a vector), and the inner product is for matrices. When $\mathbf{C}$ is calculated, the left inversion of $\mathbf{V}$ is given by $\mathbf{U}={\mathbf{C}}^{\text{T}}$.

The above MCGM is suitable to find the inversion of a well-conditioned matrix; however, for a given ill-conditioned matrix with a large condition number, we need more study to find its inversion. Let(17) $$\begin{array}{c}\hfill \mathbf{V}{\mathbf{x}}_0={\mathbf{y}}_0,\end{array}$$(17) through which, given ${\mathbf{x}}_0$, say ${\mathbf{x}}_0=\mathbf{1}={[1,\dots ,1]}^{\text{T}}$, we can calculate ${\mathbf{y}}_0$ readily, because $\mathbf{V}$ is a given matrix. Hence, multiplying the above equation by $\mathbf{U}$ from the left side and using Equation (13(13) $$\begin{array}{c}\hfill {\mathbf{V}}^{\text{T}}{\mathbf{U}}^{\text{T}}={\mathbf{I}}_m,\text{i.e.}{(\mathbf{U}\mathbf{V})}^{\text{T}}={\mathbf{I}}_m,\end{array}$$(13) ) we have(18) $$\begin{array}{c}\hfill {\mathbf{y}}_0^{\text{T}}{\mathbf{U}}^{\text{T}}={\mathbf{x}}_0^{\text{T}},\text{i.e.}{\mathbf{x}}_0=\mathbf{U}{\mathbf{y}}_0.\end{array}$$(18) Together, Equations (13(13) $$\begin{array}{c}\hfill {\mathbf{V}}^{\text{T}}{\mathbf{U}}^{\text{T}}={\mathbf{I}}_m,\text{i.e.}{(\mathbf{U}\mathbf{V})}^{\text{T}}={\mathbf{I}}_m,\end{array}$$(13) ) and (22(22) $$\begin{array}{c}\hfill \mathbf{V}\mathbf{U}={\mathbf{I}}_m,\end{array}$$(22) ) constitute an over-determined system to calculate ${\mathbf{U}}^{\text{T}}$. This over-determined system can be written as(19) $$\begin{array}{c}\hfill \mathbf{W}{\mathbf{U}}^{\text{T}}=\left[\begin{array}{c}\hfill {\mathbf{I}}_m\hfill \\ \hfill {\mathbf{x}}_0^{\text{T}}\hfill \end{array}\right],\end{array}$$(19) where(20) $$\begin{array}{c}\hfill \mathbf{W}:=\left[\begin{array}{c}\hfill {\mathbf{V}}^{\text{T}}\hfill \\ \hfill {\mathbf{y}}_0^{\text{T}}\hfill \end{array}\right]\end{array}$$(20) is an $n\times m$ matrix with $n=m+1$. Multiplying Equation (23(23) $$\begin{array}{c}\hfill {\mathbf{y}}_0^{\text{T}}\mathbf{U}={\mathbf{x}}_0^{\text{T}},\text{i.e.}{\mathbf{y}}_0={\mathbf{V}}^{\text{T}}{\mathbf{x}}_0.\end{array}$$(23) ) by ${\mathbf{W}}^{\text{T}}$, we obtain an $m\times m$ matrix equation again:(21) $$\begin{array}{c}\hfill [\mathbf{V}{\mathbf{V}}^{\text{T}}+{\mathbf{y}}_0{\mathbf{y}}_0^{\text{T}}]{\mathbf{U}}^{\text{T}}=\mathbf{V}+{\mathbf{y}}_0{\mathbf{x}}_0^{\text{T}},\end{array}$$(21) which, similar to Equation (14(14) $$\begin{array}{c}\hfill \mathbf{D}{\mathbf{U}}^{\text{T}}=\mathbf{V},\mathbf{D}:=\mathbf{V}{\mathbf{V}}^{\text{T}},\end{array}$$(14) ), is solved by the MCGM with $\mathbf{D}=\mathbf{V}{\mathbf{V}}^{\text{T}}+{\mathbf{y}}_0{\mathbf{y}}_0^{\text{T}}$ and $\mathbf{V}$ being replaced by $\mathbf{V}+{\mathbf{y}}_0{\mathbf{x}}_0^{\text{T}}$. This algorithm for solving the left inversion $\mathbf{U}$ of an ill-conditioned matrix $\mathbf{V}$ has been labelled as the MCGML method.

The above algorithm is suitable for finding the left inversion of $\mathbf{V}$, i.e. $\mathbf{U}\mathbf{V}={\mathbf{I}}_m$; however, we need to solve(22) $$\begin{array}{c}\hfill \mathbf{V}\mathbf{U}={\mathbf{I}}_m,\end{array}$$(22) when we want $\mathbf{U}$ to be a right inversion of $\mathbf{V}$. Mathematically, the left inversion is equal to the right inversion. But, numerically, they are hardly being equal, especially for ill-conditioned matrices.

For the right inversion, we can supplement, as in Equation (21(21) $$\begin{array}{c}\hfill [\mathbf{V}{\mathbf{V}}^{\text{T}}+{\mathbf{y}}_0{\mathbf{y}}_0^{\text{T}}]{\mathbf{U}}^{\text{T}}=\mathbf{V}+{\mathbf{y}}_0{\mathbf{x}}_0^{\text{T}},\end{array}$$(21) ), another equation:(23) $$\begin{array}{c}\hfill {\mathbf{y}}_0^{\text{T}}\mathbf{U}={\mathbf{x}}_0^{\text{T}},\text{i.e.}{\mathbf{y}}_0={\mathbf{V}}^{\text{T}}{\mathbf{x}}_0.\end{array}$$(23) Then, the combination of Equations (26(26) $$\begin{array}{cc}\hfill & {\mathit{\alpha }}_k=\frac{{\parallel {\mathbf{R}}_{k-1}\parallel }^2}{{\mathbf{P}}_k·(\mathbf{D}{\mathbf{P}}_k)},\hfill \\ \hfill & {\mathbf{U}}_k={\mathbf{U}}_{k-1}+{\mathit{\alpha }}_k{\mathbf{P}}_k,\hfill \\ \hfill & {\mathbf{R}}_k={\mathbf{V}}_1-\mathbf{D}{\mathbf{U}}_k,\hfill \\ \hfill & {\mathit{\eta }}_k=\frac{\parallel {\mathbf{R}}_k{\parallel }^2}{\parallel {\mathbf{R}}_{k-1}{\parallel }^2},\hfill \\ \hfill & {\mathbf{P}}_{k+1}={\mathbf{R}}_k+{\mathit{\eta }}_k{\mathbf{P}}_k.\hfill \end{array}$$(26) ) and (27(27) $$\begin{array}{c}\hfill \parallel {\mathbf{R}}_k\parallel <{\mathit{\epsilon }}_2,\end{array}$$(27) ) leads to the following over-determined system:(24) $$\begin{array}{c}\hfill \left[\begin{array}{c}\hfill \mathbf{V}\hfill \\ \hfill {\mathbf{y}}_0^{\text{T}}\hfill \end{array}\right]\mathbf{U}=\left[\begin{array}{c}\hfill {\mathbf{I}}_m\hfill \\ \hfill {\mathbf{x}}_0^{\text{T}}\hfill \end{array}\right].\end{array}$$(24) Multiplying the transpose of the leading matrix on both sides, we can obtain an $m\times m$ matrix equation:(25) $$\begin{array}{c}\hfill [{\mathbf{V}}^{\text{T}}\mathbf{V}+{\mathbf{y}}_0{\mathbf{y}}_0^{\text{T}}]\mathbf{U}={\mathbf{V}}^{\text{T}}+{\mathbf{y}}_0{\mathbf{x}}_0^{\text{T}},\end{array}$$(25) which is then solved by the following MCGMR:

1. Let $\mathbf{D}={\mathbf{V}}^{\text{T}}\mathbf{V}+{\mathbf{y}}_0{\mathbf{y}}_0^{\text{T}}$, and ${\mathbf{V}}_1={\mathbf{V}}^{\text{T}}+{\mathbf{y}}_0{\mathbf{x}}_0^{\text{T}}$.

2. Assume an initial value ${\mathbf{U}}_0$.

3. Calculate ${\mathbf{R}}_0={\mathbf{V}}_1-\mathbf{D}{\mathbf{U}}_0$, and ${\mathbf{P}}_0={\mathbf{R}}_0$.

4. For $k=1,2,\dots$, we repeat the following iterations:(26) $$\begin{array}{cc}\hfill & {\mathit{\alpha }}_k=\frac{{\parallel {\mathbf{R}}_{k-1}\parallel }^2}{{\mathbf{P}}_k·(\mathbf{D}{\mathbf{P}}_k)},\hfill \\ \hfill & {\mathbf{U}}_k={\mathbf{U}}_{k-1}+{\mathit{\alpha }}_k{\mathbf{P}}_k,\hfill \\ \hfill & {\mathbf{R}}_k={\mathbf{V}}_1-\mathbf{D}{\mathbf{U}}_k,\hfill \\ \hfill & {\mathit{\eta }}_k=\frac{\parallel {\mathbf{R}}_k{\parallel }^2}{\parallel {\mathbf{R}}_{k-1}{\parallel }^2},\hfill \\ \hfill & {\mathbf{P}}_{k+1}={\mathbf{R}}_k+{\mathit{\eta }}_k{\mathbf{P}}_k.\hfill \end{array}$$(26) If ${\mathbf{U}}_k$ converges according to a given stopping criterion,(27) $$\begin{array}{c}\hfill \parallel {\mathbf{R}}_k\parallel <{\mathit{\epsilon }}_2,\end{array}$$(27) then stop; otherwise, go to step (iv).

Equations (25(25) $$\begin{array}{c}\hfill [{\mathbf{V}}^{\text{T}}\mathbf{V}+{\mathbf{y}}_0{\mathbf{y}}_0^{\text{T}}]\mathbf{U}={\mathbf{V}}^{\text{T}}+{\mathbf{y}}_0{\mathbf{x}}_0^{\text{T}},\end{array}$$(25) ) and (29(29) $$\begin{array}{c}\hfill \mathbf{r}=\mathbf{B}\mathbf{x}-\mathbf{b},\end{array}$$(29) ) are two regularized and non-perturbed algebraic equations to find, respectively, the left and right inversion of a given ill-conditioned matrix $\mathbf{V}$. Due to the appearance of ${\mathbf{y}}_0$, we have a chance to reduce the condition numbers of the coefficient matrices of these two equations; however, we refer the paper [21] for a detailed description of how to find the best value of ${\mathbf{y}}_0$.

Invariant manifold method

The most simple way for solving the linear equations system (1(1) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(1) ) is(28) $$\begin{array}{c}\hfill \mathbf{x}={\mathbf{B}}^{-1}\mathbf{b},\end{array}$$(28) where we can apply the MCGML to find ${\mathbf{B}}^{-1}$ from the given matrix $\mathbf{B}$. This inversion method is usually quite dangerous and unstable when there exists a noise on $\mathbf{b}$. The error of noise will be amplified by ${\mathbf{B}}^{-1}$ to cause a large error of $\mathbf{x}$, when the singular values of $\mathbf{B}$ are clustered near to zero value. In Section 5.1, we will give a numerical example to reveal this type phenomenon.

Instead of Equation (32), we search an iterative method based on the idea of MCGMR. For the linear equations system (1(1) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(1) ), which is expressed to be $\mathbf{r}=\mathbf{0}$ in terms of the residual vector:(29) $$\begin{array}{c}\hfill \mathbf{r}=\mathbf{B}\mathbf{x}-\mathbf{b},\end{array}$$(29) we can introduce a scalar homotopy function:(30) $$\begin{array}{c}\hfill h(\mathbf{x},t)=\frac{Q(t)}{2}\parallel \mathbf{r}(\mathbf{x}){\parallel }^2-\frac{1}{2}\parallel \mathbf{r}({\mathbf{x}}_0){\parallel }^2=0.\end{array}$$(30) We expect $h(\mathbf{x},t)=0$ to be an invariant manifold in the space-time domain $(\mathbf{x},t)$ for a dynamical system $h(\mathbf{x}(t),t)=0$ to be specified further. When $Q>0$, the manifold defined by Equation (34(34) $$\begin{array}{c}\hfill \mathbf{A}\mathbf{r}={\mathbf{B}}^{-1}\mathbf{r}.\end{array}$$(34) ) is continuous and differentiable, and thus the following differential operation makes sense:(31) $$\begin{array}{c}\hfill \frac{1}{2}\stackrel{·}{Q}(t)\parallel \mathbf{r}(\mathbf{x}){\parallel }^2+Q(t)\mathbf{r}·(\mathbf{B}\stackrel{·}{\mathbf{x}})=0,\end{array}$$(31) which is obtained by taking the time differential of Equation (34(34) $$\begin{array}{c}\hfill \mathbf{A}\mathbf{r}={\mathbf{B}}^{-1}\mathbf{r}.\end{array}$$(34) ) with respect to t, considering $\mathbf{x}=\mathbf{x}(t)$ and using Equation (33(33) $$\begin{array}{c}\hfill \mathbf{u}=\mathbf{A}\mathbf{r}.\end{array}$$(33) ).

We suppose that the evolution of $\mathbf{x}$ is governed by a vector $\mathbf{u}$:(32) $$\begin{array}{c}\hfill \stackrel{·}{\mathbf{x}}=\mathit{\lambda }\mathbf{u},\end{array}$$(32) where(33) $$\begin{array}{c}\hfill \mathbf{u}=\mathbf{A}\mathbf{r}.\end{array}$$(33) We hope $\mathbf{A}\mathbf{r}$ is near to ${\mathbf{B}}^{-1}\mathbf{r}$ for a fast convergence (see Section 4.2), i.e.(34) $$\begin{array}{c}\hfill \mathbf{A}\mathbf{r}={\mathbf{B}}^{-1}\mathbf{r}.\end{array}$$(34) Then, we can apply the MCGMR to find the right inversion $\mathbf{A}$ of $\mathbf{B}$ by(35) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{A}={\mathbf{I}}_n.\end{array}$$(35) Inserting Equation (36(36) $$\begin{array}{c}\hfill \stackrel{·}{\mathbf{x}}=-q(t)\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{v}}\mathbf{u},\end{array}$$(36) ) into Equation (35(35) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{A}={\mathbf{I}}_n.\end{array}$$(35) ) we can derive(36) $$\begin{array}{c}\hfill \stackrel{·}{\mathbf{x}}=-q(t)\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{v}}\mathbf{u},\end{array}$$(36) where(37) $$\begin{array}{cc}\hfill & \mathbf{v}:=\mathbf{B}\mathbf{u}=\mathbf{B}\mathbf{A}\mathbf{r},\hfill \\ \hfill & q(t):=\frac{\stackrel{·}{Q}(t)}{2Q(t)}.\hfill \end{array}$$(37) Hence, in our algorithm if Q(t) can be guaranteed to be a monotonically increasing function of t, we have an absolutely convergent property in solving the linear equations system (1(1) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(1) ) by decreasing $\parallel \mathbf{r}{\parallel }^2$ according to(38) $$\begin{array}{c}\hfill \parallel \mathbf{r}(\mathbf{x}){\parallel }^2=\frac{C}{Q(t)},\end{array}$$(38) where(39) $$\begin{array}{c}\hfill C=\parallel \mathbf{r}({\mathbf{x}}_0){\parallel }^2\end{array}$$(39) is determined by the initial value ${\mathbf{x}}_0$.

Dynamics on the invariant manifold

In order to keep $\mathbf{x}$ on the manifold (43(43) $$\begin{array}{c}\hfill \mathbf{x}(t+\mathrm{\Delta }t)=\mathbf{x}(t)-\mathit{\eta }\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{v}}\mathbf{u},\end{array}$$(43) ), we can consider the evolution of $\mathbf{r}$ along the path $\mathbf{x}(t)$ by(40) $$\begin{array}{c}\hfill \stackrel{·}{\mathbf{r}}=\mathbf{B}\stackrel{·}{\mathbf{x}}=-q(t)\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{v}}\mathbf{v}.\end{array}$$(40) Because of $q(t)>0$ we can introduce a new independent variable $\mathit{\tau }={\int }_0^{t}q(\mathit{\xi })d\mathit{\xi }$, such that the above equation can be written as(41) $$\begin{array}{c}\hfill \frac{d\mathbf{r}}{d\mathit{\tau }}=-\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{B}\mathbf{A}\mathbf{r}}\mathbf{B}\mathbf{A}\mathbf{r}.\end{array}$$(41) where we have inserted Equation (41(41) $$\begin{array}{c}\hfill \frac{d\mathbf{r}}{d\mathit{\tau }}=-\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{B}\mathbf{A}\mathbf{r}}\mathbf{B}\mathbf{A}\mathbf{r}.\end{array}$$(41) ) for $\mathbf{v}$. It is an autonomous non-linear dynamical system for $\mathbf{r}$.

First, we note that $\mathbf{r}=\mathbf{0}$ is an equilibrium point of Equation (46(46) $$\begin{array}{c}\hfill \frac{C}{Q(t+\mathrm{\Delta }t)}=\frac{C}{Q(t)}-2\mathit{\eta }\frac{C}{Q(t)}+{\mathit{\eta }}^2\frac{C}{Q(t)}\frac{\parallel \mathbf{r}{\parallel }^2}{{({\mathbf{r}}^{\text{T}}\mathbf{v})}^2}\parallel \mathbf{v}{\parallel }^2.\end{array}$$(46) ). It is known that the Lyapunov’s second, or direct, method provides a stronger stability condition of the equilibrium point of a nonlinear dynamical system.[27] To describe the Lyapunov theorem we need to define the positive-definite function. A real scalar function $V(\mathbf{r})$ is defined to be positive-definite in some closed bounded region D of state space if for all $\mathbf{r}$ in D,

1. $V(\mathbf{r})$ is continuously differentiable with respect to $\mathbf{r}$,

2. $V(\mathbf{0})=0$, and

3. $V(\mathbf{r})>0$, for all $\mathbf{r}\ne \mathbf{0}$.

Then $V(\mathbf{r})$ is a Lyapunov function in a neighbourhood D of the origin if

1. $V(\mathbf{r})$ is positive-definite, and

2. $\mathit{dV}(\mathbf{r})/d\mathit{\tau }$ is negative-semidefinite for all $\mathbf{r}\in D$.

The Lyapunov theorem of stability says that the origin is stable if there exists a Lyapunov function $V(\mathbf{r})$ throughout D; and that the origin is asymptotically stable if there exists a Lyapunov function $V(\mathbf{r})$ throughout D, such that $\mathit{dV}(\mathbf{r})/d\mathit{\tau }$ is negative-definite for all $\mathbf{r}\in D/\mathbf{0}$.

By using the Lyapunov function $V=\parallel \mathbf{r}{\parallel }^2/2$ and from Equation (45(45) $$\begin{array}{c}\hfill \mathbf{r}(t+\mathrm{\Delta }t)=\mathbf{r}(t)-\mathit{\eta }\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{v}}\mathbf{v},\end{array}$$(45) ), it is easy to prove that(42) $$\begin{array}{cc}\hfill & V(\mathbf{0})=0,V(\mathbf{r})=\frac{\parallel \mathbf{r}{\parallel }^2}{2}>0,\forall \mathbf{r}\ne \mathbf{0},\hfill \\ \hfill & \stackrel{·}{V}=\mathbf{r}·\stackrel{·}{\mathbf{r}}=-q(t)\parallel \mathbf{r}{\parallel }^2<0,\forall \mathbf{r}\ne \mathbf{0}.\hfill \end{array}$$(42) In Section 4.2, we will prove $\mathit{\eta }=q\mathrm{\Delta }t>0$. Then, by using the Lyapunov stability theory, the ODEs in Equation (40(40) $$\begin{array}{c}\hfill \stackrel{·}{\mathbf{r}}=\mathbf{B}\stackrel{·}{\mathbf{x}}=-q(t)\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{v}}\mathbf{v}.\end{array}$$(40) ) are asymptotically stable to $\mathbf{r}=\mathbf{0}$, and the iterative algorithm derived from it with a suitable selection of $q>0$ is stable.

Discretizing, yet keeping $\mathbf{x}$ on the manifold

Now we discretize the foregoing continuous time dynamics (40(40) $$\begin{array}{c}\hfill \stackrel{·}{\mathbf{r}}=\mathbf{B}\stackrel{·}{\mathbf{x}}=-q(t)\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{v}}\mathbf{v}.\end{array}$$(40) ) into a discrete time dynamics by applying the forward Euler scheme:(43) $$\begin{array}{c}\hfill \mathbf{x}(t+\mathrm{\Delta }t)=\mathbf{x}(t)-\mathit{\eta }\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{v}}\mathbf{u},\end{array}$$(43) where(44) $$\begin{array}{c}\hfill \mathit{\eta }=q(t)\mathrm{\Delta }t\end{array}$$(44) is a steplength.

Similarly, we use the forward Euler scheme to integrate Equation (45(45) $$\begin{array}{c}\hfill \mathbf{r}(t+\mathrm{\Delta }t)=\mathbf{r}(t)-\mathit{\eta }\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{v}}\mathbf{v},\end{array}$$(45) ):(45) $$\begin{array}{c}\hfill \mathbf{r}(t+\mathrm{\Delta }t)=\mathbf{r}(t)-\mathit{\eta }\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{v}}\mathbf{v},\end{array}$$(45) and taking the square norms of both the sides and using Equation (43(43) $$\begin{array}{c}\hfill \mathbf{x}(t+\mathrm{\Delta }t)=\mathbf{x}(t)-\mathit{\eta }\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{v}}\mathbf{u},\end{array}$$(43) ), we can obtain(46) $$\begin{array}{c}\hfill \frac{C}{Q(t+\mathrm{\Delta }t)}=\frac{C}{Q(t)}-2\mathit{\eta }\frac{C}{Q(t)}+{\mathit{\eta }}^2\frac{C}{Q(t)}\frac{\parallel \mathbf{r}{\parallel }^2}{{({\mathbf{r}}^{\text{T}}\mathbf{v})}^2}\parallel \mathbf{v}{\parallel }^2.\end{array}$$(46) Thus, the following scalar equation is derived:(47) $$\begin{array}{c}\hfill a_0{\mathit{\eta }}^2-2\mathit{\eta }+1-\frac{Q(t)}{Q(t+\mathrm{\Delta }t)}=0,\end{array}$$(47) where(48) $$\begin{array}{c}\hfill a_0:=\frac{\parallel \mathbf{r}{\parallel }^2\parallel \mathbf{v}{\parallel }^2}{{({\mathbf{r}}^{\text{T}}\mathbf{v})}^2}\ge 1\end{array}$$(48) by using the Cauchy–Schwarz inequality:$${\mathbf{r}}^{\text{T}}\mathbf{v}\le \parallel \mathbf{r}\parallel \parallel \mathbf{v}\parallel .$$As a result, $h(\mathbf{x},t)=0$ remains to be an invariant manifold in the space time of $(\mathbf{x},t)$ for the discrete time dynamical system $h(\mathbf{x}(t),t)=0$, $t\in \{0,1,2,\dots \}$, which will be explored further in the next section.

An iterative dynamics

Let(49) $$\begin{array}{c}\hfill s:=\frac{Q(t)}{Q(t+\mathrm{\Delta }t)}=\frac{\parallel \mathbf{r}(\mathbf{x}(t+\mathrm{\Delta }t)){\parallel }^2}{\parallel \mathbf{r}(\mathbf{x}(t)){\parallel }^2},\end{array}$$(49) which is an important quantity to assess the convergent property of our numerical algorithm for solving linear equations system (1(1) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(1) ).

From Equations (53(53) $$\begin{array}{c}\hfill \mathit{\eta }=\frac{1-\mathit{\gamma }}{a_0}>0,\end{array}$$(53) ) and (55(55) $$\begin{array}{c}\hfill \mathbf{x}(t+\mathrm{\Delta }t)=\mathbf{x}(t)-(1-\mathit{\gamma })\frac{{\mathbf{r}}^{\text{T}}\mathbf{v}}{\parallel \mathbf{v}{\parallel }^2}\mathbf{u}.\end{array}$$(55) ), it follows that(50) $$\begin{array}{c}\hfill a_0{\mathit{\eta }}^2-2\mathit{\eta }+1-s=0,\end{array}$$(50) of which we can take a preferred solution of $\mathit{\eta }$ to be(51) $$\begin{array}{c}\hfill \mathit{\eta }=\frac{1-\sqrt{1-(1-s)a_0}}{a_0},\text{if}1-(1-s)a_0\ge 0.\end{array}$$(51) Let(52) $$\begin{array}{cc}\hfill & 1-(1-s)a_0={\mathit{\gamma }}^2\ge 0,\hfill \\ \hfill & s=1-\frac{1-{\mathit{\gamma }}^2}{a_0},\hfill \end{array}$$(52) and the condition $1-(1-s)a_0\ge 0$ in Equation (57(57) $$\begin{array}{c}\hfill \text{Convergence}\text{Rate}:=\frac{\parallel \mathbf{r}(t)\parallel }{\parallel \mathbf{r}(t+\mathrm{\Delta }t)\parallel }=\frac{1}{\sqrt{s}}>1.\end{array}$$(57) ) is automatically satisfied; hence, from Equations (57(57) $$\begin{array}{c}\hfill \text{Convergence}\text{Rate}:=\frac{\parallel \mathbf{r}(t)\parallel }{\parallel \mathbf{r}(t+\mathrm{\Delta }t)\parallel }=\frac{1}{\sqrt{s}}>1.\end{array}$$(57) ) and (54(54) $$\begin{array}{c}\hfill 0\le \mathit{\gamma }<1\end{array}$$(54) ), it follows that(53) $$\begin{array}{c}\hfill \mathit{\eta }=\frac{1-\mathit{\gamma }}{a_0}>0,\end{array}$$(53) where(54) $$\begin{array}{c}\hfill 0\le \mathit{\gamma }<1\end{array}$$(54) is a parameter. Finally, from Equations (49(49) $$\begin{array}{c}\hfill s:=\frac{Q(t)}{Q(t+\mathrm{\Delta }t)}=\frac{\parallel \mathbf{r}(\mathbf{x}(t+\mathrm{\Delta }t)){\parallel }^2}{\parallel \mathbf{r}(\mathbf{x}(t)){\parallel }^2},\end{array}$$(49) ), (54(54) $$\begin{array}{c}\hfill 0\le \mathit{\gamma }<1\end{array}$$(54) ) and (60(60) $$\begin{array}{cc}\hfill & {\mathbf{r}}_k=\mathbf{B}{\mathbf{x}}_k-\mathbf{b},\hfill \\ \hfill & {\mathbf{u}}_k=\mathbf{A}{\mathbf{r}}_k,\hfill \\ \hfill & {\mathbf{v}}_k=\mathbf{B}\mathbf{A}{\mathbf{r}}_k,\hfill \\ \hfill & {\mathbf{x}}_{k+1}={\mathbf{x}}_k-(1-\mathit{\gamma })\frac{{\mathbf{r}}_k·{\mathbf{v}}_k}{\parallel {\mathbf{v}}_k{\parallel }^2}{\mathbf{u}}_k.\hfill \end{array}$$(60) ), we can obtain the following algorithm:(55) $$\begin{array}{c}\hfill \mathbf{x}(t+\mathrm{\Delta }t)=\mathbf{x}(t)-(1-\mathit{\gamma })\frac{{\mathbf{r}}^{\text{T}}\mathbf{v}}{\parallel \mathbf{v}{\parallel }^2}\mathbf{u}.\end{array}$$(55) Under conditions (54(54) $$\begin{array}{c}\hfill 0\le \mathit{\gamma }<1\end{array}$$(54) ) and (61(61) $$\begin{array}{cc}\hfill & u_t(x,t)=\mathit{\alpha }{u}_{\mathit{xx}}(x,t),0<t<T,0<x<\ell ,\hfill \\ \hfill & u(0,t)=u_0(t),u(\ell ,t)=u_{\ell }(t),\hfill \end{array}$$(61) ), from Equations (55(55) $$\begin{array}{c}\hfill \mathbf{x}(t+\mathrm{\Delta }t)=\mathbf{x}(t)-(1-\mathit{\gamma })\frac{{\mathbf{r}}^{\text{T}}\mathbf{v}}{\parallel \mathbf{v}{\parallel }^2}\mathbf{u}.\end{array}$$(55) ) and (59(59) $$\begin{array}{c}\hfill {\mathbf{x}}_{k+1}={\mathbf{x}}_k-(1-\mathit{\gamma })\frac{{\mathbf{r}}_k^{\text{T}}{\mathbf{v}}_k}{\parallel {\mathbf{v}}_k{\parallel }^2}{\mathbf{u}}_k.\end{array}$$(59) ), we can prove that the new algorithm satisfies(56) $$\begin{array}{c}\hfill \frac{\parallel \mathbf{r}(t+\mathrm{\Delta }t)\parallel }{\parallel \mathbf{r}(t)\parallel }=\sqrt{s}<1,\end{array}$$(56) which means that the residual error is absolutely decreased. In other words, the convergence rate of present iterative algorithm is greater than one:(57) $$\begin{array}{c}\hfill \text{Convergence}\text{Rate}:=\frac{\parallel \mathbf{r}(t)\parallel }{\parallel \mathbf{r}(t+\mathrm{\Delta }t)\parallel }=\frac{1}{\sqrt{s}}>1.\end{array}$$(57) The property in Equation (64(64) $$\begin{array}{c}\hfill u(\mathbf{z})=\sum _{j=1}^N{c}_{j}U(\mathbf{z},{\mathbf{s}}_j),{\mathbf{s}}_j=({\mathit{\eta }}_j,{\mathit{\tau }}_j)\in {\mathrm{\Omega }}^c,\end{array}$$(64) ) is very important, since it guarantees that the new algorithm is absolutely convergent to the true solution.

From Equations (48(48) $$\begin{array}{c}\hfill a_0:=\frac{\parallel \mathbf{r}{\parallel }^2\parallel \mathbf{v}{\parallel }^2}{{({\mathbf{r}}^{\text{T}}\mathbf{v})}^2}\ge 1\end{array}$$(48) ), (50(50) $$\begin{array}{c}\hfill a_0{\mathit{\eta }}^2-2\mathit{\eta }+1-s=0,\end{array}$$(50) ) and (60(60) $$\begin{array}{cc}\hfill & {\mathbf{r}}_k=\mathbf{B}{\mathbf{x}}_k-\mathbf{b},\hfill \\ \hfill & {\mathbf{u}}_k=\mathbf{A}{\mathbf{r}}_k,\hfill \\ \hfill & {\mathbf{v}}_k=\mathbf{B}\mathbf{A}{\mathbf{r}}_k,\hfill \\ \hfill & {\mathbf{x}}_{k+1}={\mathbf{x}}_k-(1-\mathit{\gamma })\frac{{\mathbf{r}}_k·{\mathbf{v}}_k}{\parallel {\mathbf{v}}_k{\parallel }^2}{\mathbf{u}}_k.\hfill \end{array}$$(60) ), we can derive(58) $$\begin{array}{c}\hfill \mathrm{\Delta }V=-\frac{1-\mathit{\gamma }}{a_0}\parallel \mathbf{r}{\parallel }^2.\end{array}$$(58) By using the Lyapunov stability, the best choice of $a_0$ is the one that makes $\mathrm{\Delta }V$ as negative as possible and which can be achieved by rendering $a_0\ge 1$ as small as possible. In principle, if we can use $\mathbf{u}={\mathbf{B}}^{-1}\mathbf{r}$ as a search direction, by Equations (41(41) $$\begin{array}{c}\hfill \frac{d\mathbf{r}}{d\mathit{\tau }}=-\frac{\parallel \mathbf{r}{\parallel }^2}{{\mathbf{r}}^{\text{T}}\mathbf{B}\mathbf{A}\mathbf{r}}\mathbf{B}\mathbf{A}\mathbf{r}.\end{array}$$(41) ) and (54(54) $$\begin{array}{c}\hfill 0\le \mathit{\gamma }<1\end{array}$$(54) ) we have $a_0=1$ and with $\mathrm{\Delta }V=-(1-\mathit{\gamma })\parallel \mathbf{r}{\parallel }^2$ being the minimum of $\mathrm{\Delta }V$. This is, however, impossible because the exact inverse ${\mathbf{B}}^{-1}$ is hard to be found, and so instead, we use $\mathbf{u}=\mathbf{A}\mathbf{r}$ as a search direction and solve $\mathbf{A}$ to near ${\mathbf{B}}^{-1}$ by using the MCGMR in Section 2. In doing so, we have a fast convergence iterative algorithm to solve the ill-posed linear problem (1(1) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(1) ) on one hand, and on the other hand, because $\mathbf{A}$ is not exactly equal to ${\mathbf{B}}^{-1}$, we can avoid the ill-posedness to magnify the noisy error by $\mathbf{A}\mathbf{r}$. Indeed, the present iterative algorithm is a trade-off between accuracy and regularization. We need to point out that for an ill-posed linear system (1(1) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(1) ), the solution given by ${\mathbf{B}}^{-1}\mathbf{b}$ is unstable. Our algorithms are finding $\mathbf{A}$, not finding ${\mathbf{B}}^{-1}$, which is less ill-conditioned than the finding of ${\mathbf{B}}^{-1}$. The descent direction detected by $\mathbf{A}\mathbf{r}$ is not exactly equal to the best descent direction ${\mathbf{B}}^{-1}\mathbf{r}$, which is an approximation. Because we have taken the direction ${\mathbf{B}}^{-1}\mathbf{r}$ into account, the iterative algorithm based on $\mathbf{A}\mathbf{r}$ can converge quite fast.

vector regularization iterative algorithm

Since the fictitious time variable is now discrete, $t\in \{0,1,2,\dots \}$, we let ${\mathbf{x}}_k$ denote the numerical value of $\mathbf{x}$ at the $k$-th step. Thus, we arrive at a purely iterative algorithm from Equation (62(62) $$\begin{array}{c}\hfill u(x,T)=u^T(x).\end{array}$$(62) ):(59) $$\begin{array}{c}\hfill {\mathbf{x}}_{k+1}={\mathbf{x}}_k-(1-\mathit{\gamma })\frac{{\mathbf{r}}_k^{\text{T}}{\mathbf{v}}_k}{\parallel {\mathbf{v}}_k{\parallel }^2}{\mathbf{u}}_k.\end{array}$$(59) Then, the following VRIA is available:

1. For a given $\mathbf{B}$, find $\mathbf{A}$ by using the MCGMR.

2. Select $\mathit{\gamma }$, and give an initial value of ${\mathbf{x}}_0$ or ${\mathbf{x}}_0=\mathbf{A}\mathbf{b}$.

3. For $k=0,1,2,\dots$, we repeat the following iterations:(60) $$\begin{array}{cc}\hfill & {\mathbf{r}}_k=\mathbf{B}{\mathbf{x}}_k-\mathbf{b},\hfill \\ \hfill & {\mathbf{u}}_k=\mathbf{A}{\mathbf{r}}_k,\hfill \\ \hfill & {\mathbf{v}}_k=\mathbf{B}\mathbf{A}{\mathbf{r}}_k,\hfill \\ \hfill & {\mathbf{x}}_{k+1}={\mathbf{x}}_k-(1-\mathit{\gamma })\frac{{\mathbf{r}}_k·{\mathbf{v}}_k}{\parallel {\mathbf{v}}_k{\parallel }^2}{\mathbf{u}}_k.\hfill \end{array}$$(60) If ${\mathbf{x}}_{k+1}$ converges according to a given stopping criterion $\parallel {\mathbf{r}}_{k+1}\parallel <{\mathit{\epsilon }}_1$, then stop; otherwise, go to step (iii). Here, $\mathit{\gamma }$ is a relaxation parameter, chosen by the user.

Linear inverse problems

In this section, we will apply the method of fundamental solutions (MFS) to discretize some inverse problems into a set of linear algebraic equations. In recent years, a few different meshless boundary collocation methods, like the singular boundary method, have been proposed and developed which are different but highly related to the MFS examined in this paper.[28, 29] The regularization method proposed in this paper can also be an efficient alternative for these methods for solving the ill-posed linear inverse problems.[30, 31]

Example 1

When the backward heat conduction problem (BHCP) is considered in a spatial interval of $0<x<\ell$ by subjecting to the boundary conditions at two ends of a slab:(61) $$\begin{array}{cc}\hfill & u_t(x,t)=\mathit{\alpha }{u}_{\mathit{xx}}(x,t),0<t<T,0<x<\ell ,\hfill \\ \hfill & u(0,t)=u_0(t),u(\ell ,t)=u_{\ell }(t),\hfill \end{array}$$(61) we solve $u$ under a final time condition:(62) $$\begin{array}{c}\hfill u(x,T)=u^T(x).\end{array}$$(62) The fundamental solution of Equation (68(68) $$\begin{array}{c}\hfill b_i=u(x_i,T)+\mathit{\sigma }R(i),\end{array}$$(68) ) is given as follows:(63) $$\begin{array}{c}\hfill K(x,t)=\frac{H(t)}{2\sqrt{\mathit{\alpha }\mathit{\pi }t}}\exp \left(\frac{-x^2}{4\mathit{\alpha }t}\right),\end{array}$$(63) where H(t) is the Heaviside function.

The method of fundamental solutions (MFSs) has a broad application in engineering computations. However, the MFS has a serious drawback in that the resulting system of linear equations is always highly ill-conditioned. In the MFS, the solution of u at the field point $\mathbf{z}=(x,t)$ can be expressed as a linear combination of the fundamental solutions $U(\mathbf{z},{\mathbf{s}}_j)$:(64) $$\begin{array}{c}\hfill u(\mathbf{z})=\sum _{j=1}^N{c}_{j}U(\mathbf{z},{\mathbf{s}}_j),{\mathbf{s}}_j=({\mathit{\eta }}_j,{\mathit{\tau }}_j)\in {\mathrm{\Omega }}^c,\end{array}$$(64) where N is the number of source points, $c_j$ are unknown coefficients and ${\mathbf{s}}_j$ are source points located in the complement ${\mathrm{\Omega }}^c$ of $\mathrm{\Omega }=[0,\ell ]\times [0,T]$. For the heat conduction equation, we have the basis functions(65) $$\begin{array}{c}\hfill U(\mathbf{z},{\mathbf{s}}_j)=K(x-{\mathit{\eta }}_j,t-{\mathit{\tau }}_j).\end{array}$$(65) It is known that the location of source points in the MFS has a great influence on the accuracy and stability. In a practical application of MFS to solve the BHCP, the source points are uniformly located on two straight lines parallel to the t-axis and not over $t=T$, which was adopted by Hon and Li [32] and Liu [33], showing a large improvement than the line location of source points below the initial time. After imposing the boundary conditions and the final time condition on Equation (72(72) $$\begin{array}{c}\hfill \ddot{y}(t)+\stackrel{·}{y}(t)+y(t)=F(t).\end{array}$$(72) ), we can obtain a linear equations system:(66) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(66) where(67) $$\begin{array}{cc}\hfill & B_{\mathit{ij}}=U({\mathbf{z}}_i,{\mathbf{s}}_j),\mathbf{x}={(c_1,\cdots ,c_N)}^{\text{T}},\hfill \\ \hfill & \mathbf{b}={(u_{\ell }(t_i),i=1,\dots ,m_1;u^T(x_j),j=1,\dots ,m_2;u_0(t_k),k=m_1,\dots ,1)}^{\text{T}}.\hfill \end{array}$$(67) The number $n=2m_1+m_2$ of collocation points does not necessarily equal to the number N of source points.

Since the BHCP is highly ill-posed,[34] the ill-conditioning of the coefficient matrix $\mathbf{B}$ in Equation (74(74) $$\begin{array}{c}\hfill c_k=\frac{a_k\cos (k{\mathit{\theta }}_k)}{R_{2k}^k}+\frac{b_k\sin (k{\mathit{\theta }}_k)}{R_{2k+1}^k},\end{array}$$(74) ) is serious. To overcome the ill-posedness of Equation (74(74) $$\begin{array}{c}\hfill c_k=\frac{a_k\cos (k{\mathit{\theta }}_k)}{R_{2k}^k}+\frac{b_k\sin (k{\mathit{\theta }}_k)}{R_{2k+1}^k},\end{array}$$(74) ), we can employ both the DIM and VRIA to solve this problem. Here, we compare the numerical solution with an exact solution:$$u(x,t)=\cos (\mathit{\pi }x)\exp (-{\mathit{\pi }}^{2}t).$$For $T=1$ the value of final data is in the order of ${10}^{-4}$, which is small in comparison with the value of the initial temperature $u_0(x)=\cos (\mathit{\pi }x)$ to be retrieved, which is $O(1)$.

In order to test the stability of the proposed algorithm, we add a random noise on the final time data by(68) $$\begin{array}{c}\hfill b_i=u(x_i,T)+\mathit{\sigma }R(i),\end{array}$$(68) where $\mathit{\sigma }$ denotes the level of noise and R(i) are random numbers between $[-1,1]$.

Fig. 1 For example 1 of a BHCP under an adding noise 0.001, comparing the exact solution with the numerical solutions obtained by the inversions from MCGML and MCGMR.

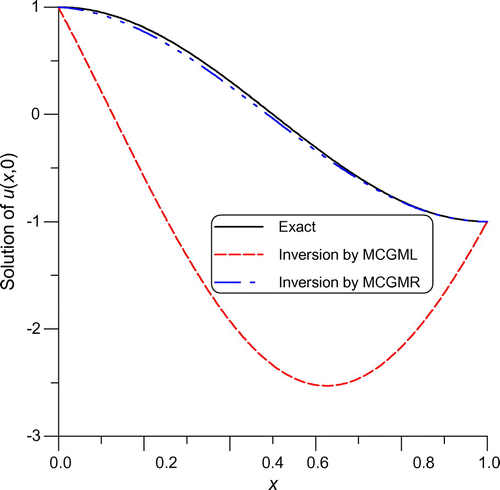
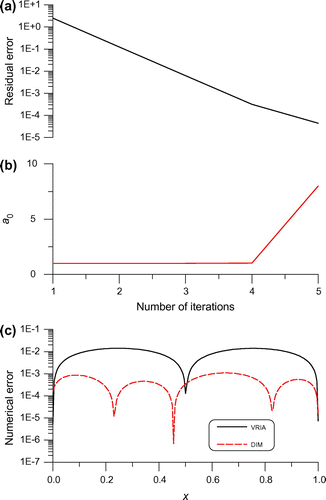
Fig. 2 For example 1 of a BHCP under a large relative noise 0.1, (a) the residual error, (b) the value of $a_0$, and (c) comparing the numerical errors.

We take $m_1=15$, $m_2=10$, and hence $n=40$, and the noise with an intensity $\mathit{\sigma }={10}^{-3}$ is adding on the right-hand side. We first apply the MCGML to find the left inversion of $\mathbf{B}$ under a convergence criterion ${\mathit{\epsilon }}_2={10}^{-6}$, which is convergent with 714 iterations to find the inverse matrix ${\mathbf{B}}^{-1}$, such that the solution of $\mathbf{x}$ can be written as(69) $$\begin{array}{c}\hfill \mathbf{x}={\mathbf{B}}^{-1}\mathbf{b}.\end{array}$$(69) Unfortunately, the noisy error is largely amplified in the above solution, which causes an incorrect solution as shown in Figure 1 by the red dashed line with the maximum error being 2.34. Conversely, when we apply the MCGMR to find the right inversion $\mathbf{A}$ of $\mathbf{B}$, which is convergent with 914 iterations, and give the solution by(70) $$\begin{array}{c}\hfill \mathbf{x}=\mathbf{A}\mathbf{b},\end{array}$$(70) which is named a DIM in this paper, the numerical solution is close to the exact solution as shown in Figure 1 by the blue dashed-dotted line, with the maximum error being 0.0478.

The MCGML is a feasible algorithm to find the left inversion of an ill-conditioned matrix. When the MCGML can provide a very accurate solution of ${\mathbf{B}}^{-1}$ in Equation (77(77) $$\begin{array}{c}\hfill p(x)=a_0+\sum _{k=1}^m[a_k{\left(\frac{x}{R_{2k}}\right)}^k\cos (k{\mathit{\theta }}_k)+b_k{\left(\frac{x}{R_{2k+1}}\right)}^k\sin (k{\mathit{\theta }}_k)],\end{array}$$(77) ), the noise is also being magnified, which pollutes the numerical solution of $\mathbf{x}$. Hence, we do not suggest to directly use Equation (77(77) $$\begin{array}{c}\hfill p(x)=a_0+\sum _{k=1}^m[a_k{\left(\frac{x}{R_{2k}}\right)}^k\cos (k{\mathit{\theta }}_k)+b_k{\left(\frac{x}{R_{2k+1}}\right)}^k\sin (k{\mathit{\theta }}_k)],\end{array}$$(77) ) to find the solution of $\mathbf{x}$, when the data $\mathbf{b}$ are noisy and $\mathbf{B}$ is ill-conditioned. The reason is that the noise in $\mathbf{b}$ would be enlarged when the elements in ${\mathbf{B}}^{-1}$ are quite large.

We take $m_1=15$, $m_2=10$, and hence $n=40$, and a relative random noise with intensity ${\mathit{\sigma }}_r=10\%$ is added in the final time data:(71) $$\begin{array}{c}\hfill b_i=u(x_i,T)[1+{\mathit{\sigma }}_{r}R(i)].\end{array}$$(71) We first apply the MCGMR to find the right inversion of $\mathbf{B}$ by imposing a convergence criterion ${\mathit{\epsilon }}_2={10}^{-3}$, which is convergent with 74 iterations to find the right inverse matrix $\mathbf{A}$. Then, we use the DIM as shown in Equation (78(78) $$\begin{array}{c}\hfill p(x_i)=y_i,i=0,\dots ,n-1.\end{array}$$(78) ) to solve this BHCP, of which the maximum error of initial condition is 0.088. Moreover, when the value of ${\mathit{\epsilon }}_2$ is reduced to ${\mathit{\epsilon }}_2={10}^{-4}$, the MCGMR is convergent with 128 iterations to find the inverse matrix $\mathbf{A}$, and the DIM used $\mathbf{A}$ in Equation (78(78) $$\begin{array}{c}\hfill p(x_i)=y_i,i=0,\dots ,n-1.\end{array}$$(78) ) leads to the maximum error being $1.085\times {10}^{-3}$, which is shown in Figure 2(c). To the best knowledge of the author, this accuracy is never seen before for this highly ill-posed BHCP under a large noise with ${\mathit{\sigma }}_r=0.1$.

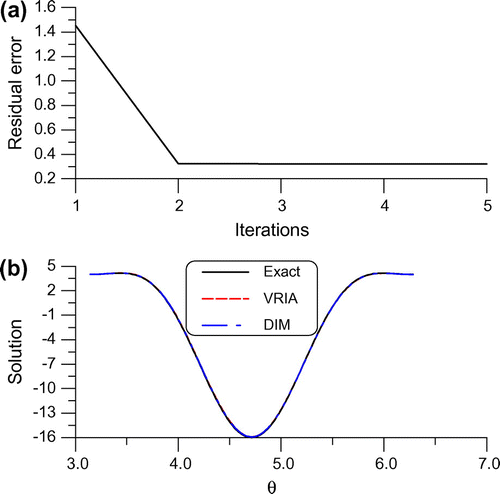
With $\mathit{\gamma }=0.05$, we also apply the VRIA in Section 4.3 to solve this problem, where we take ${\mathit{\epsilon }}_1={10}^{-4}$ and ${\mathit{\epsilon }}_2={10}^{-4}$ and with $\mathbf{A}\mathbf{b}$ as an initial guess. In Figure 2(a), we show the residual error obtained by the VRIA, which is convergent only through 5 iterations. By adding 127 for the number of finding $\mathbf{A}$, the total number of iterations for the VRIA is 132, which is larger than 128 iterations for the DIM. The values of $a_0$ as shown in Figure 2(b) is very small, which causes a fast convergence of the VRIA. It can be seen that the algorithm of VRIA is convergent very fast only through five iterations that its residual error reduces from 2.5 to $4.448\times {10}^{-5}$. We found that more smaller convergence criterion of ${\mathit{\epsilon }}_1$ would not lead to more accurate solution. The numerical error is compared with that obtained by the DIM in Figure 2(c) with the maximum error being 0.014, which is greater than that obtained by the DIM. This result is much better than that obtained by Liu [21, 22], and also than that obtained by Liu et al. [35].

Example 2

Let us consider the following inverse problem to recover the external force $F(t)$ for an ODE:(72) $$\begin{array}{c}\hfill \ddot{y}(t)+\stackrel{·}{y}(t)+y(t)=F(t).\end{array}$$(72) In a time interval of $t\in [0,t_f]$, the discretized data $y_i=y(t_i)$ are supposed to be measurable, which are subjected to the random noise with an intensity $\mathit{\sigma }=0.01$. Usually, it is very difficult to recover the external force $F\mathrm{(}{t}_i\mathrm{)}$ from Equation (80(80) $$\begin{array}{cc}\hfill & R_{2k}={\mathit{\beta }}_0{(\frac{1}{2m+1}\sum _{j=0}^{2m}{x}_j^{2k}(\cos k{\mathit{\theta }}_k{)}^2)}^{1/(2k)},k=1,2,\dots ,m,\hfill \\ \hfill & R_{2k+1}={\mathit{\beta }}_0{(\frac{1}{2m+1}\sum _{j=0}^{2m}{x}_j^{2k}(\sin k{\mathit{\theta }}_k{)}^2)}^{1/(2k)},k=1,2,\dots ,m,\hfill \end{array}$$(80) ) by the direct differentials of the noisy data of the displacements, because the differential is an ill-posed linear operator.

To approach this inverse problem by the polynomial interpolation, we begin with(73) $$\begin{array}{c}\hfill p_m(x)=c_0+\sum _{k=1}^m{c}_k{x}^k.\end{array}$$(73) Now, the coefficient $c_k$ is split into two coefficients $a_k$ and $b_k$ to absorb more interpolation points; in the meanwhile, $\cos (k{\mathit{\theta }}_k)$ and $\sin (k{\mathit{\theta }}_k)$ are introduced to reduce the condition number of the coefficient matrix.[36] We suppose that(74) $$\begin{array}{c}\hfill c_k=\frac{a_k\cos (k{\mathit{\theta }}_k)}{R_{2k}^k}+\frac{b_k\sin (k{\mathit{\theta }}_k)}{R_{2k+1}^k},\end{array}$$(74) and(75) $$\begin{array}{c}\hfill {\mathit{\theta }}_k=\frac{2k\mathit{\pi }}{m},k=1,\dots ,m.\end{array}$$(75) The problem domain is $[a,b]$, and the interpolating points are:(76) $$\begin{array}{c}\hfill a=x_0<x_1<x_2<\dots <x_{2m-1}<x_{2m}=b.\end{array}$$(76) Substituting Equation (82(82) $$\begin{array}{c}\hfill u(\mathbf{z})=\sum _{j=1}^n{c}_{j}U(\mathbf{z},{\mathbf{s}}_j),{\mathbf{s}}_j\in {\mathrm{\Omega }}^c,\end{array}$$(82) ) into Equation (81(81) $$\begin{array}{cc}\hfill & \mathrm{\Delta }u=u_{\mathit{rr}}+\frac{1}{r}{u}_r+\frac{1}{r^2}{u}_{\mathit{\theta }\mathit{\theta }}=0,r<\mathit{\rho },0\le \mathit{\theta }\le 2\mathit{\pi },\hfill \\ \hfill & u(\mathit{\rho },\mathit{\theta })=h(\mathit{\theta }),0\le \mathit{\theta }\le \mathit{\pi },\hfill \\ \hfill & u_n(\mathit{\rho },\mathit{\theta })=g(\mathit{\theta }),0\le \mathit{\theta }\le \mathit{\pi },\hfill \end{array}$$(81) ), we can obtain(77) $$\begin{array}{c}\hfill p(x)=a_0+\sum _{k=1}^m[a_k{\left(\frac{x}{R_{2k}}\right)}^k\cos (k{\mathit{\theta }}_k)+b_k{\left(\frac{x}{R_{2k+1}}\right)}^k\sin (k{\mathit{\theta }}_k)],\end{array}$$(77) where we let $c_0=a_0$. Here, $a_k$ and $b_k$ are unknown coefficients. In order to obtain them, we impose the following $n$ interpolated conditions:(78) $$\begin{array}{c}\hfill p(x_i)=y_i,i=0,\dots ,n-1.\end{array}$$(78) Thus, we obtain a linear equations system to determine $a_k$ and $b_k$:(79) $$\begin{array}{cc}\hfill & \left[\begin{array}{cccccc}\hfill 1\hfill & \hfill \frac{x_0\cos {\mathit{\theta }}_1}{R_2}\hfill & \hfill \frac{x_0\sin {\mathit{\theta }}_1}{R_3}\hfill & \hfill \dots \hfill & \hfill {\left(\frac{x_0}{R_{2m}}\right)}^m\cos m{\mathit{\theta }}_m\hfill & \hfill {\left(\frac{x_0}{R_{2m+1}}\right)}^m\sin m{\mathit{\theta }}_m\hfill \\ \hfill 1\hfill & \hfill \frac{x_1\cos {\mathit{\theta }}_1}{R_2}\hfill & \hfill \frac{x_1\sin {\mathit{\theta }}_1}{R_3}\hfill & \hfill \dots \hfill & \hfill {\left(\frac{x_1}{R_{2m}}\right)}^m\cos m{\mathit{\theta }}_m\hfill & \hfill {\left(\frac{x_1}{R_{2m+1}}\right)}^m\sin m{\mathit{\theta }}_m\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill \frac{x_{2m-1}\cos {\mathit{\theta }}_1}{R_2}\hfill & \hfill \frac{x_{2m-1}\sin {\mathit{\theta }}_1}{R_3}\hfill & \hfill \dots \hfill & \hfill {\left(\frac{x_{2m-1}}{R_{2m}}\right)}^m\cos m{\mathit{\theta }}_m\hfill & \hfill {\left(\frac{x_{2m-1}}{R_{2m+1}}\right)}^m\sin m{\mathit{\theta }}_m\hfill \\ \hfill 1\hfill & \hfill \frac{x_{2m}\cos {\mathit{\theta }}_1}{R_2}\hfill & \hfill \frac{x_{2m}\sin {\mathit{\theta }}_1}{R_3}\hfill & \hfill \dots \hfill & \hfill {\left(\frac{x_{2m}}{R_{2m}}\right)}^m\cos m{\mathit{\theta }}_m\hfill & \hfill {\left(\frac{x_{2m}}{R_{2m+1}}\right)}^m\sin m{\mathit{\theta }}_m\hfill \end{array}\right]\left[\begin{array}{c}\hfill a_0\hfill \\ \hfill a_1\hfill \\ \hfill b_1\hfill \\ \hfill ⋮\hfill \\ \hfill a_m\hfill \\ \hfill b_m\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{c}\hfill y_0\hfill \\ \hfill y_1\hfill \\ \hfill y_2\hfill \\ \hfill ⋮\hfill \\ \hfill y_{2m-1}\hfill \\ \hfill y_{2m}\hfill \end{array}\right].\hfill \end{array}$$(79) We note that the norm of the first column of the above coefficient matrix is $\sqrt{2m+1}$. According to the concept of equilibrated matrix,[37] we can derive the optimal scales for the current interpolation with a half-order technique as(80) $$\begin{array}{cc}\hfill & R_{2k}={\mathit{\beta }}_0{(\frac{1}{2m+1}\sum _{j=0}^{2m}{x}_j^{2k}(\cos k{\mathit{\theta }}_k{)}^2)}^{1/(2k)},k=1,2,\dots ,m,\hfill \\ \hfill & R_{2k+1}={\mathit{\beta }}_0{(\frac{1}{2m+1}\sum _{j=0}^{2m}{x}_j^{2k}(\sin k{\mathit{\theta }}_k{)}^2)}^{1/(2k)},k=1,2,\dots ,m,\hfill \end{array}$$(80) where ${\mathit{\beta }}_0$ is a scaling factor.[38] The improved method uses m order polynomial to interpolate $n=2m+1$ data nodes, while regular method with a full order can only interpolate $m+1$ data points.

Fig. 3 For example 2 under a large noise 0.01, (a) comparing the numerical and exact solutions, and (b) the numerical errors.

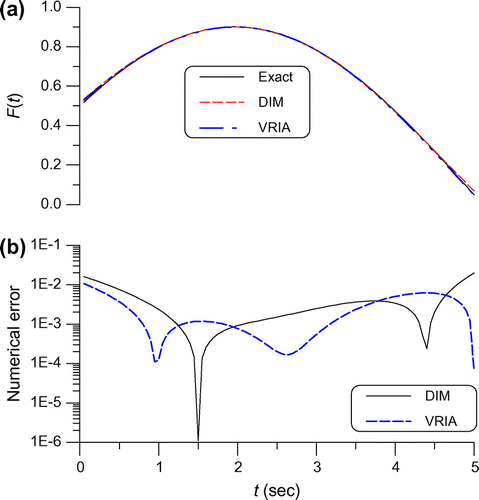
Now, we fix $m=25$ and $t_f=5$ and consider the exact solution to be $F(t)=\mathit{\omega }\cos (\mathit{\omega }t)+(1-{\mathit{\omega }}^2)\sin (\mathit{\omega }t)$, which is obtained by inserting the exact value of $y(t)=\sin (\mathit{\omega }t)$ into Equation (80(80) $$\begin{array}{cc}\hfill & R_{2k}={\mathit{\beta }}_0{(\frac{1}{2m+1}\sum _{j=0}^{2m}{x}_j^{2k}(\cos k{\mathit{\theta }}_k{)}^2)}^{1/(2k)},k=1,2,\dots ,m,\hfill \\ \hfill & R_{2k+1}={\mathit{\beta }}_0{(\frac{1}{2m+1}\sum _{j=0}^{2m}{x}_j^{2k}(\sin k{\mathit{\theta }}_k{)}^2)}^{1/(2k)},k=1,2,\dots ,m,\hfill \end{array}$$(80) ). The parameters used are $\mathit{\omega }=0.5$, and ${\mathit{\beta }}_0=5$. When we use the MCGMR, it is convergent with nine iterations under ${\mathit{\epsilon }}_2={10}^{-4}$. We compare the numerical solution obtained by the DIM with the data given by $F(t)=\mathit{\omega }\cos (\mathit{\omega }t)+(1-{\mathit{\omega }}^2)\sin (\mathit{\omega }t)$ in Figure 3(a), of which the maximum error is found to be $0.0196$ as shown in Figure 3(b) by solid line. Then, we apply the VRIA to solve this problem under $\mathit{\gamma }=0.05$ and ${\mathit{\beta }}_0=5$, where we first use the MCGMR to find $\mathbf{A}$, which is convergent with five iterations under ${\mathit{\epsilon }}_2={10}^{-3}$. Then, using the initial guess ${\mathbf{x}}_0=\mathbf{A}\mathbf{b}$, we let VRIA run 20 for iterations. We compare the numerical solution obtained by the VRIA with the exact data in Figure 3(a) by dashed-dotted line, of which the maximum error is 0.0106 as shown in Figure 3(b) by dashed line.

Example 3

We solve the Cauchy problem of the Laplace equation under the incomplete boundary conditions:(81) $$\begin{array}{cc}\hfill & \mathrm{\Delta }u=u_{\mathit{rr}}+\frac{1}{r}{u}_r+\frac{1}{r^2}{u}_{\mathit{\theta }\mathit{\theta }}=0,r<\mathit{\rho },0\le \mathit{\theta }\le 2\mathit{\pi },\hfill \\ \hfill & u(\mathit{\rho },\mathit{\theta })=h(\mathit{\theta }),0\le \mathit{\theta }\le \mathit{\pi },\hfill \\ \hfill & u_n(\mathit{\rho },\mathit{\theta })=g(\mathit{\theta }),0\le \mathit{\theta }\le \mathit{\pi },\hfill \end{array}$$(81) where $h(\mathit{\theta })$ and $g(\mathit{\theta })$ are given functions, and $\mathit{\rho }=\mathit{\rho }(\mathit{\theta })$ is a given contour to describe the boundary shape. The contour in the polar coordinates is specified by $\mathrm{\Gamma }=\{(r,\mathit{\theta })|r=\mathit{\rho }(\mathit{\theta }),0\le \mathit{\theta }\le 2\mathit{\pi }\}$, which is the boundary of the problem domain $\mathrm{\Omega }$, and $n$ denotes the outward normal direction. We need to find the boundary data on the lower half contour for the completeness of boundary data.

In the MFS, the trial solution of u at the field point  $\mathbf{z}=(r\cos \mathit{\theta },r\sin \mathit{\theta })$ can be expressed as a linear combination of the fundamental solutions $U(\mathbf{z},{\mathbf{s}}_j)$:(82) $$\begin{array}{c}\hfill u(\mathbf{z})=\sum _{j=1}^n{c}_{j}U(\mathbf{z},{\mathbf{s}}_j),{\mathbf{s}}_j\in {\mathrm{\Omega }}^c,\end{array}$$(82) where n is the number of source points, $c_j$ are the unknown coefficients, ${\mathbf{s}}_j$ are the source points and ${\mathrm{\Omega }}^c$ is the complementary set of $\mathrm{\Omega }$. For the Laplace Equation (90(90) $$\begin{array}{c}\hfill u(x,t)={\int }_0^{t}v(x,\mathit{\xi })d\mathit{\xi }+f(x),\end{array}$$(90) ), we have the fundamental solutions:(83) $$\begin{array}{c}\hfill U(\mathbf{z},{\mathbf{s}}_j)=\ln r_j,r_j=\parallel \mathbf{z}-{\mathbf{s}}_j\parallel .\end{array}$$(83) In the practical application of MFS, usually the source points are distributed uniformly on a circle with a radius R, such that after imposing the boundary conditions (91(91) $$\begin{array}{c}\hfill u_{\mathit{xx}}(x,t)={\int }_0^t{v}_{\mathit{xx}}(x,\mathit{\xi })d\mathit{\xi }+f^{\prime \prime }(x),\end{array}$$(91) ) and (92(92) $$\begin{array}{c}\hfill v(x,t)={\int }_0^t{v}_{\mathit{xx}}(x,\mathit{\xi })d\mathit{\xi }+f^{\prime \prime }(x)+H(x).\end{array}$$(92) ) on Equation (93(93) $$\begin{array}{c}\hfill H(x)=v(x,0)-f^{\prime \prime }(x).\end{array}$$(93) ), we can obtain a linear equations system:(84) $$\begin{array}{c}\hfill \mathbf{B}\mathbf{x}=\mathbf{b},\end{array}$$(84) where(85) $$\begin{array}{cc}\hfill & {\mathbf{z}}_i=(z_i^1,z_i^2)=(\mathit{\rho }({\mathit{\theta }}_i)\cos {\mathit{\theta }}_i,\mathit{\rho }({\mathit{\theta }}_i)\sin {\mathit{\theta }}_i),\hfill \\ \hfill & {\mathbf{s}}_j=(s_j^1,s_j^2)=(R\cos {\mathit{\theta }}_j,R\sin {\mathit{\theta }}_j),\hfill \\ \hfill & B_{\mathit{ij}}=\ln \parallel {\mathbf{z}}_i-{\mathbf{s}}_j\parallel ,\text{if}i\text{is}\text{odd},\hfill \\ \hfill & B_{\mathit{ij}}=\frac{\mathit{\eta }({\mathit{\theta }}_i)}{\parallel {\mathbf{z}}_i-{\mathbf{s}}_j{\parallel }^2}(\mathit{\rho }({\mathit{\theta }}_i)-s_j^1\cos {\mathit{\theta }}_i-s_j^2\sin {\mathit{\theta }}_i\hfill \\ \hfill & -\frac{{\mathit{\rho }}^{\prime }({\mathit{\theta }}_i)}{\mathit{\rho }({\mathit{\theta }}_i)}[s_j^1\sin {\mathit{\theta }}_i-s_j^2\cos {\mathit{\theta }}_i]),\text{if}i\text{is}\text{even},\hfill \\ \hfill & \mathbf{x}={(c_1,\dots ,c_n)}^{\text{T}},\mathbf{b}={(h({\mathit{\theta }}_1),g({\mathit{\theta }}_1),\dots ,h({\mathit{\theta }}_m),g({\mathit{\theta }}_m))}^{\text{T}},\hfill \end{array}$$(85) in which $n=2m$, and(86) $$\begin{array}{c}\hfill \mathit{\eta }(\mathit{\theta })=\frac{\mathit{\rho }(\mathit{\theta })}{\sqrt{{\mathit{\rho }}^2(\mathit{\theta })+{[{\mathit{\rho }}^{\prime }(\mathit{\theta })]}^2}}.\end{array}$$(86) This example poses a great challenge to test the efficiency of linear equations solver, because the Cauchy problem is highly ill-posed. A noise with intensity $\mathit{\sigma }=10\%$ is imposed on the given data. We fix $n=30$ and take a circle with radius $R=500$ to distribute the source points. Under ${\mathit{\epsilon }}_2={10}^{-4}$, we can find $\mathbf{A}$ through six iterations. Then, we start from the initial guess ${\mathbf{x}}_0=\mathbf{A}\mathbf{b}$, and apply the VRIA to solve Equation (95(95) $$\begin{array}{c}\hfill {\mathbf{x}}_{k+1}={\mathbf{x}}_k-(1-\mathit{\gamma })\frac{{\mathbf{r}}_k·{\mathbf{v}}_k}{\parallel {\mathbf{v}}_k{\parallel }^2}{\mathbf{u}}_k,\end{array}$$(95) ) through 5 iterations as shown in Figure 4(a). In Figure 4(b), we compare the numerical solution with the exact data given by $u={\mathit{\rho }}^2\cos (2\mathit{\theta }),\mathit{\pi }\le \mathit{\theta }<2\mathit{\pi }$, where $\mathit{\rho }=\sqrt{10-6\cos (2\mathit{\theta })}$, of which the maximum error is $0.106$. The DIM converges with 25 iterations under the convergence criterion ${\mathit{\epsilon }}_2={10}^{-5}$. As shown in Figure 4(b) the maximum error of DIM is 0.0957.

Fig. 4 For example 3 of a Cauchy problem under a large noise 0.1, (a) showing residual error, and (b) comparing the numerical and exact solutions.

Fig. 5 For example 4 of an inverse heat source problem under a large noise 0.1, (a) the residual error, (b) the value of $a_0$ and (c) comparing the numerical errors.

Example 4

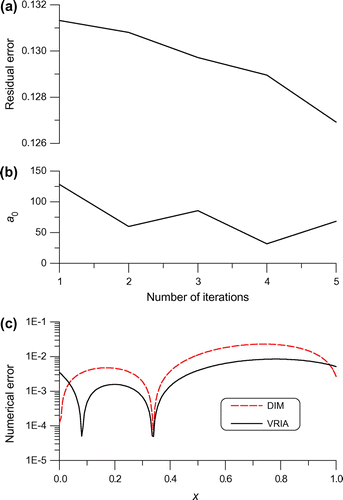
In this section, we apply the VRIA and DIM to identify an unknown space-dependent heat source function H(x) for a one-dimensional heat conduction equation:(87) $$\begin{array}{cc}\hfill & u_t(x,t)=u_{\mathit{xx}}(x,t)+H(x),0<x<\ell ,0<t<t_f,\hfill \\ \hfill & u(0,t)=u_0(t),u(\ell ,t)=u_{\ell }(t),\hfill \\ \hfill & u(x,0)=f(x).\hfill \end{array}$$(87) In order to identify H(x), we can impose an extra condition:(88) $$\begin{array}{c}\hfill u_x(0,t)=q(t).\end{array}$$(88) We propose a numerical differential method by letting $v=u_t$. Taking the differentials of Equations (98), (99), (101) with respect to t, and letting $v=u_t$, we can derive(89) $$\begin{array}{cc}\hfill & v_t(x,t)=v_{\mathit{xx}}(x,t),0<x<\ell ,0<t<t_f,\hfill \\ \hfill & v(0,t)={\stackrel{·}{u}}_0(t),\hfill \\ \hfill & v(\ell ,t)={\stackrel{·}{u}}_{\ell }(t),\hfill \\ \hfill & v_x(0,t)=\stackrel{·}{q}(t).\hfill \end{array}$$(89) This is an inverse heat conduction problem (IHCP) for v(x, t) without using the initial condition.

Therefore, as being a numerical method, we can first solve the above IHCP for v(x, t) by using the MFS in Section 5.1 to obtain a linear equations system, and then the method introduced in Section 4 is used to solve the resultant linear equations system; hence, we can construct u(x, t) by(90) $$\begin{array}{c}\hfill u(x,t)={\int }_0^{t}v(x,\mathit{\xi })d\mathit{\xi }+f(x),\end{array}$$(90) which automatically satisfies the initial condition in Equation (100).

From Equation (106), it follows that(91) $$\begin{array}{c}\hfill u_{\mathit{xx}}(x,t)={\int }_0^t{v}_{\mathit{xx}}(x,\mathit{\xi })d\mathit{\xi }+f^{\prime \prime }(x),\end{array}$$(91) which together with $u_t=v$ being inserted into Equation (98), leads to(92) $$\begin{array}{c}\hfill v(x,t)={\int }_0^t{v}_{\mathit{xx}}(x,\mathit{\xi })d\mathit{\xi }+f^{\prime \prime }(x)+H(x).\end{array}$$(92) Inserting Equation (102) for $v_{\mathit{xx}}=v_t$ into the above equation and integrating it, we can derive the following equation to recover H(x):(93) $$\begin{array}{c}\hfill H(x)=v(x,0)-f^{\prime \prime }(x).\end{array}$$(93) For the purpose of comparison we consider the following exact solutions:(94) $$\begin{array}{cc}\hfill & u(x,t)=x^2+2\mathit{xt}+\sin (2\mathit{\pi }x),\hfill \\ \hfill & H(x)=2x-2+4{\mathit{\pi }}^2\sin (2\mathit{\pi }x).\hfill \end{array}$$(94) In Equation (109), we disregard the ill-posedness of $f^{\prime \prime }(x)$, and suppose that the data $f^{\prime \prime }(x)$ are given exactly. We solve this problem by the DIM and VRIA with ${\mathit{\gamma }}_0=0.05$ and the convergence criterion is ${\mathit{\epsilon }}_2={10}^{-4}$. A random noise with an intensity $\mathit{\sigma }=10\%$ is added on the data $\stackrel{·}{q}(t)$. In the solution of $\mathbf{A}$, the DIM is convergent through 57 iterations and its numerical error as shown in Figure 5(c) by dashed line is small with the maximum error being 0.023. We compute $\mathbf{A}$ under ${\mathit{\epsilon }}_2={10}^{-3}$, which is convergent with 28 iterations. Then, by starting from the initial guess of $\mathbf{x}$ by ${\mathbf{x}}_0=\mathbf{A}\mathbf{b}$, we let the VRIA run five iterations, whose residual error and $a_0$ are respectively shown in Figure 5(a) and (b). The numerical error obtained by the VRIA is shown in Figure 5(c) by solid line with the maximum error being 0.0086. It is amazing that the accuracy of the VRIA is very good when one knows that the maximum value of H(x) is about 38. This example shows again that the proposed DIM and VRIA can solve linear inverse problems with good efficiency and accuracy, and as well is robustness against the large noise with intensity $\mathit{\sigma }=0.1$ being imposed on the data in the right-hand side.

Conclusions

For solving an ill-posed linear equations system $\mathbf{B}\mathbf{x}=\mathbf{b}$ under a large noisy disturbance and with $\mathbf{r}=\mathbf{B}\mathbf{x}-\mathbf{b}$ as being a residual vector, we have derived a very simple iterative algorithm including a parameter $\mathit{\gamma }$:(95) $$\begin{array}{c}\hfill {\mathbf{x}}_{k+1}={\mathbf{x}}_k-(1-\mathit{\gamma })\frac{{\mathbf{r}}_k·{\mathbf{v}}_k}{\parallel {\mathbf{v}}_k{\parallel }^2}{\mathbf{u}}_k,\end{array}$$(95) where(96) $$\begin{array}{c}\hfill {\mathbf{u}}_k=\mathbf{A}{\mathbf{r}}_k,{\mathbf{v}}_k=\mathbf{B}{\mathbf{u}}_k.\end{array}$$(96) The Lyapunov stability theorem guarantees that the present algorithm is stable and fast convergent because the search direction $\mathbf{A}\mathbf{r}$ is close to the best descent direction ${\mathbf{B}}^{-1}\mathbf{r}$ with $\mathbf{A}$ being a right inversion of $\mathbf{B}$. The new algorithm is a VRIA, which has a superior computational efficiency and accuracy in solving ill-posed linear problems. This assertion is further identified by four linear inverse problems, revealing that the proposed DIM and VRIA can solve very well the linear inverse problem with a high robustness against a large noise $\mathit{\sigma }=0.1$ being imposed on the data in the right-hand side.

Acknowledgments

First, the author is grateful to the anonymous referees for their comments which substantially improved the quality of this paper. Taiwan’s National Science Council project NSC-99-2221-E-002-074-MY3 granted to the author is highly appreciated. On the other hand, the author would acknowledge the promotion to be a Lifetime Distinguished Professor of National Taiwan University, since 2013.