Numerical reconstruction of an inhomogeneity in an elliptic equation

Abstract

In this paper, the inverse problem which consists of reconstructing an unknown inner boundary of a domain from a single pair of boundary Cauchy data associated to an elliptic equation is solved numerically using the meshless method of fundamental solutions. A nonlinear minimization of the objective function is regularized. The stability of the numerical results is investigated for several test examples with respect to noise in the input data and various values of the regularization parameters.

Keywords:

• elliptic equation
• inverse problem
• method of fundamental solutions
• regularization
• inhomogeneity

Introduction

The determination of an inhomogeneity (anomaly) contained in a given domain from the knowledge of the imposed voltage (boundary temperature) and the measured current (heat) flux arises in many non-destructive tomography testing of materials. In particular, in this paper, we consider the inverse problem of determining an inhomogeneity ${\mathrm{\Omega }}_2$ (with Lipschitz boundary $\mathit{\partial }{\mathrm{\Omega }}_2$) compactly contained in a bounded domain $\mathrm{\Omega }$ (with smooth boundary $\mathit{\partial }\mathrm{\Omega }$) entering in the modified Helmholtz elliptic equation(1) $$\begin{array}{c}\hfill {\nabla }^{2}u-k^{2}u=0\mathrm{i}n\mathrm{\Omega },\end{array}$$(1) where $k^2=k_1^2+(k_2^2-k_1^2){\mathit{\chi }}_{{\mathrm{\Omega }}_2}$ is a given positive function with $k_2>k_1⩾0$ and of class $C^2(\mathrm{\Omega })$, ${\mathit{\chi }}_{{\mathrm{\Omega }}_2}$ is the characteristic function of the domain ${\mathrm{\Omega }}_2$, and $u$ is the potential (temperature). In heat transfer, Equation (1(1) $$\begin{array}{c}\hfill {\nabla }^{2}u-k^{2}u=0\mathrm{i}n\mathrm{\Omega },\end{array}$$(1) ) stands as the governing equation for a (two-dimensional) dry fin-tube heat exchanger with $k^2=\frac{2h}{\mathit{\kappa }\mathit{\delta }}$, where $\mathit{\kappa }$ is the thermal conductivity of the fin, $h$ is the convective heat transfer coefficient and $\mathit{\delta }$ is the fin thickness, see [1]. By defining(2) $$\begin{array}{c}\hfill u:=\{\begin{array}{c}{u}_1\mathrm{i}n{\mathrm{\Omega }}_1:=\mathrm{\Omega }\setminus {\mathrm{\Omega }}_2,\hfill \\ u_2\mathrm{i}n{\mathrm{\Omega }}_2,\hfill \end{array}\end{array}$$(2) Equation (1(1) $$\begin{array}{c}\hfill {\nabla }^{2}u-k^{2}u=0\mathrm{i}n\mathrm{\Omega },\end{array}$$(1) ) can be rewritten as the following transmission problem:(3) $$\begin{array}{cc}\hfill & {\nabla }^2{u}_1-k_1^2{u}_1=0\mathrm{i}n{\mathrm{\Omega }}_1,\hfill \end{array}$$(3) (4) $$\begin{array}{cc}\hfill & {\nabla }^2{u}_2-k_2^2{u}_2=0\mathrm{i}n{\mathrm{\Omega }}_2,\hfill \end{array}$$(4) (5) $$\begin{array}{cc}\hfill & u_1=u_2,\mathrm{o}n\mathit{\partial }{\mathrm{\Omega }}_2.\hfill \end{array}$$(5) (6) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}\mathrm{o}n\mathit{\partial }{\mathrm{\Omega }}_2\hfill \end{array}$$(6) where $\underset{¯}{n}$ denotes the outward unit normal to the boundary.

Associated to the above problem (3(3) $$\begin{array}{cc}\hfill & {\nabla }^2{u}_1-k_1^2{u}_1=0\mathrm{i}n{\mathrm{\Omega }}_1,\hfill \end{array}$$(3) )–(6(6) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}\mathrm{o}n\mathit{\partial }{\mathrm{\Omega }}_2\hfill \end{array}$$(6) ), we also have the Cauchy boundary conditions on $\mathit{\partial }\mathrm{\Omega }$ given by(7) $$\begin{array}{cc}\hfill & u_1=f\mathrm{o}n\mathit{\partial }\mathrm{\Omega },\hfill \end{array}$$(7) (8) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=g\mathrm{o}n\mathit{\partial }\mathrm{\Omega }.\hfill \end{array}$$(8) Such a problem arises in the determination of the contact resistivity of planar electronic devices.[2] Other formulations of inverse obstacle problems can be found in the topical review by Isakov.[3] Uniqueness of the inhomogeneity ${\mathrm{\Omega }}_2$ entering the inverse problem (3(3) $$\begin{array}{cc}\hfill & {\nabla }^2{u}_1-k_1^2{u}_1=0\mathrm{i}n{\mathrm{\Omega }}_1,\hfill \end{array}$$(3) )–(8(8) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=g\mathrm{o}n\mathit{\partial }\mathrm{\Omega }.\hfill \end{array}$$(8) ) has been established in the class of balls, star-shaped domains, convex hulls of polygons and other classes of subdomains in [4–7], respectively.

Recently, in [8, 9] the authors determined inner rigid inclusions, cavities and absorbing obstacles in modified Helmholtz inverse geometric problems using the method of fundamental solutions (MFS). This method has proved rather versatile and easy to use for solving a wide range of inverse problems, see the recent review of Karageorghis et al. [10]. In this study, we provide yet another application of the MFS for solving the inverse transmission problem (3(3) $$\begin{array}{cc}\hfill & {\nabla }^2{u}_1-k_1^2{u}_1=0\mathrm{i}n{\mathrm{\Omega }}_1,\hfill \end{array}$$(3) )–(8(8) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=g\mathrm{o}n\mathit{\partial }\mathrm{\Omega }.\hfill \end{array}$$(8) ).

The outline of this paper is as follows. In Section 2, we present the MFS for the modified Helmholtz equation in composite bi-materials. In Section 3, we present and discuss the numerically obtained results. In Section 4, we give some conclusions and possible future work.

Fig. 1 Sketch of the curves on which the source $(---)$ and the boundary collocation (—) points are located in the MFS.

Fig. 2 The unregularized objective function for $p\in \{0,1,5,10\}\%$ noise, as a function of the number of iterations, for example 1.

The method of fundamental solutions (MFS)

In the MFS for a composite bi-material $\mathrm{\Omega }={\mathrm{\Omega }}_1\cup {\mathrm{\Omega }}_2$, ${\mathrm{\Omega }}_1\cap {\mathrm{\Omega }}_2=\mathrm{\varnothing }$, we approximate the solutions $u_1$ and $u_2$ of the modified Helmholtz Equations (3(3) $$\begin{array}{cc}\hfill & {\nabla }^2{u}_1-k_1^2{u}_1=0\mathrm{i}n{\mathrm{\Omega }}_1,\hfill \end{array}$$(3) ) and (4(4) $$\begin{array}{cc}\hfill & {\nabla }^2{u}_2-k_2^2{u}_2=0\mathrm{i}n{\mathrm{\Omega }}_2,\hfill \end{array}$$(4) ) by a linear combination of fundamental solutions in the form [11],(9) $$\begin{array}{cc}\hfill u_{1,2N}(\underset{¯}{X})& =\sum _{j=1}^{2N}{a}_j{G}_{\mathit{HM}}(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_1^j;k_1),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_1,\hfill \end{array}$$(9) (10) $$\begin{array}{cc}\hfill u_{2,N}(\underset{¯}{X})& =\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_2^j;k_2),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_2,\hfill \end{array}$$(10) where $G_{\mathit{MH}}$ is the fundamental solution for the modified Helmholtz equations which in two dimensions, for example, is given by,(11) $$\begin{array}{c}\hfill G_{\mathit{MH}}(\underset{¯}{X},\underset{¯}{\mathit{\xi }};k_i)=K_0(k_i\parallel \underset{¯}{X}-\underset{¯}{\mathit{\xi }}\parallel ),i=1,2,\end{array}$$(11) where $K_0$ is the modified Bessel function of the second kind of order zero. For simplicity, the constant $\frac{1}{2\mathit{\pi }}$, which does not appear in (11(11) $$\begin{array}{c}\hfill G_{\mathit{MH}}(\underset{¯}{X},\underset{¯}{\mathit{\xi }};k_i)=K_0(k_i\parallel \underset{¯}{X}-\underset{¯}{\mathit{\xi }}\parallel ),i=1,2,\end{array}$$(11) ), has been embedded in the unknown coefficients ${(b_j)}_{j=\overline{1,N}}$ in (10(10) $$\begin{array}{cc}\hfill u_{2,N}(\underset{¯}{X})& =\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_2^j;k_2),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_2,\hfill \end{array}$$(10) ). The modified Bessel function $K_0$ is computed using the NAG routine S18ACF. In the case that the background medium ${\mathrm{\Omega }}_1$ is harmonic, i.e. $k_1=0$, we should replace $G_{\mathit{MH}}(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_1;k_1)$ in (9(9) $$\begin{array}{cc}\hfill u_{1,2N}(\underset{¯}{X})& =\sum _{j=1}^{2N}{a}_j{G}_{\mathit{HM}}(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_1^j;k_1),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_1,\hfill \end{array}$$(9) ) by the fundamental solution for the Laplace equation(12) $$\begin{array}{c}\hfill {\nabla }^2{u}_1=0\mathrm{i}n{\mathrm{\Omega }}_1\end{array}$$(12) which in two dimensions is given by(13) $$\begin{array}{c}\hfill G_L(\underset{¯}{X},\underset{¯}{\mathit{\xi }})=-\frac{1}{2\mathit{\pi }}\ln \parallel \underset{¯}{X}-\underset{¯}{\mathit{\xi }}\parallel .\end{array}$$(13) In this case, the MFS approximation for (12(12) $$\begin{array}{c}\hfill {\nabla }^2{u}_1=0\mathrm{i}n{\mathrm{\Omega }}_1\end{array}$$(12) ) is(14) $$\begin{array}{c}\hfill u_{1,2N}(\underset{¯}{X})=\sum _{j=1}^{2N}{a}_j{G}_L(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_1^j),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_1,\end{array}$$(14) The source points ${\left({\underset{¯}{\mathit{\xi }}}_1^j\right)}_{j=\overline{1,2N}}$ in (9(9) $$\begin{array}{cc}\hfill u_{1,2N}(\underset{¯}{X})& =\sum _{j=1}^{2N}{a}_j{G}_{\mathit{HM}}(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_1^j;k_1),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_1,\hfill \end{array}$$(9) ) or (14(14) $$\begin{array}{c}\hfill u_{1,2N}(\underset{¯}{X})=\sum _{j=1}^{2N}{a}_j{G}_L(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_1^j),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_1,\end{array}$$(14) ) are located outside the domain $\overline{\mathrm{\Omega }}$ and inside the domain ${\mathrm{\Omega }}_2$, whilst the source points ${\left({\underset{¯}{\mathit{\xi }}}_2^j\right)}_{j=\overline{1,N}}$ in (10(10) $$\begin{array}{cc}\hfill u_{2,N}(\underset{¯}{X})& =\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_2^j;k_2),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_2,\hfill \end{array}$$(10) ) are located outside ${\overline{\mathrm{\Omega }}}_2$. More precisely, ${\left({\underset{¯}{\mathit{\xi }}}_1^j\right)}_{j=\overline{N+1,2N}}\in {\mathrm{\Omega }}_2$ and ${\left({\underset{¯}{\mathit{\xi }}}_2^j\right)}_{j=\overline{1,N}}\notin {\mathrm{\Omega }}_2$ are placed on (moving) pseudo-boundaries $\mathit{\partial }{\mathrm{\Omega }}_2^{{}^{\prime }}$ and $\mathit{\partial }{\mathrm{\Omega }}_2^{{}^{\prime \prime }}$ similar to $\mathit{\partial }{\mathrm{\Omega }}_2$ at a distance $\mathit{\delta }>0$ inwards and outwards, respectively. The rest of source points ${\left({\underset{¯}{\mathit{\xi }}}_1^j\right)}_{j=\overline{1,N}}\in {\mathbb{R}}^2\setminus \overline{\mathrm{\Omega }}$ are placed on a (fixed) pseudo-boundary $\mathit{\partial }{\mathrm{\Omega }}^{{}^{\prime }}$ similar to $\mathit{\partial }\mathrm{\Omega }$. 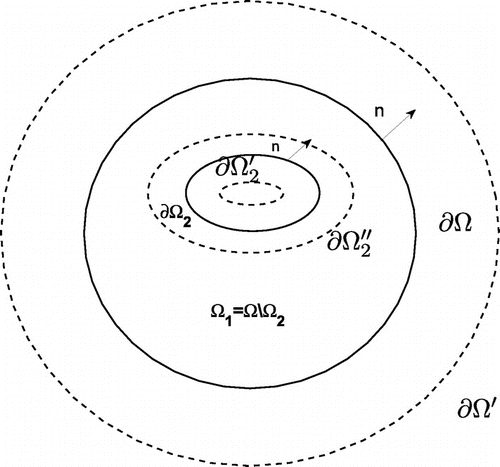A sketch of the fictitions curves $\mathit{\partial }{\mathrm{\Omega }}_2^{{}^{\prime }}$, $\mathit{\partial }{\mathrm{\Omega }}_2^{{}^{\prime \prime }}$ and $\mathit{\partial }{\mathrm{\Omega }}^{{}^{\prime }}$ on which the source points are located is shown in Figure 1.

Fig. 3 The reconstructed inner boundary with no regularization for $p\in \{0,1,5,10\}\%$ noise, for Example 1.

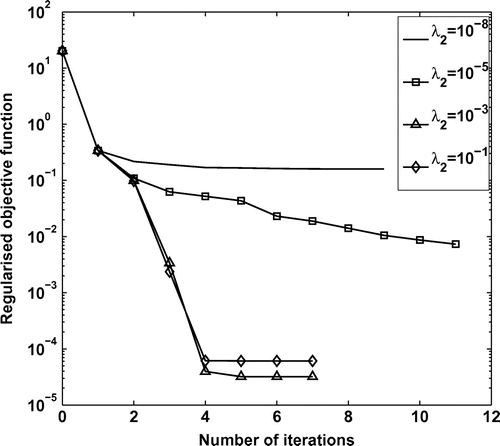
Fig. 4 The regularized objective function with various regularization parameters ${\mathit{\lambda }}_1=0,$${\mathit{\lambda }}_2\in \{{10}^{-8},{10}^{-5},{10}^{-3},{10}^{-1}\}$ for $p=10\%$ noise, as a function of the number of iterations, for Example 1.

For simplicity, we assume that $\mathrm{\Omega }$ is the unit circle $B(\underset{¯}{0};1)$ and that the unknown domain ${\mathrm{\Omega }}_2$ is star shaped with respect to the origin, i.e. $\mathit{\partial }{\mathrm{\Omega }}_2=\{(r(\mathit{\theta })\cos (\mathit{\theta }),r(\mathit{\theta })\sin (\mathit{\theta }))|\mathit{\theta }\in [0,2\mathit{\pi })\}$, where $r$ is a $2\mathit{\pi }$-periodic smooth function with values in the interval (0,1). We take$${\underset{¯}{X}}_i=(\cos ({\mathit{\theta }}_i),\sin ({\mathit{\theta }}_i)),i=\overline{1,N}$$to be the outer boundary collocation points uniformly distributed on $\mathit{\partial }\mathrm{\Omega }=\mathit{\partial }B(\underset{¯}{0};1)$, where ${\mathit{\theta }}_i=2\mathit{\pi }i/N$ for $i=\overline{1,N}$, and the source points$${\underset{¯}{\mathit{\xi }}}_1^j=(R\cos ({\mathit{\theta }}_j),R\sin ({\mathit{\theta }}_j)),j=\overline{1,N},$$where $R>1$ is fixed. We also take(15) $$\begin{array}{c}\hfill {\underset{¯}{X}}_i=(r_{i-N}\cos ({\mathit{\vartheta }}_{i-N}),r_{i-N}\sin ({\mathit{\vartheta }}_{i-N})),i=\overline{N+1,2N}\end{array}$$(15) to be the inner unknown boundary collocation points on $\mathit{\partial }{\mathrm{\Omega }}_2$, and the inner and outer source points$$\begin{array}{c}\hfill {\underset{¯}{\mathit{\xi }}}_1^j=(1-\mathit{\delta }){\underset{¯}{X}}_j,{\underset{¯}{\mathit{\xi }}}_2^{j-N}=(1+\mathit{\delta }){\underset{¯}{X}}_j,j=\overline{N+1,2N},\end{array}$$where $\mathit{\delta }\in (0,1)$. In Equation (15(15) $$\begin{array}{c}\hfill {\underset{¯}{X}}_i=(r_{i-N}\cos ({\mathit{\vartheta }}_{i-N}),r_{i-N}\sin ({\mathit{\vartheta }}_{i-N})),i=\overline{N+1,2N}\end{array}$$(15) ), $r_i:=r({\mathit{\theta }}_i)$ for $i=\overline{1,N}$.

The MFS coefficient vectors $\underset{¯}{a}={(a_j)}_{j=\overline{1,2N}}$, $\underset{¯}{b}={(b_j)}_{j=\overline{1,N}}$ in (9(9) $$\begin{array}{cc}\hfill u_{1,2N}(\underset{¯}{X})& =\sum _{j=1}^{2N}{a}_j{G}_{\mathit{HM}}(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_1^j;k_1),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_1,\hfill \end{array}$$(9) ) or (14(14) $$\begin{array}{c}\hfill u_{1,2N}(\underset{¯}{X})=\sum _{j=1}^{2N}{a}_j{G}_L(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_1^j),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_1,\end{array}$$(14) ), and (10(10) $$\begin{array}{cc}\hfill u_{2,N}(\underset{¯}{X})& =\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_2^j;k_2),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_2,\hfill \end{array}$$(10) ), and the radii vector $\underset{¯}{r}={(r_i)}_{i=\overline{1,N}}$ characterizing the star-shaped inner boundary $\mathit{\partial }{\mathrm{\Omega }}_2$ are determined by imposing the transmission conditions (5(5) $$\begin{array}{cc}\hfill & u_1=u_2,\mathrm{o}n\mathit{\partial }{\mathrm{\Omega }}_2.\hfill \end{array}$$(5) ), (6(6) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}\mathrm{o}n\mathit{\partial }{\mathrm{\Omega }}_2\hfill \end{array}$$(6) ) and the Cauchy data (7(7) $$\begin{array}{cc}\hfill & u_1=f\mathrm{o}n\mathit{\partial }\mathrm{\Omega },\hfill \end{array}$$(7) ), (8(8) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=g\mathrm{o}n\mathit{\partial }\mathrm{\Omega }.\hfill \end{array}$$(8) ) at the boundary collocation points ${({\underset{¯}{X}}_i)}_{i=\overline{1,2N}}$ in a least-squares sense which recasts into minimizing the non-linear objective function(16) $$\begin{array}{cc}\hfill T(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})& :=\parallel u_1-f{\parallel }_{L^2(\mathit{\partial }\mathrm{\Omega })}^2+\parallel \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}-g{\parallel }_{L^2(\mathit{\partial }\mathrm{\Omega })}^2+\parallel u_1-u_2{\parallel }_{L^2(\mathit{\partial }{\mathrm{\Omega }}_2)}^2\hfill \\ \hfill & +\parallel \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}-\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}{\parallel }_{L^2(\mathit{\partial }{\mathrm{\Omega }}_2)}^2+{\mathit{\lambda }}_1\{\parallel \underset{¯}{a}{\parallel }^2+\parallel \underset{¯}{b}{\parallel }^2\}+{\mathit{\lambda }}_2\parallel {\underset{¯}{r}}^{\prime }{\parallel }^2,\hfill \end{array}$$(16) where ${\mathit{\lambda }}_1,{\mathit{\lambda }}_2\ge 0$ are regularization parameters to be prescribed. Introducing the MFS approximations (10(10) $$\begin{array}{cc}\hfill u_{2,N}(\underset{¯}{X})& =\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_2^j;k_2),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_2,\hfill \end{array}$$(10) ), and say (14(14) $$\begin{array}{c}\hfill u_{1,2N}(\underset{¯}{X})=\sum _{j=1}^{2N}{a}_j{G}_L(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_1^j),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_1,\end{array}$$(14) ) (with obvious modifications if (9(9) $$\begin{array}{cc}\hfill u_{1,2N}(\underset{¯}{X})& =\sum _{j=1}^{2N}{a}_j{G}_{\mathit{HM}}(\underset{¯}{X},{\underset{¯}{\mathit{\xi }}}_1^j;k_1),\underset{¯}{X}\in {\overline{\mathrm{\Omega }}}_1,\hfill \end{array}$$(9) ) is used) into (16(16) $$\begin{array}{cc}\hfill T(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})& :=\parallel u_1-f{\parallel }_{L^2(\mathit{\partial }\mathrm{\Omega })}^2+\parallel \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}-g{\parallel }_{L^2(\mathit{\partial }\mathrm{\Omega })}^2+\parallel u_1-u_2{\parallel }_{L^2(\mathit{\partial }{\mathrm{\Omega }}_2)}^2\hfill \\ \hfill & +\parallel \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}-\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}{\parallel }_{L^2(\mathit{\partial }{\mathrm{\Omega }}_2)}^2+{\mathit{\lambda }}_1\{\parallel \underset{¯}{a}{\parallel }^2+\parallel \underset{¯}{b}{\parallel }^2\}+{\mathit{\lambda }}_2\parallel {\underset{¯}{r}}^{\prime }{\parallel }^2,\hfill \end{array}$$(16) ) yields(17) $$\begin{array}{cc}\hfill T(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})& =\sum _{i=1}^N{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_i,{\underset{¯}{\mathit{\xi }}}_1^j)-f({\underset{¯}{X}}_i)]}^2\hfill \\ \hfill & +\sum _{i=N+1}^{2N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-g\left({\underset{¯}{X}}_{i-N}\right)]}^2\hfill \\ \hfill & +\sum _{i=2N+1}^{3N}{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +\sum _{i=3N+1}^{4N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j\frac{\mathit{\partial }{G}_{\mathit{MH}}}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1\{\sum _{j=1}^{2N}{a}_j^2+\sum _{j=1}^N{b}_j^2\}+{\mathit{\lambda }}_2\sum _{j=1}^{N-1}{(r_{j+1}-r_j)}^2.\hfill \end{array}$$(17) The minimization of (17(17) $$\begin{array}{cc}\hfill T(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})& =\sum _{i=1}^N{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_i,{\underset{¯}{\mathit{\xi }}}_1^j)-f({\underset{¯}{X}}_i)]}^2\hfill \\ \hfill & +\sum _{i=N+1}^{2N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-g\left({\underset{¯}{X}}_{i-N}\right)]}^2\hfill \\ \hfill & +\sum _{i=2N+1}^{3N}{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +\sum _{i=3N+1}^{4N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j\frac{\mathit{\partial }{G}_{\mathit{MH}}}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1\{\sum _{j=1}^{2N}{a}_j^2+\sum _{j=1}^N{b}_j^2\}+{\mathit{\lambda }}_2\sum _{j=1}^{N-1}{(r_{j+1}-r_j)}^2.\hfill \end{array}$$(17) ) imposes $4N$ non-linear equations in the $4N$ unknowns $(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})$. We can obviously have more equations than the unknowns if we take more boundary collocation points than sources. If there is noise in the measured data (8(8) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=g\mathrm{o}n\mathit{\partial }\mathrm{\Omega }.\hfill \end{array}$$(8) ), we replace the exact $g$ in (17(17) $$\begin{array}{cc}\hfill T(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})& =\sum _{i=1}^N{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_i,{\underset{¯}{\mathit{\xi }}}_1^j)-f({\underset{¯}{X}}_i)]}^2\hfill \\ \hfill & +\sum _{i=N+1}^{2N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-g\left({\underset{¯}{X}}_{i-N}\right)]}^2\hfill \\ \hfill & +\sum _{i=2N+1}^{3N}{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +\sum _{i=3N+1}^{4N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j\frac{\mathit{\partial }{G}_{\mathit{MH}}}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1\{\sum _{j=1}^{2N}{a}_j^2+\sum _{j=1}^N{b}_j^2\}+{\mathit{\lambda }}_2\sum _{j=1}^{N-1}{(r_{j+1}-r_j)}^2.\hfill \end{array}$$(17) ) by the noisy $g^{\mathit{\epsilon }}$ given by(18) $$\begin{array}{c}\hfill g^{\mathit{ϵ}}({\underset{¯}{X}}_i)=g({\underset{¯}{X}}_i)+{\mathit{ϵ}}_i,i=\overline{1,N},\end{array}$$(18) where ${\mathit{ϵ}}_i$ are random variables generated (using the NAG routine D05DDF) from a Gaussian normal distribution with mean zero and standard deviation(19) $$\begin{array}{c}\hfill \mathit{\sigma }=p\times \underset{\mathit{\partial }\mathrm{\Omega }}{\max }|g|,\end{array}$$(19) where $p$ represents the percentage of noise. In Equation (17(17) $$\begin{array}{cc}\hfill T(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})& =\sum _{i=1}^N{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_i,{\underset{¯}{\mathit{\xi }}}_1^j)-f({\underset{¯}{X}}_i)]}^2\hfill \\ \hfill & +\sum _{i=N+1}^{2N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-g\left({\underset{¯}{X}}_{i-N}\right)]}^2\hfill \\ \hfill & +\sum _{i=2N+1}^{3N}{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +\sum _{i=3N+1}^{4N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j\frac{\mathit{\partial }{G}_{\mathit{MH}}}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1\{\sum _{j=1}^{2N}{a}_j^2+\sum _{j=1}^N{b}_j^2\}+{\mathit{\lambda }}_2\sum _{j=1}^{N-1}{(r_{j+1}-r_j)}^2.\hfill \end{array}$$(17) ), the normal derivatives of $G_L$ and $G_{\mathit{MH}}$, via (12(12) $$\begin{array}{c}\hfill {\nabla }^2{u}_1=0\mathrm{i}n{\mathrm{\Omega }}_1\end{array}$$(12) ) and (11(11) $$\begin{array}{c}\hfill G_{\mathit{MH}}(\underset{¯}{X},\underset{¯}{\mathit{\xi }};k_i)=K_0(k_i\parallel \underset{¯}{X}-\underset{¯}{\mathit{\xi }}\parallel ),i=1,2,\end{array}$$(11) ), are given by(20) $$\begin{array}{ccc}\hfill \frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}(\underset{¯}{X},\underset{¯}{\mathit{\xi }})=& -\frac{(\underset{¯}{X}-\underset{¯}{\mathit{\xi }})·\underset{¯}{n}}{2\mathit{\pi }\parallel \underset{¯}{X}-\underset{¯}{\mathit{\xi }}{\parallel }^2},\hfill & \hfill \\ \hfill \frac{\mathit{\partial }{G}_{\mathit{MH}}}{\mathit{\partial }n}(\underset{¯}{X},\underset{¯}{\mathit{\xi }};k_2)=& -\frac{k_2(\underset{¯}{X}-\underset{¯}{\mathit{\xi }})·\underset{¯}{n}}{\parallel \underset{¯}{X}-\underset{¯}{\mathit{\xi }}\parallel }\hfill & \hfill K_1(k_2\parallel \underset{¯}{X}-\underset{¯}{\mathit{\xi }}\parallel ),\end{array}$$(20) where $K_1$ is the modified Bessel function of the second kind of order one, and(21) $$\begin{array}{c}\hfill \underset{¯}{n}(\underset{¯}{X})=\{\begin{array}{c}\cos (\mathit{\theta })\underset{¯}{i}+\sin (\mathit{\theta })\underset{¯}{j},\underset{¯}{X}\in \mathit{\partial }\mathrm{\Omega },\hfill \\ \frac{1}{\sqrt{r^2(\mathit{\theta })+r^{\prime 2}(\mathit{\theta })}}[-(r^{\prime }(\mathit{\theta })\sin (\mathit{\theta })+r(\mathit{\theta })\cos (\mathit{\theta }))\underset{¯}{i}\hfill \\ +(r^{\prime }(\mathit{\theta })\cos (\mathit{\theta })-r(\mathit{\theta })\sin (\mathit{\theta }))\underset{¯}{j}],\underset{¯}{X}\in \mathit{\partial }{\mathrm{\Omega }}_2,\hfill \end{array}\end{array}$$(21) where $\underset{¯}{i}=(1,0)$ and $\underset{¯}{j}=(0,1)$. The modified Bessel function $K_1$ is computed using the NAG routine S18ADF. In Equation (21(21) $$\begin{array}{c}\hfill \underset{¯}{n}(\underset{¯}{X})=\{\begin{array}{c}\cos (\mathit{\theta })\underset{¯}{i}+\sin (\mathit{\theta })\underset{¯}{j},\underset{¯}{X}\in \mathit{\partial }\mathrm{\Omega },\hfill \\ \frac{1}{\sqrt{r^2(\mathit{\theta })+r^{\prime 2}(\mathit{\theta })}}[-(r^{\prime }(\mathit{\theta })\sin (\mathit{\theta })+r(\mathit{\theta })\cos (\mathit{\theta }))\underset{¯}{i}\hfill \\ +(r^{\prime }(\mathit{\theta })\cos (\mathit{\theta })-r(\mathit{\theta })\sin (\mathit{\theta }))\underset{¯}{j}],\underset{¯}{X}\in \mathit{\partial }{\mathrm{\Omega }}_2,\hfill \end{array}\end{array}$$(21) ), the derivative $r^{\prime }$ is approximated using backward finite differences as(22) $$\begin{array}{c}\hfill r^{\prime }(\mathit{\theta })\approx \frac{r_i-r_{i-1}}{{\mathit{\theta }}_i-{\mathit{\theta }}_{i-1}},i=\overline{1,N},\end{array}$$(22) with the convention that $r_0=r_N$ and ${\mathit{\theta }}_0=0$.

Fig. 5 The reconstructed inner boundary with various regularisation parameters ${\mathit{\lambda }}_1=0,$${\mathit{\lambda }}_2\in \{{10}^{-8},{10}^{-5},{10}^{-3},{10}^{-1}\}$ for $p=10\%$ noise, for Example 1.

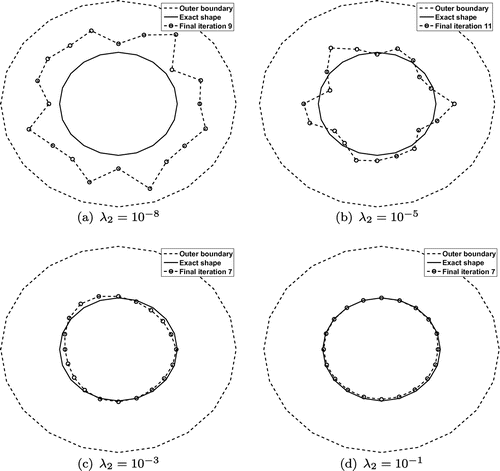
Fig. 6 The numerical solutions for the normal derivative $\mathit{\partial }{u}_1/\mathit{\partial }n(1,\mathit{\theta })$, obtained for various values of $M=N\in \{20,40,80\}$ with (a) no regularisation, and (b) regularisation parameter $\mathit{\lambda }={10}^{-6}$ for the direct problem associated to Example 2.

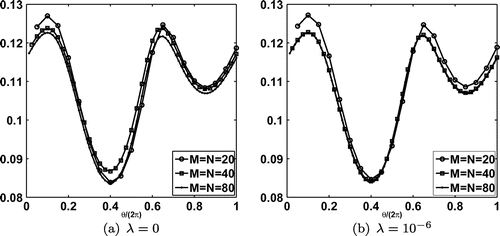
Fig. 7 The unregularized objective function for $p\in \{0,1,3,5\}\%$ noise, as a function of the number of iterations, for Example 2.

Fig. 8 The reconstructed inner boundary with no regularization for $p\in \{0,1,3,5\}\%$ noise, for Example 2.

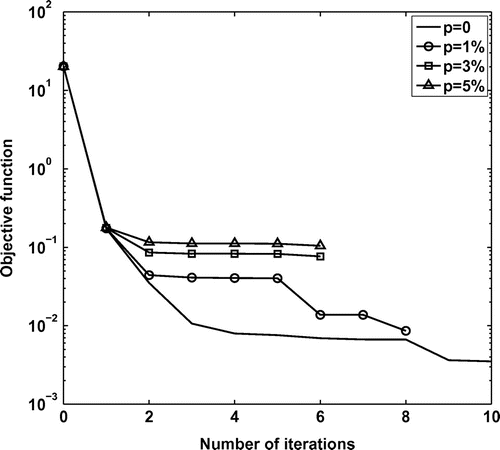
Fig. 9 The regularized objective function with various regularization parameters ${\mathit{\lambda }}_2=0$, ${\mathit{\lambda }}_1\in \{{10}^{-8},{10}^{-5},{10}^{-3},{10}^{-1}\}$ for $p=5\%$ noise, as a function of the number of iterations, for Example 2.

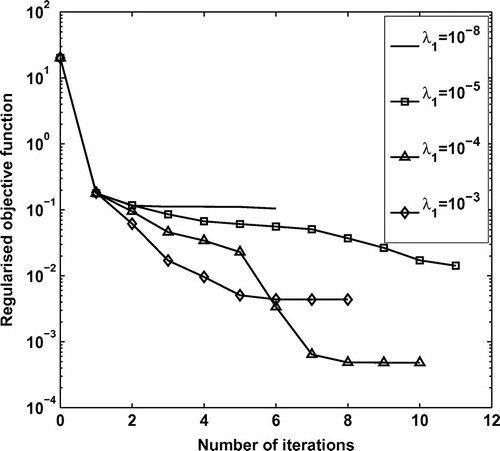
Fig. 10 The reconstructed inner boundary with various regularization parameters ${\mathit{\lambda }}_2=0$, ${\mathit{\lambda }}_1\in \{{10}^{-8},{10}^{-5},{10}^{-4},{10}^{-3}\}$ for $p=5\%$ noise, for Example 2.

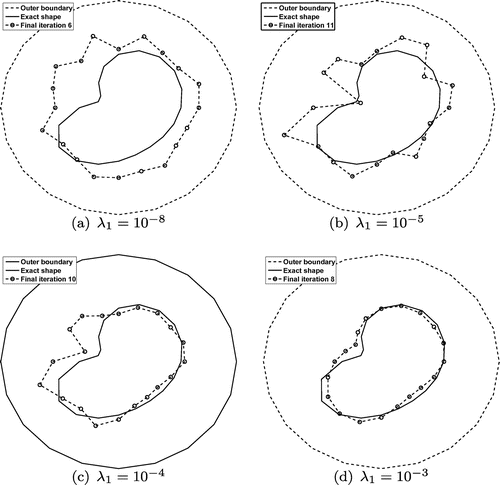
Fig. 11 The reconstructed inner boundary with various regularization parameters ${\mathit{\lambda }}_2=0$, ${\mathit{\lambda }}_1\in \{{10}^{-8},{10}^{-5},{10}^{-3},{10}^{-1}\}$ for $p=5\%$ noise, for Example 3.

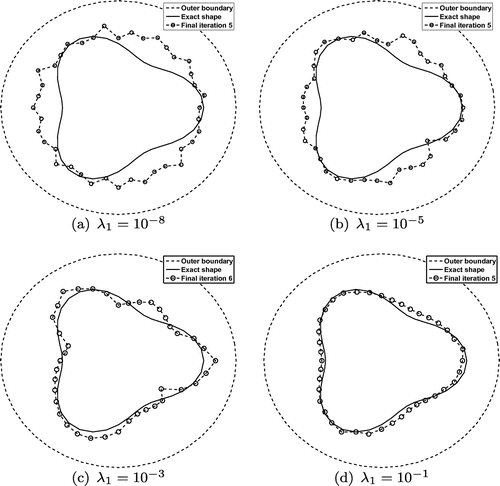
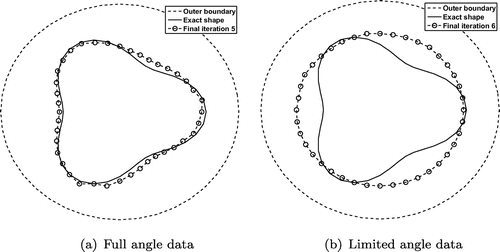
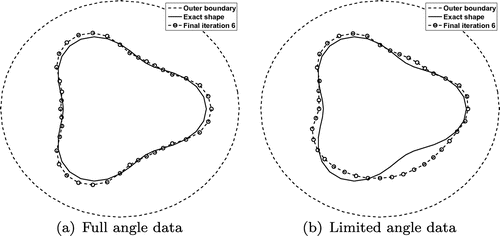
Fig. 12 The reconstructed inner boundary for (a) full angle data for ${\mathit{\lambda }}_1={10}^{-1},{\mathit{\lambda }}_2=0$, and (b) limited angle data for ${\mathit{\lambda }}_1={\mathit{\lambda }}_2={10}^{-9}$, for no noise, for Example 3.

The minimization of the objective function (17(17) $$\begin{array}{cc}\hfill T(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})& =\sum _{i=1}^N{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_i,{\underset{¯}{\mathit{\xi }}}_1^j)-f({\underset{¯}{X}}_i)]}^2\hfill \\ \hfill & +\sum _{i=N+1}^{2N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-g\left({\underset{¯}{X}}_{i-N}\right)]}^2\hfill \\ \hfill & +\sum _{i=2N+1}^{3N}{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +\sum _{i=3N+1}^{4N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j\frac{\mathit{\partial }{G}_{\mathit{MH}}}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1\{\sum _{j=1}^{2N}{a}_j^2+\sum _{j=1}^N{b}_j^2\}+{\mathit{\lambda }}_2\sum _{j=1}^{N-1}{(r_{j+1}-r_j)}^2.\hfill \end{array}$$(17) ) is accomplished computationally using the NAG routine E04FCF, which is a comprehensive algorithm for minimizing an unconstrained sum of squares of nonlinear functions. Note that the NAG routine E04FCF does not require the user to supply the gradient of (17(17) $$\begin{array}{cc}\hfill T(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})& =\sum _{i=1}^N{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_i,{\underset{¯}{\mathit{\xi }}}_1^j)-f({\underset{¯}{X}}_i)]}^2\hfill \\ \hfill & +\sum _{i=N+1}^{2N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-g\left({\underset{¯}{X}}_{i-N}\right)]}^2\hfill \\ \hfill & +\sum _{i=2N+1}^{3N}{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +\sum _{i=3N+1}^{4N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j\frac{\mathit{\partial }{G}_{\mathit{MH}}}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1\{\sum _{j=1}^{2N}{a}_j^2+\sum _{j=1}^N{b}_j^2\}+{\mathit{\lambda }}_2\sum _{j=1}^{N-1}{(r_{j+1}-r_j)}^2.\hfill \end{array}$$(17) ). If required, the physical constraints $0<r_i<1$ for $i=\overline{1,N}$, that the inhomogeneity ${\mathrm{\Omega }}_2$ stays within the host domain $\mathrm{\Omega }$ during the iteration proccess can be imposed manually during the iterative procedure by adjustment at each iteration. The minimization process usually terminates when either a user-specified tolerance is achieved, or when a user-specified maximum number of iterations is reached.

Numerical results and discussion

In this section, three examples in two dimensions are presented in order to show the accuracy and stability of the MFS described in the previous section.

We take $k_1=0$ and $k_2=1$. In all numerical experiments, the initial guess for the unknown vectors $\underset{¯}{a}$, $\underset{¯}{b}$ are $\underset{¯}{0}$ and the initial guess for the inner boundary is taken to be a circle located at the origin with radius $0.7$, i.e. the initial guess for $\underset{¯}{r}$ is $\underset{¯}{0.7}$. Moreover, as required by the NAG routine E04FCF used, the tolerance XTOL was set to ${10}^{-6}$ and the maximum number of function evaluations, MAXCAL, was set to 1000. However, it is noted that by increasing the MAXCAL to be large, say 400 $\times$ (number of unknowns), as suggested by the NAG Fortran library manual, the computational time increases significantly and moreover, it does not produce more accurate numerical results. We also take $R=2$, $M=N=20$ for examples 1 and 2, and $M=N=40$ for example 3. Clearly, the rigorous choice of the regularization two-parameter family ${\mathit{\lambda }}_1$ and ${\mathit{\lambda }}_2$ in the nonlinear Tikhonov functional (16(16) $$\begin{array}{cc}\hfill T(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})& :=\parallel u_1-f{\parallel }_{L^2(\mathit{\partial }\mathrm{\Omega })}^2+\parallel \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}-g{\parallel }_{L^2(\mathit{\partial }\mathrm{\Omega })}^2+\parallel u_1-u_2{\parallel }_{L^2(\mathit{\partial }{\mathrm{\Omega }}_2)}^2\hfill \\ \hfill & +\parallel \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}-\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}{\parallel }_{L^2(\mathit{\partial }{\mathrm{\Omega }}_2)}^2+{\mathit{\lambda }}_1\{\parallel \underset{¯}{a}{\parallel }^2+\parallel \underset{¯}{b}{\parallel }^2\}+{\mathit{\lambda }}_2\parallel {\underset{¯}{r}}^{\prime }{\parallel }^2,\hfill \end{array}$$(16) ) is very challenging. One can attempt the usual discrepancy principle or the more recent L-surface criterion [12] but the calculations are very expensive and close to being prohibitive. In our study, we have investigated by trial and error several values for ${\mathit{\lambda }}_1$ and ${\mathit{\lambda }}_2$, and although we are not optimal in their difficult choice, at least we can discard the unstable solutions and provide some nearly optimal plausible stable candidates. Nevertheless, more work should be undertaken on the subject of multiple regularization in the future.

Example 1

We first consider an example for which the analytical solution is available and given by, see [5],(23) $$\begin{array}{c}\hfill u_1(r,\mathit{\theta })=1+a_0\ln (r),R_0<r<1,\end{array}$$(23) where $a_0=\frac{R_0{I}_1(R_0)}{I_0(R_0)-R_0{I}_1(R_0)\ln (R_0)}$,(24) $$\begin{array}{c}\hfill u_2(r,\mathit{\theta })=A_0{I}_0(r),0<r<R_0,\end{array}$$(24) where $A_0=\frac{1}{I_0(R_0)-R_0{I}_1(R_0)\ln (R_0)}$. The modified Bessel functions of the first kind of order 0 and 1, namely $I_0$ and $I_1$ are computed using the NAG routines S18AEF and S18AFF, respectively.

In this example, the unknown inner boundary is the disk(25) $$\begin{array}{c}\hfill {\mathrm{\Omega }}_2=B(\underset{¯}{0};R_0)=\{(x,y)\in {\mathbb{R}}^2|x^2+y^2<R_0^2\}\end{array}$$(25) of radius $R_0=0.5$ and $\mathit{\delta }$ is taken to be 0.5. This analytical solution satisfies problem (4(4) $$\begin{array}{cc}\hfill & {\nabla }^2{u}_2-k_2^2{u}_2=0\mathrm{i}n{\mathrm{\Omega }}_2,\hfill \end{array}$$(4) )–(8(8) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=g\mathrm{o}n\mathit{\partial }\mathrm{\Omega }.\hfill \end{array}$$(8) ) and (12(12) $$\begin{array}{c}\hfill {\nabla }^2{u}_1=0\mathrm{i}n{\mathrm{\Omega }}_1\end{array}$$(12) ), with(26) $$\begin{array}{c}\hfill f(\mathit{\theta })=1,\mathit{\theta }\in (0,2\mathit{\pi }]\end{array}$$(26) and(27) $$\begin{array}{c}\hfill \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}(1,\mathit{\theta })=g(\mathit{\theta })=a_0,\mathit{\theta }\in (0,2\mathit{\pi }].\end{array}$$(2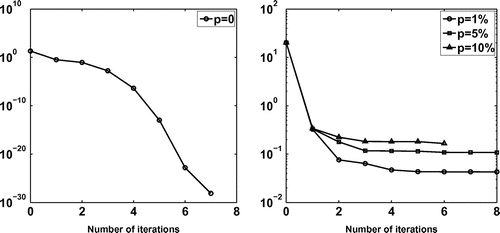7) Figure 2 shows the objective function (17(17) $$\begin{array}{cc}\hfill T(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})& =\sum _{i=1}^N{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_i,{\underset{¯}{\mathit{\xi }}}_1^j)-f({\underset{¯}{X}}_i)]}^2\hfill \\ \hfill & +\sum _{i=N+1}^{2N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-g\left({\underset{¯}{X}}_{i-N}\right)]}^2\hfill \\ \hfill & +\sum _{i=2N+1}^{3N}{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +\sum _{i=3N+1}^{4N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j\frac{\mathit{\partial }{G}_{\mathit{MH}}}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1\{\sum _{j=1}^{2N}{a}_j^2+\sum _{j=1}^N{b}_j^2\}+{\mathit{\lambda }}_2\sum _{j=1}^{N-1}{(r_{j+1}-r_j)}^2.\hfill \end{array}$$(17) ) with no regularization, i.e. ${\mathit{\lambda }}_1={\mathit{\lambda }}_2=0$, when $p\in \{0,1,5,10\}\%$ noise is added in the input data (27(27) $$\begin{array}{c}\hfill \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}(1,\mathit{\theta })=g(\mathit{\theta })=a_0,\mathit{\theta }\in (0,2\mathit{\pi }].\end{array}$$(27) ), as a function of the number of iterations. From this figure, it can be seen that the unregularized objective cost functional decreases rapidly within 6–8 iterations to either a very low value of $\mathbf{O}\left({10}^{-29}\right)$ for $p=0$, or to a stationary level for $p>0$. Moreover, as expected, this level of stationarity decreases with decreasing the level of noise $p$.

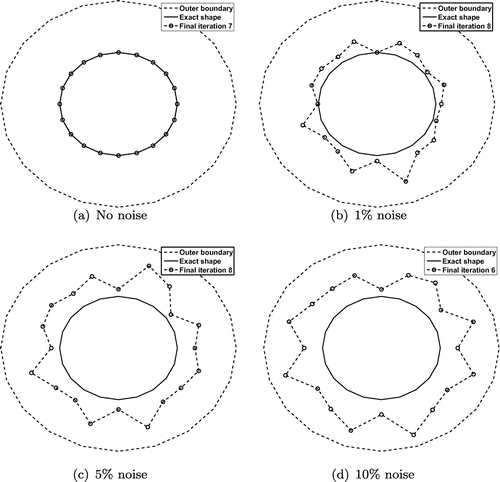
In Figure 3, we present the reconstructed inner boundary and the exact shape (25(25) $$\begin{array}{c}\hfill {\mathrm{\Omega }}_2=B(\underset{¯}{0};R_0)=\{(x,y)\in {\mathbb{R}}^2|x^2+y^2<R_0^2\}\end{array}$$(25) ) with no regularization for $p\in \{0,1,5,10\}\%$. As expected, as the level of noise increases, since no regularization is imposed, the reconstructed inner boundary becomes unstable.

Next, regularization is used in (17(17) $$\begin{array}{cc}\hfill T(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})& =\sum _{i=1}^N{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_i,{\underset{¯}{\mathit{\xi }}}_1^j)-f({\underset{¯}{X}}_i)]}^2\hfill \\ \hfill & +\sum _{i=N+1}^{2N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-g\left({\underset{¯}{X}}_{i-N}\right)]}^2\hfill \\ \hfill & +\sum _{i=2N+1}^{3N}{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +\sum _{i=3N+1}^{4N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j\frac{\mathit{\partial }{G}_{\mathit{MH}}}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1\{\sum _{j=1}^{2N}{a}_j^2+\sum _{j=1}^N{b}_j^2\}+{\mathit{\lambda }}_2\sum _{j=1}^{N-1}{(r_{j+1}-r_j)}^2.\hfill \end{array}$$(17) ) in order to stablize the numerical solutions. Figures 4 and 5 show the regularized objective function (17(17) $$\begin{array}{cc}\hfill T(\underset{¯}{a},\underset{¯}{b},\underset{¯}{r})& =\sum _{i=1}^N{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_i,{\underset{¯}{\mathit{\xi }}}_1^j)-f({\underset{¯}{X}}_i)]}^2\hfill \\ \hfill & +\sum _{i=N+1}^{2N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-g\left({\underset{¯}{X}}_{i-N}\right)]}^2\hfill \\ \hfill & +\sum _{i=2N+1}^{3N}{[\sum _{j=1}^{2N}{a}_j{G}_L({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j{G}_{\mathit{MH}}({\underset{¯}{X}}_{i-N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +\sum _{i=3N+1}^{4N}{[\sum _{j=1}^{2N}{a}_j\frac{\mathit{\partial }{G}_L}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_1^j)-\sum _{j=1}^N{b}_j\frac{\mathit{\partial }{G}_{\mathit{MH}}}{\mathit{\partial }n}({\underset{¯}{X}}_{i-2N},{\underset{¯}{\mathit{\xi }}}_2^j;k_2)]}^2\hfill \\ \hfill & +{\mathit{\lambda }}_1\{\sum _{j=1}^{2N}{a}_j^2+\sum _{j=1}^N{b}_j^2\}+{\mathit{\lambda }}_2\sum _{j=1}^{N-1}{(r_{j+1}-r_j)}^2.\hfill \end{array}$$(17) ) and the reconstructed inner boundary, respectively, for $p=10\%$ noise and various regularization parameters ${\mathit{\lambda }}_1=0$, ${\mathit{\lambda }}_2\in \{{10}^{-8},{10}^{-5},{10}^{-3},{10}^{-1}\}$. From Figure 5, it can be seen that accurate and stable numerical solutions are achieved for ${\mathit{\lambda }}_1=0$ and ${\mathit{\lambda }}_2$ in the range ${10}^{-3}$ to ${10}^{-1}$, whilst clearly for ${\mathit{\lambda }}_2\le {10}^{-5}$ the obtained reconstructions become unstable.

Example 2

In the second example, we consider a more complicated bean-shaped inclusion $\mathit{\partial }{\mathrm{\Omega }}_2$ given by the radial parameterization(28) $$\begin{array}{c}\hfill r(\mathit{\theta })=\frac{0.5+0.4\cos (\mathit{\theta })+0.1\sin (2\mathit{\theta })}{1+0.7\cos (\mathit{\theta })},\mathit{\theta }\in (0,2\mathit{\pi }]\end{array}$$(28) within the unit circle $\mathrm{\Omega }=B(\underset{¯}{0},1)$. The Dirichlet data (7(7) $$\begin{array}{cc}\hfill & u_1=f\mathrm{o}n\mathit{\partial }\mathrm{\Omega },\hfill \end{array}$$(7) ) on $\mathit{\partial }\mathrm{\Omega }$ is taken to be the same as in Example 1 and given by Equation (26(26) $$\begin{array}{c}\hfill f(\mathit{\theta })=1,\mathit{\theta }\in (0,2\mathit{\pi }]\end{array}$$(26) ). We also choose $\mathit{\delta }=0.3$.

Since in this case no analytical solution is available, the Neumann flux data (8(8) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=g\mathrm{o}n\mathit{\partial }\mathrm{\Omega }.\hfill \end{array}$$(8) ) on $\mathit{\partial }\mathrm{\Omega }$ is simulated numerically by solving, using the MFS, the direct problem given by Equations (3(3) $$\begin{array}{cc}\hfill & {\nabla }^2{u}_1-k_1^2{u}_1=0\mathrm{i}n{\mathrm{\Omega }}_1,\hfill \end{array}$$(3) )–(6(6) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=\frac{\mathit{\partial }{u}_2}{\mathit{\partial }n}\mathrm{o}n\mathit{\partial }{\mathrm{\Omega }}_2\hfill \end{array}$$(6) ) and (26(26) $$\begin{array}{c}\hfill f(\mathit{\theta })=1,\mathit{\theta }\in (0,2\mathit{\pi }]\end{array}$$(26) ), when $\mathit{\partial }{\mathrm{\Omega }}_2$ is known and given by (28(28) $$\begin{array}{c}\hfill r(\mathit{\theta })=\frac{0.5+0.4\cos (\mathit{\theta })+0.1\sin (2\mathit{\theta })}{1+0.7\cos (\mathit{\theta })},\mathit{\theta }\in (0,2\mathit{\pi }]\end{array}$$(28) ). In this case, the numerical solutions for the normal derivative $\mathit{\partial }{u}_1/\mathit{\partial }n(1,\mathit{\theta })$ on $\mathit{\partial }\mathrm{\Omega }$, obtained for various values of $M=N\in \{20,40,80\}$ with no regularization $\mathit{\lambda }=0$, and with regularization $\mathit{\lambda }={10}^{-6}$ are shown in Figure 6. From Figure 6 it can be seen that the numerical results are convergent as the number of degrees of freedom increases. Furthermore, a small regularization with $\mathit{\lambda }={10}^{-6}$ tends to improve the independance of the mesh between $M=N=40$ and $80$. Twenty evenly spread points out of the curve $M=N=80$ with $\mathit{\lambda }={10}^{-6}$ of Figure 6(b) are chosen as input Neumann numerically simulated data (8(8) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=g\mathrm{o}n\mathit{\partial }\mathrm{\Omega }.\hfill \end{array}$$(8) ) in the inverse problem. Next, in order to avoid committing an inverse crime we solve the inverse problem with $M=N=20$.

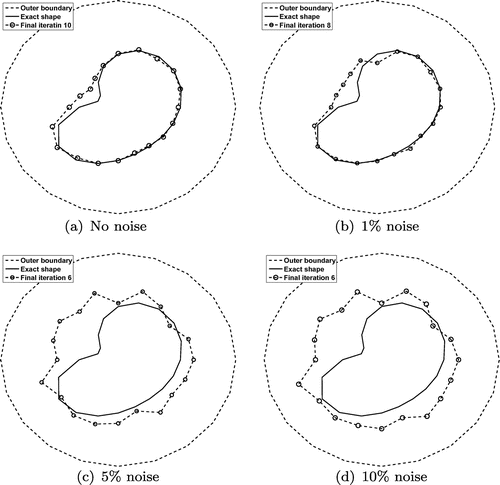
Figures 7 and 8 for Example 2 are anologous to Figures 2 and 3 for Example 1 and the same conclusions about the unstable nature of the unregularized solution, as the level of noise $p$ increases, can be drawn. Figures 9 and 10 for Example 2 present similar characteristics to Figures 4 and 5 for Example 1. In order to investigate a different situation to that in Example 1 we regularize with ${\mathit{\lambda }}_1>0$ instead of ${\mathit{\lambda }}_2>0$. From Figure 10, it can be seen that a stable and reasonably accurate numerical solution is obtained for ${\mathit{\lambda }}_1={10}^{-3}$ (and ${\mathit{\lambda }}_2=0$), whilst clearly for ${\mathit{\lambda }}_1\le {10}^{-4}$ the obtained reconstructions become unstable.

Example 3

We finally consider reconstructing a complicated pear-shaped inclusion $\mathit{\partial }{\mathrm{\Omega }}_2$ given by the radial parameterization(29) $$\begin{array}{c}\hfill r(\mathit{\theta })=0.6+0.125\cos (3\mathit{\theta }),\mathit{\theta }\in (0,2\mathit{\pi }],\end{array}$$(29) within the unit circle $\mathrm{\Omega }=B(\underset{¯}{0},1)$. The Dirichlet voltage (2(2) $$\begin{array}{c}\hfill u:=\{\begin{array}{c}{u}_1\mathrm{i}n{\mathrm{\Omega }}_1:=\mathrm{\Omega }\setminus {\mathrm{\Omega }}_2,\hfill \\ u_2\mathrm{i}n{\mathrm{\Omega }}_2,\hfill \end{array}\end{array}$$(2) ) on $\mathit{\partial }\mathrm{\Omega }$ was taken to be the same as in Example 1 and given by Equation (26(26) $$\begin{array}{c}\hfill f(\mathit{\theta })=1,\mathit{\theta }\in (0,2\mathit{\pi }]\end{array}$$(26) ). We also take $\mathit{\delta }=0.3$. Since no analytical solution of this example is available, the Neumann flux data (8(8) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=g\mathrm{o}n\mathit{\partial }\mathrm{\Omega }.\hfill \end{array}$$(8) ) on $\mathit{\partial }\mathrm{\Omega }$ is simulated numerically by solving the direct problem (5(5) $$\begin{array}{cc}\hfill & u_1=u_2,\mathrm{o}n\mathit{\partial }{\mathrm{\Omega }}_2.\hfill \end{array}$$(5) )–(8(8) $$\begin{array}{cc}\hfill & \frac{\mathit{\partial }{u}_1}{\mathit{\partial }n}=g\mathrm{o}n\mathit{\partial }\mathrm{\Omega }.\hfill \end{array}$$(8) ) and (26(26) $$\begin{array}{c}\hfill f(\mathit{\theta })=1,\mathit{\theta }\in (0,2\mathit{\pi }]\end{array}$$(26) ), when $\mathit{\partial }{\mathrm{\Omega }}_2$ is known and given by (29(29) $$\begin{array}{c}\hfill r(\mathit{\theta })=0.6+0.125\cos (3\mathit{\theta }),\mathit{\theta }\in (0,2\mathit{\pi }],\end{array}$$(29) ), using the MFS with $M=N=80$ and $\mathit{\lambda }={10}^{-6}$. In order to avoid committing an inverse crime, we use a different number $M=N=40$ in the inverse problem. Next, two cases are considered for this example, as follows.

Recovery from full angle data

We consider the first case when the full data of measurment of the flux $g$ on the outer boundary $\mathit{\partial }\mathrm{\Omega }$ is available. Figure 11 shows reconstructed inner boundary with $p=5\%$, for various regularization parameters ${\mathit{\lambda }}_1\in \{{10}^{-8},{10}^{-5},{10}^{-3},{10}^{-1}\}$, ${\mathit{\lambda }}_2=0$. From this figure it can be seen that a stable and reasonably accurate numerical solution is obtained for ${\mathit{\lambda }}_1$ between ${10}^{-3}$ and ${10}^{-1}$ (and ${\mathit{\lambda }}_2=0$).

Recovery from limited angle data

Finally, we consider the case of limited flux measurment data $g$ prescribed on the subportion $\{(1,\mathit{\theta })|\mathit{\theta }\in [0,\mathit{\pi }]\}$ of the full outer boundary $\mathit{\partial }\mathrm{\Omega }=\mathit{\partial }B(\underset{¯}{0},1)$. Figures 12 and 13 show the reconstructed inner boundary for both full and limited flux data with or without noise. From these figures it can be seen that, as expected, the reconstructed inner boundary from full angle data is much more accurate than that obtained from limited angle data.

Fig. 13 The reconstructed inner boundary for (a) full angle data for ${\mathit{\lambda }}_1={10}^{-1},{\mathit{\lambda }}_2=0$, and (b) limited angle data for ${\mathit{\lambda }}_1={\mathit{\lambda }}_2={10}^{-9}$, for $p=5\%$ noise, for Example 3.

Conclusions

In this paper, a novel numerical method based on a regularized iterative MFS has been developed for the reconstruction of an inhomogeneity in an inverse problem for the elliptic (modified Helmholtz) equation. The choice of the two-family multiple regularization parameters was based on trial and error. More rigorous choices of these parameters should be investigated in any future work. Several examples have been investigated showing that the MFS is accurate (for exact data) and stable (for noisy data). Future work will concern extending the MFS developed in this paper to the reconstruction of a source domain from Cauchy data.[13]

Acknowledgments

B. Bin-Mohsin would like to thank King Saud University for their financial support in this research.