The method of fundamental solutions for the two-dimensional inverse Stefan problem

Abstract

We propose an application of the method of fundamental solutions (MFS) for the two-dimensional inverse Stefan problem, where data are to be reconstructed from knowledge of the moving surface and the given Stefan conditions on this surface. We present numerical results for several examples both when the initial data are given but also when it is not specified. These results show good accuracy with low computational cost and are compared with results obtained by other methods.

Keywords:

• heat conduction
• method of fundamental solutions (MFS)
• inverse Stefan problem
• Tikhonov’s regularization

AMS Subject Classifications:

• 35K05
• 35A35
• 65N35

Introduction

The method of fundamental solutions (MFS) is a powerful meshless approximation technique which is easy to use, has low computational cost and is applicable to problems where the governing partial differential operator possesses a fundamental solution available in an explicit form, see e.g. [1, 2]. Namely, it is applicable to all problems for which the boundary element method (BEM) is applicable, see e.g. [3]. Thus, it shares all the advantages the BEM has over domain discretization methods such as the finite difference method (FDM) and the finite element method (FEM). In addition, the MFS does not require any boundary integral evaluations as in the BEM, and it has an exponential convergence rate for analytic input data. In the MFS, the solution is represented as the discretization of a ‘non-singular’ single layer potential in which the ‘singularities’ (sources) are located outside the solution domain, see e.g. [4]. Thus, one possible drawback of the MFS may be that one has to make a choice for positioning the fictitious pseudo-boundary on which the sources are to be placed. However, there are two main approaches to handle this issue, namely, the case where the positions of the sources are pre-assigned and the dynamic case where they are determined as part of the solution, see e.g. [5–8]. More recently, the MFS has been applied to both elliptic (Laplace, Helmholtz, biharmonic, Lamé, Stokes) and parabolic (heat) partial differential equations, and to both direct and inverse problems.[9–11] In this paper, the focus is on applying the MFS to higher dimensional (two-dimensional) inverse parabolic Stefan problems by extending the one-dimensional analyses performed by the authors.[1, 12]

Both direct [13] and inverse [14] Stefan problems model many physical situations including the melting of a solid (ice), solidification of metals, crystal growth and recrystallization, etc. The classical direct Stefan problem is a free boundary problem which requires determining both the temperature and the free boundary when the initial and boundary conditions are known along with the thermal properties. In the case of two or more space variables, the geometry can become irregular and complicated, leading to both mathematical and numerical difficulties. This fact has motivated researchers to consider inverse Stefan problems, i.e. given the “free” boundary, find the corresponding boundary and/or initial data.[14, 15] These belong to a very important class of improperly posed problems which have application in the technology of refining a material by means of recrystalization, i.e. “how must a given solid be heated in order for it to melt in a prescribed manner?”.[13, 15] However, difficulties arise since the inverse Stefan problem, as a non-characteristic Cauchy problem, is ill-posed.[15–17] Although there exists an extensive literature on the one-dimensional inverse Stefan problem, the two-dimensional case has been less examined. Prior to this study, Colton and Reemtsen [18] developed an effective numerical procedure based on the use of a complete family of heat polynomials to minimize the maximal defect in the given initial-boundary data subject to regularizing constraints. The other two approaches by Saguez [19] and Jochum [20] minimize the defect in the given free boundary, but these non-linear approaches are numerically very expensive. More recently, Ang et al. [21] regularized the problem by means of a convolution equation, but the domain considered in their paper is semi-infinite.

In this paper, we develop the meshless method of fundamental solutions (MFS)combined with the Tikhonov regularization procedure for solving the linear inverse Stefan problem in two dimensions. Numerical results for several benchmark test examples are presented and discussed. Furthermore, a comparison with the numerical results of [18] is made.

Mathematical formulation

In this section we follow the mathematical set up of [18]. Let $T>0$ and for $t\in [0,T]$ define the liquid zone$$\mathrm{\Omega }(t)=\{(x,y)\in {\mathbb{R}}^2|0<x<s(y,t),0<y<1\},$$where the “free” surface $s(y,t)$ is given. The boundary $\mathit{\partial }\mathrm{\Omega }(t)=\mathrm{\Gamma }(t)\cup \mathrm{\Sigma }(t),$ where $\mathrm{\Sigma }(t)=\{(x,y)\in {\mathbb{R}}^2|x=s(y,t),0<y<1\}$ and $\mathrm{\Gamma }(t)=\mathit{\partial }\mathrm{\Omega }(t)\setminus \mathrm{\Sigma }(t).$ The whole solution domain is denoted by $\mathrm{\Omega }=\bigcup _{t\in (0,T]}\mathrm{\Omega }(t),$ and we observe that the boundary $\mathit{\partial }\mathrm{\Omega }$ of $\mathrm{\Omega }$ consists of the “bottom” $\overline{\mathrm{\Omega }(0)}=\{(x,y)\in {\mathbb{R}}^2|0\le x\le s(y,0),0\le y\le 1\},$ the “top” $\overline{\mathrm{\Omega }(T)}=\{(x,y)\in {\mathbb{R}}^2|0\le x\le s(y,T),0\le y\le 1\},$ the “free” boundary $\mathrm{\Sigma }=\bigcup _{t\in (0,T)}\mathrm{\Sigma }(t)$, and the “fixed” boundary $\mathrm{\Gamma }=\bigcup _{t\in (0,T)}\mathrm{\Gamma }(t).$

We assume that $s\in (0,1)$ is sufficiently smooth, and denote by $C^{p,q}$ the space of functions which are $p$ times continuously differentiable with respect to the space variables and $q$ times continuously differentiable with respect to the time variable. Let$$f\in C^1(\overline{\mathrm{\Omega }(0)}),g_1\in C^1(\overline{\mathrm{\Sigma }})\text{and}{g}_2\in C(\overline{\mathrm{\Sigma }})$$be given data that are compatible, i.e. $f=g_1$ on $\overline{\mathrm{\Omega }(0)}\cap \overline{\mathrm{\Sigma }}.$

The two-dimensional inverse Stefan problem then requires finding the temperature solution $u\in C^{2,1}(\mathrm{\Omega })\cap C^{1,0}(\overline{\mathrm{\Omega }})$ satisfying the heat equation(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) where $\mathit{\alpha }>0$ is the thermal diffusivity, subject to the Cauchy boundary conditions on $\mathrm{\Sigma }$(2) $$\begin{array}{c}\hfill u=g_1\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(2) (3) $$\begin{array}{c}\hfill k\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(3) and the initial condition(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) In (3(3) $$\begin{array}{c}\hfill k\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(3) ), $k>0$ is the thermal conductivity and $\mathit{\nu }$ is the inward unit normal, with respect to the space variables, pointing into the liquid zone $\mathrm{\Omega }$. In the application of melting of ice in water,[22](5) $$\begin{array}{c}\hfill g_1=0\text{and}{g}_2=\frac{\mathrm{\Lambda }\mathit{\rho }}{|\nabla \mathrm{\Phi }|}\frac{\mathit{\partial }\mathrm{\Phi }}{\mathit{\partial }t}\text{on}\overline{\mathrm{\Sigma }},\end{array}$$(5) where $\mathit{\rho }$ is the density, $\mathrm{\Lambda }$ is the latent heat of fusion, $\mathrm{\Phi }(x,y,t)=x-s(y,t),$ and the gradient $\nabla$ is taken with respect to the space variables. Note that the “free” boundary $\mathrm{\Sigma }$ is overspecified by prescribing on it both Dirichlet (2(2) $$\begin{array}{c}\hfill u=g_1\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(2) ) and Neumann data (3(3) $$\begin{array}{c}\hfill k\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(3) ), i.e. the Cauchy data, whilst the “fixed” boundary $\mathrm{\Gamma }$ is underspecified since no conditions are specified on it. We also remark that when $s(y,t)\equiv$ constant, the problem (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) becomes the more classical inverse heat conduction problem which has been well investigated, see e.g. [23] and [24]. In Figure 1 we present the domain and boundary conditions.

Fig. 1 Representation of the two-dimensional inverse Stefan problem, with locations of the initial and boundary conditions (2(2) $$\begin{array}{c}\hfill u=g_1\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(2) )–(4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ).

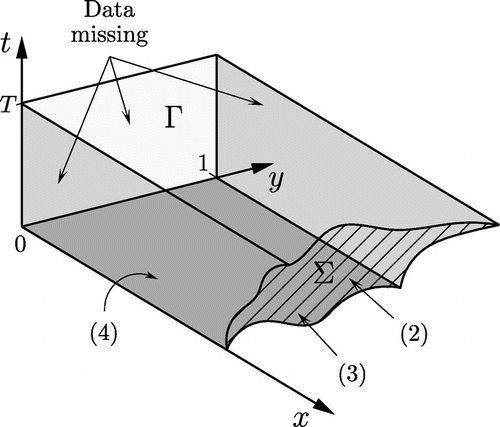
It is well-known that, in general, the inverse Stefan problem does not have a solution even if the surface $\mathrm{\Sigma }$ is analytic.[15] Further, even if a solution does exist, it will not depend continuously on the Cauchy data (2(2) $$\begin{array}{c}\hfill u=g_1\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(2) ) and (3(3) $$\begin{array}{c}\hfill k\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(3) ). As was pointed out in [23], the knowledge of the initial condition (4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) is not needed for obtaining the uniqueness of the solution of the inverse Cauchy-Stefan problem (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) )–(3(3) $$\begin{array}{c}\hfill k\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(3) ). In this paper, we shall investigate both cases when the initial condition (4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) is imposed and not.

The method of fundamental solutions (MFS)

An overview of the MFS has been given at the beginning of Section 1. The only additional point to note is that the literature on the applications of the MFS for the parabolic heat Equation (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) ) is more scarce than that for the corresponding steady-state elliptic Laplace’s equation. The reason for this is that until recently,[10] there were no density results for the set of ‘non-singular’ fundamental solutions of the heat operator, although some ideas have been previously proposed over 50 years ago, see [25].

The fundamental solution of the two-dimensional heat equation (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) ) is given by(6) $$\begin{array}{c}\hfill F(\mathbf{x},t;\mathbf{y},\mathit{\tau })=\frac{H(t-\mathit{\tau })}{4\mathit{\pi }\mathit{\alpha }(t-\mathit{\tau })}\exp (-\frac{|\mathbf{x}-\mathbf{y}{|}^2}{4\mathit{\alpha }(t-\mathit{\tau })}),\end{array}$$(6) where $H$ is the Heaviside function. At this stage, it is worth mentioning that the MFS presented in this paper can easily be extended to anisotropic transient heat conduction governed by(7) $$\begin{array}{c}\hfill \sum _{i,j=1}^2{K}_{\mathit{ij}}\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}_i\mathit{\partial }{x}_j}=\frac{\mathit{\partial }u}{\mathit{\partial }t},\end{array}$$(7) where ${(K_{\mathit{ij}})}_{i,j=1,2}$ is a symmetric and positive definite thermal diffusivity tensor, using the fundamental solution for the equation defined in (7(7) $$\begin{array}{c}\hfill \sum _{i,j=1}^2{K}_{\mathit{ij}}\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}_i\mathit{\partial }{x}_j}=\frac{\mathit{\partial }u}{\mathit{\partial }t},\end{array}$$(7) ) given by, see [26],(8) $$\begin{array}{c}\hfill F_{\mathbf{K}}(\mathbf{x},t;\mathbf{y},\mathit{\tau })=H(t-\mathit{\tau })\frac{\text{det}({\mathbf{K}}^{-1})}{4\mathit{\pi }(t-\mathit{\tau })}\exp (-\frac{{(\mathbf{x}-\mathbf{y})}^{\mathit{tr}}{\mathbf{K}}^{-1}(\mathbf{x}-\mathbf{y})}{4(t-\mathit{\tau })}),\end{array}$$(8) where ${\mathbf{K}}^{-1}$ is the inverse of the matrix $\mathbf{K}$.

The MFS for the two-dimensional transient heat Equation (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) ) in a fixed domain has been described in detail in [27]. Herein, we extend it to the inverse Stefan problem, i.e. to a problem with a moving boundary surface. According to the density results of [10], we search for an approximation to the solution of Equations (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) as a linear combination of ‘non-singular’ fundamental solutions (6(6) $$\begin{array}{c}\hfill F(\mathbf{x},t;\mathbf{y},\mathit{\tau })=\frac{H(t-\mathit{\tau })}{4\mathit{\pi }\mathit{\alpha }(t-\mathit{\tau })}\exp (-\frac{|\mathbf{x}-\mathbf{y}{|}^2}{4\mathit{\alpha }(t-\mathit{\tau })}),\end{array}$$(6) ), namely(9) $$\begin{array}{c}\hfill u_{M,N}(\mathbf{x},t)=\sum _{m=1}^{2M}\sum _{j=1}^N{c}_m^{(j)}F(\mathbf{x},t;{\mathbf{y}}_j^{(m)},{\mathit{\tau }}_m),(\mathbf{x},t)\in \overline{\mathrm{\Omega }},\end{array}$$(9) where the sources ‘singularities’ are located outside $\overline{\mathrm{\Omega }}.$ In particular, we take the instants ${({\mathit{\tau }}_m)}_{m=\overline{1,2M}}$ uniformly distributed in $(-T,T)$ as$${\mathit{\tau }}_m=\frac{(2m-2M-1)T}{2M},m=\overline{1,2M},$$and the space points ${\left({\mathbf{y}}_j^{(m)}\right)}_{j=\overline{1,N}}^{m=\overline{1,2M}}$ on a fictitious lateral boundary $\mathit{\partial }{\mathrm{\Omega }}^{\prime }(t)$, which embraces the domain $\mathrm{\Omega }(t),$ where we define$$\mathit{\partial }\mathrm{\Omega }(t)=\{(x,y)\in {\mathbb{R}}^2|0<x<s(y,-t),0<y<1\}\text{for}t\in [-T,0),$$as the mirror image of $\mathit{\partial }\mathrm{\Omega }(t)$ for $t\in [0,T].$ At the fixed time $\mathit{\tau }={\mathit{\tau }}_m$, we have$${\mathbf{y}}_j^{(m)}=\{\begin{array}{cc}(s(\frac{2j-1}{N/2},{\mathit{\tau }}_m)+h,\frac{2j-1}{N/2})\hfill & \text{for}j=\overline{1,N/4},\hfill \\ (s(1,{\mathit{\tau }}_m)-\frac{s(1,{\mathit{\tau }}_m)(2(j-N/4)-1)}{N/2},1+h)\hfill & \text{for}j=\overline{N/4+1,N/2},\hfill \\ (-h,1-\frac{2(j-N/2)-1}{N/2})\hfill & \text{for}j=\overline{N/2+1,3N/4},\hfill \\ (\frac{s(0,{\mathit{\tau }}_m)(2(j-3N/4)-1)}{N/2},-h)\hfill & \text{for}j=\overline{3N/4+1,N}.\hfill \end{array}$$The parameter $h>0$, characterizing the distance between the boundary of the solution domain and the exterior dilated boundary on which the source points are located, can be chosen such that the error between the numerical MFS solution (9(9) $$\begin{array}{c}\hfill u_{M,N}(\mathbf{x},t)=\sum _{m=1}^{2M}\sum _{j=1}^N{c}_m^{(j)}F(\mathbf{x},t;{\mathbf{y}}_j^{(m)},{\mathit{\tau }}_m),(\mathbf{x},t)\in \overline{\mathrm{\Omega }},\end{array}$$(9) ) and the data $g_1$ and $f$ on the boundary $\overline{\mathrm{\Sigma }}\cup \mathrm{\Omega }(0)$ are minimized (viz maximum principle for the heat equation). Once we have selected the $N\times 2M$ source points $\left({\mathbf{y}}_j^{(m)}\right)$ on $\bigcup _{t\in [-T,T]}\mathit{\partial }{\mathrm{\Omega }}^{\prime }(t),$ we now select the collocation points on $\overline{\mathrm{\Sigma }}\cup \mathrm{\Omega }(0)$. Let $t_i=\mathit{iT}/M_1$ for $i=\overline{0,M_1}$ be a uniform selection of time points on the interval $[0,T]$. At the fixed time $t=t_i$ we define the collocation points$${\mathbf{x}}_k^{(i)}=(s(\frac{2k-1}{N_1/2},t_i),\frac{2k-1}{N_1/2})\text{for}k=\overline{1,N_1/4}.$$Collocating the Cauchy data (2(2) $$\begin{array}{c}\hfill u=g_1\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(2) ) and (3(3) $$\begin{array}{c}\hfill k\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(3) ) at the points ${\mathbf{x}}_k^{(i)},$ we obtain $\frac{N_1}{2}\times (M_1+1)$ equations. If the initial condition (4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) is also prescribed, we additionally need to collocate it on $\mathrm{\Omega }(0)$. 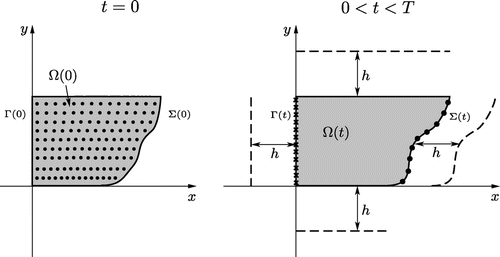At the time $t=0$, we take some regular distribution of points$${\mathbf{z}}_l^{(i)}=(\frac{l}{M_2}s(y_i,0),\frac{i}{\frac{N_1}{2}+1}),\text{for}l=\overline{1,M_2-1},i=\overline{1,N_1/2}.$$Collocating the initial condition (4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) at these points we obtain an extra $\frac{N_1}{2}\times (M_2-1)$ equations. In Figure 2, is shown an illustration of our placement of collocation and source points.

Fig. 2 Representation of the placement of the collocation ($•$) and source points (- - -), along with the unknown boundary data ($\times$).

Therefore, we get $N_1\times \frac{(M_1+M_2)}{2}$ equations with $N\times 2M$ unknowns. Taking $N_1=N$ and $M_1=M_2\ge M$, we obtain an over-determined system of linear equations which we can represent generically in the form(10) $$\begin{array}{c}\hfill \mathbf{A}\mathbf{c}=\mathbf{d},\end{array}$$(10) where $\mathbf{c}$ is the vector of unknowns $c_m^{(j)}$, $\mathbf{d}$ is the vector representing the input values of the functions $g_1,g_2$ and $f$ at the respective collocation points, and $\mathbf{A}$ is the matrix containing the values of the fundamental solution at the source and collocation points outlined above. To solve this system, it might be possible to invert the matrix $\mathbf{A}$ and solve the system directly. However, it is well-known that the MFS matrix $\mathbf{A}$ is ill-conditioned, see [28, 29], and therefore regularization is necessary, i.e. instead of (9(9) $$\begin{array}{c}\hfill u_{M,N}(\mathbf{x},t)=\sum _{m=1}^{2M}\sum _{j=1}^N{c}_m^{(j)}F(\mathbf{x},t;{\mathbf{y}}_j^{(m)},{\mathit{\tau }}_m),(\mathbf{x},t)\in \overline{\mathrm{\Omega }},\end{array}$$(9) ), we solve the modified regularized system(11) $$\begin{array}{c}\hfill ({\mathbf{A}}^{\mathit{tr}}\mathbf{A}+\mathit{\lambda }\mathbf{I})\mathbf{c}={\mathbf{A}}^{\mathit{tr}}\mathbf{d},\end{array}$$(11) where $\mathbf{I}$ is the identity matrix, the superscript ${}^{\mathit{tr}}$ denotes the transpose of a matrix, and $\mathit{\lambda }>0$ is a regularization parameter to be prescribed by trial and error, or according to some specialized criterion such as the discrepancy principle, the generalized cross-validation or the $L$-curve criterion. Herein, trial and error means that we choose the smallest $\mathit{\lambda }>0$ for which a stable (free of oscillations and unbounded behaviour) numerical solution is still obtained.

Numerical results and discussion

In this section, we investigate numerically three examples of two-dimensional inverse Stefan problems. The first two correspond to the problem (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) in which the initial condition (4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) is known and taken into account, whilst the third one corresponds to the problem (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) )–(3(3) $$\begin{array}{c}\hfill k\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(3) ) in which the initial condition (4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) is not known. The first example is taken from [30], which applied the MFS to an inverse free boundary problem, and the second and third examples have previously been considered in [18] using different approximation methods. We also take, for simplicity, the dimensional physical quantities $\mathit{\alpha }$, $k$, $\mathit{\rho }$, $\mathrm{\Lambda }$ and $T$ equal to unity.

Example 1

In this first example, we solve the problem (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) with input data given by$$s(y,t)=1-\frac{t}{10}-\frac{{(y+1)}^2}{20},$$(12) $$\begin{array}{cc}\hfill u=g_1=1,& \frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2=\sqrt{{\left(\frac{y+1}{10}\right)}^2+1}\hfill \\ \hfill & \text{on}\overline{\mathrm{\Sigma }}=\{(x,y,t)\in {\mathbb{R}}^3|y\in [0,1],t\in [0,1],x=s(y,t)\},\hfill \end{array}$$(12) (13) $$\begin{array}{cc}\hfill u(x,y,0)& =f(x,y)=x+\frac{{(y+1)}^2}{20},\hfill \\ \hfill & (x,y)\in \mathrm{\Omega }(0)=\{(x,y)\in {\mathbb{R}}^2|y\in (0,1),x\in (0,s(y,0))\},\hfill \end{array}$$(13) where the inward unit normal to the free boundary $\mathrm{\Sigma }$ is given by$$\mathit{\nu }=\frac{1}{\sqrt{{\left(\frac{y+1}{10}\right)}^2+1}}(1,\frac{y+1}{10}).$$The analytic solution of the problem (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) with the above data, is given by$$u(x,y,t)=\frac{{(y+1)}^2}{20}+x+\frac{t}{10},$$$$(x,y,t)\in \overline{\mathrm{\Omega }}=\{(x,y,t)\in {\mathbb{R}}^3|y\in [0,1],t\in [0,1],0\le x\le s(y,t)\}.$$The unknown data which are sought are given by$$u(0,y,t)=\frac{{(y+1)}^2}{20}+\frac{t}{10},\frac{\mathit{\partial }u}{\mathit{\partial }x}(0,y,t)=1,(y,t)\in (0,1)\times (0,1),$$$$u(x,0,t)=\frac{1}{20}+x+\frac{t}{10},t\in (0,1),0<x<s(0,t)=\frac{19}{20}-\frac{t}{10},$$$$u(x,1,t)=\frac{1}{5}+x+\frac{t}{10},t\in (0,1),0<x<s(1,t)=\frac{4}{5}-\frac{t}{10},$$Noise is added to the flux data on $\overline{\mathrm{\Sigma }}$ as(14) $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2(1+p\mathit{\rho }),\end{array}$$(14) where $p$ is the percentage of noise and $\mathit{\rho }$ are random variables taken from a uniform distribution in $[-1,1]$.

In Figures 3 and 4 we have produced plots of the exact solution and exact normal derivative, the MFS approximation and absolute error on the fixed boundary $x=0.$ From Figures 3(b) and 4(b) we can see that the MFS has produced accurate and stable results, even for the normal derivative, which is usually difficult to recover. This accuracy can be seen in the plots of the absolute error provided in Figures 3(c) and 4(c).

Fig. 3 (a) The exact solution, (b) the MFS approximation and (c) the absolute error for $(y,t)\in [0,1]\times [0,1],$ on the fixed boundary $x=0$. All plots obtained with $h=3$, $\mathit{\lambda }={10}^{-14}$, $M=10$, $N=40$, $M_1=20$, $N_1=40$, ($800$ collocation points and $800$ source points) and $p=0$, for Example 1.

Fig. 4 (a) The exact normal derivative, (b) the MFS approximation and (c) the absolute error for $(y,t)\in [0,1]\times [0,1],$ on the fixed boundary $x=0$. All plots obtained with $h=3$, $\mathit{\lambda }={10}^{-14}$, $M=10$, $N=40$, $M_1=20$, $N_1=40$, ($800$ collocation points and $800$ source points) and $p=0$, for Example 1.

The parameters, such as the distance $h,$ and $M,N,M_1=M_2,N_1$, in these numerical results have been chosen by trial and error; however, as was pointed out in Section 3, the parameter $h$ can be found by solving a non-linear minimization problem. Choosing the number of collocation and source points is usually a balance between having a matrix of sufficient size to generate accurate MFS approximations, the conditioning of this matrix, and the running time of the programme. In the authors’ study of the one-dimensional Stefan problem in [1], a typical value of the condition number was $\mathcal{O}({10}^{28})$; however, the condition number of the matrix $A$ used in producing Figures 3 and 4 is $\mathcal{O}({10}^{59})$ and, in Figures 10(b) and 10(c), it can become as high as $\mathcal{O}({10}^{118})$. Therefore, we see that the condition number for the two-dimensional problem has increased compared to the one-dimensional case, affecting the solution more when noise is added to the boundary data, and making the appropriate choice of the Tikhonov regularization parameter $\mathit{\lambda }$ in (11(11) $$\begin{array}{c}\hfill ({\mathbf{A}}^{\mathit{tr}}\mathbf{A}+\mathit{\lambda }\mathbf{I})\mathbf{c}={\mathbf{A}}^{\mathit{tr}}\mathbf{d},\end{array}$$(11) ) even more important.

Additionally, in Figures 5 and 6, we have attempted to reconstruct the data along the boundaries $y=0$ and $y=1$, and again the absolute error plots in Figures 5(c) and 6(c) show the very good accuracy of the proposed method.

Fig. 5 (a) The exact solution, (b) the MFS approximation and (c) the absolute error for $(x,t)\in [0,s(0,t)]\times [0,1],$ on $y=0$. All plots obtained with $h=3$, $\mathit{\lambda }={10}^{-14}$, $M=10$, $N=40$, $M_1=20$, $N_1=40$, ($800$ collocation points and $800$ source points) and $p=0$, for Example 1.

Fig. 6 (a) The exact solution, (b) the MFS approximation and (c) the absolute error for $(x,t)\in [0,s(1,t)]\times [0,1],$ on $y=1$. All plots obtained with $h=3$, $\mathit{\lambda }={10}^{-14}$, $M=10$, $N=40$, $M_1=20$, $N_1=40$, ($800$ collocation points and $800$ source points) and $p=0$, for Example 1.

Figures 7(a)–7(d) contain plots of the absolute error when we have added $p=5\%$ noise to the flux data in (12(12) $$\begin{array}{cc}\hfill u=g_1=1,& \frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2=\sqrt{{\left(\frac{y+1}{10}\right)}^2+1}\hfill \\ \hfill & \text{on}\overline{\mathrm{\Sigma }}=\{(x,y,t)\in {\mathbb{R}}^3|y\in [0,1],t\in [0,1],x=s(y,t)\},\hfill \end{array}$$(12) ). These plots show that the error is of the same order as the amount of noise.

Fig. 7 Plots of the absolute error of the exact solution and the MFS approximation for (a) $(y,t)\in [0,1]\times [0,1]$ on $x=0$, (c) $(x,t)\in [0,s(0,t)]\times [0,1]$ on $y=0$, (d) $(x,t)\in [0,s(1,t)]\times [0,1]$ on $y=1$, and (b) the absolute error of the normal derivative and the MFS approximation for $(y,t)\in [0,1]\times [0,1]$ on $x=0$. All plots were obtained with $h=3$, $\mathit{\lambda }={10}^{-6}$, $M=10$, $N=40$, $M_1=20$, $N_1=40$, ($800$ collocation points and $800$ source points) and $p=5\%$, for Example 1.

Next, we experiment with a different arrangement of collocation points on the initial base. This time we equally distribute points on a rectangle, which contains $\mathrm{\Omega }(0)$, and remove any points not in $\mathrm{\Omega }(0)$, see Figure 8 for a representation of this placement. In Figures 9(a) and 9(b), we plot the absolute error of the exact solution and normal derivative, respectively, and the MFS approximation when we have changed the placement of the collocation points on the initial base.

Fig. 8 Representation of an alternative placement of the collocation points ($•$); on the initial base we simply equally distribute them over a larger rectangular domain, ignoring points ($\circ$) outside $\mathrm{\Omega }(0)$.

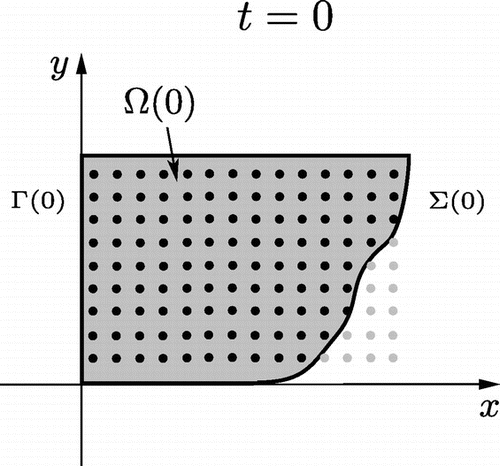
Comparing Figures 7(a) and 7(b) to Figures 9(a) and 9(b) we find that the positioning of the collocation points on $\mathrm{\Omega }(0)$ changes the approximation very little. In fact, we find that the boundary data on the free boundary plays more of a part in the approximation than the initial data, which is not even required, see Example 3.

Fig. 9 Plots of the absolute error for (a) the exact solution and the MFS approximation and (b) the exact normal derivative and the MFS approximation, for $(y,t)\in [0,1]\times [0,1]$ on $x=0$, when the collocation points on the initial base at time $t=0$ have been equally distributed. Both plots obtained with $h=3$, $\mathit{\lambda }={10}^{-6}$, $M=10$, $N=40$, $M_1=20$, $N_1=40$, ($780$ collocation points and $800$ source points) and $p=5\%$, for Example 1.

Lastly, in this example we provide an analysis in the form of error plots, when changing the parameters $h,M,N,M_1,N_1$ and the Tikhonov regularization parameter $\mathit{\lambda }$. In Figure 10(a) we have plotted the maximum absolute error of the exact solution and the MFS approximation over $(y,t)\in [0,1]\times [0,1]$ on $x=0$ for varying values of $h$ and $\mathit{\lambda }$. We observe that the best results are produced for $h\in [2,4]$ and for very small values of $\mathit{\lambda }$ (near machine precision). Figures 10(b) and 10(c) shows that as all of $M,N,M_1,N_1$ increase, so does the accuracy of the approximation; however, MATLAB was only able to produce plots for values up to $M=24,N=48,M_1=48,$ and $N_1=48$.

Fig. 10 Plots of the maximum absolute error of the exact solution and the MFS approximation over $(y,t)\in [0,1]\times [0,1]$ on $x=0$, for (a) $(h,\mathit{\lambda })\in (0,6]\times [{10}^{-15},{10}^{-1}]$, obtained with $M=10$, $N=40$, $M_1=20$ and $N_1=40$, ($800$ collocation points and $800$ source points), (b) $(M_1,N_1)\in [8,48]\times [8,48]$ ($N_1\times M_1$ collocation points and $N\times 2M$ ($N=N_1$ and $M_1=2M$) source points), obtained with $h=3$ and $\mathit{\lambda }={10}^{-14}$, and (c) $(h,M_1)\in (0,6]\times [8,48]$ ($N_1\times M_1$ ($N_1=M_1$) collocation and source points), obtained with $\mathit{\lambda }={10}^{-14}$. All plots obtained with $p=0$, for Example 1.

 

Example 2

We consider solving the problem (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) with the input data given by$$s(y,t)=\frac{y+1}{2}+\frac{5t}{4},(y,t)\in (0,1)\times (0,1),$$(15) $$\begin{array}{cc}\hfill u=g_1=0,& \frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2=-\frac{1}{|\nabla \mathrm{\Phi }|}\frac{\mathit{\partial }\mathrm{\Phi }}{\mathit{\partial }t}=\sqrt{5/4}\hfill \\ \hfill & \text{on}\overline{\mathrm{\Sigma }}=\{(x,y,t)\in {\mathbb{R}}^3|y\in [0,1],t\in [0,1],x=s(y,t)\},\hfill \end{array}$$(15) $$u(x,y,0)=f(x,y)=\exp (-x+\frac{y+1}{2})-1,$$$$(x,y)\in \mathrm{\Omega }(0)=\{(x,y)\in {\mathbb{R}}^2|y\in (0,1),x\in (0,s(y,0))\},$$where the inward unit normal to the free boundary $\mathrm{\Sigma }$ is given by $\mathit{\nu }=-\frac{\nabla \mathrm{\Phi }}{|\nabla \mathrm{\Phi }|}=\frac{1}{\sqrt{5/4}}(-1,\frac{1}{2})$ and $\mathrm{\Phi }(x,y,t)=x-s(y,t)$. In [18] the minus sign in the data $g_2$ is missing, most likely due to the fact that the outward unit normal has been used although it was stated that the normal should be pointing inwards.

The analytic solution of the problem (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) with the above data is given by(16) $$\begin{array}{cc}\hfill & u(x,y,t)=\exp (-x+\frac{y+1}{2}+\frac{5t}{4})-1,\hfill \\ \hfill & (x,y,t)\in \overline{\mathrm{\Omega }}=\{(x,y,t)\in {\mathbb{R}}^3|y\in [0,1],t\in [0,1],0\le x\le s(y,t)\}.\hfill \end{array}$$(16) The unknown data which is sought is given by(17) $$\begin{array}{cc}\hfill u(0,y,t)=\exp (\frac{y+1}{2}+\frac{5t}{4})-1,\frac{\mathit{\partial }u}{\mathit{\partial }x}(0,y,t)& =-\exp (\frac{y+1}{2}+\frac{5t}{4}),\hfill \\ \hfill & (y,t)\in (0,1)\times (0,1).\hfill \end{array}$$(17) $$u(x,0,t)=\exp (-x+\frac{1}{2}+\frac{5t}{4})-1,t\in (0,1),0<x<s(0,t)=\frac{1}{2}+\frac{5t}{4}.$$$$u(x,1,t)=\exp (-x+1+\frac{5t}{4})-1,t\in (0,1),0<x<s(1,t)=1+\frac{5t}{4}.$$Noise is applied to the flux data similar to (12(12) $$\begin{array}{cc}\hfill u=g_1=1,& \frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2=\sqrt{{\left(\frac{y+1}{10}\right)}^2+1}\hfill \\ \hfill & \text{on}\overline{\mathrm{\Sigma }}=\{(x,y,t)\in {\mathbb{R}}^3|y\in [0,1],t\in [0,1],x=s(y,t)\},\hfill \end{array}$$(12) ).

As in Example 1, we have plotted in this example the MFS approximation of the exact solution on $x=0$, $y=0$ and $y=1$, in Figures 11, 13 and 14, respectively, and the MFS approximation of the exact normal derivative on $x=0$ in Figure 12. The absolute errors in these figures seem quite large; however, when compared to the size of the data being reconstructed and the ill-posedness of the problem, we believe that the approximation is good, with all results being stable when noise is not applied to the flux data. We note however, that the error increases as $t$ increases, which is a usual feature when solving inverse heat problems, and the fact that $s(x,t)$ is increasing with respect to $x$ and $t$ in this example (in contrast to Example 1, where it was decreasing).

Fig. 11 (a) The exact solution, (b) the MFS approximation and (c) the absolute error for $(y,t)\in [0,1]\times [0,1]$, on the fixed boundary $x=0$. All plots obtained with $h=3$, $\mathit{\lambda }={10}^{-14}$, $M=10$, $N=40$, $M_1=20$, $N_1=40$, ($800$ collocation points and $800$ source points) and $p=0$, for Example2.

Fig. 12 (a) The exact normal derivative, (b) the MFS approximation and (c) the absolute error for $(y,t)\in [0,1]\times [0,1],$ on the fixed boundary $x=0$. All plots obtained with $h=3$, $\mathit{\lambda }={10}^{-14}$, $M=10$, $N=40$, $M_1=20$, $N_1=40$, ($800$ collocation points and $800$ source points) and $p=0$, for Example 2.

Fig. 13 (a) The exact solution, (b) the MFS approximation and (c) the absolute error for $(x,t)\in [0,s(0,t)]\times [0,1],$ on $y=0$. All plots obtained with $h=3$, $\mathit{\lambda }={10}^{-14}$, $M=10$, $N=40$, $M_1=20$, $N_1=40$, ($800$ collocation points and $800$ source points) and $p=0$, for Example 2.

Fig. 14 (a) The exact solution, (b) the MFS approximation and (c) the absolute error for $(x,t)\in [0,s(1,t)]\times [0,1],$ on $y=1$. All plots obtained with $h=3$, $\mathit{\lambda }={10}^{-14}$, $M=10$, $N=40$, $M_1=20$, $N_1=40$, ($800$ collocation points and $800$ source points) and $p=0$, for Example 2.

Next we applied $p=5\%$ noise to the flux data (12(12) $$\begin{array}{cc}\hfill u=g_1=1,& \frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2=\sqrt{{\left(\frac{y+1}{10}\right)}^2+1}\hfill \\ \hfill & \text{on}\overline{\mathrm{\Sigma }}=\{(x,y,t)\in {\mathbb{R}}^3|y\in [0,1],t\in [0,1],x=s(y,t)\},\hfill \end{array}$$(12) ). We have plotted the absolute error of the best, average and least accurate MFS approximations after ten trials in Figures 15(a), 15(b) and 15(c), respectively. We find that in this example that the inclusion of noise produced very large maximum errors, at the final time point $T$, however the mean error (used to determine the ordering of the plots) is reasonable, see the caption of Figure 15, and the MFS approximation still matches the shape of the exact solution.

Fig. 15 Plots of the absolute error for $(y,t)\in [0,1]\times [0,1]$ on $x=0$, for the (a) best (mean error: $0.1591$), (b) average (mean error: $0.2005$) and (c) least (mean error: $0.2360$) accurate MFS approximations from ten different sets of noisy data with noise level $p=5\%$. All plots obtained with $h=3$, $\mathit{\lambda }={10}^{-7}$, $M=10$, $N=40$, $M_1=20$ and $N_1=40$, ($800$ collocation points and $800$ source points), for Example 2.

We provide an analysis, similar to the previous example, in the form of error plots, and find that results are also similar. In Figure 16(a) we have plotted the maximum absolute error over $(y,t)\in [0,1]\times [0,1]$ on $x=0$ for varying values of $h$ and $\mathit{\lambda }$, and again find that the best results are produced for $h\in [2,4]$ Figures 16(b) and 16(c) also show that increasing the size of $M,N,M_1,N_1$ improves the accuracy of the approximation.

Fig. 16 Plots of the maximum absolute error of the exact solution and the MFS approximation over $(y,t)\in [0,1]\times [0,1]$ on $x=0$, for (a) $(h,\mathit{\lambda })\in (0,6]\times [{10}^{-15},{10}^{-1}]$, obtained with $M=10$, $N=40$, $M_1=20$ and $N_1=40$, ($800$ collocation points and $800$ source points), (b) $(M_1,N_1)\in [8,48]\times [8,48]$ ($N_1\times M_1$ collocation points and $N\times 2M$ ($N=N_1$ and $M_1=2M$) source points), obtained with $h=3$ and $\mathit{\lambda }={10}^{-14}$, and (c) $(h,M_1)\in (0,6]\times [8,48]$ ($N_1\times M_1$ ($N_1=M_1$) collocation and source points), obtained with $\mathit{\lambda }={10}^{-14}$. All plots obtained with $p=0$, for Example 2.

Fig. 17 A plot of the MFS approximation for $(x,t)=(0,0.7)$, and for $y\in [0,1]$. The plot was obtained with $h=3$, $\mathit{\lambda }={10}^{-14}$, $M=10$, $N=40$, $M_1=20$, $N_1=40$ ($800$ collocation points and $800$ source points) and $p=0$, for Example 3.

Fig. 18 Plots of the MFS approximation for (a) $(y,t)\in [0,1]\times [0,1]$ on $x=0$, (b) $(x,t)\in [0,s(0,t)]\times [0,1]$ on $y=0$, (c) $(x,t)\in [0,s(1,t)]\times [0,1]$ on $y=1$, and (d) the MFS approximation of the normal derivative for $(y,t)\in [0,1]\times [0,1]$ on $x=0$. All plots obtained with $h=3$, $\mathit{\lambda }={10}^{-14}$, $M=10$, $N=40$, $M_1=40$, $N_1=40$ ($820$ collocation points and $800$ source points) and $p=0$, for Example 3.

Fig. 19 Plots of the MFS approximation for (a) $(y,t)\in [0,1]\times [0,1]$ on $x=0$, (c) $(x,t)\in [0,s(0,t)]\times [0,1]$ on $y=0$, (d) $(x,t)\in [0,s(1,t)]\times [0,1]$ on $y=1$, and (b) the MFS approximation of the normal derivative for $(y,t)\in [0,1]\times [0,1]$ on $x=0$. All plots obtained with $h=3$, $\mathit{\lambda }={10}^{-8}$, $M=10$, $N=40$, $M_1=40$, $N_1=40$ ($820$ collocation points and $800$ source points) and $p=5\%$, for Example 3.

 

Example 3

In the third example, the initial condition (4(4) $$\begin{array}{c}\hfill u=f\text{on}\mathrm{\Omega }(0).\end{array}$$(4) ) is not specified. In this case for the system of Equations (10(10) $$\begin{array}{c}\hfill \mathbf{A}\mathbf{c}=\mathbf{d},\end{array}$$(10) ), we need to take$$\frac{N_1}{2}\times (M_1+1)\ge N\times 2M.$$The input data for the problem (1(1) $$\begin{array}{c}\hfill \mathit{\alpha }{\nabla }^{2}u=\frac{\mathit{\partial }u}{\mathit{\partial }t}\text{in}\mathrm{\Omega },\end{array}$$(1) )–(3(3) $$\begin{array}{c}\hfill k\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2\text{on}\overline{\mathrm{\Sigma }}\end{array}$$(3) ) are given by$$s(y,t)=\frac{{(y+1/2)}^2}{\ln (2)}\ln (1+t),(y,t)\in (0,1)\times (0,1),$$$$u=g_1=0,\frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2=-\frac{1}{|\nabla \mathrm{\Phi }|}\frac{\mathit{\partial }\mathrm{\Phi }}{\mathit{\partial }t}=\frac{{(2y+1)}^2}{4(1+t)\sqrt{{\ln }^2(2)+{(2y+1)}^2{\ln }^2(1+t)}}\text{on}\overline{\mathrm{\Sigma }},$$ where $\mathit{\nu }=-\frac{\nabla \mathrm{\Phi }}{|\nabla \mathrm{\Phi }|}$ and $\mathrm{\Phi }(x,y,t)=x-s(y,t).$ Noise is applied to the flux data, as in (12(12) $$\begin{array}{cc}\hfill u=g_1=1,& \frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2=\sqrt{{\left(\frac{y+1}{10}\right)}^2+1}\hfill \\ \hfill & \text{on}\overline{\mathrm{\Sigma }}=\{(x,y,t)\in {\mathbb{R}}^3|y\in [0,1],t\in [0,1],x=s(y,t)\},\hfill \end{array}$$(12) ).

There is no available analytical solution for this example, but we can compare our results with the results of Figures 1–4 from [18].

In Figure 17 we plot the MFS approximation for $(x,t)=(0,0.7)$, and for $y\in [0,1]$. Comparing Figure 1 of [18] to Figure 17, we find that the plots for $n=25$ and $n=49$ in [18] suggest convergence to the result we have in Figure 17, however our result differs from the approximation generated for $n=64$ in [18]. It is noted in the text of [18] that no regularization constraint was used and that the approximation does not converge uniformly, therefore, this might explain the difference in the results for $n=64$.

Figure 18 contains plots of the MFS approximation for the exact solution and exact normal derivative. We observe similarities when comparing the plots in Figure 18 to the plots produced in [18]; however, in [18] a large spike is produced near $(x,y,t)=(0,0,1)$. The data do not suggest the presence of a singularity at this point, and we are led to conclude that the difficulty of the numerical method in [18] to converge uniformly has produced results with a large error near $(x,y,t)=(0,0,1)$.

To test the stability in this example we have again included $p=5\%$ noise to the flux data (12(12) $$\begin{array}{cc}\hfill u=g_1=1,& \frac{\mathit{\partial }u}{\mathit{\partial }\mathit{\nu }}=g_2=\sqrt{{\left(\frac{y+1}{10}\right)}^2+1}\hfill \\ \hfill & \text{on}\overline{\mathrm{\Sigma }}=\{(x,y,t)\in {\mathbb{R}}^3|y\in [0,1],t\in [0,1],x=s(y,t)\},\hfill \end{array}$$(12) ), and in Figure 19 we have produced plots of the MFS approximation to the exact solution and exact normal derivative. To better observe this stability, we provide the values of the mean and maximum differences between the MFS approximations obtained for $p=0$ and $p=5\%$ in Table 1.

Table 1 Mean and maximum differences between the MFS approximations obtained for $p=0$ and $5\%$.

Figures to compare	18(a) & 19(a)	18(b) & 19(b)	18(c) & 19(c)	18(d) & 19(d)
Mean difference	$8.7473\times {10}^{-4}$	$0.0219$	$0.0034$	$1.6608\times {10}^{-4}$
Max difference	$0.0967$	$0.4058$	$0.0246$	$0.0967$

 

Conclusions

We have extended the MFS of [1] to the two-dimensional inverse Stefan problem, i.e. to the problem of reconstructing boundary (and additionally initial) data from the knowledge of the moving surface and given Cauchy data on this surface. The Tikhonov regularization was incorporated to solve the linear system obtained from the MFS approximation in a stable way. Three examples were numerically investigated both when the initial data was specified and not specified, with noise added to the input flux data.

It was found that accurate and stable numerical results were obtained in all cases with small computational effort. The dependence of the results on the placement of the source points and the regularizing parameter were investigated, as well as on the collocation arrangement on the initial base. Future work will concern possible extensions to three-dimensions.

Acknowledgments

The third author would like to thank the financial support received from the EPSRC. The comments and suggestions made by the referees are gratefully acknowledged.