Numerical methods for solving a boundary-value inverse heat conduction problem

Abstract

This paper considers the boundary-value inverse heat conduction problem with steady boundary. To solve this problem, different approaches based on the Laplace and Fourier transforms are proposed. Application of the Laplace transform makes it possible to obtain an operator equation describing the explicit dependence of the desired boundary-value function on the initial data at the other boundary. This approach to solving the problem is used for the first time. The method based on the direct and inverse Fourier transforms with respect to the time variable provides stable solutions. The estimation of error of these solutions is the best with respect to the order. The range of application of each of the proposed methods and the stability of the solutions obtained by these methods was evaluated by a computational experiment.

Keywords:

• heat conduction equation
• Fourier transform
• Laplace transform
• regularization method

AMS Subject Classifications:

• 58J35
• 35R30
• 80M30

Introduction

In experimental studies of non-stationary thermal processes, it is often impossible to directly measure the desired physical quantity, and its characteristics are therefore found from the results of indirect measurements. In this situation, one way to determine the desired physical quantity is to solve boundary-value inverse heat conduction problems. This paper presents methods for solving a fixed-boundary inverse heat conduction problem based on the Laplace and Fourier transforms.

The use of direct and inverse Laplace transforms to solve inverse heat conduction problems is of great interest. For example, Kolodziej et al. [1] and Cialkowski and Grysa [2] used the Laplace transform to solve the Cauchy problem. Monde et al. [3] applied the Laplace transform to the two-dimensional problem.

In existing approaches, the equations resulting from the Laplace transform are usually solved by regularization methods, and the inverse transform is then applied to the regularized solution. However, the main difficulty in using the inverse Laplace transform is that this operation is highly unstable.

In this paper, a different approach is proposed. In this approach, the explicit dependence of the boundary function on one of the boundaries on the known data on the other boundary is described by an operator equation, and regularization methods are then used to solve this equation. This eliminates the need to perform the unstable procedure of numerical inversion of the Laplace transform in the computational process. The proposed method was used in a computational experiment to obtain a numerical solution of the inverse problem.

The Fourier transform with respect to the space variable has been widely used to solve the inverse heat conduction problems. In particular, Jonas and Louis [4] applied the Fourier transform and a stabilizing functional to obtain regularized solutions. Prud’homme and Hguyen [5] make use of the Fourier transform and a conjugate gradient for the purpose of regularization of solutions and evaluation of their convergence. Fu et al. [6] and Qian and Feng [7] took the direct Fourier transform with respect to the space variable and, as a result, obtained the Fourier transform of the solution of the inverse boundary-value problem.

The approach proposed in this paper is to use the direct and inverse Fourier transforms with respect to the time variable. The regularization algorithm is based on the projection regularization method for the direct and inverse Fourier transforms. This method provides regularized solutions with the best possible error bounds. This property provided the basis for comparative analysis of the solutions obtained by the Laplace and Fourier transform methods.

The developed methods were employed to perform a computational experiment. The objectives of this experiment were to test the performance of the algorithms and to evaluate the errors of the regularized solutions provided by each approach.

Statement of the problem

We consider the following inverse heat conduction problem:(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) (2) $$\begin{array}{c}\hfill u(x,0)=0,u(0,t)=0,x\in (0,1),t⩾0,\end{array}$$(2) (3) $$\begin{array}{c}\hfill u_x(0,t)=g\left(t\right),t⩾0.\end{array}$$(3) In this problem, it is required to find the boundary value of the function:(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) Let $g\in C^{2+\mathit{\eta }}[0,T]$ for all $T>0$ and there exists constants $M,m$ such that $\parallel g(t)\parallel \le M{e}^{\mathit{mt}}$ for all $t\in [0,T]$ for any $T>0$, where $C^{2+\mathit{\eta }}[0,T]$ is the Hölder space space and $\mathit{\eta }\in (0,1)$.

It is known that for $g\left(t\right)=g_0\left(t\right)$, there exists an exact solution $u(1,t)={\mathit{\varphi }}_0\left(t\right)$. However, instead of $g_0$ we are given some approximations $g_{\mathit{\delta }}$ and an error level $\mathit{\delta }>0$, such that $\parallel g_{\mathit{\delta }}-g_0\parallel ⩽\mathit{\delta }$. Using these initial data, it is required to construct a regularized solution of the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ).

Uniqueness of the solution of the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ) was proved in [8]. In this paper, we propose methods based on Laplace and Fourier transforms to solve the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ).

Construction of the operator equation using the Laplace transform

The problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ) can be reduced to an integral equation. To do this, we find the solution of the direct problem, assuming that the required function $u(1,t)=\mathit{\varphi }\left(t\right)$ is known. Thus, we consider the following direct problem:(5) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(5) (6) $$\begin{array}{c}\hfill u(x,0)=0,x\in (0,1),\end{array}$$(6) (7) $$\begin{array}{c}\hfill u(0,t)=0,u(1,t)=\mathit{\varphi }\left(t\right),t⩾0.\end{array}$$(7) It is required in this direct problem to find the function $u(x,t)$ for $(x,t)\in (0,1)\times (0,\infty )$.

Suppose that there exist such constants $C>0$ and ${\mathit{\beta }}_0⩾0$ that for any $x\in [0,1]$ and for any $t\in [0,\infty )$ the following inequality holds $\left|u(x,t)\right|⩽{\mathit{Ce}}^{{\mathit{\beta }}_{0}t}$. In addition, we assume that the function $\mathit{\varphi }\left(t\right)$ satisfies the Dirichlet conditions for $t\in [0,T]$ for any $T\in [0,\infty ]$. Then, we can apply the Laplace transform [9] to function $u(1,t)$ for solving of the direct problem (5(5) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(5) )–(7(7) $$\begin{array}{c}\hfill u(0,t)=0,u(1,t)=\mathit{\varphi }\left(t\right),t⩾0.\end{array}$$(7) ). Such approach allows obtain an equation relating $u(1,t)=\mathit{\varphi }\left(t\right)$ and $u_x(0,t)=g\left(t\right)$.

Let $\overline{u}(x,p)$ be the Laplace transform of the function $u(x,t)$, and $\overline{\mathit{\varphi }}(p)$ be the Laplace transform of the function $u(1,t)=\mathit{\varphi }(t)$. Then, the operator representation of the problem (5(5) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(5) )–(7(7) $$\begin{array}{c}\hfill u(0,t)=0,u(1,t)=\mathit{\varphi }\left(t\right),t⩾0.\end{array}$$(7) ) is given by:$$\begin{array}{c}\hfill \frac{d^2\overline{u}}{{\mathit{dx}}^2}-p\overline{u}=0,\end{array}$$$$\overline{u}(0,p)=0,\overline{u}(1,p)=\overline{\mathit{\varphi }}\left(p\right).$$The solution of this problem has the following form:(8) $$\begin{array}{c}\hfill \overline{u}(x,p)=\overline{\mathit{\varphi }}\left(p\right)\frac{\mathit{sh}\left(\sqrt{p}x\right)}{\mathit{sh}\left(\sqrt{p}\right)}.\end{array}$$(8)

Theorem 3.1

The function $\overline{\mathit{\psi }}(x,p)=\frac{\mathit{sh}\left(\sqrt{p}x\right)}{\mathit{sh}\left(\sqrt{p}\right)}$ can be represented as:(9) $$\begin{array}{c}\hfill \overline{\mathit{\psi }}(x,p)=x+\frac{2}{\mathit{\pi }}\sum _{n=1}^{\infty }\frac{{(-1)}^n}{n}\sin \left(\mathit{\pi }\mathit{nx}\right)\frac{p}{p+n^2{\mathit{\pi }}^2}.\end{array}$$(9)

Proof

Because the function $\overline{\mathit{\psi }}(x,p)$ has simple poles at the points $q_n=\sqrt{p}=\pm i\mathit{\pi }n$, $n=1,2,3\dots$ and the point $p=0$ is a regular point of the function $\overline{\mathit{\psi }}(x,p)$ and$$\underset{p\to 0}{\lim }\frac{\mathit{sh}\left(\sqrt{p}x\right)}{\mathit{sh}\left(\sqrt{p}\right)}=x,$$it follows that the function $\overline{\mathit{\psi }}(x,p)$ is meromorphic.

Consider a system of contours $|p|=\mathit{\pi }(n+\frac{1}{2})$. Each contour contains only a finite number of poles and exists certain number $K$ such that for any contour:(10) $$\begin{array}{c}\hfill |\overline{\mathit{\psi }}(x,p)|\le K.\end{array}$$(10) Hence, we obtain the boundedness of the function for any contour.

Thus, for $\overline{\mathit{\psi }}(x,p)$, we can use the Mittag–Leffler theorem on the expansion of functions in series of simple fractions, according to which the function $\overline{\mathit{\psi }}(x,p)$ may be represented as the series:(11) $$\begin{array}{c}\hfill \overline{\mathit{\psi }}(x,p)=h(x,p)+\sum _{n=1}^{\infty }(g_n(x,p)-h_n(x,p)),\end{array}$$(11) where $g_n(x,p)$ is the main part of the expansion of the function $\overline{\mathit{\psi }}(x,p)$ at the poles $q_n$ and $h(x,p)$ and $h_n(x,p)$ are given by the relations:(12) $$\begin{array}{c}\hfill h(x,p)=\sum _{k=0}^{m_n}\frac{{\overline{\mathit{\psi }}}^{(k)}(0)}{k!}{p}^k,\end{array}$$(12) (13) $$\begin{array}{c}\hfill h_n(x,p)=\sum _{k=0}^{m_n}\frac{g^{(k)}(0)}{k!}{p}^k.\end{array}$$(13) Since the estimate (10(10) $$\begin{array}{c}\hfill |\overline{\mathit{\psi }}(x,p)|\le K.\end{array}$$(10) ) does not depend on $p$, the function (11(11) $$\begin{array}{c}\hfill \overline{\mathit{\psi }}(x,p)=h(x,p)+\sum _{n=1}^{\infty }(g_n(x,p)-h_n(x,p)),\end{array}$$(11) ) becomes:(14) $$\begin{array}{c}\hfill \overline{\mathit{\psi }}(x,p)=\overline{\mathit{\psi }}(x,0)+\sum _{n=1}^{\infty }(g_n(x,p)-g_n(x,0))=x+\sum _{n=1}^{\infty }(g_n(x,p)-g_n(x,0)),\end{array}$$(14) Cauchy’s theorem implies that$$g_n(x,p)=\frac{2·{(-1)}^n·\mathit{sh}(\pm i\mathit{\pi }nx)·(\pm i\mathit{\pi }n)}{p+{\mathit{\pi }}^2{n}^2},$$$$g_n(x,0)=\frac{2·{(-1)}^n·\mathit{sh}(\pm i\mathit{\pi }nx)·(\pm i)}{\mathit{\pi }n}$$and, hence,$$g_n(x,p)-g_n(x,0)=\frac{2·{(-1)}^n·\sin (\mathit{\pi }nx)}{\mathit{\pi }n}·\frac{p}{p+{\mathit{\pi }}^2{n}^2}.$$Substitution of the last relation into (14(14) $$\begin{array}{c}\hfill \overline{\mathit{\psi }}(x,p)=\overline{\mathit{\psi }}(x,0)+\sum _{n=1}^{\infty }(g_n(x,p)-g_n(x,0))=x+\sum _{n=1}^{\infty }(g_n(x,p)-g_n(x,0)),\end{array}$$(14) ) yields:$$\overline{\mathit{\psi }}(x,p)=x+\frac{2}{\mathit{\pi }}\sum _{n=1}^{\infty }\frac{{(-1)}^n}{n}\sin \left(\mathit{\pi }\mathit{nx}\right)\frac{p}{p+n^2{\mathit{\pi }}^2}.$$Thus, the theorem is proved. $\square$

Applying the inverse Laplace transform to both the sides of (8(8) $$\begin{array}{c}\hfill \overline{u}(x,p)=\overline{\mathit{\varphi }}\left(p\right)\frac{\mathit{sh}\left(\sqrt{p}x\right)}{\mathit{sh}\left(\sqrt{p}\right)}.\end{array}$$(8) ), using (9(9) $$\begin{array}{c}\hfill \overline{\mathit{\psi }}(x,p)=x+\frac{2}{\mathit{\pi }}\sum _{n=1}^{\infty }\frac{{(-1)}^n}{n}\sin \left(\mathit{\pi }\mathit{nx}\right)\frac{p}{p+n^2{\mathit{\pi }}^2}.\end{array}$$(9) ), the convolution theorem [9] and the presence multiplier p in the second part in (), we obtain:(15) $$\begin{array}{c}\hfill u(x,t)=x\mathit{\varphi }(t)+\frac{2}{\mathit{\pi }}\frac{d}{\mathit{dt}}\sum _{n=1}^{\infty }\frac{{(-1)}^n}{n}\sin (\mathit{\pi }\mathit{nx})e^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }.\end{array}$$(15)

Theorem 3.2

Suppose that there exist such constant $C>0$ and ${\mathit{\beta }}_0⩾0$ that for any $t\in [0,\infty )$ holds $\left|\mathit{\varphi }\left(t\right)\right|⩽{\mathit{Ce}}^{{\mathit{\beta }}_{0}t}$. In addition, we assume that the function $\mathit{\varphi }\left(t\right)$ satisfies the Dirichlet conditions for $t\in [0,T]$ for any $T\in [0,\infty ]$. Then, the series (15(15) $$\begin{array}{c}\hfill u(x,t)=x\mathit{\varphi }(t)+\frac{2}{\mathit{\pi }}\frac{d}{\mathit{dt}}\sum _{n=1}^{\infty }\frac{{(-1)}^n}{n}\sin (\mathit{\pi }\mathit{nx})e^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }.\end{array}$$(15) ) converges all $x\in [0,1),t\in [0,\infty )$ and for $x\in [0,1)$ the solution $u(x,t)$ of the problem (5(5) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(5) )–(7(7) $$\begin{array}{c}\hfill u(0,t)=0,u(1,t)=\mathit{\varphi }\left(t\right),t⩾0.\end{array}$$(7) ) has the following form:(16) $$\begin{array}{c}\hfill u(x,t)=2\mathit{\pi }\sum _{n=1}^{\infty }{(-1)}^{n+1}n\sin \left(\mathit{\pi }\mathit{nx}\right)e^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }.\end{array}$$(16)

Proof

Because the function $\mathit{\varphi }\left(t\right)$ satisfies the Dirichlet conditions, using the properties of functionals in linear normed spaces [11] and the estimate of the quantity $|\mathit{\varphi }(t)|$, for $a_n=\frac{|\sin (\mathit{\pi }\mathit{nx})|}{n}{e}^{-{\mathit{\pi }}^2{n}^{2}t}|\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }|$ we obtain:$$a_n⩽\frac{\left|\sin \left(\mathit{\pi }\mathit{nx}\right)\right|}{n}{e}^{-{\mathit{\pi }}^2{n}^{2}t}\frac{{\mathit{Ce}}^{({\mathit{\pi }}^2{n}^2+{\mathit{\beta }}_0)t}}{({\mathit{\pi }}^2{n}^2+{\mathit{\beta }}_0)}⩽\frac{\left|\sin \left(\mathit{\pi }\mathit{nx}\right)\right|{\mathit{Ce}}^{{\mathit{\beta }}_{0}t}}{n({\mathit{\pi }}^2{n}^2+{\mathit{\beta }}_0)}⩽\frac{{\mathit{Ce}}^{{\mathit{\beta }}_{0}t}}{{\mathit{\pi }}^2{n}^3}.$$The series$$\sum _{n=1}^{\infty }\frac{{\mathit{Ce}}^{{\mathit{\beta }}_{0}t}}{{\mathit{\pi }}^2{n}^3}=\frac{{\mathit{Ce}}^{{\mathit{\beta }}_{0}t}}{{\mathit{\pi }}^2}\sum _{n=1}^{\infty }\frac{1}{n^3}$$converges and the sum of this series is of the form $S=\frac{{\mathit{Ce}}^{{\mathit{\beta }}_{0}t}}{{\mathit{\pi }}^2}\mathit{\zeta }\left(3\right)$, where $\mathit{\zeta }\left(q\right)$ is the Riemann zeta function and $\mathit{\zeta }\left(3\right)\approx 1,20206$, [12]. Thus, the convergence of the series (15(15) $$\begin{array}{c}\hfill u(x,t)=x\mathit{\varphi }(t)+\frac{2}{\mathit{\pi }}\frac{d}{\mathit{dt}}\sum _{n=1}^{\infty }\frac{{(-1)}^n}{n}\sin (\mathit{\pi }\mathit{nx})e^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }.\end{array}$$(15) ) follows from the Weierstrass theorem.

Using the property of convergent series and expanding the operator $\frac{d}{\mathit{dt}}$ in the relation (15(15) $$\begin{array}{c}\hfill u(x,t)=x\mathit{\varphi }(t)+\frac{2}{\mathit{\pi }}\frac{d}{\mathit{dt}}\sum _{n=1}^{\infty }\frac{{(-1)}^n}{n}\sin (\mathit{\pi }\mathit{nx})e^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }.\end{array}$$(15) ), we have that for $x\in [0,1)$, the function $u(x,t)$ defined by the following relation:(17) $$\begin{array}{c}\hfill u(x,t)=2\mathit{\pi }\sum _{n=1}^{\infty }{(-1)}^{n+1}n\sin \left(\mathit{\pi }\mathit{nx}\right)e^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }.\end{array}$$(17) $\square$

The differentiation of the series (17(17) $$\begin{array}{c}\hfill u(x,t)=2\mathit{\pi }\sum _{n=1}^{\infty }{(-1)}^{n+1}n\sin \left(\mathit{\pi }\mathit{nx}\right)e^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }.\end{array}$$(17) ) with respect to the variable $x$ presents some difficulties. However, since we only need the function $u_x(0,t)$, we proceeded as follows. Following the ideas proposed in [13] and [14], we approximate the functions $u_x(0,t)$ as the truncated series:(18) $$\begin{array}{c}\hfill u_x(0,t)=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }.\end{array}$$(18) Since the function $u_x(0,t)=g\left(t\right)$ is known, the solution of the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ) reduces to solving the following equation:(19) $$\begin{array}{c}\hfill A\mathit{\varphi }=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }=g(t).\end{array}$$(19) Using (19(19) $$\begin{array}{c}\hfill A\mathit{\varphi }=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }=g(t).\end{array}$$(19) ), it is required to find(20) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }\left(t\right),\end{array}$$(20) provided that, instead of $g\left(t\right)$ we know its approximations $g_{\mathit{\delta }}\left(t\right)$ and $\mathit{\delta }>0$ such that for all $t⩾0$ holds $\parallel g\left(t\right)-g_0\left(t\right)\parallel ⩽\mathit{\delta }$.

Thus, the problem (19(19) $$\begin{array}{c}\hfill A\mathit{\varphi }=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }=g(t).\end{array}$$(19) ),(20(20) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }\left(t\right),\end{array}$$(20) ) is solved in two steps. The first step involves choosing an optimal number of terms in the partial sum of the series (19(19) $$\begin{array}{c}\hfill A\mathit{\varphi }=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }=g(t).\end{array}$$(19) ) and reducing the solution to solving an equation with a finite number of terms. Then, the resulting equation is solved using the method proposed by Lavrentiev.

To evaluate the effectiveness of the proposed approach, we performed a computational experiment and made a comparative analysis of the obtained solutions and solutions with the best possible error bounds. Solutions with the desired error bound were constructed using a method based on the Fourier transform with respect to the time variable and the projection regularization method.

Remark.

As one of anonymous referees has kindly pointed out to the author, the formula (5.9) of the paper [15] is exactly formula () of Theorem 3.1. Still, the author believes that it makes sense to present the full proof of Theorem 3.1 here, because the above derivation of (9(9) $$\begin{array}{c}\hfill \overline{\mathit{\psi }}(x,p)=x+\frac{2}{\mathit{\pi }}\sum _{n=1}^{\infty }\frac{{(-1)}^n}{n}\sin \left(\mathit{\pi }\mathit{nx}\right)\frac{p}{p+n^2{\mathit{\pi }}^2}.\end{array}$$(9) ) uses an idea which is different from the one in [15].

Projection regularization method

Suppose that $H$ is a Hilbert space, $A:H\to H$ is a linear, injective, bounded operator, $A_1=A^{\ast }A$, the spectrum $\mathit{Sp}\left(A_1\right)=[0,\parallel A\parallel {}^2]$. We consider the operator equation:(21) $$\begin{array}{c}\hfill \mathit{Au}=g,u,g\in H.\end{array}$$(21) The lemma proved in [16] implies the existence of a unitary operator $Q$, such that the following polar decomposition of the operator $A$ holds:$$A={\mathit{QA}}_1^{1/2}.$$Let $Q^{\ast }$ be conjugate to $Q$ and ${\overline{g}}_{\mathit{\delta }}=Q^{\ast }{g}_{\mathit{\delta }}$. The projection regularization method is proposed in and its regularization family $\{{\overline{T}}_{\mathit{\delta }}^{\mathit{\alpha }}:\mathit{\delta }\in (0,{\mathit{\delta }}_0],\mathit{\alpha }\in (0,\parallel A\parallel ]\}$ is defined by the formula:(22) $$\begin{array}{c}\hfill {\overline{T}}_{\mathit{\delta }}^{\mathit{\alpha }}{g}_{\mathit{\delta }}=\underset{\mathit{\alpha }}{\overset{\parallel A\parallel }{\int }}\frac{1}{\mathit{\sigma }}{\mathit{dE}}_{\mathit{\sigma }}{\overline{g}}_{\mathit{\delta }}.\end{array}$$(22) where $\{E_{\mathit{\sigma }}:\mathit{\sigma }\in [0,\parallel A\parallel ]\}$ use the spectral decomposition of $E$ generated by the operator $A_1^{1/2}$, and the regularization parameter $\mathit{\alpha }$ chosen as follows.

Let $u_{\mathit{\delta }}^{\mathit{\alpha }}={\overline{T}}_{\mathit{\delta }}^{\mathit{\alpha }}{g}_{\mathit{\delta }}$. Then, as the regularization parameter $\mathit{\alpha }$ we choose one of the solutions of the equation:(23) $$\begin{array}{c}\hfill \parallel {\mathit{Au}}_{\mathit{\delta }}^{\mathit{\alpha }}-g_{\mathit{\delta }}\parallel {}^2=9\parallel A\parallel {}^2{\mathit{\delta }}^2.\end{array}$$(23) Note that Equation (23(23) $$\begin{array}{c}\hfill \parallel {\mathit{Au}}_{\mathit{\delta }}^{\mathit{\alpha }}-g_{\mathit{\delta }}\parallel {}^2=9\parallel A\parallel {}^2{\mathit{\delta }}^2.\end{array}$$(23) ) can have a several solutions. This fact does not affect the accuracy of the approximate solution of Equation (21(21) $$\begin{array}{c}\hfill \mathit{Au}=g,u,g\in H.\end{array}$$(21) ).

The appearance of the number ‘9’ in (23(23) $$\begin{array}{c}\hfill \parallel {\mathit{Au}}_{\mathit{\delta }}^{\mathit{\alpha }}-g_{\mathit{\delta }}\parallel {}^2=9\parallel A\parallel {}^2{\mathit{\delta }}^2.\end{array}$$(23) ) is due to the proof of the optimality of the projection regularization method [17]. The constant ‘9’ is an upper estimate of all possible occurring constants in this procedure. Although, one might probably obtain a lower constant, this one is sufficient for our goal.

In the proposed approach, the approximate solution of Equation (21(21) $$\begin{array}{c}\hfill \mathit{Au}=g,u,g\in H.\end{array}$$(21) ) is given by:(24) $$\begin{array}{c}\hfill u_{\mathit{\delta }}^{\overline{\mathit{\alpha }}}={\hat{T}}_{\mathit{\delta }}^{\mathit{\alpha }}{g}_{\mathit{\delta }}=\{\begin{array}{c}{\overline{T}}_{\mathit{\delta }}^{\overline{\mathit{\alpha }}}{g}_{\mathit{\delta }},\text{for}\parallel g_{\mathit{\delta }}\parallel >3\parallel A\parallel \mathit{\delta }\text{,}\hfill \\ 0,\text{for}\parallel g_{\mathit{\delta }}\parallel \le 3\parallel A\parallel \mathit{\delta }\text{,}\hfill \end{array}\end{array}$$(24) where the operator ${\overline{T}}_{\mathit{\delta }}^{\overline{\mathit{\alpha }}}{g}_{\mathit{\delta }}$ is given by formula (22(22) $$\begin{array}{c}\hfill {\overline{T}}_{\mathit{\delta }}^{\mathit{\alpha }}{g}_{\mathit{\delta }}=\underset{\mathit{\alpha }}{\overset{\parallel A\parallel }{\int }}\frac{1}{\mathit{\sigma }}{\mathit{dE}}_{\mathit{\sigma }}{\overline{g}}_{\mathit{\delta }}.\end{array}$$(22) ), and $\overline{\mathit{\alpha }}$ is one solution of Equation (23(23) $$\begin{array}{c}\hfill \parallel {\mathit{Au}}_{\mathit{\delta }}^{\mathit{\alpha }}-g_{\mathit{\delta }}\parallel {}^2=9\parallel A\parallel {}^2{\mathit{\delta }}^2.\end{array}$$(23) ).

It has been proved previously [17] that the operators given by the formula (24(24) $$\begin{array}{c}\hfill u_{\mathit{\delta }}^{\overline{\mathit{\alpha }}}={\hat{T}}_{\mathit{\delta }}^{\mathit{\alpha }}{g}_{\mathit{\delta }}=\{\begin{array}{c}{\overline{T}}_{\mathit{\delta }}^{\overline{\mathit{\alpha }}}{g}_{\mathit{\delta }},\text{for}\parallel g_{\mathit{\delta }}\parallel >3\parallel A\parallel \mathit{\delta }\text{,}\hfill \\ 0,\text{for}\parallel g_{\mathit{\delta }}\parallel \le 3\parallel A\parallel \mathit{\delta }\text{,}\hfill \end{array}\end{array}$$(24) ) is a regularization method for Equation (21(21) $$\begin{array}{c}\hfill \mathit{Au}=g,u,g\in H.\end{array}$$(21) )and the error estimate of the regularized solutions is the best with respect to the order. This property of regularized solutions provided the basis for comparative analysis of the numerical methods developed using Fourier and Laplace transforms.

Numerical simulation of the solution of the inverse problem for the Laplace transform

Let $g_{\mathit{\delta }}\left(t\right)\in L_1([0,\infty ))$ and $g\left(0\right)=0$. The numerical scheme for solving the problem (19(19) $$\begin{array}{c}\hfill A\mathit{\varphi }=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }=g(t).\end{array}$$(19) ), (20(20) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }\left(t\right),\end{array}$$(20) ) is as follows. The first step of the solution is to transform the initial data. For this, we orthogonalize the system of functions ${\left\{e^{-k^2{\mathit{\pi }}^{2}t}\right\}}_{k=1}^{\infty }$ for each $t⩾0$ and denote the obtained orthogonalized system of functions by ${\left\{c_k{e}^{-k^2{\mathit{\pi }}^{2}t}\right\}}_{k=1}^{\infty }$. The function $g_{\mathit{\delta }}(t)$ is represented in terms of this system as:(25) $$\begin{array}{c}\hfill g_{\mathit{\delta }k}\left(t\right)=c_k\underset{0}{\overset{t}{\int }}{g}_{\mathit{\delta }}\left(\mathit{\tau }\right)e^{-k^2{\mathit{\pi }}^2\mathit{\tau }}d\mathit{\tau }.\end{array}$$(25) Then, the function $g_{\mathit{\delta }}\left(t\right)$ can be expressed as:(26) $$\begin{array}{c}\hfill g_{\mathit{\delta }}\left(t\right)=\sum _{k=1}^{\infty }{g}_{\mathit{\delta }k}\left(t\right)e^{-k^2{\mathit{\pi }}^{2}t}=\sum _{k=1}^{\infty }{c}_k\left(\underset{0}{\overset{t}{\int }}{g}_{\mathit{\delta }}\left(\mathit{\tau }\right)e^{-k^2{\mathit{\pi }}^2\mathit{\tau }}d\mathit{\tau }\right)e^{-k^2{\mathit{\pi }}^{2}t}.\end{array}$$(26) Taking into account (19(19) $$\begin{array}{c}\hfill A\mathit{\varphi }=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }=g(t).\end{array}$$(19) ) and (26(26) $$\begin{array}{c}\hfill g_{\mathit{\delta }}\left(t\right)=\sum _{k=1}^{\infty }{g}_{\mathit{\delta }k}\left(t\right)e^{-k^2{\mathit{\pi }}^{2}t}=\sum _{k=1}^{\infty }{c}_k\left(\underset{0}{\overset{t}{\int }}{g}_{\mathit{\delta }}\left(\mathit{\tau }\right)e^{-k^2{\mathit{\pi }}^2\mathit{\tau }}d\mathit{\tau }\right)e^{-k^2{\mathit{\pi }}^{2}t}.\end{array}$$(26) ) and using the approach proposed in [8], we find that the regularization parameter defined by formula (23(23) $$\begin{array}{c}\hfill \parallel {\mathit{Au}}_{\mathit{\delta }}^{\mathit{\alpha }}-g_{\mathit{\delta }}\parallel {}^2=9\parallel A\parallel {}^2{\mathit{\delta }}^2.\end{array}$$(23) ) is the number of terms in the partial sum of the series (26(26) $$\begin{array}{c}\hfill g_{\mathit{\delta }}\left(t\right)=\sum _{k=1}^{\infty }{g}_{\mathit{\delta }k}\left(t\right)e^{-k^2{\mathit{\pi }}^{2}t}=\sum _{k=1}^{\infty }{c}_k\left(\underset{0}{\overset{t}{\int }}{g}_{\mathit{\delta }}\left(\mathit{\tau }\right)e^{-k^2{\mathit{\pi }}^2\mathit{\tau }}d\mathit{\tau }\right)e^{-k^2{\mathit{\pi }}^{2}t}.\end{array}$$(26) ). Thus, the regularization parameter is determined from the following equation:(27) $$\begin{array}{c}\hfill \parallel A\mathit{\varphi }\left(t\right)-g_{\mathit{\delta }}\left(t\right)\parallel {}^2={\parallel \sum _{k=1}^N{g}_{\mathit{\delta }k}{e}^{-{\mathit{\pi }}^2{k}^{2}t}-g_{\mathit{\delta }}\left(t\right)\parallel }^2=9{\mathit{\delta }}^2.\end{array}$$(27) Let $N$ be the number of terms found from (27(27) $$\begin{array}{c}\hfill \parallel A\mathit{\varphi }\left(t\right)-g_{\mathit{\delta }}\left(t\right)\parallel {}^2={\parallel \sum _{k=1}^N{g}_{\mathit{\delta }k}{e}^{-{\mathit{\pi }}^2{k}^{2}t}-g_{\mathit{\delta }}\left(t\right)\parallel }^2=9{\mathit{\delta }}^2.\end{array}$$(27) ). Then, Equation (19(19) $$\begin{array}{c}\hfill A\mathit{\varphi }=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }=g(t).\end{array}$$(19) ) is transformed to:(28) $$\begin{array}{c}\hfill A\mathit{\varphi }=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }=g_{\mathit{\delta }}\left(t\right)\end{array}$$(28) If $g\left(t\right)\in C\left([0,T]\right)$ for any $T\ne \infty$. Then, we use the following computational scheme for numerical solution of Equation (28(28) $$\begin{array}{c}\hfill A\mathit{\varphi }=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }=g_{\mathit{\delta }}\left(t\right)\end{array}$$(28) ). Let(29) $$\begin{array}{c}\hfill K_N(t-\mathit{\tau })=\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^2(t-\mathit{\tau })},\end{array}$$(29) $$K_N\left(0\right)=\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2,$$then for any $T\ne \infty$ at $t\in [0;T]$ Equation (28(28) $$\begin{array}{c}\hfill A\mathit{\varphi }=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }=g_{\mathit{\delta }}\left(t\right)\end{array}$$(28) ) becomes:(30) $$\begin{array}{c}\hfill A\mathit{\varphi }(t)=\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })K_N(t-\mathit{\tau })d\mathit{\tau }=g(t).\end{array}$$(30) It is necessary to find the function $\mathit{\varphi }\left(\mathit{\tau }\right)$ from Equation (30(30) $$\begin{array}{c}\hfill A\mathit{\varphi }(t)=\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })K_N(t-\mathit{\tau })d\mathit{\tau }=g(t).\end{array}$$(30) ). Thus, the solution of the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ) reduces to solving a Volterra equation of the first kind, provided that $\parallel A\mathit{\varphi }(\mathit{\tau })-g_{\mathit{\delta }}\parallel ⩽\mathit{\delta }$ .

To solve the problem (30(30) $$\begin{array}{c}\hfill A\mathit{\varphi }(t)=\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })K_N(t-\mathit{\tau })d\mathit{\tau }=g(t).\end{array}$$(30) ), we use Lavrentiev method [18]. According to this approach, the regularized solution of the problem is obtained from the equation:(31) $$\begin{array}{c}\hfill A\mathit{\varphi }+\mathit{\alpha }\mathit{\varphi }=2\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })K_N(t-\mathit{\tau })d\mathit{\tau }+\mathit{\alpha }\mathit{\varphi }(\mathit{\tau })=g_{\mathit{\delta }},\end{array}$$(31) provided that $\parallel A\mathit{\varphi }-g_{\mathit{\delta }}\parallel ⩽\mathit{\delta }$ and the regularization parameter $\mathit{\alpha }$ may be chosen by various ways.

In our research the regularization parameter is chosen as follows. Let ${\mathit{\varphi }}_{\mathit{\delta }}^{\mathit{\alpha }}$ be a regularized solution of Equation (31(31) $$\begin{array}{c}\hfill A\mathit{\varphi }+\mathit{\alpha }\mathit{\varphi }=2\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })K_N(t-\mathit{\tau })d\mathit{\tau }+\mathit{\alpha }\mathit{\varphi }(\mathit{\tau })=g_{\mathit{\delta }},\end{array}$$(31) ). We set $P=\parallel A{\mathit{\varphi }}_{\mathit{\delta }}^{\mathit{\alpha }}\parallel$ and $M=\frac{P}{\parallel {\mathit{\varphi }}_{\mathit{\delta }}^{\mathit{\alpha }}\parallel }$. Following the idea proposed in [19] and taking into account relation (23(23) $$\begin{array}{c}\hfill \parallel {\mathit{Au}}_{\mathit{\delta }}^{\mathit{\alpha }}-g_{\mathit{\delta }}\parallel {}^2=9\parallel A\parallel {}^2{\mathit{\delta }}^2.\end{array}$$(23) ), we obtain that the regularization parameter is defined by the formula:(32) $$\begin{array}{c}\hfill {(\frac{\mathit{\alpha }P}{{(\mathit{\alpha }+M)}^2}-2\frac{\mathit{\delta }}{\mathit{\alpha }}-12\frac{P}{{\mathit{\alpha }}^2})}^2=9\frac{\mathit{\alpha }P}{{(\mathit{\alpha }+M)}^2}.\end{array}$$(32) The proposed method of solving the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ) based on the Laplace transform was used to develop a numerical method consisting of the following steps.

1. Determining the number $N$ of terms in the series (28(28) $$\begin{array}{c}\hfill A\mathit{\varphi }=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }=g_{\mathit{\delta }}\left(t\right)\end{array}$$(28) ). This is done by applying an iterative process and calculating the elements $g_{\mathit{\delta }k}\left(t_i\right)$. The integrals are approximated by sums using the right rectangle quadrature formula. The values of $N$ should be chosen so as to ensure positive definiteness of the kernel in relation (30(30) $$\begin{array}{c}\hfill A\mathit{\varphi }(t)=\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })K_N(t-\mathit{\tau })d\mathit{\tau }=g(t).\end{array}$$(30) ).

2. Verifying the condition $\parallel \sum _{k=1}^N{g}_{\mathit{\delta }k}{e}^{-{\mathit{\pi }}^2{k}^{2}t}-g_{\mathit{\delta }}\left(t\right)\parallel {}^2=9{\mathit{\delta }}^2$. The iterative process is performed until the required equality is satisfied.

3. Solving Equation (31(31) $$\begin{array}{c}\hfill A\mathit{\varphi }+\mathit{\alpha }\mathit{\varphi }=2\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })K_N(t-\mathit{\tau })d\mathit{\tau }+\mathit{\alpha }\mathit{\varphi }(\mathit{\tau })=g_{\mathit{\delta }},\end{array}$$(31) ). For this, a certain initial value of the parameter $\mathit{\alpha }={\mathit{\alpha }}_0$ is chosen, and the integrals in (31(31) $$\begin{array}{c}\hfill A\mathit{\varphi }+\mathit{\alpha }\mathit{\varphi }=2\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })K_N(t-\mathit{\tau })d\mathit{\tau }+\mathit{\alpha }\mathit{\varphi }(\mathit{\tau })=g_{\mathit{\delta }},\end{array}$$(31) ) are approximated by sums using the right rectangle quadrature formula. The values of ${\mathit{\varphi }}_{\mathit{\delta }}^{\mathit{\alpha }}\left(t\right)$ are determined from the obtained system of algebraic equations.

4. Checking condition (32(32) $$\begin{array}{c}\hfill {(\frac{\mathit{\alpha }P}{{(\mathit{\alpha }+M)}^2}-2\frac{\mathit{\delta }}{\mathit{\alpha }}-12\frac{P}{{\mathit{\alpha }}^2})}^2=9\frac{\mathit{\alpha }P}{{(\mathit{\alpha }+M)}^2}.\end{array}$$(32) ). If it is satisfied, the process is stopped; otherwise, a new value of the parameter $\mathit{\alpha }={\mathit{\alpha }}_1$ is chosen and step 3 is repeated.

Note that the convergence of the obtained solutions for Equation (31(31) $$\begin{array}{c}\hfill A\mathit{\varphi }+\mathit{\alpha }\mathit{\varphi }=2\underset{0}{\overset{t}{\int }}\mathit{\varphi }(\mathit{\tau })K_N(t-\mathit{\tau })d\mathit{\tau }+\mathit{\alpha }\mathit{\varphi }(\mathit{\tau })=g_{\mathit{\delta }},\end{array}$$(31) ) depends on the regularization parameter. Therefore, it is important to choose an appropriate initial parameter ${\mathit{\alpha }}_0$. In addition, the next values of the parameter that satisfy condition (32(32) $$\begin{array}{c}\hfill {(\frac{\mathit{\alpha }P}{{(\mathit{\alpha }+M)}^2}-2\frac{\mathit{\delta }}{\mathit{\alpha }}-12\frac{P}{{\mathit{\alpha }}^2})}^2=9\frac{\mathit{\alpha }P}{{(\mathit{\alpha }+M)}^2}.\end{array}$$(32) ) can be chosen by different methods, which will also affect the rate of convergence of the computational process.

In order to test the reliability of the results and evaluate the effectiveness of the proposed scheme, we performed a computational experiment for a series of model examples. The experimental results were used for comparative analysis of the solutions obtained by applying the Laplace and Fourier transforms.

Numerical simulation of the inverse problem for the Fourier transform

We proceed to construct a numerical method based on the Fourier transform to solve (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ). If it is known that the solution $u(x,t)$ of the direct problem (5(5) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(5) )–(7(7) $$\begin{array}{c}\hfill u(0,t)=0,u(1,t)=\mathit{\varphi }\left(t\right),t⩾0.\end{array}$$(7) ) satisfies the conditions:$$\begin{array}{c}u(x,t),u_x(x,t)\in C([0,1]\times [0,\infty ))\cap L_2([0,1]\times [0,\infty )),\hfill \\ u_t(x,t),u_{\mathit{xx}}(x,t)\in L_2([0,1]\times [0,\infty ))\hfill \end{array}$$and the function $\mathit{\varphi }\left(t\right)\in H^{2,1}\left([0,\infty )\right)$ such that $\parallel \mathit{\varphi }\left(t\right)\parallel {}_{H^{2,1}\left([0,\infty )\right)}⩽r$, then the Fourier transform with respect to the variable $t$ can be used for solving of the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ).

Let $\parallel g_{\mathit{\delta }}\parallel {}_{L_2}>3\mathit{\delta }$. We apply the Fourier transform $F_t$ with respect to the variable $t$ for $g_{\mathit{\delta }}$. Since the transform is used for $t⩾0$, it is necessary to perform the projection of the images onto $R\left(F_t\right)$. Then, the function $g_{\mathit{\delta }}$ corresponds to a function ${\overline{g}}_{\mathit{\delta }}(\mathit{\lambda },\overline{\mathit{\alpha }}\left(\mathit{\delta }\right))$ such that:(33) $$\begin{array}{c}\hfill {\overline{g}}_{\mathit{\delta }}(\mathit{\lambda },\overline{\mathit{\alpha }}(\mathit{\delta }))=\{\begin{array}{cc}{\stackrel{\sim }{g}}_{\mathit{\delta }}(\mathit{\lambda }),\hfill & \text{for}|\mathit{\lambda }|⩽\overline{\mathit{\alpha }}(\mathit{\delta })\text{,}\hfill \\ 0,\hfill & \text{for}|\mathit{\lambda }|>\overline{\mathit{\alpha }}(\mathit{\delta })\mathit{bad}\mathit{hbox}\hfill \end{array}\end{array}$$(33) The regularization parameter $\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)$ given by formula (23(23) $$\begin{array}{c}\hfill \parallel {\mathit{Au}}_{\mathit{\delta }}^{\mathit{\alpha }}-g_{\mathit{\delta }}\parallel {}^2=9\parallel A\parallel {}^2{\mathit{\delta }}^2.\end{array}$$(23) ) is chosen to be the solution of the following equation:(34) $$\begin{array}{c}\hfill \underset{-\infty }{\overset{-\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)}{\int }}{\left|{\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)\right|}^{2}d\mathit{\lambda }+\underset{\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)}{\overset{+\infty }{\int }}{\left|{\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)\right|}^{2}d\mathit{\lambda }=9{\mathit{\delta }}^2.\end{array}$$(34) Applying the Fourier transform $F_t$ with respect to the variable $t$, we find that the operator representation of the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ) of the form:(35) $$\begin{array}{c}\hfill i\mathit{\lambda }\stackrel{\sim }{u}(x,\mathit{\lambda })=\frac{d^2}{{\mathit{dx}}^2}\stackrel{\sim }{u}(x,\mathit{\lambda }),x\in (0,1),\mathit{\lambda }\in R,\end{array}$$(35) $$\stackrel{\sim }{u}(0,\mathit{\lambda })=0,{\stackrel{\sim }{u}}_x(0,\mathit{\lambda })={\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right),$$where $\stackrel{\sim }{u}(x,\mathit{\lambda })=F_t\left(u(x,t)\right)$, ${\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)=F_t\left(g_{\mathit{\delta }}\left(t\right)\right)$.

Solving the problem (35(35) $$\begin{array}{c}\hfill i\mathit{\lambda }\stackrel{\sim }{u}(x,\mathit{\lambda })=\frac{d^2}{{\mathit{dx}}^2}\stackrel{\sim }{u}(x,\mathit{\lambda }),x\in (0,1),\mathit{\lambda }\in R,\end{array}$$(35) ) and using the transformations (33(33) $$\begin{array}{c}\hfill {\overline{g}}_{\mathit{\delta }}(\mathit{\lambda },\overline{\mathit{\alpha }}(\mathit{\delta }))=\{\begin{array}{cc}{\stackrel{\sim }{g}}_{\mathit{\delta }}(\mathit{\lambda }),\hfill & \text{for}|\mathit{\lambda }|⩽\overline{\mathit{\alpha }}(\mathit{\delta })\text{,}\hfill \\ 0,\hfill & \text{for}|\mathit{\lambda }|>\overline{\mathit{\alpha }}(\mathit{\delta })\mathit{bad}\mathit{hbox}\hfill \end{array}\end{array}$$(33) ), (34(34) $$\begin{array}{c}\hfill \underset{-\infty }{\overset{-\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)}{\int }}{\left|{\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)\right|}^{2}d\mathit{\lambda }+\underset{\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)}{\overset{+\infty }{\int }}{\left|{\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)\right|}^{2}d\mathit{\lambda }=9{\mathit{\delta }}^2.\end{array}$$(34) ) we obtain the desired function $\stackrel{\sim }{u}(1,\mathit{\lambda })$ given by the formula:(36) $$\begin{array}{c}\hfill \stackrel{\sim }{u}(1,\mathit{\lambda })=\frac{2\mathit{sh}\left({\mathit{\mu }}_0\sqrt{\mathit{\lambda }}\right)}{{\mathit{\mu }}_0\sqrt{\mathit{\lambda }}}{\overline{g}}_{\mathit{\delta }}(\mathit{\lambda },\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)),\end{array}$$(36) where ${\mathit{\mu }}_0=\frac{1}{\sqrt{2}}(1+i)$, the regularization parameter $\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)$ satisfies Equation (34(34) $$\begin{array}{c}\hfill \underset{-\infty }{\overset{-\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)}{\int }}{\left|{\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)\right|}^{2}d\mathit{\lambda }+\underset{\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)}{\overset{+\infty }{\int }}{\left|{\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)\right|}^{2}d\mathit{\lambda }=9{\mathit{\delta }}^2.\end{array}$$(34) ) and the function ${\overline{g}}_{\mathit{\delta }}(\mathit{\lambda },\overline{\mathit{\alpha }}\left(\mathit{\delta }\right))$ is given by relation (33(33) $$\begin{array}{c}\hfill {\overline{g}}_{\mathit{\delta }}(\mathit{\lambda },\overline{\mathit{\alpha }}(\mathit{\delta }))=\{\begin{array}{cc}{\stackrel{\sim }{g}}_{\mathit{\delta }}(\mathit{\lambda }),\hfill & \text{for}|\mathit{\lambda }|⩽\overline{\mathit{\alpha }}(\mathit{\delta })\text{,}\hfill \\ 0,\hfill & \text{for}|\mathit{\lambda }|>\overline{\mathit{\alpha }}(\mathit{\delta })\mathit{bad}\mathit{hbox}\hfill \end{array}\end{array}$$(33) ).

Applying the inverse Fourier transform $F_{\mathit{\lambda }}^{-1}$ to the function $\stackrel{\sim }{u}(1,\mathit{\lambda })$, we get:(37) $$\begin{array}{c}\hfill {\overline{u}}_{\mathit{\delta }}(1,t)=F_{\mathit{\lambda }}^{-1}({\stackrel{\sim }{u}}_{\mathit{\delta }}(1,\mathit{\lambda })).\end{array}$$(37) Using the projection regularization method for the function ${\overline{u}}_{\mathit{\delta }}(1,t)$ the regularized solution of the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ) has the form:(38) $$\begin{array}{c}\hfill u_{\mathit{\delta }}(1,t)=\{\begin{array}{cc}\mathit{Re}({\overline{u}}_{\mathit{\delta }}(1,t)),\hfill & \mathrm{for}t⩾0,\hfill \\ 0,\hfill & \mathrm{for}t<0.\hfill \end{array}\end{array}$$(38) The proposed scheme (33(33) $$\begin{array}{c}\hfill {\overline{g}}_{\mathit{\delta }}(\mathit{\lambda },\overline{\mathit{\alpha }}(\mathit{\delta }))=\{\begin{array}{cc}{\stackrel{\sim }{g}}_{\mathit{\delta }}(\mathit{\lambda }),\hfill & \text{for}|\mathit{\lambda }|⩽\overline{\mathit{\alpha }}(\mathit{\delta })\text{,}\hfill \\ 0,\hfill & \text{for}|\mathit{\lambda }|>\overline{\mathit{\alpha }}(\mathit{\delta })\mathit{bad}\mathit{hbox}\hfill \end{array}\end{array}$$(33) )–(38(38) $$\begin{array}{c}\hfill u_{\mathit{\delta }}(1,t)=\{\begin{array}{cc}\mathit{Re}({\overline{u}}_{\mathit{\delta }}(1,t)),\hfill & \mathrm{for}t⩾0,\hfill \\ 0,\hfill & \mathrm{for}t<0.\hfill \end{array}\end{array}$$(38) ) was used to develop a numerical method for solving the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ). The computational scheme of the method is as follows:

1. Apply the Fourier transform to the elements $g_{\mathit{\delta }}$ to find ${\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)$.

2. Find the parameter $\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)$ from Equation (34(34) $$\begin{array}{c}\hfill \underset{-\infty }{\overset{-\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)}{\int }}{\left|{\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)\right|}^{2}d\mathit{\lambda }+\underset{\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)}{\overset{+\infty }{\int }}{\left|{\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)\right|}^{2}d\mathit{\lambda }=9{\mathit{\delta }}^2.\end{array}$$(34) ). For this, the integrals on the left-hand side of this equation are replaced by integral sums, and Equation (34(34) $$\begin{array}{c}\hfill \underset{-\infty }{\overset{-\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)}{\int }}{\left|{\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)\right|}^{2}d\mathit{\lambda }+\underset{\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)}{\overset{+\infty }{\int }}{\left|{\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)\right|}^{2}d\mathit{\lambda }=9{\mathit{\delta }}^2.\end{array}$$(34) ) is solved taking into account the convergence of the integrals on the left-hand side.

3. Transform the initial data according to formulas (34(34) $$\begin{array}{c}\hfill \underset{-\infty }{\overset{-\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)}{\int }}{\left|{\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)\right|}^{2}d\mathit{\lambda }+\underset{\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)}{\overset{+\infty }{\int }}{\left|{\stackrel{\sim }{g}}_{\mathit{\delta }}\left(\mathit{\lambda }\right)\right|}^{2}d\mathit{\lambda }=9{\mathit{\delta }}^2.\end{array}$$(34) ).

4. Find the Fourier transform $\stackrel{\sim }{u}(1,\mathit{\lambda })$ of the regularized solution using formula (36(36) $$\begin{array}{c}\hfill \stackrel{\sim }{u}(1,\mathit{\lambda })=\frac{2\mathit{sh}\left({\mathit{\mu }}_0\sqrt{\mathit{\lambda }}\right)}{{\mathit{\mu }}_0\sqrt{\mathit{\lambda }}}{\overline{g}}_{\mathit{\delta }}(\mathit{\lambda },\overline{\mathit{\alpha }}\left(\mathit{\delta }\right)),\end{array}$$(36) ).

5. Obtain the regularized solution using formulas (37(37) $$\begin{array}{c}\hfill {\overline{u}}_{\mathit{\delta }}(1,t)=F_{\mathit{\lambda }}^{-1}({\stackrel{\sim }{u}}_{\mathit{\delta }}(1,\mathit{\lambda })).\end{array}$$(37) ) and (38(38) $$\begin{array}{c}\hfill u_{\mathit{\delta }}(1,t)=\{\begin{array}{cc}\mathit{Re}({\overline{u}}_{\mathit{\delta }}(1,t)),\hfill & \mathrm{for}t⩾0,\hfill \\ 0,\hfill & \mathrm{for}t<0.\hfill \end{array}\end{array}$$(38) ).

From the results of [17] it follows that this approach provides solutions with the best possible errors bounds. This property was used for comparative analysis of the numerical methods developed using the Laplace and Fourier transforms.

Computational results

To test the effectiveness of the proposed approaches and to perform comparative analysis of the solutions obtained, we performed a computational experiment for a series of model examples. In the experiment, the direct and inverse problems were solved and norms of the deviations of the regularized solutions from the model functions were determined. The model functions differed in the monotonicity and continuity of their derivatives. In each series, several recalculations for each function were perfumed.

The computational experiment was carried out for $t\in [0,T]$ using a uniform grid of $m+1$ points $T=\mathit{hm}$, and $t_i=(i-1)h$, $i=\overline{1,(m+1)}$. The numerical experiments includes the following steps:

1. The direct problem (5(5) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(5) )–(7(7) $$\begin{array}{c}\hfill u(0,t)=0,u(1,t)=\mathit{\varphi }\left(t\right),t⩾0.\end{array}$$(7) ) for the model function is solved by the finite difference method, and the values of the function $g\left(t\right)$ at the grid points $t_i$ are obtained by numerical differentiation.

2. The values of $g_{\mathit{\delta }}$ are simulated at each grid point $t_i$ as values of a normally distributed random variable with expectation $a=g\left(t_i\right)$ and standard deviation $\mathit{\sigma }=\mathit{\delta }$.

3. The inverse problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ) with the initial data $g_{\mathit{\delta }}\left(t\right)$ is solved using the computational schemes based on the Laplace and Fourier transforms.

4. The quantity $\parallel u_{\mathit{\delta }}-u_0\parallel$ is calculated, where $u_0$ is the model function and $u_{\mathit{\delta }}$ is a regularized solution obtained using the corresponding approach.

The results of the numerical experiment for several model functions are illustrated in the figures below. In all the figures, the same notation is employed. The calculation error is denoted by $\mathit{\delta }$. In the upper plot, the designation ‘model’ corresponds to the exact value of $g\left(t\right)$, and in the lower plot, it corresponds to the exact value of the model function $u_0(1,t)$. The perturbed value of the function $g\left(t\right)$ is denoted by $g_{\mathit{\delta }}$. The designation $u_{\mathit{\delta }}$ corresponds to the regularized solution obtained using the Fourier transform, and the designation $u_{\mathit{\delta }t}$ to the regularized solution obtained using the Laplace transform. The symbols $\mathit{\alpha }$ and ${\mathit{\alpha }}_t$ denote the regularization parameters for approaches using the Fourier and Laplace transforms, respectively.

Fig. 1 Results of the numerical solution for the boundary function $u(1,t)={\mathit{te}}^{-t}$ with $\mathit{\delta }=0.03$.

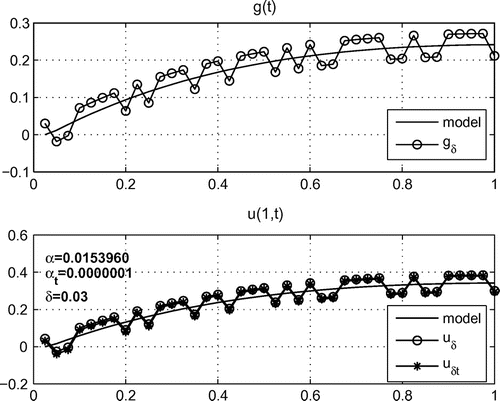
Example 1.

In this series of experiments, continuous monotonic functions were used. The experiment was performed for different levels of error. Figure 1 shows the results of the numerical solution of the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ) for the model function $u={\mathit{te}}^{-t}$ with $\mathit{\delta }=0.03$.

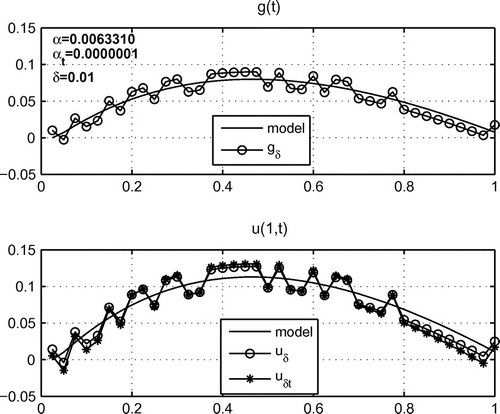
Example 2.

In this series of experiments, continuous smooth functions with a single extremum were used. The experiment was carried out for different levels of error. Figure 2 shows the experimental results for one of the model functions $u(1,t)=t(e^{-t}-e^{-1})$ with $\mathit{\delta }=0.01$.

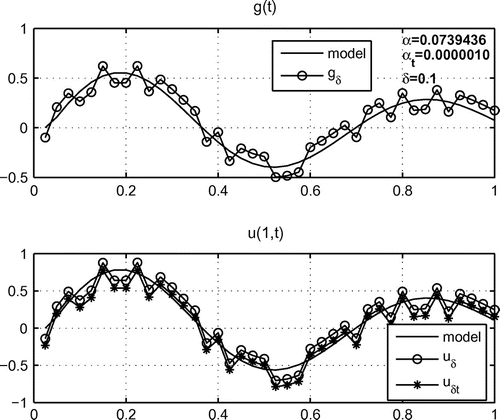
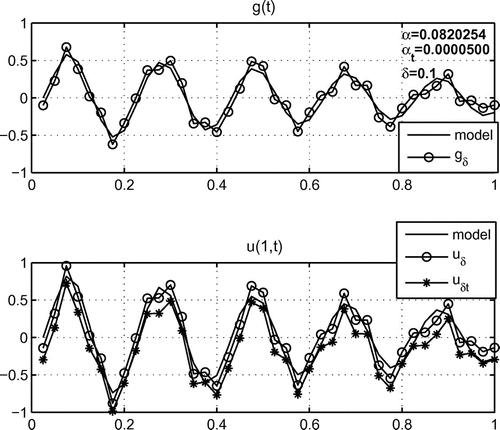
Example 3.

In this series of experiments, continuous smooth function with several extremes were used. The experiment was carried out for different levels of error. Figure 3 shows the results of numerical solution of the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ) for the function $u(1,t)=\sin \left(3\mathit{\pi }t\right)e^{-t}$ with $\mathit{\delta }=0.1$, Figure 4 shows the results of the experiment for the model function $u(1,t)=\sin \left(10\mathit{\pi }t\right)e^{-t}$ with $\mathit{\delta }=0.1$.

Fig. 2 Results of the numerical solution for the boundary function $u(1,t)=t(e^{-t}-e^{-1})$ with $\mathit{\delta }=0.01$.

Fig. 3 Results of the numerical solution for the boundary function $u(1,t)=\sin \left(3\mathit{\pi }t\right)e^{-t}$ with $\mathit{\delta }=0.1$.

Fig. 4 Results of the numerical solution for the boundary function $u(1,t)=\sin (10\mathit{\pi }t)e^{-t}$ with $\mathit{\delta }=0.1$.

Fig. 5 Results of the numerical solution for the function $u(1,t)=\{\begin{array}{c}-40t,t\in [0;0.025],\hfill \\ -1,t\in (0.025;0.5],\hfill \\ 80t-39,t\in (0.5;0.525],\hfill \\ 1,t\in (0.525;1].\hfill \end{array}$.

Fig. 6 Results of the numerical solution for the function $u(1,t)=\{\begin{array}{c}\sin (5\mathit{\pi }t)-2.5t^2,t\in [0;0.5),\hfill \\ \cos (5\mathit{\pi }t),t\in [0.5;1].\hfill \end{array}$.

Example 4.

In this series of experiments, continuous functions with discontinuous derivatives were used. A difficulty in this experiment was that Equation (28(28) $$\begin{array}{c}\hfill A\mathit{\varphi }=2\sum _{n=1}^N{(-1)}^{n+1}{\mathit{\pi }}^2{n}^2{e}^{-{\mathit{\pi }}^2{n}^{2}t}\underset{0}{\overset{t}{\int }}\mathit{\varphi }\left(\mathit{\tau }\right)e^{{\mathit{\pi }}^2{n}^2\mathit{\tau }}d\mathit{\tau }=g_{\mathit{\delta }}\left(t\right)\end{array}$$(28) ) was reduced to the Volterra equation of the first kind, so that a necessary condition for the stability of the process was the continuity of the model function. The results of the numerical solution of the problem (1(1) $$\begin{array}{c}\hfill u_t=u_{\mathit{xx}},x\in (0,1),t⩾0,\end{array}$$(1) )–(4(4) $$\begin{array}{c}\hfill u(1,t)=\mathit{\varphi }(t),t⩾0.\end{array}$$(4) ) for $\mathit{\delta }=0.1$ are presented in Figure 5, and in Figure 6.

To study the stability of the regularized solutions and obtain experimental estimates for the deviations of these solutions from the given model functions in each series of experiments, we measured the quantities $\parallel u_{\mathit{\delta }}-u_0\parallel$ and $\parallel u_{\mathit{\delta }t}-u_0\parallel$, which characterize the deviations of the regularized solutions $u_{\mathit{\delta }}$ and $u_{\mathit{\delta }t}$ obtained using the Fourier and Laplace transforms of the model function $u_0$. Average values of these quantities obtained in each series of experiments are shown in Table 1.

Table 1 Experimental estimates of deviation for regularized solutions.

model function	values of $\mathit{\delta }$	average $\parallel u_{\mathit{\delta }}^L-u_0\parallel$	average $\parallel u_{\mathit{\delta }}^F-u_0\parallel$
$u(1,t)={\mathit{te}}^{-t}$	0.01	0.0167	0.0141
	0.03	0.0175	0.0142
$u(1,t)=t(e^{-t}-e^{-1})$	0.01	0.0169	0.0142
	0.03	0.0409	0.0421
$u(1,t)=\sin (3\mathit{\pi }t)e^{-t}$	0.01	0.0983	0.01441
	0.1	0.1233	0.1414
$u(1,t)=\sin (10\mathit{\pi }t)e^{-t}$	0.01	0.0965	0.01415
	0.1	0.1001	0.1415
$u(1,t)=\{\begin{array}{cc}-40t,\hfill & t\in [0;0.025],\hfill \\ -1,\hfill & t\in (0.025;0.5],\hfill \\ 80t-39,\hfill & t\in (0.5;0.525],\hfill \\ 1,\hfill & t\in (0.525;1].\hfill \end{array}$	0.05	0.1508	0.0425
	0.1	0.1776	0.1457
$u(1,t)=\{\begin{array}{cc}\sin (5\mathit{\pi }t)-2.5t^2,\hfill & t\in [0;0.5),\hfill \\ \cos (5\mathit{\pi }t),\hfill & t\in [0.5;1].\hfill \end{array}$	0.05	0.1501	0.0615
	0.1	0.1860	0.1424

The results of the experiments leads to the the following conclusions. Both methods provide regularized solutions with reasonable accuracy. The approach based on the Fourier transform and the projection regularization method allows results to be obtained with guaranteed accuracy, which is confirmed by the theoretical estimates for the projection regularization method given in [17]. The estimates of the error for the solutions obtained by this method depends from the order of the error of the initial data, and the properties of the model functions do not significantly affect the magnitude of the error.

The approach based on the Laplace transform provides approximate solutions with a sufficient accuracy. In this case, the order of error of the initial data does not significantly affect the accuracy of the solutions. It should be noted that these equations were solved using the Lavrentiev method which depends greatly on the choice of the regularization parameter. To evaluate the error estimates of the solutions obtained using this method and improve the convergence of the solutions, it is planned to to consider a numerical solution of this type of equation using the right (central) rectangle quadrature formulas, by analogy to [20].

Conclusions

Different approaches to solving the inverse boundary problems based on the use of Laplace and Fourier transforms were proposed.

The approach based on the regularization method for the direct and inverse Fourier transforms yields approximate solutions with guaranteed accuracy. The estimation of errors of these solutions are the exact with respect to the order.

The approach based on the Laplace transform can be applied to a wider class of functions than the approach based on the Fourier transform. Moreover, this method reduces the solution of the original problem to regularization of integral operator equations and eliminates elements of operational calculus from the numerical solution procedure. Experimental error estimates of the obtained solutions show sufficient stability of these solutions. However, further studies are needed to evaluate the error estimates and convergence of numerical solutions.

Acknowledgments

The author thanks anonymous referees for their valuable comments.