Efficient iterative tip/tilt reconstruction for atmospheric tomography

Abstract

The planned new generation of extremely large telescopes (ELT) requires highly efficient algorithms for its adaptive optics systems. Recently, a new iterative reconstruction approach for multi conjugate adaptive optics (MCAO) and multi object adaptive optics (MOAO) was introduced that computes the mirror corrections without the use of matrix-vector multiplications. The method splits the MCAO/MOAO problem into three subproblems – wavefront reconstruction, atmospheric tomography and mirror deformation – sequently. If an AO system uses laser guide stars, then the reconstruction methods have to be extended in order to consider the cone effect and the tip/tilt indetermination. For the reconstruction of an atmosphere with correct tip/tilt we assume that additional measurements from a tip/tilt sensor are available, and propose two iterative reconstruction methods for the atmosphere. In the first approach, the tip/tilt reconstruction is included into the atmospheric tomography, whereas in the second approach the tip/tilt is reconstructed separately and added to the atmosphere after the atmospheric tomography. Both algorithms are tested numerically. The reconstruction quality of our methods is evaluated for ELT.

Keywords:

• adaptive optics
• inverse problems
• regularization
• Kaczmarz method
• iterative methods

1 Introduction

The image quality of large ground based-telescopes is severely affected by atmospheric turbulences. Adaptive optics systems correct for the disturbances by using appropriately shaped deformable mirrors (DM) to obtain sharper images. The shape of the DMs depends on the turbulences in the atmosphere and has to be recomputed with a frequency of 500–1000$$Hz, which requires powerful reconstruction methods for future systems with thousands of degrees of freedom. An introduction to adaptive optics can be found in [1–3].

Adaptive optics systems of the new generation, as multi conjugate adaptive optics (MCAO) and multi object adaptive optics (MOAO) aim at a correction not only into a single direction on the sky but over a large field of view. This can be achieved by the use of measurements from several artificially created stars, laser guide stars, pointed at different directions and several DM, which are conjugated to different heights in the atmosphere. The mirror shapes have to be obtained with a tomographic algorithm. For the description of an MCAO system, we refer to [4, 5]. Contrary to MCAO, an MOAO system has a separate mirror to correct for each direction of interest, i.e. for each observed scientific object, see [6, 7].

In [8], we have proposed a reconstruction method that solves the three required subproblems – wavefront reconstruction, atmospheric tomography, mirror fitting – sequently. In particular for the wavefront reconstruction and the mirror fitting we have presented accurate as well as fast methods. For the atmospheric tomography, we have used a fast iterative algorithm, the Kaczmarz method. However, so far we only considered measurements from natural guide stars for the reconstruction of the atmosphere. When using laser guide stars, additional effects have to be taken into account, e.g. the cone effect and tip/tilt indeterminacy due to the nature of the laser guide star (see [1] for details). The goal of the paper is to investigate a variant of the Kaczmarz iteration that takes these effects into account.

Due to the finite height of the laser guide star, the light is not propagated through the atmosphere in a cylindrical but rather in a conical form. This so called cone effect can be taken into account by a redefinition of the operator that describes the measurements from a laser guide star.

Tip/tilt indeterminacy refers to the impossibility to reconstruct the correct linear part of the atmosphere from laser guide star measurements only. This is related to the fact that the laser light passes all turbulent layers twice – on its way up and down. In order to reconstruct the tip/tilt correctly, additional natural guide stars and tip/tilt sensors are used.

In most of the proposed numerical methods for MCAO (or for the atmospheric tomography problem), a large system matrix is set up that maps the atmospheric turbulences to the sensor measurements of incoming wavefronts from the guide stars. The implementation of cone effect and tip/tilt indetermination into the system matrix is straight forward, see, e.g. [9]. The solution of the resulting matrix vector system involves either the computation of the generalized inverse of the underlying matrix [10] or iterative methods for the solution of the linear system.[11–21]

In the following, we will propose two methods for the combination of laser guide star measurements with the natural guide star measurements in the framework of the Kaczmarz reconstructor proposed in [8]. As in the therein proposed three-step approach, we will assume that we already have the incoming wavefronts from the laser guide stars, that is, we have already reconstructed the wavefronts from Shack–Hartmann wavefront sensor measurements. The sensor can mathematically be described as the averaged gradient of the wavefront on the subapertures,1.1 $$\begin{array}{c}\hfill s_x[i,j]=\left({\mathbf{P}}_x,,\mathit{\varphi }\right)[i,j]:=\frac{1}{|{\mathrm{\Omega }}_{ij}|}{\int }_{{\mathrm{\Omega }}_{ij}}{\mathit{\varphi }}_x(x,y)d(x,y)\end{array}$$1.1 and $s_y$, respectively (see [1], Section 5.3.2). For the inversion of the operator $\mathbf{P}=({\mathbf{P}}_x,{\mathbf{P}}_y)$, the Cumulative Reconstructor (CuRe) or CuReD, a variant of CuRe with domain decomposition, is used.[22–24] These algorithms are currently the fastest ones available, and will guarantee – together with the Kaczmarz iteration and the fitting step – a reconstruction for MCAO/MOAO well within the time frame available for the planned extremely large telescopes (ELT).

The paper is organized as follows. In Section 2, the model for atmospheric tomography is presented followed by a derivation of some mathematical properties of the tip/tilt sensor models. In Section 3, two methods for atmospheric tomography with tip/tilt correction are proposed, the separate and the integrated tip/tilt reconstruction. The corresponding numerical results and computational complexities of both methods are presented in Section 4.

2 Atmospheric tomography

The goal of atmospheric tomography is the reconstruction of $L$ turbulent layers ${\mathrm{\Phi }}^{(l)}$, located at heights $h_l$, $l=1,\dots ,L$ from a combination of natural and laser guide star measurements. We assume that $G$ different laser guide stars, located at finite height in directions ${\mathit{\alpha }}_g$, $g=1,\dots ,G$, are available, as well as $N$ tip/tilt measurements from tip/tilt sensors aligned to natural guide stars in directions ${\mathit{\beta }}_n$, $n=1,\dots ,N$. Associated to each laser guide star, we have measurements of the incoming wavefront ${\mathit{\phi }}_{{\mathit{\alpha }}_g}$, and for each natural guide star measurements ${\mathbf{t}}_{{\mathit{\beta }}_n}\in {\mathbb{R}}^2$.

Due to the fact that a laser guide star is located at a finite altitude, the models for the propagation of the light from laser guide stars and natural guide stars differ slightly, as we will point out below. Following Fusco et al. [25], we only aim at the reconstruction of a finite number of turbulent layers in the atmosphere. Each layer is represented as a function ${\mathrm{\Phi }}^{(l)}:{\mathbf{\Omega }}_l\subset {\mathbb{R}}^2\to \mathbb{R}$. For simplicity, we will drop the coordinate for the height of the layer, which is implicitly assigned to each layer via its number.

Note that the restriction to the reconstruction of a finite number of functions defined on a plane instead of reconstructing a volume reduces the ill-posedness of the problem.

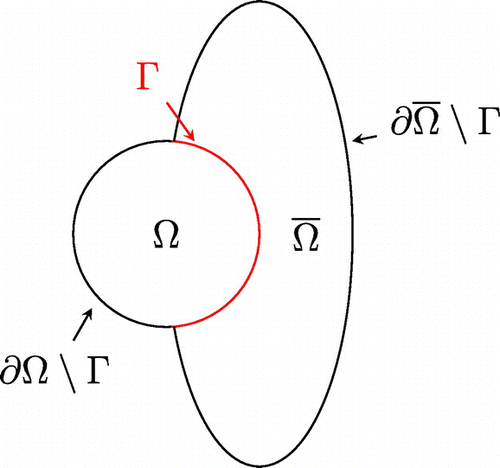
Let ${\mathbf{\Omega }}_D$ denote a disc with radius $D$, centred at the origin and representing the telescope, i.e.$$\begin{array}{c}\hfill {\mathbf{\Omega }}_D=\{\mathbf{r}=(x,y)\in {\mathbb{R}}^2:\Vert \mathbf{r}\Vert \le D\}.\end{array}$$Following [25], the incoming wavefront from a natural guide star in a direction ${\mathit{\alpha }}_g$ is given as2.1 $$\begin{array}{c}\hfill {\mathit{\phi }}_{{\mathit{\alpha }}_g}(\mathbf{r})=\sum _{l=1}^L{\mathrm{\Phi }}^{(l)}(\mathbf{r}+h_l{\mathit{\alpha }}_g),\mathbf{r}\in {\mathbf{\Omega }}_D,\end{array}$$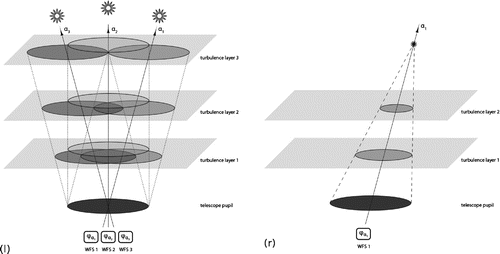2.1 see Figure 1(l). In contrast, the light from a laser guide star propagates in a cone towards the telescope, see Figure 1(r). The measured wavefronts from laser guide stars are therefore given by2.2 $$\begin{array}{c}\hfill {\mathbf{A}}_{{\mathit{\alpha }}_g}\mathbf{\Phi }:=\sum _{l=1}^L{\mathrm{\Phi }}^{(l)}(c_l\mathbf{r}+h_l{\mathit{\alpha }}_g)={\mathit{\phi }}_{{\mathit{\alpha }}_g}(\mathbf{r}),\mathbf{r}\in {\mathbf{\Omega }}_D.\end{array}$$2.2 The parameter $c_l$ depends on the location of the layer and the laser guide star and is defined as2.3 $$\begin{array}{c}\hfill c_l=1-\frac{h_l}{h_{LGS}},\end{array}$$2.3 where $h_{LGS}$ denotes the height of the laser guide star.

At altitude $h_l$, we can only reconstruct what is ‘seen’ by the guide star sensors, i.e. within the area2.4 $$\begin{array}{c}\hfill {\mathbf{\Omega }}_l=\bigcup _{g=1}^G{\mathbf{\Omega }}_D(h_l{\mathit{\alpha }}_g,c_l)\cup \bigcup _{n=1}^N{\mathbf{\Omega }}_D(h_l{\mathit{\beta }}_n,1).\end{array}$$2.4 Here,2.5 $$\begin{array}{c}\hfill {\mathbf{\Omega }}_D(h\mathit{\alpha },c):=\{\mathbf{r}\in {\mathbb{R}}^2:c\mathbf{r}-h\mathit{\alpha }\in {\mathbf{\Omega }}_D\}.\end{array}$$2.5 If $c=1$, we will frequently drop the second parameter, that is,2.6 $$\begin{array}{c}\hfill {\mathbf{\Omega }}_D(h\mathit{\alpha }):={\mathbf{\Omega }}_D(h\mathit{\alpha },1).\end{array}$$2.6 Thus, the set ${\mathbf{\Omega }}_l$ is simply the union of shifted versions of ${\mathbf{\Omega }}_D$, see also Figure 1. Please note that, even at a large altitude, there will be a significant overlap of the shifted versions of ${\mathbf{\Omega }}_D$ due to the small field of view.

Figure 1. Atmospheric tomography: measurements from natural guide stars (l) and influence of the cone effect (r).

In what follows, we will consider ${\mathrm{\Phi }}^{(l)}$ as a function in the spaces $L_2({\mathbf{\Omega }}_l)$, the space of square integrable functions or the Sobolev space $H^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)$, which is defined by$$\begin{array}{c}\hfill H^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)=\left\{\mathit{\varphi },:,{\mathbf{\Omega }}_l,\to ,{\mathbb{R}|\Vert \mathit{\varphi }\Vert }_{H^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)},<,\infty \right\}\end{array}$$with$$\begin{array}{c}\hfill {\Vert \mathit{\varphi }\Vert }_{H^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)}^2:=\underset{{\mathbf{\Omega }}_l}{\int }{|\mathit{\varphi }(x)|}^{2}dx+\mathit{\sigma }\underset{{\mathbf{\Omega }}_l}{\int }{|\nabla \mathit{\varphi }(x)|}^{2}dx,\end{array}$$where $\mathit{\sigma }>0$ is a fixed parameter. It is well known that $H^{1,\mathit{\sigma }}$ is a Hilbert space with inner product2.7 $$\begin{array}{c}\hfill {〈\mathit{\varphi },\mathit{\psi }〉}_{H^{1,\mathit{\sigma }}}:={〈\mathit{\varphi },\mathit{\psi }〉}_{L_2}+\mathit{\sigma }{〈\nabla \mathit{\varphi },\nabla \mathit{\psi }〉}_{L_2}.\end{array}$$2.7 Next, we collect all layers in a vector $\mathbf{\Phi }$,$$\begin{array}{c}\hfill \mathbf{\Phi }={({\mathrm{\Phi }}^{(1)},\dots ,{\mathrm{\Phi }}^{(L)})}^T\end{array}$$and define an inner product via$$\begin{array}{c}\hfill {〈\mathbf{\Phi },\mathbf{\Psi }〉}_{\mathbf{L}}=\sum _{l=1}^L\frac{1}{{\mathit{\gamma }}_l}〈{\mathrm{\Phi }}^{(l)},{\mathrm{\Psi }}^{(l)}〉,\end{array}$$where we can choose either the $L_2$ or the $H^{1,\mathit{\sigma }}$ inner product on the right hand side. The parameters ${\mathit{\gamma }}_l$ are the (known) relative strengths of layers in the atmosphere, fulfilling2.8 $$\begin{array}{c}\hfill \sum _{l=1}^L{\mathit{\gamma }}_l=1.\end{array}$$2.8 The parameter ${\mathit{\gamma }}_l$ denotes the $c_n^2$-profile of layer $l$, that is an additional information about the strength of the turbulence on that layer and is, therefore, used as a weighting factor for the inner product.

The task is to reconstruct the atmosphere $\mathbf{\Phi }$ from measurements ${\mathit{\phi }}_{{\mathit{\alpha }}_g}$. As mentioned in Section 1, the reconstruction from the incoming laser guide star wavefronts leads to a wrongly reconstructed tip/tilt. In order to obtain a correct reconstruction of the atmosphere, additional tip/tilt sensors are needed, which will be investigated in the following.

2.1 Some mathematical properties of the operators describing tip/tilt sensors

The MCAO / MOAO systems which will be used, e.g. at the European extremely large telescope (E-ELT), use additional tip/tilt sensors to determine the tip/tilt of an incoming wavefront from additional natural guide stars. A mathematical model for the sensor measurements of an incoming wavefront from a natural guide star is given by2.9 $$\begin{array}{cc}\hfill {\mathbf{N}}_{{\mathit{\beta }}_i}\mathbf{\Phi }& ={\mathbf{t}}_{{\mathit{\beta }}_i}=\left(\begin{array}{c}{t}_{{\mathit{\beta }}_i}^x\\ t_{{\mathit{\beta }}_i}^y\end{array}\right)\in {\mathbb{R}}^2,i=1,\dots ,N.\hfill \end{array}$$2.9 2.10 $$\begin{array}{cc}\hfill t_{{\mathit{\beta }}_i}^x& =\sum _{l=1}^L\underset{{\mathbf{\Omega }}_D}{\int }\frac{\mathit{\partial }}{\mathit{\partial }x}{\mathrm{\Phi }}^{(l)}(\mathbf{r}+h_l{\mathit{\beta }}_i)d\mathbf{r}\hfill \end{array}$$2.10 2.11 $$\begin{array}{cc}\hfill t_{{\mathit{\beta }}_i}^y& =\sum _{l=1}^L\underset{{\mathbf{\Omega }}_D}{\int }\frac{\mathit{\partial }}{\mathit{\partial }y}{\mathrm{\Phi }}^{(l)}(\mathbf{r}+h_l{\mathit{\beta }}_i)d\mathbf{r},\hfill \end{array}$$2.11 $\mathbf{r}=(x,y)\in {\mathbf{\Omega }}_D$, i.e. it is assumed that the sensor measures the average values of the partial derivative of the incoming wavefront over the whole aperture. We wish to remark that other models for the measurements are also frequently used, e.g. the RMS best-fit tilt to the wavefront, see, e.g. [15]. Please note that the operator ${\mathbf{N}}_{{\mathit{\beta }}_i}$ is not well defined on $L_2$; thus, we will here consider it in the $H^{1,\mathit{\sigma }}$ setting only. The reconstruction algorithms presented later will always use the adjoint operator ${\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast }$, which will be derived in the following section.

2.1.1 The operator ${\mathbf{N}}_{{\mathit{\beta }}_i}$ defined on $H^{1,\mathit{\sigma }}$ spaces

We consider the operator$$\begin{array}{c}\hfill {\mathbf{N}}_{{\mathit{\beta }}_i}:\underset{l=1}{\overset{L}{⨂}}{H}^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)\to {\mathbb{R}}^2.\end{array}$$Let us now derive the adjoint operator$$\begin{array}{c}\hfill {\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast }:{\mathbb{R}}^2\to \underset{l=1}{\overset{L}{⨂}}{H}^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l).\end{array}$$For $\mathbf{t}=(t^x,t^y)\in {\mathbb{R}}^2$, set $u(\mathbf{r})=u(x,y)=t^x·x+t^y·y$. In particular, we have $\mathrm{\Delta }u=0$ and obtain by Green’s theorem$$\begin{array}{cc}\hfill 〈{\mathbf{N}}_{{\mathit{\beta }}_i}\mathbf{\Phi },\mathbf{t}〉& =\sum _{l=1}^L\underset{{\mathbf{\Omega }}_D}{\int }{t}^x·\frac{\mathit{\partial }}{\mathit{\partial }x}{\mathrm{\Phi }}^{(l)}(\mathbf{r}+h_l{\mathit{\beta }}_i)d\mathbf{r}+\sum _{l=1}^L\underset{{\mathbf{\Omega }}_D}{\int }{t}^y·\frac{\mathit{\partial }}{\mathit{\partial }y}{\mathrm{\Phi }}^{(l)}(\mathbf{r}+h_l{\mathit{\beta }}_i)d\mathbf{r}\hfill \\ & =\sum _{l=1}^L{〈\nabla {\mathrm{\Phi }}^{(l)}(·+h_l{\mathit{\beta }}_i),\nabla u〉}_{L_2({\mathbf{\Omega }}_D)}\hfill \\ & =\sum _{l=1}^L\left(〈{\mathrm{\Phi }}^{(l)}(·+h_l{\mathit{\beta }}_i),-\mathrm{\Delta }u〉,+,\underset{\mathit{\partial }{\mathbf{\Omega }}_D}{\int },{\mathrm{\Phi }}^{(l)},(\mathbf{r}+h_l{\mathit{\beta }}_i),\frac{\mathit{\partial }u}{\mathit{\partial }e},(\mathbf{r}),,d,\mathbf{r}\right)\hfill \\ & =\sum _{l=1}^L\underset{\mathit{\partial }{\mathbf{\Omega }}_D}{\int }{\mathrm{\Phi }}^{(l)}(\mathbf{r}+h_l{\mathit{\beta }}_i)\frac{\mathit{\partial }u}{\mathit{\partial }n}(\mathbf{r})d\mathbf{r}\hfill \\ & =\sum _{l=1}^L\underset{\mathit{\partial }{\mathbf{\Omega }}_D}{\int }{\mathrm{\Phi }}^{(l)}(\mathbf{r}+h_l{\mathit{\beta }}_i)\frac{\mathit{\partial }u}{\mathit{\partial }n}(\mathbf{r}+h_l{\mathit{\beta }}_i)d\mathbf{r},\hfill \end{array}$$where the last equality holds as $u$ is a linear function. By $n$ we denote the normal vector to $\mathit{\partial }{\mathbf{\Omega }}_D$. Using (2.52.5 $$\begin{array}{c}\hfill {\mathbf{\Omega }}_D(h\mathit{\alpha },c):=\{\mathbf{r}\in {\mathbb{R}}^2:c\mathbf{r}-h\mathit{\alpha }\in {\mathbf{\Omega }}_D\}.\end{array}$$2.5 ), we obtain2.12 $$\begin{array}{c}\hfill 〈{\mathbf{N}}_{{\mathit{\beta }}_i}\mathbf{\Phi },\mathbf{t}〉=\sum _{l=1}^L\underset{\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)}{\int }{\mathrm{\Phi }}^{(l)}(\mathbf{r})\frac{\mathit{\partial }u}{\mathit{\partial }{n}_{li}}(\mathbf{r})d\mathbf{r},\end{array}$$2.12 where $n_{li}$ now denotes the normal vector to $\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)$.

In the next step, we need to rewrite the inner product ${〈\mathbf{\Phi },\mathbf{\Psi }〉}_{\mathbf{L}}$. We first derive

Proposition 2.1

Let ${\mathrm{\Phi }}^{(l)}\in H^1({\mathbf{\Omega }}_l)$, ${\mathrm{\Psi }}^{(l)}\in H^2({\mathbf{\Omega }}_l)$. Then2.13 $$\begin{array}{cc}\hfill {〈{\mathrm{\Phi }}^{(l)},{\mathrm{\Psi }}^{(l)}〉}_{H^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)}& =\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }\left({\mathrm{\Psi }}^{(l)},-,\mathit{\sigma },\mathrm{\Delta },{\mathrm{\Psi }}^{(l)}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }\left({\mathrm{\Psi }}^{(l)},-,\mathit{\sigma },\mathrm{\Delta },{\mathrm{\Psi }}^{(l)}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\mathit{\sigma }\underset{{\mathrm{\Gamma }}_l}{\int }\left({\mathrm{\Psi }}_1^{(l)},-,{\mathrm{\Psi }}_2^{(l)}\right)\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}+\mathit{\sigma }\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }{\mathrm{\Phi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}\hfill \\ & +\mathit{\sigma }\underset{{\mathrm{\Gamma }}_l}{\int }{\mathrm{\Phi }}^{(l)}\left(\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}},-,\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}\right)d\mathbf{r}+\mathit{\sigma }\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Phi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}d\mathbf{r}.\hfill \end{array}$$2.13 Here, $\overline{\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)}:={\mathbf{\Omega }}_l\backslash \mathbf{\Omega }({\mathit{\beta }}_i{h}_l)$, $n_{li}$ is a normal vector with respect to $\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)$, ${\overline{n}}_{li}$ a normal vector with respect to $\overline{\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)}$, ${\mathrm{\Gamma }}_l:=\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash \mathit{\partial }{\mathbf{\Omega }}_l$ and2.14 $$\begin{array}{c}\hfill {\mathrm{\Psi }}^{(l)}={\mathrm{\Psi }}_1^{(l)}+{\mathrm{\Psi }}_2^{(l)},\end{array}$$2.14 with ${\mathrm{\Psi }}_1^{(l)}$defined only on $\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)$, ${\mathrm{\Psi }}_2^{(l)}$ defined only on $\overline{\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)}$, respectively.

Proof

The proof is based on Green’s theorem which is used in its weak form. We have2.15 $$\begin{array}{cc}\hfill & {〈{\mathrm{\Phi }}^{(l)},{\mathrm{\Psi }}^{(l)}〉}_{H^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)}=\underset{{\mathbf{\Omega }}_l}{\int }{\mathrm{\Phi }}^{(l)}{\mathrm{\Psi }}^{(l)}d\mathbf{r}+\mathit{\sigma }\underset{{\mathbf{\Omega }}_l}{\int }\nabla {\mathrm{\Phi }}^{(l)}\nabla {\mathrm{\Psi }}^{(l)}d\mathbf{r}\hfill \\ \hfill & =\underset{{\mathbf{\Omega }}_l}{\int }{\mathrm{\Phi }}^{(l)}{\mathrm{\Psi }}^{(l)}d\mathbf{r}-\mathit{\sigma }\underset{{\mathbf{\Omega }}_l}{\int }{\mathrm{\Psi }}^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\mathit{\sigma }\underset{\mathit{\partial }{\mathbf{\Omega }}_l}{\int }{\mathrm{\Psi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }n}d\mathbf{r}\hfill \\ \hfill & =\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }{\mathrm{\Psi }}_1^{(l)}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Psi }}_2^{(l)}{\mathrm{\Phi }}^{(l)}d\mathbf{r}-\mathit{\sigma }\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }{\mathrm{\Psi }}_1^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & -\mathit{\sigma }\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Psi }}_2^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\mathit{\sigma }\underset{\mathit{\partial }{\mathbf{\Omega }}_l}{\int }{\mathrm{\Psi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }n}d\mathbf{r}.\hfill \end{array}$$2.15 Applying Green’s theorem twice, we get2.16 $$\begin{array}{cc}\hfill -\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }{\mathrm{\Psi }}_1^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}& =-\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }\mathrm{\Delta }{\mathrm{\Psi }}_1^{(l)}{\mathrm{\Phi }}^{(l)}d\mathbf{r}-\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }{\mathrm{\Psi }}_1^{(l)}\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}\hfill \\ & +\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }{\mathrm{\Phi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r},\hfill \end{array}$$2.16 2.17 $$\begin{array}{cc}\hfill -\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Psi }}_2^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}& =-\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }\mathrm{\Delta }{\mathrm{\Psi }}_2^{(l)}{\mathrm{\Phi }}^{(l)}d\mathbf{r}-\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Psi }}_2^{(l)}\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}\hfill \\ & +\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Phi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}.\hfill \end{array}$$2.17 Combining (2.152.15 $$\begin{array}{cc}\hfill & {〈{\mathrm{\Phi }}^{(l)},{\mathrm{\Psi }}^{(l)}〉}_{H^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)}=\underset{{\mathbf{\Omega }}_l}{\int }{\mathrm{\Phi }}^{(l)}{\mathrm{\Psi }}^{(l)}d\mathbf{r}+\mathit{\sigma }\underset{{\mathbf{\Omega }}_l}{\int }\nabla {\mathrm{\Phi }}^{(l)}\nabla {\mathrm{\Psi }}^{(l)}d\mathbf{r}\hfill \\ \hfill & =\underset{{\mathbf{\Omega }}_l}{\int }{\mathrm{\Phi }}^{(l)}{\mathrm{\Psi }}^{(l)}d\mathbf{r}-\mathit{\sigma }\underset{{\mathbf{\Omega }}_l}{\int }{\mathrm{\Psi }}^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\mathit{\sigma }\underset{\mathit{\partial }{\mathbf{\Omega }}_l}{\int }{\mathrm{\Psi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }n}d\mathbf{r}\hfill \\ \hfill & =\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }{\mathrm{\Psi }}_1^{(l)}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Psi }}_2^{(l)}{\mathrm{\Phi }}^{(l)}d\mathbf{r}-\mathit{\sigma }\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }{\mathrm{\Psi }}_1^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & -\mathit{\sigma }\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Psi }}_2^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\mathit{\sigma }\underset{\mathit{\partial }{\mathbf{\Omega }}_l}{\int }{\mathrm{\Psi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }n}d\mathbf{r}.\hfill \end{array}$$2.15 )–(2.172.17 $$\begin{array}{cc}\hfill -\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Psi }}_2^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}& =-\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }\mathrm{\Delta }{\mathrm{\Psi }}_2^{(l)}{\mathrm{\Phi }}^{(l)}d\mathbf{r}-\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Psi }}_2^{(l)}\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}\hfill \\ & +\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Phi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}.\hfill \end{array}$$2.17 ), we get2.18 $$\begin{array}{cc}\hfill {〈{\mathrm{\Phi }}^{(l)},{\mathrm{\Psi }}^{(l)}〉}_{H^{1,\mathit{\sigma }}}& =\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }\left({\mathrm{\Psi }}_1^{(l)},-,\mathit{\sigma },\mathrm{\Delta },{\mathrm{\Psi }}_1^{(l)}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }\left({\mathrm{\Psi }}_2^{(l)},-,\mathit{\sigma },\mathrm{\Delta },{\mathrm{\Psi }}_2^{(l)}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}+\mathit{\sigma }B,\hfill \end{array}$$2.18 where $B$ denotes the sum of all boundary integrals appearing in (2.152.15 $$\begin{array}{cc}\hfill & {〈{\mathrm{\Phi }}^{(l)},{\mathrm{\Psi }}^{(l)}〉}_{H^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)}=\underset{{\mathbf{\Omega }}_l}{\int }{\mathrm{\Phi }}^{(l)}{\mathrm{\Psi }}^{(l)}d\mathbf{r}+\mathit{\sigma }\underset{{\mathbf{\Omega }}_l}{\int }\nabla {\mathrm{\Phi }}^{(l)}\nabla {\mathrm{\Psi }}^{(l)}d\mathbf{r}\hfill \\ \hfill & =\underset{{\mathbf{\Omega }}_l}{\int }{\mathrm{\Phi }}^{(l)}{\mathrm{\Psi }}^{(l)}d\mathbf{r}-\mathit{\sigma }\underset{{\mathbf{\Omega }}_l}{\int }{\mathrm{\Psi }}^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\mathit{\sigma }\underset{\mathit{\partial }{\mathbf{\Omega }}_l}{\int }{\mathrm{\Psi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }n}d\mathbf{r}\hfill \\ \hfill & =\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }{\mathrm{\Psi }}_1^{(l)}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Psi }}_2^{(l)}{\mathrm{\Phi }}^{(l)}d\mathbf{r}-\mathit{\sigma }\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }{\mathrm{\Psi }}_1^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & -\mathit{\sigma }\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Psi }}_2^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\mathit{\sigma }\underset{\mathit{\partial }{\mathbf{\Omega }}_l}{\int }{\mathrm{\Psi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }n}d\mathbf{r}.\hfill \end{array}$$2.15 )–(2.172.17 $$\begin{array}{cc}\hfill -\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Psi }}_2^{(l)}\mathrm{\Delta }{\mathrm{\Phi }}^{(l)}d\mathbf{r}& =-\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }\mathrm{\Delta }{\mathrm{\Psi }}_2^{(l)}{\mathrm{\Phi }}^{(l)}d\mathbf{r}-\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Psi }}_2^{(l)}\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}\hfill \\ & +\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Phi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}.\hfill \end{array}$$2.17 ). Setting2.19 $$\begin{array}{c}\hfill {\mathrm{\Gamma }}_l:=\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash \mathit{\partial }{\mathbf{\Omega }}_l,\end{array}$$2.19 we get2.20 $$\begin{array}{c}\hfill \mathit{\partial }{\mathbf{\Omega }}_l=\left(\mathit{\partial },\mathbf{\Omega },({\mathit{\beta }}_i{h}_l),\backslash ,{\mathrm{\Gamma }}_l\right)\cup \left(\mathit{\partial },\overline{\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)},\backslash ,{\mathrm{\Gamma }}_l\right),\end{array}$$2.20 i.e.2.21 $$\begin{array}{cc}\hfill B=& -\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Psi }}_1^{(l)}d\mathbf{r}-\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Psi }}_1^{(l)}d\mathbf{r}+\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}-\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Psi }}_2^{(l)}d\mathbf{r}-\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Psi }}_2^{(l)}d\mathbf{r}\hfill \\ & +\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{{\mathbf{\Omega }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }n}{\mathrm{\Psi }}^{(l)}d\mathbf{r}\hfill \\ \hfill =& \underset{{\mathrm{\Gamma }}_l}{\int }\left({\mathrm{\Psi }}_2^{(l)},-,{\mathrm{\Psi }}_1^{(l)}\right)\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}+\underset{{\mathrm{\Gamma }}_l}{\int }\left(\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}},-,\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}.\hfill \end{array}$$2.21 For the last equality, we have in particular used the relation $n_{li}=-{\overline{n}}_{li}$ for the normal vectors on common boundaries. Together, (2.182.18 $$\begin{array}{cc}\hfill {〈{\mathrm{\Phi }}^{(l)},{\mathrm{\Psi }}^{(l)}〉}_{H^{1,\mathit{\sigma }}}& =\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }\left({\mathrm{\Psi }}_1^{(l)},-,\mathit{\sigma },\mathrm{\Delta },{\mathrm{\Psi }}_1^{(l)}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }\left({\mathrm{\Psi }}_2^{(l)},-,\mathit{\sigma },\mathrm{\Delta },{\mathrm{\Psi }}_2^{(l)}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}+\mathit{\sigma }B,\hfill \end{array}$$2.18 ) and (2.212.21 $$\begin{array}{cc}\hfill B=& -\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Psi }}_1^{(l)}d\mathbf{r}-\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Psi }}_1^{(l)}d\mathbf{r}+\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}-\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Psi }}_2^{(l)}d\mathbf{r}-\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Psi }}_2^{(l)}d\mathbf{r}\hfill \\ & +\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{{\mathbf{\Omega }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }n}{\mathrm{\Psi }}^{(l)}d\mathbf{r}\hfill \\ \hfill =& \underset{{\mathrm{\Gamma }}_l}{\int }\left({\mathrm{\Psi }}_2^{(l)},-,{\mathrm{\Psi }}_1^{(l)}\right)\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}+\underset{{\mathrm{\Gamma }}_l}{\int }\left(\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}},-,\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}.\hfill \end{array}$$2.21 ) gives (2.132.13 $$\begin{array}{cc}\hfill {〈{\mathrm{\Phi }}^{(l)},{\mathrm{\Psi }}^{(l)}〉}_{H^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)}& =\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }\left({\mathrm{\Psi }}^{(l)},-,\mathit{\sigma },\mathrm{\Delta },{\mathrm{\Psi }}^{(l)}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }\left({\mathrm{\Psi }}^{(l)},-,\mathit{\sigma },\mathrm{\Delta },{\mathrm{\Psi }}^{(l)}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\mathit{\sigma }\underset{{\mathrm{\Gamma }}_l}{\int }\left({\mathrm{\Psi }}_1^{(l)},-,{\mathrm{\Psi }}_2^{(l)}\right)\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}+\mathit{\sigma }\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }{\mathrm{\Phi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}\hfill \\ & +\mathit{\sigma }\underset{{\mathrm{\Gamma }}_l}{\int }{\mathrm{\Phi }}^{(l)}\left(\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}},-,\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}\right)d\mathbf{r}+\mathit{\sigma }\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Phi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}d\mathbf{r}.\hfill \end{array}$$2.13 ). $\square$

Please note that statistics of the atmosphere predict for the layers ${\mathrm{\Phi }}^{(l)}\in H^{\frac{11}{6}}$ (see, e.g. [2]), and thus the atmosphere fulfills the condition ${\mathrm{\Phi }}^{(l)}\in H^1$.

We can now derive the adjoint of the operator ${\mathbf{N}}_{{\mathit{\beta }}_i}$:

Proposition 2.2

For $i=1,\dots ,N$ and given $\mathbf{t}\in {\mathbb{R}}^2$, the function2.22 $$\begin{array}{c}\hfill \mathbf{\Psi }={\left({\mathrm{\Psi }}_1^{(1)},+,{\mathrm{\Psi }}_2^{(1)},,,\dots ,,,{\mathrm{\Psi }}_1^{(L)},+,{\mathrm{\Psi }}_2^{(L)}\right)}^T={\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast }\mathbf{t}\end{array}$$2.22 is given as (weak) solution of the differential equations2.23 $$\begin{array}{cc}\hfill {\mathrm{\Psi }}_1^{(l)}-\mathit{\sigma }\mathrm{\Delta }{\mathrm{\Psi }}_1^{(l)}& =0\text{in}\mathbf{\Omega }(h_l{\mathit{\beta }}_i),\hfill \\ \hfill {\mathrm{\Psi }}_2^{(l)}-\mathit{\sigma }\mathrm{\Delta }{\mathrm{\Psi }}_2^{(l)}& =0\text{in}\overline{\mathbf{\Omega }(h_l{\mathit{\beta }}_i)},\hfill \\ \hfill {\mathrm{\Psi }}_1^{(l)}& ={\mathrm{\Psi }}_2^{(l)}\text{on}{\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}& =\frac{{\mathit{\gamma }}_l}{\mathit{\sigma }}·{\mathbf{t}}^T·n_{li}\text{on}\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)\backslash {\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}& =0\text{on}\overline{\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)}\backslash {\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}-\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}& =\frac{{\mathit{\gamma }}_l}{\mathit{\sigma }}·{\mathbf{t}}^T·n_{li}\text{on}{\mathrm{\Gamma }}_l,\hfill \end{array}$$2.23 $l=1,\dots ,L$.

Proof

The adjoint operator is defined by the equation$$\begin{array}{c}\hfill {〈{\mathbf{N}}_{{\mathit{\beta }}_i}\mathbf{\Phi },\mathbf{t}〉}_{{\mathbb{R}}^2}={〈\mathbf{\Phi },{\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast }\mathbf{t}〉}_{\mathbf{L}}={〈\mathbf{\Phi },\mathbf{\Psi }〉}_{\mathbf{L}}.\end{array}$$Using the definition of the inner product on the atmosphere and (2.122.12 $$\begin{array}{c}\hfill 〈{\mathbf{N}}_{{\mathit{\beta }}_i}\mathbf{\Phi },\mathbf{t}〉=\sum _{l=1}^L\underset{\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)}{\int }{\mathrm{\Phi }}^{(l)}(\mathbf{r})\frac{\mathit{\partial }u}{\mathit{\partial }{n}_{li}}(\mathbf{r})d\mathbf{r},\end{array}$$2.12 ), we obtain the condition2.24 $$\begin{array}{c}\hfill \sum _{l=1}^L\underset{\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)}{\int }{\mathrm{\Phi }}^{(l)}(\mathbf{r})\frac{\mathit{\partial }u}{\mathit{\partial }{n}_{li}}(\mathbf{r})d\mathbf{r}=\sum _{l=1}^L\frac{1}{{\mathit{\gamma }}_l}{〈{\mathrm{\Phi }}^{(l)},{\mathrm{\Psi }}^{(l)}〉}_{H^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)},\end{array}$$2.24 for all $\mathbf{\Phi },\mathbf{\Psi }$, and thus2.25 $$\begin{array}{c}\hfill {\mathit{\gamma }}_l·\underset{\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)}{\int }{\mathrm{\Phi }}^{(l)}(\mathbf{r})\frac{\mathit{\partial }u}{\mathit{\partial }{n}_{li}}(\mathbf{r})d\mathbf{r}={〈{\mathrm{\Phi }}^{(l)},{\mathrm{\Psi }}^{(l)}〉}_{H^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)}\end{array}$$2.25 has to hold for $l=1,\dots ,L$. Now keeping in mind that $\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)=\left(\mathit{\partial },\mathbf{\Omega },(h_l{\mathit{\beta }}_i),\backslash ,{\mathrm{\Gamma }}_l\right)\cup {\mathrm{\Gamma }}_l$ and $\frac{\mathit{\partial }u}{\mathit{\partial }{n}_{li}}(\mathbf{r})={\mathbf{t}}^T·n_{li}$ we conclude by comparing the right hand side of (2.132.13 $$\begin{array}{cc}\hfill {〈{\mathrm{\Phi }}^{(l)},{\mathrm{\Psi }}^{(l)}〉}_{H^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)}& =\underset{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }\left({\mathrm{\Psi }}^{(l)},-,\mathit{\sigma },\mathrm{\Delta },{\mathrm{\Psi }}^{(l)}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }\left({\mathrm{\Psi }}^{(l)},-,\mathit{\sigma },\mathrm{\Delta },{\mathrm{\Psi }}^{(l)}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\mathit{\sigma }\underset{{\mathrm{\Gamma }}_l}{\int }\left({\mathrm{\Psi }}_1^{(l)},-,{\mathrm{\Psi }}_2^{(l)}\right)\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}+\mathit{\sigma }\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)}{\int }{\mathrm{\Phi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}\hfill \\ & +\mathit{\sigma }\underset{{\mathrm{\Gamma }}_l}{\int }{\mathrm{\Phi }}^{(l)}\left(\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}},-,\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}\right)d\mathbf{r}+\mathit{\sigma }\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}}{\int }{\mathrm{\Phi }}^{(l)}\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}d\mathbf{r}.\hfill \end{array}$$2.13 ) with the left hand side of (2.303.2 $$\begin{array}{c}\hfill \mathbf{P}=\left(\begin{array}{c}{\mathbf{P}}_x\\ {\mathbf{P}}_y\end{array}\right),\end{array}$$3.2 ) that equality only holds for all $\mathbf{\Phi },\mathbf{\Psi }$ if Equations (2.232.23 $$\begin{array}{cc}\hfill {\mathrm{\Psi }}_1^{(l)}-\mathit{\sigma }\mathrm{\Delta }{\mathrm{\Psi }}_1^{(l)}& =0\text{in}\mathbf{\Omega }(h_l{\mathit{\beta }}_i),\hfill \\ \hfill {\mathrm{\Psi }}_2^{(l)}-\mathit{\sigma }\mathrm{\Delta }{\mathrm{\Psi }}_2^{(l)}& =0\text{in}\overline{\mathbf{\Omega }(h_l{\mathit{\beta }}_i)},\hfill \\ \hfill {\mathrm{\Psi }}_1^{(l)}& ={\mathrm{\Psi }}_2^{(l)}\text{on}{\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}& =\frac{{\mathit{\gamma }}_l}{\mathit{\sigma }}·{\mathbf{t}}^T·n_{li}\text{on}\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)\backslash {\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}& =0\text{on}\overline{\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)}\backslash {\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}-\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}& =\frac{{\mathit{\gamma }}_l}{\mathit{\sigma }}·{\mathbf{t}}^T·n_{li}\text{on}{\mathrm{\Gamma }}_l,\hfill \end{array}$$2.23 )–(2.282.27 $$\begin{array}{c}\hfill \mathcal{R}({\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast })=\text{span}\{{\mathbf{u}}_i^1,{\mathbf{u}}_i^2\},\end{array}$$2.27 ) hold. $\square$

According to Proposition 2.2, we have to solve two pde’s with appropriate boundary/interface conditions for each layer for the evaluation of the adjoint operator. However, as$$\mathbf{t}=t^x\left(\begin{array}{c}1\\ 0\end{array}\right)+t^y\left(\begin{array}{c}0\\ 1\end{array}\right)$$and as the adjoint operator is linear, it is sufficient to evaluate the operator ${\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast }$ only once for the (two) unit vectors, i.e. solve the pde’s only twice, and obtain the adjoint applied to an arbitrary vector in ${\mathbb{R}}^2$ by superposition. Defining2.26 $$\begin{array}{c}\hfill {\mathbf{u}}_i^1:={\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast }\left(\begin{array}{c}1\\ 0\end{array}\right),{\mathbf{u}}_i^2:={\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast }\left(\begin{array}{c}0\\ 1\end{array}\right),\end{array}$$2.26 we observe2.27 $$\begin{array}{c}\hfill \mathcal{R}({\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast })=\text{span}\{{\mathbf{u}}_i^1,{\mathbf{u}}_i^2\},\end{array}$$2.27 which will be needed in Section 3.2.

3 Atmospheric tomography with tip/tilt correction

If the atmosphere is reconstructed from the incoming wavefronts from laser guide stars only, then the part of the atmosphere related to the unknown tip/tilt is not properly reconstructed, and thus the obtained mirror corrections are not optimal. Therefore, the reconstruction process has to take into account the additional information from the tip/tilt sensors. In the following, we will investigate two different approaches for a tip/tilt correction.

3.1 Integrated tip/tilt correction

In our first approach, we will integrate the tip/tilt correction into the atmospheric reconstruction from guide star measurements. We will follow now a more classical approach, which was, e.g. presented in [5]. However, we will reformulate the approach in such a way that we can still use the reconstructedwavefronts ${\mathit{\phi }}_{{\mathit{\alpha }}_g}$ instead of the measurements of the Shack–Hartmann sensor.

To describe the average values over the whole aperture of the partial derivative of the incoming wavefront from a laser guide star, we need the operator ${\mathbf{N}}_{{\mathit{\alpha }}_g}^L$, similar to ${\mathbf{N}}_{{\mathit{\beta }}_i}$ defined in (2.92.9 $$\begin{array}{cc}\hfill {\mathbf{N}}_{{\mathit{\beta }}_i}\mathbf{\Phi }& ={\mathbf{t}}_{{\mathit{\beta }}_i}=\left(\begin{array}{c}{t}_{{\mathit{\beta }}_i}^x\\ t_{{\mathit{\beta }}_i}^y\end{array}\right)\in {\mathbb{R}}^2,i=1,\dots ,N.\hfill \end{array}$$2.9 ) but with the cone effect included:3.1 $$\begin{array}{cc}\hfill {\mathbf{N}}_{{\mathit{\alpha }}_g}^L\mathbf{\Phi }& ={\mathbf{t}}_{{\mathit{\alpha }}_g}=\left(\begin{array}{c}{t}_{{\mathit{\alpha }}_g}^x\\ t_{{\mathit{\alpha }}_g}^y\end{array}\right)\in {\mathbb{R}}^2,i=1,\dots ,N.\hfill \\ \hfill t_{{\mathit{\alpha }}_g}^x& =\sum _{l=1}^L\underset{{\mathbf{\Omega }}_D}{\int }\frac{\mathit{\partial }}{\mathit{\partial }x}{\mathrm{\Phi }}^{(l)}(c_l\mathbf{r}+h_l{\mathit{\alpha }}_g)d\mathbf{r}\hfill \\ \hfill t_{{\mathit{\alpha }}_g}^y& =\sum _{l=1}^L\underset{{\mathbf{\Omega }}_D}{\int }\frac{\mathit{\partial }}{\mathit{\partial }y}{\mathrm{\Phi }}^{(l)}(c_l\mathbf{r}+h_l{\mathit{\alpha }}_g)d\mathbf{r},\hfill \end{array}$$3.1 with $\mathbf{r}=(x,y)\in {\mathbf{\Omega }}_D$ and $c_l$ as in (2.32.3 $$\begin{array}{c}\hfill c_l=1-\frac{h_l}{h_{LGS}},\end{array}$$2.3 ). Denoting3.2 $$\begin{array}{c}\hfill \mathbf{P}=\left(\begin{array}{c}{\mathbf{P}}_x\\ {\mathbf{P}}_y\end{array}\right),\end{array}$$3.2 where ${\mathbf{P}}_x,{\mathbf{P}}_y$ are defined as in (1.11.1 $$\begin{array}{c}\hfill s_x[i,j]=\left({\mathbf{P}}_x,,\mathit{\varphi }\right)[i,j]:=\frac{1}{|{\mathrm{\Omega }}_{ij}|}{\int }_{{\mathrm{\Omega }}_{ij}}{\mathit{\varphi }}_x(x,y)d(x,y)\end{array}$$1.1 ), the measurements from a Shack–Hartmann sensor with a laser guide star in direction ${\mathit{\alpha }}_g$ can be modelled as3.3 $$\begin{array}{cc}\hfill \left({\mathbf{P}}_x,{\mathbf{A}}_{{\mathit{\alpha }}_g},\mathbf{\Phi }\right)[i,j]-t_{{\mathit{\alpha }}_g}^x& =\left({\mathbf{P}}_x,{\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr}\right)[i,j],\hfill \\ \hfill \left({\mathbf{P}}_y,{\mathbf{A}}_{{\mathit{\alpha }}_g},\mathbf{\Phi }\right)[i,j]-t_{{\mathit{\alpha }}_g}^y& =\left({\mathbf{P}}_y,{\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr}\right)[i,j],\hfill \end{array}$$3.3 where ${\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr},g=1,\dots ,G$ denote the tip/tilt removed incoming wavefronts from laser guide stars. Setting$$\begin{array}{cc}\hfill t^x[i,j]& =t_{{\mathit{\alpha }}_g}^x,\hfill \\ \hfill t^y[i,j]& =t_{{\mathit{\alpha }}_g}^y,\hfill \end{array}$$$$\mathbf{Q}\mathbf{t}=\left(\begin{array}{c}{t}^x[i,j]\\ t^y[i,j]\end{array}\right),i,j=1,\dots ,s$$Equations (3.53.5 $$\begin{array}{c}\hfill (\mathbf{S}\mathbf{t})(\mathbf{r}):=t^x·x+t^y·y,\mathbf{r}=(x,y).\end{array}$$3.5 )–(3.63.6 $$\begin{array}{c}\hfill \mathbf{Q}{\mathbf{N}}_{{\mathit{\alpha }}_g}^L\mathbf{\Phi }=\mathbf{P}\mathbf{S}{\mathbf{N}}_{{\mathit{\alpha }}_g}^L\mathbf{\Phi },\end{array}$$3.6 ) can be written as3.4 $$\begin{array}{c}\hfill \mathbf{P}{\mathbf{A}}_{{\mathit{\alpha }}_g}\mathbf{\Phi }-\mathbf{Q}{\mathbf{N}}_{{\mathit{\alpha }}_g}^L\mathbf{\Phi }=\mathbf{P}{\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr},g=1,\dots ,G.\end{array}$$3.4 In a next step, we want to derive a relation between the operators $\mathbf{P}$ and $\mathbf{Q}$: For $\mathbf{t}={(t^x,t^y)}^T$, we define the linear and bounded operator3.5 $$\begin{array}{c}\hfill (\mathbf{S}\mathbf{t})(\mathbf{r}):=t^x·x+t^y·y,\mathbf{r}=(x,y).\end{array}$$3.5 and obtain$$\begin{array}{cc}\hfill \left({\mathbf{P}}_x,\mathbf{S},\right)[i,j]& =\frac{1}{|{\mathrm{\Omega }}_{ij}|}{\int }_{{\mathrm{\Omega }}_{ij}}\frac{\mathit{\partial }}{\mathit{\partial }x}(\mathbf{S}\mathbf{t})(\mathbf{r})d\mathbf{r}=t^x,\hfill \\ \hfill \left({\mathbf{P}}_y,\mathbf{S},\right)[i,j]& =\frac{1}{|{\mathrm{\Omega }}_{ij}|}{\int }_{{\mathrm{\Omega }}_{ij}}\frac{\mathit{\partial }}{\mathit{\partial }y}(\mathbf{S}\mathbf{t})(\mathbf{r})d\mathbf{r}=t^y.\hfill \end{array}$$Thus, we derive3.6 $$\begin{array}{c}\hfill \mathbf{Q}{\mathbf{N}}_{{\mathit{\alpha }}_g}^L\mathbf{\Phi }=\mathbf{P}\mathbf{S}{\mathbf{N}}_{{\mathit{\alpha }}_g}^L\mathbf{\Phi },\end{array}$$3.6 and the model (3.73.7 $$\begin{array}{c}\hfill \mathbf{P}{\mathbf{A}}_{{\mathit{\alpha }}_g}\mathbf{\Phi }-\mathbf{P}\mathbf{S}{\mathbf{N}}_{{\mathit{\alpha }}_g}^L\mathbf{\Phi }=\mathbf{P}{\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr},g=1,\dots ,G.\end{array}$$3.7 ) for the laser guide star measurements can be rewritten as3.7 $$\begin{array}{c}\hfill \mathbf{P}{\mathbf{A}}_{{\mathit{\alpha }}_g}\mathbf{\Phi }-\mathbf{P}\mathbf{S}{\mathbf{N}}_{{\mathit{\alpha }}_g}^L\mathbf{\Phi }=\mathbf{P}{\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr},g=1,\dots ,G.\end{array}$$3.7 The above equation is fulfilled if3.8 $$\begin{array}{c}\hfill {\mathbf{A}}_{{\mathit{\alpha }}_g}\mathbf{\Phi }-\mathbf{S}{\mathbf{N}}_{{\mathit{\alpha }}_g}^L\mathbf{\Phi }={\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr},g=1,\dots ,G.\end{array}$$3.8 which is now an equation that has to be solved from the reconstructed and tip/tilt removed phases ${\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr}$. In order to integrate the tip/tilt sensor measurements into the reconstruction of the atmosphere, we have to solve the following set of $G+N$ operator equations simultaneously:3.9 $$\begin{array}{cc}\hfill \left({\mathbf{A}}_{{\mathit{\alpha }}_g},-,\mathbf{S},{\mathbf{N}}_{{\mathit{\alpha }}_g}^L\right)\mathbf{\Phi }& ={\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr},g=1,\dots ,G,\hfill \\ \hfill {\mathbf{N}}_{{\mathit{\beta }}_n}\mathbf{\Phi }& ={\mathbf{t}}_{{\mathit{\beta }}_n},n=1,\dots ,N.\hfill \end{array}$$3.9 This can again be achieved with a Kaczmarz iteration, see Algorithm 3.1. As we have to take the adjoint operators of ${\mathbf{A}}_{{\mathit{\alpha }}_g}$ and ${\mathbf{N}}_{{\mathit{\alpha }}_g}^L$ at the same time, it is essential for the convergence results to consider the operators in the same function spaces, that is, we need to choose the numerically more expensive $H^{1,\mathit{\sigma }}$ setting. As a plus, we would expect better reconstruction results compared to the separate tip/tilt reconstruction.

In order to perform the Kaczmarz iteration, we also need the adjoint of the operator $\mathbf{S}$. As ${\mathbf{A}}_{{\mathit{\alpha }}_g}$ and $\mathbf{S}$ have the same range, it seems suitable to consider$$\begin{array}{c}\hfill \mathbf{S}:{\mathbb{R}}^2⟶L_2({\mathrm{\Omega }}_D).\end{array}$$We obtain

Proposition 3.1

The adjoint of the operator $\mathbf{S}$ in the $L_2$ setting is given by3.10 $$\begin{array}{ccc}\hfill {\mathbf{S}}^{\ast }& :\hfill & \hfill L_2⟶{\mathbb{R}}^2,\\ \hfill {\mathbf{S}}^{\ast }u& =\left(\begin{array}{c}\underset{{\mathrm{\Omega }}_D}{\int }x·u(x,y)dxdy\\ \underset{{\mathrm{\Omega }}_D}{\int }y·u(x,y)dxdy\end{array}\right).\hfill \end{array}$$3.10

Proof

For the proof, we simply have to use the relation$$\begin{array}{c}\hfill {〈S\mathbf{t},u〉}_{L_2}=\underset{{\mathrm{\Omega }}_D}{\int }(t^x·x+t^y·y)·u(x,y)dxdy={〈\mathbf{t},{\mathbf{S}}^{\ast }u〉}_{{\mathbb{R}}^2}\end{array}$$with ${\mathbf{S}}^{\ast }u$ defined in (3.143.14 $$\begin{array}{c}\hfill \left({\mathbf{A}}_{{\mathit{\alpha }}_g},-,\mathbf{S},{\mathbf{N}}_{{\mathit{\alpha }}_g}^L\right)\mathbf{\Phi }={\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr},g=1,\dots ,G.\end{array}$$3.14 ). $\square$

It is interesting to note that the adjoint of $\mathbf{S}$ considered with respect to the inner product ${〈u,v〉}_{\diamond }:={〈\nabla u,\nabla v〉}_{L_2}$ is given by$${\mathbf{S}}^{\ast }u=\left(\begin{array}{c}\underset{{\mathrm{\Omega }}_D}{\int }\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }x}dxdy\\ \underset{{\mathrm{\Omega }}_D}{\int }\frac{\mathit{\partial }u(x,y)}{\mathit{\partial }y}dxdy\end{array}\right)$$i.e. represents tip/tilt measurements of $u$.

3.2 Separate tip/tilt reconstruction

We will now propose a method that considers the information coming from laser guide stars and natural guide stars separately, and obtains the reconstruction of the atmosphere as a combination of the atmospheres reconstructed from the LGS and the NGS. We wish to remark that the idea of a separate treatment of LGS/NGS information was already proposed as Split Tomography in [15] in a finite-dimensional setting leading to a different method then the here presented one.

In the first step of our approach, we decompose the atmosphere $\mathbf{\Phi }$ into3.11 $$\begin{array}{c}\hfill \mathbf{\Phi }={\mathbf{\Phi }}_{{}_{LGS}}+{\mathbf{\Phi }}_{{}_{TT}},\end{array}$$3.11 where ${\mathbf{\Phi }}_{{}_{LGS}}$ is the part of the atmosphere that is reconstructable from the incoming wavefronts from LGSs, and ${\mathbf{\Phi }}_{{}_{TT}}$ is the part of the atmosphere that is not seen by LGS measurements.

We again consider the Equations (3.13.1 $$\begin{array}{cc}\hfill {\mathbf{N}}_{{\mathit{\alpha }}_g}^L\mathbf{\Phi }& ={\mathbf{t}}_{{\mathit{\alpha }}_g}=\left(\begin{array}{c}{t}_{{\mathit{\alpha }}_g}^x\\ t_{{\mathit{\alpha }}_g}^y\end{array}\right)\in {\mathbb{R}}^2,i=1,\dots ,N.\hfill \\ \hfill t_{{\mathit{\alpha }}_g}^x& =\sum _{l=1}^L\underset{{\mathbf{\Omega }}_D}{\int }\frac{\mathit{\partial }}{\mathit{\partial }x}{\mathrm{\Phi }}^{(l)}(c_l\mathbf{r}+h_l{\mathit{\alpha }}_g)d\mathbf{r}\hfill \\ \hfill t_{{\mathit{\alpha }}_g}^y& =\sum _{l=1}^L\underset{{\mathbf{\Omega }}_D}{\int }\frac{\mathit{\partial }}{\mathit{\partial }y}{\mathrm{\Phi }}^{(l)}(c_l\mathbf{r}+h_l{\mathit{\alpha }}_g)d\mathbf{r},\hfill \end{array}$$3.1 )–(3.33.3 $$\begin{array}{cc}\hfill \left({\mathbf{P}}_x,{\mathbf{A}}_{{\mathit{\alpha }}_g},\mathbf{\Phi }\right)[i,j]-t_{{\mathit{\alpha }}_g}^x& =\left({\mathbf{P}}_x,{\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr}\right)[i,j],\hfill \\ \hfill \left({\mathbf{P}}_y,{\mathbf{A}}_{{\mathit{\alpha }}_g},\mathbf{\Phi }\right)[i,j]-t_{{\mathit{\alpha }}_g}^y& =\left({\mathbf{P}}_y,{\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr}\right)[i,j],\hfill \end{array}$$3.3 ). Integration of the partial derivatives of ${\mathbf{A}}_{{\mathit{\alpha }}_g}{\mathbf{\Phi }}_{{}_{TT}}$ yields3.12 $$\begin{array}{c}\hfill \left(\begin{array}{c}\underset{{\mathbf{\Omega }}_D}{\int }\frac{\mathit{\partial }}{\mathit{\partial }x}\left({\mathbf{A}}_{{\mathit{\alpha }}_g},{\mathbf{\Phi }}_{{}_{TT}}\right)(\mathbf{r})d\mathbf{r}\\ \underset{{\mathbf{\Omega }}_D}{\int }\frac{\mathit{\partial }}{\mathit{\partial }y}\left({\mathbf{A}}_{{\mathit{\alpha }}_g},{\mathbf{\Phi }}_{{}_{TT}}\right)(\mathbf{r})d\mathbf{r}\end{array}\right)={\mathbf{N}}_{{\mathit{\alpha }}_g}^L{\mathbf{\Phi }}_{{}_{TT}}.\end{array}$$3.12 As a consequence, we can approximately determine ${\mathbf{\Phi }}_{{}_{TT}}$ by solving the equation ${\mathbf{N}}_{{\mathit{\alpha }}_g}^L{\mathbf{\Phi }}_{{}_{TT}}={\mathbf{t}}_{{\mathit{\alpha }}_g}$. Unfortunately, measurements of the tip/tilt are not available in the laser guide star direction. Therefore, we propose to reconstruct ${\mathbf{\Phi }}_{{}_{TT}}$ from the tip/tilt measurements, i.e. to determine ${\mathbf{\Phi }}_{{}_{TT}}$ as solution to the equations3.13 $$\begin{array}{c}\hfill {\mathbf{N}}_{{\mathit{\beta }}_i}{\mathbf{\Phi }}_{{}_{TT}}={\mathbf{t}}_{{\mathit{\beta }}_i},i=1,\dots ,N,\end{array}$$3.13 and ${\mathbf{\Phi }}_{{}_{LGS}}$ as solution of3.14 $$\begin{array}{c}\hfill \left({\mathbf{A}}_{{\mathit{\alpha }}_g},-,\mathbf{S},{\mathbf{N}}_{{\mathit{\alpha }}_g}^L\right)\mathbf{\Phi }={\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr},g=1,\dots ,G.\end{array}$$3.14 Note that the reconstruction of ${\mathbf{\Phi }}_{{}_{TT}}$ and ${\mathbf{\Phi }}_{{}_{LGS}}$ can be done independently and in parallel. We also wish to remark that, as the involved operators do not admit a unique solution, the reconstructed atmosphere $\mathbf{\Phi }={\mathbf{\Phi }}_{{}_{LGS}}+{\mathbf{\Phi }}_{{}_{TT}}$ is only a promising candidate for the true atmosphere.

Let us start with the computation of ${\mathbf{\Phi }}_{{}_{TT}}$ by solving (3.173.17 $$\begin{array}{c}\hfill \mathcal{R}({\mathbf{N}}^{\ast })=\bigcup _{i=1}^N\mathcal{R}({\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast })=\text{span}\{{\mathbf{u}}_i^1,{\mathbf{u}}_i^2|i=1,\dots ,N\}.\end{array}$$3.17 ) for $i=1,\dots ,N$ or, equivalently,3.15 $$\begin{array}{c}\hfill \mathbf{N}{\mathbf{\Phi }}_{{}_{TT}}=\mathbf{T},\end{array}$$3.15 with $\mathbf{N}:{⨂}_{l=1}^L{H}^{1,\mathit{\sigma }}({\mathbf{\Omega }}_l)\to {\mathbb{R}}^{2·N}$ and3.16 $$\begin{array}{c}\hfill \mathbf{N}{\mathbf{\Phi }}_{{}_{TT}}=\left(\begin{array}{c}{\mathbf{N}}_{{\mathit{\beta }}_1}{\mathbf{\Phi }}_{{}_{TT}}\\ ⋮\\ {\mathbf{N}}_{{\mathit{\beta }}_N}{\mathbf{\Phi }}_{{}_{TT}}\end{array}\right),\mathbf{T}=\left(\begin{array}{c}{t}_{{\mathit{\beta }}_1}^x\\ t_{{\mathit{\beta }}_1}^y\\ ⋮\\ t_{{\mathit{\beta }}_N}^x\\ t_{{\mathit{\beta }}_N}^y\end{array}\right).\end{array}$$3.16 Note that Equation (3.193.19 $$\begin{array}{c}\hfill \sum _{j=1}^2\sum _{i=1}^N{\mathit{\kappa }}_{ji}{\mathbf{N}}_{{\mathit{\beta }}_k}{\mathbf{u}}_k^j=\left(\begin{array}{c}{t}_{{\mathit{\beta }}_k}^x\\ t_{{\mathit{\beta }}_k}^y\end{array}\right),k=1,\dots ,N.\end{array}$$3.19 ) might only have a generalized solution, i.e. a solution of the equation$${\mathbf{N}}^{\ast }\mathbf{N}{\mathbf{\Phi }}_{{}_{TT}}={\mathbf{N}}^{\ast }\mathbf{T},{\mathbf{N}}^{\ast }=\left(\begin{array}{c}{\mathbf{N}}_{{\mathit{\beta }}_1}^{\ast }\\ ⋮\\ {\mathbf{N}}_{{\mathit{\beta }}_N}^{\ast }\end{array}\right).$$In the following, we are aiming at the reconstruction of a solution of (3.193.19 $$\begin{array}{c}\hfill \sum _{j=1}^2\sum _{i=1}^N{\mathit{\kappa }}_{ji}{\mathbf{N}}_{{\mathit{\beta }}_k}{\mathbf{u}}_k^j=\left(\begin{array}{c}{t}_{{\mathit{\beta }}_k}^x\\ t_{{\mathit{\beta }}_k}^y\end{array}\right),k=1,\dots ,N.\end{array}$$3.19 ) fulfilling$$\begin{array}{c}\hfill {\mathbf{\Phi }}_{{}_{TT}}\in \mathcal{N}{(\mathbf{N})}^{\perp }=\mathcal{R}({\mathbf{N}}^{\ast }),\end{array}$$i.e. a solution of (3.193.19 $$\begin{array}{c}\hfill \sum _{j=1}^2\sum _{i=1}^N{\mathit{\kappa }}_{ji}{\mathbf{N}}_{{\mathit{\beta }}_k}{\mathbf{u}}_k^j=\left(\begin{array}{c}{t}_{{\mathit{\beta }}_k}^x\\ t_{{\mathit{\beta }}_k}^y\end{array}\right),k=1,\dots ,N.\end{array}$$3.19 ) with minimal norm. According to (2.323.4 $$\begin{array}{c}\hfill \mathbf{P}{\mathbf{A}}_{{\mathit{\alpha }}_g}\mathbf{\Phi }-\mathbf{Q}{\mathbf{N}}_{{\mathit{\alpha }}_g}^L\mathbf{\Phi }=\mathbf{P}{\mathit{\phi }}_{{\mathit{\alpha }}_g}^{ttr},g=1,\dots ,G.\end{array}$$3.4 ), we can characterize $\mathcal{R}({\mathbf{N}}^{\ast })$ as3.17 $$\begin{array}{c}\hfill \mathcal{R}({\mathbf{N}}^{\ast })=\bigcup _{i=1}^N\mathcal{R}({\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast })=\text{span}\{{\mathbf{u}}_i^1,{\mathbf{u}}_i^2|i=1,\dots ,N\}.\end{array}$$3.17 Thus, if ${\mathbf{\Phi }}_{{}_{TT}}$ exists as a solution of (3.193.19 $$\begin{array}{c}\hfill \sum _{j=1}^2\sum _{i=1}^N{\mathit{\kappa }}_{ji}{\mathbf{N}}_{{\mathit{\beta }}_k}{\mathbf{u}}_k^j=\left(\begin{array}{c}{t}_{{\mathit{\beta }}_k}^x\\ t_{{\mathit{\beta }}_k}^y\end{array}\right),k=1,\dots ,N.\end{array}$$3.19 ), it admits a decomposition3.18 $$\begin{array}{c}\hfill {\mathbf{\Phi }}_{{}_{TT}}=\sum _{j=1}^2\sum _{i=1}^N{\mathit{\kappa }}_{ji}{\mathbf{u}}_i^j,\end{array}$$3.18 with the matrix $\mathbf{K}={({\mathit{\kappa }}_{ji})}_{i=1,\dots ,N}^{j=1,2}$. Applying the operators ${\mathbf{N}}_{{\mathit{\beta }}_k}$ to (3.222.21 $$\begin{array}{cc}\hfill B=& -\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Psi }}_1^{(l)}d\mathbf{r}-\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Psi }}_1^{(l)}d\mathbf{r}+\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}-\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Psi }}_2^{(l)}d\mathbf{r}-\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Psi }}_2^{(l)}d\mathbf{r}\hfill \\ & +\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{{\mathbf{\Omega }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }n}{\mathrm{\Psi }}^{(l)}d\mathbf{r}\hfill \\ \hfill =& \underset{{\mathrm{\Gamma }}_l}{\int }\left({\mathrm{\Psi }}_2^{(l)},-,{\mathrm{\Psi }}_1^{(l)}\right)\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}+\underset{{\mathrm{\Gamma }}_l}{\int }\left(\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}},-,\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}.\hfill \end{array}$$2.21 ) yields

Proposition 3.2

Assume that a solution of (3.193.19 $$\begin{array}{c}\hfill \sum _{j=1}^2\sum _{i=1}^N{\mathit{\kappa }}_{ji}{\mathbf{N}}_{{\mathit{\beta }}_k}{\mathbf{u}}_k^j=\left(\begin{array}{c}{t}_{{\mathit{\beta }}_k}^x\\ t_{{\mathit{\beta }}_k}^y\end{array}\right),k=1,\dots ,N.\end{array}$$3.19 ) exists. Then, the solution with minimal norm admits a decomposition (3.222.21 $$\begin{array}{cc}\hfill B=& -\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Psi }}_1^{(l)}d\mathbf{r}-\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Psi }}_1^{(l)}d\mathbf{r}+\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}-\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Psi }}_2^{(l)}d\mathbf{r}-\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Psi }}_2^{(l)}d\mathbf{r}\hfill \\ & +\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{{\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{{\mathbf{\Omega }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }n}{\mathrm{\Psi }}^{(l)}d\mathbf{r}\hfill \\ \hfill =& \underset{{\mathrm{\Gamma }}_l}{\int }\left({\mathrm{\Psi }}_2^{(l)},-,{\mathrm{\Psi }}_1^{(l)}\right)\frac{\mathit{\partial }{\mathrm{\Phi }}^{(l)}}{\mathit{\partial }{n}_{li}}d\mathbf{r}+\underset{{\mathrm{\Gamma }}_l}{\int }\left(\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}},-,\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}\right){\mathrm{\Phi }}^{(l)}d\mathbf{r}\hfill \\ & +\underset{\mathit{\partial }\mathbf{\Omega }({\mathit{\beta }}_i{h}_l)\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}+\underset{\mathit{\partial }\overline{\mathrm{\Omega }({\mathit{\beta }}_i{h}_l)}\backslash {\mathrm{\Gamma }}_l}{\int }\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}{\mathrm{\Phi }}^{(l)}d\mathbf{r}.\hfill \end{array}$$2.21 ), and the coefficients ${\mathit{\kappa }}_{ji}$ are determined as the solution of the finite-dimensional system3.19 $$\begin{array}{c}\hfill \sum _{j=1}^2\sum _{i=1}^N{\mathit{\kappa }}_{ji}{\mathbf{N}}_{{\mathit{\beta }}_k}{\mathbf{u}}_k^j=\left(\begin{array}{c}{t}_{{\mathit{\beta }}_k}^x\\ t_{{\mathit{\beta }}_k}^y\end{array}\right),k=1,\dots ,N.\end{array}$$3.19 Solving (3.193.19 $$\begin{array}{c}\hfill \sum _{j=1}^2\sum _{i=1}^N{\mathit{\kappa }}_{ji}{\mathbf{N}}_{{\mathit{\beta }}_k}{\mathbf{u}}_k^j=\left(\begin{array}{c}{t}_{{\mathit{\beta }}_k}^x\\ t_{{\mathit{\beta }}_k}^y\end{array}\right),k=1,\dots ,N.\end{array}$$3.19 ), therefore, reduces the inversion of a $2N\times 2N$ matrix $\mathbf{K}$.

Note that a similar characterization of ${\mathbf{\Phi }}_{{}_{TT}}$ is possible if there exists a generalized solution only. However, we observed in our numerical examples that the matrix $\mathbf{K}$ had full rank, i.e. (3.193.19 $$\begin{array}{c}\hfill \sum _{j=1}^2\sum _{i=1}^N{\mathit{\kappa }}_{ji}{\mathbf{N}}_{{\mathit{\beta }}_k}{\mathbf{u}}_k^j=\left(\begin{array}{c}{t}_{{\mathit{\beta }}_k}^x\\ t_{{\mathit{\beta }}_k}^y\end{array}\right),k=1,\dots ,N.\end{array}$$3.19 ) is always solvable. Equation (3.183.18 $$\begin{array}{c}\hfill {\mathbf{\Phi }}_{{}_{TT}}=\sum _{j=1}^2\sum _{i=1}^N{\mathit{\kappa }}_{ji}{\mathbf{u}}_i^j,\end{array}$$3.18 ) can be solved by appropriate iterative methods, in particular by a Kaczmarz method, which was introduced in [8] for the atmospheric tomography problem. The method computes cyclic updates for each of the Equations (3.183.18 $$\begin{array}{c}\hfill {\mathbf{\Phi }}_{{}_{TT}}=\sum _{j=1}^2\sum _{i=1}^N{\mathit{\kappa }}_{ji}{\mathbf{u}}_i^j,\end{array}$$3.18 ) and (3.173.17 $$\begin{array}{c}\hfill \mathcal{R}({\mathbf{N}}^{\ast })=\bigcup _{i=1}^N\mathcal{R}({\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast })=\text{span}\{{\mathbf{u}}_i^1,{\mathbf{u}}_i^2|i=1,\dots ,N\}.\end{array}$$3.17 ), separately. It has been shown that the method converges fast and gives a good reconstruction quality. The method is easily adapted in order to include the cone effect, see Algorithm 2. Note that the wavefronts ${\mathit{\phi }}_{{\mathit{\alpha }}_g}$ have to be tip/tilt removed.

For more information on the Kaczmarz method and its convergence properties we refer to [26–30].

Let us point out a significant advantage of Algorithm 3.2. As we are solving (3.183.18 $$\begin{array}{c}\hfill {\mathbf{\Phi }}_{{}_{TT}}=\sum _{j=1}^2\sum _{i=1}^N{\mathit{\kappa }}_{ji}{\mathbf{u}}_i^j,\end{array}$$3.18 ) and (3.173.17 $$\begin{array}{c}\hfill \mathcal{R}({\mathbf{N}}^{\ast })=\bigcup _{i=1}^N\mathcal{R}({\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast })=\text{span}\{{\mathbf{u}}_i^1,{\mathbf{u}}_i^2|i=1,\dots ,N\}.\end{array}$$3.17 ) separately, we can consider the operators in different function spaces. As already mentioned, the operators ${\mathbf{N}}_{{\mathit{\beta }}_i}$ are not well defined on $L_2$, thus we have to consider them as operators defined on a direct product of $H^{1,\mathit{\sigma }}$ spaces. The operators ${\mathbf{A}}_{{\mathit{\alpha }}_g}$ are well defined both on $L_2$ and $H^{1,\mathit{\sigma }}$ spaces. However, the implementation of the adjoint operator in an $H^{1,\mathit{\sigma }}$ setting requires significantly more numerical operations than in the $L_2$ setting (see [8]); therefore, it makes sense to consider the operators ${\mathbf{A}}_{{\mathit{\alpha }}_g}$ defined on $L_2$.

4 Numerical results

4.1 The application of the operator ${\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast }$

Let us first illustrate the result of the application of the adjoint operator to a single layer. As mentioned in Section 2.1, Equations (2.232.23 $$\begin{array}{cc}\hfill {\mathrm{\Psi }}_1^{(l)}-\mathit{\sigma }\mathrm{\Delta }{\mathrm{\Psi }}_1^{(l)}& =0\text{in}\mathbf{\Omega }(h_l{\mathit{\beta }}_i),\hfill \\ \hfill {\mathrm{\Psi }}_2^{(l)}-\mathit{\sigma }\mathrm{\Delta }{\mathrm{\Psi }}_2^{(l)}& =0\text{in}\overline{\mathbf{\Omega }(h_l{\mathit{\beta }}_i)},\hfill \\ \hfill {\mathrm{\Psi }}_1^{(l)}& ={\mathrm{\Psi }}_2^{(l)}\text{on}{\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}& =\frac{{\mathit{\gamma }}_l}{\mathit{\sigma }}·{\mathbf{t}}^T·n_{li}\text{on}\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)\backslash {\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}& =0\text{on}\overline{\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)}\backslash {\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}-\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}& =\frac{{\mathit{\gamma }}_l}{\mathit{\sigma }}·{\mathbf{t}}^T·n_{li}\text{on}{\mathrm{\Gamma }}_l,\hfill \end{array}$$2.23 )–(2.282.27 $$\begin{array}{c}\hfill \mathcal{R}({\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast })=\text{span}\{{\mathbf{u}}_i^1,{\mathbf{u}}_i^2\},\end{array}$$2.27 ) have to be solved for the unit vectors ${(1,0)}^T$ and ${(0,1)}^T$ only, the application of the adjoint to an arbitrary vector in ${\mathbb{R}}^2$ is obtained by superposition. We will present now the solutions of (2.232.23 $$\begin{array}{cc}\hfill {\mathrm{\Psi }}_1^{(l)}-\mathit{\sigma }\mathrm{\Delta }{\mathrm{\Psi }}_1^{(l)}& =0\text{in}\mathbf{\Omega }(h_l{\mathit{\beta }}_i),\hfill \\ \hfill {\mathrm{\Psi }}_2^{(l)}-\mathit{\sigma }\mathrm{\Delta }{\mathrm{\Psi }}_2^{(l)}& =0\text{in}\overline{\mathbf{\Omega }(h_l{\mathit{\beta }}_i)},\hfill \\ \hfill {\mathrm{\Psi }}_1^{(l)}& ={\mathrm{\Psi }}_2^{(l)}\text{on}{\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}& =\frac{{\mathit{\gamma }}_l}{\mathit{\sigma }}·{\mathbf{t}}^T·n_{li}\text{on}\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)\backslash {\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}& =0\text{on}\overline{\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)}\backslash {\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}-\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}& =\frac{{\mathit{\gamma }}_l}{\mathit{\sigma }}·{\mathbf{t}}^T·n_{li}\text{on}{\mathrm{\Gamma }}_l,\hfill \end{array}$$2.23 )–(2.282.27 $$\begin{array}{c}\hfill \mathcal{R}({\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast })=\text{span}\{{\mathbf{u}}_i^1,{\mathbf{u}}_i^2\},\end{array}$$2.27 ) for a simple geometrical set-up, consisting of a circle intersecting an ellipse, see Figure 2.

Figure 2. Domain for the evaluation of ${\mathbf{N}}_{{\mathit{\beta }}_1}^{\ast }$.

For this simple example, we assume that we have tip/tilt measurements ${\mathbf{t}}_{{\mathit{\beta }}_1}$ available on the circle $\mathrm{\Omega }$, and have to construct $\mathbf{\Phi }={\mathbf{\Phi }}_1+{\mathbf{\Phi }}_2={\mathbf{N}}_{{\mathit{\beta }}_1}^{\ast }{\mathbf{t}}_{{\mathit{\beta }}_1}$ on $\mathrm{\Omega }\cup \overline{\mathrm{\Omega }}$. Considering a single layer ($L=1$), with the direction ${\mathit{\beta }}_1$ and setting the parameter $\mathit{\sigma }={\mathit{\gamma }}_1=1$, we have, according to (2.232.23 $$\begin{array}{cc}\hfill {\mathrm{\Psi }}_1^{(l)}-\mathit{\sigma }\mathrm{\Delta }{\mathrm{\Psi }}_1^{(l)}& =0\text{in}\mathbf{\Omega }(h_l{\mathit{\beta }}_i),\hfill \\ \hfill {\mathrm{\Psi }}_2^{(l)}-\mathit{\sigma }\mathrm{\Delta }{\mathrm{\Psi }}_2^{(l)}& =0\text{in}\overline{\mathbf{\Omega }(h_l{\mathit{\beta }}_i)},\hfill \\ \hfill {\mathrm{\Psi }}_1^{(l)}& ={\mathrm{\Psi }}_2^{(l)}\text{on}{\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}& =\frac{{\mathit{\gamma }}_l}{\mathit{\sigma }}·{\mathbf{t}}^T·n_{li}\text{on}\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)\backslash {\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{\overline{n}}_{li}}& =0\text{on}\overline{\mathit{\partial }\mathbf{\Omega }(h_l{\mathit{\beta }}_i)}\backslash {\mathrm{\Gamma }}_l,\hfill \\ \hfill \frac{\mathit{\partial }{\mathrm{\Psi }}_1^{(l)}}{\mathit{\partial }{n}_{li}}-\frac{\mathit{\partial }{\mathrm{\Psi }}_2^{(l)}}{\mathit{\partial }{n}_{li}}& =\frac{{\mathit{\gamma }}_l}{\mathit{\sigma }}·{\mathbf{t}}^T·n_{li}\text{on}{\mathrm{\Gamma }}_l,\hfill \end{array}$$2.23 )–(2.282.27 $$\begin{array}{c}\hfill \mathcal{R}({\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast })=\text{span}\{{\mathbf{u}}_i^1,{\mathbf{u}}_i^2\},\end{array}$$2.27 ), to solve the pde system$$\begin{array}{cc}\hfill {\mathbf{\Phi }}_1-\mathit{\sigma }\mathrm{\Delta }{\mathbf{\Phi }}_1& =0\text{in}\mathbf{\Omega }\hfill \\ \hfill {\mathbf{\Phi }}_2-\mathit{\sigma }\mathrm{\Delta }{\mathbf{\Phi }}_2& =0\text{in}\overline{\mathbf{\Omega }}\hfill \\ \hfill {\mathbf{\Phi }}_1& ={\mathbf{\Phi }}_2\text{on}\mathrm{\Gamma }\hfill \\ \hfill \frac{\mathit{\partial }{\mathbf{\Phi }}_1}{\mathit{\partial }n}& ={\mathbf{t}}_{{\mathit{\beta }}_1}^T·n\text{on}\mathit{\partial }\mathbf{\Omega }\backslash \mathrm{\Gamma }\hfill \\ \hfill \frac{\mathit{\partial }{\mathbf{\Phi }}_2}{\mathit{\partial }\overline{n}}& =0\text{on}\overline{\mathit{\partial }\mathbf{\Omega }}\backslash \mathrm{\Gamma }\hfill \\ \hfill \frac{\mathit{\partial }{\mathbf{\Phi }}_1}{\mathit{\partial }n}-\frac{\mathit{\partial }{\mathbf{\Phi }}_2}{\mathit{\partial }n}& ={\mathbf{t}}_{{\mathit{\beta }}_1}^T·n\text{on}\mathrm{\Gamma },\hfill \end{array}$$

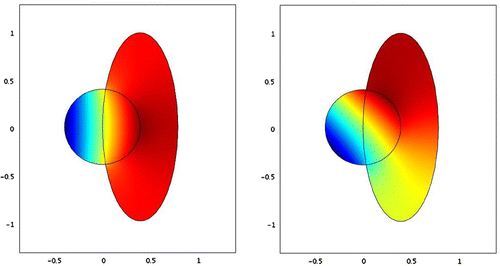
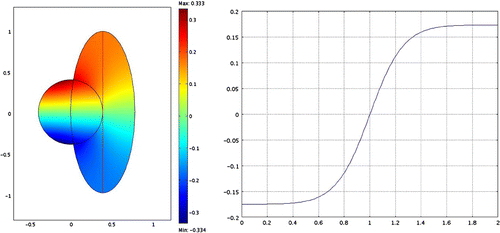
Figure 3. Reconstructed $\mathbf{\Phi }$ for ${\mathbf{t}}_{{\mathit{\beta }}_1}={(0,1)}^T$ (left) and function values of $\mathbf{\Phi }$ along a vertical line through the center of the ellipse (right, the line is also depicted in the left image).

Figure 4. Reconstructed $\mathbf{\Phi }$ for ${\mathbf{t}}_{{\mathit{\beta }}_1}={(1,0)}^T$ (left) and for ${\mathbf{t}}_{{\mathit{\beta }}_1}{(\sqrt{2},\sqrt{2})}^T$ (right).

where $n$ denotes the normal vector to $\mathit{\partial }\mathbf{\Omega }$, and $\overline{n}=-n$. As pointed out, we only solve the system for the unit tip/tilt vectors ${(1,0)}^T$ and ${(0,1)}^T$. Figure 3 shows the resulting phase for the vector ${(0,1)}^T$. The reconstructed function within the circle (see Figure 3) resembles a plane, thus, a tip/tilt. Outside the circle, where no tip/tilt measurements are available, the reconstruction of the tip/tilt in the circle is smoothly extended to the ellipse, see Figure 3. In Figure 4, the reconstructions of $\mathbf{\Phi }$ for ${\mathbf{t}}_{{\mathit{\beta }}_1}={(1,0)}^T$ and ${\mathbf{t}}_{{\mathit{\beta }}_1}={(\sqrt{2},\sqrt{2})}^T$ are displayed.

Note that in Figure 4, the extension of the tip/tilt outside the circle is almost constant, which is due to the fact that the geometry of our example and the chosen tip/tilt measurements allow a smooth continuation. This is, however, not the case for the other examples.

4.2 Reconstruction of a nine-layer atmosphere

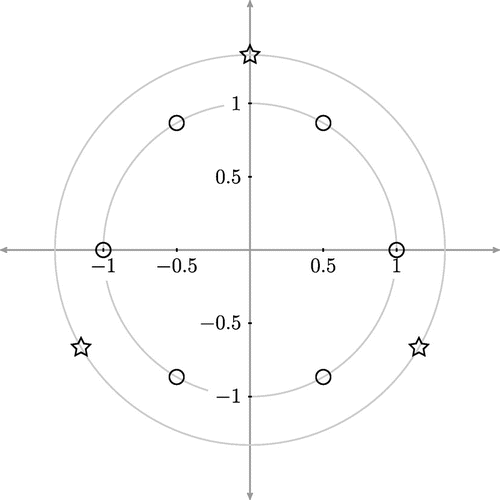
We will now present numerical results for a tip/tilt reconstruction using six-laser guide stars and three-tip/tilt sensors.

The physical set-up used for our simulations is closely related to the definition of the MAORY system in [31]. The NGS are located on a circle with radius 1.33 arcmin, the LGS on a circle with radius 1 arcmin. The height of the laser guide stars is assumed to be $h_{LGS}=90$km. For simulation and reconstruction, we use the nine-layer atmosphere defined in Table 1. The Fried parameter of the atmosphere was set to $r_0=0.129$m.

Figure 5 shows the positions of the NGS and LGS. In the wavefronts ${\mathit{\phi }}_{{\mathit{\alpha }}_g}$, $g=1,\dots ,G$, originating from LGS, the (incorrect) tip/tilt was removed, and the tip/tilt on each layer was reconstructed based on the NGS measurements only. For the reconstruction, we used both the separated (Algorithm 2) and the integrated approach (Algorithm 1).

Table 1. Location of the layers in the atmosphere.

Layer	1	2	3	4	5	6	7	8	9
Height (m)	47	140	281	562	1125	2250	4500	9000	18,000
$c_n^2$-profile	0.52	0.027	0.04	0.12	0.1	0.03	0.06	0.043	0.06

Figure 5. Position of NGS (star) and LGS (circle).

As the tip/tilt reconstruction is needed on each layer, the functions $\{{\mathbf{u}}_i^1,{\mathbf{u}}_i^2|i=1,\dots ,3\}$, spanning the range of the operator ${\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast }$, are needed on each layer. As pointed out in Section 2.1, we, therefore, have to evaluate the operators ${\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast }$ on the unit vectors ${(1,0)}^T$ and ${(0,1)}^T$. The functions were reconstructed on a square containing the area ${\mathbf{\Omega }}_l$. Figure 6 shows the functions ${\mathbf{u}}_i^1,{\mathbf{u}}_i^2,i=1,2,3$ on layer $9$ only (note that the functions ${\mathbf{u}}_i^j$ have a contribution on each layer).

The system of pde’s was solved using a Finite Element method with quadratic ansatz functions. The results have been studied with respect to different choices of the parameter $\mathit{\sigma }$. In Figure 6 and all numerical results below, a value of $\mathit{\sigma }=$ 10,000 has been used in the computations. Additionally, we would like to remark that the use of the operators ${\mathbf{N}}_{{\mathit{\beta }}_i}^{\ast }$ yields a smooth continuation of the tip/tilt reconstruction over the whole square area, including ${\mathbf{\Omega }}_l$.

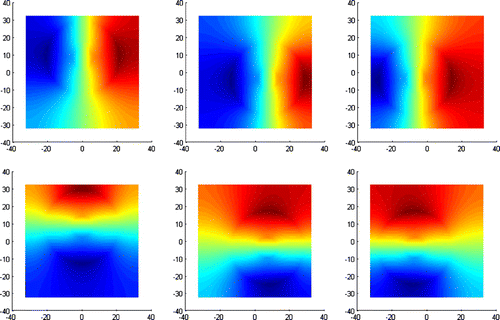
Finally, we compare the performance of the separated approach, the integrated approach and an MVM reconstructor. All simulations and reconstructions have been performed within ESO’s Octopus simulation tool.[32] The used MVM method is an internal Octopus MAP reconstructor, based on a standard (bilinear) discretization. The simulations have been carried out in pseudo-open loop for 500 time steps, which equals a simulation time of 1 s. As time control, a simple integrator has been applied. The Strehl ratio has been used as quality measure (a Strehl ratio equal to 1 resembles the best possible image quality for a telescope with fixed diameter). Figure 7 shows a contour plot of the achievable reconstruction quality over the field of view for the separated as well as the integrated approach.

Figure 6. Tip/tilt ansatz functions ${\mathbf{u}}_i^1,i=1,2,3$ (first row) and ${\mathbf{u}}_i^2,i=1,2,3$ (second row) on layer 9.

Figure 7. Contour plot of the Strehl ratio for the integrated (left) and separated (right) approach.

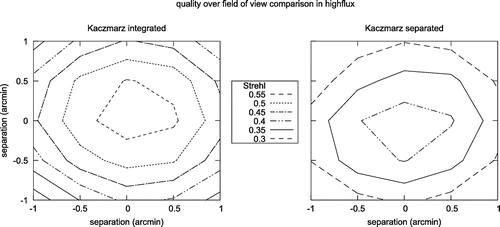
Figure 8. Short and long exposure on-axis Strehl ratios for MVM, separated and integrated reconstructors. The test was carried out with a photon flux of 10,000.

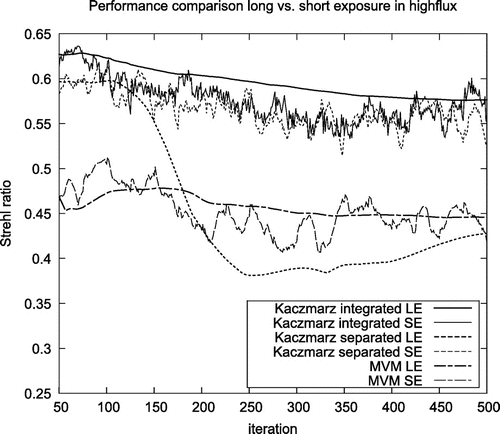
Figure 9. Short and long exposure on-axis Strehl ratios for MVM, separated and integrated reconstructors. The test was carried out with a photon flux of 500.

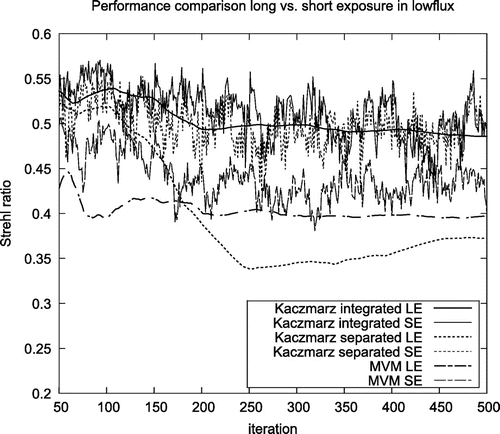
Figure 10. LE Strehl ratios, averaged over the field of view, over photon flux level for MVM, separated and integrated reconstructors.

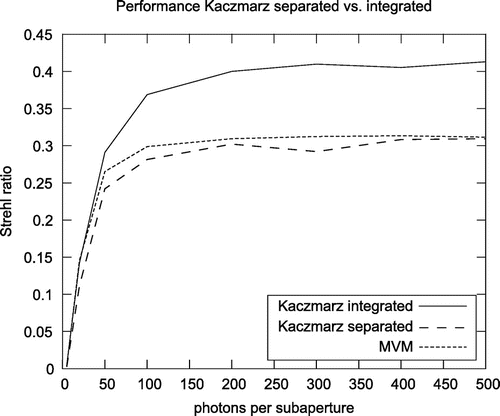
Figures 8 and 9 show the development of the Short- and Long-Exposure (LE) Strehl ratios for the MVM reconstructor as well as the separated and integrated approaches. Both the separated and the integrated approach show a better Short Exposure (SE) Strehl ratio compared to the MVM reconstructor. However, the LE Strehl of the integrated approach is significantly higher than the values for the two other approaches. Additionally, the Short and LE Strehls are close to each other for the integrated approach, which is an indication for a good tip/tilt reconstruction. Note that the LE Strehls of the separated approach and the MVM reconstructor are close to each other. These results are confirmed by Figure 10, where the LE Strehl, averaged over the field of view, is displayed for different photon flux levels, corresponding to different levels of noise. Again, the integrated approach gives the best results, whereas MVM and the separated approach display comparable results.

One of the main reasons for a new algorithm in adaptive optics is the high computational effort for the standard method. The MVM has a complexity of $4(G\ast n_{wfs}+N)n_{dm}$, where $n_{wfs}$ is the number of subapertures in a Shack–Hartmann wavefront sensor and $n_{dm}$ is the number of all actuators in the DM. For future big telescopes this number is too high to perform the calculation within the time available.

For the Kaczmarz method, we have to add the complexity of the different steps. The reconstruction of the wavefronts with CuReD can be performed in $20n_{wfs}$ operations, as stated in [24]. Assuming the use of bilinear ansatz functions on a rectangular grid, a single Kaczmarz iteration has a total number of $G\ast (18L-14)\ast n_{wfs}$ operations, with $L$ the number of layers considered. The handling of the tip/tilt indetermination gives another $2G\ast n_{wfs}$ operations, the additional NGS add $N\ast (L-1)\ast 8n_{wfs}+2\ast L\ast n_{wfs}$ to the total amount. The projection onto the mirrors is done with Kaczmarz iterations as well. This can be performed in $D\ast (18L-14)\ast n_{wfs}$, where $D$ is the number of optimization directions.

For a better understanding, we computed the numbers for the standard setting with six LGS with $84\times 84$ subapertures (approx. 75% active), three NGS with tip/tilt sensors and three DM with a total of about 9300 actuators. For the MVM, this leads to a computational complexity of $11.8\times {10}^8$ operations. For the Kaczmarz algorithm, we need $6.4\times {10}^5$ operations for the wavefront reconstructions. If the reconstruction is performed on the nine layers of the atmosphere with five iterations, the effort sums up to $2.9\times {10}^7$ operations. In the projection step, 25 optimization directions are assumed. This leads to an additional computational complexity of $2.65\times {10}^7$ operations. Therefore, we can state that the Kaczmarz algorithm is approximately 20 times faster than the MVM algorithm.

Based on our numerical results, we conclude that the integrated approach delivers the best results for the reconstruction of the atmosphere from combined LGS/NGS measurements. The achieved reconstruction quality is even higher than the quality from the standard MVM reconstructor. The separated approach delivers a quality comparable to MVM. As the separated approach is numerically cheaper than the integrated approach, one might consider to use its tip/tilt reconstruction as an initial guess for the integrated approach.

Acknowledgments

This work was supported by the Austrian Ministry of Science within the framework of the ESO Austrian In-kind contribution. Furthermore, the authors would like to thank in particular Stefan Kindermann from Industrial Mathematics Institute, JKU Linz for helpful discussions.