Elasticity imaging of biological soft tissue using a combined finite element and non-linear optimization method

Abstract

A novel material reconstruction method combining finite element (FE)-based direct inverse method and non-linear optimization algorithm is proposed for elasticity imaging of biological soft tissue. The biological soft tissue is represented using Neo-Hookean hyperelastic model. The FE-based direct inverse method provides an estimation of material parameter distribution which serves as the initial guess of the Levenberg–Marquardt optimization algorithm. Direct calculation of Jacobian matrix is proposed to improve the computational efficiency of the combined algorithm. Computer simulation demonstrated that the material parameters of soft tissue can be determined rapidly and accurately within a small tolerance using the proposed method. Our experimental results on a human lower leg demonstrated the clinical viability of this method.

Keywords:

• elastography
• finite element method
• inverse problems
• non-linear optimization

AMS subject classifications:

• 15A29
• 74B20
• 74S05

1. Introduction

Elasticity is an important property for soft tissue characterization. Local changes in mechanical properties of soft tissues may indicate the presence of tumours and other diseases.[1] Palpation is traditionally used by physicians to detect the presence of tumours. However, palpation greatly depends on the experiences of physician, and is a subjective method for determining the tissue properties. Moreover, many parts of human body such as the brain and deep abdominal organs cannot be assessed simply by human hands. In order to quantitatively study the soft tissue mechanical properties, various elasticity imaging methods, including ultrasonic elastography [2–8] and magnetic resonance elastography,[9–14] have been proposed in the last two decades.

Elasticity imaging of soft tissue can be divided into two categories: dynamic methods and quasi-static methods. Dynamic methods determine soft tissue elasticity from propagating waves inside the soft tissue while quasi-static methods utilise displacement/strain image to calculate the soft tissue elasticity. Recently, Latorre-Ossa et al. proposed a method combining static method and dynamic method to determine the non-linear shear modulus by applying the acoustoelasticity theory in quasi-incompressible soft solids.[8] In this paper, we focused on quasi-static methods. Common procedure of quasi-static methods is to measure internal displacement field of soft tissue using ultrasound or magnetic resonance imaging by applying quasi-static compression to the soft tissue. The elasticity distribution of the soft tissue is then determined from the measured displacement field using various inverse methods.[7,8,15,16] Quasi-newton optimization approach was used by Gokhale et al. to minimise difference between measured and predicted displacement field assuming hyperelastic material.[17,18] Gradient was calculated using adjoint method. In Sumi and Matsuzawa’s method, soft tissue was treated as linear elastic, incompressible material.[6] Constant shear modulus is assumed on the boundary of region of interest. Relative shear modulus of soft tissue is obtained by solving a partial differential equation. Mcgrath et al. used an iterative method to update Young’s modulus of soft tissue based on numerically calculated stress distribution assuming linear elastic material.[19]

Among these methods, optimization method is commonly used.[20–24] Firstly, soft tissue is modelled by a number of elements in finite element (FE) method. Simulated displacement field is calculated using the FE model. Secondly, the residual between the simulated displacement field and the measured displacement field is minimised using the optimization method. This method approaches the solution through an iterative process. A uniform initial guess of the element stiffness is often used in the first iteration. Finite difference approximation is usually used to calculate the entries of the Jacobian matrix J.[2,25] The entries of J are obtained by slightly perturbing the stiffness of each element separately, and then solving the forward FE analysis for each perturbation. Since the finite difference approximation method needs to perform forward FE analysis repeatedly, this method is computationally expensive, particularly for FE model that has a large number of elements.

Another commonly used method is a FE-based direct inverse method.[26,27] In this method, the solution is obtained by minimising an objective function defined as the sum of the square of the force residual norms at all nodes. Measured nodal displacement vector is directly applied to equilibrium equations at the element level. After global assembly in FE method, material stiffness vector can be expressed explicitly and calculated directly. This method is efficient since no forward FE analysis is needed. However, this method is sensitive to noise and is only applicable to linear elastic material. Soft biological tissue is a highly incompressible hyperelastic material.[28–30] Mechanical behaviour of hyperelastic material differs significantly from that of linear elastic material. It is important to develop a computationally efficient method which is applicable to hyperelastic material models.

In this paper, we propose a novel material parameter reconstruction method for hyperelastic material models. This method combines the advantages of the FE-based direct inverse method and the non-linear optimization algorithm. In the optimization method, the initial guess is important since a poor guess may result in much iteration for convergence or even non-convergence. The widely used uniform initial guess may not be the optimal initial guess. In our method, an estimation of the true material stiffness distribution is first determined using the FE-based direct inverse method. This estimation is then input to the Levenberg–Marquardt (LM) optimization algorithm as the initial guess. Final solution is obtained after the optimization process. In the optimization method, a new algorithm is proposed for the calculation of Jacobian matrix. There is no need to perform the repeated forward FE analysis using this algorithm. Neo-Hookean hyperelastic model is used to represent the biological soft tissue. Forward FE analysis is performed using Abaqus which is commercial FE software. The execution of Abaqus in our implementation is controlled via customised Python scripts.

Section 2 describes the proposed inverse algorithm. In Section 3, the proposed algorithm is implemented, and verified with applications to solve 2D plane strain compression problems. In Section 4, the proposed method is used to determine the elasticity distribution of a human lower leg. This paper concludes with a discussion on the efficiency of the proposed algorithm and its contributions in Section 5.

2. Method

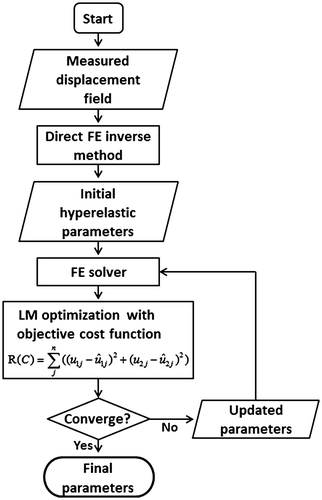
A novel elasticity imaging method is proposed by combining FE-based direct inverse method and non-linear optimization algorithm. Instead of using a uniform material stiffness distribution as an initial guess, an estimation of the true material stiffness distribution calculated by FE-based direct inverse method is used. Since the initial guess is estimated and is relatively closer to the true material stiffness distribution, smaller number of iterations is required for convergence. Instead of relying on finite difference method for Jacobian calculation, direct calculation of Jacobian matrix is introduced to improve the computational efficiency.

2.1. Neo-Hookean hyperelastic model

In this study, isotropic hyperelastic model is used to represent the nearly incompressible biological soft tissue. Hyperelastic materials may be described in terms of ‘strain energy potential’ which defines the strain energy stored in the material per unit of reference volume as a function of the strain at that point in the material. Deformation gradient is defined by (1) $$[F]=\frac{\mathit{\partial }x}{\mathit{\partial }X}=[I]+\frac{\mathit{\partial }u}{\mathit{\partial }X}$$(1)

where X is a material point in the reference configuration, x is the current position of the point and u is the displacement. Both x and u are a function of time. The implementation of Neo-Hookean model in ABAQUS is given by (2) $$U=C\left(\overline{I_1}-3\right)+\frac{1}{D}{(J-1)}^2$$(2)

where U is the strain energy per unit of reference volume, C and D are material parameters. $\overline{I_1}$ and J are the strain invariants of the deviatoric left Cauchy–Green deformation tensor which is defined by(3) $$\left[\overline{B}\right]=\overline{[F]}·{\overline{[F]}}^T$$(3)

where $\overline{[F]}=J^{-\frac{1}{3}}[F]$. The material Jacobian is given by(4) $$E_{ijkl}=\frac{2}{J}C\left(\frac{1}{2}\left({\mathit{\delta }}_{ik}{\overline{B}}_{jl}+{\overline{B}}_{ik}{\mathit{\delta }}_{jl}+{\mathit{\delta }}_{il}{\overline{B}}_{jk}+{\overline{B}}_{il}{\mathit{\delta }}_{jk}\right)-\frac{2}{3}{\mathit{\delta }}_{ij}{\overline{B}}_{kl}-\frac{2}{3}{\overline{B}}_{ij}{\mathit{\delta }}_{kl}+\frac{2}{9}{\mathit{\delta }}_{ij}{\mathit{\delta }}_{kl}{\overline{B}}_{mm}\right)+\frac{2}{D}(2J-1){\mathit{\delta }}_{ij}{\mathit{\delta }}_{kl}.$$(4)

2.2. Material stiffness estimation

The continuum is first discretized into a number of elements and each material parameter is an unknown variable. The displacement within an element can be approximated by [31](5) $$\left\{u(x)\right\}=\left[N(x)\right]\left\{u^e\right\}$$(5)

where {u^e}is the element nodal displacement vector, N(x) is the shape function matrix. Strain tensor is calculated using(6) $$\mathit{\epsilon }(x)=[L]·\left[N(x)\right]\{u^e\}=[B]\{u^e\}$$(6)

where [L] is a differential operation matrix, [B] is the strain matrix. The element tangential stiffness matrix can be expressed as (7) $$\left[K_T^e(C^e)\right]=\int {{}_{{\mathrm{\Omega }}^e}{[B]}^T[E_T][B]d\mathrm{\Omega }}^e=C^e[\overline{K_1^e]}+\frac{1}{D}[\overline{K_2^e}]$$(7)

where $\overline{[K_1^e]}$ and $\overline{[K_2^e]}$ are the respective reference element tangential stiffness matrices associated with a unit material parameters, [E_T] is the material tangential elasticity matrix, C^e is the material parameter of the element, D represents the soft tissue compressibility and is assumed to be constant over the entire domain for simplification. The element internal force vector is(8) $$\{f^e(e)\}\approx C^e[\overline{K_1^e}]\{u^e\}+\frac{1}{D}[\overline{K_2^e}]\{u^e\}=C^e\{\overline{f_1^e}\}+\frac{1}{D}\{\overline{f_2^e}\}$$(8)

where $\{\overline{f_1^e}\}$ and $\{\overline{f_2^e}\}$ are the respective reference element internal force vectors associated with a unit material parameters.

Reduced Gauss integration and isoparametric coordinates mapping are used to calculate the integrations and element shape functions. The global force vector is obtained through an assembling process over the entire domain. Boundary conditions need to be incorporated during this assembling process. Similar to forward FE analysis, ‘fixed’ boundary degree of freedoms (DOFs) are removed from the system equations. By defining an element assembly matrix [H^e], the ‘fixed’ boundary DOFs can be eliminated in the inverse problem. Each DOF is assigned an index i, i  =  1, 2 … n_d, where n_d is the total system DOF. For each element e, an $n_d\ast n_d^e$ element assembly matrix [H^e] is defined, where $n_d^e$ is the DOF of a single element. The entry of [H^e] is $H_{ij}^e=1$, if the jth DOF of the element is assigned the ith system DOF and not a ‘fixed’ boundary DOF. Otherwise, $H_{ij}^e=0$. When constructing the global internal force vector, a material parameter selective vector {G^e} needs to be defined. For the ith element, $\{G^{e_i}\}$ is defined as $G_j^{e_i}={\mathit{\delta }}_{ij}$. After the DOFs corresponding to the ‘fixed’ displacement boundary are removed, the global internal force vector can be expressed as(9) $$\{F\}=\sum _{\text{all}}[H^e]\{{\overline{f_1}}^e\}\{G^e\}\{C\}+\sum _{\text{all}}[H^e]\{{\overline{f_2}}^e\}\{G^e\}\left\{\frac{1}{D}\right\}=\{\overline{F_1}\}\{C\}+\{\overline{F_2}\}\left\{\frac{1}{D}\right\}$$(9)

where [H^e] is an element assembly mapping matrix, {G^e} is a material parameter selective matrix, and $\{\overline{F_1}\}$ and $\{\overline{F_2}\}$ are global reference internal force vector associated with unit material parameters, respectively. After assembling, the global equilibrium equation reads(10) $$[\overline{F_1}]\{C\}+[\overline{F_2}]\left\{\frac{1}{D}\right\}=\{P\}$$(10)

where {P} is external force vector.

The dimension of vector $[\overline{F_1}]$ and $[\overline{F_2}]$ is n_d× n_e. The dimensions of {C} and {P} are n_e× 1 and n_d× 1, respectively. In other words, there are n_d equations and n_e unknowns in the system. If n_d  <  n_e, there is not enough spatial information for material parameter reconstruction problem. In this situation, the solution is generally not unique. Extra displacement tracking points or a prior-known material parameter is required to derive a unique solution. If n_d = n_e, which rarely happens, {C} can be obtained directly by(11) $$\{C\}={[\overline{F_1}]}^{-1}\left(\{P\}-\{\overline{F_2}\}\left\{\frac{1}{D}\right\}\right)$$(11)

when $[\overline{F_1}]$ is non-singular. In most cases, n_d  >  n_e, by minimising the global force residue, the solution can be given by(12) $$\{C\}={\left\{{[\overline{F_1}]}^T[\overline{F_1}]\right\}}^{-1}{[\overline{F_1}]}^T\left(\{P\}-\{\overline{F_2}\}\left\{\frac{1}{D}\right\}\right)$$(12)

when ${[\overline{F_1}]}^T[\overline{F_1}]$ is non-singular. If the matrix ${[\overline{F_1}]}^T[\overline{F_1}]$ is singular, the solution will not be unique. New displacement tracking points or remeshing of the FE model is required to solve this problem.[16]

2.3. LM optimization

In FE analysis, hyperelastic non-linear problem is usually solved through an iterative procedure. Traction boundary condition is applied using an incremental method. The material tangential elasticity matrix varies in every incremental step due to the strain dependency property of the hyperelastic model. Since the stiffness matrix in (7) is used to estimate the incrementally changing tangential stiffness matrix, the material parameter calculated by (12) is only an estimation of the true material stiffness distribution. This estimation then serves as the initial guess of the LM optimization algorithm to calculate the material stiffness distribution.

Unknown Neo-Hookean material parameters are determined by minimising the least-square difference between the simulated nodal displacement and the measured displacement. The objective function can be expressed as(13) $$R(C)=\sum _j^n\left({(u_{1j}-{\widehat{u}}_{1j})}^2+{(u_{2j}-{\widehat{u}}_{2j})}^2\right)$$(13)

where C is the material parameter to be optimised, $u_{1j},u_{2j}$ are the measured displacement vectors in x and y direction, respectively, ${\widehat{u}}_{1j}$, ${\widehat{u}}_{2j}$ are the simulated displacement vectors, and n is the total number of nodes in the system.

Finite difference approximation is usually used to calculate the Jacobian matrix J.[2,25] The forward FE analysis has to be solved repeatedly by slightly perturbing one material parameter in each forward FE analysis. If there are N elements in the FE model, the forward FE analysis has to be solved N times to obtain the Jacobian matrix J. In order to improve the computational efficiency of the algorithm, we introduce a new algorithm to calculate the Jacobian matrix directly. Consider a FE model with linear material, the FE equilibrium equation reads(14) $$[K]\{u\}=\{f\},\text{and}\{u\}={[K]}^{-1}\{f\}.$$(14)

Taking the first derivatives of u with respect to C, we have(15) $$\{J_i\}=\left\{\frac{\mathit{\partial }u}{\mathit{\partial }{C}_i}\right\}=\left[\frac{\mathit{\partial }{K}^{-1}}{\mathit{\partial }{C}_i}\right]\{f\}=-{[K]}^{-1}\left[\frac{\mathit{\partial }K}{\mathit{\partial }{C}_i}\right]{[K]}^{-1}\{f\}\approx -{[K]}^{-1}[H^e][\overline{K_1^i}]{[H^e]}^T{[K]}^{-1}\{f\}$$(15)

where i = 1, 2 … N is the element number, C_i is the material parameter of ith element, K is the global stiffness matrix, f is the global nodal force vector, $[\overline{K_1^i}]$is the derivative of element stiffness matrix with respect to the ith elemental material parameter and [H^e] is the element assembly mapping matrix.(16) $$[J]=[J_1,J_2,\dots J_N].$$(16)

The Jacobian matrix J can be estimated directly by substituting the stiffness matrix K with tangential stiffness matrix K_T. Computational efficiency of the algorithm is greatly improved with this method.

To tackle the ill-posedness, a traditional Tikhonov regularisation technique is implemented by means of (17) $$\{\widehat{C}\}={({[J]}^T[J]+\mathit{\mu }I)}^{-1}{[J]}^T\{P\}$$(17)

where $\{\widehat{C}\}$ is optimization step, μ is a damping factor which influences both the direction and size of the optimization step, and {P} is the external force vector. Refer to [32,33] for the use of damping factor μ during regularizations.

3. Numerical simulation and sensitivity study

In order to evaluate the performance of the proposed algorithm, two experiments with different strain levels and inclusion geometries were performed with example models as shown in Figures 1 and 2. Different levels of noise were added to the input displacement field to test the noise sensitivity of our method. Plain strain condition was assumed in both FE models.

Figure 1. (a) The geometry and boundary conditions of the FE model, (b) FE mesh.

Figure 2. (a) The geometry and boundary conditions of the FE model, (b) FE mesh.

3.1. Rectangular inclusion with small strain level

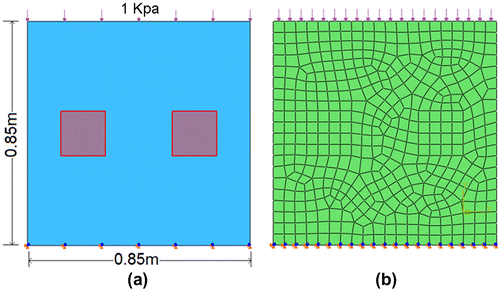
The two shadowed regions in the model represented the hard inclusions embedded within the softer homogeneous background. Neo-Hookean model was used in the analysis. In the forward FE analysis, material parameter D was set to 2× 10⁻⁷ Pa⁻¹ while material parameter C of the hard inclusions and soft background were set to 7× 10⁵ Pa and 5× 10⁵ Pa, respectively. Uniform pressure load of 1× 10³ Pa was applied onto the top surface. Both horizontal and vertical DOF of bottom surface were constrained. Each hard inclusion was divided into 16 elements and the entire domain was divided into 446 elements with 487 nodes. Quadrilateral element type CPE4R was used throughout the domain. Both material non-linearity and geometric non-linearity were considered in a static step.

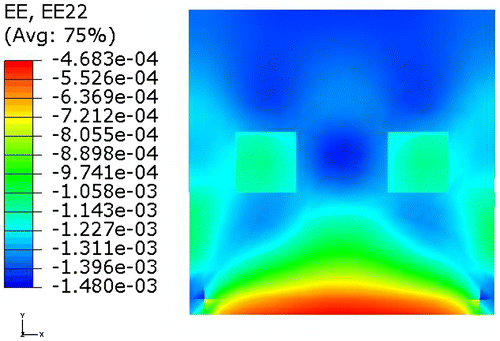
In order to examine the numerical consistency of the proposed algorithm, the nodal displacement field calculated in the forward FE analysis was used for elasticity reconstruction. Simulation was performed under small strain level. Figure 3 shows the contour of the vertical normal strain without mesh on the deformed shape.

Figure 3. Contours of the normal strain in the vertical direction.

An estimation of the material stiffness distribution was first calculated using the method described in Section 2.2. Final solution was obtained after LM optimization with this estimation as the initial guess. Results including 3D and side elevations of the material stiffness distribution are shown in Figure 4.

Figure 4. (a1)(a2) Estimated and final parameters obtained with exact displacement data, (b1)(b2) Estimated and final parameters obtained with ±1% noise added, (c1)(c2) Estimated and final parameters obtained with ±3% noise added.

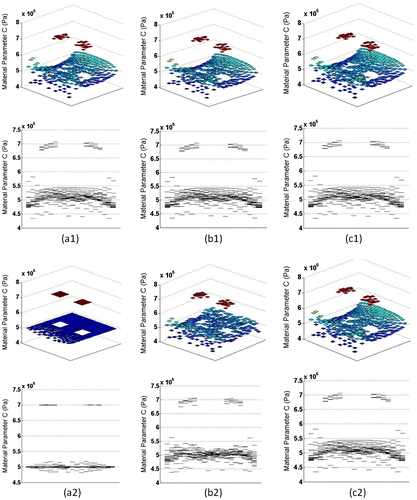
The proposed algorithm recovered the exact material stiffness distribution using the exact displacement field. The error in the final solution will eventually become negligible with a harsher convergence condition. In practice, the available displacement field data always suffer from a certain level of noise. In order to evaluate the noise sensitivity of the algorithm, random noise was added to all the component of the exact displacement field. The noise was defined as (u_input/u_exact− 1), where u_input was the noise-impaired data. Displacement field with random noise of level ±1 and ±3% were tested and convergence occurs within an average error of 2.32 and 3.26% of the known parameters, respectively. Objective cost and relative error of the reconstructed material parameters are shown in Table 1. Compared to the initial estimation, better material reconstruction was obtained after the LM optimization. For reconstruction using data with ±3% noise, the final solution was the same as that of the initial guess. In this case, the optimization procedure did not improve upon the initial guess due to the noise.

Table 1. Sensitivity study result when different level of noise is added.

Condition	Initial guess				Final convergence
	Objective cost (R)	Relative error in stiffness (%)			Objective cost (R)	Relative error in stiffness (%)
		Min	Mean	Max		Min	Mean	Max
Exact data with no noise	5.07e − 6	7.21e − 3	3.26	16.42	1.37e − 11	2.43e − 5	0.29	3.60
Exact data with ±1% noise	8.52e − 6	7.21e − 3	3.26	16.42	3.40e − 6	0.01	2.32	12.56
Exact data with ±3% noise	3.49e − 5	7.21e − 3	3.26	16.42	3.49e − 5	7.21e − 3	3.26	16.42

3.2. Circular inclusion with large strain level

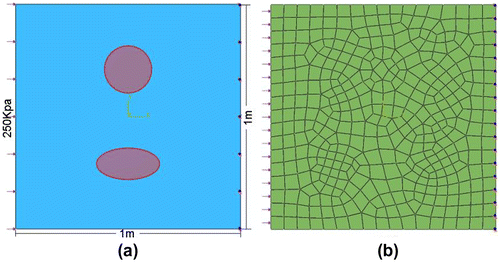
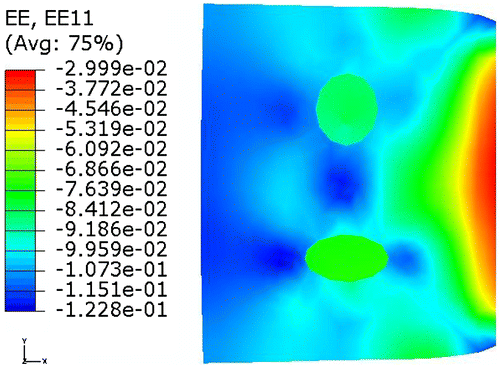
A circular and ellipsoidal inclusion was modelled with material parameter C set to be 7× 10⁵ Pa and 5× 10⁵ Pa, respectively. Material parameter C of the soft background was 3× 10⁵ Pa. Material parameter D was chosen to be 2× 10⁻⁷ Pa⁻¹ . Uniform pressure load of 200× 10³ Pa was applied onto the left surface. Both horizontal and vertical DOF of the right surface were constrained. The entire domain was divided into 388 elements with 423 nodes. Quadrilateral element type CPE4R was used throughout the domain. Both material non-linearity and geometric non-linearity were considered in a static step. The model reached a maximum normal strain level of 12%. Figure 5 shows the contour of the strain in the horizontal direction on the deformed shape.

Figure 5. Contour of the normal strain in the horizontal direction.

The proposed algorithm recovered the exact material stiffness distribution using the exact displacement field. Displacement data with random noise of ±0.5% were tested. Final stiffness distribution was obtained after the LM optimization. Results including 3D and side elevations of the material stiffness distribution are shown in Figure 6. Objective cost and relative error of the reconstructed material parameters are shown in Table 2. The result showed that the proposed algorithm performed well in large strain level.

Figure 6. (a1)(b1) Estimated and final parameters obtained with exact displacement data, (a2)(b2) Estimated and final parameters obtained with ±0.5% noise added.

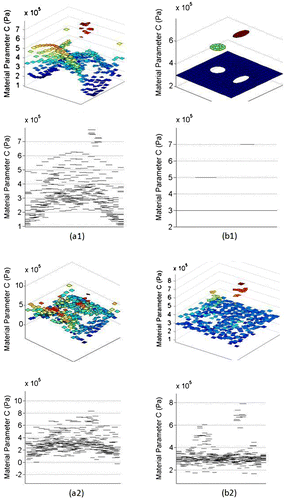
Table 2. Sensitivity study result when different level of noise is added.

Condition	Initial guess				Final convergence
	Objective cost (R)	Relative error in stiffness (%)			Objective cost (R)	Relative error in stiffness (%)
		Min	Mean	Max		Min	Mean	Max
Exact data with no noise	1.74e − 2	4.76e − 2	26.35	108.13	5.29e − 13	6.78e − 6	2.95e − 3	2.03e − 2
Exact data with ±0.5% noise	2.92e − 2	0.91	31.57	144.91	0.56e − 5	0.14e − 2	9.19	48.66

3.3. Computational time

The proposed algorithm was implemented using Matlab while the FE problem was solved using Abaqus based on customised Python scripts. The code was run on a workstation with a 2.4 GHz dual core Intel CPU and 2 GB of main memory. For comparison, the two models in Sections 3.2 and 3.3 were performed using a pure optimization method with a uniform initial guess of 6× 10⁵ Pa. Execution time of our method was compared to that of the pure optimization method under the same convergence condition. The execution time is shown in Table 3.

Table 3. Computational time. Method 1: proposed method. Method 2: pure optimization method (uniform initial guess, finite difference to calculated Jacobian matrix).

Methods	Model in Section 3.2		Model in Section 3.3
	Iteration number	Execution time	Iteration number	Execution time
Method 1	8	5 min	6	3 min
Method 2	16	>6 h	10	>6 h

Our method converged faster than that of the pure optimization method. This is because an estimated initial guess from our method is closer to the true solution than the uniform initial guess. Since Jacobian matrix is calculated directly, the execution time has been greatly reduced.

4. Experiments on human leg

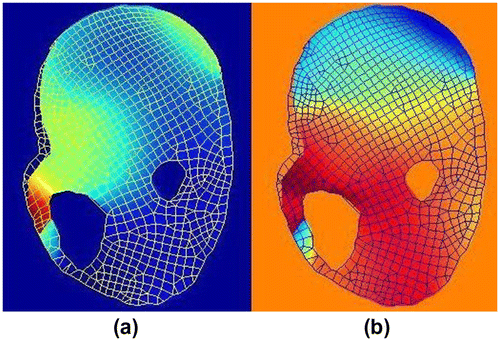
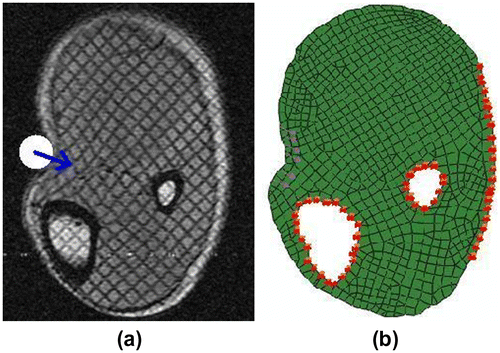
Tagged MR images of tissue deformation were acquired using our imaging system reported in [34]. A volunteer’s lower leg was indented using an MR-compatible actuator while the indentation force was recorded by a force sensor. FE model of the indentation experiment and boundary conditions are shown in Figure 7(a) and (b), respectively. The bones were modelled as rigid body. The entire domain was divided into 865 elements with 898 nodes. Triangular element type CPE3 and Quadrilateral element type CPE4R were used in the domain. Some nodal displacements were not considered in the optimization process since these nodal displacements were poorly measured. Only nodal displacements that were measured with high fidelity were the input of the proposed algorithm.

Figure 7. Images of human lower leg (a) MR image, white circle represents the indenter, blue arrow represents the indentation direction, (b) FE boundary conditions.

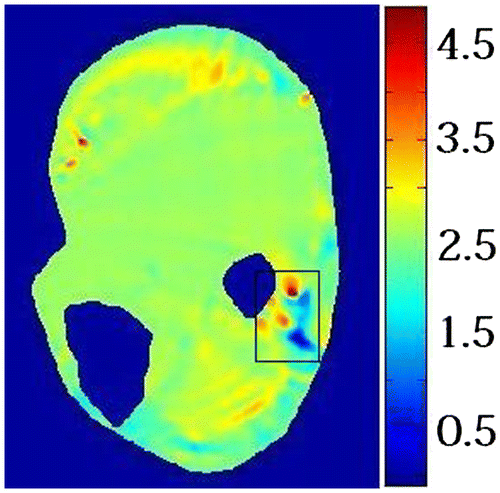
The proposed method was tested using measured displacement field from MR-tagged images. Displacement field was calculated from tagged MR image as illustrated in Figure 8(a) and (b). Signal to noise ratio (SNR) of the measured displacement on a specific tissue point is determined by the MR imaging modality and the displacement amplitude of this specific tissue point. The SNR was low where the tissue displacement was small. Since the deformation in the rectangle is hindered by the bone, SNR of the measured displacement in this region is low. Figure 9 shows the elasticity distribution of the human lower leg at rest computed using our method. The elasticity was uniformly distributed over the leg domain except for the region indicated by rectangle. The large elasticity variation in this region is due to the low SNR. The average shear modulus of the leg muscle was 5.53× 10³ Pa which was comparable to the results reported by Bensamoun et al. [35].

Figure 8. (a) Measured displacement in the horizontal direction, (b) Measured displacement in the vertical direction.

Figure 9. Elastography of human lower leg (Material Parameter: C, unit: kPa).

5. Discussion and conclusion

A new material parameter reconstruction method is proposed for hyperelastic material models by combining the FE-based direct inverse method and non-linear optimization method. Flowchart of our method is shown in Figure 10. The direct FE inverse method provides an estimation of the true material parameter distribution. This estimation serves as the initial guess of LM optimization algorithm. Direct calculation of Jacobian matrix is proposed to improve the computational efficiency of the LM optimization algorithm. Both numerical consistency and noise sensitivity of the proposed method are tested in its application to solve 2D plain strain problems. The proposed method was also verified using different inclusion shapes under different strain levels. Computer simulation results show that our method is computationally efficient, and is accurate for determining the material parameter distribution. The improved computational efficiency can be attributed to both estimated initial guess that is close to the true material parameter distribution and direct calculation of the Jacobian matrix.

Figure 10. Flowchart of the combined finite element and non-linear optimization method.

If the exact displacement field obtained by forward FE analysis is used, material stiffness can be recovered totally after the optimization process. When the data were contaminated with random noise, exact solution to material parameter {C} may not exist. Since the system tangential matrix is strain-dependent for hyperelastic material, the proposed method performed better in small strain level than that of large strain level. Calculation of strain involves differentiation of the measured displacement field. This differentiation may magnify the effect of the noise. The solution may diverge from the known solution due to the noise. It is important to use regularisation techniques to regularise the optimization process. Prior knowledge of the applied force is required to accurately compute the absolute elasticity distribution.

Although Neo-Hookean model has been used to model biological soft tissue in this algorithm, other polynomial hyperelastic models such as Mooney–Rivlin model can also be used. In this study, an example of pure compression is applied and plane strain condition is assumed for material reconstruction. Reduced integration is adopted in this paper. Since reduced integration may sometimes give poor results, full integration can be implemented if necessary. Although quadrilateral element is used throughout the FE model in this study, mixed element type meshing can be used in the proposed algorithm. Higher order elements can be used within the field of interest to improve the accuracy of FE model.[36] For different element type, different number of integration points should be used accordingly. This algorithm can be readily extended to 3D using 3D formulations of the system equilibrium equations. One limitation of this study is that it does not apply to complete incompressible material models which could be the future work of this ongoing project.

Our experimental results on a human lower leg demonstrated that the proposed method is clinically viable. Boundary condition was one of the most important factors that determine the accuracy of the stiffness calculation. MRI experiments with clear boundary conditions should be designed so that the FE model can be built with clearly defined boundary conditions. Other important factors were the quality of the MR images and force measurement during experiment. In order to obtain tissue stiffness map with high accuracy, good imaging modality and experimental design were required.

The material reconstruction algorithm was implemented using Matlab and Abaqus. There is a tight coupling between the Matlab codes and customised Abaqus subroutines written in Python scripts. The Matlab codes could be easily replaced with a more efficient programming language such as C or C++. The direct computation of the Jacobian matrix should be implemented in an efficient manner especially for FE models with a large number of elements. The Python scripting language is a convenient way of controlling the FE solution process in Abaqus. Nevertheless, FE solvers other than Abaqus could also be used.

Acknowledgements

This research is partially supported by NUS-JSPS Joint Research Project Grant (R-265-000-285-646 and R-265-000-285-123).