Spectral method for ill-posed problems based on the balancing principle

Abstract

In this article, we consider a class of ill-posed problems in two-dimensional setting which can be formulated as the problem of solving ill-posed operator equation. The spectral method is a simple and effective regularization method for such a class of ill-posed problems. For the spectral method, we obtain the error estimates with optimal order under an adaptive a posteriori parameter choice rule called balancing principle. Two ill-posed examples including an inverse diffraction problem and a deblurring problem are provided.

Keywords:

• ill-posedness
• regularization
• error estimate
• source condition

1 Introduction

Many PDE-based ill-posed problems in mathematical physics can be formulated as the problem for solving an operator equation, e.g. the inverse diffraction problem [1–4] and the deblurring problem.[5, 6] Therefore, theory analysis, such as error estimate for the spectral method, is possible for this kind of ill-posed problems. In this paper, we discuss this kind of ill-posed problems in two-dimensional space, which involves the numerical computation of pseudodifferential operator.

Let1.1 $$\begin{array}{c}\hfill \widehat{h}(\mathit{\xi },\mathit{\eta })=\frac{1}{2\mathit{\pi }}{\int }_{{\mathbb{R}}^2}h(x,y)e^{-i(\mathit{\xi }x+\mathit{\eta }y)}dxdy\end{array}$$1.1 be the Fourier transform of the function $h(x,y)\in L^2\left({\mathbb{R}}^2\right)$. The Sobolev function space $H^p\left({\mathbb{R}}^2\right)$ is defined by1.2 $$\begin{array}{cc}\hfill H^p\left({\mathbb{R}}^2\right)& =\left\{h(x,y)|h\in ,L^2,\left({\mathbb{R}}^2\right),,,{\Vert h\Vert }_p\right.\hfill \\ \hfill & \left.:,=,{\left({\int }_{{\mathbb{R}}^2},{\left(1,+,{\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)}^p,{|\widehat{h}\left(\mathit{\xi },,,\mathit{\eta }\right)|}^2,d,\mathit{\xi },d,\mathit{\eta }\right)}^{\frac{1}{2}},<,\infty \right\},\hfill \end{array}$$1.2 where $\widehat{h}(\mathit{\xi },\mathit{\eta })$ is the Fourier transform of function $h(x,y)$ and $\Vert ·\Vert :={\Vert ·\Vert }_0$ denotes the norm in $L^2\left({\mathbb{R}}^2\right)$.

Consider the numerical computation of the pseudodifferential operator with an unbounded symbol $a(\mathit{\xi },\mathit{\eta },s)$ given by1.3 $$\begin{array}{c}\hfill f(x,y,s)=\frac{1}{2\mathit{\pi }}{\int }_{{\mathbb{R}}^2}a(\mathit{\xi },\mathit{\eta },s)\widehat{g}(\mathit{\xi },\mathit{\eta })e^{i(\mathit{\xi }x+\mathit{\eta }y)}d\mathit{\xi }d\mathit{\eta },\end{array}$$1.3 where $s\in (0,L]$ is a fixed constant and $\widehat{g}(\mathit{\xi },\mathit{\eta })$ is the Fourier transform of the exact data $g(x,y)\in L^2\left({\mathbb{R}}^2\right)$; the data $g(x,y)$ is only given approximately by $g_{\mathit{\delta }}(x,y)\in L^2\left({\mathbb{R}}^2\right)$ satisfying1.4 $$\begin{array}{c}\hfill \Vert g(·,·)-g_{\mathit{\delta }}(·,·)\Vert \le \mathit{\delta },\end{array}$$1.4 where $\mathit{\delta }$ is the noise level and is assumed to be known.

We assume that the symbol $a(\mathit{\xi },\mathit{\eta },s)$ satisfies the following growth condition:1.5 $$\begin{array}{cc}\hfill C_{1}exp\left(s,\mathit{\varphi },\left({\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)\right)& \le |a\left(\mathit{\xi },,,\mathit{\eta },,,s\right)|\hfill \\ \hfill & \le C_{2}exp\left(s,\mathit{\varphi },\left({\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)\right),{\mathit{\xi }}^2+{\mathit{\eta }}^2\ge c_1,s\in (0,L],\hfill \\ \hfill & |a(\mathit{\xi },\mathit{\eta },s)|\le z(s),{\mathit{\xi }}^2+{\mathit{\eta }}^2<c_1,\hfill \end{array}$$1.5 where the function $\mathit{\varphi }(x)$ is strictly increasing with ${lim}_{x\to \infty }\mathit{\varphi }(x)=\infty$, the function $z(s)\in C[0,L]$ with $z(s)>0$ and $C_1,C_2,c_1>0$ are constants.

If $a(\mathit{\xi },\mathit{\eta },s)$ satisfies $|a(\mathit{\xi },\mathit{\eta },s)|=O(exp(c{({\mathit{\xi }}^2+{\mathit{\eta }}^2)}^b))$ as ${\mathit{\xi }}^2+{\mathit{\eta }}^2\to \infty$ with $c,b>0$, then we call the problem of numerical computation of the above pseudodifferential operators as a severely ill-posed problem. Likewise, if $a(\mathit{\xi },\mathit{\eta },s)$ satisfies $|a(\mathit{\xi },\mathit{\eta },s)|=O\left({\left({\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)}^b\right)$ as ${\mathit{\xi }}^2+{\mathit{\eta }}^2\to \infty$ with $b>0$, then we call the problem of numerical computation of above pseudodifferential operators as a mildly ill-posed problem. In this paper, we only consider the severely ill-posed problem since the mildly ill-posed problems can be solved more easily. The problem (1.31.3 $$\begin{array}{c}\hfill f(x,y,s)=\frac{1}{2\mathit{\pi }}{\int }_{{\mathbb{R}}^2}a(\mathit{\xi },\mathit{\eta },s)\widehat{g}(\mathit{\xi },\mathit{\eta })e^{i(\mathit{\xi }x+\mathit{\eta }y)}d\mathit{\xi }d\mathit{\eta },\end{array}$$1.3 ) in one-dimensional space has been discussed in [7] by the a posteriori Fourier method based on Morozov’s discrepancy principle. But, many ill-posed problems with important application backgrounds such as inverse diffraction and deblurring problems are set in two-dimensional case. This motivates us to consider the two-dimensional inverse problems. Although the authors in [7] analysed the Fourier method with a posteriori parameter choice rule by using a direct method, here we stress that we give a rule for selecting regularization parameter based on the theory of regularization framework. The analysis involved is more general.

A priori information about unknown solution has been proved to be essential in the analysis of ill-posed problems in mathematical physics. Otherwise, without the a priori information, the convergence rate of the constructed regularization method will be arbitrarily slow.[8] For analysis, we assume that there holds the a-priori bound for the unknown solution1.6 $$\begin{array}{c}\hfill {\Vert f(·,·,L)\Vert }_p\le E,p\ge 0.\end{array}$$1.6 Let $f_{\mathit{\alpha }}^{\mathit{\delta }}(·,·,s)$ denote a regularization solution. If $0\le s<L$, we call the $f_{\mathit{\alpha }}^{\mathit{\delta }}(·,·,s)$ as interior inversion. If $s=L$, we call the $f_{\mathit{\alpha }}^{\mathit{\delta }}(·,·,s)$ as boundary inversion.

Obviously, the ill-posedness of problem (1.31.3 $$\begin{array}{c}\hfill f(x,y,s)=\frac{1}{2\mathit{\pi }}{\int }_{{\mathbb{R}}^2}a(\mathit{\xi },\mathit{\eta },s)\widehat{g}(\mathit{\xi },\mathit{\eta })e^{i(\mathit{\xi }x+\mathit{\eta }y)}d\mathit{\xi }d\mathit{\eta },\end{array}$$1.3 ) is caused by components of high frequency. If $c_1\ne 0$, we only need to regularize the solution in the case of ${\mathit{\xi }}^2+{\mathit{\eta }}^2\ge c_1$, because for the case of ${\mathit{\xi }}^2+{\mathit{\eta }}^2\le c_1$ the problem (1.31.3 $$\begin{array}{c}\hfill f(x,y,s)=\frac{1}{2\mathit{\pi }}{\int }_{{\mathbb{R}}^2}a(\mathit{\xi },\mathit{\eta },s)\widehat{g}(\mathit{\xi },\mathit{\eta })e^{i(\mathit{\xi }x+\mathit{\eta }y)}d\mathit{\xi }d\mathit{\eta },\end{array}$$1.3 ) is well posed which can be observed by the following discussion:

Let the sets $W(\mathit{\xi },\mathit{\eta })=\{(\mathit{\xi },\mathit{\eta })|{\mathit{\xi }}^2+{\mathit{\eta }}^2\le c_1\}$ and $I(\mathit{\xi },\mathit{\eta })=\{(\mathit{\xi },\mathit{\eta })|{\mathit{\xi }}^2+{\mathit{\eta }}^2\ge c_1\}$, and we have $L^2\left({\mathbb{R}}^2\right)=L^2(W)⨁L^2(I)$.

Consider the difference$$\begin{array}{cc}& \Vert \widehat{f}(\mathit{\xi },\mathit{\eta },s)-{\widehat{f}}_{\mathit{\delta }}(\mathit{\xi },\mathit{\eta },s)\Vert {{}^2}_{L^2(W)}={\int }_W{|a(\mathit{\xi },\mathit{\eta },s)|}^2{|\widehat{g}(\mathit{\xi },\mathit{\eta })-{\widehat{g}}_{\mathit{\delta }}(\mathit{\xi },\mathit{\eta })|}^{2}d\mathit{\xi }d\mathit{\eta }\hfill \\ \hfill & \le z^2(s){\mathit{\delta }}^2\le C{\mathit{\delta }}^2,\hfill \end{array}$$where ${\widehat{f}}_{\mathit{\delta }}(\mathit{\xi },\mathit{\eta },s)$ denotes the solution with noisy data $g_{\mathit{\delta }}$.

The same technique has been used in.[9, 10] Throughout this paper, we mainly deal with the case of ${\mathit{\xi }}^2+{\mathit{\eta }}^2\ge c_1$.

By the balance principle,[11] we can derive a Hölder-type error estimate like $\Vert f_{\mathit{\alpha }}^{\mathit{\delta }}(·,·,s)-f(·,·,s)\Vert =O(E^{s/L}{\mathit{\delta }}^{1-\frac{s}{L}}),\mathit{\delta }\to 0$ under the a priori bound (1.61.6 $$\begin{array}{c}\hfill {\Vert f(·,·,L)\Vert }_p\le E,p\ge 0.\end{array}$$1.6 ) with $p=0$. However, when $s=L$, in which we should be more interested, we cannot get any convergence. To overcome the difficulty, usually a stronger a priori bound on the unknown solution is added, i.e. we should require $p>0$ for (1.61.6 $$\begin{array}{c}\hfill {\Vert f(·,·,L)\Vert }_p\le E,p\ge 0.\end{array}$$1.6 ) to obtain the convergence rate at $s=L$. In the following, we will construct the interior and boundary inversions by a spectral regularization method.

The outline of this paper is as follows. In Section 2, we present the spectral method. In Section 3, the spectral method is applied to solve problem (1.31.3 $$\begin{array}{c}\hfill f(x,y,s)=\frac{1}{2\mathit{\pi }}{\int }_{{\mathbb{R}}^2}a(\mathit{\xi },\mathit{\eta },s)\widehat{g}(\mathit{\xi },\mathit{\eta })e^{i(\mathit{\xi }x+\mathit{\eta }y)}d\mathit{\xi }d\mathit{\eta },\end{array}$$1.3 ); some applications are given in Section 4. In Section 5, some numerical results are presented. Finally, Section 6 concludes the paper.

2 The spectral method [12, 13]

2.1 Preliminaries

Ill-posed operator equations arise in several contexts and various aspects have been treated in the literature.[8, 14, 15] We cannot give here an exhaustive survey. In this paper, we are interested in solving the solution $x^{†}\in H_1$ of linear ill-posed problems by spectral cut-off method. Consider2.1 $$\begin{array}{c}\hfill Ax=y,\end{array}$$2.1 where $A:H_1\to H_2$ is a linear injective, closed operator between infinite-dimensional Hilbert spaces $H_1$ and $H_2$ with non-closed range $R(A)$. We suppose that $y^{\mathit{\delta }}\in H_2$ are the noisy data with2.2 $$\begin{array}{c}\hfill \Vert y-y^{\mathit{\delta }}\Vert \le \mathit{\delta }\end{array}$$2.2 and known noise level $\mathit{\delta }$.

If we consider the ill-posed problem $Kx=y$ where only noisy data $y^{\mathit{\delta }}$ are available, $K$ is a compact operator with singular system ${\{{\mathit{\sigma }}_n,v_n,u_n\}}_{n=1}^{\infty }$ since the ill-posedness is associated with the small singular values, an obvious idea is to truncate or damp the smaller singular values. That is the well-known truncated singular value decomposition method. These methods are simple and effective. In practical computation, we can implement the spectral cut-off method by mollification method discovered by Hào [16].

For problem (2.12.1 $$\begin{array}{c}\hfill Ax=y,\end{array}$$2.1 ), most regularization operators can be written in the form,2.3 $$\begin{array}{c}\hfill R_{\mathit{\alpha }}:=g_{\mathit{\alpha }}(A^{\ast }A)A^{\ast }\end{array}$$2.3 with some function $g_{\mathit{\alpha }}$ satisfying$$\begin{array}{c}\hfill \underset{\mathit{\alpha }\to 0}{lim}{g}_{\mathit{\alpha }}(\mathit{\lambda })=\frac{1}{\mathit{\lambda }},\end{array}$$where the operator function $g_{\mathit{\alpha }}(A^{\ast }A)$ is well defined via the spectral representation $g_{\mathit{\alpha }}(A^{\ast }A)={\int }_0^{a}g(\mathit{\lambda })d{E}_{\mathit{\lambda }}$. Here, $A^{\ast }A={\int }_0^a\mathit{\lambda }d{E}_{\mathit{\lambda }}$, $\{E_{\mathit{\lambda }}\}$ denotes the spectral family of the operator $A^{\ast }A$ and $a$ is a constant satisfying $\Vert A^{\ast }A\Vert \le a$ with $a=\infty$ if $A^{\ast }A$ is unbounded.

Then, for the regularization solution with unperturbed data, we have $x_{\mathit{\alpha }}:=R_{\mathit{\alpha }}y$ and $x^{†}-x_{\mathit{\alpha }}=r_{\mathit{\alpha }}(A^{\ast }A)x^{†}$ with $r_{\mathit{\alpha }}(\mathit{\lambda })=1-\mathit{\lambda }{g}_{\mathit{\alpha }}(\mathit{\lambda })$. For example, for spectral cut-off method,2.4 $$\begin{array}{c}\hfill g_{\mathit{\alpha }}(\mathit{\lambda })=\left\{\begin{array}{cc}\frac{1}{\mathit{\lambda }},\hfill & \mathit{\lambda }\ge \mathit{\alpha },\hfill \\ 0,\hfill & \mathit{\lambda }<\mathit{\alpha }.\hfill \end{array}\right.\end{array}$$2.4 In general, the exact solution $x^{†}\in X$ is required to satisfy a so-called source condition, otherwise the convergence of the regularization method approximating the problem can be arbitrarily slow. For ill-posed problems, the source condition is chosen as2.5 $$\begin{array}{c}\hfill x^{†}={\left[\mathit{\phi },(,A^{\ast },A,)\right]}^{1/2}\mathit{\omega },\Vert \mathit{\omega }\Vert \le E,\end{array}$$2.5 i.e. $x^{†}$ belongs to the source set2.6 $$\begin{array}{c}\hfill M_{\mathit{\phi },E}=\left\{{\left[\mathit{\phi },(,A^{\ast },A,)\right]}^{1/2},\mathit{\omega },,,,\mathit{\omega },\in ,X,,\text{and},\Vert \mathit{\omega }\Vert ,\le ,E\right\},\end{array}$$2.6 where $\mathit{\phi }(\mathit{\lambda })$ satisfies some properties:

Assumption 1

${lim}_{\mathit{\lambda }\to 0}\mathit{\phi }(\mathit{\lambda })=0$and$\mathit{\phi }(\mathit{\lambda })$is strict monotonically increasing, $\mathit{\rho }(\mathit{\lambda })=\mathit{\lambda }{\mathit{\phi }}^{-1}(\mathit{\lambda })$is convex.

For the stable approximate solution of problem (2.12.1 $$\begin{array}{c}\hfill Ax=y,\end{array}$$2.1 ) some regularization technique has to be applied, which provides regularized approximations $x_{\mathit{\alpha }}^{\mathit{\delta }}=R_{\mathit{\alpha }}^{\mathit{\delta }}{y}^{\mathit{\delta }}$ with property $x_{\mathit{\alpha }}^{\mathit{\delta }}\to x^{†}$ as $\mathit{\delta }\to 0$.

Any operator $R:H_2\to H_1$ can be considered as a special method for solving problem (2.12.1 $$\begin{array}{c}\hfill Ax=y,\end{array}$$2.1 ). the approximate solution to (2.12.1 $$\begin{array}{c}\hfill Ax=y,\end{array}$$2.1 ) is then given by $R{y}^{\mathit{\delta }}$. Consider the worst case error $\mathrm{\Delta }(\mathit{\delta },R)$ for identifying the solution $x^{†}$ of problem (2.12.1 $$\begin{array}{c}\hfill Ax=y,\end{array}$$2.1 ) from noisy data $y^{\mathit{\delta }}$ under the assumptions $\Vert y-y^{\mathit{\delta }}\Vert \le \mathit{\delta }$ and $x^{†}$ belongs to a source set $M_{\mathit{\phi },E}$ which is defined by2.7 $$\begin{array}{c}\hfill \mathrm{\Delta }(\mathit{\delta },R)=sup\left\{\Vert R,y^{\mathit{\delta }},-,x^{†},\Vert |,x^{†},\in ,M_{\mathit{\phi },E},,,y^{\mathit{\delta }},\in ,H_2,,,\Vert y-y^{\mathit{\delta }}\Vert ,\le ,\mathit{\delta }\right\}.\end{array}$$2.7 This worst case error characterizes the maximal error of the method $R$ if the solution $x^{†}$ of problem (2.12.1 $$\begin{array}{c}\hfill Ax=y,\end{array}$$2.1 ) varies in the set $M_{\mathit{\phi },E}$. An optimal method $R_{opt}$ is characterized by $\mathrm{\Delta }(\mathit{\delta },R_{opt})={inf}_R\mathrm{\Delta }(\mathit{\delta },R)$. It can easily be realized that2.8 $$\begin{array}{c}\hfill \underset{R}{inf}\mathrm{\Delta }(\mathit{\delta },R)\ge \mathit{\omega }(\mathit{\delta },M_{\mathit{\phi },E}),\end{array}$$2.8 where $\mathit{\omega }(\mathit{\delta },M_{\mathit{\phi },E})=sup\{\Vert x\Vert |x\in M_{\mathit{\phi },E},\Vert Ax\Vert \le \mathit{\delta }\}.$

The following theorem and definition can be found in [15].

Theorem 1.1

Let $M_{\mathit{\phi },E}$ is given by (2.62.6 $$\begin{array}{c}\hfill M_{\mathit{\phi },E}=\left\{{\left[\mathit{\phi },(,A^{\ast },A,)\right]}^{1/2},\mathit{\omega },,,,\mathit{\omega },\in ,X,,\text{and},\Vert \mathit{\omega }\Vert ,\le ,E\right\},\end{array}$$2.6 ), and Assumption 1 be satisfied. If $\frac{\mathit{\delta }}{E}\in \mathit{\sigma }(A^{\ast }A\mathit{\phi }(A^{\ast }A))$, then2.9 $$\begin{array}{c}\hfill \mathit{\omega }\left(\mathit{\delta },,,M_{\mathit{\phi },E}\right)=E\sqrt{{\mathit{\rho }}^{-1}\left(\frac{{\mathit{\delta }}^2}{E^2}\right)},\end{array}$$2.9 where $\mathit{\rho }$ is given by $\mathit{\rho }(\mathit{\lambda })=\mathit{\lambda }{\mathit{\phi }}^{-1}(\mathit{\lambda })$.

Definition 1.1

Let Assumption 1 be satisfied. Any regularization method $R_{\mathit{\alpha }}^{\mathit{\delta }}$ for problem (2.12.1 $$\begin{array}{c}\hfill Ax=y,\end{array}$$2.1 ) with noisy data is called

(i)	Optimal on the set $M_{\mathit{\phi },E}$ if $\Vert x_{\mathit{\alpha }}^{\mathit{\delta }}-x^{†}\Vert \le E\sqrt{{\mathit{\rho }}^{-1}(\frac{{\mathit{\delta }}^2}{E^2})}$;
(ii)	Order optimal on the set $M_{\mathit{\phi },E}$ if $\Vert x_{\mathit{\alpha }}^{\mathit{\delta }}-x^{†}\Vert \le cE\sqrt{{\mathit{\rho }}^{-1}(\frac{{\mathit{\delta }}^2}{E^2})}$ with $c\ge 1$.

2.2 The balancing principle

Now, we prove some estimates for the spectral regularization method under the a posteriori parameter choice rule based on balance principle.

First we have [12]:

Theorem 2.1

Let $x^{†}\in M_{\mathit{\phi },E}$, Assumption 1 is satisfied, then there holds2.10 $$\begin{array}{c}\hfill \Vert x_{\mathit{\alpha }}^{\mathit{\delta }}-x^{†}\Vert \le E\sqrt{\mathit{\phi }(\mathit{\alpha })}+\mathit{\delta }/\sqrt{\mathit{\alpha }}.\end{array}$$2.10

Now denote $C(\mathit{\alpha }):=E\sqrt{\mathit{\phi }(\mathit{\alpha })}$, $D(\mathit{\alpha }):=\mathit{\delta }/\sqrt{\mathit{\alpha }}$. Since $C(\mathit{\alpha })$ increases with $\mathit{\alpha }$ but $D(\mathit{\alpha })$ decreases with $\mathit{\alpha }$, let us rewrite (2.102.10 $$\begin{array}{c}\hfill \Vert x_{\mathit{\alpha }}^{\mathit{\delta }}-x^{†}\Vert \le E\sqrt{\mathit{\phi }(\mathit{\alpha })}+\mathit{\delta }/\sqrt{\mathit{\alpha }}.\end{array}$$2.10 ) as2.11 $$\begin{array}{c}\hfill \Vert x_{\mathit{\alpha }}^{\mathit{\delta }}-x^{†}\Vert \le C(\mathit{\alpha })+D(\mathit{\alpha }).\end{array}$$2.11 By virtue of the behaviour of the functions $C(\mathit{\alpha })$ and $D(\mathit{\alpha })$, we can choose an $\tilde{\mathit{\alpha }}$ such that $C(\tilde{\mathit{\alpha }})=D(\tilde{\mathit{\alpha }})$. Therefore,2.12 $$\begin{array}{c}\hfill \Vert x_{\mathit{\alpha }}^{\mathit{\delta }}-x^{†}\Vert \le 2C(\tilde{\mathit{\alpha }}).\end{array}$$2.12 However, since the a priori bound $E$ of the unknown solution is seldom known such that $C(\mathit{\alpha })$ is unknown, the a priori choice of the theoretically value of $\tilde{\mathit{\alpha }}$ is impossible. Therefore it is necessary to use some a-posteriori rule of $\mathit{\alpha }$.

For this purpose, we use the balancing principle.

Consider a discrete set of possible values of regularization parameter2.13 $$\begin{array}{c}\hfill {▵}_N=\left\{{\mathit{\alpha }}_i,=,{\left(q^2\right)}^i,{\mathit{\alpha }}_0,,,,i,=,1,,,2,,,\dots ,,,N\right\},q>1,\end{array}$$2.13 where ${\mathit{\alpha }}_0={\mathit{\delta }}^2$, $N$ sufficiently large such that ${\mathit{\alpha }}_N\simeq 1$.

Denote the set2.14 $$\begin{array}{c}\hfill M^{+}\left({▵}_N\right)=\left\{{\mathit{\alpha }}_i,\in ,{▵}_N,:,,\Vert x_{{\mathit{\alpha }}_i}^{\mathit{\delta }}-x_{{\mathit{\alpha }}_j}^{\mathit{\delta }}\Vert ,\le ,4,D,({\mathit{\alpha }}_j),,,j,=,1,,,\dots ,,,i\right\}.\end{array}$$2.14 Choose the value of regularization parameter by the rule2.15 $$\begin{array}{c}\hfill \mathit{\alpha }={\mathit{\alpha }}_{+}:=max\left\{\mathit{\alpha },\in ,M^{+},({▵}_N)\right\}.\end{array}$$2.15 Below we show that the choice of $\mathit{\alpha }={\mathit{\alpha }}_{+}$ gives the error estimate, which differs from (2.122.12 $$\begin{array}{c}\hfill \Vert x_{\mathit{\alpha }}^{\mathit{\delta }}-x^{†}\Vert \le 2C(\tilde{\mathit{\alpha }}).\end{array}$$2.12 ) only by a factor of $3q$.

To prove this conclusion, denote the auxiliary set2.16 $$\begin{array}{c}\hfill M\left({▵}_N\right)=\left\{{\mathit{\alpha }}_i,\in ,{▵}_N,:,,C,\left({\mathit{\alpha }}_j\right),\le ,D,({\mathit{\alpha }}_i),,,j,=,1,,,\dots ,,,i\right\}.\end{array}$$2.16 and the auxiliary quantity2.17 $$\begin{array}{c}\hfill {\mathit{\alpha }}_{\ast }:=max\left\{\mathit{\alpha },\in ,M,(,{▵}_N,)\right\}.\end{array}$$2.17 Without loss of generality, we assume that$$\begin{array}{c}\hfill M\left({▵}_N\right)\ne \varnothing ,{▵}_N\backslash M\left({▵}_N\right)\ne \varnothing .\end{array}$$

Theorem 2.2

Let the parameter be chosen by (2.152.15 $$\begin{array}{c}\hfill \mathit{\alpha }={\mathit{\alpha }}_{+}:=max\left\{\mathit{\alpha },\in ,M^{+},({▵}_N)\right\}.\end{array}$$2.15 ), then there holds2.18 $$\begin{array}{c}\hfill \Vert x_{{\mathit{\alpha }}^{+}}^{\mathit{\delta }}-x^{†}\Vert \le 6qC(\tilde{\mathit{\alpha }})=6qE\sqrt{\mathit{\phi }(\tilde{\mathit{\alpha }})}.\end{array}$$2.18

Proof

As the process is similar to [11], we omit it. $\square$

3 Spectral regularization for problem (1.31.3 $$\begin{array}{c}\hfill f(x,y,s)=\frac{1}{2\mathit{\pi }}{\int }_{{\mathbb{R}}^2}a(\mathit{\xi },\mathit{\eta },s)\widehat{g}(\mathit{\xi },\mathit{\eta })e^{i(\mathit{\xi }x+\mathit{\eta }y)}d\mathit{\xi }d\mathit{\eta },\end{array}$$1.3 )

Now, in order to apply the spectral regularization method, we formulate problem (1.31.3 $$\begin{array}{c}\hfill f(x,y,s)=\frac{1}{2\mathit{\pi }}{\int }_{{\mathbb{R}}^2}a(\mathit{\xi },\mathit{\eta },s)\widehat{g}(\mathit{\xi },\mathit{\eta })e^{i(\mathit{\xi }x+\mathit{\eta }y)}d\mathit{\xi }d\mathit{\eta },\end{array}$$1.3 ) as an operator equation in the frequency domain:$$\begin{array}{c}\hfill A(s)\widehat{f}:=a^{-1}(\mathit{\xi },\mathit{\eta },s)\widehat{f}(\mathit{\xi },\mathit{\eta },s)=\widehat{g}(\mathit{\xi },\mathit{\eta }),\end{array}$$where $A(s):L^2\left({\mathbb{R}}^2\right)\to L^2\left({\mathbb{R}}^2\right)$ is a multiplication operator. Obviously $A(s)=a^{-1}(\mathit{\xi },\mathit{\eta },s)$, and the adjoint operator of $A(s)$ is $A^{\ast }(s)=\overline{a^{-1}(\mathit{\xi },\mathit{\eta },s)}$, where the symbol $\overline{\mathrm{\Pi }}$ denotes the complex conjugate of $\mathrm{\Pi }$. Therefore, $A^{\ast }A(s)=|a^{-1}{(\mathit{\xi },\mathit{\eta },s)|}^2={|a(\mathit{\xi },\mathit{\eta },s)|}^{-2}$. In this section, we deal with problem (1.31.3 $$\begin{array}{c}\hfill f(x,y,s)=\frac{1}{2\mathit{\pi }}{\int }_{{\mathbb{R}}^2}a(\mathit{\xi },\mathit{\eta },s)\widehat{g}(\mathit{\xi },\mathit{\eta })e^{i(\mathit{\xi }x+\mathit{\eta }y)}d\mathit{\xi }d\mathit{\eta },\end{array}$$1.3 ) for two cases separately:

Case I    (the case of the interior inversion): $p=0$ in (1.61.6 $$\begin{array}{c}\hfill {\Vert f(·,·,L)\Vert }_p\le E,p\ge 0.\end{array}$$1.6 ).

Case II    (the case of the boundary inversion): $p>0$ in (1.61.6 $$\begin{array}{c}\hfill {\Vert f(·,·,L)\Vert }_p\le E,p\ge 0.\end{array}$$1.6 ).

Now we investigate the spectral method for two cases.

First, we can write the spectral regularization according to (2.42.4 $$\begin{array}{c}\hfill g_{\mathit{\alpha }}(\mathit{\lambda })=\left\{\begin{array}{cc}\frac{1}{\mathit{\lambda }},\hfill & \mathit{\lambda }\ge \mathit{\alpha },\hfill \\ 0,\hfill & \mathit{\lambda }<\mathit{\alpha }.\hfill \end{array}\right.\end{array}$$2.4 ):3.1 $$\begin{array}{c}\hfill {\widehat{f}}_{\mathit{\alpha }}^{\mathit{\delta }}(\mathit{\xi },\mathit{\eta },s)=\left\{\begin{array}{cc}a(\mathit{\xi },\mathit{\eta },s){\widehat{g}}_{\mathit{\delta }}(\mathit{\xi },\mathit{\eta }),\hfill & |a(\mathit{\xi },\mathit{\eta },s)|\le \frac{1}{\sqrt{\mathit{\alpha }}},\hfill \\ 0,\hfill & else.\hfill \end{array}\right.\end{array}$$3.1 In order to obtain the explicit expression of the error bound, we need to know the expression of $\mathit{\phi }(·)$ in (2.52.5 $$\begin{array}{c}\hfill x^{†}={\left[\mathit{\phi },(,A^{\ast },A,)\right]}^{1/2}\mathit{\omega },\Vert \mathit{\omega }\Vert \le E,\end{array}$$2.5 ).

3.1 Interior inversion

In this subsection, we note that $p=0$ in (1.61.6 $$\begin{array}{c}\hfill {\Vert f(·,·,L)\Vert }_p\le E,p\ge 0.\end{array}$$1.6 ) and we want to recover the solution $\widehat{f}(\mathit{\xi },\mathit{\eta },s)$ with $0\le s<L$. First we use the equality$$\begin{array}{c}\hfill \widehat{f}(\mathit{\xi },\mathit{\eta },s)=\frac{a(\mathit{\xi },\mathit{\eta },s)}{a(\mathit{\xi },\mathit{\eta },L)}\widehat{f}(\mathit{\xi },\mathit{\eta },L).\end{array}$$Now (1.61.6 $$\begin{array}{c}\hfill {\Vert f(·,·,L)\Vert }_p\le E,p\ge 0.\end{array}$$1.6 ) reads$$\begin{array}{c}\hfill \Vert \widehat{f}{(\mathit{\xi },\mathit{\eta },L)\Vert }^2={∥\frac{a(\mathit{\xi },\mathit{\eta },L)}{a(\mathit{\xi },\mathit{\eta },s)},\widehat{f},(\mathit{\xi },\mathit{\eta },s)∥}^2\le E^2.\end{array}$$Denote the sets3.2 $$\begin{array}{cc}\hfill M_1& =\left\{\widehat{f},(\mathit{\xi },\mathit{\eta },s),\in ,L^2,|,{∥\frac{a(\mathit{\xi },\mathit{\eta },L)}{a(\mathit{\xi },\mathit{\eta },s)},\widehat{f},(\mathit{\xi },\mathit{\eta },s)∥}^2,\le ,E^2\right\}.\hfill \end{array}$$3.2 3.3 $$\begin{array}{cc}\hfill M& =\left\{\widehat{f},(\mathit{\xi },\mathit{\eta },s),\in ,L^2,|,{∥\frac{C_1}{C_2^2},{|a(\mathit{\xi },\mathit{\eta },s)|}^{\frac{L-s}{s}},\widehat{f},(\mathit{\xi },\mathit{\eta },s)∥}^2,\le ,E^2\right\}.\hfill \end{array}$$3.3 In fact, by $A^{\ast }A(s)=|a^{-1}{(\mathit{\xi },\mathit{\eta },s)|}^2={|a(\mathit{\xi },\mathit{\eta },s)|}^{-2}$, $M$ is equivalent to $M_2$ given in the form of (2.62.6 $$\begin{array}{c}\hfill M_{\mathit{\phi },E}=\left\{{\left[\mathit{\phi },(,A^{\ast },A,)\right]}^{1/2},\mathit{\omega },,,,\mathit{\omega },\in ,X,,\text{and},\Vert \mathit{\omega }\Vert ,\le ,E\right\},\end{array}$$2.6 )3.4 $$\begin{array}{c}\hfill M_2=\left\{\widehat{f},(\mathit{\xi },\mathit{\eta },s),\in ,L^2,|,{\Vert {\left[\mathit{\phi },(A^{\ast }A(s))\right]}^{-\frac{1}{2}}\widehat{f}(\mathit{\xi },\mathit{\eta },s)\Vert }^2,\le ,E^2\right\},\end{array}$$3.4 where3.5 $$\begin{array}{c}\hfill \mathit{\phi }(\mathit{\lambda })=\frac{C_2^4}{C_1^2}{\mathit{\lambda }}^{\frac{L-s}{s}}.\end{array}$$3.5 Now we only need to show that every element from $M_1$ belongs to the set $M$. For any element $\widehat{f}(\mathit{\xi },\mathit{\eta },s)\in M_1$, we have3.6 $$\begin{array}{c}\hfill {\displaystyle \int {\left|\frac{a(\mathit{\xi },\mathit{\eta },L)}{a(\mathit{\xi },\mathit{\eta },s)}\right|}^2{\left|\widehat{f},(\mathit{\xi },\mathit{\eta },s)\right|}^{2}d\mathit{\xi }\le E^2.}\end{array}$$3.6 By (1.51.5 $$\begin{array}{cc}\hfill C_{1}exp\left(s,\mathit{\varphi },\left({\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)\right)& \le |a\left(\mathit{\xi },,,\mathit{\eta },,,s\right)|\hfill \\ \hfill & \le C_{2}exp\left(s,\mathit{\varphi },\left({\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)\right),{\mathit{\xi }}^2+{\mathit{\eta }}^2\ge c_1,s\in (0,L],\hfill \\ \hfill & |a(\mathit{\xi },\mathit{\eta },s)|\le z(s),{\mathit{\xi }}^2+{\mathit{\eta }}^2<c_1,\hfill \end{array}$$1.5 ), this implies3.7 $$\begin{array}{c}\hfill \int {\left|\frac{C_1}{C_2},exp,\left((L-s),\mathit{\varphi },\left({\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)\right)\right|}^2{\left|\widehat{f},\left(\mathit{\xi },,,\mathit{\eta },,,s\right)\right|}^{2}d\mathit{\xi }\le E^2.\end{array}$$3.7 On the other hand, for any element $\widehat{f}(\mathit{\xi },\mathit{\eta },s)\in M$, we have two-side estimates$$\begin{array}{cc}& \int \frac{C_1^2}{C_2^4}|C_{1}exp\left((L-s),\mathit{\varphi },\left({\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)\right){|}^2{|\widehat{f}(\mathit{\xi },\mathit{\eta },s)|}^{2}d\mathit{\xi }d\mathit{\eta }\hfill \\ \hfill & \le \int \frac{C_1^2}{C_2^4}{|a(\mathit{\xi },\mathit{\eta },s)|}^{\frac{2(L-s)}{s}}{|\widehat{f}(\mathit{\xi },\mathit{\eta },s)|}^{2}d\mathit{\xi }d\mathit{\eta }\hfill \\ \hfill & \le \int \frac{C_1^2}{C_2^4}|C_{2}exp\left((L-s),\mathit{\varphi },\left({\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)\right){|}^2{|\widehat{f}(\mathit{\xi },\mathit{\eta },s)|}^{2}d\mathit{\xi }d\mathit{\eta }\le E^2.\hfill \end{array}$$Thus, we have shown that every element from $M_1$ belongs to the set $M=M_2$. Likewise, we can also show that every element from $M_0$ belongs to the set $M_1$ by constructing another set $M_0$ similar to $M$. We have another $\mathit{\phi }(·)$ which differs from (3.53.5 $$\begin{array}{c}\hfill \mathit{\phi }(\mathit{\lambda })=\frac{C_2^4}{C_1^2}{\mathit{\lambda }}^{\frac{L-s}{s}}.\end{array}$$3.5 ) only by a constant factor. Now we summarize what we have:

Conclusion 1

If the a-priori bound (1.61.6 $$\begin{array}{c}\hfill {\Vert f(·,·,L)\Vert }_p\le E,p\ge 0.\end{array}$$1.6 ) with $p=0$ holds, for problem (1.31.3 $$\begin{array}{c}\hfill f(x,y,s)=\frac{1}{2\mathit{\pi }}{\int }_{{\mathbb{R}}^2}a(\mathit{\xi },\mathit{\eta },s)\widehat{g}(\mathit{\xi },\mathit{\eta })e^{i(\mathit{\xi }x+\mathit{\eta }y)}d\mathit{\xi }d\mathit{\eta },\end{array}$$1.3 ), the function $\mathit{\phi }(·)$ in the source set (3.53.5 $$\begin{array}{c}\hfill \mathit{\phi }(\mathit{\lambda })=\frac{C_2^4}{C_1^2}{\mathit{\lambda }}^{\frac{L-s}{s}}.\end{array}$$3.5 ) has the form of $\mathit{\phi }(\mathit{\lambda })=\mathit{\gamma }{\mathit{\lambda }}^{\frac{L-s}{s}}$ with $\mathit{\gamma }$ is a constant which only depends on $C_1$ and $C_2$. Thus, the function $\mathit{\rho }(\mathit{\lambda })=\mathit{\lambda }{\mathit{\phi }}^{-1}(\mathit{\lambda })=c_2{\mathit{\lambda }}^{\frac{L}{L-s}}$ and ${\mathit{\rho }}^{-1}(\mathit{\lambda })=c_3{\mathit{\lambda }}^{\frac{L-s}{L}}$. Therefore for problem (1.31.3 $$\begin{array}{c}\hfill f(x,y,s)=\frac{1}{2\mathit{\pi }}{\int }_{{\mathbb{R}}^2}a(\mathit{\xi },\mathit{\eta },s)\widehat{g}(\mathit{\xi },\mathit{\eta })e^{i(\mathit{\xi }x+\mathit{\eta }y)}d\mathit{\xi }d\mathit{\eta },\end{array}$$1.3 ) for solving $\widehat{f}(\mathit{\xi },\mathit{\eta },s)$, the optimal convergence order for error estimates is given by3.8 $$\begin{array}{c}\hfill E{(\mathit{\delta }/E)}^{\frac{L-s}{L}}=E^{\frac{s}{L}}{\mathit{\delta }}^{\frac{L-s}{L}}.\end{array}$$3.8

3.2 Boundary inversion

In this subsection, we note that $p>0$ in (1.61.6 $$\begin{array}{c}\hfill {\Vert f(·,·,L)\Vert }_p\le E,p\ge 0.\end{array}$$1.6 ) and we want to recover the solution $\widehat{f}(\mathit{\xi },\mathit{\eta },L)$. Now (1.61.6 $$\begin{array}{c}\hfill {\Vert f(·,·,L)\Vert }_p\le E,p\ge 0.\end{array}$$1.6 ) with $p>0$ reads$$\begin{array}{c}\hfill \Vert \widehat{f}{(\mathit{\xi },\mathit{\eta },L)\Vert }_p^2={∥{\left(1,+,{\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)}^{p/2},\widehat{f},(\mathit{\xi },\mathit{\eta },L)∥}^2\le E^2.\end{array}$$Denote the sets3.9 $$\begin{array}{cc}\hfill M_3& =\left\{\widehat{f},(\mathit{\xi },\mathit{\eta },L),\in ,L^2,|,{∥{\left(1,+,{\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)}^{p/2},\widehat{f},(\mathit{\xi },\mathit{\eta },L)∥}^2,\le ,E^2\right\}.\hfill \\ \hfill M_4& =\left\{\widehat{f},(\mathit{\xi },\mathit{\eta },L),\in ,L^2,|,{∥{\left[{\mathit{\varphi }}^{-1},\left(\frac{{\mathit{\gamma }}_0}{2L},ln,\left({\left[A^{\ast },A,(L)\right]}^{-1}\right)\right)\right]}^p,\widehat{f},(\mathit{\xi },\mathit{\eta },L)∥}^2,\le ,E^2\right\},\hfill \\ \hfill \end{array}$$3.9 where the ${\mathit{\varphi }}^{-1}(·)$ denotes the inverse function of $\mathit{\varphi }(·)$ and ${\mathit{\gamma }}_0$ is a positive constant depending on $C_1,C_2$. Similar to Conclusion 1, we can prove that every element from $M_3$ belongs to the set $M_4$. Thus, we can obtain the expression of $\mathit{\phi }(\mathit{\lambda })$:3.10 $$\begin{array}{c}\hfill \mathit{\phi }(\mathit{\lambda })={\left[{\mathit{\varphi }}^{-1},\left(\frac{{\mathit{\gamma }}_0}{2L},ln,({[\mathit{\lambda }]}^{-1})\right)\right]}^{-p}.\end{array}$$3.10 By an elementary calculation, it yields3.11 $$\begin{array}{c}\hfill {\mathit{\rho }}^{-1}(\mathit{\lambda })={\left[{\mathit{\varphi }}^{-1},\left(\tilde{c},ln,{\mathit{\lambda }}^{-1}\right)\right]}^{-p},\end{array}$$3.11 where $\tilde{c}$ is a constant depends on ${\mathit{\gamma }}_0,L$.

Conclusion 2

If the a-priori bound (1.61.6 $$\begin{array}{c}\hfill {\Vert f(·,·,L)\Vert }_p\le E,p\ge 0.\end{array}$$1.6 ) with $p>0$ holds, the optimal convergence order for solving $\widehat{f}(\mathit{\xi },\mathit{\eta },L)$ is given by3.12 $$\begin{array}{c}\hfill {\left[{\mathit{\varphi }}^{-1},\left(\tilde{c},ln,\left(E^2,/,{\mathit{\delta }}^2\right)\right)\right]}^{-p}.\end{array}$$3.12

4 Applications

Now, we give some applications of Theorem 2.3. Throughout this section, the $\tilde{c},c$ are the positive constants which are not dependent on $\mathit{\delta }$ and $E$.

Example 4.1

The reconstruction problem of aperture in the plane from their diffraction patterns arises in acoustics and optics. Let us consider the following inverse diffraction problem. Let $D$ be a bounded aperture in an infinite perfectly soft screen which is located in the plane $z=0$ in ${\mathbb{R}}^3$. A harmonic plane wave with wave-number $k$ propagates along with the positive $z$ direction. It hits the screen and escapes through the aperture $D$. The measured data at receiving screen $z=L>0$ are given. The problem is to reconstruct the shape (domain) of the aperture $D$. By Kirchhoff approximation, the mathematical modelling can be formulated as follows.

Let $u(x,y,z)$ be the solution of the following problem:4.1 $$\begin{array}{cc}& u_{xx}+u_{yy}+u_{zz}+k^{2}u=0,(x,y)\in {\mathbb{R}}^2,z>0\hfill \end{array}$$4.1 4.2 $$\begin{array}{cc}& u(x,y,L)=g(x,y),(x,y)\in {\mathbb{R}}^2,\hfill \end{array}$$4.2 4.3 $$\begin{array}{cc}& \underset{r\to \infty }{lim}r\left(\frac{\mathit{\partial }u}{\mathit{\partial }r},-,i,k,u\right)=0,\text{where}r=\sqrt{x^2+y^2+z^2}.\hfill \end{array}$$4.3

Here we wish to find the $u(x,y,0)={\mathit{\chi }}_D(x,y)$ from the measured data $g_{\mathit{\delta }}(x,y)\in L^2$, where ${\mathit{\chi }}_D(x,y)$ is the characteristic function of the domain $D$.

As usual, we assume that there exists a priori bound:4.4 $$\begin{array}{c}\hfill {\Vert u(·,·,0)\Vert }_p\le E,\end{array}$$4.4 where ${\Vert ·\Vert }_p$ denotes the norm of Sobolev space $H^p({\mathbb{R}}^2)$ with $p\ge 0$ and $E$ is a positive constant.

We have the solution in the frequency domain:4.5 $$\begin{array}{c}\hfill \widehat{{\mathit{\chi }}_D}(\mathit{\xi },\mathit{\eta })=e^{L\sqrt{{\mathit{\xi }}^2+{\mathit{\eta }}^2-k^2}}\widehat{g}(\mathit{\xi },\mathit{\eta }).\end{array}$$4.5 Therefore, the symbol of pseudodifferential operator is given by4.6 $$\begin{array}{c}\hfill a(\mathit{\xi },\mathit{\eta },L)=e^{L\sqrt{{\mathit{\xi }}^2+{\mathit{\eta }}^2-k^2}}.\end{array}$$4.6 Now let $\mathit{\varphi }(\mathit{\omega })=\sqrt{\mathit{\omega }-k^2}$ and its inverse function ${\mathit{\varphi }}^{-1}(\mathit{\omega })={\mathit{\omega }}^2+k^2$, $f(x,y,L)=u(x,y,0)={\mathit{\chi }}_D(x,y)$; by (3.113.11 $$\begin{array}{c}\hfill {\mathit{\rho }}^{-1}(\mathit{\lambda })={\left[{\mathit{\varphi }}^{-1},\left(\tilde{c},ln,{\mathit{\lambda }}^{-1}\right)\right]}^{-p},\end{array}$$3.11 ), we have4.7 $$\begin{array}{c}\hfill \mathit{\phi }(\tilde{\mathit{\alpha }})={\left[{\mathit{\varphi }}^{-1},\left(\frac{{\mathit{\gamma }}_0}{2L},ln,\left({\left[\tilde{\mathit{\alpha }}\right]}^{-1}\right)\right)\right]}^{-p}=O\left(E,{\left(ln,\frac{1}{\tilde{\mathit{\alpha }}}\right)}^{-2p}\right),\tilde{\mathit{\alpha }}\to 0.\end{array}$$4.7 Therefore, by Theorem 2.3, we have the following error estimate:4.8 $$\begin{array}{c}\hfill \Vert f_{{\mathit{\alpha }}^{+}}^{\mathit{\delta }}(·,·,L)-u(·,·,0)\Vert \le cE{\left(ln,\frac{1}{\tilde{\mathit{\alpha }}}\right)}^{-p}.\end{array}$$4.8 Now we need to estimate $\tilde{\mathit{\alpha }}$. At $\mathit{\alpha }=\tilde{\mathit{\alpha }}$, we have $C(\tilde{\mathit{\alpha }})=D(\tilde{\mathit{\alpha }})$. Therefore,$$cE{\left(ln,\frac{1}{\tilde{\mathit{\alpha }}}\right)}^{-p}=\mathit{\delta }/\sqrt{\tilde{\mathit{\alpha }}},$$i.e.$$\tilde{\mathit{\alpha }}=\frac{{\mathit{\delta }}^2}{{(cE)}^2}{ln}^{2p}\frac{1}{\tilde{\mathit{\alpha }}}.$$Since ${ln}^{m}x<x^{\mathit{\upsilon }}$ holds for any $x>0,\mathit{\upsilon }>0,m>0$, we have$$\tilde{\mathit{\alpha }}=\frac{{\mathit{\delta }}^2}{{(cE)}^2}{ln}^{2p}\frac{1}{\tilde{\mathit{\alpha }}}\le \frac{{\mathit{\delta }}^2}{{(cE)}^2}\frac{1}{\tilde{\mathit{\alpha }}},$$i.e.4.9 $$\begin{array}{c}\hfill \tilde{\mathit{\alpha }}\le \frac{\mathit{\delta }}{cE}.\end{array}$$4.9 As a result, we have the error estimate4.10 $$\begin{array}{c}\hfill \Vert f_{{\mathit{\alpha }}^{+}}^{\mathit{\delta }}(·,·,L)-u(·,·,0)\Vert \le \tilde{c}E{\left(ln,\frac{E}{\mathit{\delta }}\right)}^{-p}.\end{array}$$4.10 The convergence order is optimal.

Example 4.2

Consider the linear diffusion final value problem in $L^2\left({\mathbb{R}}^2\right)$,4.11 $$\begin{array}{c}\hfill u_t(x,y,t)=\mathrm{\Delta }u(x,y,t),t>0,u(x,y,T)=g(x,y),\end{array}$$4.11 where $\mathrm{\Delta }$ is the Laplacian operator, usually $g(x,y)\in L^2\left({\mathbb{R}}^2\right)$ are the data with approximation $g^{\mathit{\delta }}(x,y)\in L^2\left({\mathbb{R}}^2\right)$. As usual, we assume that there exists a priori bound:4.12 $$\begin{array}{c}\hfill {\Vert u(·,·,0)\Vert }_p\le E,\end{array}$$4.12 where ${\Vert ·\Vert }_p$ denotes the norm of Sobolev space $H^p\left({\mathbb{R}}^2\right)$ with $p\ge 0$ and $E$ is a positive constant.

This problem can be associated with a deblurring problem. Consider a space invariant point spread functions $p(x,y)$ and formulate the deblurring problem as4.13 $$\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^2}p(x-\mathit{\mu },y-\mathit{\nu })f(\mathit{\mu },\mathit{\nu })d\mathit{\mu }d\mathit{\nu }=g(x,y),\end{array}$$4.13 where $f(x,y)$ is the desired unblurred image and $g(x,y)$ is the blurred image that would have been recorded in the absence of noise. In general, the image $f(x,y)$ is viewed as originally defined on a bounded rectangle-like domain; we could extend $f(x,y)$ periodically to all of ${\mathbb{R}}^2$.

We can easily get the unique Fourier space solution for problem (4.114.11 $$\begin{array}{c}\hfill u_t(x,y,t)=\mathrm{\Delta }u(x,y,t),t>0,u(x,y,T)=g(x,y),\end{array}$$4.11 )4.14 $$\begin{array}{c}\hfill \widehat{u}(\mathit{\xi },\mathit{\eta },t)=exp\left((T-t),\left({\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)\right)\widehat{g}(\mathit{\xi },\mathit{\eta }),t>0,\end{array}$$4.14 If we take $\widehat{p}(\mathit{\xi },\mathit{\eta })=exp(T({\mathit{\xi }}^2+{\mathit{\eta }}^2)),T>0$, we may identity the blurred image $g(x,y)$ with the temperature distribution at time $t=T$ in an infinite two-dimensional medium whose initial temperature distribution is given by the unblurred image $u(x,y,0):=f(x,y)$. This involves solving the diffusion equation backwards in time. For a fixed $0<t<T$, we call the solution $u(x,y,t)$ a partial restoration. For the case $t=0$, we call the solution $u(x,y,0)$ a full restoration.

Therefore, the symbol of pseudodifferential operator is given by4.15 $$\begin{array}{c}\hfill a(\mathit{\xi },\mathit{\eta },t)=exp\left((T-t),\left({\mathit{\xi }}^2,+,{\mathit{\eta }}^2\right)\right).\end{array}$$4.15 Now let $s=T-t$, $L=T$, $\mathit{\varphi }(\mathit{\omega })=\mathit{\omega }$ and its inverse function ${\mathit{\varphi }}^{-1}(\mathit{\omega })=\mathit{\omega }$, $f(x,y,L)=u(x,y,0)$.

Boundary inversion. By (3.113.11 $$\begin{array}{c}\hfill {\mathit{\rho }}^{-1}(\mathit{\lambda })={\left[{\mathit{\varphi }}^{-1},\left(\tilde{c},ln,{\mathit{\lambda }}^{-1}\right)\right]}^{-p},\end{array}$$3.11 ), we have4.16 $$\begin{array}{c}\hfill \mathit{\phi }(\tilde{\mathit{\alpha }})={\left[{\mathit{\varphi }}^{-1},\left(\frac{{\mathit{\gamma }}_0}{2L},ln,\left({\left[\tilde{\mathit{\alpha }}\right]}^{-1}\right)\right)\right]}^{-p}=O\left(E,{\left(ln,\frac{1}{\tilde{\mathit{\alpha }}}\right)}^{-p}\right),\tilde{\mathit{\alpha }}\to 0.\end{array}$$4.16 Therefore, similar to Example 4.1, by Theorem 2.3, we have the following error estimate:4.17 $$\begin{array}{c}\hfill \Vert f_{{\mathit{\alpha }}^{+}}^{\mathit{\delta }}(·,·,L)-u(·,·,0)\Vert \le cE{\left(ln,\frac{E}{\mathit{\delta }}\right)}^{-p/2}.\end{array}$$4.17 Interior inversion. By (3.53.5 $$\begin{array}{c}\hfill \mathit{\phi }(\mathit{\lambda })=\frac{C_2^4}{C_1^2}{\mathit{\lambda }}^{\frac{L-s}{s}}.\end{array}$$3.5 ), we have4.18 $$\begin{array}{c}\hfill \mathit{\phi }(\tilde{\mathit{\alpha }})=O\left(E,{\tilde{\mathit{\alpha }}}^{\frac{t}{2(T-t)}}\right),\tilde{\mathit{\alpha }}\to 0.\end{array}$$4.18 Therefore, by Theorem 2.3, we have the following error estimate:4.19 $$\begin{array}{c}\hfill \Vert f_{{\mathit{\alpha }}^{+}}^{\mathit{\delta }}(·,·,s)-u(·,·,t)\Vert \le cE{\tilde{\mathit{\alpha }}}^{\frac{t}{2(T-t)}}.\end{array}$$4.19 Now we need to estimate $\tilde{\mathit{\alpha }}$. At $\mathit{\alpha }=\tilde{\mathit{\alpha }}$, we have $C(\tilde{\mathit{\alpha }})=D(\tilde{\mathit{\alpha }})$. Therefore,$$cE{\tilde{\mathit{\alpha }}}^{\frac{t}{2(T-t)}}=\mathit{\delta }/\sqrt{\tilde{\mathit{\alpha }}},$$i.e.$$\tilde{\mathit{\alpha }}={\left(\frac{\mathit{\delta }}{cE}\right)}^{\frac{2(T-t)}{T}}.$$As a result, we have the error estimate4.20 $$\begin{array}{c}\hfill \Vert f_{{\mathit{\alpha }}^{+}}^{\mathit{\delta }}(·,·,L)-u(·,·,0)\Vert \le \tilde{c}{\mathit{\delta }}^{t/T}{E}^{1-t/T}.\end{array}$$4.20 The convergence order in (4.174.17 $$\begin{array}{c}\hfill \Vert f_{{\mathit{\alpha }}^{+}}^{\mathit{\delta }}(·,·,L)-u(·,·,0)\Vert \le cE{\left(ln,\frac{E}{\mathit{\delta }}\right)}^{-p/2}.\end{array}$$4.17 ) and (4.204.20 $$\begin{array}{c}\hfill \Vert f_{{\mathit{\alpha }}^{+}}^{\mathit{\delta }}(·,·,L)-u(·,·,0)\Vert \le \tilde{c}{\mathit{\delta }}^{t/T}{E}^{1-t/T}.\end{array}$$4.20 ) are optimal.

5 Numerical results

In this section, we only consider the numerical results of Example 4.1. The numerical results of Example 4.2 can be found in [6], we do not repeat them here. Although the examples are described in an unbounded domain in the plane $(x,y)$, we are interested in the domain $(x,y)\in [0,1]\times [0,1]$. This is reasonable because the problem can be solved by periodic extension in the $(x,y)$ plane.

Define the discrete $L^2$ norm of $u(x,y)$ by5.1 $$\begin{array}{c}\hfill \Vert u\Vert ={\left(n^{-2},\sum _{j,k=1}^n,u,{(x_j,y_k)}^2\right)}^{\frac{1}{2}}.\end{array}$$5.1 where $n$ is the total number of sampled points. In this section, we take $n=100$.

In order to measure the accuracy of numerical results, we define the discrete $L^2$-norm error for the exact solution $u$ between the approximate solution $u_a$ as follows:5.2 $$\begin{array}{c}\hfill E={\left(n^{-2},\sum _{j,k=1}^n,{|u(x_j,y_k)-u_a(x_j,y_k)|}^2\right)}^{\frac{1}{2}}.\end{array}$$5.2 The noise was added to $g(x,y)$ by setting $\mathit{\delta }(x_j,t_k)=\mathit{\sigma }{r}_{jk}max\{g(x_j,y_k)\})$, where $\mathit{\sigma }$ denotes the noise level and $r_{jk}$ is a random number drawn from a uniform distribution in the range $[0,1]$. In numerical experiment, we use (5.25.2 $$\begin{array}{c}\hfill E={\left(n^{-2},\sum _{j,k=1}^n,{|u(x_j,y_k)-u_a(x_j,y_k)|}^2\right)}^{\frac{1}{2}}.\end{array}$$5.2 ) to compute $\mathit{\delta }=\Vert g-g_{\mathit{\delta }}\Vert$.

Figure 1. The original $D$ (a) and the data $g$ (b).

Figure 2. The reconstructed D by spectral method.

We shall illustrate the reconstruction method (3.13.1 $$\begin{array}{c}\hfill {\widehat{f}}_{\mathit{\alpha }}^{\mathit{\delta }}(\mathit{\xi },\mathit{\eta },s)=\left\{\begin{array}{cc}a(\mathit{\xi },\mathit{\eta },s){\widehat{g}}_{\mathit{\delta }}(\mathit{\xi },\mathit{\eta }),\hfill & |a(\mathit{\xi },\mathit{\eta },s)|\le \frac{1}{\sqrt{\mathit{\alpha }}},\hfill \\ 0,\hfill & else.\hfill \end{array}\right.\end{array}$$3.1 ) with different numerical examples although we have used some ‘inverse crimes’.[17] The Fourier formula (3.13.1 $$\begin{array}{c}\hfill {\widehat{f}}_{\mathit{\alpha }}^{\mathit{\delta }}(\mathit{\xi },\mathit{\eta },s)=\left\{\begin{array}{cc}a(\mathit{\xi },\mathit{\eta },s){\widehat{g}}_{\mathit{\delta }}(\mathit{\xi },\mathit{\eta }),\hfill & |a(\mathit{\xi },\mathit{\eta },s)|\le \frac{1}{\sqrt{\mathit{\alpha }}},\hfill \\ 0,\hfill & else.\hfill \end{array}\right.\end{array}$$3.1 ) is based on FFT algorithm.

Example 1

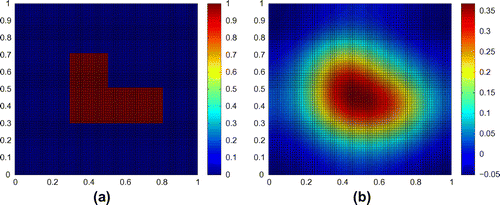
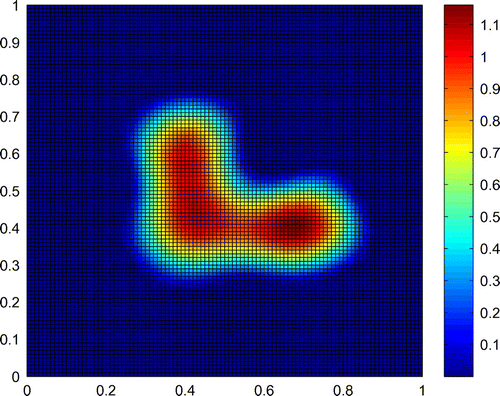
We choose the aperture $D$ in the shape of the letter ‘L’ for our test. The characteristic function, as shown in Figure 1(a) on the domain $D$, is to be constructed. And Figure 1(b) displays data $g$ which is a very blurred picture of the original aperture.

In this example, $1\%$ relative error is added to the data $g(x,y)$ at the sampled points in the simulation and we can get $\mathit{\delta }=0.02$. In the computation, we used $q=1.2$, ${\mathit{\alpha }}_{+}=4.7\ast {10}^{-5}$. Figure 2 corresponds to the results obtained by the spectral method, where the distance from the receiving plane to the screen is $L=0.2$ with the wave-number $k=5$.

Figure 3. The original $D$ (a) and the data $g$ (b).

Figure 4. The reconstructed D by spectral method.

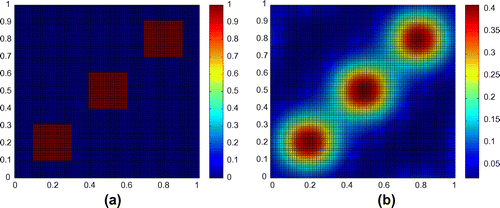
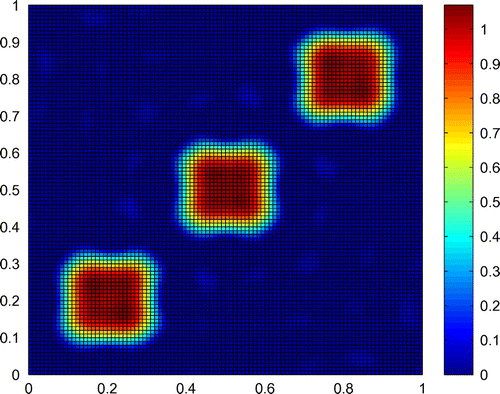
Example 2

The aperture $D$ consists of three independent squares. The characteristic function to be constructed and the data $g$ are displayed in Figure 3.

In this example, $1\%$ relative error is added to the data $g(x,y)$ at the sampled points in the simulation as the Example 5.1. And we can get $\mathit{\delta }=0.02$. In the computation, we used $q=1.2$, ${\mathit{\alpha }}_{+}=1.1\ast {10}^{-4}$.

Figure 4 correspond to the results by the spectral method, where the distance from receiving plane to the screen is $L=0.1$ with the wave-number $k=5$.

In the numerical tests, we find that the reconstruction gets more severe as the receiving plane is moved away from the aperture and as the wave-number $k$ is decreased. Because if $k$ is decreased and $d$ is increased, the degree of ill-posedness of the problem increases.

6 Concluding remark

Numerical solutions for many ill-posed problems can be recast as the numerical computation of a class of pseudodifferential operators. In this paper, for the numerical computation of a class of pseudodifferential operators, we investigate the spectral method. Under the balancing principle, we derived the error bounds for the numerical computation of a class of pseudodifferential operators. The obtained error bounds have the optimal convergence order. Two numerical examples are provided and the numerical experiment shows that the method works well.

Acknowledgments

The reviewers are thanked for their very careful reading and for pointing out several mistakes as well as for their useful comments and suggestions.

Notes

1 The work described in this paper was partially supported by a grant from the National Natural Science Foundation of China [grant number 11001223]; the Research Fund for the Doctoral Program of Higher Education of China [grant number 20106203120001]; the Key (Keygrant) Project of Chinese Ministry of Education [grant number 212179]; and the Doctoral Foundation of Northwest Normal University, China [grant number 5002–577].