Determination of a time-dependent diffusivity in a nonlinear parabolic problem

Abstract

In this article, an inverse nonlinear convection–diffusion problem is considered for the identification of an unknown solely time-dependent diffusion coefficient in a subregion of a bounded domain in ${\mathbb{R}}^d,d⩾1$. The missing data are compensated by boundary observations on a part of the surface of the subdomain: the total flux through that surface or the values of the solution at that surface are measured. Two solution methods are discussed. In both cases, the solvability of the problem is proved using coefficient to data mappings. More specific, a nonlinear numerical algorithm based on Rothe’s method is designed and the convergence of approximations towards the weak solution in suitable function spaces is shown. In the proofs, also the monotonicity methods and the Minty–Browder argument are employed. The results of numerical experiments are discussed.

Keywords:

• inverse problems
• nonlinear parabolic initial boundary value problem
• parameter identification
• nonlocal boundary condition
• time discretization
• Minty–Browder
• convergence

AMS Subject Classifications:

• 35R30
• 35K61
• 35B30
• 65M32

1 Introduction

Recovery of missing parameters in partial differential equations from overspecified data plays an important role in inverse problems arising in engineering and physics. These problems are widely encountered in the modelling of interesting phenomena, e.g. heat conduction and hydrology. Another challenge of mathematical modelling is to determine what additional information is necessary and/or sufficient to ensure the (unique) solvability of an unknown physical parameter of a given process.

This contribution is devoted to these subjects. More specific, the purpose of this paper is a study on recovery of a time-dependent diffusion coefficient in nonlinear parabolic problems. It is assumed to have some overposed nonlocal data as a side condition. Similar but steady-state settings can be found in the so-called ‘Spontaneous potential well-logging’, which is an important technique to detect parameters of the formation in petroleum exploitation, cf. [1–4]. The determination of a time-dependent diffusivity in parabolic equations has been considered in papers [5, 6]. Nonlinear problems have been studied in [7–10]. The problems studied in these papers are all one-dimensional in space. However, the analysis made in this article is valid for every dimension $d⩾1$.

The mathematical setting is the following. Let $\mathrm{\Omega }\subset {\mathbb{R}}^d$ be a bounded domain with a Lipschitz continuous boundary $\mathrm{\Gamma }$. The domain $\mathrm{\Omega }$ is split into two nonoverlapping parts ${\mathrm{\Omega }}_0\ne \mathrm{\varnothing }$ and $\mathrm{\Omega }\backslash {\overline{\mathrm{\Omega }}}_0$ with the assumption that $\mathrm{\Omega }\backslash {\overline{\mathrm{\Omega }}}_0$ cannot surround ${\mathrm{\Omega }}_0$. A transient convection–diffusion process is considered in $\mathrm{\Omega }$. The diffusion coefficient $K$ takes the form $K=k(t,\mathit{x})\mathit{\kappa }(t,\mathit{x})$ for a known $\mathit{\kappa }$ and $k(t,\mathit{x})=1$ for $\mathit{x}\in \mathrm{\Omega }\backslash {\overline{\mathrm{\Omega }}}_0$ and $k(t,\mathit{x})=k(t)$ for $\mathit{x}\in {\mathrm{\Omega }}_0$. The boundary $\mathrm{\Gamma }$ is split into three nonoverlapping parts, namely ${\mathrm{\Gamma }}_N$ (Neumann part), ${\mathrm{\Gamma }}_D$ (Dirichlet part) and ${\mathrm{\Gamma }}_0\subset \mathrm{\Gamma }\cap \mathit{\partial }{\mathrm{\Omega }}_0$, on which beside a Dirichlet boundary condition (BC) also the total flux through this part is prescribed. It is assumed that ${\overline{\mathrm{\Gamma }}}_D\cap {\overline{\mathrm{\Gamma }}}_0=\mathrm{\varnothing }$ with $\mathit{\mu }({\mathrm{\Gamma }}_0)>0$, where $\mathit{\mu }$ is the Lebesgue measure. The purpose of this article is to study the following nonlinear parabolic initial boundary value problem (IBVP) (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\mathit{\partial }}_t\mathit{\theta }(u)-\mathrm{\nabla }·\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,)\right)}& =f\hfill & \mathrm{in}{Q}_T:=(0,T)\times \mathrm{\Omega };\hfill \\ \hfill u& =g^D\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }& =g^N\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_N;\hfill \\ \hfill u(0)& =u_0\hfill & \mathrm{in}\mathrm{\Omega };\hfill \end{array}\right.\end{array}$$1 )–(22 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }}& =h(t)\hfill & \mathrm{in}(0,T);\hfill \\ \hfill {\displaystyle u}& =U(t)\hfill & \mathrm{on}(0,T)\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$2 ): find a couple $(K,u)$ such that ($T>0$ fixed)1 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\mathit{\partial }}_t\mathit{\theta }(u)-\mathrm{\nabla }·\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,)\right)}& =f\hfill & \mathrm{in}{Q}_T:=(0,T)\times \mathrm{\Omega };\hfill \\ \hfill u& =g^D\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }& =g^N\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_N;\hfill \\ \hfill u(0)& =u_0\hfill & \mathrm{in}\mathrm{\Omega };\hfill \end{array}\right.\end{array}$$1 and such that the following boundary measurements are satisfied2 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }}& =h(t)\hfill & \mathrm{in}(0,T);\hfill \\ \hfill {\displaystyle u}& =U(t)\hfill & \mathrm{on}(0,T)\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$2 More specific, the inverse problem of determining the unknown coefficient $K$ from the measured data (22 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }}& =h(t)\hfill & \mathrm{in}(0,T);\hfill \\ \hfill {\displaystyle u}& =U(t)\hfill & \mathrm{on}(0,T)\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$2 ) is considered. It is determined under which assumptions on the data this inverse problem has a weak solution $(K,u)$. Also, a nonlinear numerical algorithm based on backward Euler method is designed to approximate the solution $(K,u)$ and the convergence of approximations towards the weak solution in suitable function spaces is shown. An easier case with $\mathit{\theta }(u)=u$ and $\mathit{a}\equiv \mathbf{0}$ is studied in [11].

The remainder of this paper is organized as follows. Section 2 summarizes the mathematical tools and the assumptions on the data that are needed. Two different solution methods are presented in detail in Section 3. The existence of a solution to (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\mathit{\partial }}_t\mathit{\theta }(u)-\mathrm{\nabla }·\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,)\right)}& =f\hfill & \mathrm{in}{Q}_T:=(0,T)\times \mathrm{\Omega };\hfill \\ \hfill u& =g^D\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }& =g^N\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_N;\hfill \\ \hfill u(0)& =u_0\hfill & \mathrm{in}\mathrm{\Omega };\hfill \end{array}\right.\end{array}$$1 ) and (22 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }}& =h(t)\hfill & \mathrm{in}(0,T);\hfill \\ \hfill {\displaystyle u}& =U(t)\hfill & \mathrm{on}(0,T)\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$2 ) for each solution method is shown in Section 4. Finally, some numerical experiments are developed in Section 5.

2 Variational setting and assumptions

First, some standard notations are introduced. The euclidian norm of a vector $\mathit{v}$ in ${\mathbb{R}}^d$ is denoted by $|\mathit{v}|$. To increase the readability of the text, it is assumed without loss of generality that $g^D=0$ and $g^N=0$. The suitable choice of a test space is$$V:=\left\{\mathit{\phi },\in ,H^1,(\mathrm{\Omega }),;,,\mathit{\phi },{{|}_{{\mathrm{\Gamma }}_D}=0,\mathit{\phi }|}_{{\mathrm{\Gamma }}_0},=,\mathit{constant}\right\},$$which is clearly a Hilbert space with norm ${∥,u∥}_V^2={∥,u∥}^2+{∥,\mathrm{\nabla },u∥}^2$, where $∥,·∥$ represents the norm in $L_2(\mathrm{\Omega })$. Also a subspace of $V$ is considered, namely$$W:=\left\{\mathit{\phi },\in ,H^1,{(\mathrm{\Omega });\mathit{\phi }|}_{{\mathrm{\Gamma }}_0\cup {\mathrm{\Gamma }}_D},=,0\right\}.$$Due to the homogeneous Dirichlet boundary condition (BC) on the boundary ${\mathrm{\Gamma }}_D$, the following Friedrichs inequality holds for every function $u\in V$3 $$\begin{array}{c}\hfill {∥,u∥}_V⩽C∥,\mathrm{\nabla },u∥.\end{array}$$3 Consequently, the norm in the space $V$ is equivalent with the seminorm $∥,\mathrm{\nabla },u∥$. The norm in the trace space $L_2(\mathit{\gamma })$, with $\mathit{\gamma }\subset \mathrm{\Gamma }$, is written by ${∥,·∥}_{L_2(\mathit{\gamma })}$. The dual space of $V$ is denoted by $V^{\ast }$.

What now follows is a list of assumptions that are necessary to prove the existence of a weak solution to the nonlinear problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\mathit{\partial }}_t\mathit{\theta }(u)-\mathrm{\nabla }·\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,)\right)}& =f\hfill & \mathrm{in}{Q}_T:=(0,T)\times \mathrm{\Omega };\hfill \\ \hfill u& =g^D\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }& =g^N\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_N;\hfill \\ \hfill u(0)& =u_0\hfill & \mathrm{in}\mathrm{\Omega };\hfill \end{array}\right.\end{array}$$1 ) and (22 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }}& =h(t)\hfill & \mathrm{in}(0,T);\hfill \\ \hfill {\displaystyle u}& =U(t)\hfill & \mathrm{on}(0,T)\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$2 ) on a single time step. The continuous function $\mathit{\theta }:\mathbb{R}\to \mathbb{R}$ (diffusion term) has to satisfy4 $$\begin{array}{cc}\hfill \mathit{\theta }(0)& =0;\hfill \end{array}$$4 5 $$\begin{array}{ccc}\hfill |\mathit{\theta }(s)|& ⩽\hfill & \hfill C(1+|s|)\text{a.e. in}\mathbb{R}.\end{array}$$5 Moreover,6 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle {\mathit{\theta }}^{\prime }(s)⩾0}\hfill & \text{a.e. in}\mathbb{R}\text{if}\mathit{a}(u)=\mathit{a}(\mathit{a}\text{independent of}u);\hfill \\ {\mathit{\theta }}^{\prime }(s)⩾{\mathit{\theta }}_0>0\hfill & \text{a.e. in}\mathbb{R}\text{if}\mathit{a}(u)\ne \mathit{a}(\mathit{a}\text{depends on}u).\hfill \end{array}\right.\end{array}$$6

Remark 2.1

The condition $\mathit{a}(u(t,\mathbf{x}))=\mathit{a}(t,\mathbf{x})$ in (66 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle {\mathit{\theta }}^{\prime }(s)⩾0}\hfill & \text{a.e. in}\mathbb{R}\text{if}\mathit{a}(u)=\mathit{a}(\mathit{a}\text{independent of}u);\hfill \\ {\mathit{\theta }}^{\prime }(s)⩾{\mathit{\theta }}_0>0\hfill & \text{a.e. in}\mathbb{R}\text{if}\mathit{a}(u)\ne \mathit{a}(\mathit{a}\text{depends on}u).\hfill \end{array}\right.\end{array}$$6 ) means that $\mathit{a}$ does not depend on the solution $u$, but only on time and position, i.e. $(t,\mathbf{x})\in Q_T$. If $\mathit{a}(u)\ne \mathit{a}$, then $\mathit{a}$ is depending on $u$, for instance $\mathit{a}(u)=\mathit{b}u$ with $\mathit{b}:Q_T\to {\mathbb{R}}^d$.

The vector-valued function $\mathit{a}:\mathbb{R}\to {\mathbb{R}}^d$ (convection term) is also continuous and7 $$\begin{array}{ccc}\hfill |\mathit{a}(s)|& =|\left({\mathit{a}}_1,(s),,,{\mathit{a}}_2,(s),,,\dots ,,,{\mathit{a}}_d,(s)\right)|⩽C\hfill & \hfill \text{a.e. in}\mathbb{R};\end{array}$$7 8 $$\begin{array}{ccc}\hfill |{\mathit{a}}^{\prime }(s)|& =|\left({\mathit{a}}_1^{\prime },(s),,,{\mathit{a}}_2^{\prime },(s),,,\dots ,,,{\mathit{a}}_d^{\prime },(s)\right)|⩽C\hfill & \hfill \text{a.e. in}\mathbb{R}.\end{array}$$8

Remark 2.2

If $\mathit{a}(u)=\mathit{a}$, then the right-hand side (RHS) $f$ of (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\mathit{\partial }}_t\mathit{\theta }(u)-\mathrm{\nabla }·\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,)\right)}& =f\hfill & \mathrm{in}{Q}_T:=(0,T)\times \mathrm{\Omega };\hfill \\ \hfill u& =g^D\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }& =g^N\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_N;\hfill \\ \hfill u(0)& =u_0\hfill & \mathrm{in}\mathrm{\Omega };\hfill \end{array}\right.\end{array}$$1 ) can be redefined as $f+\mathrm{\nabla }·\mathit{a}$. From now on, it is assumed that $\mathrm{\nabla }·{\mathit{\partial }}_t\mathit{a}\in L_2((0,T),L_2(\mathrm{\Omega }))$ such that the $\mathit{a}(u)$-term in problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\mathit{\partial }}_t\mathit{\theta }(u)-\mathrm{\nabla }·\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,)\right)}& =f\hfill & \mathrm{in}{Q}_T:=(0,T)\times \mathrm{\Omega };\hfill \\ \hfill u& =g^D\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }& =g^N\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_N;\hfill \\ \hfill u(0)& =u_0\hfill & \mathrm{in}\mathrm{\Omega };\hfill \end{array}\right.\end{array}$$1 ) and (22 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }}& =h(t)\hfill & \mathrm{in}(0,T);\hfill \\ \hfill {\displaystyle u}& =U(t)\hfill & \mathrm{on}(0,T)\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$2 ) can be cancelled out of the equations if $\mathit{a}(u)=\mathit{a}$, see also equation (1414 $$\begin{array}{cc}& {\displaystyle {\mathit{\partial }}_{t}f\in L_2((0,T),L_2(\mathrm{\Omega }))\Rightarrow f\in C([0,T],L^2(\mathrm{\Omega })).}\hfill \end{array}$$14 ). Therefore, assumptions (77 $$\begin{array}{ccc}\hfill |\mathit{a}(s)|& =|\left({\mathit{a}}_1,(s),,,{\mathit{a}}_2,(s),,,\dots ,,,{\mathit{a}}_d,(s)\right)|⩽C\hfill & \hfill \text{a.e. in}\mathbb{R};\end{array}$$7 ) and (88 $$\begin{array}{ccc}\hfill |{\mathit{a}}^{\prime }(s)|& =|\left({\mathit{a}}_1^{\prime },(s),,,{\mathit{a}}_2^{\prime },(s),,,\dots ,,,{\mathit{a}}_d^{\prime },(s)\right)|⩽C\hfill & \hfill \text{a.e. in}\mathbb{R}.\end{array}$$8 ) are only necessary if $\mathit{a}(u)\ne \mathit{a}$.

Remark 2.3

The source function $f$ in problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\mathit{\partial }}_t\mathit{\theta }(u)-\mathrm{\nabla }·\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,)\right)}& =f\hfill & \mathrm{in}{Q}_T:=(0,T)\times \mathrm{\Omega };\hfill \\ \hfill u& =g^D\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }& =g^N\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_N;\hfill \\ \hfill u(0)& =u_0\hfill & \mathrm{in}\mathrm{\Omega };\hfill \end{array}\right.\end{array}$$1 ) and (22 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }}& =h(t)\hfill & \mathrm{in}(0,T);\hfill \\ \hfill {\displaystyle u}& =U(t)\hfill & \mathrm{on}(0,T)\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$2 ) depends only on the time and space variable. However, our numerical procedure can be generalized to a nonlinear $f(u)$, assuming ${\mathit{\theta }}^{\prime }⩾{\mathit{\theta }}_0>0$ if $\mathit{a}(u)=\mathit{a}$. The purpose of this paper is to keep the regularity as low as possible during the analysis. This is the reason why is started with the lowest plausible assumptions. Further, during the analysis, more assumptions are necessary on the function $\mathit{\theta }$.

The following assumptions on the other data functions are adopted9 $$\begin{array}{cc}& {\displaystyle 0<C_0⩽k⩽C_1;}\hfill \end{array}$$9 10 $$\begin{array}{cc}& {\displaystyle 0<D_0⩽\mathit{\kappa }⩽D_1;}\hfill \end{array}$$10 11 $$\begin{array}{cc}& {\displaystyle \mathit{\kappa }\in C([0,T],H^1(\mathrm{\Omega }));}\hfill \end{array}$$11 12 $$\begin{array}{cc}& {\displaystyle U\in C([0,T]);}\hfill \end{array}$$12 13 $$\begin{array}{cc}& {\displaystyle h^{\prime }\in L_2((0,T))\Rightarrow h\in C([0,T]);}\hfill \end{array}$$13 14 $$\begin{array}{cc}& {\displaystyle {\mathit{\partial }}_{t}f\in L_2((0,T),L_2(\mathrm{\Omega }))\Rightarrow f\in C([0,T],L^2(\mathrm{\Omega })).}\hfill \end{array}$$14

The initial datum satisfies15 $$\begin{array}{c}\hfill u_0\in H^1(\mathrm{\Omega }).\end{array}$$15 Note that the data function $U$ can be prolonged into the whole domain $\mathrm{\Omega }$ by a function $\tilde{U}$ in such a way that [12, Lemma 5.1]16 $$\begin{array}{c}\hfill \tilde{U}\in C\left([0,T],,,H^1,(\mathrm{\Omega })\right),\tilde{U}=\left\{\begin{array}{cc}0\hfill & \text{on}\left[0,,,T\right]\times {\mathrm{\Gamma }}_D;\hfill \\ U\hfill & \text{on}\left[0,,,T\right]\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$16 Finally, some useful (in)equalities are stated, which can easily be derived:$$\begin{array}{c}\hfill 2\sum _{i=1}^n(a_i-a_{i-1})a_i=a_n^2-a_0^2+\sum _{i=1}^n{(a_i-a_{i-1})}^2,a_i\in \mathbb{R};\text{Abel's summation rule}\end{array}$$and$$\begin{array}{c}\hfill ab⩽\mathit{\epsilon }{a}^2+C_{\mathit{\epsilon }}{b}^2,a,b\in \mathbb{R},\mathit{\epsilon }>0.\text{Young's inequality}\end{array}$$

Remark 2.4

In this contribution, the values $C,\mathit{\epsilon },C_{\mathit{\epsilon }}$ are generic and positive constants independent of the discretization parameter $\mathit{\tau }$, see Section 3. They can be different from place to place. The value $\mathit{\epsilon }$ is small and $C_{\mathit{\epsilon }}=C\left({\mathit{\epsilon }}^{-1}\right)$. To reduce the number of arbitrary constants, we use the notation $a\lesssim b$ if there exists a positive constant $C$ such that $a⩽Cb$.

3 A single time step

Rothe’s method [13] is applied to prove the existence of a weak solution to problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\mathit{\partial }}_t\mathit{\theta }(u)-\mathrm{\nabla }·\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,)\right)}& =f\hfill & \mathrm{in}{Q}_T:=(0,T)\times \mathrm{\Omega };\hfill \\ \hfill u& =g^D\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }& =g^N\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_N;\hfill \\ \hfill u(0)& =u_0\hfill & \mathrm{in}\mathrm{\Omega };\hfill \end{array}\right.\end{array}$$1 ) and (22 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }}& =h(t)\hfill & \mathrm{in}(0,T);\hfill \\ \hfill {\displaystyle u}& =U(t)\hfill & \mathrm{on}(0,T)\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$2 ). An equidistant time-partitioning is used with time step $\mathit{\tau }=T/n<1,$ for any $n\in \mathbb{N}$. Let us introduce the notations $t_i=i\mathit{\tau }$ and for any function $z$$$z_i=z(t_i),\mathit{\delta }{z}_i=\frac{z_i-z_{i-1}}{\mathit{\tau }}.$$The following recursive approximation scheme is proposed for $i=1,\cdots ,n$: find the unknown couple $(k_i,u_i)\in {\mathbb{R}}_{+}\times V$ on each time step that satisfies17 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =h_i\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$17 where $K_i=k_i{\mathit{\kappa }}_i$. In this section, the existence of $(K_i,u_i)$ for any $i=1,\cdots ,n$ is shown in two ways: two different methods for solving (1717 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =h_i\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$17 ) are presented.

In the first one, it is assumed that $k_i$ is given and a solution of the direct problem18 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill {\displaystyle \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =h_i\hfill \end{array}\right.\end{array}$$18 is looked for. Afterwards, it is shown that the trace of $u_i$ on ${\mathrm{\Gamma }}_0$ depends continuously on $k_i$. Then, $k_i$ is determined such that $u_i{|}_{{\mathrm{\Gamma }}_0}=U_i$. This solution method is discussed in detail in Section 3.1.

In the second solution method, the following direct problem is solved19 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0\hfill \end{array}\right.\end{array}$$19 for a given $k_i$. It is proved that the total flux through ${\mathrm{\Gamma }}_0$, ${\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu },$ depends continuously on $k_i$. At the end, $k_i$ is found such that ${\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }=h_i$. The reader can find more details in Section 3.2. Only the differences with the previous solution method are pointed out.

Finally, in Section 3.3, a lemma is stated about the existence of a solution on a single time step of problem (1717 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =h_i\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$17 ). This lemma is based on the results of Sections 3.1 and 3.2.

3.1 First solution method

First, the variational formulation of (1818 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill {\displaystyle \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =h_i\hfill \end{array}\right.\end{array}$$18 ) is considered20 $$\begin{array}{c}\hfill {\displaystyle \frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-h_i{\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}+\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_{i-1},),,,\mathit{\phi }\right),(\mathit{\phi }\in V).}\end{array}$$20 In the following lemma, the theory of monotone operators is applied to prove the existence of a weak solution to (2020 $$\begin{array}{c}\hfill {\displaystyle \frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-h_i{\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}+\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_{i-1},),,,\mathit{\phi }\right),(\mathit{\phi }\in V).}\end{array}$$20 ) for given $K_i$. The interested reader is referred to [14] for further information.

Lemma 3.1

(Unicity)    Assume (44 $$\begin{array}{cc}\hfill \mathit{\theta }(0)& =0;\hfill \end{array}$$4 )–(1515 $$\begin{array}{c}\hfill u_0\in H^1(\mathrm{\Omega }).\end{array}$$15 ). For any given $k_i>0$, $i=1,\dots ,n$, there exist a ${\mathit{\tau }}_0>0$ and an uniquely determined $u_{k_i}\in V$ solving (1818 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill {\displaystyle \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =h_i\hfill \end{array}\right.\end{array}$$18 ) for $\mathit{\tau }<{\mathit{\tau }}_0$.

Proof

We consider the nonlinear operators $A_i:V\to V^{\ast },i=1,\dots ,n,$ defined as$$\begin{array}{c}\hfill 〈A_i(u),\mathit{\phi }〉:=\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },u,+,\mathit{a},(u),,,\mathrm{\nabla },\mathit{\phi }\right),\end{array}$$together with the linear functionals $F_i:V\to \mathbb{R},i=1,\dots ,n,$ such that$$\begin{array}{c}\hfill 〈F_i,,,\mathit{\phi }〉:=\left(f_i,,,\mathit{\phi }\right)-h_i{\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}+\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_{i-1},),,,\mathit{\phi }\right).\end{array}$$We proof that $A_i$ is strictly monotone, coercive and demicontinuous. In the case of $\mathit{a}(u)=\mathit{a}$, it follows from the monotonicity of $\mathit{\theta }$ that$$\begin{array}{cc}\hfill 〈A_i(u)-A_i(v),u-v〉& =\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u,),-,\mathit{\theta },(,v,),,,u,-,v\right)+\left(K_i,\mathrm{\nabla },(u-v),,,\mathrm{\nabla },(u-v)\right)\hfill \\ \hfill & ⩾\hfill & \hfill C_0{D}_0{∥,\mathrm{\nabla },(,u,-,v,)∥}^2.\end{array}$$The strict monotonicity of $A_i$ follows by an application of the Friedrichs inequality (33 $$\begin{array}{c}\hfill {∥,u∥}_V⩽C∥,\mathrm{\nabla },u∥.\end{array}$$3 ). Secondly, we do the case that $\mathit{a}(u)\ne \mathit{a}$. Using the mean value theorem and the Young’s inequality, we have$$\begin{array}{cc}& 〈A_i(u)-A_i(v),u-v〉\hfill \\ \hfill & =\frac{1}{\mathit{\tau }}\left({\mathit{\theta }}^{\prime },({\mathit{\xi }}_1),[u-v],,,u,-,v\right)+\left(K_i,\mathrm{\nabla },(u-v),,,\mathrm{\nabla },(u-v)\right)+\left({\mathit{a}}^{\prime },({\mathit{\xi }}_2),[u-v],,,\mathrm{\nabla },(u-v)\right)\hfill \\ \hfill \\ \hfill & ⩾\frac{{\mathit{\theta }}_0}{\mathit{\tau }}{∥,u,-,v∥}^2+C_0{D}_0{∥,\mathrm{\nabla },(,u,-,v,)∥}^2-C_{\mathit{\epsilon }}{∥,{\mathit{a}}^{\prime },({\mathit{\xi }}_2),[u-v]∥}^2-\mathit{\epsilon }{∥,\mathrm{\nabla },(,u,-,v,)∥}^2\hfill \\ \hfill & ⩾\left(\frac{{\mathit{\theta }}_0}{\mathit{\tau }},-,C_{\mathit{\epsilon }}\right){∥,u,-,v∥}^2+\left(C_0,D_0,-,\mathit{\epsilon }\right){∥,\mathrm{\nabla },(,u,-,v,)∥}^2.\hfill \end{array}$$Fixing a sufficiently small $\mathit{\epsilon }>0$ and $\mathit{\tau }(\mathit{\epsilon })>0$ gives the strict monotonicity of the operator $A_i$. The operator $A_i$ is coercive if$${\displaystyle \underset{{∥,u∥}_V\to +\infty }{lim}\frac{〈A_i(u),u〉}{{∥,u∥}_V}=+\infty .}$$This is always satisfied. If $\mathit{a}(u)\ne \mathit{a}$, then the following lower bound is valid for sufficiently small $\mathit{\epsilon }$$$\begin{array}{cc}\hfill 〈A_i(u),u〉& =\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u,),,,u\right)+\left(K_i,\mathrm{\nabla },u,+,\mathit{a},(u),,,\mathrm{\nabla },u\right)\hfill \\ \hfill & \stackrel{(4)}{⩾}\frac{{\mathit{\theta }}_0}{\mathit{\tau }}{∥,u∥}^2+C_0{D}_0{∥,\mathrm{\nabla },u∥}^2-C_{\mathit{\epsilon }}{∥,\mathit{a},(,u,)∥}^2-\mathit{\epsilon }{∥,\mathrm{\nabla },u∥}^2\hfill \\ \hfill & \stackrel{(7)}{⩾}C{∥,u∥}_V^2-C.\hfill \end{array}$$In the case $\mathit{a}(u)=\mathit{a}$, the second constant in this lower bound disappears$$〈A_i(u),u〉⩾C_0{D}_0{∥,\mathrm{\nabla },u∥}^2\stackrel{(3)}{⩾}C{∥,u∥}_V^2.$$The demicontinuity of $A_i$ follows from the continuity of $\mathit{\theta }$ and $\mathit{a}$. The functionals $F_i$ belong to $V^{\ast }$ if $u_{i-1}\in L_2(\mathrm{\Omega })$ due to $f_i\in L_2(\mathrm{\Omega })$, the boundedness of $h$, the trace theorem (cf. [15, Theorem 3.9]) and the growth condition on $\mathit{\theta }$$$|〈F_i,\mathit{\phi }〉|⩽∥,f_i∥∥,\mathit{\phi }∥+|h_i|\frac{{∥,\mathit{\phi }∥}_{L_2({\mathrm{\Gamma }}_0)}}{\sqrt{|{\mathrm{\Gamma }}_0|}}+\frac{1}{\mathit{\tau }}∥,\mathit{\theta },(,u_{i-1},)∥∥,\mathit{\phi }∥\lesssim (1+∥,u_{i-1}∥){∥,\mathit{\phi }∥}_V.$$Consequently, since $u_0\in L_2(\mathrm{\Omega })$, the equation $A_i(u)=F_i$ admits a unique solution for $i=1,\dots ,n$. $\square$

In the subsequent Lemma, the existence of an uniform bound for $u_{k_i}$ independent of $k_i$ is proved.

Lemma 3.2

(Uniform bound for $u_{k_i}$)    Assume (44 $$\begin{array}{cc}\hfill \mathit{\theta }(0)& =0;\hfill \end{array}$$4 )–(1515 $$\begin{array}{c}\hfill u_0\in H^1(\mathrm{\Omega }).\end{array}$$15 ). There exists a positive constant $C$ such that$${∥,u_{k_i}∥}_V^2⩽\frac{C}{{\mathit{\tau }}^2}\text{for}{C}_0⩽k_i⩽C_1,i=1,\dots ,n.$$

Proof

We consider $k_i>0$ as a parameter. We set $\mathit{\phi }=u_{k_i}$ into (2020 $$\begin{array}{c}\hfill {\displaystyle \frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-h_i{\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}+\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_{i-1},),,,\mathit{\phi }\right),(\mathit{\phi }\in V).}\end{array}$$20 ) and get$$\begin{array}{c}\hfill \frac{1}{\mathit{\tau }}\left(\mathit{\theta },(u_{k_i}),,,u_{k_i}\right)+\left(K_i,\mathrm{\nabla },u_{k_i},,,\mathrm{\nabla },u_{k_i}\right)\\ \hfill & {\displaystyle =\left(f_i,,,u_{k_i}\right)-h_i{u}_{k_i}{|}_{{\mathrm{\Gamma }}_0}+\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(u_{i-1}),,,u_{k_i}\right)-\left(\mathit{a},(u_{k_i}),,,\mathrm{\nabla },u_{k_i}\right).}\hfill \end{array}$$Remark that the solution on the previous time step, $u_{i-1}$, belongs to $L_2(\mathrm{\Omega })$. First, we consider the case $\mathit{a}(u)=\mathit{a}$. Using the Cauchy’s and Young’s inequalities together with the growth condition on $\mathit{\theta }$, we obtain the trace theorem and the Friedrichs inequality (33 $$\begin{array}{c}\hfill {∥,u∥}_V⩽C∥,\mathrm{\nabla },u∥.\end{array}$$3 )$$\begin{array}{cc}\hfill \left|\left(f_i,,,u_{k_i}\right)\right|& ⩽C_{\mathit{\epsilon }}{∥,f_i∥}^2+\mathit{\epsilon }{∥,u_{k_i}∥}^2⩽C_{\mathit{\epsilon }}+\mathit{\epsilon }{∥,\mathrm{\nabla },u_{k_i}∥}^2,\hfill \\ \hfill \left|,h_i,u_{k_i},{|}_{{\mathrm{\Gamma }}_0}\right|& ⩽C_{\mathit{\epsilon }}{h}_i^2+\mathit{\epsilon }\frac{{∥,u_{k_i}∥}_{L_2({\mathrm{\Gamma }}_0)}^2}{|{\mathrm{\Gamma }}_0|}⩽C_{\mathit{\epsilon }}+\mathit{\epsilon }{∥,\mathrm{\nabla },u_{k_i}∥}^2,\hfill \\ \hfill \left|\frac{1}{\mathit{\tau }},\left(\mathit{\theta },(u_{i-1}),,,u_{k_i}\right)\right|& ⩽\frac{C_{\mathit{\epsilon }}}{{\mathit{\tau }}^2}{∥,\mathit{\theta },(,u_{i-1},)∥}^2+\mathit{\epsilon }{∥,u_{k_i}∥}^2⩽\frac{C_{\mathit{\epsilon }}}{{\mathit{\tau }}^2}+\mathit{\epsilon }{∥,\mathrm{\nabla },u_{k_i}∥}^2.\hfill \end{array}$$Using the monotonicity of $\mathit{\theta }$ and the uniform bounds (99 $$\begin{array}{cc}& {\displaystyle 0<C_0⩽k⩽C_1;}\hfill \end{array}$$9 ) and (1010 $$\begin{array}{cc}& {\displaystyle 0<D_0⩽\mathit{\kappa }⩽D_1;}\hfill \end{array}$$10 ) one can easily get$$\left(C_0,D_0,-,\mathit{\epsilon }\right){∥,\mathrm{\nabla },u_{k_i}∥}^2⩽\frac{C_{\mathit{\epsilon }}}{{\mathit{\tau }}^2}.$$Analogue, in the case $\mathit{a}(u)\ne \mathit{a}$, we can readily obtain$$\left|\left(\mathit{a},(u_{k_i}),,,\mathrm{\nabla },u_{k_i}\right)\right|⩽C_{\mathit{\epsilon }}{∥,\mathit{a},(,u_{k_i},)∥}^2+\mathit{\epsilon }{∥,\mathrm{\nabla },u_{k_i}∥}^2\stackrel{(7)}{⩽}{C}_{\mathit{\epsilon }}+\mathit{\epsilon }{∥,\mathrm{\nabla },u_{k_i}∥}^2$$and therefore$$\frac{{\mathit{\theta }}_0}{\mathit{\tau }}{∥,u_{k_i}∥}^2+\left(C_0,D_0,-,\mathit{\epsilon }\right){∥,\mathrm{\nabla },u_{k_i}∥}^2⩽\frac{C_{\mathit{\epsilon }}}{{\mathit{\tau }}^2}.$$Fixing a sufficiently small positive $\mathit{\epsilon }$ in both cases and applying the Friedrichs inequality if $\mathit{a}(u)=\mathit{a}$, we conclude the proof. $\square$

To prove that the trace of $u_i$ on ${\mathrm{\Gamma }}_0$ depends continuously on $k_i$, it is necessary to define the following coefficient to data map$$\mathcal{T}:[C_0,C_1]\to \mathbb{R}:k_i\mapsto \mathcal{T}(k_i):=u_{k_i}{|}_{{\mathrm{\Gamma }}_0}.$$Then, the inverse problem with the measured output data $U(t)$ can be formulated as the following operator equation: search $k_i$ such that$$\mathcal{T}(k_i)=U_i.$$The continuity of this input–output map $\mathcal{T}$ is investigated in the following lemma. It is this property that leads to the existence of a solution to problem (1717 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =h_i\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$17 ), see Lemma 3.7.

Lemma 3.3

($u_{k_i}$ depends continuously on $k_i$)   Assume (44 $$\begin{array}{cc}\hfill \mathit{\theta }(0)& =0;\hfill \end{array}$$4 )–(1515 $$\begin{array}{c}\hfill u_0\in H^1(\mathrm{\Omega }).\end{array}$$15 ). There exists a ${\mathit{\tau }}_0>0$ such that the function $\mathcal{T}$ is continuous for $\mathit{\tau }<{\mathit{\tau }}_0$.

Proof

Subtract (2020 $$\begin{array}{c}\hfill {\displaystyle \frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-h_i{\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}+\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_{i-1},),,,\mathit{\phi }\right),(\mathit{\phi }\in V).}\end{array}$$20 ) for $k_i=\mathit{\beta }$ from (2020 $$\begin{array}{c}\hfill {\displaystyle \frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-h_i{\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}+\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_{i-1},),,,\mathit{\phi }\right),(\mathit{\phi }\in V).}\end{array}$$20 ) for $k_i=\mathit{\alpha }$ and set $\mathit{\phi }=u_{\mathit{\alpha }}-u_{\mathit{\beta }}$ to get$$\begin{array}{cc}& \frac{1}{\mathit{\tau }}\left(\mathit{\theta },(u_{\mathit{\alpha }}),-,\mathit{\theta },(u_{\mathit{\beta }}),,,u_{\mathit{\alpha }},-,u_{\mathit{\beta }}\right)+\left(\mathit{\alpha },{\mathit{\kappa }}_i,\mathrm{\nabla },(u_{\mathit{\alpha }}-u_{\mathit{\beta }}),,,\mathrm{\nabla },(u_{\mathit{\alpha }}-u_{\mathit{\beta }})\right)\hfill \\ \hfill & =\left((\mathit{\beta }-\mathit{\alpha }),{\mathit{\kappa }}_i,\mathrm{\nabla },u_{\mathit{\beta }},,,\mathrm{\nabla },(u_{\mathit{\alpha }}-u_{\mathit{\beta }})\right)-\left(\mathit{a},(u_{\mathit{\alpha }}),-,\mathit{a},(u_{\mathit{\beta }}),,,\mathrm{\nabla },(u_{\mathit{\alpha }}-u_{\mathit{\beta }})\right).\hfill \end{array}$$The first term in the RHS can be bounded using the Cauchy’s and Young’s inequality, Lemma 3.2 and the uniform bound (1010 $$\begin{array}{cc}& {\displaystyle 0<D_0⩽\mathit{\kappa }⩽D_1;}\hfill \end{array}$$10 )$$\begin{array}{cc}\hfill \left((\mathit{\beta }-\mathit{\alpha }),{\mathit{\kappa }}_i,\mathrm{\nabla },u_{\mathit{\beta }},,,\mathrm{\nabla },(u_{\mathit{\alpha }}-u_{\mathit{\beta }})\right)& ⩽C_{\mathit{\epsilon }}{∥,(\mathit{\beta }-\mathit{\alpha }),{\mathit{\kappa }}_i,\mathrm{\nabla },u_{\mathit{\beta }}∥}^2+\mathit{\epsilon }{∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥}^2\hfill \\ \hfill & ⩽\frac{C_{\mathit{\epsilon }}}{{\mathit{\tau }}^2}{(\mathit{\beta }-\mathit{\alpha })}^2+\mathit{\epsilon }{∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥}^2.\hfill \end{array}$$The second term in the RHS disappears if $\mathit{a}(u)=\mathit{a}$. An obvious calculation employing the monotonicity of $\mathit{\theta }$ gives21 $$\begin{array}{c}\hfill (\mathit{\alpha }{D}_0-\mathit{\epsilon }){∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥}^2⩽\frac{C_{\mathit{\epsilon }}}{{\mathit{\tau }}^2}{(\mathit{\alpha }-\mathit{\beta })}^2.\end{array}$$21 We use the mean value theorem in the case of $\mathit{a}(u)\ne \mathit{a}$ to get$$\begin{array}{cc}\hfill \left(\mathit{a},(u_{\mathit{\alpha }}),-,\mathit{a},(u_{\mathit{\beta }}),,,\mathrm{\nabla },(u_{\mathit{\alpha }}-u_{\mathit{\beta }})\right)& ⩽C_{\mathit{\epsilon }}{∥,\mathit{a},(u_{\mathit{\alpha }}),-,\mathit{a},(u_{\mathit{\beta }})∥}^2+\mathit{\epsilon }{∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥}^2\hfill \\ \hfill & ⩽C_{\mathit{\epsilon }}{∥,u_{\mathit{\alpha }},-,u_{\mathit{\beta }}∥}^2+\mathit{\epsilon }{∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥}^2.\hfill \end{array}$$Therefore, we can derive the following estimate22 $$\begin{array}{c}\hfill \left(\frac{{\mathit{\theta }}_0}{\mathit{\tau }},-,C_{\mathit{\epsilon }}\right){∥,u_{\mathit{\alpha }},-,u_{\mathit{\beta }}∥}^2+(\mathit{\alpha }{D}_0-\mathit{\epsilon }){∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥}^2⩽\frac{C_{\mathit{\epsilon }}}{{\mathit{\tau }}^2}{(\mathit{\alpha }-\mathit{\beta })}^2.\end{array}$$22 We fix a sufficiently small $\mathit{\epsilon }$ and $\mathit{\tau }(\mathit{\epsilon })$ to conclude that in both cases23 $$\begin{array}{c}\hfill {∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥}^2\lesssim \frac{{(\mathit{\alpha }-\mathit{\beta })}^2}{{\mathit{\tau }}^2}.\end{array}$$23 Using the trace theorem and the Friedrichs inequality, we deduce in both cases that24 $$\begin{array}{c}\hfill \begin{array}{c}\hfill {\displaystyle \left|\mathcal{T},(,\mathit{\alpha },),-,\mathcal{T},(,\mathit{\beta },)\right|=\frac{{∥,u_{\mathit{\alpha }},-,u_{\mathit{\beta }}∥}_{L_2({\mathrm{\Gamma }}_0)}}{\sqrt{|{\mathrm{\Gamma }}_0|}}\lesssim ∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥\stackrel{(21)}{\lesssim }\frac{1}{\mathit{\tau }}|\mathit{\alpha }-\mathit{\beta }|.}\end{array}\end{array}$$24 $\square$

3.2 Second solution method

In contrast to the first solution method, the Lipschitz continuity of $\mathit{\theta }$ is needed in the second solution method, i.e. there exists a real constant ${\mathit{\theta }}_1$ such that25 $$\begin{array}{c}\hfill {\mathit{\theta }}^{\prime }(s)⩽{\mathit{\theta }}_1\text{a.e. in}\mathbb{R}.\end{array}$$25 To get rid of the nonhomogeneous Dirichlet BC on ${\mathrm{\Gamma }}_0$, the solution of (1919 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0\hfill \end{array}\right.\end{array}$$19 ) is prescribed as $u_i:=v_i+{\tilde{U}}_i,i=1,\dots ,n$, where $v_i$ is unknown. Next, define the functions $\mathit{\vartheta }:\mathbb{R}\to \mathbb{R}$ and $\mathit{b}:\mathbb{R}\to {\mathbb{R}}^d$ by setting$$\mathit{\vartheta }(s)=\mathit{\theta }(s+{\tilde{U}}_i)\text{and}\mathit{b}(s)=\mathit{a}(s+{\tilde{U}}_i).$$Thanks to the properties of $\mathit{\theta }$ and $\mathit{a}$, the function $\mathit{\vartheta }$ is monotonically increasing if $\mathit{b}$ is independent of $v_i$ and strict monotonically increasing if $\mathit{b}$ depends on $v_i$. Using the preceding assumptions, the variational formulation of (1919 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0\hfill \end{array}\right.\end{array}$$19 ) can be rewritten (for given $K_i$) for all $\mathit{\phi }\in W$ as26 $$\begin{array}{c}\hfill \frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(,v_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },v_i,+,\mathit{b},(v_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-\left(K_i,\mathrm{\nabla },{\tilde{U}}_i,,,\mathrm{\nabla },\mathit{\phi }\right)+\frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(,v_{i-1},),,,\mathit{\phi }\right).\end{array}$$26 The following growth condition on $\mathit{\vartheta }$ is satisfied due to the growth condition on $\mathit{\theta }$$$∥,\mathit{\vartheta },(,v,)∥\lesssim 1+∥,v,+,{\tilde{U}}_i∥\stackrel{(16)}{\lesssim }1+∥,v∥,v:\mathrm{\Omega }\to \mathbb{R}.$$Analogue as in the previous subsection one can state three lemmas.

Lemma 3.4

(Unicity)    Assume (44 $$\begin{array}{cc}\hfill \mathit{\theta }(0)& =0;\hfill \end{array}$$4 )–(1616 $$\begin{array}{c}\hfill \tilde{U}\in C\left([0,T],,,H^1,(\mathrm{\Omega })\right),\tilde{U}=\left\{\begin{array}{cc}0\hfill & \text{on}\left[0,,,T\right]\times {\mathrm{\Gamma }}_D;\hfill \\ U\hfill & \text{on}\left[0,,,T\right]\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$16 ). For any given $k_i>0$, $i=1,\dots ,n$, there exist a ${\mathit{\tau }}_0>0$ and an uniquely determined $v_{k_i}\in W$ solving (2323 $$\begin{array}{c}\hfill {∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥}^2\lesssim \frac{{(\mathit{\alpha }-\mathit{\beta })}^2}{{\mathit{\tau }}^2}.\end{array}$$23 ) for $\mathit{\tau }<{\mathit{\tau }}_0$. Moreover, the function $u_{k_i}=v_{k_i}+{\tilde{U}}_i\in V$ is solving (1919 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0\hfill \end{array}\right.\end{array}$$19 ).

Proof

This is almost an exact analogue of the proof of Lemma 3.1, except for the appearance of the following lower bound that is valid for each $v\in W$27 $$\begin{array}{cc}\hfill \left(\mathit{\vartheta },(,v,),,,v\right)& =\left(\mathit{\theta },(v+{\tilde{U}}_i),,,v,+,{\tilde{U}}_i\right)-\left(\mathit{\theta },(v+{\tilde{U}}_i),,,{\tilde{U}}_i\right)\hfill \\ \hfill & ⩾-\left|\left(\mathit{\theta },(v+{\tilde{U}}_i),,,{\tilde{U}}_i\right)\right|\hfill \\ \hfill & ⩾-C\left(1,+,∥,v∥,+,∥,{\tilde{U}}_i∥\right)∥,{\tilde{U}}_i∥\hfill \\ \hfill & \stackrel{(3)}{⩾}-C_{\mathit{\epsilon }}-\mathit{\epsilon }{∥,\mathrm{\nabla },v∥}^2.\hfill \end{array}$$27 $\square$

Lemma 3.5

(Uniform bound for $u_{k_i}$)    Assume (44 $$\begin{array}{cc}\hfill \mathit{\theta }(0)& =0;\hfill \end{array}$$4 )–(1616 $$\begin{array}{c}\hfill \tilde{U}\in C\left([0,T],,,H^1,(\mathrm{\Omega })\right),\tilde{U}=\left\{\begin{array}{cc}0\hfill & \text{on}\left[0,,,T\right]\times {\mathrm{\Gamma }}_D;\hfill \\ U\hfill & \text{on}\left[0,,,T\right]\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$16 ). There exists a positive constant $C$ such that for $i=1,\dots ,n$$${∥,v_{k_i}∥}_V^2⩽\frac{C}{{\mathit{\tau }}^2}\text{for}{C}_0⩽k_i⩽C_1,i=1,\dots ,n.$$

Proof

The proof follows very closely the proof of Lemma 3.2 using the lower bound (2424 $$\begin{array}{c}\hfill \begin{array}{c}\hfill {\displaystyle \left|\mathcal{T},(,\mathit{\alpha },),-,\mathcal{T},(,\mathit{\beta },)\right|=\frac{{∥,u_{\mathit{\alpha }},-,u_{\mathit{\beta }}∥}_{L_2({\mathrm{\Gamma }}_0)}}{\sqrt{|{\mathrm{\Gamma }}_0|}}\lesssim ∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥\stackrel{(21)}{\lesssim }\frac{1}{\mathit{\tau }}|\mathit{\alpha }-\mathit{\beta }|.}\end{array}\end{array}$$24 ). $\square$

At this point, define the coefficient to data map $\mathrm{\Psi }$ by$$\mathrm{\Psi }:[C_0,C_1]\to \mathbb{R}:k_i\mapsto \mathrm{\Psi }(k_i):=-{\int }_{{\mathrm{\Gamma }}_0}\left(k_i,{\mathit{\kappa }}_i,\mathrm{\nabla },u_{k_i},+,\mathit{a},(u_{k_i})\right)·\mathit{\nu }.$$Now, the inverse problem with the measured output data $h(t)$ can be formulated as the following operator equation: search $k_i$ such that$$\mathrm{\Psi }(k_i)=h_i.$$In the following lemma, the continuity of the map $\mathcal{T}$ is proved.

Lemma 3.6

($u_{k_i}$ depends continuously on $k_i$)   Assume (44 $$\begin{array}{cc}\hfill \mathit{\theta }(0)& =0;\hfill \end{array}$$4 )–(1616 $$\begin{array}{c}\hfill \tilde{U}\in C\left([0,T],,,H^1,(\mathrm{\Omega })\right),\tilde{U}=\left\{\begin{array}{cc}0\hfill & \text{on}\left[0,,,T\right]\times {\mathrm{\Gamma }}_D;\hfill \\ U\hfill & \text{on}\left[0,,,T\right]\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$16 ). There exists a ${\mathit{\tau }}_0>0$ such that the function $\mathrm{\Psi }$ is continuous for $\mathit{\tau }<{\mathit{\tau }}_0$.

Proof

Subtract (2323 $$\begin{array}{c}\hfill {∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥}^2\lesssim \frac{{(\mathit{\alpha }-\mathit{\beta })}^2}{{\mathit{\tau }}^2}.\end{array}$$23 ) for $k_i=\mathit{\beta }$ from (2323 $$\begin{array}{c}\hfill {∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥}^2\lesssim \frac{{(\mathit{\alpha }-\mathit{\beta })}^2}{{\mathit{\tau }}^2}.\end{array}$$23 ) for $k_i=\mathit{\alpha }$ and set $\mathit{\phi }=v_{\mathit{\alpha }}-v_{\mathit{\beta }}$ to get$$\begin{array}{cc}& \frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(v_{\mathit{\alpha }}),-,\mathit{\vartheta },(v_{\mathit{\beta }}),,,v_{\mathit{\alpha }},-,v_{\mathit{\beta }}\right)+\left(\mathit{\alpha },{\mathit{\kappa }}_i,\mathrm{\nabla },(v_{\mathit{\alpha }}-v_{\mathit{\beta }}),,,\mathrm{\nabla },(v_{\mathit{\alpha }}-v_{\mathit{\beta }})\right)\hfill \\ \hfill & =\left((\mathit{\beta }-\mathit{\alpha }),{\mathit{\kappa }}_i,\mathrm{\nabla },v_{\mathit{\beta }},,,\mathrm{\nabla },(v_{\mathit{\alpha }}-v_{\mathit{\beta }})\right)+\left((\mathit{\beta }-\mathit{\alpha }),{\mathit{\kappa }}_i,\mathrm{\nabla },{\tilde{U}}_i,,,\mathrm{\nabla },(v_{\mathit{\alpha }}-v_{\mathit{\beta }})\right)\hfill \\ \hfill & -\left(\mathit{b},(v_{\mathit{\alpha }}),-,\mathit{b},(v_{\mathit{\beta }}),,,\mathrm{\nabla },(v_{\mathit{\alpha }}-v_{\mathit{\beta }})\right),\hfill \end{array}$$which implies using Lemma 3.528 $$\begin{array}{c}\hfill {∥,\mathrm{\nabla },(,v_{\mathit{\alpha }},-,v_{\mathit{\beta }},)∥}^2\lesssim \frac{{(\mathit{\alpha }-\mathit{\beta })}^2}{{\mathit{\tau }}^2}.\end{array}$$28 Recall that ${\overline{\mathrm{\Gamma }}}_D\cap {\overline{\mathrm{\Gamma }}}_0=\mathrm{\varnothing }$. Hence, the existence of a function $\mathrm{\Phi }\in C^{\infty }(\overline{\mathrm{\Omega }})$ such that ${\mathrm{\Phi }|}_{{\mathrm{\Gamma }}_D}=0$ and ${\mathrm{\Phi }|}_{{\mathrm{\Gamma }}_0}=1$ is guaranteed by Friedman [12, Lemma 5.1]. Using problem (1919 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0\hfill \end{array}\right.\end{array}$$19 ), we have that$$\begin{array}{cc}\hfill \mathrm{\Psi }(k_i)& =-{\left(\left(k_i,{\mathit{\kappa }}_i,\mathrm{\nabla },u_{k_i},+,\mathit{a},(u_{k_i})\right),·,\mathit{\nu },,,1\right)}_{{\mathrm{\Gamma }}_0}\hfill \\ \hfill & =\left(f_i,,,\mathrm{\Phi }\right)-\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_{k_i},),,,\mathrm{\Phi }\right)-\left(k_i,{\mathit{\kappa }}_i,\mathrm{\nabla },u_{k_i},+,\mathit{a},(u_{k_i}),,,\mathrm{\nabla },\mathrm{\Phi }\right)+\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_{i-1},),,,\mathrm{\Phi }\right).\hfill \end{array}$$Therefore, using the mean value theorem we deduce that$$\begin{array}{cc}\hfill |\mathrm{\Psi }(\mathit{\alpha })-\mathrm{\Psi }(\mathit{\beta })|& {\displaystyle =|{\mathit{\tau }}^{-1}\left(\mathit{\theta },(u_{\mathit{\alpha }}),-,\mathit{\theta },(u_{\mathit{\beta }}),,,\mathrm{\Phi }\right)+\left(\mathit{a},(u_{\mathit{\alpha }}),-,\mathit{a},(u_{\mathit{\beta }}),,,\mathrm{\nabla },\mathrm{\Phi }\right)}\hfill \\ \hfill & {\displaystyle +\left(\mathit{\alpha },{\mathit{\kappa }}_i,\mathrm{\nabla },(u_{\mathit{\alpha }}-u_{\mathit{\beta }}),,,\mathrm{\nabla },\mathrm{\Phi }\right)+\left((\mathit{\alpha }-\mathit{\beta }),{\mathit{\kappa }}_i,\mathrm{\nabla },u_{\mathit{\beta }},,,\mathrm{\nabla },\mathrm{\Phi }\right)|}\hfill \\ \hfill & {\displaystyle \stackrel{(22)}{\lesssim }\frac{{\mathit{\theta }}_1}{\mathit{\tau }}∥,v_{\mathit{\alpha }},-,v_{\mathit{\beta }}∥∥,\mathrm{\Phi }∥+∥,v_{\mathit{\alpha }},-,v_{\mathit{\beta }}∥∥,\mathrm{\nabla },\mathrm{\Phi }∥}\hfill \\ \hfill & {\displaystyle +∥,\mathrm{\nabla },(,v_{\mathit{\alpha }},-,v_{\mathit{\beta }},)∥∥,\mathrm{\nabla },\mathrm{\Phi }∥+|\mathit{\alpha }-\mathit{\beta }|\left(∥,\mathrm{\nabla },v_{\mathit{\beta }}∥,+,∥,\mathrm{\nabla },{\tilde{U}}_i∥\right)∥,\mathrm{\nabla },\mathrm{\Phi }∥}\hfill \\ \hfill & {\displaystyle \stackrel{(3)}{\lesssim }\frac{1}{\mathit{\tau }}\left(∥,\mathrm{\nabla },(,v_{\mathit{\alpha }},-,v_{\mathit{\beta }},)∥,+,|\mathit{\alpha }-\mathit{\beta }|\right)}\hfill \\ \hfill & {\displaystyle \stackrel{(25)}{\lesssim }\frac{|\mathit{\alpha }-\mathit{\beta }|}{{\mathit{\tau }}^2}.}\hfill \end{array}$$This completes the proof. $\square$

3.3 Solvability of (1717 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =h_i\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$17 )

The following Lemma is a consequence of Sections 3.1 and 3.2.

Lemma 3.7

Assume (44 $$\begin{array}{cc}\hfill \mathit{\theta }(0)& =0;\hfill \end{array}$$4 )–(1616 $$\begin{array}{c}\hfill \tilde{U}\in C\left([0,T],,,H^1,(\mathrm{\Omega })\right),\tilde{U}=\left\{\begin{array}{cc}0\hfill & \text{on}\left[0,,,T\right]\times {\mathrm{\Gamma }}_D;\hfill \\ U\hfill & \text{on}\left[0,,,T\right]\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$16 ). If $U(t)\in \mathcal{T}([C_0,C_1])\forall t\in [0,T]$, then there exist a ${\mathit{\tau }}_0>0$ and a couple $(k_i,u_i)\in {\mathbb{R}}_{+}\times V$ that solves (1717 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =h_i\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$17 ) for $\mathit{\tau }<{\mathit{\tau }}_0$. If $\mathit{\theta }$ is Lipschitz continuous and $h(t)\in \mathrm{\Psi }([C_0,C_1])\forall t\in [0,T]$, then there exist a ${\mathit{\tau }}_0>0$ and a couple $(k_i,u_i)\in {\mathbb{R}}_{+}\times V$ that solves (1717 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =h_i\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0,\hfill \end{array}\right.\end{array}$$17 ) for $\mathit{\tau }<{\mathit{\tau }}_0$.

4 Convergence

In this section, the stability estimates are derived. Afterwards, the limit for $n\to \infty$ is passed to get the existence of a solution to problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\mathit{\partial }}_t\mathit{\theta }(u)-\mathrm{\nabla }·\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,)\right)}& =f\hfill & \mathrm{in}{Q}_T:=(0,T)\times \mathrm{\Omega };\hfill \\ \hfill u& =g^D\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }& =g^N\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_N;\hfill \\ \hfill u(0)& =u_0\hfill & \mathrm{in}\mathrm{\Omega };\hfill \end{array}\right.\end{array}$$1 )–(22 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }}& =h(t)\hfill & \mathrm{in}(0,T);\hfill \\ \hfill {\displaystyle u}& =U(t)\hfill & \mathrm{on}(0,T)\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$2 ). Again, the two different solution methods are considered.

4.1 First solution method

The variational formulation of (1818 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill {\displaystyle \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }}& =h_i\hfill \end{array}\right.\end{array}$$18 ) on time step $t_i$ reads as29 $$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \left(\mathit{\delta },\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i),,,\mathrm{\nabla },\mathit{\phi }\right)+h_i{\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}}& =\left(f_i,,,\mathit{\phi }\right)\mathit{\phi }\in V\hfill \\ \hfill u_i{|}_{{\mathrm{\Gamma }}_0}& {\displaystyle =U_i.}\hfill \end{array}\end{array}$$29 The formulation (2626 $$\begin{array}{c}\hfill \frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(,v_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },v_i,+,\mathit{b},(v_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-\left(K_i,\mathrm{\nabla },{\tilde{U}}_i,,,\mathrm{\nabla },\mathit{\phi }\right)+\frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(,v_{i-1},),,,\mathit{\phi }\right).\end{array}$$26 ) has a solution on $t_i$ according to Lemma 3.7. The next step is the stability analysis. First, two functions are introduced, which simplifies the proofs. Let $\mathit{\gamma }$ be any monotone increasing real function with $\mathit{\gamma }(0)=0$. A primitive function of $\mathit{\gamma }$ is denoted by ${\displaystyle {\mathrm{\Phi }}_{\mathit{\gamma }}(z):={\int }_0^z\mathit{\gamma }(s)\text{d}s}$. The function ${\mathrm{\Phi }}_{\mathit{\gamma }}(z)$ is convex because ${\mathrm{\Phi }}_{\mathit{\gamma }}^{″}(z)={\mathit{\gamma }}^{\prime }(z)⩾0$. One can check that30 $$\begin{array}{c}\hfill \mathit{\gamma }(z_1)(z_2-z_1)⩽{\mathrm{\Phi }}_{\mathit{\gamma }}(z_2)-{\mathrm{\Phi }}_{\mathit{\gamma }}(z_1)⩽\mathit{\gamma }(z_2)(z_2-z_1),\forall z_1,z_2\in \mathbb{R}.\end{array}$$30 According to $\mathit{\gamma }(0)=0$ and (2727 $$\begin{array}{cc}\hfill \left(\mathit{\vartheta },(,v,),,,v\right)& =\left(\mathit{\theta },(v+{\tilde{U}}_i),,,v,+,{\tilde{U}}_i\right)-\left(\mathit{\theta },(v+{\tilde{U}}_i),,,{\tilde{U}}_i\right)\hfill \\ \hfill & ⩾-\left|\left(\mathit{\theta },(v+{\tilde{U}}_i),,,{\tilde{U}}_i\right)\right|\hfill \\ \hfill & ⩾-C\left(1,+,∥,v∥,+,∥,{\tilde{U}}_i∥\right)∥,{\tilde{U}}_i∥\hfill \\ \hfill & \stackrel{(3)}{⩾}-C_{\mathit{\epsilon }}-\mathit{\epsilon }{∥,\mathrm{\nabla },v∥}^2.\hfill \end{array}$$27 ), a function ${\tilde{\mathrm{\Phi }}}_{\mathit{\gamma }}(z)$ can be defined such that$${\tilde{\mathrm{\Phi }}}_{\mathit{\gamma }}(z):=z\mathit{\gamma }(z)-{\mathrm{\Phi }}_{\mathit{\gamma }}(z)⩾0,\forall z\in \mathbb{R}.$$Some estimates on the function $u_i$ are deduced in the following lemma. These a priori estimates will serve as uniform bounds in order to prove convergence.

Lemma 4.1

Let the assumptions of Lemma 3.7 be fulfilled. Then there exists a positive constant $C$ such that

(i)	${\displaystyle \sum _{i=1}^n{∥,u_i∥}_V^2\mathit{\tau }⩽C;}$
(ii)	${\displaystyle \underset{1⩽i⩽n}{max}{∥,u_i∥}_V^2+\sum _{i=1}^n{∥,u_i,-,u_{i-1}∥}_V^2⩽C}$        if $\mathit{a}(u)=\mathit{a}$ and ${\displaystyle \sum _{i=1}^n{∥,\mathit{\delta },u_i∥}^2\mathit{\tau }+\underset{1⩽i⩽n}{max}{∥,u_i∥}_V^2+\sum _{i=1}^n{∥,u_i,-,u_{i-1}∥}_V^2⩽C}$        if $\mathit{a}(u)\ne \mathit{a};$
(iii)	${\displaystyle \underset{1⩽i⩽n}{max}{∥,\mathit{\theta },(,u_i,)∥}_V^2⩽C;}$
(iv)	${\displaystyle \underset{1⩽i⩽n}{max}{\Vert \mathit{\delta }\mathit{\theta }(u_i)\Vert }_{V^{\ast }}⩽C}$        and       ${\displaystyle \sum _{i=1}^n{\Vert \mathit{\delta }\mathit{\theta }(u_i)\Vert }_{V^{\ast }}^2\mathit{\tau }⩽C;}$

Proof

(i) Setting $\mathit{\phi }=u_i$ into (2626 $$\begin{array}{c}\hfill \frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(,v_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },v_i,+,\mathit{b},(v_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-\left(K_i,\mathrm{\nabla },{\tilde{U}}_i,,,\mathrm{\nabla },\mathit{\phi }\right)+\frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(,v_{i-1},),,,\mathit{\phi }\right).\end{array}$$26 ), multiplying by $\mathit{\tau }$ and summing it up for $i=1,\cdots ,j$ we have$$\sum _{i=1}^j\left(\mathit{\delta },\mathit{\theta },(u_i),,,u_i\right)\mathit{\tau }+\sum _{i=1}^j\left(K_i,\mathrm{\nabla },u_i,,,\mathrm{\nabla },u_i\right)\mathit{\tau }=\sum _{i=1}^j\left(f_i,,,u_i\right)\mathit{\tau }-\sum _{i=1}^j{h}_i{u}_i{|}_{{\mathrm{\Gamma }}_0}\mathit{\tau }-\sum _{i=1}^j\left(\mathit{a},(u_i),,,\mathrm{\nabla },u_i\right)\mathit{\tau }.$$According to Abel’s summation rule, the assumption that $\mathit{\theta }$ is monotonically nondecreasing, the growth condition on $\mathit{\theta }$ and $u_0\in L_2(\mathrm{\Omega })$, we can derive a lower bound for the first term on the left-hand side (LHS) of the above equation:$$\begin{array}{cc}\hfill \sum _{i=1}^j\left(\mathit{\theta },(u_i),-,\mathit{\theta },(u_{i-1}),,,u_i\right)& =\left(\mathit{\theta },(u_j),,,u_j\right)-\left(\mathit{\theta },(u_0),,,u_0\right)-\sum _{i=1}^j\left(\mathit{\theta },(u_{i-1}),,,u_i,-,u_{i-1}\right)\hfill \\ \hfill & \stackrel{(27)}{⩾}\left(\mathit{\theta },(u_j),,,u_j\right)-\left(\mathit{\theta },(u_0),,,u_0\right)-\sum _{i=1}^j{\int }_{\mathrm{\Omega }}\left[{\mathrm{\Phi }}_{\mathit{\theta }},(u_i),-,{\mathrm{\Phi }}_{\mathit{\theta }},(u_{i-1})\right]\hfill \\ \hfill & =\left[\left(\mathit{\theta },(u_j),,,u_j\right),-,{\int }_{\mathrm{\Omega }},{\mathrm{\Phi }}_{\mathit{\theta }},(u_j)\right]-\left[\left(\mathit{\theta },(u_0),,,u_0\right),-,{\int }_{\mathrm{\Omega }},{\mathrm{\Phi }}_{\mathit{\theta }},(u_0)\right]\hfill \\ \hfill & ={\int }_{\mathrm{\Omega }}{\tilde{\mathrm{\Phi }}}_{\mathit{\theta }}(u_j)-{\int }_{\mathrm{\Omega }}{\tilde{\mathrm{\Phi }}}_{\mathit{\theta }}(u_0)\hfill \\ \hfill & ⩾-{\int }_{\mathrm{\Omega }}{u}_0\mathit{\theta }(u_0)\hfill \\ \hfill & ⩾-C.\hfill \end{array}$$On the first term of the right-hand side, we apply the Cauchy and Young inequalities and the Friedrichs inequality to obtain$$\left|\sum _{i=1}^j,\left(f_i,,,u_i\right),\mathit{\tau }\right|⩽C_{\mathit{\epsilon }}\sum _{i=1}^j{∥,f_i∥}^2\mathit{\tau }+\mathit{\epsilon }\sum _{i=1}^j{∥,u_i∥}^2\mathit{\tau }⩽C_{\mathit{\epsilon }}+\mathit{\epsilon }\sum _{i=1}^j{∥,\mathrm{\nabla },u_i∥}^2\mathit{\tau }.$$In the same way, using the trace theorem, one can prove that$$\begin{array}{cc}\hfill \left|\sum _{i=1}^j,h_i,u_i,{|}_{{\mathrm{\Gamma }}_0},\mathit{\tau }\right|& ⩽C_{\mathit{\epsilon }}\sum _{i=1}^j{|h_i|}^2\mathit{\tau }+\mathit{\epsilon }\sum _{i=1}^j{∥,u_i∥}_{L_2({\mathrm{\Gamma }}_0)}^2\mathit{\tau }⩽C_{\mathit{\epsilon }}+\mathit{\epsilon }\sum _{i=1}^j{∥,\mathrm{\nabla },u_i∥}^2\mathit{\tau };\hfill \\ \hfill \left|\sum _{i=1}^j,\left(\mathit{a},(u_i),,,\mathrm{\nabla },u_i\right),\mathit{\tau }\right|& ⩽C_{\mathit{\epsilon }}\sum _{i=1}^j{∥,\mathit{a},(,u_i,)∥}^2\mathit{\tau }+\mathit{\epsilon }\sum _{i=1}^j{∥,\mathrm{\nabla },u_i∥}^2\mathit{\tau }⩽C_{\mathit{\epsilon }}+\mathit{\epsilon }\sum _{i=1}^j{∥,\mathrm{\nabla },u_i∥}^2\mathit{\tau }.\hfill \end{array}$$After fixing a sufficiently small positive $\mathit{\epsilon }$, an application of the Friedrichs inequality concludes the proof.

(ii) Choosing $\mathit{\phi }=\mathit{\delta }{u}_i$ into (2626 $$\begin{array}{c}\hfill \frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(,v_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },v_i,+,\mathit{b},(v_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-\left(K_i,\mathrm{\nabla },{\tilde{U}}_i,,,\mathrm{\nabla },\mathit{\phi }\right)+\frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(,v_{i-1},),,,\mathit{\phi }\right).\end{array}$$26 ), multiplying by $\mathit{\tau }$ and summing up over $i=1,\cdots ,j$, one can get$$\begin{array}{cc}& \sum _{i=1}^j\left(\mathit{\delta },\mathit{\theta },(u_i),,,\mathit{\delta },u_i\right)\mathit{\tau }+\sum _{i=1}^j\left(K_i,\mathrm{\nabla },u_i,,,\mathrm{\nabla },\mathit{\delta },u_i\right)\mathit{\tau }MYAMP{]=\sum _{i=1}^j\left(f_i,,,\mathit{\delta },u_i\right)\mathit{\tau }-\sum _{i=1}^j{h}_i\mathit{\delta }{u}_i|}_{{\mathrm{\Gamma }}_0}\mathit{\tau }-\sum _{i=1}^j\left(\mathit{a},(u_i),,,\mathrm{\nabla },\mathit{\delta },u_i\right)\mathit{\tau }.\hfill \end{array}$$Using the monotonicity of $\mathit{\theta }$ and the mean value theorem, the first term on the LHS can be estimated by$$\begin{array}{ccc}\hfill \sum _{i=1}^j\left(\mathit{\delta },\mathit{\theta },(u_i),,,\mathit{\delta },u_i\right)\mathit{\tau }& =\sum _{i=1}^j\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(u_i),-,\mathit{\theta },(u_{i-1}),,,u_i,-,u_{i-1}\right)⩾0\hfill & \hfill \text{if}\mathit{a}(u)=\mathit{a};\\ \hfill \sum _{i=1}^j\left(\mathit{\delta },\mathit{\theta },(u_i),,,\mathit{\delta },u_i\right)\mathit{\tau }& ⩾\frac{{\mathit{\theta }}_0}{\mathit{\tau }}\sum _{i=1}^j{∥,u_i,-,u_{i-1}∥}^2={\mathit{\theta }}_0\sum _{i=1}^j{∥,\mathit{\delta },u_i∥}^2\mathit{\tau }\hfill & \hfill \text{if}\mathit{a}(u)\ne \mathit{a}.\end{array}$$The second term on the LHS can be rewritten using Abel’s summation rule, namely$$\sum _{i=1}^j\left(K_i,\mathrm{\nabla },u_i,,,\mathrm{\nabla },\mathit{\delta },u_i\right)\mathit{\tau }⩾\frac{C_0{D}_0}{2}\left({∥,\mathrm{\nabla },u_j∥}^2,-,{∥,\mathrm{\nabla },u_0∥}^2,+,\sum _{i=1}^j,{∥,\mathrm{\nabla },(,u_i,-,u_{i-1},)∥}^2\right).$$We apply Abel’s summation rule, the Cauchy and Young inequalities, the trace theorem, (1313 $$\begin{array}{cc}& {\displaystyle h^{\prime }\in L_2((0,T))\Rightarrow h\in C([0,T]);}\hfill \end{array}$$13 ), the Friedrichs inequality (33 $$\begin{array}{c}\hfill {∥,u∥}_V⩽C∥,\mathrm{\nabla },u∥.\end{array}$$3 ) and Lemma 4.1(i) on the second term of the RHS to get$$\begin{array}{cc}\hfill \left|\sum _{i=1}^j,h_i,\mathit{\delta },u_i,{|}_{{\mathrm{\Gamma }}_0},\mathit{\tau }\right|& =\left|,u_j,{|}_{{\mathrm{\Gamma }}_0},h_j,-,u_0,{{|}_{{\mathrm{\Gamma }}_0}{h}_0-\sum _{i=1}^j\mathit{\delta }{h}_i{u}_{i-1}|}_{{\mathrm{\Gamma }}_0},\mathit{\tau }\right|\hfill \\ \hfill & ⩽\mathit{\epsilon }{∥,u_j∥}_{L_2({\mathrm{\Gamma }}_0)}^2+C_{\mathit{\epsilon }}|h_j{|}^2+C+C\sum _{i=1}^j{|\mathit{\delta }{h}_i|}^2\mathit{\tau }+C\sum _{i=1}^j{∥,u_{i-1}∥}_{L_2({\mathrm{\Gamma }}_0)}^2\mathit{\tau }\hfill \\ \hfill & ⩽C_{\mathit{\epsilon }}+\mathit{\epsilon }{∥,\mathrm{\nabla },u_j∥}^2+C{∥,\mathrm{\nabla },u_0∥}^2\mathit{\tau }+C\sum _{i=1}^j{∥,\mathrm{\nabla },u_i∥}^2\mathit{\tau }\hfill \\ \hfill & ⩽C_{\mathit{\epsilon }}+\mathit{\epsilon }{∥,\mathrm{\nabla },u_j∥}^2,\hfill \end{array}$$when $\mathit{\tau }<{\mathit{\tau }}_0$. Analogue one can prove that for $\mathit{\tau }<{\mathit{\tau }}_0$, it holds that$$\sum _{i=1}^j\left(f_i,,,\mathit{\delta },u_i\right)\mathit{\tau }=\left(f_j,,,u_j\right)-\left(f_0,,,u_0\right)-\sum _{i=1}^j\left(\mathit{\delta },f_i,,,u_{i-1}\right)\mathit{\tau }⩽C_{\mathit{\epsilon }}+\mathit{\epsilon }{∥,\mathrm{\nabla },u_j∥}^2.$$If $\mathit{a}(u)=\mathit{a}$, collecting all considerations above results in$$\frac{C_0{D}_0}{2}\left({∥,\mathrm{\nabla },u_j∥}^2,-,{∥,\mathrm{\nabla },u_0∥}^2,+,\sum _{i=1}^j,{∥,\mathrm{\nabla },(,u_i,-,u_{i-1},)∥}^2\right)⩽C_{\mathit{\epsilon }}+\mathit{\epsilon }{∥,\mathrm{\nabla },u_j∥}^2.$$Secondly, we discuss the case $\mathit{a}(u)\ne \mathit{a}$. Also, the following partial summation formula is satisfied$$\begin{array}{cc}\hfill \sum _{i=1}^j\left(\mathit{a},(u_i),,,\mathrm{\nabla },\mathit{\delta },u_i\right)\mathit{\tau }& =\left(\mathit{a},(u_j),,,\mathrm{\nabla },u_j\right)-\left(\mathit{a},(u_0),,,\mathrm{\nabla },u_0\right)-\sum _{i=1}^j\left(\mathit{\delta },\mathit{a},(u_i),,,\mathrm{\nabla },u_{i-1}\right)\mathit{\tau }.\hfill \end{array}$$Employing the mean value theorem, assumption (88 $$\begin{array}{ccc}\hfill |{\mathit{a}}^{\prime }(s)|& =|\left({\mathit{a}}_1^{\prime },(s),,,{\mathit{a}}_2^{\prime },(s),,,\dots ,,,{\mathit{a}}_d^{\prime },(s)\right)|⩽C\hfill & \hfill \text{a.e. in}\mathbb{R}.\end{array}$$8 ) and Lemma 4.1(i), we get for $\mathit{\tau }<{\mathit{\tau }}_0$$$\begin{array}{cc}\hfill \left|\sum _{i=1}^j,\left(\mathit{a},(u_i),,,\mathrm{\nabla },\mathit{\delta },u_i\right),\mathit{\tau }\right|& ⩽C_{\mathit{\epsilon }}+\mathit{\epsilon }{∥,\mathrm{\nabla },u_j∥}^2+\mathit{\epsilon }\sum _{i=1}^j{∥,\mathit{\delta },u_i∥}^2\mathit{\tau }.\hfill \end{array}$$We arrive at$$\begin{array}{cc}& {\mathit{\theta }}_0\sum _{i=1}^j{∥,\mathit{\delta },u_i∥}^2\mathit{\tau }+\frac{C_0{D}_0}{2}\left({∥,\mathrm{\nabla },u_j∥}^2,+,\sum _{i=1}^j,{∥,\mathrm{\nabla },(,u_i,-,u_{i-1},)∥}^2\right)\hfill \\ \hfill & ⩽C_{\mathit{\epsilon }}+\mathit{\epsilon }{∥,\mathrm{\nabla },u_j∥}^2+\mathit{\epsilon }\sum _{i=1}^j{∥,\mathit{\delta },u_i∥}^2\mathit{\tau }.\hfill \end{array}$$Fixing a sufficiently small $\mathit{\epsilon }$ and applying the Friedrichs inequality in both cases give the estimates.

(iii) This follows immediately from Lemma 4.1(ii) coupled with the growth condition on $\mathit{\theta }$.

(iv) The relation (2626 $$\begin{array}{c}\hfill \frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(,v_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },v_i,+,\mathit{b},(v_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-\left(K_i,\mathrm{\nabla },{\tilde{U}}_i,,,\mathrm{\nabla },\mathit{\phi }\right)+\frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(,v_{i-1},),,,\mathit{\phi }\right).\end{array}$$26 ) can be rewritten for $\mathit{\phi }\in V$ as$$\left(\mathit{\delta },\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-\left(K_i,\mathrm{\nabla },u_i,,,\mathrm{\nabla },\mathit{\phi }\right)-\left(\mathit{a},(,u_i,),,,\mathrm{\nabla },\mathit{\phi }\right)-h_i{\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}.$$A standard argumentation yields$$|\left(\mathit{\delta },\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)|\lesssim \left(1+\Vert ,f_i,\Vert +|,h_i,|+,∥,\mathrm{\nabla },u_i∥\right){∥,\mathit{\phi }∥}_V,$$which implies31 $$\begin{array}{c}\hfill {∥,\mathit{\delta },\mathit{\theta },(,u_i,)∥}_{V^{\ast }}=\underset{\genfrac{}{}{0.0pt}{}{\mathit{\phi }\in V}{{∥,\mathit{\phi }∥}_V⩽1}}{sup}|\left(\mathit{\delta },\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)|\lesssim 1+\Vert f_i\Vert +|h_i|+∥,\mathrm{\nabla },u_i∥.\end{array}$$31 An application of Lemma 4.1(ii) gives the first inequality. Taking the second power in (2828 $$\begin{array}{c}\hfill {∥,\mathrm{\nabla },(,v_{\mathit{\alpha }},-,v_{\mathit{\beta }},)∥}^2\lesssim \frac{{(\mathit{\alpha }-\mathit{\beta })}^2}{{\mathit{\tau }}^2}.\end{array}$$28 ), multiplying the inequality by $\mathit{\tau }$, summing it up for $i=1,\dots ,j$, and applying Lemma 4.1(i), we get the second inequality. $\square$

The existence of a weak solution will be proved using Rothe’s method. The variational formulation of (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\mathit{\partial }}_t\mathit{\theta }(u)-\mathrm{\nabla }·\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,)\right)}& =f\hfill & \mathrm{in}{Q}_T:=(0,T)\times \mathrm{\Omega };\hfill \\ \hfill u& =g^D\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }& =g^N\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_N;\hfill \\ \hfill u(0)& =u_0\hfill & \mathrm{in}\mathrm{\Omega };\hfill \end{array}\right.\end{array}$$1 ) and (22 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }}& =h(t)\hfill & \mathrm{in}(0,T);\hfill \\ \hfill {\displaystyle u}& =U(t)\hfill & \mathrm{on}(0,T)\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$2 ) reads as: find $(K,u)$ such that32a $$\begin{array}{cc}\hfill \left({\mathit{\partial }}_t,\mathit{\theta },(u),,,\mathit{\phi }\right)+\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,),,,\mathrm{\nabla },\mathit{\phi }\right){+h\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}& {\displaystyle =\left(f,,,\mathit{\phi }\right)\mathit{\phi }\in V}\hfill \end{array}$$32a 32b $$\begin{array}{cc}\hfill {u|}_{{\mathrm{\Gamma }}_0}& {\displaystyle =U.}\hfill \end{array}$$32b

Now, let us introduce the following piecewise linear in time functions ${\mathit{\theta }}_n$ and $u_n$$$\begin{array}{ccc}{\mathit{\theta }}_n(0)& =\mathit{\theta }(u_0)\hfill & \\ {\mathit{\theta }}_n(t)& =\mathit{\theta }(u_{i-1})+(t-t_{i-1})\mathit{\delta }\mathit{\theta }(u_i)\hfill & \text{for}t\in (t_{i-1},t_i];\hfill \\ u_n(0)& =u_0\hfill \\ u_n(t)& =u_{i-1}+(t-t_{i-1})\mathit{\delta }{u}_i\hfill & \text{for}t\in (t_{i-1},t_i];\hfill \end{array}$$and the step functions ${\overline{u}}_n$ and ${\overline{\mathit{\theta }}}_n$$$\begin{array}{ccccccc}\hfill {\overline{u}}_n(0)& =u_0,\hfill & & \hfill {\overline{u}}_n(t)& =u_i,\hfill & & \hfill \text{for}t\in (t_{i-1},t_i];\\ \hfill {\overline{\mathit{\theta }}}_n(0)& =\mathit{\theta }(u_0),\hfill & & \hfill {\overline{\mathit{\theta }}}_n(t)& =\mathit{\theta }(u_i),\hfill & & \hfill \text{for}t\in (t_{i-1},t_i].\end{array}$$Similarly, the functions ${\overline{K}}_n,{\overline{h}}_n,{\overline{U}}_n$ and ${\overline{f}}_n$ are defined. The variational formulation (2626 $$\begin{array}{c}\hfill \frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(,v_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },v_i,+,\mathit{b},(v_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-\left(K_i,\mathrm{\nabla },{\tilde{U}}_i,,,\mathrm{\nabla },\mathit{\phi }\right)+\frac{1}{\mathit{\tau }}\left(\mathit{\vartheta },(,v_{i-1},),,,\mathit{\phi }\right).\end{array}$$26 ) can be rewritten as ($t\in (0,T)$ and $\mathit{\phi }\in V$)33a $$\begin{array}{cc}\hfill \left({\mathit{\partial }}_t,{\mathit{\theta }}_n,(t),,,\mathit{\phi }\right)+\left({\overline{K}}_n,(t),\mathrm{\nabla },{\overline{u}}_n,(t),+,\mathit{a},({\overline{u}}_n(t)),,,\mathrm{\nabla },\mathit{\phi }\right)+{\overline{h}}_n{(t)\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}& =\left({\overline{f}}_n,(t),,,\mathit{\phi }\right)\mathit{\phi }\in V\hfill \end{array}$$33a 33b $$\begin{array}{cc}\hfill {\overline{u}}_n{|}_{{\mathrm{\Gamma }}_0}& ={\overline{U}}_n.\hfill \end{array}$$33b

Now, (29) follows after passage to the limit as $\mathit{\tau }\to 0$ in (30). In the case that $\mathit{a}$ is independent of $u$, the assumptions made so far are not strong enough to prove convergence. Namely, to establish convergence, the strong convergence of ${\overline{u}}_n$ in $L_2((0,T),L_2(\mathrm{\Omega }))$ is needed. The preceding observation leads to the assumption$${\mathit{\theta }}^{\prime }(s)⩾{\mathit{\theta }}_0>0\text{a.e. in}\mathbb{R}.$$

Corollary 4.2

(i) There exists a $w\in C([0,T],V^{\ast })\cap L_{\infty }((0,T),L_2(\mathrm{\Omega }))$ with ${\mathit{\partial }}_{t}w\in L_2((0,T),V^{\ast })$ (i.e. $w$ is a.e. differentiable in $(0,T)$). Moreover, there exists a subsequence of ${\mathit{\theta }}_n$ (denoted by ${\mathit{\theta }}_n$ again) such that ($t\in (0,T)$)$$\begin{array}{ccccccc}\hfill {\mathit{\theta }}_n& \to w\hfill & \text{in}C([0,T],V^{\ast }),\hfill & \hfill {\overline{\mathit{\theta }}}_n(t)& \rightharpoonup w(t)\hfill & & \text{in}{L}_2(\mathrm{\Omega }),\hfill \\ \hfill {\mathit{\theta }}_n(t)& \rightharpoonup w(t)\hfill & \text{in}{L}_2(\mathrm{\Omega }),\hfill & \hfill {\mathit{\partial }}_t{\mathit{\theta }}_n& \rightharpoonup {\mathit{\partial }}_{t}w\hfill & & \text{in}{L}_2((0,T),V^{\ast }).\hfill \end{array}$$(ii) Let ${\mathit{\theta }}^{\prime }⩾{\mathit{\theta }}_0>0$. There exists a $u\in C([0,T],L_2(\mathrm{\Omega }))\cap L_{\infty }((0,T),L_2(\mathrm{\Omega }))$ with ${\mathit{\partial }}_{t}u\in L_2((0,T),L_2(\mathrm{\Omega }))$ (i.e. $u$ is a.e. differentiable in $(0,T)$). Moreover, there exists a subsequence of $u_n$ (denoted by $u_n$ again) such that ($t\in (0,T)$)$$\begin{array}{ccccccc}\hfill u_n& \to u\hfill & \text{in}C([0,T],L_2(\mathrm{\Omega })),\hfill & \hfill {\overline{u}}_n(t)& \rightharpoonup u(t)\hfill & & \text{in}V,\hfill \\ \hfill u_n(t)& \rightharpoonup u(t)\hfill & \text{in}V,\hfill & \hfill {\mathit{\partial }}_t{u}_n& \rightharpoonup {\mathit{\partial }}_{t}u\hfill & & \text{in}{L}_2((0,T),L_2(\mathrm{\Omega })).\hfill \end{array}$$

Proof

Thanks to the Rellich-Kondrachov Compactness Theorem [16, Theorem 1, p.272], we have that$$V\hookrightarrow \hookrightarrow L_2(\mathrm{\Omega })\cong {(L_2(\mathrm{\Omega }))}^{\ast }\hookrightarrow \hookrightarrow V^{\ast }.$$

(i)	Applying Lemma 4.1(iii) and (iv), we get$$\underset{t\in [0,T]}{max}{∥,{\overline{\mathit{\theta }}}_n,(t)∥}^2+{\int }_0^T{∥,{\mathit{\partial }}_t,{\mathit{\theta }}_n∥}_{V^{\ast }}^2⩽C.$$

Consequently, an application of [13, Lemma 1.3.13] gives the proof.

(ii)	Applying Lemma 4.1(ii), we have$$\underset{t\in [0,T]}{max}{∥,{\overline{u}}_n,(t)∥}_V^2+{\int }_0^T{∥,{\mathit{\partial }}_t,u_n∥}^2⩽C.$$

Hence, an application of [13, Lemma 1.3.13] concludes the proof. $\square$

Finally, the theorem to be proved is the following.

Theorem 4.3

Let the assumptions of Lemma 3.7 be fulfilled. Suppose that there exists a positive real constant ${\mathit{\theta }}_0$ such that ${\mathit{\theta }}^{\prime }⩾{\mathit{\theta }}_0>0$. Then there exists a weak solution to (29).

Proof

Take any $\mathit{\xi }\in (0,T)$ and integrate (30a) on $(0,\mathit{\xi })$ to get for each $\mathit{\phi }\in V$34 $$\begin{array}{cc}& {\int }_0^{\mathit{\xi }}\left({\mathit{\partial }}_t,{\mathit{\theta }}_n,(t),,,\mathit{\phi }\right)+{\int }_0^{\mathit{\xi }}\left({\overline{K}}_n,(t),\mathrm{\nabla },{\overline{u}}_n,(t),+,\mathit{a},({\overline{u}}_n(t)),,,\mathrm{\nabla },\mathit{\phi }\right)+{\int }_0^{\mathit{\xi }}{\overline{h}}_n{(t)\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}\hfill \\ \hfill & ={\int }_0^{\mathit{\xi }}\left({\overline{f}}_n,(t),,,\mathit{\phi }\right).\hfill \end{array}$$34 We have to pass to the limit for $n\to \infty$ in (3131 $$\begin{array}{c}\hfill {∥,\mathit{\delta },\mathit{\theta },(,u_i,)∥}_{V^{\ast }}=\underset{\genfrac{}{}{0.0pt}{}{\mathit{\phi }\in V}{{∥,\mathit{\phi }∥}_V⩽1}}{sup}|\left(\mathit{\delta },\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)|\lesssim 1+\Vert f_i\Vert +|h_i|+∥,\mathrm{\nabla },u_i∥.\end{array}$$31 ). Each term in (3131 $$\begin{array}{c}\hfill {∥,\mathit{\delta },\mathit{\theta },(,u_i,)∥}_{V^{\ast }}=\underset{\genfrac{}{}{0.0pt}{}{\mathit{\phi }\in V}{{∥,\mathit{\phi }∥}_V⩽1}}{sup}|\left(\mathit{\delta },\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)|\lesssim 1+\Vert f_i\Vert +|h_i|+∥,\mathrm{\nabla },u_i∥.\end{array}$$31 ) is considered separately. The Rothe sequence ${\{{\overline{u}}_n\}}_{n\in \mathbb{N}}$ is bounded in the space $L_2((0,T),V)$ thanks to Lemma 4.1(i), indeed$${\displaystyle \Vert {\overline{u}}_n{\Vert }_{L_2((0,T),V)}^2={\int }_0^T\Vert {\overline{u}}_n{(t)\Vert }_V^2\text{d}t=\sum _{i=1}^n{\int }_{t_{i-1}}^{t_i}\Vert {\overline{u}}_n{(t)\Vert }_V^2\text{d}t=\sum _{i=1}^n{\Vert u_i\Vert }_V^2\mathit{\tau }⩽C.}$$Therefore, the reflexivity of $L_2((0,T),V)$ implies (for a subsequence denoted by ${\overline{u}}_n$ again) the following useful result35 $$\begin{array}{c}\hfill {\overline{u}}_n\rightharpoonup u\text{in}{L}_2((0,T),V).\end{array}$$35 Thus $u\in L_2((0,T),V)\cap C([0,T],L_2(\mathrm{\Omega }))$. Firstly, we apply the Minty–Browder’s trick [16] to prove that $w=\mathit{\theta }(u)$. It holds that for $t\in (t_{i-1},t_i]$$$\left({\mathit{\theta }}_n,-,{\overline{\mathit{\theta }}}_n\right)(t)=\mathit{\theta }(u_{i-1})+\left(\frac{t-t_{i-1}}{\mathit{\tau }}\right)\left(\mathit{\theta },(u_i),-,\mathit{\theta },(u_{i-1})\right)-\mathit{\theta }(u_i)=(t-t_i){\mathit{\partial }}_t{\mathit{\theta }}_n(t).$$Hence, using Lemma 4.1(iv), we obtain for $t\in (t_{i-1},t_i]$$${\displaystyle {∥,\left({\mathit{\theta }}_n,-,{\overline{\mathit{\theta }}}_n\right),(t)∥}_{V^{\ast }}⩽\mathit{\tau }{∥,{\mathit{\partial }}_t,{\mathit{\theta }}_n,(t)∥}_{V^{\ast }}\lesssim \mathit{\tau }.}$$Therefore, according to Corollary 4.2(i)36 $$\begin{array}{c}\hfill {\overline{\mathit{\theta }}}_n\to w\text{in}C([0,T],V^{\ast }).\end{array}$$36 Thanks to the monotonicity of the function $\mathit{\theta }$, it yields for any fixed $v\in L_2((0,T),L_2(\mathrm{\Omega }))$ that$${\displaystyle {\int }_0^T\left(\mathit{\theta },({\overline{u}}_n),-,\mathit{\theta },(v),,,{\overline{u}}_n,-,v\right)⩾0.}$$Due to (3232a $$\begin{array}{cc}\hfill \left({\mathit{\partial }}_t,\mathit{\theta },(u),,,\mathit{\phi }\right)+\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,),,,\mathrm{\nabla },\mathit{\phi }\right){+h\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}& {\displaystyle =\left(f,,,\mathit{\phi }\right)\mathit{\phi }\in V}\hfill \end{array}$$32a ) and (3332b $$\begin{array}{cc}\hfill {u|}_{{\mathrm{\Gamma }}_0}& {\displaystyle =U.}\hfill \end{array}$$32b ), we have that, for $\mathit{\tau }\to 0$,$${\displaystyle {\int }_0^T\left(w,-,\mathit{\theta },(,v,),,,u,-,v\right)⩾0.}$$Firstly, suppose that $v=u+\mathit{\epsilon }z$ with $\mathit{\epsilon }>0$ and $z\in L_2((0,T),L_2(\mathrm{\Omega }))$. We get$${\displaystyle {\int }_0^T\left(w,-,\mathit{\theta },(,u,+,\mathit{\epsilon },z,),,,-,\mathit{\epsilon },z\right)⩾0.}$$Next, dividing this equation by $-\mathit{\epsilon }$, taking the limit $\mathit{\epsilon }\to 0$ and using the continuity of $\mathit{\theta }$, we arrive at$${\displaystyle {\int }_0^T\left(w,-,\mathit{\theta },(,u,),,,z\right)⩽0.}$$Secondly, assume that $v=u-\mathit{\epsilon }z$ with $\mathit{\epsilon }>0$ and $z\in L_2((0,T),L_2(\mathrm{\Omega }))$. Then$${\displaystyle {\int }_0^T\left(w,-,\mathit{\theta },(,u,),,,z\right)⩾0.}$$Combining the previous results give us$${\displaystyle {\int }_0^T\left(w,-,\mathit{\theta },(,u,),,,z\right)=0,\forall z\in L_2((0,T),L_2(\mathrm{\Omega })).}$$Therefore, $w=\mathit{\theta }(u)\in L_2((0,T),L_2(\mathrm{\Omega }))$. Applying Corollary 4.2(i) gives for all $\mathit{\phi }\in V$ that$$\left|{\int }_0^{\mathit{\xi }},\left({\mathit{\partial }}_t,{\mathit{\theta }}_n,(t),,,\mathit{\phi }\right),-,{\int }_0^{\mathit{\xi }},\left({\mathit{\partial }}_t,\mathit{\theta },(u(t)),,,\mathit{\phi }\right)\right|\to 0\text{if}n\to \infty .$$Now, we focus on the second term in the LHS. This term can be split into two parts. Firstly, we consider the second part. The sequences $u_n$ and ${\overline{u}}_n$ have the same limit in the space $L_2((0,T),V)$. Employing Lemma 4.1(ii) gives37 $$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}{\Vert u_n-{\overline{u}}_n\Vert }_{L_2((0,T),V)}^2& =\underset{n\to \infty }{lim}\sum _{i=1}^n{\int }_{t_{i-1}}^{t_i}{∥,(u_n-{\overline{u}}_n),(t)∥}_V^2\text{d}t\hfill \\ \hfill & =\underset{n\to \infty }{lim}\sum _{i=1}^n{\int }_{t_{i-1}}^{t_i}{∥,u_{i-1},+,\frac{t-t_{i-1}}{\mathit{\tau }},(u_i-u_{i-1}),-,u_i∥}_V^2\text{d}t\hfill \\ \hfill & ⩽4\underset{n\to \infty }{lim}\sum _{i=1}^n{∥,u_i,-,u_{i-1}∥}_V^2\mathit{\tau }\hfill \\ \hfill & ⩽\underset{n\to \infty }{lim}\frac{C}{n}=0.\hfill \end{array}$$37 Therefore, if $\mathit{a}(u)\ne \mathit{a}$, it holds, thanks to assumption (88 $$\begin{array}{ccc}\hfill |{\mathit{a}}^{\prime }(s)|& =|\left({\mathit{a}}_1^{\prime },(s),,,{\mathit{a}}_2^{\prime },(s),,,\dots ,,,{\mathit{a}}_d^{\prime },(s)\right)|⩽C\hfill & \hfill \text{a.e. in}\mathbb{R}.\end{array}$$8 ) and Corollary 4.2(ii), that for all $\mathit{\phi }\in V$$$\left|{\int }_0^{\mathit{\xi }},\left(\mathit{a},({\overline{u}}_n(t)),-,\mathit{a},(u(t)),,,\mathrm{\nabla },\mathit{\phi }\right)\right|\lesssim ∥,\mathrm{\nabla },\mathit{\phi }∥\sqrt{T}\sqrt{{\int }_0^T{∥,{\overline{u}}_n,(t),-,u,(t)∥}^2}\to 0\text{if}n\to \infty .$$Secondly, applying the Green theorem and taking ${\displaystyle \mathit{\phi }\in \{\mathit{\psi }\in C^{\infty }(\mathrm{\Omega }):\mathit{\psi }{|}_{{\mathrm{\Gamma }}_D}=0,\mathit{\psi }{|}_{{\mathrm{\Gamma }}_0}=\mathit{constant}\}}$ in the first part, we deduce that38 $$\begin{array}{cc}& {\int }_0^{\mathit{\xi }}\left({\overline{K}}_n,\mathrm{\nabla },{\overline{u}}_n,,,\mathrm{\nabla },\mathit{\phi }\right)\hfill \\ \hfill & {\displaystyle ={\int }_0^{\mathit{\xi }}{\overline{k}}_n{\left({\overline{\mathit{\kappa }}}_n,\mathrm{\nabla },{\overline{u}}_n,,,\mathrm{\nabla },\mathit{\phi }\right)}_{{\mathrm{\Omega }}_0}+{\int }_0^{\mathit{\xi }}{\left({\overline{\mathit{\kappa }}}_n,\mathrm{\nabla },{\overline{u}}_n,,,\mathrm{\nabla },\mathit{\phi }\right)}_{\mathrm{\Omega }\backslash {\mathrm{\Omega }}_0}}\hfill \\ \hfill & {\displaystyle ={\int }_0^{\mathit{\xi }}{\overline{k}}_n{\left({\overline{u}}_n,,,{\overline{\mathit{\kappa }}}_n,\mathrm{\nabla },\mathit{\phi },·,\mathit{\nu }\right)}_{\mathit{\partial }{\mathrm{\Omega }}_0}-{\int }_0^{\mathit{\xi }}{\overline{k}}_n{\left({\overline{u}}_n,,,\mathrm{\nabla },·,({\overline{\mathit{\kappa }}}_n\mathrm{\nabla }\mathit{\phi })\right)}_{{\mathrm{\Omega }}_0}+{\int }_0^{\mathit{\xi }}{\left({\overline{\mathit{\kappa }}}_n,\mathrm{\nabla },{\overline{u}}_n,,,\mathrm{\nabla },\mathit{\phi }\right)}_{\mathrm{\Omega }\backslash {\mathrm{\Omega }}_0}}\hfill \\ \hfill & {\displaystyle ={\int }_0^{\mathit{\xi }}{\overline{k}}_n{\left({\overline{u}}_n,,,{\overline{\mathit{\kappa }}}_n,\mathrm{\nabla },\mathit{\phi },·,\mathit{\nu }\right)}_{\mathit{\partial }{\mathrm{\Omega }}_0}-{\int }_0^{\mathit{\xi }}{\overline{k}}_n{\left({\overline{u}}_n,,,\mathrm{\nabla },{\overline{\mathit{\kappa }}}_n,·,\mathrm{\nabla },\mathit{\phi },+,{\overline{\mathit{\kappa }}}_n,\mathrm{\Delta },\mathit{\phi }\right)}_{{\mathrm{\Omega }}_0}MYAMP]+{\int }_0^{\mathit{\xi }}{\left({\overline{\mathit{\kappa }}}_n,\mathrm{\nabla },{\overline{u}}_n,,,\mathrm{\nabla },\mathit{\phi }\right)}_{\mathrm{\Omega }\backslash {\mathrm{\Omega }}_0}.}\hfill \end{array}$$38 At this point, we need some auxiliary results. In light of equation (3232a $$\begin{array}{cc}\hfill \left({\mathit{\partial }}_t,\mathit{\theta },(u),,,\mathit{\phi }\right)+\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,),,,\mathrm{\nabla },\mathit{\phi }\right){+h\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}& {\displaystyle =\left(f,,,\mathit{\phi }\right)\mathit{\phi }\in V}\hfill \end{array}$$32a ) and Lemma 4.1(i), applying the Nečas inequality [17]$$\begin{array}{c}\hfill {∥,z∥}_{\mathrm{\Gamma }}^2⩽\mathit{\epsilon }{∥,\mathrm{\nabla },z∥}^2+C_{\mathit{\epsilon }}{∥,z∥}^2,\forall z\in H^1(\mathrm{\Omega }),0<\mathit{\epsilon }<{\mathit{\epsilon }}_0,\end{array}$$implies$${\int }_0^T{∥,{\overline{u}}_n,-,u∥}_{\mathrm{\Gamma }}^2⩽\mathit{\epsilon }{\int }_0^T{∥,\mathrm{\nabla },(,{\overline{u}}_n,-,u,)∥}^2+C_{\mathit{\epsilon }}{\int }_0^T{∥,{\overline{u}}_n,-,u∥}^2⩽\mathit{\epsilon }+C_{\mathit{\epsilon }}{\int }_0^T{∥,{\overline{u}}_n,-,u∥}^2.$$Passing to the limit for $\mathit{\tau }\to 0$ and applying Corollary 4.2(ii), we obtain$$\underset{\mathit{\tau }\to 0}{lim}{\int }_0^T{∥,{\overline{u}}_n,-,u∥}_{\mathrm{\Gamma }}^2⩽\mathit{\epsilon },$$which is valid for any small $\mathit{\epsilon }>0$. Hence,39 $$\begin{array}{c}\hfill \underset{\mathit{\tau }\to 0}{lim}{\int }_0^T{∥,{\overline{u}}_n,-,u∥}_{\mathrm{\Gamma }}^2=0\text{and}{\overline{u}}_n\to u\text{a.e. in}(0,T)\times \mathrm{\Gamma }.\end{array}$$39 Repeating this consideration for ${\mathrm{\Omega }}_0$ instead of $\mathrm{\Omega }$ gives40 $$\begin{array}{c}\hfill \underset{\mathit{\tau }\to 0}{lim}{\int }_0^T{∥,{\overline{u}}_n,-,u∥}_{\mathit{\partial }{\mathrm{\Omega }}_0}^2=0\text{and}{\overline{u}}_n\to u\text{a.e. in}(0,T)\times \mathit{\partial }{\mathrm{\Omega }}_0.\end{array}$$40 Due to the construction, we have that $C_0⩽{\overline{k}}_n⩽C_1$. This yields that ${\overline{k}}_n\rightharpoonup k$ (for a subsequence) in $L_2((0,T))$. Therefore, employing ${\overline{k}}_n\rightharpoonup k$, (1010 $$\begin{array}{cc}& {\displaystyle 0<D_0⩽\mathit{\kappa }⩽D_1;}\hfill \end{array}$$10 ), (3232a $$\begin{array}{cc}\hfill \left({\mathit{\partial }}_t,\mathit{\theta },(u),,,\mathit{\phi }\right)+\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,),,,\mathrm{\nabla },\mathit{\phi }\right){+h\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}& {\displaystyle =\left(f,,,\mathit{\phi }\right)\mathit{\phi }\in V}\hfill \end{array}$$32a ), (3434 $$\begin{array}{cc}& {\int }_0^{\mathit{\xi }}\left({\mathit{\partial }}_t,{\mathit{\theta }}_n,(t),,,\mathit{\phi }\right)+{\int }_0^{\mathit{\xi }}\left({\overline{K}}_n,(t),\mathrm{\nabla },{\overline{u}}_n,(t),+,\mathit{a},({\overline{u}}_n(t)),,,\mathrm{\nabla },\mathit{\phi }\right)+{\int }_0^{\mathit{\xi }}{\overline{h}}_n{(t)\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}\hfill \\ \hfill & ={\int }_0^{\mathit{\xi }}\left({\overline{f}}_n,(t),,,\mathit{\phi }\right).\hfill \end{array}$$34 ) and (3636 $$\begin{array}{c}\hfill {\overline{\mathit{\theta }}}_n\to w\text{in}C([0,T],V^{\ast }).\end{array}$$36 ), we get after passage to the limit as $\mathit{\tau }\to 0$ in (3535 $$\begin{array}{c}\hfill {\overline{u}}_n\rightharpoonup u\text{in}{L}_2((0,T),V).\end{array}$$35 ) that$$\begin{array}{cc}\hfill {\displaystyle }& {lim}_{\mathit{\tau }\to 0}{\int }_0^{\mathit{\xi }}\left({\overline{K}}_n,\mathrm{\nabla },{\overline{u}}_n,,,\mathrm{\nabla },\mathit{\phi }\right)\hfill \\ \hfill & {\displaystyle ={\int }_0^{\mathit{\xi }}k{\left(u,,,\mathit{\kappa },\mathrm{\nabla },\mathit{\phi },·,\mathit{\nu }\right)}_{\mathit{\partial }{\mathrm{\Omega }}_0}-{\int }_0^{\mathit{\xi }}k{\left(u,,,\mathrm{\nabla },\mathit{\kappa },·,\mathrm{\nabla },\mathit{\phi },+,\mathit{\kappa },\mathrm{\Delta },\mathit{\phi }\right)}_{{\mathrm{\Omega }}_0}+{\int }_0^{\mathit{\xi }}{\left(\mathit{\kappa },\mathrm{\nabla },u,,,\mathrm{\nabla },\mathit{\phi }\right)}_{\mathrm{\Omega }\backslash {\mathrm{\Omega }}_0}}\hfill \\ \hfill & {\displaystyle ={\int }_0^{\mathit{\xi }}k{\left(u,,,\mathit{\kappa },\mathrm{\nabla },\mathit{\phi },·,\mathit{\nu }\right)}_{\mathit{\partial }{\mathrm{\Omega }}_0}-{\int }_0^{\mathit{\xi }}k{\left(u,,,\mathrm{\nabla },·,(,\mathit{\kappa },\mathrm{\nabla },\mathit{\phi },)\right)}_{{\mathrm{\Omega }}_0}+{\int }_0^{\mathit{\xi }}{\left(\mathit{\kappa },\mathrm{\nabla },u,,,\mathrm{\nabla },\mathit{\phi }\right)}_{\mathrm{\Omega }\backslash {\mathrm{\Omega }}_0}}\hfill \\ \hfill & {\displaystyle ={\int }_0^{\mathit{\xi }}k{\left(\mathit{\kappa },\mathrm{\nabla },u,,,\mathrm{\nabla },\mathit{\phi }\right)}_{{\mathrm{\Omega }}_0}+{\int }_0^{\mathit{\xi }}{\left(\mathit{\kappa },\mathrm{\nabla },u,,,\mathrm{\nabla },\mathit{\phi }\right)}_{\mathrm{\Omega }\backslash {\mathrm{\Omega }}_0}}\hfill \\ \hfill & {\displaystyle ={\int }_0^{\mathit{\xi }}\left(K,\mathrm{\nabla },u,,,\mathrm{\nabla },\mathit{\phi }\right).}\hfill \end{array}$$Applying the density argument ${\displaystyle \overline{\{\mathit{\psi }\in C^{\infty }(\mathrm{\Omega }):\mathit{\psi }{|}_{{\mathrm{\Gamma }}_D}=0,\mathit{\psi }{|}_{{\mathrm{\Gamma }}_0}=\mathit{constant}\}}=V}$, we conclude that$$\underset{\mathit{\tau }\to 0}{lim}{\int }_0^{\mathit{\xi }}\left({\overline{K}}_n,\mathrm{\nabla },{\overline{u}}_n,,,\mathrm{\nabla },\mathit{\phi }\right)={\int }_0^{\mathit{\xi }}\left(K,\mathrm{\nabla },u,,,\mathrm{\nabla },\mathit{\phi }\right),\forall \mathit{\phi }\in V.$$Moreover, due the continuity of $h$ and $f,$ one can deduce that, for any $\mathit{\phi }\in V,$$$\begin{array}{cc}\hfill \left|{\int }_0^{\mathit{\xi }},\left({\overline{h}}_n,(t),-,h,(t)\right),{\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}\right|& \lesssim {∥,\mathit{\phi }∥}_V{\int }_0^T|{\overline{h}}_n(t)-h(t)|\lesssim \mathit{\tau }\hfill \\ \hfill \left|{\int }_0^{\mathit{\xi }},\left({\overline{f}}_n,(t),-,f,(t),,,\mathit{\phi }\right)\right|& ⩽∥,\mathit{\phi }∥{\int }_0^T∥,{\overline{f}}_n,(t),-,f,(t)∥\lesssim \mathit{\tau }.\hfill \end{array}$$Collecting all considerations above and passing to the limit for $\mathit{\tau }\to 0$ in (3131 $$\begin{array}{c}\hfill {∥,\mathit{\delta },\mathit{\theta },(,u_i,)∥}_{V^{\ast }}=\underset{\genfrac{}{}{0.0pt}{}{\mathit{\phi }\in V}{{∥,\mathit{\phi }∥}_V⩽1}}{sup}|\left(\mathit{\delta },\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)|\lesssim 1+\Vert f_i\Vert +|h_i|+∥,\mathrm{\nabla },u_i∥.\end{array}$$31 ), we arrive at$$\begin{array}{c}\hfill {\displaystyle {\int }_0^{\mathit{\xi }}\left({\mathit{\partial }}_t,\mathit{\theta },(u),,,\mathit{\phi }\right)+{\int }_0^{\mathit{\xi }}\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,),,,\mathrm{\nabla },\mathit{\phi }\right)+{\int }_0^{\mathit{\xi }}{h\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}={\int }_0^{\mathit{\xi }}\left(f,,,\mathit{\phi }\right)\mathit{\phi }\in V.}\end{array}$$This is valid for any $\mathit{\xi }\in (0,T)$. Differentiation with respect to $\mathit{\xi }$ gives (29a). Taking the limit $\mathit{\tau }\to 0$ in (30b) and using the continuity of $U$ we get (29b), which concludes the proof. $\square$

4.2 Second solution method

Consider the notations in Section 3.2. The variational formulation of (1919 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle \mathit{\delta }\mathit{\theta }(u_i)-\mathrm{\nabla }·\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i)\right)}& =f_i\hfill & \text{in}\mathrm{\Omega };\hfill \\ \hfill u_i& =0\hfill & \text{on}{\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K_i,\mathrm{\nabla },u_i,-,\mathit{a},(u_i)\right)·\mathit{\nu }& =0\hfill & \text{on}{\mathrm{\Gamma }}_N;\hfill \\ \hfill {\displaystyle u_i}& =U_i\hfill & \text{on}{\mathrm{\Gamma }}_0\hfill \end{array}\right.\end{array}$$19 ) on time step $t_i$ for all $\mathit{\phi }\in W$ is41 $$\begin{array}{c}\hfill \begin{array}{c}\hfill {\displaystyle \left(\mathit{\delta },\mathit{\vartheta },(,v_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },(v_i+{\tilde{U}}_i),+,\mathit{b},(v_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right),}\\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },(v_i+{\tilde{U}}_i),-,\mathit{b},(v_i)\right)·\mathit{\nu }}& {\displaystyle =h_i,}\hfill \end{array}\end{array}$$41 with $u_i=v_i+{\tilde{U}}_i$. Using analogous notations as in the previous Section 4.1, the variational formulation (3737 $$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}{\Vert u_n-{\overline{u}}_n\Vert }_{L_2((0,T),V)}^2& =\underset{n\to \infty }{lim}\sum _{i=1}^n{\int }_{t_{i-1}}^{t_i}{∥,(u_n-{\overline{u}}_n),(t)∥}_V^2\text{d}t\hfill \\ \hfill & =\underset{n\to \infty }{lim}\sum _{i=1}^n{\int }_{t_{i-1}}^{t_i}{∥,u_{i-1},+,\frac{t-t_{i-1}}{\mathit{\tau }},(u_i-u_{i-1}),-,u_i∥}_V^2\text{d}t\hfill \\ \hfill & ⩽4\underset{n\to \infty }{lim}\sum _{i=1}^n{∥,u_i,-,u_{i-1}∥}_V^2\mathit{\tau }\hfill \\ \hfill & ⩽\underset{n\to \infty }{lim}\frac{C}{n}=0.\hfill \end{array}$$37 ) can be rewritten as42a $$\begin{array}{cc}\hfill \left({\mathit{\partial }}_t,{\mathit{\vartheta }}_n,,,\mathit{\phi }\right)+\left({\overline{K}}_n,\mathrm{\nabla },({\overline{v}}_n+{\overline{\tilde{U}}}_n),+,\mathit{b},({\overline{v}}_n),,,\mathrm{\nabla },\mathit{\phi }\right)& {\displaystyle =\left({\overline{f}}_n,,,\mathit{\phi }\right),}\hfill \\ \hfill {\int }_{{\mathrm{\Gamma }}_0}\left(-,{\overline{K}}_n,\mathrm{\nabla },({\overline{v}}_n+{\overline{\tilde{U}}}_n),-,\mathit{b},({\overline{v}}_n)\right)·\mathit{\nu }& {\displaystyle ={\overline{h}}_n,}\hfill \end{array}$$42a where $\mathit{\phi }\in W$ and ${\overline{u}}_n={\overline{v}}_n+{\overline{\tilde{U}}}_n$. The variational formulation of (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\mathit{\partial }}_t\mathit{\theta }(u)-\mathrm{\nabla }·\left(K,\mathrm{\nabla },u,+,\mathit{a},(,u,)\right)}& =f\hfill & \mathrm{in}{Q}_T:=(0,T)\times \mathrm{\Omega };\hfill \\ \hfill u& =g^D\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_D;\hfill \\ \hfill \left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }& =g^N\hfill & \mathrm{in}(0,T)\times {\mathrm{\Gamma }}_N;\hfill \\ \hfill u(0)& =u_0\hfill & \mathrm{in}\mathrm{\Omega };\hfill \end{array}\right.\end{array}$$1 ) and (22 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}\hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K,\mathrm{\nabla },u,-,\mathit{a},(,u,)\right)·\mathit{\nu }}& =h(t)\hfill & \mathrm{in}(0,T);\hfill \\ \hfill {\displaystyle u}& =U(t)\hfill & \mathrm{on}(0,T)\times {\mathrm{\Gamma }}_0.\hfill \end{array}\right.\end{array}$$2 ) for all $\mathit{\phi }\in W$ reads as: find $(K,u)$ with $u=v+\tilde{U}$ such that43a $$\begin{array}{cc}\hfill \left({\mathit{\partial }}_t,\mathit{\vartheta },(v),,,\mathit{\phi }\right)+\left(K,\mathrm{\nabla },(v+\tilde{U}),+,\mathit{b},(v),,,\mathrm{\nabla },\mathit{\phi }\right)& {\displaystyle =\left(f,,,\mathit{\phi }\right),}\hfill \\ \hfill {\int }_{{\mathrm{\Gamma }}_0}\left(-,K,\mathrm{\nabla },(v+\tilde{U}),-,\mathit{b},(v)\right)·\mathit{\nu }& {\displaystyle =h.}\hfill \end{array}$$43a

Analysis similar to that in the previous Section 4.1 shows that the limit $\mathit{\tau }\to 0$ in (38a) results into (39a). There is an extra term to take under consideration, namely ($\mathit{\xi }\in (0,T)$ and $\mathit{\phi }\in W$)$$\begin{array}{c}\hfill \left|{\int }_0^{\mathit{\xi }},\left({\overline{k}}_n,{\overline{\mathit{\kappa }}}_n,\mathrm{\nabla },{\overline{\tilde{U}}}_n,-,k,\mathit{\kappa },\mathrm{\nabla },\tilde{U},,,\mathrm{\nabla },\mathit{\phi }\right)\right|\to 0.\end{array}$$The convergence of (38b)–(39b) for any $t\in (0,T)$ follows from the continuity of $h$.

This subsection concludes with an analogue of Theorem 4.3.

Theorem 4.4

Let the assumptions of Lemma 3.7 be fulfilled. Moreover, suppose that there exist real constants ${\mathit{\theta }}_0$ and ${\mathit{\theta }}_1$ such that $0<{\mathit{\theta }}_0<{\mathit{\theta }}^{\prime }⩽{\mathit{\theta }}_1$. Then there exists a weak solution to (39).

5 Numerical experiments

The aim of the simulations is to analyse both algorithms proposed in Sections 3 and 4. The 2D Finite Elements code Freefem++ is used.

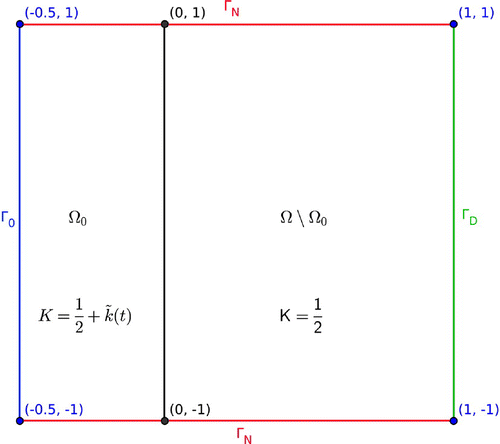
The domain under consideration is the rectangle $\mathrm{\Omega }=\left(-,\frac{1}{2},,,1\right)\times \left(-,1,,,1\right)$, with ${\mathrm{\Omega }}_0=\left(-,\frac{1}{2},,,0\right)\times \left(-,1,,,1\right)$ in ${\mathbb{R}}^2$. The time interval is $[0,1]$, i.e. $T=1$. The boundary $\mathrm{\Gamma }$ is split into three nonoverlapping parts, namely ${\mathrm{\Gamma }}_D$ (right), ${\mathrm{\Gamma }}_N$ (top and bottom) and ${\mathrm{\Gamma }}_0$ (left part of $\mathrm{\Gamma }$), see Figure 1.

Figure 1. The domain used in the numerical experiments.

In the experiments, the exact solution $(K,u)$ is prescribed as follows$$\begin{array}{c}\hfill {\displaystyle K(t,x,y)=\left(1,+,sin,(,10,t,)\right)1{\text{I}}_{\left\{x,<,0\right\}}+\frac{1}{2};u(t,x,y)=(1+t)sin\left(\frac{\mathit{\pi }}{2},(1-x)\right).}\end{array}$$The function $1{\text{I}}_{\left\{x,<,0\right\}}$ is the indicator function of the subset $\left\{(x,y),\in ,{\mathbb{R}}^2,:,x,<,0\right\}$ of ${\mathbb{R}}^2$. Moreover, it is assumed that$$\mathit{\theta }(s)=\sqrt{s^2+1}\text{and}\mathit{a}\equiv \mathbf{0}.$$Some simple calculations give the exact data for the numerical experiment$$\begin{array}{c}\hfill {\displaystyle g^D=g^N=0;U(t)=\frac{1+t}{\sqrt{2}};h(t)=\frac{\mathit{\pi }}{\sqrt{2}}\left(1,+,t\right)\left(1.5,+,sin,(,10,t,)\right).}\end{array}$$This section is split into two subsections. The first two are devoted to a different solution method. The results are summarized in the third subsection. The purpose is the recovery of$$\tilde{k}(t):=1+sin(10t).$$For the time discretization, an equidistant time partitioning is chosen with time step $\mathit{\tau }=0.02$ and for the space discretization, a fixed uniform mesh is used consisting of $144528$ triangles.

5.1 First solution method

An uncorrelated noise is added to the additional condition $U(t)$ in order to simulate the errors present in real measurements. The noise is generated randomly with given magnitude $e=0,$$0.5$ and $1\%$. Applying the backward Euler difference scheme into (2020 $$\begin{array}{c}\hfill {\displaystyle \frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },u_i,+,\mathit{a},(u_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-h_i{\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}+\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_{i-1},),,,\mathit{\phi }\right),(\mathit{\phi }\in V).}\end{array}$$20 ), a recurrent system of nonlinear elliptic BVPs for $(K_i,u_i)\approx \left(K,(t_i),,,u,(t_i)\right),i=1,2,\dots ,50$ and $\mathit{\phi }\in V$ have to be solved44 $$\begin{array}{c}\hfill {\displaystyle \frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },u_i,,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)-h_i{\mathit{\phi }|}_{{\mathrm{\Gamma }}_0}+\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_{i-1},),,,\mathit{\phi }\right);u_0=u_0;}\end{array}$$44 with45 $$\begin{array}{cc}\hfill \left(f_i,,,\mathit{\phi }\right)& =\left(\frac{\left(1,+,t_i\right){\left(sin,\left(\frac{\mathit{\pi }}{2},\left(1,-,x\right)\right)\right)}^2}{\sqrt{{\left(1,+,t_i\right)}^2{\left(sin,\left(\frac{\mathit{\pi }}{2},\left(1,-,x\right)\right)\right)}^2+1}},,,\mathit{\phi }\right)\hfill \\ \hfill & +{\left(\left(1.5,+,sin,(,10,t_i,)\right),{\left(\frac{\mathit{\pi }}{2}\right)}^2,\left(1,+,t_i\right),sin,\left(\frac{\mathit{\pi }}{2},(1-x)\right),,,\mathit{\phi }\right)}_{{\mathrm{\Omega }}_0}\hfill \\ \hfill & +{\left(0.5,{\left(\frac{\mathit{\pi }}{2}\right)}^2,\left(1,+,t_i\right),sin,\left(\frac{\mathit{\pi }}{2},(1-x)\right),,,\mathit{\phi }\right)}_{\mathrm{\Omega }\backslash {\mathrm{\Omega }}_0}.\hfill \end{array}$$45 On every time level, Newton’s method is applied to deal with the nonlinearity. More precisely, given a solution $u_i^l$ from iteration $l$, a perturbation $d{u}_i$ is searched such that$$u_i^{l+1}=u_i^l+d{u}_i$$fulfills the nonlinear problem (4040 $$\begin{array}{c}\hfill \underset{\mathit{\tau }\to 0}{lim}{\int }_0^T{∥,{\overline{u}}_n,-,u∥}_{\mathit{\partial }{\mathrm{\Omega }}_0}^2=0\text{and}{\overline{u}}_n\to u\text{a.e. in}(0,T)\times \mathit{\partial }{\mathrm{\Omega }}_0.\end{array}$$40 ). The perturbation $d{u}_i$ is zero at the boundaries where the Dirichlet conditions are applied. Inserting $u_i^{l+1}$ in the BVP (4040 $$\begin{array}{c}\hfill \underset{\mathit{\tau }\to 0}{lim}{\int }_0^T{∥,{\overline{u}}_n,-,u∥}_{\mathit{\partial }{\mathrm{\Omega }}_0}^2=0\text{and}{\overline{u}}_n\to u\text{a.e. in}(0,T)\times \mathit{\partial }{\mathrm{\Omega }}_0.\end{array}$$40 ), the $\mathit{\theta }$ term in the LHS is linearized as$$\mathit{\theta }(u_i^{l+1})\approx \mathit{\theta }(u_i^l)+{\mathit{\theta }}^{\prime }(u_i^l)d{u}_i.$$As initial guess $u_i^0$, the solution of the linear problem with $\mathit{\theta }(s)=1$ and $\mathit{a}(s)=\mathbf{0}$ is taken. The iterations are stopped when $\Vert u_i^{l+1}-u_i^l{\Vert }_{L_{\infty }(\mathrm{\Omega })}={\Vert d{u}_i\Vert }_{L_{\infty }(\mathrm{\Omega })}<{10}^{-5}$ or when the number of iterations exceed the limit $25$. The unknowns ${\tilde{k}}_i\approx \tilde{k}(t_i),i=1,\dots ,50,$ are determined by the nonlinear conjugate gradient method. On each time step $t_i,i=1,\dots ,50,$ the functional$$\begin{array}{c}\hfill J_1({\tilde{k}}_i):={\Vert u_i-U(t_i)\Vert }_{L_2({\mathrm{\Gamma }}_0)}^2\end{array}$$is minimized. The starting point for this algorithm on the first time step is set as ${\tilde{k}}_1^0=1$. The starting point on the following time steps is ${\tilde{k}}_{i-1}$, the minimizing value of the functional in the previous time step. The algorithm stops after maximum $10$ iterations with the prescribed error tolerance ${10}^{-6}$.

Figure 2. Noise $e=0\%$: numerical value of ${\tilde{k}}_i$ using the first solution method (a) and the second solution method (b); $i=1,\dots ,50.$

Figure 3. Noise $e=0.5\%$: numerical value of ${\tilde{k}}_i$ using the first solution method (a) and the second solution method (b); $i=1,\dots ,50.$

5.2 Second solution method

Again, an uncorrelated noise with magnitude $e=0,0.5$ and $1\%$ is added to the additional condition $h(t)$. Utilizing the backward Euler difference scheme into (2323 $$\begin{array}{c}\hfill {∥,\mathrm{\nabla },(,u_{\mathit{\alpha }},-,u_{\mathit{\beta }},)∥}^2\lesssim \frac{{(\mathit{\alpha }-\mathit{\beta })}^2}{{\mathit{\tau }}^2}.\end{array}$$23 ), a recurrent system of linear elliptic BVPs for $(K_i,u_i)\approx \left(K,(t_i),,,u,(t_i)\right),i=1,2,\dots ,50$ and $\mathit{\phi }\in W$ has to be solved46 $$\begin{array}{c}\hfill {\displaystyle \frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },u_i,,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right)+\frac{1}{\mathit{\tau }}\left(\mathit{\theta },(,u_{i-1},),,,\mathit{\phi }\right),u_0=u_0;}\end{array}$$46 where $\left(f_i,,,\mathit{\phi }\right)$ is as in (4141 $$\begin{array}{c}\hfill \begin{array}{c}\hfill {\displaystyle \left(\mathit{\delta },\mathit{\vartheta },(,v_i,),,,\mathit{\phi }\right)+\left(K_i,\mathrm{\nabla },(v_i+{\tilde{U}}_i),+,\mathit{b},(v_i),,,\mathrm{\nabla },\mathit{\phi }\right)=\left(f_i,,,\mathit{\phi }\right),}\\ \hfill {\displaystyle {\int }_{{\mathrm{\Gamma }}_0}\left(-,K_i,\mathrm{\nabla },(v_i+{\tilde{U}}_i),-,\mathit{b},(v_i)\right)·\mathit{\nu }}& {\displaystyle =h_i,}\hfill \end{array}\end{array}$$41 ) and $u_i={\tilde{U}}_i$ on ${\mathrm{\Gamma }}_0$. The nonlinearity is handled in the same way as in the first solution method. Now, on each time step $t_i,i=1,\dots ,50,$ the functional$$\begin{array}{c}\hfill J_2({\tilde{k}}_i):={\left(-,{\int }_{{\mathrm{\Gamma }}_0},({\tilde{k}}_i+0.5),\mathrm{\nabla },u_i,·,\mathit{\nu },-,h,(t_i)\right)}^2\end{array}$$is minimized.

5.3 Results

At each time step, the resulting elliptic BVP’s (4040 $$\begin{array}{c}\hfill \underset{\mathit{\tau }\to 0}{lim}{\int }_0^T{∥,{\overline{u}}_n,-,u∥}_{\mathit{\partial }{\mathrm{\Omega }}_0}^2=0\text{and}{\overline{u}}_n\to u\text{a.e. in}(0,T)\times \mathit{\partial }{\mathrm{\Omega }}_0.\end{array}$$40 ) and (4240 $$\begin{array}{c}\hfill \underset{\mathit{\tau }\to 0}{lim}{\int }_0^T{∥,{\overline{u}}_n,-,u∥}_{\mathit{\partial }{\mathrm{\Omega }}_0}^2=0\text{and}{\overline{u}}_n\to u\text{a.e. in}(0,T)\times \mathit{\partial }{\mathrm{\Omega }}_0.\end{array}$$40 ) are solved numerically by the finite element method (FEM) using second-order (P2-FEM) Lagrange polynomials. The results from the recovery of $\tilde{k}(t)$ using both solution methods for the different values of the amplitude $e$ are shown in Figures 2–4. The exact $\tilde{k}(t_i)$ is denoted by a solid line and the approximations ${\tilde{k}}_i$ by linespoints; $i=1,\dots ,50$. The evolution of the absolute ${\tilde{k}}_i$-error for the different time steps is shown in Figure 5.

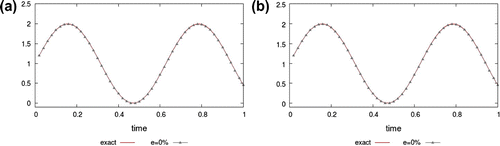
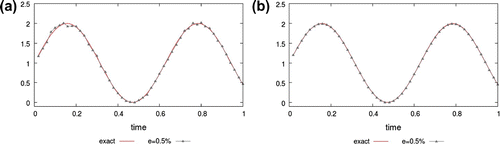
Figure 4. Noise $e=1\%$: numerical value of ${\tilde{k}}_i$ using the first solution method (a) and the second solution method (b); $i=1,\dots ,50.$

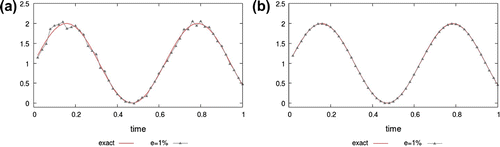
Figure 5. The absolute ${\tilde{k}}_i$-error using the first solution method (a) and using the second solution method (b) for the different noise levels; $i=1,\dots ,50.$

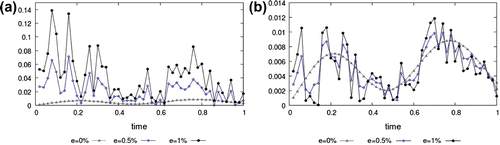
The experiments demonstrate that the approximation becomes less accurate with increasing magnitude $e$ when the number of time discretization intervals and the number of triangles in the space discretization is fixed. In this experiment, the second solution method is more accurate.

6 Conclusion

In this contribution, a nonlinear parabolic problem of second order with an unknown diffusion coefficient in a subregion is considered. In this subregion, the diffusion coefficient is only time dependent. Two different solution methods are considered. In the first solution method, an additional Dirichlet condition is prescribed on a part of the surface of the region with unknown coefficient. In the second solution method, an additional total flux condition is prescribed through the same surface. First, for both solution methods, the existence of a solution on a single time step is proved using coefficient to data mappings. Afterwards, a numerical algorithm based on Rothe’s method is established and the convergence of this scheme is shown. No uniqueness of the solution can be assured. The convergence of the numerical algorithm is illustrated by a numerical experiment.

Acknowledgments

The authors thank the reviewers for closely reading the manuscript and for their useful suggestions.