A Slepian framework for the inverse problem of equivalent gravitational potential generated by discrete point masses

Abstract

We solve a geodetic inverse problem for the determination of a distribution of point masses (characterized by their intensities and positions), such that the potential generated by them best approximates a given potential field. On the whole Earth, a potential function is usually expressed in terms of spherical harmonics which are basis functions with global support. The identification of the two potentials is done by solving a least-squares problem. When only a limited area of the Earth is studied, the estimation of the point-mass parameters by means of spherical harmonics is prone to error, since they are no longer orthogonal over a partial domain of the sphere. The point-mass determination problem on a limited region is treated by the construction of a local spherical harmonic basis that is orthogonal over the specified limited domain of the sphere. We propose an iterative algorithm for the numerical solution of the local point mass determination problem and give some results on the robustness of this reconstruction process. We also study the stability of this problem against added noise. Some numerical tests are presented and commented.

Keywords:

• inverse problem
• point masses
• gravitational potential
• spherical harmonics
• global basis
• local basis
• band-limited functions
• Slepian functions

AMS Subject Classifications:

• 86A22
• 86A30
• 94A12

1 Introduction

One of the main problems in physical geodesy is the determination of the geoid: the equipotential surface for the gravitational potential which coincides with the mean ocean surface. During the past few decades there has been a growing interest in developing methods, with increasing levels of accuracy, for the determination of the high-resolution geoid (and/or regional geoid). Among the methods widely used by the geodetic community for the gravimetric determination of the geoid we mention the Stokes’ integration approach,[1] the least-squares collocation approach,[2, 3] and the point-mass inversion approach.[4, 5]

The point-mass approach is based on the simple idea that, in principle, it is possible to find an equivalent distribution of discrete point masses placed below the Earth’s surface for which the gravitational potential field generated by them closely approximates the true gravity field in the region of interest. This approach can also be considered as a model reduction for which the representation by the inverse-distance Newtonian potential functions can be seen as simple alternative to the classical representation by spherical harmonics.

There are many methods based on the point-mass inversion approach which differ by the procedure used for the determination of the positions and intensities of the point masses. While some of these methods place the point masses on a fixed regular grid beneath the Earth’s surface and try to find their depths and intensities,[6] other methods use freely positioned point masses and thus seek full positions and intensities of the point masses.[4] We also note that the strategy used for the optimization of the positions and intensities differs from one method to another.

In this paper, we are interested in using the theory of localized functions to construct a distribution of buried point masses in such a way that the potential generated by them best fits, in the sense of least squares, a given potential gravitational field in a specified region of the Earth. In fact, in the case where the region of interest is the whole Earth, the orthonormal spherical harmonics basis is used to expand the given and synthesized potentials in order to formulate the problem of the determination of the positions and intensities of buried masses as an inverse problem. On the other hand, when only a limited region of the Earth is considered, the spherical harmonics basis is no longer orthogonal. Consequently, the spherical harmonic basis for the determination of the local point-mass problem is not appropriate and hence one has to find another basis which is localized in the region of interest. Once such a basis has been found, by expanding the given and synthesized potentials over this basis, the problem of the determination of the positions and intensities of buried masses can then be formulated as an inverse problem.

We note that the question of finding a local basis was first studied by Slepian, Pollak and Landau for an interval of the real line and for a rectangular region of the plane.[7–12] They discovered by serendipity a basis of functions (now called Slepian functions) whose energies are concentrated in the considered region. This procedure was very useful in several domains of applied mathematics and physics, notably geophysics,[13, 14] cosmology [15] and image processing.[16, 17]

The problem of localization (or concentration) on a limited region of the sphere has been an active area of research for many years. We particularly mention the pioneering works of Simons and his coauthors [18–21] on spherical Slepian functions and their applications in geodesy. Other authors use different approaches to this problem. For example, Michel and his collaborators [22–24] use multiresolution splines to deal with the problem of localization. We also mention zooming-in approximation by locally supported wavelets.[25]

The remaining of this paper is structured as follows. In Section 2, we start by gathering some background materials on spherical harmonics that will be used in the sequel. Then, we give the expansions of the given (observed) gravitational potential and the potential generated by the distribution of point masses (synthesized potential) in terms of spherical harmonics. In Section 3, we first formulate the problem of equivalent point-mass determination for the whole Earth as a minimization problem. Then, we use Slepian analysis to formulate the problem of the determination of equivalent point masses which generate a gravitational potential that closely approximates the given gravitational potential on a specified region. Some numerical results are presented and commented in Section 5. Finally, some conclusions and perspectives are given in Section 6.

2 The gravitational and synthesized potentials

2.1 Spherical harmonics

Let $\mathbb{S}$ denote the unit sphere in ${\mathbb{R}}^3$ and let $(\mathit{\theta },\mathit{\varphi })$ denote a generic point on the sphere where $\mathit{\theta }$ is the co-latitude and $\mathit{\varphi }$ is the longitude. On the space of square-integrable real functions on $\mathbb{S}$, we have the inner product ${〈·,·〉}_{\mathbb{S}}$ defined by1 $$\begin{array}{c}\hfill {〈f,g〉}_{\mathbb{S}}={\int }_{\mathbb{S}}f(\mathit{\theta },\mathit{\varphi })g(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma }={\int }_0^{2\mathit{\pi }}{\int }_0^{\mathit{\pi }}f(\mathit{\theta },\mathit{\varphi })g(\mathit{\theta },\mathit{\varphi })sin\mathit{\theta }d\mathit{\theta }d\mathit{\varphi },\end{array}$$1 where $d\mathit{\sigma }=sin\mathit{\theta }d\mathit{\theta }d\mathit{\varphi }$ denotes the surface element on the unit sphere $\mathbb{S}$. The associated norm is given by2 $$\begin{array}{c}\hfill {\Vert f\Vert }_{\mathbb{S}}^2={\int }_{\mathbb{S}}{|f(\mathit{\theta },\mathit{\varphi })|}^{2}d\mathit{\sigma }.\end{array}$$2 We recall that any square-integrable function on the unit sphere $\mathbb{S}$ can be expanded in terms of spherical harmonics as [26]3 $$\begin{array}{c}\hfill f(\mathit{\theta },\mathit{\varphi })=\sum _{n=0}^{\infty }\sum _{m=-n}^n{f}_{mn}{Y}_{nm}(\mathit{\theta },\mathit{\varphi }),\end{array}$$3 where$$f_{nm}={〈f,Y_{nm}〉}_{\mathbb{S}}={\int }_{\mathbb{S}}f(\mathit{\theta },\mathit{\varphi })Y_{nm}(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma },$$is the spherical harmonic coefficient of $f$ associated with $Y_{nm}(\mathit{\theta },\mathit{\varphi })$, the spherical harmonic of degree $n$ and order $m$ which is given by4 $$\begin{array}{c}\hfill Y_{nm}(\mathit{\theta },\mathit{\varphi })=\left\{,,\begin{array}{cc}{\overline{P}}_{nm}(cos\mathit{\theta })cos(m\mathit{\varphi })\hfill & \mathrm{if}m\ge 0,\hfill \\ {\overline{P}}_{nm}(cos\mathit{\theta })sin(|m|\mathit{\varphi })\hfill & \mathrm{if}m<0.\hfill \end{array}\right.\end{array}$$4 Here, ${\overline{P}}_{nm}(cos\mathit{\theta })$ is a normalized version of $P_{nm}(cos\mathit{\theta })$, the Legendre’s associated function of degree $n$ and order $m$ given by5 $$\begin{array}{c}\hfill {\overline{P}}_{nm}(cos\mathit{\theta })=\sqrt{k\frac{2n+1}{4\mathit{\pi }}\frac{(n-m)!}{(n+m)!}}{P}_{nm}(cos\mathit{\theta }),\text{where}\left\{\begin{array}{c}\hfill k=1\text{for}m=0,\\ \hfill k=2\text{for}m\ne 0.\end{array}\right.\end{array}$$5 The spherical harmonics functions $Y_{nm}(\mathit{\theta },\mathit{\varphi })$ are orthonormal with respect to the inner product (11 $$\begin{array}{c}\hfill {〈f,g〉}_{\mathbb{S}}={\int }_{\mathbb{S}}f(\mathit{\theta },\mathit{\varphi })g(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma }={\int }_0^{2\mathit{\pi }}{\int }_0^{\mathit{\pi }}f(\mathit{\theta },\mathit{\varphi })g(\mathit{\theta },\mathit{\varphi })sin\mathit{\theta }d\mathit{\theta }d\mathit{\varphi },\end{array}$$1 ), i.e. [2]$${〈Y_{nm},Y_{n^{\prime }{m}^{\prime }}〉}_{\mathbb{S}}={\int }_{\mathbb{S}}{Y}_{nm}(\mathit{\theta },\mathit{\varphi })Y_{n^{\prime }{m}^{\prime }}(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma }={\mathit{\delta }}_{l{l}^{\prime }}{\mathit{\delta }}_{m{m}^{\prime }}.$$Finally, we recall that for two points $(\mathit{\theta },\mathit{\varphi })$ and $({\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })$ on the unit sphere, by the addition theorem of spherical harmonics we have the identity [18]6 $$\begin{array}{c}\hfill \sum _{m=-n}^n{Y}_{nm}(\mathit{\theta },\mathit{\varphi })Y_{nm}({\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })=\frac{2n+1}{4\mathit{\pi }}{P}_n(cos\mathit{\psi }),\end{array}$$6 where $\mathit{\psi }$ is the spherical distance between $(\mathit{\theta },\mathit{\varphi })$ and $({\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })$ given by7 $$\begin{array}{c}\hfill cos\mathit{\psi }=cos{\mathit{\theta }}^{\prime }cos\mathit{\theta }+sin{\mathit{\theta }}^{\prime }sin\mathit{\theta }cos({\mathit{\varphi }}^{\prime }-\mathit{\varphi }).\end{array}$$7

2.2 The gravitational potential in terms of spherical harmonics

The gravitational potential $V$ satisfies [2]$$\begin{array}{cc}\mathrm{\Delta }V=0,\hfill & \text{in}{\mathbb{R}}^3\backslash \mathbb{E},\hfill \\ \mathrm{\Delta }V=-4\mathit{\pi }G\mathit{\rho },\hfill & \text{in}\mathbb{E},\hfill \end{array}$$where $\mathbb{E}$ is the Earth, $\mathit{\rho }$ is the mass density and $G$ is the universal gravitational constant. Furthermore, across the Earth’s surface we have continuity of both the potential and its normal derivative.

Since the gravitational potential is a harmonic function outside the Earth, for a point $\mathit{P}$ with spherical coordinates $(r,\mathit{\theta },\mathit{\varphi })$ that lies outside the Earth we have the following expansion in spherical harmonics [2]8 $$\begin{array}{c}\hfill V(r,\mathit{\theta },\mathit{\varphi })=\frac{GM}{r}\sum _{n=0}^{+\infty }\sum _{m=-n}^n{c}_{nm}{\left(\frac{a}{r}\right)}^n{Y}_{nm}(\mathit{\theta },\mathit{\varphi }).\end{array}$$8 Here $M=5.9736\times {10}^{24}\mathrm{k}g$ is the total mass of the Earth, $a$ is the equatorial radius of the Earth and $c_{nm}$ is the geopotential coefficient of degree $n$ and order $m$. The values of $M$ and $c_{nm}$ depend on the choice of the geopotential model (e.g. EGM96, OSU91, etc.) at the considered zone. Note that the first term in the summation, i.e. for $n=0,$ is $GM/r$ which represents the potential generated by a homogeneous body of mass $M$ located at the origin.

Geopotential dedicated Earth-orbiting satellites, like CHAMP (CHAllenging Minisatellite Payload) and GRACE (Gravity Recovery and Climate Experiment), provide data that are incorporated to determine the spherical harmonics coefficients of the Earth gravitational potential. In the EGM96 model, the coefficients $c_{nm}$ in this expansion are determined up to the degree $n=360$, see e.g. [27, 28]. The higher resolution model, EGM08, provides the coefficients $c_{nm}$ up to the degree $n=2160$, see [29].

2.3 The synthesized potential in terms of spherical harmonics

The inverse gravimetric problem of finding the mass density $\mathit{\rho }$ inside the Earth from information of the gravitational potential $V$ outside the Earth is not well posed in the sense of Hadamard. In fact, this problem does not have a unique solution as the associated Fredholm integral operator is of the first kind and has an infinite dimensional null space.[22] This null space corresponds to the space of functions which are $L^2(\mathbb{E})$-orthogonal to the space, $\mathrm{H}arm(\mathbb{E})$, of harmonic functions in $\mathbb{E}$. Furthermore, even when restricting this operator to $\mathrm{H}arm(\mathbb{E})$, it still has a discontinuous inverse and thus stability is not guaranteed.

In the point-mass approach, the true mass density $\mathit{\rho }$ is approximated by a finite distribution of point masses$$\tilde{\mathit{\rho }}=\sum _{k=1}^N{m}_k{\mathit{\delta }}_{{\mathit{x}}_k},$$where $m_k$ and ${\mathit{x}}_k$ are the mass and location of the point mass $k$ and $\mathit{\delta }$ is the Dirac distribution.

We here recall the following identifiability result [30]:

Theorem 2.1

Let $V^{(i)}$, $i=1,2$ be the solutions of the problems$$\left\{\begin{array}{cc}\mathrm{\Delta }{V}^{(i)}=-4\mathit{\pi }G{\sum }_{k=1}^{N^i}{m}_k^{(i)}{\mathit{\delta }}_{{\mathit{x}}_k^{(i)}},\hfill & \mathrm{in}\mathbb{E},\hfill \\ {\displaystyle \frac{\mathit{\partial }{V}^{(i)}}{\mathit{\partial }\mathit{\nu }}=g,}\hfill & \mathrm{on}\mathit{\partial }\mathbb{E}.\hfill \end{array}\right.$$If $V^{(1)}=V^{(2)}$ on a subset of $\mathit{\partial }\mathbb{E}$ with non-empty interior then $N^1=N^2$ and (up to a permutation of the indices) $m_k^{(1)}=m_k^{(2)}$ and ${\mathit{x}}_k^{(1)}={\mathit{x}}_k^{(2)}$ for $k=1,\dots N^1$.

It is interesting to note that this result does not hold for an infinite distribution of point masses. Lipschitz stability results for the problem of determining the intensities of the point-masses and their locations from measurements of the generated potential are given in [31].

Similar to what we did for the potential $V$ generated with the mass density $\mathit{\rho }$, we will expand the gravitational potential $\tilde{V}$ generated by the discrete mass density $\tilde{\mathit{\rho }}$ in spherical harmonics. Let $\mathcal{S}=$${\{{\mathit{M}}_k\equiv (r_k,{\mathit{\theta }}_k,{\mathit{\varphi }}_k;m_k)\}}_{k=1}^N$ be a distribution of $N$ points located at $(r_k,{\mathit{\theta }}_k,{\mathit{\varphi }}_k)$ and with masses $m_k$. Recall that the potential at a spacial point $\mathit{P}$ with coordinates $(r,\mathit{\theta },\mathit{\varphi })$ generated by a point mass ${\mathit{M}}_k$ is given by9 $$\begin{array}{c}\hfill {\tilde{V}}_k(r,\mathit{\theta },\mathit{\varphi })=\frac{G{m}_k}{{\ell }_k},\end{array}$$9 where ${\ell }_k$ is the Euclidean distance between the two points ${\mathit{M}}_k$ and $\mathit{P}$. If we denote by ${\mathit{\psi }}_k$ the spherical distance between ${\mathit{M}}_k$ and $\mathit{P}$ which is obtained by taking $({\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })=({\mathit{\theta }}_k,{\mathit{\varphi }}_k)$ in (77 $$\begin{array}{c}\hfill cos\mathit{\psi }=cos{\mathit{\theta }}^{\prime }cos\mathit{\theta }+sin{\mathit{\theta }}^{\prime }sin\mathit{\theta }cos({\mathit{\varphi }}^{\prime }-\mathit{\varphi }).\end{array}$$7 ), then10 $$\begin{array}{c}\hfill {\displaystyle {\ell }_k=\sqrt{r^2-2r{r}_{k}cos{\mathit{\psi }}_k+r_k^2}.}\end{array}$$10 As the point masses are buried, we have $r_k<r$, $1\le k\le N$, and as a consequence, the inverse of the distance between ${\mathit{M}}_k$ and $\mathit{P}$, admits a convergent Legendre series expansion. Indeed, if we set ${\mathit{\alpha }}_k=r_k/r$, then11 $$\begin{array}{c}\hfill {\ell }_k=r\sqrt{1-2{\mathit{\alpha }}_{k}cos{\mathit{\psi }}_k+{\mathit{\alpha }}_k^2},\end{array}$$11 and therefore $r/{\ell }_k=1/\sqrt{1-2{\mathit{\alpha }}_{k}cos{\mathit{\psi }}_k+{\mathit{\alpha }}_k^2}$ can be expanded into power series with respect to ${\mathit{\alpha }}_k$ [2]:12 $$\begin{array}{c}\hfill \frac{r}{{\ell }_k}=\sum _{n=0}^{+\infty }{\mathit{\alpha }}_k^n{P}_n(cos{\mathit{\psi }}_k).\end{array}$$12 Then, it follows from (66 $$\begin{array}{c}\hfill \sum _{m=-n}^n{Y}_{nm}(\mathit{\theta },\mathit{\varphi })Y_{nm}({\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })=\frac{2n+1}{4\mathit{\pi }}{P}_n(cos\mathit{\psi }),\end{array}$$6 ) that13 $$\begin{array}{c}\hfill \frac{1}{{\ell }_k}=\frac{1}{r}\sum _{n=0}^{+\infty }{\mathit{\alpha }}_k^n{P}_n(cos{\mathit{\psi }}_k)=\frac{1}{r}\sum _{n=0}^{+\infty }\sum _{m=-n}^n{\mathit{\alpha }}_k^n\frac{4\mathit{\pi }}{2n+1}{Y}_{nm}({\mathit{\theta }}_k,{\mathit{\varphi }}_k)Y_{nm}(\mathit{\theta },\mathit{\varphi }).\end{array}$$13 The expression (99 $$\begin{array}{c}\hfill {\tilde{V}}_k(r,\mathit{\theta },\mathit{\varphi })=\frac{G{m}_k}{{\ell }_k},\end{array}$$9 ) of the potential ${\tilde{V}}_k$ at the spacial point $\mathit{P}$ becomes$${\tilde{V}}_k(r,\mathit{\theta },\mathit{\varphi })=\frac{G{m}_k}{r}\sum _{n=0}^{+\infty }\sum _{m=-n}^n{\mathit{\alpha }}_k^n\frac{4\mathit{\pi }}{2n+1}{Y}_{nm}({\mathit{\theta }}_k,{\mathit{\varphi }}_k)Y_{nm}(\mathit{\theta },\mathit{\varphi }).$$The potential $\tilde{V}$ at $\mathit{P}$ generated by the $N$ point masses is the sum of the potentials generated by the considered elementary buried masses14 $$\begin{array}{c}\hfill \tilde{V}(r,\mathit{\theta },\mathit{\varphi })=\frac{G}{r}\sum _{k=1}^N{m}_k\sum _{n=0}^{+\infty }{\left(\frac{r_k}{r}\right)}^n\sum _{m=-n}^n\frac{4\mathit{\pi }}{2n+1}{Y}_{nm}({\mathit{\theta }}_k,{\mathit{\varphi }}_k)Y_{nm}(\mathit{\theta },\mathit{\varphi }).\end{array}$$14 On a selected sphere (i.e. for a fixed value $\tilde{R}$ of $r$), we seek the masses and positions of the buried points, so that the resulting generated potential best approximates the gravitational potential for the considered region. This involves solving an inverse problem which we formulate in the following section.

3 Formulation as inverse problems

3.1 Inverse problem on the whole Earth

The problem of determining the potential generated by a finite distribution of point masses of given positions and intensities can be solved by considering the expression of the elementary potential (99 $$\begin{array}{c}\hfill {\tilde{V}}_k(r,\mathit{\theta },\mathit{\varphi })=\frac{G{m}_k}{{\ell }_k},\end{array}$$9 ), we gave in (1414 $$\begin{array}{c}\hfill \tilde{V}(r,\mathit{\theta },\mathit{\varphi })=\frac{G}{r}\sum _{k=1}^N{m}_k\sum _{n=0}^{+\infty }{\left(\frac{r_k}{r}\right)}^n\sum _{m=-n}^n\frac{4\mathit{\pi }}{2n+1}{Y}_{nm}({\mathit{\theta }}_k,{\mathit{\varphi }}_k)Y_{nm}(\mathit{\theta },\mathit{\varphi }).\end{array}$$14 ). Thus, the potential caused by a distribution of point masses at a spacial point $\mathit{P}$ with spherical coordinates $(\tilde{R},\mathit{\theta },\mathit{\varphi })$, is the sum of the elementary potentials generated by all the point masses. Such a problem is called the forward problem.

The inverse problem is then to find the masses $\mathit{m}={(m_1,\dots ,m_N)}^T$ and positions $\mathit{\xi }={(r_1,{\mathit{\theta }}_1,{\mathit{\varphi }}_1,\dots ,r_N,{\mathit{\theta }}_N,{\mathit{\varphi }}_N)}^T$ of the point masses that generate a gravitational potential close to a given one, i.e. for which the difference between the given gravitational potential and the one generated by these masses is minimized. Eventually, some constraints on those unknowns need to be imposed to make the computations more stable. If we assume that the point masses co-latitudes and longitudes $({\mathit{\theta }}_k,{\mathit{\varphi }}_k)$ are distributed on a fixed regular grid on the unit sphere then the unknown parameters are the masses $\mathit{m}={(m_1,\dots ,m_N)}^T$ and radii $\mathit{r}={(r_1,\dots ,r_N)}^T$. The approach we use here, is based on the expansion of the two potentials (i.e. the modelled and the predicted) in the same orthogonal basis. In the following sections, we describe the orthogonal basis to be used which depends on the region of interest: the whole Earth or on a limited region of the Earth.

To find the distribution of point masses which generates a potential field that best fits (in the sense of least squares) a given potential field over the whole Earth we introduce the real-valued function defined on ${\mathbb{R}}^{3N}\times {\mathbb{R}}^N$ by$${\displaystyle F(\mathit{\xi },\mathit{m})=\frac{1}{2}{\int }_{\mathbb{S}}{|V(\tilde{R},\mathit{\theta },\mathit{\varphi })-\tilde{V}(\tilde{R},\mathit{\theta },\mathit{\varphi })|}^{2}d\mathit{\sigma },}$$and we consider the following minimization problem15 $$\begin{array}{c}\hfill \underset{\mathit{\xi }\in {\mathbb{R}}^{3N},\mathit{m}\in {\mathbb{R}}^N}{min}F(\mathit{\xi },\mathit{m}).\end{array}$$15 That is we are interested in finding the masses $\mathit{m}$ and positions $\mathit{\xi }$ of the points so that the function $F(\mathit{\xi },\mathit{m})$ attains its minimum.

Using the spherical harmonic expansions (88 $$\begin{array}{c}\hfill V(r,\mathit{\theta },\mathit{\varphi })=\frac{GM}{r}\sum _{n=0}^{+\infty }\sum _{m=-n}^n{c}_{nm}{\left(\frac{a}{r}\right)}^n{Y}_{nm}(\mathit{\theta },\mathit{\varphi }).\end{array}$$8 ) and (1414 $$\begin{array}{c}\hfill \tilde{V}(r,\mathit{\theta },\mathit{\varphi })=\frac{G}{r}\sum _{k=1}^N{m}_k\sum _{n=0}^{+\infty }{\left(\frac{r_k}{r}\right)}^n\sum _{m=-n}^n\frac{4\mathit{\pi }}{2n+1}{Y}_{nm}({\mathit{\theta }}_k,{\mathit{\varphi }}_k)Y_{nm}(\mathit{\theta },\mathit{\varphi }).\end{array}$$14 ) and the orthonormality of the spherical harmonics on $\mathbb{S}$, this minimization problem can be written as16 $$\begin{array}{c}\hfill {\displaystyle \underset{\mathit{\xi }\in {\mathbb{R}}^{3N},\mathit{m}\in {\mathbb{R}}^N}{min}\frac{1}{2}{\Vert \mathit{b}-A(\mathit{\xi })\mathit{m}\Vert }^2,}\end{array}$$16 where $\mathit{b}$ is a vector with infinite numbers of rows and $A(\mathit{\xi })$ is a matrix function of $\mathit{\xi }$ with an infinite number of rows and $N$ columns. The entries of $\mathit{b}$ and $A(\mathit{\xi })$ are$$\begin{array}{cc}\hfill b_{I(n,m)}& =M{c}_{nm}{\left(\frac{a}{\tilde{R}}\right)}^n,I(n,m)=1,2,\dots ,\hfill \\ \hfill A_{I(n,m)k}(\mathit{\xi })& =\frac{4\mathit{\pi }}{(2n+1)}{\left(\frac{r_k}{\tilde{R}}\right)}^n{Y}_{nm}({\mathit{\theta }}_k,{\mathit{\varphi }}_k),I(n,m)=1,2,\dots ,k=1,\dots ,N,\hfill \end{array}$$where $I(n,m)=n(n+1)+m+1$. We shall assume that the positions of the point masses are such that the matrix $A(\mathit{\xi })$ has full column rank. Otherwise, we can arrange by adding/removing a point mass so that $A(\mathit{\xi })$ satisfies this hypothesis.

To solve the minimization problem (1616 $$\begin{array}{c}\hfill {\displaystyle \underset{\mathit{\xi }\in {\mathbb{R}}^{3N},\mathit{m}\in {\mathbb{R}}^N}{min}\frac{1}{2}{\Vert \mathit{b}-A(\mathit{\xi })\mathit{m}\Vert }^2,}\end{array}$$16 ), we use an alternating minimization algorithm which consists in an iterative procedure that solves alternatively a linear problem $({\mathcal{P}}_{\mathit{m}})$ for the masses $\mathit{m}$ (which are assumed non-negative) and a non-linear problem $({\mathcal{P}}_{\mathit{\xi }})$ for the positions $\mathit{\xi }$. The main steps of this algorithm are as follows:

(i)

Given fixed positions $\mathit{\xi }$ for the masses, we solve17 $$\begin{array}{c}\hfill {\displaystyle ({\mathcal{P}}_{\mathit{m}})\underset{m_k\ge 0,k=1,\dots ,N}{min}\frac{1}{2}{\Vert \mathit{b}-A(\mathit{\xi })\mathit{m}\Vert }^2.}\end{array}$$17 This least-squares problem is linear but with non-negative constraints for the masses. This problem is solved, for example, by using the non-negative least squares algorithm (NNLS) of Lawson and Hanson [32]. We denote by $\widehat{\mathit{m}}$ the solution of the problem (1717 $$\begin{array}{c}\hfill {\displaystyle ({\mathcal{P}}_{\mathit{m}})\underset{m_k\ge 0,k=1,\dots ,N}{min}\frac{1}{2}{\Vert \mathit{b}-A(\mathit{\xi })\mathit{m}\Vert }^2.}\end{array}$$17 ).

(ii)

Given the masses $\widehat{\mathit{m}}$, we solve (iteratively) for $\mathit{\xi }$ the problem18 $$\begin{array}{c}\hfill {\displaystyle ({\mathcal{P}}_{\mathit{\xi }})\underset{\mathit{\xi }\in {\mathbb{R}}^N}{min}\frac{1}{2}{\Vert \mathit{b}-A(\mathit{\xi })\widehat{\mathit{m}}\Vert }^2.}\end{array}$$18 The first-order optimality condition for this problem is the vanishing of the gradient of its objective function, i.e.$${(\mathrm{\nabla }F(\mathit{\xi }))}_i=-{(\mathit{b}-A(\mathit{\xi })\widehat{\mathit{m}})}^T\frac{\mathit{\partial }A(\mathit{\xi })}{\mathit{\partial }{\mathit{\xi }}_i}\widehat{\mathit{m}}.$$ Of course, to initialize the process, an initial position ${\mathit{\xi }}_{\mathbf{0}}$ is set for all the point masses.

3.2 Point-mass determination on a limited region of the Earth

The fact that, for a scalar product defined on a limited region of the Earth defined by19 $$\begin{array}{c}\hfill {〈f,g〉}_{\mathrm{\Omega }}:={\int }_{\mathrm{\Omega }}f(\mathit{\theta },\mathit{\varphi })g(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma },\end{array}$$19 the spherical harmonics basis is no longer orthogonal for the $L^2$-inner product, makes the computations of the entries of the matrix $A(\mathit{\xi })$ and vector $\mathit{b}$ more complicated. A new basis of functions that are concentrated on the region of interest is now defined.

3.2.1 Slepian basis of localized functions

As stated earlier, a square-integrable function $f$ on $\mathbb{S}$ can be represented as$$f(\mathit{\theta },\mathit{\varphi })=\sum _{n=0}^{+\infty }\sum _{m=-n}^n{f}_{nm}{Y}_{nm}(\mathit{\theta },\mathit{\varphi })\text{with}{f}_{nm}={\int }_{\mathbb{S}}f(\mathit{\theta },\mathit{\varphi })Y_{nm}(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma }.$$We say that $f$ is band limited with band width $K$ if $f_{nm}=0$ for all $n>K$, i.e. it has the finite sum representation20 $$\begin{array}{c}\hfill f(\mathit{\theta },\mathit{\varphi })=\sum _{n=0}^K\sum _{m=-n}^n{f}_{nm}{Y}_{nm}(\mathit{\theta },\mathit{\varphi }).\end{array}$$20 Following the pioneering work of Slepian, to find a basis of functions that are localized on a given region $\mathrm{\Omega }$ of the unit sphere, we seek functions $f$ such that the ratio21 $$\begin{array}{c}\hfill \mathit{\lambda }=\frac{{\int }_{\mathrm{\Omega }}{f}^2(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma }}{{\int }_{\mathbb{S}}{f}^2(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma }},\end{array}$$21 between their energy over $\mathrm{\Omega }$ and their energy over $\mathbb{S}$ is maximized. When the set $\mathrm{\Omega }\subset \mathbb{S}$ has positive measure and is not equal to $\mathbb{S}$, we have $0<\mathit{\lambda }<1$ for any $f$.

This maximization problem is equivalent to an eigenvalue and eigenfunction problem. Indeed, if $f$ is band-limited with band width $K$ then (2121 $$\begin{array}{c}\hfill \mathit{\lambda }=\frac{{\int }_{\mathrm{\Omega }}{f}^2(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma }}{{\int }_{\mathbb{S}}{f}^2(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma }},\end{array}$$21 ) reduces to22 $$\begin{array}{c}\hfill \mathit{\lambda }=\frac{1}{{\Vert \mathit{f}\Vert }_{\mathbb{S}}^2}\sum _{n=0}^K\sum _{m=-n}^n{f}_{nm}\sum _{n^{\prime }=0}^K\sum _{m^{\prime }=-n^{\prime }}^{n^{\prime }}{D}_{nm,n^{\prime }{m}^{\prime }}{f}_{n^{\prime }{m}^{\prime }},\end{array}$$22 where$$D_{nm,n^{\prime }{m}^{\prime }}={\int }_{\mathrm{\Omega }}{Y}_{nm}(\mathit{\theta },\mathit{\varphi })Y_{n^{\prime }{m}^{\prime }}(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma }.$$If we denote by $D$ the ${(K+1)}^2\times {(K+1)}^2$ matrix with coefficients $D_{nm,n^{\prime }{m}^{\prime }}$ and by $\mathit{f}={(f_{00},\dots ,f_{nm},\dots ,f_{KK})}^T$ the $f$-spherical harmonic coefficient vector, then ${\displaystyle \mathit{\lambda }=\frac{{\mathit{f}}^{T}D\mathit{f}}{{\mathit{f}}^T\mathit{f}}}$, and the maximization problem becomes the following algebraic eigenvalue problem23 $$\begin{array}{c}\hfill D\mathit{f}=\mathit{\lambda }\mathit{f}.\end{array}$$23 Since the matrix $D$ is real, symmetric and positive definite, its eigenvalues ${\mathit{\lambda }}_p$, $p=1,2,\dots ,{(K+1)}^2$, are all positive. We shall assume that they are ordered such that $1>{\mathit{\lambda }}_1\ge {\mathit{\lambda }}_2\dots \ge {\mathit{\lambda }}_{{(K+1)}^2}>0$. Furthermore, the symmetry of $D$ guarantees that the eigenvectors are real and orthonormal. Consequently,24 $$\begin{array}{c}\hfill {\mathit{f}}_p^T{\mathit{f}}_q={\mathit{\delta }}_{pq},{\mathit{f}}_p^{T}D{\mathit{f}}_q={\mathit{\lambda }}_p{\mathit{\delta }}_{pq}.\end{array}$$24 Every eigenvector ${\mathit{f}}_p$, $p=1,2,\dots ,{(K+1)}^2$ defines an associated spatially band-limited eigenfunction $f_p(\mathit{\theta },\mathit{\varphi })$ of the form (2020 $$\begin{array}{c}\hfill f(\mathit{\theta },\mathit{\varphi })=\sum _{n=0}^K\sum _{m=-n}^n{f}_{nm}{Y}_{nm}(\mathit{\theta },\mathit{\varphi }).\end{array}$$20 ). We remark that these functions are at the same time orthonormal with respect to the inner product (11 $$\begin{array}{c}\hfill {〈f,g〉}_{\mathbb{S}}={\int }_{\mathbb{S}}f(\mathit{\theta },\mathit{\varphi })g(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma }={\int }_0^{2\mathit{\pi }}{\int }_0^{\mathit{\pi }}f(\mathit{\theta },\mathit{\varphi })g(\mathit{\theta },\mathit{\varphi })sin\mathit{\theta }d\mathit{\theta }d\mathit{\varphi },\end{array}$$1 ) and orthogonal with respect to the inner product (1919 $$\begin{array}{c}\hfill {〈f,g〉}_{\mathrm{\Omega }}:={\int }_{\mathrm{\Omega }}f(\mathit{\theta },\mathit{\varphi })g(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma },\end{array}$$19 ), i.e.25 $$\begin{array}{c}\hfill {\int }_{\mathbb{S}}{f}_p(\mathit{\theta },\mathit{\varphi })f_q(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma }={\mathit{\delta }}_{pq},{\int }_{\mathrm{\Omega }}{f}_p(\mathit{\theta },\mathit{\varphi })f_q(\mathit{\theta },\mathit{\varphi })d\mathit{\sigma }={\mathit{\lambda }}_p{\mathit{\delta }}_{pq}.\end{array}$$25 Now, if we multiply the eigenvalue Equation (2323 $$\begin{array}{c}\hfill D\mathit{f}=\mathit{\lambda }\mathit{f}.\end{array}$$23 ) by $Y_{nm}(\mathit{\theta },\mathit{\varphi })$ and sum over all $0\le n\le K$ and $-n\le m\le n,$ we deduce that the eigenfunction $f$ satisfies the homogeneous Fredholm integral equation of the second kind$$\mathcal{D}(f)(\mathit{\theta },\mathit{\varphi }):={\int }_{\mathrm{\Omega }}D((\mathit{\theta },\mathit{\varphi }),({\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime }))f({\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })d\mathit{\sigma }=\mathit{\lambda }f(\mathit{\theta },\mathit{\varphi }),(\mathit{\theta },\mathit{\varphi })\in \mathrm{\Omega },$$where $\mathcal{D}$ is the integral operator associated with the kernel$$D((\mathit{\theta },\mathit{\varphi }),({\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime }))=\sum _{n=0}^K\frac{2n+1}{4\mathit{\pi }}{P}_n(cos\mathit{\psi }),$$which is symmetric and depends only on the spherical distance, $\mathit{\psi }$, between $(\mathit{\theta },\mathit{\varphi })$ and $({\mathit{\theta }}^{\prime },{\mathit{\varphi }}^{\prime })$ and given in (77 $$\begin{array}{c}\hfill cos\mathit{\psi }=cos{\mathit{\theta }}^{\prime }cos\mathit{\theta }+sin{\mathit{\theta }}^{\prime }sin\mathit{\theta }cos({\mathit{\varphi }}^{\prime }-\mathit{\varphi }).\end{array}$$7 ).

3.2.2 Point-mass determination using the Slepian basis

The problem of point-mass determination on a limited region of the Earth is solved in an analogous manner to that we used for the one formulated on the whole Earth but using the Slepian basis functions instead of the spherical harmonics. The main steps are essentially:

(i)	Initialization    We choose the geographic region to study and we compute its associated Slepian basis. Only the basis vectors associated with eigenvalues ${\mathit{\lambda }}_k>{10}^{-10},k=1,\dots ,K$ are kept. We also define the grid of the point-masses (see Section 3.2.1).
(ii)	Construction of the right-hand side    We compute the coefficients of the Earth gravitational potential $V$ over the considered region relative to the spherical harmonics basis. We note that we used the geoid model EGM96 for which the potential decomposition on the spherical harmonics basis is truncated to degree $n=360$. The spherical harmonic coefficients $c_{nm}$, $n=0,\dots ,360$, $m=-n,\dots ,n$ for this model are available from [33]. The right-hand side of our problem is the vector of the spherical harmonics components of the gravitational potential (see Section 3.1). Then, we project this vector on the orthogonal Slepian basis. To start the iterative process, we fix the initial depth of all point masses to ${\mathit{\xi }}_0=30\mathrm{k}m$.
(iii)	Alternating minimization Set $j=0$ and repeat (a) and (b) until convergence: (a) Solve the problem $({\mathcal{P}}_{\mathit{m}})$: • For $\mathit{\xi }={\mathit{\xi }}^{(j)}$, construct the matrix $A({\mathit{\xi }}^{(j)})$ (see Section 3.1). • Compute the solution, ${\mathit{m}}^{(j)}$, of problem $({\mathcal{P}}_{\mathit{m}})$. (b) Solve the problem$({\mathcal{P}}_{\mathit{\xi }})$: • For $\mathit{m}={\mathit{m}}^{(j)}$ find ${\mathit{\xi }}^{(j+1)}$ solution of the problem $({\mathcal{P}}_{\mathit{\xi }})$. • Set $j=j+1$ and go to a).

4 Determination of a distribution of point masses on a grid

4.1 Minimum separation distance between point masses

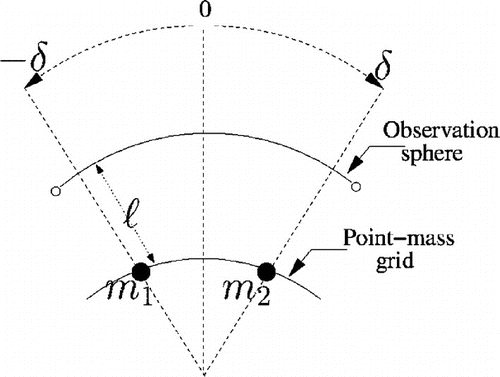
To test the robustness of the results of the reconstruction process it is instructive to start by analysing the sensibility of the identification of two point masses $({\mathit{P}}_k(r_k,{\mathit{\varphi }}_k,{\mathit{\theta }}_k),m_k),k=1,2$ (possibly with distinct masses) with respect to their separating distance and the ratio ${\displaystyle \mathit{\alpha }=\frac{r_k}{r},k=1,2}$. In our computations, we take $r=(R_m+30)\mathrm{km}$ which is the radius of an observation sphere concentric with the Earth, and we consider two point masses $({\mathit{P}}_1,m_1)$ and $({\mathit{P}}_2,m_2)$ located on a regular grid buried at a constant depth ${\mathit{\xi }}_0$. Let us denote by $V_{12}$ the potential generated by both point masses at a spacial point $\mathit{P}(\tilde{R},\mathit{\theta },\mathit{\varphi })$ located on an observation sphere which has the same centre as the Earth and a radius $\tilde{R}$. We restrict our analysis to the case where the point $\mathit{P}$ belongs to the planar section containing ${\mathit{P}}_1$, ${\mathit{P}}_2$ and the geocenter. We then have$${\displaystyle V_{12}(\tilde{R},\mathit{\theta },\mathit{\varphi })=\frac{G{m}_1}{{\ell }_1}+\frac{G{m}_2}{{\ell }_2},}$$where, as stated in (1010 $$\begin{array}{c}\hfill {\displaystyle {\ell }_k=\sqrt{r^2-2r{r}_{k}cos{\mathit{\psi }}_k+r_k^2}.}\end{array}$$10 ), ${\ell }_k=\mathit{P}{\mathit{P}}_k=\tilde{R}\sqrt{1-2\mathit{\alpha }cos{\mathit{\psi }}_k+{\mathit{\alpha }}^2}$ for $k=1,2$.

As ${\ell }_k$ depends only on the spherical distance between $\mathit{P}$ and ${\mathit{P}}_k$, we assume, without loss of generality, that the two point masses are on the same meridian, i.e. with fixed $\mathit{\varphi }$. Therefore, from (1111 $$\begin{array}{c}\hfill {\ell }_k=r\sqrt{1-2{\mathit{\alpha }}_{k}cos{\mathit{\psi }}_k+{\mathit{\alpha }}_k^2},\end{array}$$11 ) we obtain$${\displaystyle V_{12}(\tilde{R},\mathit{\theta },\mathit{\varphi })=\frac{G}{\tilde{R}}\left(\frac{m_1}{\sqrt{1-2\mathit{\alpha }cos(\mathit{\theta }-{\mathit{\theta }}_1)+{\mathit{\alpha }}^2}},+,\frac{m_2}{\sqrt{1-2\mathit{\alpha }cos(\mathit{\theta }-{\mathit{\theta }}_2)+{\mathit{\alpha }}^2}}\right).}$$Furthermore, by shifting the latitude origin to the midpoint of the mass locations, and by denoting ${\displaystyle \mathit{\delta }=\frac{{\mathit{\theta }}_1-{\mathit{\theta }}_2}{2}}$ (see Figure 1), we get ${\mathit{\psi }}_{12}=2\mathit{\delta }$ and$${\displaystyle V_{12}(\tilde{R},\mathit{\theta },\mathit{\varphi })=\frac{G}{\tilde{R}}\left(m_1,W,(\mathit{\theta }-\mathit{\delta }),+,m_2,W,(\mathit{\theta }+\mathit{\delta })\right),}$$where$$W(\mathit{\eta })=\frac{1}{\sqrt{1-2\mathit{\alpha }cos\mathit{\eta }+{\mathit{\alpha }}^2}}.$$For $\mathit{\alpha }=0.969$, we consider the following two experiments. In the first one, the two point masses are assumed to have the same (fixed) longitude $\mathit{\varphi }$ (i.e. they are positioned on the same meridian) and have different latitudes ${\mathit{\theta }}_1,{\mathit{\theta }}_2$ which vary in the interval $[1^{\circ },{10}^{\circ }]$. In the second one, the point masses are assumed to have the same (fixed) latitude (i.e. they are placed on the same parallel) $\mathit{\theta }$ and have different longitudes ${\mathit{\varphi }}_1,{\mathit{\varphi }}_2$ which vary in $[1^{\circ },{10}^{\circ }]$.

In Figure 2 we display, for equal and distinct masses, the plots of the composite potential over the arc intersecting the plane containing the two point masses and the geocenter, with the observation sphere.

Figure 1. A schematic of the positions of the two point-masses.

Figure 2. Plots of the potential on the observation sphere $(\tilde{R}=R_m+30\mathrm{k}m,R_m=6378\mathrm{k}m)$ as function of the distance between the point masses. The coordinates are given by ${\mathit{\psi }}_i={\mathit{\psi }}_0\pm n_i\mathrm{\Delta }\mathit{\psi }$ where $\mathrm{\Delta }\mathit{\psi }=0.{2308}^{\circ }$.

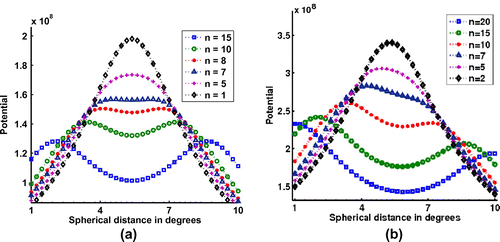
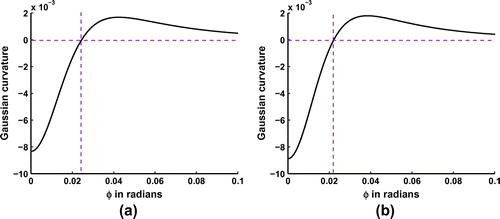
Figure 2 shows that as the distance between the point masses decreases the curve of the potential generated by two point masses changes from a two-humped form to a one-humped form. This result holds true in the case of point masses with equal and different mass values. Furthermore, there is a critical distance below which the potential generated by the two point masses appears as it is the potential generated by a single point mass located at the midpoint and with a mass equal to the sum of the masses of the two points.

This phenomenon is observed in other fields such as optics and radar signals generated by very close point sources. The Rayleigh criterion [34] is a widely accepted criterion for finding the minimum distance for which the point sources can be resolved from the signals. Consequently, for a chosen ratio $\mathit{\alpha }$, the minimal distance ${\mathit{\delta }}_{\mathrm{m}in}$ that permits us to distinguish point masses, can be determined to a prescribed precision using Rayleigh criterion.

In Figure 3, we plot the second derivative with respect to the spherical distance between the point masses. We remark that when the distance between the two point masses (in the case of equal and different masses) is less than $2\mathit{\delta }=2.{29}^{\circ }\approx 255\mathrm{k}m$, the second derivative is negative and the potential attains a local maximum at the midpoint. In this case, the identification process becomes unstable.

Figure 3. Gaussian curvature of the potential as function of the spherical distance between the point masses. (a) corresponds to the case of equal masses. (b) represents the case of two different masses.

4.2 Stability of the reconstruction process

To check the stability of point-mass determination algorithm, we proceed as follows. First, we compute the vector $\mathit{b}$ of the problem (1616 $$\begin{array}{c}\hfill {\displaystyle \underset{\mathit{\xi }\in {\mathbb{R}}^{3N},\mathit{m}\in {\mathbb{R}}^N}{min}\frac{1}{2}{\Vert \mathit{b}-A(\mathit{\xi })\mathit{m}\Vert }^2,}\end{array}$$16 ) that corresponds to the potential generated by a given distribution of point masses. Second, we add a normally distributed noise vector to the vector $\mathit{b}$ and we determine, for several values of the noise level, the masses and positions that result from the minimization problem (1616 $$\begin{array}{c}\hfill {\displaystyle \underset{\mathit{\xi }\in {\mathbb{R}}^{3N},\mathit{m}\in {\mathbb{R}}^N}{min}\frac{1}{2}{\Vert \mathit{b}-A(\mathit{\xi })\mathit{m}\Vert }^2,}\end{array}$$16 ) with the unperturbed vector $\mathit{b}$ and the perturbed one $\tilde{\mathit{b}}=\mathit{b}+\mathit{\kappa }\text{mean}(\mathit{b})\overline{\mathit{a}}$, where $\overline{\mathit{a}}$ is a vector of random normally distributed real values and $\mathit{\kappa }$ is a scalar that represents the noise level times the magnitude of $\mathit{b}$. Our experiments, which are performed on a regular grid with grid size $2.5^{\circ }$, consisted of the following two situations: a single point mass and a pair of point masses (Figure 4).

In the single point mass case, the vector $\mathit{b}$ contains the coefficients of the potential generated by $(\mathit{P}(r_0,{\mathit{\theta }}_0,{\mathit{\varphi }}_0),m_0)$. This experiment consists in recovering the point mass $\mathit{P}$ for data with and without noise. We remark that without noise we are able to recover the point mass accurately. As we add noise we observe that the recovered masses consists of a principal mass located at ${\mathit{P}}_0$, and other masses located nearby and with much smaller mass than $m_0$. We note that the sum of all identified masses is equal to $m_0$.

In the two point masses case, the vector $\mathit{b}$ contains the coefficients of the potential generated by $(\mathit{P}(r_1,{\mathit{\theta }}_1,{\mathit{\varphi }}_1),m_1)$ and $(\mathit{P}(r_1,{\mathit{\theta }}_2,{\mathit{\varphi }}_2),m_2)$. Without added noise we are able to accurately recover the masses. For a $5\%$ of noise level, we find two principal masses located at the same positions than our initial masses and some other masses nearby. However, when the noise level is $10\%$, we are not able to recover the masses.

In Table 1, we show the proportion of retrieved principal masses and the initial masses in both cases (the value $1$ in the table means that we recover the initial point masses accurately). Values lesser than $1$ are explained by the presence of other masses around the principal ones. Table 1 shows that when the noise level becomes high, our procedure fails to recover the initial masses.

Figure 4. A schematic of both cases studied in Section 4.2. In (a), we show the principal retrieved point-mass $(P_0,m_0)$ and the masses identified when adding noise. In (b), we show the second experiment dealing with identifying two point masses $(P_1,m_1)\mathrm{a}nd(P_2,m_2)$, and we see the masses identified around the principal masses. The difference between the found point masses sizes is shown in both cases.

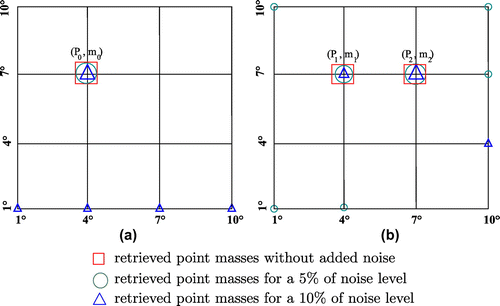
Table 1. Influence of the level of the added noise on the retrieved mass values. In the second and the third columns we give the ratios of the retrieved principal masses and the initial masses.

Noise	Single point mass	Two point masses
0%	1	(1, 1)
5%	0.966	(0.962, 1.016)
10%	1.012	(0.869, 0.982)

5 Reconstruction results for a specified geographical region

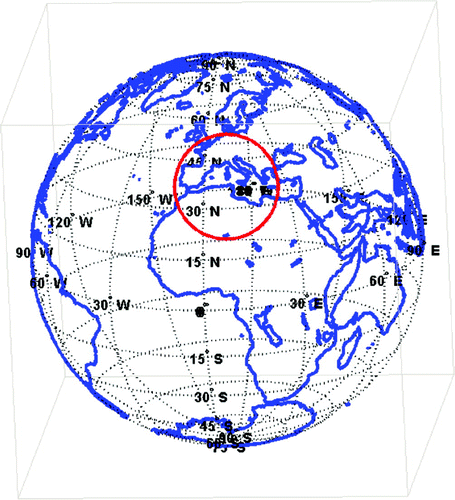
The numerical experiments presented in this section are for a domain $\mathrm{\Omega }\subset \mathbb{S}$ which corresponds to the spherical cap centred at the geographic point with coordinates $[\mathrm{L}on,\mathrm{L}at]=[{10}^{\circ },{34}^{\circ }]$, and with an epicentral distance of $2000\mathrm{k}m$, see Figure 5.

Figure 5. The geographic region under study (circle) which is a spherical cap centred at the point with longitude ${10}^{\circ }$W and latitude ${34}^{\circ }$N.

The local basis associated to the domain $\mathrm{\Omega }$ is computed using the methodology described in Section 3.2.1 for a band-width $L=30$. We have used Frederik J. Simons’ Matlab toolbox ‘Spatiospectral concentration on a sphere’.¹

Figure 6. Slepian functions for the spherical cap with $\mathrm{\Theta }\le {45}^{\circ }$ and with bandlimit $L=30$. The first two rows show the Slepian functions corresponding to the first six largest eigenvalues. The last row shows those Slepian functions which correspond to very small eigenvalues.

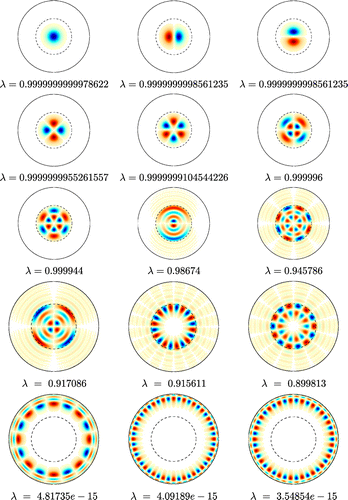
Figure 7. Spectrum of the spatio-spectral concentration problem on the spherical cap with $\mathrm{\Theta }\le {45}^{\circ }$ (domain under study) and bandwidth $L=18,20,25,30,35,40$. On the $x$-axis, we show the rank of the eigenvalues and on the $y$-axis their magnitudes.

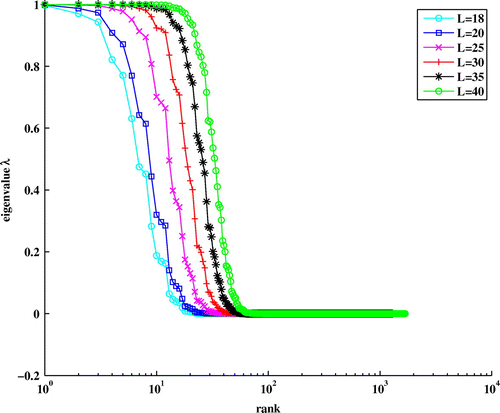
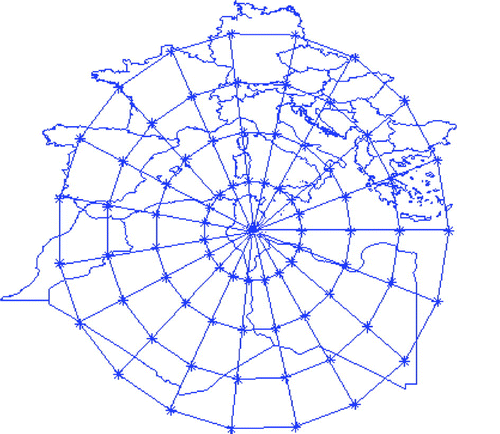
Figure 8. The grid that we use in the computations consists of a web of points regularly spaced in both the radial and tangential directions. The minimal distances between the points of this grid respect the stability condition.

In the Figure 6, we present some eigenfunctions of the operator $D$ in decreasing order of significance. Eigenfunctions that are well concentrated within the domain $\mathrm{\Omega }$ are the ones associated with the eigenvalues close to 1. Whereas those that are weakly concentrated are those associated with small eigenvalues. Accordingly, the selected basis functions are chosen to be located inside the area under study and in an appropriate neighbourhood. It should be noted that the number of significant eigenfunctions increases as the bandlimit $L$ increases. Figure 7 shows this behaviour for several bandlimit values.

We remind that our problem consists in finding point masses ${\mathit{P}}_k(m_k,{\mathit{\xi }}_k),k=1,\dots K$, defined by their masses, $m_k$, and depths, ${\mathit{\xi }}_k=R_m-r_k$, on a fixed buried grid $({\mathit{\theta }}_k,{\mathit{\varphi }}_k)$. Here $R_m=6371\mathrm{k}m$ is the Earth’s mean radius. As stated in Section 3.2.2, we use a minimization algorithm in which we alternate (until convergence) between the two minimization problems (1717 $$\begin{array}{c}\hfill {\displaystyle ({\mathcal{P}}_{\mathit{m}})\underset{m_k\ge 0,k=1,\dots ,N}{min}\frac{1}{2}{\Vert \mathit{b}-A(\mathit{\xi })\mathit{m}\Vert }^2.}\end{array}$$17 ) and (1818 $$\begin{array}{c}\hfill {\displaystyle ({\mathcal{P}}_{\mathit{\xi }})\underset{\mathit{\xi }\in {\mathbb{R}}^N}{min}\frac{1}{2}{\Vert \mathit{b}-A(\mathit{\xi })\widehat{\mathit{m}}\Vert }^2.}\end{array}$$18 ). We start with a given ${\mathit{\xi }}^{(0)}$, and for $j=0,1,\dots$ we seek ${\mathit{m}}^{(j)}$ solution of the non-negative minimization problem26 $$\begin{array}{c}\hfill \underset{m_k\ge 0}{min}\frac{1}{2}{\Vert A({\mathit{\xi }}^{(j)})\mathit{m}-\mathit{b}\Vert }^2,\end{array}$$26 and ${\mathit{\xi }}^{(j+1)}$ solution of the non-linear minimization27 $$\begin{array}{c}\hfill \underset{\mathit{\xi }}{min}\frac{1}{2}{\Vert A(\mathit{\xi }){\mathit{m}}^{(j)}-\mathit{b}\Vert }^2.\end{array}$$27 We note that (2626 $$\begin{array}{c}\hfill \underset{m_k\ge 0}{min}\frac{1}{2}{\Vert A({\mathit{\xi }}^{(j)})\mathit{m}-\mathit{b}\Vert }^2,\end{array}$$26 ) is a constrained minimization problem. To solve it we use the maximum entropy regularization method in $L^2$ proposed by Hansen [35]. In this method, we need to solve the unconstrained problem$$\underset{m_k}{min}\frac{1}{2}{\Vert A({\mathit{\xi }}^{(j)})\mathit{m}-\mathit{b}\Vert }^2+{\mathit{\alpha }}_j^2\sum _{k=1}^K{m}_{k}log(m_k)$$where ${\mathit{\alpha }}_j$ is the regularization parameter. The entropy terms $m_{k}log{m}_k$ ensure that the masses $m_k$ are positive. It has been shown that this regularization procedure is comparable to the Tikhonov regularization with non-negativity constraints.[35] Selecting an appropriate regularization parameter ${\mathit{\alpha }}_j$ is crucial and must be estimated from the given data. In our computation, we use the L-curve method [36] for estimating the optimal value for the regularization parameter.

In the following experiments the depths of all points are initialized at ${\mathit{\xi }}_0=6341\mathrm{k}m$. Our grid (Figure 8) is chosen to be a regular grid formed by four concentric circles. On each circle there are 19 grid points. This choice satisfies our stability condition related to the minimal distance separating points for which the elementary potentials are distinguishable (see Section 4.1).

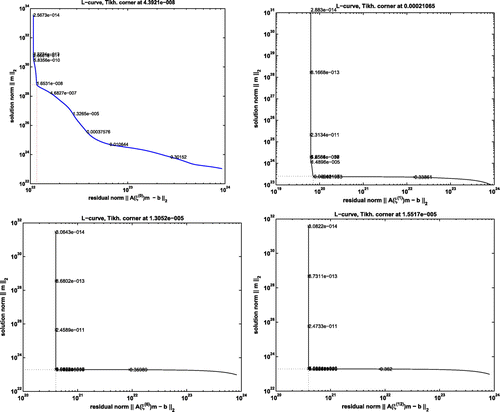
In Figure 9 we present, at different values of the iteration number $j$, the L-curve that yields the good choice of the regularization parameter at the iteration $j$. As it can be seen, all these curves clearly exhibit L-shaped graphs plotting the solution norm against the residual norm.

Figure 9. L-curves for the initial guess, and at iteration numbers 2, 6 and 12. The value of the optimal regularisation parameter is given by the value of this parameter at the corner of the L-shape.

To assess the accuracy of our reconstruction procedure we define the pointwise relative error as:$$\mathit{ϵ}(i,j)=\frac{|V(i,j)-\tilde{V}(i,j)|}{|\tilde{V}(i,j)|}$$where $V$ and $\tilde{V}$ are, respectively, the real and the point-mass gravitational potentials. Figure 10 shows the relative error $\mathit{ϵ}$ on the gravitational potential.

Figure 10. Results of pointwise relative error between the given and the approximated gravitational potentials on the studied grid.

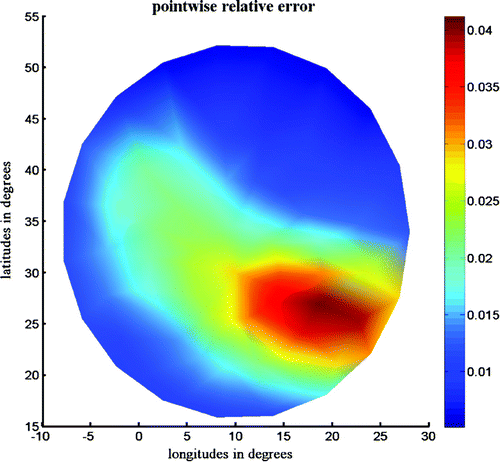
Our algorithm yields a point mass at each point of the regular grid, however only few have significant mass. We remark that the relative error values are less than $5\%$ on a small part of the domain, and less than $3\%$ on the rest of the domain.

6 Conclusion

In this paper, we have considered an important problem in geodesy, namely the inverse problem of point-mass determination relative to a limited region of the Earth. We have tackled this problem by using a localized Slepian basis. We have presented an iterative algorithm to numerically solve this problem. We have established that there is a minimum distance between the point masses that must be respected so that the identification process of the point masses works. We have computed this minimum distance of approach explicitly. We have presented several numerical examples and have studied the effects of added noise on the reconstruction process. The numerical tests of our point-mass determination algorithm on a specific geographical region show that the pointwise relative errors between the given potential and the one generated with the obtained point masses are acceptable.

Acknowledgments

The authors would like to thank the anonymous referees for their valuable comments and suggestions which helped them to improve an earlier version of this paper.

Notes

1 Available online from http://geoweb.princeton.edu/people/simons/software.html.