Nonlinear parameter identification in a corneal geometry model

Abstract

In this paper, we apply an iterative regularization technique based on Newton’s method to the ill-posed problem of parameter identification in a differential equation describing corneal surface. This equation is based on our previously derived model of corneal topography. We prove the convergence of the proposed method along with some stability estimates. When compared with real corneal data, this method gives reasonable results with error of the same order of magnitude as is introduced by measuring equipment in data acquisition. Moreover, the iteration converges very quickly to the parameters associated with the intra-ocular pressure and the elasticity of the cornea.

Keywords:

• corneal topography
• mathematical model
• parameter identification
• ill-posed problem

AMS Subject Classifications:

• 35R30
• 92C99

1 Introduction and model description

In present times, ophthalmology is one of the most rapidly developing fields in medical sciences. There is a need for a better treatment of various eye diseases since increasingly more people develop sight problems. This is mostly due to the ‘civilization’ issues present in our lives, i.e. excessive reading and computer use. Since sight is almost by anyone considered as the most important sense, keeping healthy eyes is a crucial matter. One of the most important parts of human eye is the cornea. It is a transparent, shell-like structure that constitutes a large portion of the frontal part of the eye. Together with sclera, it constitutes the outer part of the eyeball. Cornea has a layered structure with its thickness of about $0.5$ mm. It is responsible for about two-thirds of refractive power and, partly because of this, so much attention is being put in studying its nature.[1] Moreover, cornea is very durable and acts as a frontline defence against the exterior conditions. For more on biology of cornea see [2]. The beginnings of mathematical treatment of the cornea dates as back as to Helmholtz [3]. He was an inventor of ophthalmoscope, investigated optics of seeing and colour perception. For a modern mathematical consideration concerning a broad range of eye-associated issues, the reader is invited to see [4, 5]. There, fluid-mechanical models of different flows and their effect on sight disorders are proposed. The issues of tear-film dynamics and flows are considered for example in [6–8]. Particularly, Authors develop a model of so-called break-up time (BUT) which is the first moment after a blink of appearance of a dry patch on the cornea. The cited papers show that mathematics which is needed in modelling eye phenomena is far from trivial.

The development of medical equipment and new means of examination gave the need for creating mathematical descriptions and models of various phenomena associated with sight. Particularly, the shape and topography of the cornea are very important factors used in diagnosing many sight disorders. The most common corneal shape models that are presently in use are based on surfaces of revolution generated by conic sections (see [9, 10]). Unfortunately these models, although very useful and accurate, lack the physical motivation what makes them conceptually not fully justified. In that case, an usual attempt on modelling cornea is made by creating the best-fit ellipsoid to the surface of the cornea. The calculated shape parameters are then used in further reasoning (see e.g. [11]). Another group of corneal topography models consists of those based on shell theory and/or finite-element method (e.g. [12, 13]). These models are sometimes too complex to be readily computed and used in real-world applications. Nevertheless, they can serve many purposes such as reconstruction of the corneal surface by the eye measurements. A large number of scientists use the Zernike orthogonal polynomials to describe the shape of the cornea (see e.g. [14, 15]). These polynomials are orthogonal with respect to a certain scalar product and can be used to describe aberrations in (organic) lens. The advantage of these polynomials is that they are indexed by parameters which have a straightforward physical meaning (see [16, 17]). Apart from Zernike, Bessel functions have also been used for similar aim.[18] Also, adaptive techniques of approximating corneal surfaces are also being used.[19]

In [20] we have proposed a new mathematical model of a human cornea. This model was further improved in [21]. We have derived the following PDE that governs the elevation $h$ of the cornea over its domain $\mathrm{\Omega }$1 $$\begin{array}{c}\hfill -\mathrm{\Delta }h+ah=\frac{b}{\sqrt{1+{∥,\mathrm{\nabla },h∥}^2}}{\mathrm{in}\mathrm{\Omega },h|}_{\mathit{\partial }\mathrm{\Omega }}=0,\end{array}$$1 where $a$ and $b$ are nonnegative, dimensionless constants related to the tension $T$, intra-ocular pressure $P$ and elasticity constant $k$ through2 $$\begin{array}{c}\hfill a:=\frac{k{R}^2}{T},b:=\frac{PR}{T}.\end{array}$$2 Here, $h=h(r)$ and $r$ are dimensionless quantities scaled with respect to the typical corneal radius $R$ (which is on the average of about $6$ mm). The boundary condition says that the cornea has a rim at $\mathit{\partial }\mathrm{\Omega }$. This PDE has been derived by describing the corneal surface as a thin membrane with constant tension $T$, elastic force proportional to the elevation $h$ and a force caused by the intra-ocular pressure $P$ acting normally to the surface. Assumption that $a$ and $b$ are constant (hence the pressure is also constant throughout the whole cornea) suggests that we should look for an axisymmetric solution. This setting can be thought as a zero-order perturbation approximation to the real situation, where cornea is asymmetric and aspherical. This was partially justified and investigated in [22], where the inverse problem associated with variable $b$ was elaborated and shown that corrections to the axisymmetric topography are of higher order. Another simplifying assumption we make is that the pressure–force acts along the $z$-direction and not in the direction of the normal vector. From the derivation in [21], it can be seen that this clears off the square root on right-hand side of (11 $$\begin{array}{c}\hfill -\mathrm{\Delta }h+ah=\frac{b}{\sqrt{1+{∥,\mathrm{\nabla },h∥}^2}}{\mathrm{in}\mathrm{\Omega },h|}_{\mathit{\partial }\mathrm{\Omega }}=0,\end{array}$$1 ) (square root is a cosine of the angle subtended between $z$-axis and normal vector). This is not a very severe assumption, since we can assume that the corneal radius of curvature is small. This can be tentatively justified by a crude estimate: typical elevation of the cornea is about $2$ mm and its radius $6$ mm. This gives $∥,\mathrm{\nabla },h∥\approx 1/3$, which implies that3 $$\begin{array}{c}\hfill \frac{1}{\sqrt{1+{∥,\mathrm{\nabla },h∥}^2}}\approx 0.95,\end{array}$$3 which is close to $1$.

With $h=h(r)$, we get an ODE for the corneal cross-section:4 $$\begin{array}{c}\hfill -\frac{1}{r}\frac{d}{dr}\left(r,\frac{dh}{dr}\right)+ah\approx b,0\le r\le 1,\end{array}$$4 with boundary conditions5 $$\begin{array}{c}\hfill h^{\prime }(0)=0,h(1)=0.\end{array}$$5 The condition $h(1)=0$ is obvious since we want cornea to have a rim at $r=1$ and $h^{\prime }(0)=0$ gives us a smooth at origin, nonsingular surface of revolution. Equation (44 $$\begin{array}{c}\hfill -\frac{1}{r}\frac{d}{dr}\left(r,\frac{dh}{dr}\right)+ah\approx b,0\le r\le 1,\end{array}$$4 ) can be readily solved yielding6 $$\begin{array}{c}\hfill h_0(r)=\frac{b}{a}\left(1,-,\frac{I_0(\sqrt{a}r)}{I_0(\sqrt{a})}\right),\end{array}$$6 where $I_0$ is a Modified Bessel Function of the First Kind. We note that when fitting with the real corneal data we have to consider both interior and exterior corneal surfaces. This is due to the fact that cornea has a thickness. Also, we remark that in the future work, thickness will be incorporated into our differential equation model.

An easy calculation can give us the estimate on the error that is made when neglecting the square root. In [21] it was shown that the solution to the problem (44 $$\begin{array}{c}\hfill -\frac{1}{r}\frac{d}{dr}\left(r,\frac{dh}{dr}\right)+ah\approx b,0\le r\le 1,\end{array}$$4 )–(55 $$\begin{array}{c}\hfill h^{\prime }(0)=0,h(1)=0.\end{array}$$5 ) can be stated in terms of the integral equation7 $$\begin{array}{c}\hfill h(r)=b{\int }_0^1\frac{G(r,t)}{\sqrt{1+h^{\prime }{(t)}^2}}dt,\end{array}$$7 while (66 $$\begin{array}{c}\hfill h_0(r)=\frac{b}{a}\left(1,-,\frac{I_0(\sqrt{a}r)}{I_0(\sqrt{a})}\right),\end{array}$$6 ) can be rewritten as:8 $$\begin{array}{c}\hfill h_0(r)=b{\int }_0^{1}G(r,t)dt,\end{array}$$8 where $G=G(r,t)$ is a Green’s function for our problem. Taking the difference we can estimate9 $$\begin{array}{c}\hfill \left|h,(r),-,h_0,(r)\right|\le b{\int }_0^{1}G(r,t)\left|\frac{1}{\sqrt{1+h^{\prime }{(t)}^2}},-,1\right|dt\le b{\int }_0^{1}G(r,t)dt=h_0(r).\end{array}$$9 Thus making the assumption of pressure acting vertically introduces a maximal error of ${∥,h,-,h_0∥}_{\infty }\le h_0(0)=b/a\left(1,-,1,/,I_0,(\sqrt{a})\right)$. This is an a-priori theoretical estimate. We can make a more realistic calculation by utilizing the typical corneal sizes and (33 $$\begin{array}{c}\hfill \frac{1}{\sqrt{1+{∥,\mathrm{\nabla },h∥}^2}}\approx 0.95,\end{array}$$3 )10 $$\begin{array}{c}\hfill \left|h,(r),-,h_0,(r)\right|\le b{\int }_0^{1}G(r,t)\left|\frac{1}{\sqrt{1+h^{\prime }{(t)}^2}},-,1\right|dt\approx 0.05h_0(r),\end{array}$$10 which would give us ${∥,h,-,h_0∥}_{\infty }\approx 0.05h_0(0)\approx 0.1$ mm, where we took the typical corneal deflection to be equal to $2$ mm. For the accuracy of the first approximation we can thus safely neglect the square root in (44 $$\begin{array}{c}\hfill -\frac{1}{r}\frac{d}{dr}\left(r,\frac{dh}{dr}\right)+ah\approx b,0\le r\le 1,\end{array}$$4 ).

In this paper, we are mainly concerned with determining constants $a$ and $b$ in (66 $$\begin{array}{c}\hfill h_0(r)=\frac{b}{a}\left(1,-,\frac{I_0(\sqrt{a}r)}{I_0(\sqrt{a})}\right),\end{array}$$6 ) when the solution $h$ is known (usually with a noise). This is one example of so-called inverse problems (as opposed to the Direct Problems, here: solving the ODE (44 $$\begin{array}{c}\hfill -\frac{1}{r}\frac{d}{dr}\left(r,\frac{dh}{dr}\right)+ah\approx b,0\le r\le 1,\end{array}$$4 )). In applications one usually wants to make an identification of various parameters in differential equations (see [23]). In our case, knowing $a$ and $b$ will give us an approximation to the corneal topography. A problem of finding (possibly nonconstant) $b$ when $a$ is known was solved in [22].

Inverse problems are usually ill-posed, that is they can have no solutions, have a nonunique solution or be unstable with respect to the noise level in input data.[24] In our case we cannot expect that the cornea is mathematically described precisely by (66 $$\begin{array}{c}\hfill h_0(r)=\frac{b}{a}\left(1,-,\frac{I_0(\sqrt{a}r)}{I_0(\sqrt{a})}\right),\end{array}$$6 ) hence generally our inverse problem will have no solution. The simplest way of determining unknowns $a$ and $b$ in (66 $$\begin{array}{c}\hfill h_0(r)=\frac{b}{a}\left(1,-,\frac{I_0(\sqrt{a}r)}{I_0(\sqrt{a})}\right),\end{array}$$6 ) is by using maximum deflection $h(0)$ and central radius of curvature $\mathit{\rho }(0)$ as was done in [21]. However, this method is not reliable because $h(0)$ depends on a specific reference level and could be determined ambiguously. Moreover, it can give serious errors because of instability.

Due to the nonuniqueness there is a need of defining some generalized solution to the inverse problem. This is usually done by looking for the unique least-squares solution.[25] Moreover, we often do not know the exact function $h$. When doing measurements some noise $\mathit{\delta }$ would always be present, thus we have only $h^{\mathit{\delta }}$ at our disposal that is,11 $$\begin{array}{c}\hfill ∥,h,-,h^{\mathit{\delta }}∥\le \mathit{\delta }.\end{array}$$11 It is natural to expect a stable dependence of parameters $a^{\mathit{\delta }}$ and $b^{\mathit{\delta }}$ on the noise level $\mathit{\delta }$. Small errors in measurement should give small errors in parameters. In parameter identification problems usually this is not the case and we have serious instabilities in the obtained solutions. Such parameters are not of much use in applications.

We shall put our inverse problem in a slightly more abstract setting of $L^2$ space and propose a method of determining the unique solution to the inverse problem of the type we are concerned of. To overcome these problems, many regularization methods have been developed (see e.g. [26]). We present a variation of one of them which gives us a stable and unique solution to our parameter identification problem.

2 Analytical results

In this section, we propose an iterative regularization method and prove some stability results. First, we introduce the following family of linear operators defined by12 $$\begin{array}{c}\hfill \left(F_a,b\right)(x):=bf(a;x),\end{array}$$12 where $f(a;·)\in L^2\left([,0,,,1,]\right)$ is a fixed function with possibly nonlinear dependence on $a$. Here we assume that $a\in D(a)\subseteq \mathbb{R}$ ($D(a)$ compact) and $b\in \mathbb{R}$, hence13 $$\begin{array}{c}\hfill {\forall }_{a\in D(a)}{F}_a:\mathbb{R}\to L^2\left([,0,,,1,]\right).\end{array}$$13 Moreover, we assume that the family of operators $F_a$ depends smoothly (up to the second order) on $a$.

We treat the real line $\mathbb{R}$ as a Hilbert space with multiplication as a scalar product. The adjoint $F_a^{\ast }:L^2\left([,0,,,1,]\right)\to \mathbb{R}$ of $F_a$ is defined by14 $$\begin{array}{c}\hfill 〈F_a,b,,,g〉=b·F_a^{\ast }g,\end{array}$$14 for all $g\in L^2\left([,0,,,1,]\right)$. Thus, by (1212 $$\begin{array}{c}\hfill \left(F_a,b\right)(x):=bf(a;x),\end{array}$$12 ), we have $F_a^{\ast }g=〈f,(,a,;,·,),,,g〉$. It is straightforward to observe that15 $$\begin{array}{c}\hfill N_a:=∥,F_a∥=∥,F_a^{\ast }∥=∥,f,(,a,;,·,)∥,\end{array}$$15 where appropriate types of norms are understood.

By the inverse problem we will understand the determination of $a$ and $b$ from the equation16 $$\begin{array}{c}\hfill F_{a}b=h,\end{array}$$16 where $h\in L^2\left([,0,,,1,]\right)$ is a known function (in our case $h$ will describe the corneal geometry and thus $h$ must satisfy the boundary condition (55 $$\begin{array}{c}\hfill h^{\prime }(0)=0,h(1)=0.\end{array}$$5 )). It is not expected that the cornea will be exactly described by the function $bf(a,·)$ that is, $h$ does not necessarily have to be in the range of $F_a$. Moreover, $h$ is always measured with noise $\mathit{\delta }$ which also has to be taken into account. To make precise what we understand by an inverse problem, we must first make a distinction between the well-posed and ill-posed problems (in the Hadamard sense, see e.g. [27]).

Definition 2.1

A mathematical problem (for example a differential or algebraic equation) is called a well-posed problem if it has all of the following properties

• it has a solution,

• it has only one solution,

• it is continuous with respect to the perturbations in the initial data (stability).

If a problem is not well-posed it is called ill-posed. Inverse problems are usually ill-posed thus are more difficult to analyse and use in applications than the well-posed ones.

The Equation (1616 $$\begin{array}{c}\hfill F_{a}b=h,\end{array}$$16 ) is linear in $b$ and generally nonlinear in $a$. Assume for now that $a$ is fixed and consider only finding $b$ as a solution to the linear equation. We look for a generalized least-squares solution, that is $b^{†}$ is such solution when17 $$\begin{array}{c}\hfill ∥,F_a,b^{†},-,h∥=min\{∥,F_a,b,-,h∥:b\in \mathbb{R}\}.\end{array}$$17 Of course, when $b^{†}$ is an exact solution to (1616 $$\begin{array}{c}\hfill F_{a}b=h,\end{array}$$16 ), the left-hand side of (1717 $$\begin{array}{c}\hfill ∥,F_a,b^{†},-,h∥=min\{∥,F_a,b,-,h∥:b\in \mathbb{R}\}.\end{array}$$17 ) is zero, thus it is also a least-squares solution. It can be shown (see e.g. [25]) that the sufficient and necessary condition for $b^{†}$ to be the unique least-squares solution to (1616 $$\begin{array}{c}\hfill F_{a}b=h,\end{array}$$16 ) is18 $$\begin{array}{c}\hfill F_a^{\ast }{F}_a{b}^{†}=F_a^{\ast }h\mathrm{or}{F}_a^{\ast }(F_a{b}^{†}-h)=0.\end{array}$$18 From (1818 $$\begin{array}{c}\hfill F_a^{\ast }{F}_a{b}^{†}=F_a^{\ast }h\mathrm{or}{F}_a^{\ast }(F_a{b}^{†}-h)=0.\end{array}$$18 ) using (1212 $$\begin{array}{c}\hfill \left(F_a,b\right)(x):=bf(a;x),\end{array}$$12 ) and (), we obtain19 $$\begin{array}{c}\hfill b^{†}=\frac{1}{N_a^2}〈f,(,a,;,·,),,,h〉.\end{array}$$19 It is evident that this least-squares solution depends on parameter $a$ and $b^{†}=b^{†}(a)$ is uniquely determined when $a$ is known. Now, the solution to the full nonlinear problem (1616 $$\begin{array}{c}\hfill F_{a}b=h,\end{array}$$16 ) is reduced to finding only one parameter, namely $a$. To simplify notation let us define a nonlinear operator20 $$\begin{array}{c}\hfill F(a):=F_a{b}^{†}(a)\end{array}$$20 and consider finding least-squares solution $a^{†}$ to the problem $F(a)=h$. Due to the compactness of $D(a)$, the existence of this solution is provided. We will proceed by a method known as Output Least Squares (see [23]). This iterative method takes from Newton’s tangent method of finding roots of nonlinear equations. The difference is that we look for a generalized least-squares solution and not the exact one.

Fix an initial guess of unknown parameter $a_0$. We will try to find an increase $\mathrm{\Delta }{a}_0$ such that $h=F(a_0+\mathrm{\Delta }{a}_0)=F(a_1)$. We can write21 $$\begin{array}{c}\hfill h=F(a_1)=F(a_0+\mathrm{\Delta }{a}_0)=F(a_0)+F^{\prime }(a_0)\mathrm{\Delta }{a}_0+r(a_0,\mathrm{\Delta }{a}_0),\end{array}$$21 where $F^{\prime }(a_0):\mathbb{R}\to L^2\left([,0,,,1,]\right)$ is a Fr$\acute{e}$chet derivative, which is a linear operator and remainder $r(a_0,\mathrm{\Delta }{a}_0)=o(\mathrm{\Delta }{a}_0)$. In our simple case of one-dimensional operator (1212 $$\begin{array}{c}\hfill \left(F_a,b\right)(x):=bf(a;x),\end{array}$$12 ), the Fr$\acute{e}$chet derivative is just22 $$\begin{array}{c}\hfill (F^{\prime }(a)c)(x)=c·\left(\frac{\mathit{\partial }}{\mathit{\partial }a},F,(a)\right)(x)=c·\frac{\mathit{\partial }}{\mathit{\partial }a}\left(b^{†},(a),f,(a;x)\right).\end{array}$$22 It is easy to see that the adjoint $F^{\prime }{(a)}^{\ast }:L^2\left([,0,,,1,]\right)\to \mathbb{R}$ has a form23 $$\begin{array}{c}\hfill F^{\prime }{(a)}^{\ast }g=〈\frac{\mathit{\partial }}{\mathit{\partial }a},\left(b^{†},(a),f,(a;·)\right),,,g〉\end{array}$$23 with the following equalities in norms24 $$\begin{array}{c}\hfill M_a:=∥,F^{\prime },(a)∥=∥,F^{\prime },{(a)}^{\ast }∥=∥,\frac{\mathit{\partial }}{\mathit{\partial }a},\left(b^{†},(a),f,(a;·)\right)∥.\end{array}$$24 We look for $\mathrm{\Delta }{a}_0$ as a least-squares solution to (2121 $$\begin{array}{c}\hfill h=F(a_1)=F(a_0+\mathrm{\Delta }{a}_0)=F(a_0)+F^{\prime }(a_0)\mathrm{\Delta }{a}_0+r(a_0,\mathrm{\Delta }{a}_0),\end{array}$$21 ), thus discarding remainder we want to have25 $$\begin{array}{c}\hfill F^{\prime }{(a_0)}^{\ast }\left(h,-,F,(,a_0,)\right)\approx F^{\prime }{(a_0)}^{\ast }{F}^{\prime }(a_0)\mathrm{\Delta }{a}_0.\end{array}$$25 Now, using (2222 $$\begin{array}{c}\hfill (F^{\prime }(a)c)(x)=c·\left(\frac{\mathit{\partial }}{\mathit{\partial }a},F,(a)\right)(x)=c·\frac{\mathit{\partial }}{\mathit{\partial }a}\left(b^{†},(a),f,(a;x)\right).\end{array}$$22 ), () and (2424 $$\begin{array}{c}\hfill M_a:=∥,F^{\prime },(a)∥=∥,F^{\prime },{(a)}^{\ast }∥=∥,\frac{\mathit{\partial }}{\mathit{\partial }a},\left(b^{†},(a),f,(a;·)\right)∥.\end{array}$$24 ) we get26 $$\begin{array}{c}\hfill \mathrm{\Delta }{a}_0=\frac{1}{M_{a_0}^2}{F}^{\prime }{(a_0)}^{\ast }\left(h,-,F,(,a_0,)\right).\end{array}$$26 Using $a_1=a_0+\mathrm{\Delta }{a}_0$ as a new initial guess, we can continue this procedure and propose an iterative scheme27 $$\begin{array}{c}\hfill a_{n+1}=a_n+\mathrm{\Delta }{a}_n,\mathrm{\Delta }{a}_n=\frac{1}{M_{a_n}^2}{F}^{\prime }{(a_n)}^{\ast }\left(h,-,F,(,a_n,)\right).\end{array}$$27 Proposed algorithm can be summarized in the following lines, where all the formulas are consequences of (1919 $$\begin{array}{c}\hfill b^{†}=\frac{1}{N_a^2}〈f,(,a,;,·,),,,h〉.\end{array}$$19 ), (2020 $$\begin{array}{c}\hfill F(a):=F_a{b}^{†}(a)\end{array}$$20 ), (1212 $$\begin{array}{c}\hfill \left(F_a,b\right)(x):=bf(a;x),\end{array}$$12 ), () and (2727 $$\begin{array}{c}\hfill a_{n+1}=a_n+\mathrm{\Delta }{a}_n,\mathrm{\Delta }{a}_n=\frac{1}{M_{a_n}^2}{F}^{\prime }{(a_n)}^{\ast }\left(h,-,F,(,a_n,)\right).\end{array}$$27 ).

(1)	Let$$F^{\prime }(a)(x):=\frac{\mathit{\partial }}{\mathit{\partial }a}\left(\frac{⟨f(a,·),h⟩}{{∥,f,(,a,,,·,)∥}^2},f,(a,x)\right).$$
(2)	Chose a starting value $a_0$ and set $n=0$.
(3)	Compute $a_{n+1}=a_n+\mathrm{\Delta }{a}_n$, where$$\mathrm{\Delta }{a}_n=\frac{⟨h-f(a_n,·),F^{\prime }(a_n)⟩}{{∥,F^{\prime },(a_n)∥}^2}.$$
(4)	Let $n\to n+1$.
(5)	Repeat (3)–(4) until the desired accuracy $|a_{n+1}-a_n|<\mathit{ϵ}$ is achieved.

The following theorem establishes scheme’s convergence to the least-squares solution $a^{†}$ of $F(a)=h$.

Theorem 2.2

Assume that28 $$\begin{array}{c}\hfill \underset{s,t\in D(a)}{sup}\frac{∥,F^{″},(s)∥}{M_t^2}<{∥,h,-,F,(,a^{†},)∥}^{-1},\end{array}$$28 then there exists a neighbourhood of $a^{†}$ in which the iterative scheme (2727 $$\begin{array}{c}\hfill a_{n+1}=a_n+\mathrm{\Delta }{a}_n,\mathrm{\Delta }{a}_n=\frac{1}{M_{a_n}^2}{F}^{\prime }{(a_n)}^{\ast }\left(h,-,F,(,a_n,)\right).\end{array}$$27 ) is convergent to the least-squares solution of $F(a)=h$.

Remark 1

By $F^{″}(a):{\mathbb{R}}^2\to L^2\left([,0,,,1,]\right)$, we mean a bilinear functional $F^{″}(a)(k,l)=k·l·{\mathit{\partial }}^2/\mathit{\partial }{a}^{2}F(a)$. It is straightforward to see that $∥,F^{″},(a),(k,l)∥=\left|k\right|\left|l\right|∥,{\mathit{\partial }}^2,/,\mathit{\partial },a^2,,F,(a)∥$. Thus we write $∥,F^{″},(a)∥=∥,{\mathit{\partial }}^2,/,\mathit{\partial },a^2,\left(b^{†},(a),f,(a;x)\right)∥$. We also will make an abbreviation by writing $F^{″}(a)k^2$ instead of $F^{″}(a)(k,k)$.

Remark 2

The assumption (2828 $$\begin{array}{c}\hfill \underset{s,t\in D(a)}{sup}\frac{∥,F^{″},(s)∥}{M_t^2}<{∥,h,-,F,(,a^{†},)∥}^{-1},\end{array}$$28 ) is not very severe because we expect that the residue $∥,h,-,F,(,a^{†},)∥$ would usually be small (for the method to be useful). Of course in applications we do not know $a^{†}$, but sometimes we can at least try to guess its approximate location. Thus, due to minimality of $∥,h,-,F,(,a^{†},)∥$, we can impose a stronger assumption29 $$\begin{array}{c}\hfill \underset{s,t\in D(a)}{sup}\frac{∥,F^{″},(s)∥}{M_t^2}<{∥,h,-,F,(,a_0,)∥}^{-1},\end{array}$$29 which implies (2828 $$\begin{array}{c}\hfill \underset{s,t\in D(a)}{sup}\frac{∥,F^{″},(s)∥}{M_t^2}<{∥,h,-,F,(,a^{†},)∥}^{-1},\end{array}$$28 ).

Proof

Denote an error of approximation by $e_n:=a^{†}-a_n$. We will show that $e_n\to 0$. We have30 $$\begin{array}{c}\hfill e_{n+1}=a^{†}-a_{n+1}=e_n-\mathrm{\Delta }{a}_n=\frac{1}{M_{a_n}^2}\left(M_{a_n}^2,e_n,-,F^{\prime },{(a_n)}^{\ast },(h-F(a_n))\right).\end{array}$$30 Observe that31 $$\begin{array}{c}\hfill F(a^{†})-F(a_n)=F^{\prime }(a_n)e_n+\frac{1}{2}{F}^{″}({\mathit{\alpha }}_n)e_n^2,\end{array}$$31 hence application of $F^{\prime }{(a_n)}^{\ast }$ gives32 $$\begin{array}{c}\hfill M_{a_n}^2{e}_n=F^{\prime }{(a_n)}^{\ast }\left(F,(a^{†}),-,F,(a_n)\right)-\frac{1}{2}{F}^{\prime }{(a_n)}^{\ast }{F}^{″}({\mathit{\alpha }}_n)e_n^2,\end{array}$$32 where ${\mathit{\alpha }}_n$ is between $a^{†}$ and $a_n$. We can rewrite (3030 $$\begin{array}{c}\hfill e_{n+1}=a^{†}-a_{n+1}=e_n-\mathrm{\Delta }{a}_n=\frac{1}{M_{a_n}^2}\left(M_{a_n}^2,e_n,-,F^{\prime },{(a_n)}^{\ast },(h-F(a_n))\right).\end{array}$$30 ) as33 $$\begin{array}{c}\hfill e_{n+1}=-\frac{1}{M_{a_n}^2}\left(F^{\prime },{(a_n)}^{\ast },(h-F(a^{†})),+,\frac{1}{2},F^{\prime },{(a_n)}^{\ast },F^{″},({\mathit{\alpha }}_n),e_n^2\right).\end{array}$$33 We are looking for the least-squares solution $a^{†}$, thus the normal equation $F^{\prime }{(a^{†})}^{\ast }\left(h,-,F,(,a^{†},)\right)=0$ must be fulfilled (see [25]). This is the particular difference between the classical proof of Newton’s tangent method, where the exactness of the solution is utilized. Therefore, writing34 $$\begin{array}{c}\hfill F^{\prime }{(a_n)}^{\ast }(h-F(a^{†}))=〈\frac{\mathit{\partial }}{\mathit{\partial }a},F,(a_n),,,h,-,F,(a^{†})〉=〈\frac{\mathit{\partial }}{\mathit{\partial }a},F,(a^{†}),-,\frac{{\mathit{\partial }}^2}{\mathit{\partial }{a}^2},F,({\mathit{\beta }}_n),e_n,,,h,-,F,(a^{†})〉\end{array}$$34 we finally arrive at35 $$\begin{array}{c}\hfill e_{n+1}=\left(\frac{〈\frac{{\mathit{\partial }}^2}{\mathit{\partial }{a}^2},F,({\mathit{\beta }}_n),,,h,-,F,(a^{†})〉}{M_{a_n}^2},-,\frac{1}{2},\frac{F^{\prime }{(a_n)}^{\ast }{F}^{″}({\mathit{\alpha }}_n)}{M_{a_n}^2},e_n\right)e_n,\end{array}$$35 which gives36 $$\begin{array}{c}\hfill \left|e_{n+1}\right|\le \left(\underset{s,t\in D(a)}{sup},\frac{∥,F^{″},(s)∥}{M_t^2},∥,h,-,F,(,a^{†},)∥,+,\frac{1}{2},\underset{s,t\in D(a)}{sup},\frac{∥,F^{″},(s)∥}{M_t},\left|e_n\right|\right)\left|e_n\right|.\end{array}$$36 From (2828 $$\begin{array}{c}\hfill \underset{s,t\in D(a)}{sup}\frac{∥,F^{″},(s)∥}{M_t^2}<{∥,h,-,F,(,a^{†},)∥}^{-1},\end{array}$$28 ) we have ${sup}_{s,t\in D(a)}\frac{∥,F^{″},(s)∥}{M_t}<{∥,h,-,F,(,a^{†},)∥}^{-1}{sup}_{t\in D(a)}{M}_t<\infty$. Thus, when $\left|e_n\right|$ is sufficiently small, that is, if we start our iteration suitably close to $a^{†}$, the assumption (2828 $$\begin{array}{c}\hfill \underset{s,t\in D(a)}{sup}\frac{∥,F^{″},(s)∥}{M_t^2}<{∥,h,-,F,(,a^{†},)∥}^{-1},\end{array}$$28 ) implies that37 $$\begin{array}{c}\hfill \left|e_{n+1}\right|\le C_h\left|e_n\right|,\end{array}$$37 where $0\le C_h<1$. This means that $e_n\to 0$ which is what we had to show. $\square$

Now, we have a method of determining $a^{†}$ and $b^{†}$ as a least-squares solutions to $F_{a}b=h$. Next, we will show some stability results. When we know only noisy data $h^{\mathit{\delta }}$, the iteration is convergent to some $a^{\mathit{\delta }}$ which usually is different from $a^{†}$. This produces an error bound which grows with $n$. The question arises in what moment should we stop iteration (2727 $$\begin{array}{c}\hfill a_{n+1}=a_n+\mathrm{\Delta }{a}_n,\mathrm{\Delta }{a}_n=\frac{1}{M_{a_n}^2}{F}^{\prime }{(a_n)}^{\ast }\left(h,-,F,(,a_n,)\right).\end{array}$$27 ) to have the smallest bound possible. The next Theorem gives an a-priori stopping rule.

Theorem 2.3

Assume we have a noisy data $∥,h,-,h^{\mathit{\delta }}∥\le \mathit{\delta }$, then for solutions $(a^{\mathit{\delta }},b^{\mathit{\delta }})$ to $F_{a}b=h^{\mathit{\delta }}$ we have the following estimates38 $$\begin{array}{c}\hfill \left|a_{n_{\ast }(\mathit{\delta })}^{\mathit{\delta }},-,a^{†}\right|=O({\mathit{\delta }}^{\mathit{\nu }}),\left|b_{n_{\ast }(\mathit{\delta })}^{\mathit{\delta }},-,b^{†}\right|=O({\mathit{\delta }}^{\mathit{\nu }})as\mathit{\delta }\to 0,\end{array}$$38 where $0<\mathit{\nu }\le 1$ is some $h$-dependent constant and $n_{\ast }(\mathit{\delta })$ is an optimal stopping moment chosen to satisfy39 $$\begin{array}{c}\hfill n_{\ast }(\mathit{\delta })=O\left(log,\frac{1}{\mathit{\delta }}\right).\end{array}$$39

Proof

Let $a_n$ and $a_n^{\mathit{\delta }}$ be sequences (2727 $$\begin{array}{c}\hfill a_{n+1}=a_n+\mathrm{\Delta }{a}_n,\mathrm{\Delta }{a}_n=\frac{1}{M_{a_n}^2}{F}^{\prime }{(a_n)}^{\ast }\left(h,-,F,(,a_n,)\right).\end{array}$$27 ) convergent to $a^{†}$ and $a^{\mathit{\delta }}$, respectively. We will use the following fundamental estimate40 $$\begin{array}{c}\hfill \left|a_n^{\mathit{\delta }},-,a^{†}\right|\le \left|a_n^{\mathit{\delta }},-,a_n\right|+\left|a_n,-,a^{†}\right|,\end{array}$$40 where the error decomposes into two terms: one corresponding to the noise and the other connected with the convergence rate of the iterative method. We can take $a_0=a_0^{\mathit{\delta }}$ and estimate the first term as follows:41 $$\begin{array}{cc}\hfill \left|a_n^{\mathit{\delta }},-,a_n\right|& \le \sum _{j=0}^{n-1}\left|\frac{1}{M_{a_j}^2},F^{\prime },{(a_j)}^{\ast },\left(h,-,F,(,a_j,)\right),-,\frac{1}{M_{a_j^{\mathit{\delta }}}^2},F^{\prime },{(a_j^{\mathit{\delta }})}^{\ast },\left(h^{\mathit{\delta }},-,F,(a_j^{\mathit{\delta }})\right)\right|\hfill \\ \hfill & \le \sum _{j=0}^{n-1}\left|\left(\frac{1}{M_{a_j}^2},F^{\prime },{(a_j)}^{\ast },-,\frac{1}{M_{a_j^{\mathit{\delta }}}^2},F^{\prime },{(a_j^{\mathit{\delta }})}^{\ast }\right),\left(h,-,F,(,a_j,)\right)\right|\hfill \\ \hfill & +\sum _{j=0}^{n-1}\frac{1}{M_{a_j^{\mathit{\delta }}}^2}\left|F^{\prime },{(a_j^{\mathit{\delta }})}^{\ast },\left(h^{\mathit{\delta }},-,h\right)\right|+\sum _{j=0}^{n-1}\frac{1}{M_{a_j^{\mathit{\delta }}}^2}\left|F^{\prime },{(a_j^{\mathit{\delta }})}^{\ast },\left(F,(a_j^{\mathit{\delta }}),-,F,(a_j)\right)\right|.\hfill \end{array}$$41 Using the fact that $F(a)$ and $F^{\prime }(a)$ are Lipschitz continuous (since they have bounded $a$-derivatives) with respect to $a$ and that $D(a)$ is a compact set, we have42 $$\begin{array}{cc}& ∥,F,(a_j^{\mathit{\delta }}),-,F,(a_j)∥\le M_{a_j^{\ast }}\left|a_j^{\mathit{\delta }},-,a_j\right|\le \underset{a\in D(a)}{sup}{M}_a\left|a_j^{\mathit{\delta }},-,a_j\right|,\hfill \\ \hfill & ∥,\frac{1}{M_{a_j}^2},F^{\prime },{(a_j)}^{\ast },-,\frac{1}{M_{a_j^{\mathit{\delta }}}^2},F^{\prime },{(a_j^{\mathit{\delta }})}^{\ast }∥∥,h,-,F,(,a_j,)∥\le E\left|a_j^{\mathit{\delta }},-,a_j\right|,\hfill \end{array}$$42 where we used the fact that $∥,h,-,F,(,a_j,)∥$ is bounded with respect to $j$ (due to compactness of $D(a)$) and put it along other estimates under $E$. We can further write43 $$\begin{array}{c}\hfill \left|a_n^{\mathit{\delta }},-,a_n\right|\le C\left(n,\mathit{\delta },+,\sum _{j=1}^{n-1},\left|a_j^{\mathit{\delta }},-,a_j\right|\right),\end{array}$$43 where $C$ is greatest constant of the following44 $$\begin{array}{c}\hfill \underset{s,t\in D(a)}{sup}{M}_t/M_s+E,\underset{t\in D(a)}{sup}1/M_t.\end{array}$$44 Using (4343 $$\begin{array}{c}\hfill \left|a_n^{\mathit{\delta }},-,a_n\right|\le C\left(n,\mathit{\delta },+,\sum _{j=1}^{n-1},\left|a_j^{\mathit{\delta }},-,a_j\right|\right),\end{array}$$43 ) it is easy to see that $\left|a_1^{\mathit{\delta }},-,a_1\right|\le C\mathit{\delta }$ and $\left|a_2^{\mathit{\delta }},-,a_2\right|\le (C^2+2C)\mathit{\delta }$. By induction we can finally prove that45 $$\begin{array}{c}\hfill \left|a_n^{\mathit{\delta }},-,a_n\right|\le \mathit{\delta }\sum _{j=1}^n\left(\genfrac{}{}{0.0pt}{}{n}{j}\right)C^j\le {(1+C)}^n\mathit{\delta }.\end{array}$$45 The second term in (4040 $$\begin{array}{c}\hfill \left|a_n^{\mathit{\delta }},-,a^{†}\right|\le \left|a_n^{\mathit{\delta }},-,a_n\right|+\left|a_n,-,a^{†}\right|,\end{array}$$40 ) is by (3737 $$\begin{array}{c}\hfill \left|e_{n+1}\right|\le C_h\left|e_n\right|,\end{array}$$37 ) dominated by $C_h^n{e}_0$, thus we can write46 $$\begin{array}{c}\hfill \left|a_n^{\mathit{\delta }},-,a^{†}\right|\le {(1+C)}^n\mathit{\delta }+C_h^n{e}_0.\end{array}$$46 We see that with increasing $n$ one error bound grows without a limit and the other goes to zero. Thus, in order to provide its convergence with $\mathit{\delta }$ we must find a minimizing $n_{\ast }$ as a function of $\mathit{\delta }$. Simple calculations give this minimizing argument equal to47 $$\begin{array}{c}\hfill n_{\ast }(\mathit{\delta })=\frac{log\left(-,\frac{log(1+C)}{e_{0}log{C}_h},\mathit{\delta }\right)}{log{C}_h-log(1+C)}=O\left(log,\frac{1}{\mathit{\delta }}\right)\text{as}\mathit{\delta }\to 0.\end{array}$$47 Plugging this expression into the estimate (4646 $$\begin{array}{c}\hfill \left|a_n^{\mathit{\delta }},-,a^{†}\right|\le {(1+C)}^n\mathit{\delta }+C_h^n{e}_0.\end{array}$$46 ) we obtain48 $$\begin{array}{c}\hfill \left|a_{n_{\ast }}^{\mathit{\delta }},-,a_{n_{\ast }}\right|\le \mathit{\delta }{(1+C)}^{\frac{log\left(-,\frac{log(1+C)}{e_{0}log{C}_h},\mathit{\delta }\right)}{log{C}_h-log(1+C)}}+e_0{C}_h^{\frac{log\left(-,\frac{log(1+C)}{e_{0}log{C}_h},\mathit{\delta }\right)}{log{C}_h-log(1+C)}}.\end{array}$$48 By some elementary manipulations along with the identity $x^{lny}=y^{lnx}$ we arrive at49 $$\begin{array}{c}\hfill \left|a_{n_{\ast }}^{\mathit{\delta }},-,a_{n_{\ast }}\right|\le {\mathit{\delta }}^{\frac{ln(1+C)}{ln{C}_h-ln(1+C)}}\left(A,\mathit{\delta },+,B\right)=O\left({\mathit{\delta }}^{\frac{log(1/C_h)}{log1/C_h+log(1+C)}}\right)\text{as}\mathit{\delta }\to 0,\end{array}$$49 whereby $A$ and $B$ we denoted the $\mathit{\delta }$-independent constants. We see that the exponent of $\mathit{\delta }$ is between $0$ and $1$. For the estimate of $b$ denote $g(a,x):=f(a,x)/N_a^2$ and by (1919 $$\begin{array}{c}\hfill b^{†}=\frac{1}{N_a^2}〈f,(,a,;,·,),,,h〉.\end{array}$$19 ) write50 $$\begin{array}{cc}& \left|b_{n_{\ast }}^{\mathit{\delta }},-,b^{†}\right|=\left|〈g,(a_{n_{\ast }}^{\mathit{\delta }},·),,,h^{\mathit{\delta }}〉,-,〈g,(,a^{†},,,·,),,,h〉\right|\hfill \\ \hfill & \le \left|〈g,(a_{n_{\ast }}^{\mathit{\delta }},·),,,h^{\mathit{\delta }},-,h〉\right|+\left|〈g,(a_{n_{\ast }}^{\mathit{\delta }},·),-,g,(a^{†},·),,,h〉\right|\hfill \\ \hfill & \le \underset{a\in D(a)}{sup}∥,g,(,a,,,·,)∥\mathit{\delta }+∥,h∥\underset{a\in D(a)}{sup}∥,\frac{\mathit{\partial }}{\mathit{\partial }a},g,(a,·)∥\left|a_{n_{\ast }}^{\mathit{\delta }},-,a^{†}\right|,\hfill \end{array}$$50 which gives us the desired estimate for the second parameter and concludes the proof. $\square$

3 Numerical simulations and application to the corneal geometry

In this section, we apply our previous abstract reasoning to the problem of finding $a$ and $b$ in the Equation (44 $$\begin{array}{c}\hfill -\frac{1}{r}\frac{d}{dr}\left(r,\frac{dh}{dr}\right)+ah\approx b,0\le r\le 1,\end{array}$$4 ) describing the corneal geometry. We will find a fit with the two data-sets consisting of $123\times 123$ points representing the interior and exterior surfaces of cornea. Unfortunately, we are in possession of this data only. A more thorough verification would only be possible provided a larger set of data.

Instead of (66 $$\begin{array}{c}\hfill h_0(r)=\frac{b}{a}\left(1,-,\frac{I_0(\sqrt{a}r)}{I_0(\sqrt{a})}\right),\end{array}$$6 ) we will use the following function51 $$\begin{array}{c}\hfill f(a;x):=\frac{1}{a{I}_0(\sqrt{a})}\left(I_0,(\sqrt{a}x),-,1\right),\end{array}$$51 which is $h(0)-h(x)$ in (66 $$\begin{array}{c}\hfill h_0(r)=\frac{b}{a}\left(1,-,\frac{I_0(\sqrt{a}r)}{I_0(\sqrt{a})}\right),\end{array}$$6 ). This is done because of the form in which data are acquired from the measuring equipment. In the case of our measurement, the noise level is $\mathit{\delta }=3\mathrm{\mu }$m. Of course, we have to return to the original dimensional model, but here we suppress the details.

Our previous work [21] gives us a hint where to look for the unknown parameters $a$ and $b$, where we tentatively found that $a_{in}\approx 2.0788$, $b_{in}\approx 2.7674$, $a_{ex}\approx 1.9439$ and $b_{ex}\approx 2.2753$. We expect that the real values of parameters will be of order of unity, thus we restrict our search of $a^{†}$ for example to the set $D(a)=[0.1,10]$. Numerical calculations show that both $M_a$ and $∥,F^{″},(a)∥$ are decreasing functions of $a$.

We note that the needed assumption of Theorem 2.2 is satisfied. Indeed, we have52 $$\begin{array}{c}\hfill \underset{s,t\in D(a)}{sup}∥,F^{″},(s)∥M_t^{-2}∥,h,-,F,(,a_0,)∥\approx 0.0075,0.011\end{array}$$52 for exterior and interior surfaces, respectively. These quantities are less than $1$ so the iteration (2727 $$\begin{array}{c}\hfill a_{n+1}=a_n+\mathrm{\Delta }{a}_n,\mathrm{\Delta }{a}_n=\frac{1}{M_{a_n}^2}{F}^{\prime }{(a_n)}^{\ast }\left(h,-,F,(,a_n,)\right).\end{array}$$27 ) is convergent. For interior and exterior surfaces we have, respectively, $a_{in}^{\mathit{\delta }}\approx 2.0288$, $b_{in}^{\mathit{\delta }}\approx 2.7749$ and $a_{ex}^{\mathit{\delta }}\approx 1.4130$, $b_{ex}^{\mathit{\delta }}\approx 1.9856$. The number of iterations needed for the convergence for different starting points is presented in Table 1. We can see that even for big differences between the starting point and the limit, only a few iterations are needed. When doing the same calculations with other iterative regularization method, namely Landweber iteration (see e.g. [26]), achieving the same precision took almost $700$ and $300$ iterations, respectively! However, Landweber’s iteration is known to converge arbitrarily slow (see [28]). Our results were verified by using some well-known algorithms for finding the least-squares solution. We have used Newton, Quasi-Newton, Levenberg-Marquardt and Conjugate Gradient methods available in the scientific environment MATHEMATICA. In any case we have obtained the same values of $a$ and $b$.

Table 1. Number of iterations needed for the convergence with different starting points $a_0$ for interior and exterior surfaces of the cornea.

	Starting points $a_0$
	0.1	1	2	3	4	5	6	7	8	9	10
Interior	4	3	2	3	3	3	4	4	4	4	3
Exterior	5	3	4	4	5	7	6	5	4	6	8

Table 2. Results of the numerical experiment for finding true values of parameters $a$ and $b$. The model was constructed from (5151 $$\begin{array}{c}\hfill f(a;x):=\frac{1}{a{I}_0(\sqrt{a})}\left(I_0,(\sqrt{a}x),-,1\right),\end{array}$$51 ) with additive noise on level $\mathit{\delta }$ and $a=1$, $b=2$.

	Noise level $\mathit{\delta }$ (mm)
	0	0.01	0.05	0.1	0.5	1.0	1.5
$a$	0.9936	0.9968	0.9627	1.0532	1.1681	0.8481	1.2239
$b$	1.9979	2.0020	1.9877	2.0187	2.0550	1.9357	2.1082

By Theorem 2.3 and by using the known value of $\mathit{\delta }$, we crudely estimate that the optimal number of iterations should be about $10$. Also, by (3838 $$\begin{array}{c}\hfill \left|a_{n_{\ast }(\mathit{\delta })}^{\mathit{\delta }},-,a^{†}\right|=O({\mathit{\delta }}^{\mathit{\nu }}),\left|b_{n_{\ast }(\mathit{\delta })}^{\mathit{\delta }},-,b^{†}\right|=O({\mathit{\delta }}^{\mathit{\nu }})as\mathit{\delta }\to 0,\end{array}$$38 ) the difference between the computed $a_{n_{\ast }}^{\mathit{\delta }}$, $b_{n_{\ast }}^{\mathit{\delta }}$ and the exact values of the unknown parameters $a^{†}$ and $b^{†}$ can be estimated to be of order of $0.1\%$. 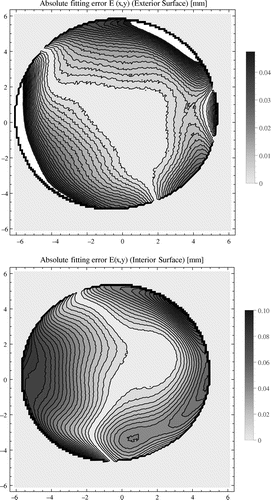The absolute fitting error was calculated from the formula53 $$\begin{array}{c}\hfill E(x,y):=\left|h,(x,y),-,F,(a_{n_{\ast }}^{†}),(x,y)\right|,\end{array}$$53 which is depicted in Figure 1. The plots show the contour plots of the magnitude of the absolute error $E(x,y)$ along the region of cornea. The means of these errors taken along the surface of the cornea are equal to $0.031$ mm for the interior surface and $0.014$ mm for the exterior. These errors are within the systematic measurement uncertainty, which is $3\mathrm{\mu }$m. Therefore we do not introduce any additional errors which are of lower order than the data. The dimensional radius of the cornea is $5.6$ mm and the reference surface of the measurement is drawn in light colour on the outside of the circular rim of the cornea (that is for $r>5.6$ mm).

Figure 1. Contur plots of the absolute errors in fitting $E(x,y)$ defined in (5353 $$\begin{array}{c}\hfill E(x,y):=\left|h,(x,y),-,F,(a_{n_{\ast }}^{†}),(x,y)\right|,\end{array}$$53 ). On the top: exterior surface, on the bottom: interior surface of cornea. Horizontal and vertical axes, shown in millimetres, depict $x$ and $y$ coordinates of the point on the corneal surface. The light colour outside the cornea represents the reference surface.

Our algorithm can also be tested for a performance with different noise levels $\mathit{\delta }$. For this numerical experiment, we produce an artificial corneal surface described by the function (5151 $$\begin{array}{c}\hfill f(a;x):=\frac{1}{a{I}_0(\sqrt{a})}\left(I_0,(\sqrt{a}x),-,1\right),\end{array}$$51 ) with an additive random noise generated from normal $\mathcal{N}(0,\mathit{\delta })$ distribution. We choose $a=1$ and $b=2$ as the true parameters in our simulation. The results of the experiment are presented in Table 2. The number of iterations for different starting points chosen from the set $[0.1,10]$ is small, ranging from $3$ to $8$. It is evident that even for a large (comparing to the maximum corneal deflection $2$ mm) noise level, the method shows decent stability yielding results that are very close to the exact parameters.

4 Conclusion and discussion

In this paper, we have applied a simple iterative regularization method to the problem of parameter identification in a differential equation describing corneal surface. At the beginning, we have reduced a double linear–nonlinear problem to a nonlinear one and applied Newton’s iteration to solve it. Sufficient conditions for convergence were proved. We have also found estimates for order of stability with respect to noise in input data.

When fitting with the real data, we saw that Newton’s method needed fewer hundred iterations that Landweber’s. The fitting error is very reasonable and is smaller for exterior than interior surface of the cornea (we have observed similar results earlier in [21]). We have calculated fitting parameters $a^{\mathit{\delta }}$ and $b^{\mathit{\delta }}$ which by Theorem 2.3 converge to the real least-squares solutions $a^{†}$ and $b^{†}$ when $\mathit{\delta }\to 0$. Thus we have obtained the unique, stable solution to our inverse problem.

In our model, parameters $a$ and $b$ are associated with physical quantities (22 $$\begin{array}{c}\hfill a:=\frac{k{R}^2}{T},b:=\frac{PR}{T}.\end{array}$$2 ) such as intra-ocular pressure. Stable method of obtaining them is crucial in the real-world applications since every measurement introduces some noise. Intra-ocular pressure is an important parameter for the diagnostics of many seeing disorders and in almost every eye examination its measurement has to be taken. Since parameter $b$ is associated with the intra-ocular pressure, our model might help to determine it in a noninvasive way, knowing only the corneal topography $h$. Nevertheless, we hope that our model will provide some new insights into the biomechanical structure of cornea and make a step to determining intra-ocular pressure without any invasive techniques.

Acknowledgements

The authors would like to thank Dr Robert Iskander from Institute of Biomedical Engineering and Instrumentation, Wroclaw University of Technology, Poland and School of Optometry, Queensland University of Technology, Australia for access to the data. This research was supported by the Polish Government funds for science: research project NCN 2012/05/N/ST1/02860.