A fourth-order compact difference scheme for the parabolic inverse problem with an overspecification at a point

Abstract

The problem of finding the solution of partial differential equation with source control parameter has appeared increasingly in physical phenomena, for example, in the study of heat conduction process, chemical diffusion and control theory. In this paper, we use a high-order scheme for determining unknown control parameter and unknown solution of parabolic inverse problem. In the proposed numerical scheme, we replace the space derivative with a fourth-order compact finite difference approximation. We will investigate the stability and convergence of proposed scheme and show that the convergence order is $\mathcal{O}({\mathit{\tau }}^2+h^4)$. Also due to the usually ill-posed nature of inverse problems, we examine the stability of method with respect to perturbations of the data. Numerical results corroborate the theoretical results and high accuracy of proposed scheme in comparison with the other methods in the literature.

Keywords:

• control parameter
• parabolic inverse problem
• compact finite difference
• stability
• convergence
• perturbation

1 Introduction

The parameter determination in a parabolic partial differential equation from the over-specified data plays a crucial role in applied mathematics and physics. This technique has been widely used to determine the unknown properties of a region by measuring only data on its boundary or a specified location in the domain. These unknown properties, such as conductivity, are important to the physical process but usually cannot be measured directly, or very expensive to be measured. The literature on the numerical approximation of solutions of parabolic partial differential equations with standard boundary conditions is large and still growing rapidly.[1] While many finite difference, finite element, spectral, finite volume and boundary element methods have been proposed to approximate such solutions, there has been less research into the numerical approximation of parabolic partial differential equations with over-specified boundary data. Over the last few years, it has become increasingly apparent that many physical phenomena can be described in terms of parabolic partial differential equations with source control parameters.[2–7] The main contribution of this paper is to propose a high-order method to approximate the solution of the following inverse problem, i.e. to find the unknown control parameter $p(t)$ in the semi-linear time-dependent diffusion equation1.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 with initial condition1.2 $$\begin{array}{c}\hfill u(x,0)=f(x),0<x<1,\end{array}$$1.2 and boundary conditions1.3 $$\begin{array}{c}\hfill u(0,t)=g_0(t),u(1,t)=g_1(t),0\le t\le T,\end{array}$$1.3 subject to the over-specification at a point in the spatial domain1.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 where $f(x),g_0(t),g_1(t),\mathit{\varphi }(x,t)$ and $E(t)$ are known functions which are positive and continuous, $E(t)$ and $f(x)$ are at least once and twice differentiable, respectively, $x^{}\ast \in (0,1)$, $u(x,t)$ and $p(t)$ are unknown functions. The existence and uniqueness and continuous dependence of the solutions to some kind of these inverse problems are discussed in [6, 8–12]. The applications of these inverse problems and some other similar parameter identification problems are discussed in [13, 14]. The inverse problem (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ) can be used to describe a heat transfer process with a source parameter $p(t)$, where for example (1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ) represents the temperature at a given point $x^{\ast }$ in a spatial domain at a time $t$, and $u$ is the temperature distribution.

Cannon et al. [7] formulated a backward Euler finite difference scheme via a transformation and proved the convergence of u with the convergence order of $\mathcal{O}(\mathrm{\Delta }t,h^2)$. Dehghan in [15–17] presented four difference schemes for the problems (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ). They are three-point explicit, five-point explicit, three-point implicit and implicit Crandalls schemes. Also a numerical scheme based on the method of radial basis function for problem (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ) is proposed in [18]. Dehghan and Saadatmandi in [19] proposed a tau method for the solution of problem (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ). A method of line approach based on the applying standard finite difference schemes and Runge-Kutta method presented in [20] for (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ). Also the approximation of moving least-square (MLS) has been used in [21] for finding the solution of problems (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ). A coefficient inverse problem of the one-dimensional parabolic equation is solved by a high-order compact finite difference method in [22]. Liao in [23] combined an efficient high-order finite difference method for solving wave equation, auto differentiation tools and globally convergent optimization algorithms to estimate the unknown coefficient in a 1-D wave equation. Another effective method based on Ritz-Galerkin method for solving an inverse heat conduction problem with a nonlinear source term via Bernstein multi-scaling functions and cubic B-spline functions is proposed in [24]. The authors of [25, 26] suggested some numerical approximations which do not use any transformation to solve inverse problem (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ). An approach for the inverse problem for a fractional parabolic equation is given in [27] and some discussions about inverse problem for elliptic equations are proposed in [28, 29]. Finite difference scheme for the estimation of heat source dependent on time variable is given in [30]. Finite volume method is used in [31] to solve a one-dimensional parabolic inverse problem with source term and Neumann boundary conditions. The inverse problem of finding the time-dependent coefficient of heat capacity together with the nonlocal boundary conditions is considered in [32]. Under some natural regularity and consistency conditions on the input data, the existence, uniqueness and continuous dependence upon the data of the solution are shown. A new method by the reproducing kernel Hilbert space in [33] is applied to generalized form of the inverse heat problem (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ). The problem is reduced to a system of linear equations. The exact and approximate solutions are both obtained in a reproducing kernel space. By the Green’s function method, the inverse problem (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ) is reduced to an operator equation of the first kind in [34]. The uniqueness of the solution for the inverse problem is obtained by the contraction mapping principle. A second order of accuracy implicit difference scheme is presented in [35] for a right-hand side identification problem. The coercive stability estimates for the solution of this difference scheme are obtained. A numerical method based on the method of lines for the solution of inverse problem (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ) is given in [36]. The radial basis functions (RBFs) method is employed in [37] to handle a class of multi-dimensional parabolic inverse problems. Based on the idea of RBF approximation, a fast and highly accurate meshless method is developed for solving an inverse problem with a control parameter. A method based on combination of compact finite difference scheme with boundary value methods is proposed in [38]. Authors of [39] proposed a numerical method of order $\mathcal{O}({\mathit{\tau }}^2+h^2)$ for Equations (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ) and proved the solvability, stability and convergence of it. Also a linearized compact scheme of order $\mathcal{O}({\mathit{\tau }}^2+h^4)$ is given in [40] with only solvability analysis. Some other numerical schemes are given in [41–45].

Some of the above finite difference methods in the literature have low order of accuracy [15–17, 30, 39] or be high-order schemes without any discussion about stability and convergence analysis.[20, 24, 38, 40] In this paper, we propose an efficient algorithm for solving problem (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ) which is of order $\mathcal{O}({\mathit{\tau }}^2+h^4)$. We analyse the stability and convergence of proposed method. We will compare the results of applied method with the results of other schemes in the literature to show the high accuracy and efficiency of proposed method. Also it is well-known that inverse heat conduction problems are highly ill-posed, that is, a small change in the input data can result in an enormous change in the computed solution. Thus, the stability of the numerical method with respect to the noise in the data is of vital importance for obtaining physically meaningful results. On the other hand, since $E(t)$ is measured, there will be a measurement error in it. We will investigate the effect of this error on the approximate solutions.

The outline of this paper is as follows: In Section 2, we introduce the derivation of compact scheme for the solution of Equation (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 ). In Section 3, we investigate the stability and convergence of applied method. The numerical results obtained from applying the new method on two test problems and comparison with analytical and other methods, are shown in Section 4. We conclude this article with a brief conclusive discussion in Section 5.

2 Derivation of proposed scheme

For positive integer numbers $M$ and $N$, let $h=\frac{L}{M}$ denotes the step size of spatial variable$,x,$ and $\mathit{\tau }=\frac{T}{N}$ denotes the step size of time variable, $t$, where $L=1$ and $T$ is the final time. So we define$$x_i=ih,i=0,1,2,...,M,$$$$t_n=n\mathit{\tau },n=0,1,2,...,N.$$Without the loss of generality, we can choose the mesh such that for some $k_0$, $1\le k_0\le M-1$, we have $x^{}\ast =k_{0}h$. The exact and approximate solutions at the point $(x_i,t_n)$ are denoted by $u_i^n$ and $U_i^n$, respectively.

We first use the following transformation [16, 38]2.1 $$\begin{array}{c}\hfill v=u{e}^{-{\int }_0^{t}p(s)ds}.\end{array}$$2.1 Then the problem (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ) can be written as follows:2.2 $$\begin{array}{cc}& v_t=v_{xx}+e^{-{\int }_0^{t}p(s)ds}\mathit{\varphi }(x,t),0<x<1,0<t\le T,\hfill \end{array}$$2.2 2.3 $$\begin{array}{cc}& v(x,0)=f(x),0<x<1,\hfill \end{array}$$2.3 2.4 $$\begin{array}{cc}& v(0,t)=g_0(t)e^{-{\int }_0^{t}p(s)ds},v(1,t)=g_1(t)e^{-{\int }_0^{t}p(s)ds},0\le t\le T.\hfill \end{array}$$2.4 It follow from (2.12.1 $$\begin{array}{c}\hfill v=u{e}^{-{\int }_0^{t}p(s)ds}.\end{array}$$2.1 ) and (1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ) that$$v(x^{}\ast ,t)=u(x^{}\ast ,t)e^{-{\int }_0^{t}p(s)ds}=E(t)e^{-{\int }_0^{t}p(s)ds},$$or,2.5 $$\begin{array}{c}\hfill e^{-{\int }_0^{t}p(s)ds}=\frac{v(x^{}\ast ,t)}{E(t)}.\end{array}$$2.5 Substituting (2.52.5 $$\begin{array}{c}\hfill e^{-{\int }_0^{t}p(s)ds}=\frac{v(x^{}\ast ,t)}{E(t)}.\end{array}$$2.5 ) into (2.22.2 $$\begin{array}{cc}& v_t=v_{xx}+e^{-{\int }_0^{t}p(s)ds}\mathit{\varphi }(x,t),0<x<1,0<t\le T,\hfill \end{array}$$2.2 )–(2.42.4 $$\begin{array}{cc}& v(0,t)=g_0(t)e^{-{\int }_0^{t}p(s)ds},v(1,t)=g_1(t)e^{-{\int }_0^{t}p(s)ds},0\le t\le T.\hfill \end{array}$$2.4 ) gives2.6 $$\begin{array}{cc}& v_t=v_{xx}+\mathit{\phi }(x,t)v(x^{}\ast ,t),0<x<1,0<t\le T,\hfill \\ \hfill & v(x,0)=f(x),0<x<1,\hfill \\ \hfill & v(0,t)=\mathit{\alpha }(t)v(x^{}\ast ,t),v(1,t)=\mathit{\beta }(t)v(x^{}\ast ,t),0\le t\le T,\hfill \end{array}$$2.6 where$$\mathit{\phi }(x,t)=\frac{\mathit{\varphi }(x,t)}{E(t)},\mathit{\alpha }(t)=\frac{g_0(t)}{E(t)},\mathit{\beta }(t)=\frac{g_1(t)}{E(t)},0<x<1,0<t\le T.$$Now we define the following mesh functions$$\begin{array}{c}{\mathit{\varphi }}_i^n=\mathit{\varphi }(x_i,t_n),E^n=E(t_n),{\left(E^{\prime }\right)}^n=E^{\prime }\left(t_n\right),0\le i\le M,0\le n\le N,\\ \\ u_i^n=u(x_i,t_n),v_i^n=v(x_i,t_n),{\mathit{\phi }}_i^n=\mathit{\phi }(x_i,t_n),0\le i\le M,0\le n\le N,\\ \\ {\mathit{\alpha }}_n=\mathit{\alpha }(t_n),{\mathit{\beta }}_n=\mathit{\beta }(t_n),0\le n\le N.\end{array}$$Also we introduce the following notations [39, 40]$$\begin{array}{c}{v}_i^{\overline{n}}=\frac{v_i^{n+1}+v_i^{n-1}}{2},{\mathit{\delta }}_x^2{v}_i^n=\frac{v_{i-1}^n-2v_i^n+v_{i+1}^n}{h^2},D_t{v}_i^n=\frac{v_i^{n+1}-v_i^{n-1}}{2\mathit{\tau }},\\ \\ ∥v^n∥={\left[h\sum _{i=0}^M{(v_i^n)}^2\right]}^{\frac{1}{2}},\Vert v^n{\Vert }_{\infty }=max\left|v_i^n\right|,0\le i\le M,0\le n\le N,\\ \\ u_i^{n+\frac{1}{2}}=\frac{u_i^{n+1}+u_i^n}{2},{\mathit{\delta }}_t{u}_i^{n+\frac{1}{2}}=\frac{u_i^{n+1}-u_i^n}{\mathit{\tau }}.\end{array}$$Let [40]2.7 $$\begin{array}{c}\hfill z=\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{x}^2}.\end{array}$$2.7 Then it follows from (2.62.6 $$\begin{array}{cc}& v_t=v_{xx}+\mathit{\phi }(x,t)v(x^{}\ast ,t),0<x<1,0<t\le T,\hfill \\ \hfill & v(x,0)=f(x),0<x<1,\hfill \\ \hfill & v(0,t)=\mathit{\alpha }(t)v(x^{}\ast ,t),v(1,t)=\mathit{\beta }(t)v(x^{}\ast ,t),0\le t\le T,\hfill \end{array}$$2.6 ) that2.8 $$\begin{array}{c}\hfill z=\frac{\mathit{\partial }v}{\mathit{\partial }t}-\mathit{\phi }(x,t)v(x^{}\ast ,t).\end{array}$$2.8 Considering Equation (2.82.8 $$\begin{array}{c}\hfill z=\frac{\mathit{\partial }v}{\mathit{\partial }t}-\mathit{\phi }(x,t)v(x^{}\ast ,t).\end{array}$$2.8 ) at the point $(x_i,t_n)$ we have2.9 $$\begin{array}{c}\hfill z(x_i,t_n)=\frac{\mathit{\partial }v}{\mathit{\partial }t}(x_i,t_n)-\mathit{\phi }(x_i,t_n)v(x^{}\ast ,t_n),0\le i\le M,0\le n\le N,\end{array}$$2.9 i.e.2.10 $$\begin{array}{c}\hfill z_i^n=\frac{\mathit{\partial }v}{\mathit{\partial }t}(x_i,t_n)-{\mathit{\phi }}_i^n{v}_{k_0}^n,0\le i\le M,0\le n\le N.\end{array}$$2.10 Using fourth-order finite difference scheme for the second-order spatial derivative,[38, 46] we obtain2.11 $$\begin{array}{c}\hfill {\mathit{\delta }}_x^2{v}_i^n=\frac{1}{12}\left(z_{i-1}^n,+,10,z_i^n,+,z_{i+1}^n\right)+\mathcal{O}(h^4),1\le i\le M-1.\end{array}$$2.11 Substituting (2.102.10 $$\begin{array}{c}\hfill z_i^n=\frac{\mathit{\partial }v}{\mathit{\partial }t}(x_i,t_n)-{\mathit{\phi }}_i^n{v}_{k_0}^n,0\le i\le M,0\le n\le N.\end{array}$$2.10 ) into (2.112.11 $$\begin{array}{c}\hfill {\mathit{\delta }}_x^2{v}_i^n=\frac{1}{12}\left(z_{i-1}^n,+,10,z_i^n,+,z_{i+1}^n\right)+\mathcal{O}(h^4),1\le i\le M-1.\end{array}$$2.11 ), we get2.12 $$\begin{array}{cc}& \frac{1}{12}\left[\frac{\mathit{\partial }v}{\mathit{\partial }t}(x_{i-1},t_n)+10\frac{\mathit{\partial }v}{\mathit{\partial }t}(x_i,t_n)+\frac{\mathit{\partial }v}{\mathit{\partial }t}(x_{i+1},t_n)\right]\hfill \\ \hfill & ={\mathit{\delta }}_x^2{v}_i^n+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right)+\mathcal{O}(h^4),1⩽i⩽M-1,1⩽n⩽N,\hfill \\ \hfill \end{array}$$2.12 2.13 $$\begin{array}{cc}& v_i^0=f(x_i),1\le i\le M-1,\hfill \end{array}$$2.13 2.14 $$\begin{array}{cc}& v_0^n={\mathit{\alpha }}_n{v}_{k_0}^n,v_M^n={\mathit{\beta }}_n{v}_{k_0}^n,0\le n\le N.\hfill \end{array}$$2.14 If we use the Taylor expansion, we obtain [40]2.15 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,v_{i-1}^n,+,10,D_t,v_i^n,+,D_t,v_{i+1}^n\right)={\mathit{\delta }}_x^2{v}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right)+{(e_1)}_i^n,\hfill \\ \hfill & 1\le i\le M-1,1\le n\le N.\hfill \end{array}$$2.15 2.16 $$\begin{array}{cc}& v_i^0=f(x_i),1\le i\le M-1,\hfill \end{array}$$2.16 2.17 $$\begin{array}{cc}& v_0^n={\mathit{\alpha }}_n{v}_{k_0}^n,v_M^n={\mathit{\beta }}_n{v}_{k_0}^n,0\le n\le N,\hfill \end{array}$$2.17 where there is a constant $c_1$ such that2.18 $$\begin{array}{c}\hfill \left|{(e_1)}_i^n\right|\le c_1({\mathit{\tau }}^2+h^4),1\le i\le M-1,1\le n\le N-1.\end{array}$$2.18 Again using the Taylor expansion, we have2.19 $$\begin{array}{cc}& v_i^1=v_i^0+{\left.\mathit{\tau }\frac{\mathit{\partial }v}{\mathit{\partial }t}\right|}_i^0+{\left.\frac{{\mathit{\tau }}^2}{2}\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{t}^2}\right|}_i^0+\mathcal{O}({\mathit{\tau }}^3)\hfill \\ \hfill & =v_i^0+\mathit{\tau }\left({\left.\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{x}^2}\right|}_i^0,+,{\mathit{\phi }}_i^0,v_{k_0}^0\right)+{(e_2)}_i,1\le i\le M-1,\hfill \end{array}$$2.19 and there is a constant $c_2$ such that2.20 $$\begin{array}{c}\hfill \left|{(e_2)}_i\right|\le c_2{\mathit{\tau }}^2,1\le i\le M-1.\end{array}$$2.20 Eliminating small terms in (2.152.15 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,v_{i-1}^n,+,10,D_t,v_i^n,+,D_t,v_{i+1}^n\right)={\mathit{\delta }}_x^2{v}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right)+{(e_1)}_i^n,\hfill \\ \hfill & 1\le i\le M-1,1\le n\le N.\hfill \end{array}$$2.15 ) and (2.192.19 $$\begin{array}{cc}& v_i^1=v_i^0+{\left.\mathit{\tau }\frac{\mathit{\partial }v}{\mathit{\partial }t}\right|}_i^0+{\left.\frac{{\mathit{\tau }}^2}{2}\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{t}^2}\right|}_i^0+\mathcal{O}({\mathit{\tau }}^3)\hfill \\ \hfill & =v_i^0+\mathit{\tau }\left({\left.\frac{{\mathit{\partial }}^{2}v}{\mathit{\partial }{x}^2}\right|}_i^0,+,{\mathit{\phi }}_i^0,v_{k_0}^0\right)+{(e_2)}_i,1\le i\le M-1,\hfill \end{array}$$2.19 ), we obtain2.21 $$\begin{array}{c}\hfill \frac{1}{12}\left(D_t,v_{i-1}^n,,+,,10,D_t,v_i^n,+,D_t,v_{i+1}^n\right)={\mathit{\delta }}_x^2{v}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right),\end{array}$$2.21 or$$\begin{array}{cc}& \left(\frac{1}{24\mathit{\tau }},-,\frac{1}{2h^2}\right)v_{i-1}^{n+1}+\left(\frac{5}{12\mathit{\tau }},+,\frac{1}{h^2}\right)v_i^{n+1}+\left(\frac{1}{24\mathit{\tau }},-,\frac{1}{2h^2}\right)v_{i+1}^{n+1}\hfill \\ \hfill & =\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right)v_{i-1}^{n-1}+\left(\frac{5}{12\mathit{\tau }},-,\frac{1}{h^2}\right)v_i^{n-1}+\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right)v_{i+1}^{n-1}\hfill \\ \hfill & +\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right),\hfill \end{array}$$and2.22 $$\begin{array}{c}\hfill v_i^1=f(x_i)+\mathit{\tau }\left(f^{″},(x_i),+,{\mathit{\phi }}_i^0,v_{k_0}^0\right),1\le i\le M-1.\end{array}$$2.22 2.23 $$\begin{array}{c}\hfill v_i^0=f(x_i),1\le i\le M-1,\end{array}$$2.23 2.24 $$\begin{array}{c}\hfill v_0^n={\mathit{\alpha }}_n{v}_{k_0}^n,v_M^n={\mathit{\beta }}_n{v}_{k_0}^n,0\le n\le N.\end{array}$$2.24 For obtaining $p(t)$, it follows from (2.12.1 $$\begin{array}{c}\hfill v=u{e}^{-{\int }_0^{t}p(s)ds}.\end{array}$$2.1 ) and (2.52.5 $$\begin{array}{c}\hfill e^{-{\int }_0^{t}p(s)ds}=\frac{v(x^{}\ast ,t)}{E(t)}.\end{array}$$2.5 ) that$$\begin{array}{c}\hfill u(x_i,t_n)=\frac{v(x_i,t_n)}{v(x^{}\ast ,t_n)}E(t_n),1\le i\le M-1,1\le n\le N,\end{array}$$or,2.25 $$\begin{array}{c}\hfill u_i^n=\frac{v_i^n}{v_{k_0}^n}{E}^n,1\le i\le M-1,1\le n\le N.\end{array}$$2.25 From (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 ) and (1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ) we have2.26 $$\begin{array}{c}\hfill p(t_n)=\frac{1}{E^n}\left[{(E^{\prime })}^n-\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}(x_{k_0},t_n)-{\mathit{\varphi }}_{k_0}^n\right],1\le n\le N,\end{array}$$2.26 where ${(E^{\prime })}^n=\frac{dE}{dt}(t_n)$. Using the following fourth-order difference scheme$$\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}(x_{k_0},t_n)=\frac{1}{12h^2}\left(-u_{k_0-2}^n+16u_{k_0-1}^n-30u_{k_0}^n+16u_{k_0+1}^n-u_{k_{0+2}}^n\right)+\mathrm{O}(h^4),$$we can write2.27 $$\begin{array}{cc}\hfill p^n& =\frac{1}{E^n}\left[{(E^{\prime })}^n-\frac{1}{12h^2}\left(-u_{k_0-2}^n+16u_{k_0-1}^n-30u_{k_0}^n+16u_{k_0+1}^n-u_{k_{0+2}}^n\right)-{\mathit{\varphi }}_{k_0}^n\right]\hfill \\ \hfill & +{(e_3)}^n,1\le n\le N,\hfill \end{array}$$2.27 and there is a constant $c_3$ such that2.28 $$\begin{array}{c}\hfill \left|{(e_3)}^n\right|\le c_3{h}^4,1\le n\le N.\end{array}$$2.28 Omitting the small term in (2.272.27 $$\begin{array}{cc}\hfill p^n& =\frac{1}{E^n}\left[{(E^{\prime })}^n-\frac{1}{12h^2}\left(-u_{k_0-2}^n+16u_{k_0-1}^n-30u_{k_0}^n+16u_{k_0+1}^n-u_{k_{0+2}}^n\right)-{\mathit{\varphi }}_{k_0}^n\right]\hfill \\ \hfill & +{(e_3)}^n,1\le n\le N,\hfill \end{array}$$2.27 ), for $1\le n\le N$ we have2.29 $$\begin{array}{c}\hfill p^n=\frac{1}{E^n}\left[{(E^{\prime })}^n-\frac{1}{12h^2}\left(-,u_{k_0-2}^n,+,16,u_{k_0-1}^n,-,30,u_{k_0}^n,+,16,u_{k_0+1}^n,-,u_{k_0+2}^n\right)-{\mathit{\varphi }}_{k_0}^n\right].\end{array}$$2.29 Note that for $n=0$ we can write2.30 $$\begin{array}{c}\hfill p^0=\frac{1}{f(x^{}\ast )}\left[{(E^{\prime })}^0-f^{″}(x^{}\ast )-{\mathit{\varphi }}_{k_0}^0\right].\end{array}$$2.30 So the final fourth-order difference scheme for the solution of (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ) is as follows:2.31 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,v_{i-1}^n,+,10,D_t,v_i^n,+,D_t,v_{i+1}^n\right)={\mathit{\delta }}_x^2{v}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right),\hfill \\ \hfill \end{array}$$2.31 2.32 $$\begin{array}{cc}& v_i^1=f(x_i)+\mathit{\tau }\left(f^{″},(x_i),+,{\mathit{\phi }}_i^0,v_{k_0}^0\right),\hfill \end{array}$$2.32 2.33 $$\begin{array}{cc}& v_i^0=f(x_i),1\le i\le M-1,\hfill \end{array}$$2.33 2.34 $$\begin{array}{cc}& v_0^n={\mathit{\alpha }}_n{v}_{k_0}^n,v_M^n={\mathit{\beta }}_n{v}_{k_0}^n,0\le n\le N,\hfill \end{array}$$2.34 2.35 $$\begin{array}{cc}& u_i^n=\frac{v_i^n}{v_{k_0}^n}{E}^n,1\le i\le M-1,1\le n\le N,\hfill \end{array}$$2.35 2.36 $$\begin{array}{cc}& p^n=\frac{1}{E^n}\left[{(E^{\prime })}^n-\frac{1}{12h^2}\left(-,u_{k_0-2}^n,+,16,u_{k_0-1}^n,-,30,u_{k_0}^n,+,16,u_{k_0+1}^n,-,u_{k_0+2}^n\right)-{\mathit{\varphi }}_{k_0}^n\right],\hfill \\ \hfill & 1\le n\le N,\hfill \end{array}$$2.36 2.37 $$\begin{array}{cc}& p^0=\frac{1}{f(x^{}\ast )}\left[{(E^{\prime })}^0-f^{″}(x^{}\ast )-{\mathit{\varphi }}_{k_0}^0\right].\hfill \end{array}$$2.37

3 Analysis of method

In this section, we analyse the stability and convergence of proposed method. Firstly we assume [39]$$\begin{array}{c}\hfill \left|\mathit{\alpha }(t)\right|\le 1,\left|\mathit{\beta }(t)\right|\le 1,0\le t\le T,\end{array}$$which will be used in the proof of Lemma 1.

Lemma 1

Let $w=\left\{w_i^n,\mid ,0\le i\le M,0\le n\le N\right\}$ be the solution of difference scheme$$w_i^1=f(x_i)+\mathit{\tau }\left(f^{″},(x_i),+,w_{k_0}^0,{\mathit{\phi }}_i^0\right),$$3.1 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,w_{i-1}^n,+,10,D_t,w_i^n,+,D_t,w_{i+1}^n\right)\hfill \\ \hfill & ={\mathit{\delta }}_x^2{w}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,w_{k_0}^n,+,10,{\mathit{\phi }}_i^n,w_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,w_{k_0}^n\right)+g_i^n,\hfill \\ \hfill & 1\le i\le M-1,1\le n\le N,\hfill \end{array}$$3.1 with initial and boundary conditions3.2 $$\begin{array}{c}\hfill w_i^0=f(x_i),1\le i\le M-1,\end{array}$$3.2 3.3 $$\begin{array}{c}\hfill w_0^n={\mathit{\alpha }}_n{w}_{k_0}^n,w_M^n={\mathit{\beta }}_n{w}_{k_0}^n,0\le n\le N,\end{array}$$3.3 then for $\frac{1}{12}⩽r=\frac{\mathit{\tau }}{h^2}⩽\frac{5}{12}$ we have$$\begin{array}{c}\hfill {∥w^n∥}_{\infty }\le e^{2cT}\left({∥w^0∥}_{\infty },+,\mathit{\gamma },+,2,\mathit{\tau },\sum _{l=1}^{n-1},{∥g^l∥}_{\infty }\right),0\le n\le N,\end{array}$$where $\mathit{\gamma }$ depends on $f$ and $\mathit{\varphi }$ and$$c=\underset{\genfrac{}{}{0pt}{}{1\le i\le M-1}{1\le n\le N}}{max}|{\mathit{\phi }}_i^n|.$$

Proof

It follows from (3.13.1 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,w_{i-1}^n,+,10,D_t,w_i^n,+,D_t,w_{i+1}^n\right)\hfill \\ \hfill & ={\mathit{\delta }}_x^2{w}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,w_{k_0}^n,+,10,{\mathit{\phi }}_i^n,w_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,w_{k_0}^n\right)+g_i^n,\hfill \\ \hfill & 1\le i\le M-1,1\le n\le N,\hfill \end{array}$$3.1 ) that$$\begin{array}{cc}& \left(\frac{1}{24\mathit{\tau }},-,\frac{1}{2h^2}\right)w_{i-1}^{n+1}+\left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right)w_i^{n+1}+\left(\frac{1}{24\mathit{\tau }},-,\frac{1}{2h^2}\right)w_{i+1}^{n+1}\hfill \\ \hfill & =\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right)w_{i-1}^{n-1}+\left(\frac{10}{24\mathit{\tau }},-,\frac{2}{2h^2}\right)w_i^{n-1}+\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right)w_{i+1}^{n-1}\hfill \\ \hfill & +\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,w_{k_0}^n,+,10,{\mathit{\phi }}_i^n,w_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,w_{k_0}^n\right)+g_i^n\hfill \\ \hfill & 1\le i\le M-1,1\le n\le N-1.\hfill \end{array}$$If $i=1$, we have$$\begin{array}{cc}\hfill \left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right)w_1^{n+1}& =\left(\frac{10}{24\mathit{\tau }},-,\frac{2}{2h^2}\right)w_1^{n-1}+\left(\frac{1}{2h^2},-,\frac{1}{24\mathit{\tau }}\right)w_0^{n+1}\hfill \\ \hfill & +\left(\frac{1}{2h^2},-,\frac{1}{24\mathit{\tau }}\right)w_2^{n+1}+\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right)w_0^{n-1}\hfill \\ \hfill & +\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right)w_2^{n-1}+\frac{1}{12}\left({\mathit{\phi }}_0^n,w_{k_0}^n,+,10,{\mathit{\phi }}_1^n,w_{k_0}^n,+,{\mathit{\phi }}_2^n,w_{k_0}^n\right)+g_1^n.\hfill \end{array}$$From (3.33.3 $$\begin{array}{c}\hfill w_0^n={\mathit{\alpha }}_n{w}_{k_0}^n,w_M^n={\mathit{\beta }}_n{w}_{k_0}^n,0\le n\le N,\end{array}$$3.3 ) we can rewrite above equation as follows:$$\begin{array}{cc}\hfill \left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right)w_1^{n+1}& =\left(\frac{10}{24\mathit{\tau }},-,\frac{2}{2h^2}\right)w_1^{n-1}+\left(\frac{1}{2h^2},-,\frac{1}{24\mathit{\tau }}\right){\mathit{\alpha }}_{n+1}{w}_{k_0}^{n+1}\hfill \\ \hfill & +\left(\frac{1}{2h^2},-,\frac{1}{24\mathit{\tau }}\right)w_2^{n+1}+\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right){\mathit{\alpha }}_{n-1}{w}_{k_0}^{n-1}\hfill \\ \hfill & +\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right)w_2^{n-1}+\frac{1}{12}\left({\mathit{\phi }}_0^n,+,10,{\mathit{\phi }}_1^n,+,{\mathit{\phi }}_2^n\right)w_{k_0}^n+g_1^n.\hfill \end{array}$$Therefore,3.4 $$\begin{array}{cc}& \left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right)\left|w_1^{n+1}\right|\hfill \\ \hfill & \le \left|\frac{10}{24\mathit{\tau }}-\frac{2}{2h^2}\right|\left|w_1^{n-1}\right|+\left|\frac{1}{2h^2}-\frac{1}{24\mathit{\tau }}\right|\left|w_{k_0}^{n+1}\right|+\left|\frac{1}{2h^2}-\frac{1}{24\mathit{\tau }}\right|\left|w_2^{n+1}\right|\hfill \\ \hfill & +\left|\frac{1}{24\mathit{\tau }}+\frac{1}{2h^2}\right|\left|w_{k_0}^{n-1}\right|+\left|\frac{1}{24\mathit{\tau }}+\frac{1}{2h^2}\right|\left|w_2^{n-1}\right|+c\left|w_{k_0}^n\right|+\left|g_1^n\right|\hfill \\ \hfill & \le \left(\left|\frac{10}{24\mathit{\tau }}-\frac{1}{h^2}\right|,+,\left(\frac{1}{12\mathit{\tau }},+,\frac{1}{h^2}\right)\right){∥w^{n-1}∥}_{\infty }^{}+\left|\frac{1}{h^2}-\frac{1}{12\mathit{\tau }}\right|{∥w^{n+1}∥}_{\infty }^{}\hfill \\ \hfill & +c{∥w^n∥}_{\infty }^{}+{∥g^n∥}_{\infty }^{}.\hfill \end{array}$$3.4 If $2\le i\le M-2$, we have$$\begin{array}{cc}& \left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right)w_i^{n+1}\hfill \\ \hfill & =\left(\frac{1}{2h^2},-,\frac{1}{24\mathit{\tau }}\right)w_{i-1}^{n+1}+\left(\frac{1}{2h^2},-,\frac{1}{24\mathit{\tau }}\right)w_{i+1}^{n+1}\hfill \\ \hfill & +\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right)w_{i-1}^{n-1}+\left(\frac{10}{24\mathit{\tau }},-,\frac{2}{2h^2}\right)w_i^{n-1}\hfill \\ \hfill & +\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right)w_{i+1}^{n-1}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,w_{k_0}^n,+,10,{\mathit{\phi }}_i^n,w_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,w_{k_0}^n\right)+g_i^n.\hfill \end{array}$$So3.5 $$\begin{array}{cc}& \left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right)\left|w_i^{n+1}\right|\hfill \\ \hfill & \le \left|\frac{1}{2h^2}-\frac{1}{24\mathit{\tau }}\right|\left(\left|w_{i-1}^{n+1}\right|,+,\left|w_{i+1}^{n+1}\right|\right)+\left|\frac{1}{24\mathit{\tau }}+\frac{1}{2h^2}\right|\left(\left|w_{i-1}^{n-1}\right|,+,\left|w_{i+1}^{n-1}\right|\right)\hfill \\ \hfill & +\left|\frac{10}{24\mathit{\tau }}-\frac{2}{2h^2}\right|\left|w_i^{n-1}\right|+c\left|w_{k_0}^n\right|+\left|g_i^n\right|\hfill \\ \hfill & \le \left(\left|\frac{10}{24\mathit{\tau }}-\frac{1}{h^2}\right|,+,\left(\frac{1}{12\mathit{\tau }},+,\frac{1}{h^2}\right)\right){∥w^{n-1}∥}_{\infty }^{}+\left|\frac{1}{h^2}-\frac{1}{12\mathit{\tau }}\right|{∥w^{n+1}∥}_{\infty }^{}\hfill \\ \hfill & +c{∥w^n∥}_{\infty }^{}+{∥g^n∥}_{\infty }^{}.\hfill \end{array}$$3.5 If $i=M-1$, we have$$\begin{array}{cc}& \left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right)w_{M-1}^{n+1}\hfill \\ \hfill & =\left(\frac{1}{2h^2},-,\frac{1}{24\mathit{\tau }}\right)w_{M-2}^{n+1}+\left(\frac{1}{2h^2},-,\frac{1}{24\mathit{\tau }}\right)w_M^{n+1}+\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right)w_{M-2}^{n-1}\hfill \\ \hfill & +\left(\frac{10}{24\mathit{\tau }},-,\frac{2}{2h^2}\right)w_{M-1}^{n-1}+\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right)w_M^{n-1}\hfill \\ \hfill & +\frac{1}{12}\left({\mathit{\phi }}_{M-2}^n,w_{k_0}^n,+,10,{\mathit{\phi }}_{M-1}^n,w_{k_0}^n,+,{\mathit{\phi }}_M^n,w_{k_0}^n\right)+g_{M-1}^n.\hfill \end{array}$$Using (3.33.3 $$\begin{array}{c}\hfill w_0^n={\mathit{\alpha }}_n{w}_{k_0}^n,w_M^n={\mathit{\beta }}_n{w}_{k_0}^n,0\le n\le N,\end{array}$$3.3 ) we can write$$\begin{array}{cc}& \left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right)w_{M-1}^{n+1}\hfill \\ \hfill & =\left(\frac{1}{2h^2},-,\frac{1}{24\mathit{\tau }}\right)w_{M-2}^{n+1}+\left(\frac{1}{2h^2},-,\frac{1}{24\mathit{\tau }}\right){\mathit{\beta }}_{n+1}{w}_{k_0}^{n+1}+\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right)w_{M-2}^{n-1}\hfill \\ \hfill & +\left(\frac{10}{24\mathit{\tau }},-,\frac{2}{2h^2}\right)w_{M-1}^{n-1}+\left(\frac{1}{24\mathit{\tau }},+,\frac{1}{2h^2}\right){\mathit{\beta }}_{n-1}{w}_{k_0}^{n-1}\hfill \\ \hfill & +\frac{1}{12}\left({\mathit{\phi }}_{M-2}^n,w_{k_0}^n,+,10,{\mathit{\phi }}_{M-1}^n,w_{k_0}^n,+,{\mathit{\phi }}_M^n,w_{k_0}^n\right)+g_{M-1}^n,\hfill \end{array}$$thus, we can state3.6 $$\begin{array}{cc}& \left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right)\left|w_{M-1}^{n+1}\right|\hfill \\ \hfill & \le \left|\frac{1}{2h^2}-\frac{1}{24\mathit{\tau }}\right|\left(\left|w_{M-2}^{n+1}\right|,+,\left|w_M^{n+1}\right|\right)+\left|\frac{1}{24\mathit{\tau }}+\frac{1}{2h^2}\right|\left(\left|w_{M-2}^{n-1}\right|,+,\left|w_M^{n-1}\right|\right)\hfill \\ \hfill & +\left|\frac{10}{24\mathit{\tau }}-\frac{2}{2h^2}\right|\left|w_{M-1}^{n-1}\right|+c\left|w_{k_0}^n\right|+\left|g_{M-1}^n\right|\hfill \\ \hfill & \le \left(\left|\frac{10}{24\mathit{\tau }}-\frac{1}{h^2}\right|,+,\left(\frac{1}{12\mathit{\tau }},+,\frac{1}{h^2}\right)\right){∥w^{n-1}∥}_{\infty }^{}+\left|\frac{1}{h^2}-\frac{1}{12\mathit{\tau }}\right|{∥w^{n+1}∥}_{\infty }^{}\hfill \\ \hfill & +c{∥w^n∥}_{\infty }^{}+{∥g^n∥}_{\infty }^{}.\hfill \end{array}$$3.6 Considering (3.43.4 $$\begin{array}{cc}& \left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right)\left|w_1^{n+1}\right|\hfill \\ \hfill & \le \left|\frac{10}{24\mathit{\tau }}-\frac{2}{2h^2}\right|\left|w_1^{n-1}\right|+\left|\frac{1}{2h^2}-\frac{1}{24\mathit{\tau }}\right|\left|w_{k_0}^{n+1}\right|+\left|\frac{1}{2h^2}-\frac{1}{24\mathit{\tau }}\right|\left|w_2^{n+1}\right|\hfill \\ \hfill & +\left|\frac{1}{24\mathit{\tau }}+\frac{1}{2h^2}\right|\left|w_{k_0}^{n-1}\right|+\left|\frac{1}{24\mathit{\tau }}+\frac{1}{2h^2}\right|\left|w_2^{n-1}\right|+c\left|w_{k_0}^n\right|+\left|g_1^n\right|\hfill \\ \hfill & \le \left(\left|\frac{10}{24\mathit{\tau }}-\frac{1}{h^2}\right|,+,\left(\frac{1}{12\mathit{\tau }},+,\frac{1}{h^2}\right)\right){∥w^{n-1}∥}_{\infty }^{}+\left|\frac{1}{h^2}-\frac{1}{12\mathit{\tau }}\right|{∥w^{n+1}∥}_{\infty }^{}\hfill \\ \hfill & +c{∥w^n∥}_{\infty }^{}+{∥g^n∥}_{\infty }^{}.\hfill \end{array}$$3.4 )–(3.63.6 $$\begin{array}{cc}& \left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right)\left|w_{M-1}^{n+1}\right|\hfill \\ \hfill & \le \left|\frac{1}{2h^2}-\frac{1}{24\mathit{\tau }}\right|\left(\left|w_{M-2}^{n+1}\right|,+,\left|w_M^{n+1}\right|\right)+\left|\frac{1}{24\mathit{\tau }}+\frac{1}{2h^2}\right|\left(\left|w_{M-2}^{n-1}\right|,+,\left|w_M^{n-1}\right|\right)\hfill \\ \hfill & +\left|\frac{10}{24\mathit{\tau }}-\frac{2}{2h^2}\right|\left|w_{M-1}^{n-1}\right|+c\left|w_{k_0}^n\right|+\left|g_{M-1}^n\right|\hfill \\ \hfill & \le \left(\left|\frac{10}{24\mathit{\tau }}-\frac{1}{h^2}\right|,+,\left(\frac{1}{12\mathit{\tau }},+,\frac{1}{h^2}\right)\right){∥w^{n-1}∥}_{\infty }^{}+\left|\frac{1}{h^2}-\frac{1}{12\mathit{\tau }}\right|{∥w^{n+1}∥}_{\infty }^{}\hfill \\ \hfill & +c{∥w^n∥}_{\infty }^{}+{∥g^n∥}_{\infty }^{}.\hfill \end{array}$$3.6 ), we have$$\begin{array}{cc}& \left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right)\left|w_i^{n+1}\right|\hfill \\ \hfill & \le \left(\left|\frac{10}{24\mathit{\tau }}-\frac{1}{h^2}\right|,+,\left(\frac{1}{12\mathit{\tau }},+,\frac{1}{h^2}\right)\right){∥w^{n-1}∥}_{\infty }^{}+\left|\frac{1}{h^2}-\frac{1}{12\mathit{\tau }}\right|{∥w^{n+1}∥}_{\infty }^{}\hfill \\ \hfill & +c{∥w^n∥}_{\infty }^{}+{∥g^n∥}_{\infty }^{},i=0,\dots ,M.\hfill \end{array}$$According to relation (3.33.3 $$\begin{array}{c}\hfill w_0^n={\mathit{\alpha }}_n{w}_{k_0}^n,w_M^n={\mathit{\beta }}_n{w}_{k_0}^n,0\le n\le N,\end{array}$$3.3 ) we can write$$\begin{array}{c}\hfill \left|w_0^n\right|\le \left|w_{k_0}^n\right|,\left|w_M^n\right|\le \left|w_{k_0}^n\right|,0\le n\le N.\end{array}$$So we have$$\begin{array}{cc}& \left(\frac{10}{24\mathit{\tau }},+,\frac{2}{2h^2}\right){∥w^{n+1}∥}_{\infty }^{}\hfill \\ \hfill & \le \left(\left|\frac{10}{24\mathit{\tau }}-\frac{1}{h^2}\right|,+,\left(\frac{1}{12\mathit{\tau }},+,\frac{1}{h^2}\right)\right){∥w^{n-1}∥}_{\infty }^{}+\left|\frac{1}{h^2}-\frac{1}{12\mathit{\tau }}\right|{∥w^{n+1}∥}_{\infty }^{}\hfill \\ \hfill & +c{∥w^n∥}_{\infty }^{}+{∥g^n∥}_{\infty }^{}.\hfill \end{array}$$Now if $\frac{1}{12}⩽r⩽\frac{5}{12}$, we have$$\frac{1}{2}{∥w^{n+1}∥}_{\infty }\le \frac{1}{2}{∥w^{n-1}∥}_{\infty }+c\mathit{\tau }{∥w^n∥}_{\infty }+\mathit{\tau }{∥g^n∥}_{\infty }.$$Changing index from $n$ to $l$ in above relation gives3.7 $$\begin{array}{c}\hfill {∥w^{l+1}∥}_{\infty }-{∥w^{l-1}∥}_{\infty }\le 2c\mathit{\tau }{∥w^l∥}_{\infty }+2\mathit{\tau }{∥g^l∥}_{\infty }.\end{array}$$3.7 Summing up (3.73.7 $$\begin{array}{c}\hfill {∥w^{l+1}∥}_{\infty }-{∥w^{l-1}∥}_{\infty }\le 2c\mathit{\tau }{∥w^l∥}_{\infty }+2\mathit{\tau }{∥g^l∥}_{\infty }.\end{array}$$3.7 ) from $1$ to $n-1$ results$$\begin{array}{c}{∥w^n∥}_{\infty }\le {∥w^0∥}_{\infty }+{∥w^1∥}_{\infty }-{∥w^{n-1}∥}_{\infty }+2c\mathit{\tau }\sum _{l=1}^{n-1}{∥w^l∥}_{\infty }+2\mathit{\tau }\sum _{l=1}^{n-1}{∥g^l∥}_{\infty }\hfill \\ \le \left({∥w^0∥}_{\infty },+,{∥w^1∥}_{\infty },+,2,\mathit{\tau },\sum _{l=1}^{n-1},{∥g^l∥}_{\infty }\right)+2c\mathit{\tau }\sum _{l=1}^{n-1}{∥w^l∥}_{\infty }.\hfill \end{array}$$According to$$\begin{array}{c}\hfill w_i^1=f(x_i)+\mathit{\tau }\left(f^{″},(x_i),+,w_{k_0}^0,{\mathit{\phi }}_i^0\right),\end{array}$$there is a positive constant $\mathit{\gamma }$ such that$$\begin{array}{c}\hfill \left|w_i^1\right|\le \left|f(x_i)\right|+\mathit{\tau }\left|f^{″}(x_i)\right|+\mathit{\tau }c\left|w_{k_0}^0\right|\le \mathit{\gamma }.\end{array}$$Consequently,$${∥w^n∥}_{\infty }\le ({∥w^0∥}_{\infty }+\mathit{\gamma }+2\mathit{\tau }\sum _{l=1}^{n-1}{∥g^l∥}_{\infty })+2c\mathit{\tau }\sum _{l=1}^{n-1}{∥w^l∥}_{\infty }.$$The discrete Gronwall lemma [47] gives us$$\begin{array}{c}\hfill {∥w^n∥}_{\infty }\le e^{2cT}({∥w^0∥}_{\infty }+\mathit{\gamma }+2\mathit{\tau }\sum _{l=1}^{n-1}{∥g^l∥}_{\infty }),\end{array}$$which completes the proof.

Theorem 1

Let $v_i^n$ be the solution of compact finite difference scheme (2.312.31 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,v_{i-1}^n,+,10,D_t,v_i^n,+,D_t,v_{i+1}^n\right)={\mathit{\delta }}_x^2{v}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right),\hfill \\ \hfill \end{array}$$2.31 )–(2.342.34 $$\begin{array}{cc}& v_0^n={\mathit{\alpha }}_n{v}_{k_0}^n,v_M^n={\mathit{\beta }}_n{v}_{k_0}^n,0\le n\le N,\hfill \end{array}$$2.34 ), then this difference scheme is stable under the assumptions of Lemma 1.

Proof

From Lemma 1 and regarding to $g=0$ in (2.312.31 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,v_{i-1}^n,+,10,D_t,v_i^n,+,D_t,v_{i+1}^n\right)={\mathit{\delta }}_x^2{v}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right),\hfill \\ \hfill \end{array}$$2.31 ), we can state that$$\begin{array}{c}\hfill {∥v^n∥}_{\infty }⩽e^{2cT}\left({∥v^0∥}_{\infty },+,\mathit{\gamma }\right),\end{array}$$which shows the stability of the proposed difference scheme. $\square$

Now we prove that the difference scheme (2.312.31 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,v_{i-1}^n,+,10,D_t,v_i^n,+,D_t,v_{i+1}^n\right)={\mathit{\delta }}_x^2{v}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right),\hfill \\ \hfill \end{array}$$2.31 )–(2.342.34 $$\begin{array}{cc}& v_0^n={\mathit{\alpha }}_n{v}_{k_0}^n,v_M^n={\mathit{\beta }}_n{v}_{k_0}^n,0\le n\le N,\hfill \end{array}$$2.34 ) converges with the spatial accuracy of fourth order.

Theorem 2

Let $V_i^n$ and $v_i^n$ be the solutions of (2.152.15 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,v_{i-1}^n,+,10,D_t,v_i^n,+,D_t,v_{i+1}^n\right)={\mathit{\delta }}_x^2{v}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right)+{(e_1)}_i^n,\hfill \\ \hfill & 1\le i\le M-1,1\le n\le N.\hfill \end{array}$$2.15 )–(2.172.17 $$\begin{array}{cc}& v_0^n={\mathit{\alpha }}_n{v}_{k_0}^n,v_M^n={\mathit{\beta }}_n{v}_{k_0}^n,0\le n\le N,\hfill \end{array}$$2.17 ) and (2.312.31 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,v_{i-1}^n,+,10,D_t,v_i^n,+,D_t,v_{i+1}^n\right)={\mathit{\delta }}_x^2{v}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right),\hfill \\ \hfill \end{array}$$2.31 )–(2.342.34 $$\begin{array}{cc}& v_0^n={\mathit{\alpha }}_n{v}_{k_0}^n,v_M^n={\mathit{\beta }}_n{v}_{k_0}^n,0\le n\le N,\hfill \end{array}$$2.34 ), respectively, then under the assumptions of Lemma 1, the difference scheme (2.312.31 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,v_{i-1}^n,+,10,D_t,v_i^n,+,D_t,v_{i+1}^n\right)={\mathit{\delta }}_x^2{v}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right),\hfill \\ \hfill \end{array}$$2.31 )–(2.352.35 $$\begin{array}{cc}& u_i^n=\frac{v_i^n}{v_{k_0}^n}{E}^n,1\le i\le M-1,1\le n\le N,\hfill \end{array}$$2.35 ) converges with the convergence order $\mathcal{O}\left({\mathit{\tau }}^2+h^4\right)$.

Proof

We define the following notation$$\begin{array}{c}\hfill e_i^n=V_i^n-v_i^n,0\le i\le M,1\le n\le N.\end{array}$$Subtracting (2.312.31 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,v_{i-1}^n,+,10,D_t,v_i^n,+,D_t,v_{i+1}^n\right)={\mathit{\delta }}_x^2{v}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right),\hfill \\ \hfill \end{array}$$2.31 )–(2.352.35 $$\begin{array}{cc}& u_i^n=\frac{v_i^n}{v_{k_0}^n}{E}^n,1\le i\le M-1,1\le n\le N,\hfill \end{array}$$2.35 ) from (2.152.15 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,v_{i-1}^n,+,10,D_t,v_i^n,+,D_t,v_{i+1}^n\right)={\mathit{\delta }}_x^2{v}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,v_{k_0}^n,+,10,{\mathit{\phi }}_i^n,v_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,v_{k_0}^n\right)+{(e_1)}_i^n,\hfill \\ \hfill & 1\le i\le M-1,1\le n\le N.\hfill \end{array}$$2.15 )–(2.172.17 $$\begin{array}{cc}& v_0^n={\mathit{\alpha }}_n{v}_{k_0}^n,v_M^n={\mathit{\beta }}_n{v}_{k_0}^n,0\le n\le N,\hfill \end{array}$$2.17 ), we obtain3.8 $$\begin{array}{cc}& \frac{1}{12}\left(D_t,e_{i-1}^n,+,10,D_t,e_i^n,+,D_t,e_{i+1}^n\right)\hfill \\ \hfill & ={\mathit{\delta }}_x^2{e}_i^{\overline{n}}+\frac{1}{12}\left({\mathit{\phi }}_{i-1}^n,e_{k_0}^n,+,10,{\mathit{\phi }}_i^n,e_{k_0}^n,+,{\mathit{\phi }}_{i+1}^n,e_{k_0}^n\right)+{(e_1)}_i^n,\hfill \\ \hfill & 1\le i\le M-1,1\le n\le N,\hfill \end{array}$$3.8 3.9 $$\begin{array}{cc}& e_i^0=0,1\le i\le M-1,\hfill \end{array}$$3.9 3.10 $$\begin{array}{cc}& e_0^n={\mathit{\alpha }}_n{e}_{k_0}^n,e_M^n={\mathit{\beta }}_n{e}_{k_0}^n,0\le n\le N.\hfill \end{array}$$3.10 According to above relations, we can set $\mathit{\gamma }=0$, so from Lemma 1 and Equation (2.182.18 $$\begin{array}{c}\hfill \left|{(e_1)}_i^n\right|\le c_1({\mathit{\tau }}^2+h^4),1\le i\le M-1,1\le n\le N-1.\end{array}$$2.18 ), we have$$\begin{array}{cc}\hfill {∥e^n∥}_{\infty }& \le e^{2cT}\left({∥e^0∥}_{\infty }+2\mathit{\tau }\sum _{l=1}^n{∥g^l∥}_{\infty }\right)\hfill \\ \hfill & \le e^{2cT}\left(2n\mathit{\tau }{c}_1({\mathit{\tau }}^2+h^4)\right)\hfill \\ \hfill & \le e^{2cT}\left(2T{c}_1({\mathit{\tau }}^2+h^4)\right)\hfill \\ \hfill & \le \tilde{c}\left({\mathit{\tau }}^2+h^4\right),\hfill \end{array}$$which completes the proof. $\square$

4 Numerical results

In this section, we present the numerical results of the new method on two test problems. We tested the accuracy and stability of the method for different values of $h$ and $\mathit{\tau }$. We performed our computations using Matlab 7 software on a Pentium IV, 2800 MHz CPU machine with 2 Gbyte of memory. To illustrate the accuracy of the method and to compare with other methods in the literature, we compute the following error norms:4.1 $$\begin{array}{cc}\hfill E_{\infty }(h,\mathit{\tau })& =max\left\{max\left|U_i^n-u_i^n\right|\right\},F_{\infty }(h,\mathit{\tau })=max\left|P^n-p^n\right|,\hfill \\ \hfill & 0\le i\le M,0\le n\le N.\hfill \end{array}$$4.1 Also we investigate a measurement error in $E(t)$ for both test problems. Let $\mathbf{E}={(E(t_0),E(t_1),\cdots ,E(t_N))}^T$, then we will replace exact value of $E(t)$ by noisy data given as follows4.2 $$\begin{array}{c}\hfill {\mathbf{E}}_{\mathit{ϵ}}=\mathbf{E}+\mathit{ϵ}randn(size(\mathbf{E})).\end{array}$$4.2 The function ‘ randn(.)’ generates arrays of random numbers whose elements are normally distributed and it is realized using the MATLAB function randn.

4.1 Test problem 1

Consider the parabolic problem with control parameter [15]$$\begin{array}{cc}& \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+[{\mathit{\pi }}^2-{(t+1)}^2]e^{-t^2}[cos(\mathit{\pi }x)+sin(\mathit{\pi }x)],0<x<1,0<t\le 1,\hfill \\ \hfill & u(x,0)=cos(\mathit{\pi }x)+sin(\mathit{\pi }x),0<x<1,\hfill \\ \hfill & u(0,t)=e^{-t^2},u(1,t)=-e^{-t^2},0\le t\le 1,\hfill \\ \hfill & u(0.25,t)=\sqrt{2}{e}^{-t^2},0\le t\le 1.\hfill \end{array}$$The exact solution is given as follows:$$\begin{array}{c}\hfill u(x,t)=e^{-t^2}[cos(\mathit{\pi }x)+sin(\mathit{\pi }x)],p(t)=1+t^2.\end{array}$$Test problem 1 is a direct problem, used to test the proposed compact scheme formulation against mentioned analytic solution. We solve this problem with the method presented in this article with several values of $h$ and $\mathit{\tau }$ at final time $T=1$. In Tables 1 and 2, we compare the absolute error of some technique for the solution of this test problem and report the CPU time of proposed method in Tables 1 and 2. As we see the results of present method are better from the results of [15, 40]. It is compatible with theoretical results, since method of [15] is of order $\mathcal{O}(\mathit{\tau }+h^2)$ and although the method of [40] is of order $\mathcal{O}({\mathit{\tau }}^2+h^4)$, but it is a linearized compact difference scheme.

Table 1. Comparison of absolute error in $u(x,1)$ for several methods.

M	N	Crandall [15]	Compact [40]	Present method	CPU time (s)
40	80	$8.098521\times {10}^{-2}$	$3.001612\times {10}^{-3}$	$1.0325\times {10}^{-14}$	0.038095
80	320	$2.378824\times {10}^{-2}$	$1.847058\times {10}^{-4}$	$2.8866\times {10}^{-15}$	0.301837
160	1280	$6.191500\times {10}^{-3}$	$1.153267\times {10}^{-5}$	$4.9960\times {10}^{-15}$	3.828022
320	5120	$1.563503\times {10}^{-3}$	$3.207327\times {10}^{-7}$	$2.1261\times {10}^{-14}$	61.293867

Table 2. Comparison of absolute error in $p(t)$ for several methods.

M	N	Crandall [15]	Compact [40]	Present method
40	80	$2.082863$	$7.537490\times {10}^{-2}$	$7.5456\times {10}^{-6}$
80	320	$6.086413\times {10}^{-1}$	$4.638067\times {10}^{-3}$	$2.6083\times {10}^{-7}$
160	1280	$1.581301\times {10}^{-1}$	$2.895918\times {10}^{-4}$	$1.6877\times {10}^{-8}$
320	5120	$3.991209\times {10}^{-2}$	$1.809814\times {10}^{-5}$	$3.5533\times {10}^{-9}$

Table 3. Comparison of absolute error in $u(x,1)$ for several methods.

	$h=1/50,\mathit{\tau }=6.6667e-005$			$h=1/40,\mathit{\tau }=0.01$
$x_i$	Saulyev I [16]	Saulyev II [16]	MOL [20]	Present method
0.1	$8.3\times {10}^{-3}$	$8.0\times {10}^{-3}$	$1.9219\times {10}^{-7}$	$1.3323\times {10}^{-15}$
0.2	$8.5\times {10}^{-3}$	$8.0\times {10}^{-3}$	$5.7795\times {10}^{-8}$	$3.3307\times {10}^{-16}$
0.3	$8.5\times {10}^{-3}$	$8.0\times {10}^{-3}$	$5.0769\times {10}^{-8}$	$2.1094\times {10}^{-15}$
0.4	$8.7\times {10}^{-3}$	$8.3\times {10}^{-3}$	$1.3041\times {10}^{-7}$	$1.7764\times {10}^{-15}$
0.5	$8.6\times {10}^{-3}$	$8.8\times {10}^{-3}$	$1.8180\times {10}^{-7}$	$1.1102\times {10}^{-16}$
0.6	$8.5\times {10}^{-3}$	$8.9\times {10}^{-3}$	$2.0885\times {10}^{-7}$	$8.8818\times {10}^{-16}$
0.7	$8.3\times {10}^{-3}$	$8.5\times {10}^{-3}$	$2.1800\times {10}^{-7}$	$1.0547\times {10}^{-15}$
0.8	$8.4\times {10}^{-3}$	$8.7\times {10}^{-3}$	$2.1716\times {10}^{-7}$	$1.2490\times {10}^{-16}$
0.9	$8.5\times {10}^{-3}$	$8.9\times {10}^{-3}$	$2.1463\times {10}^{-7}$	$3.6082\times {10}^{-16}$

Also Tables 3 and 4 show the absolute error obtain in approximating $u(x,1)$ and $p(t)$ for some methods in the literature. Again we see that the results of the present method are very satisfactory. Figure 1 presents the absolute errors for both unknown function and unknown control parameter. We show the noise in $E(t)$ and resulting error in approximate solution with $h=1/40$, $\mathit{\tau }=1/100$ and $\mathit{ϵ}=0.01$ in Figure 2 and $\mathit{ϵ}=0.1$ in Figure 3. As we see, the proposed method produces satisfactory results and is stable respect to noise in the $E(t)$.

Table 4. Comparison of absolute error in $p(t)$ for several methods.

	$h=1/50,\mathit{\tau }=6.6667e-005$			$h=1/40,\mathit{\tau }=0.01$
t	Saulyev I [16]	Saulyev II [16]	MOL [20]	Present method
0.1	$9.8\times {10}^{-3}$	$9.5\times {10}^{-3}$	$6.3751\times {10}^{-5}$	$4.170395\times {10}^{-6}$
0.2	$9.7\times {10}^{-3}$	$9.3\times {10}^{-3}$	$5.6986\times {10}^{-5}$	$4.170405\times {10}^{-6}$
0.3	$9.6\times {10}^{-3}$	$9.2\times {10}^{-3}$	$3.3660\times {10}^{-4}$	$4.170393\times {10}^{-6}$
0.4	$9.4\times {10}^{-3}$	$9.1\times {10}^{-3}$	$1.6461\times {10}^{-4}$	$4.170401\times {10}^{-6}$
0.5	$9.2\times {10}^{-3}$	$8.8\times {10}^{-3}$	$4.0586\times {10}^{-4}$	$4.170394\times {10}^{-6}$
0.6	$9.3\times {10}^{-3}$	$8.8\times {10}^{-3}$	$3.9383\times {10}^{-5}$	$4.170405\times {10}^{-6}$
0.7	$9.3\times {10}^{-3}$	$8.7\times {10}^{-3}$	$4.6266\times {10}^{-4}$	$4.170395\times {10}^{-6}$
0.8	$9.1\times {10}^{-3}$	$8.6\times {10}^{-3}$	$4.7802\times {10}^{-4}$	$4.170405\times {10}^{-6}$
0.9	$9.0\times {10}^{-3}$	$8.4\times {10}^{-3}$	$2.1816\times {10}^{-3}$	$4.170388\times {10}^{-6}$
1.0	$8.9\times {10}^{-3}$	$8.3\times {10}^{-3}$	$2.2165\times {10}^{-4}$	$4.170416\times {10}^{-6}$

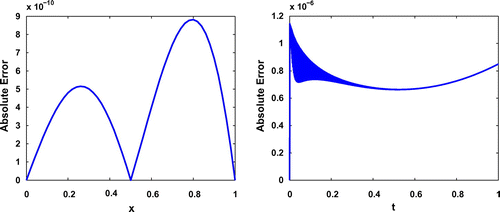
Figure 1. Errors obtained in approximating $u(x,1)$ (left panel) and $p(t)$ (right panel) with $h=1/80$ and $\mathit{\tau }=0.01$ for Test Problem 1.

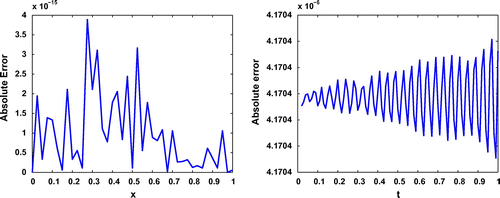
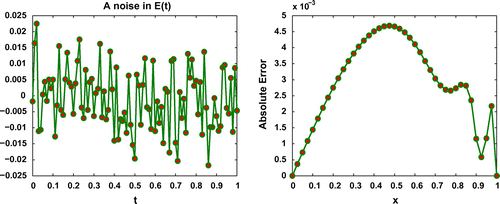
Figure 2. A noise ($\mathit{ϵ}randn(size(\mathbf{E}))$) in $E(t)$ (left panel) and resulting absolute error in approximating $u$($x$,1) (right panel) for Test problem 1 with $h=1/40$, $\mathit{\tau }=1/100$ and $\mathit{ϵ}=0.01$.

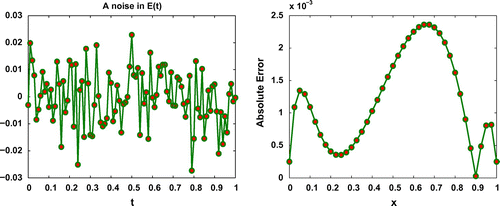
Figure 3. A noise ($\mathit{ϵ}randn(size(\mathbf{E}))$) in $E(t)$ (left panel) and resulting absolute error in approximating $u$($x$,1) (right panel) for Test problem 1 with $h=1/40$, $\mathit{\tau }=1/100$ and $\mathit{ϵ}=0.1$.

In Table 5 we present the resulting error at different times for some positions with $h=1/40$ and $\mathit{\tau }=1/100$ for Test problem 1.

4.2 Test problem 2

Consider the problem (1.11.1 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }t}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+p(t)u+\mathit{\varphi }(x,t),0<x<1,0<t\le T,\end{array}$$1.1 )–(1.41.4 $$\begin{array}{c}\hfill u(x^{}\ast ,t)=E(t),0\le t\le T,\end{array}$$1.4 ) with $T=1$, $x^{\ast }=\frac{1}{2}$,$$\begin{array}{c}\hfill f(x)=-\frac{1}{2}sin(x)exp(-x^2),\end{array}$$$$\begin{array}{c}\hfill g_0(x)=0,g_1(x)=-\frac{1}{2}sin(1)exp(-t^3-t^2-1),\end{array}$$$$\begin{array}{c}\hfill E(t)=-\frac{1}{2}sin\left(\frac{1}{2}\right)exp\left(-t^3-t^2-\frac{1}{4}\right),\end{array}$$$$\begin{array}{c}\hfill \mathit{\varphi }(x,t)=exp\left(-t^3-t^2-x^2\right)\left(tsin(x)-2sin(x)-2xcos(x)+2x^{2}sin(x)\right).\end{array}$$The exact solutions are given as follows:$$\begin{array}{c}\hfill u(x,t)=-\frac{1}{2}sin(x)exp(-t^3-t^2-x^2),p(t)=-3t^2-1.\end{array}$$This test problem is a direct inverse problem, used to test the proposed compact scheme formulation against mentioned analytic solution. Table 6 presents the numerical and the exact solutions of $u(x,t)$ at some points. Also Table 7 gives the numerical and the exact solutions of $p(t)$ at some points.

Table 5. Errors at different times for some positions with $h=1/40$ and $\mathit{\tau }=1/100$.

T	$x=0.2$	$x=0.4$	$x=0.6$
0.1	$2.2204\times {10}^{-16}$	$8.8818\times {10}^{-16}$	$7.7716\times {10}^{-16}$
0.3	$1.1102\times {10}^{-15}$	$8.8818\times {10}^{-16}$	$1.1102\times {10}^{-16}$
0.5	$1.1102\times {10}^{-15}$	$3.3307\times {10}^{-16}$	$2.1203\times {10}^{-16}$
0.7	$1.1102\times {10}^{-16}$	$1.7764\times {10}^{-15}$	$7.2164\times {10}^{-16}$
0.9	$2.2204\times {10}^{-16}$	$1.1102\times {10}^{-15}$	$5.5511\times {10}^{-17}$

Table 6. Numerical results and exact solutions of $u(x,1)$ at some points.

$x_i$
M	N	0.2	0.4	0.6	CPU time (s)
40	80	$-0.01291640$	$-0.02245489$	$-0.02665679$	0.036738
80	320	$-0.01291636$	$-0.02245486$	$-0.02665683$	0.304918
160	1280	$-0.01291635$	$-0.02245485$	$-0.026656683$	4.072580
320	5120	$-0.01291635$	$-0.02245485$	$-0.02665683$	63.530038
$u(x,1)$	-	$-0.01291635$	$-0.02245485$	$-0.02665683$

Table 7. Numerical results and exact solutions of $p(t)$ at some points.

$t_i$
M	N	0.2	0.4	0.6	0.8
40	80	$-1.11994954$	$-1.47994122$	$-2.07994051$	$-2.91994962$
80	320	$-1.1199982$	$-1.47999632$	$-2.07999628$	$-2.91999685$
160	1280	$-1.11999980$	$-1.479999977$	$-2.07999976$	$-2.91999980$
320	5120	$-1.11999998$	$-1.47999998$	$-2.07999998$	$-2.91999998$
p(t)	-	$-1.12000000$	$-1.48000000$	$-2.08000000$	$-2.92000000$

Table 8. Absolute values of the errors in approximating $u(x,1)$.

$x_i$
M	N	0.2	0.4	0.6	0.8
40	80	$5.0333\times {10}^{-8}$	$3.5002\times {10}^{-8}$	$4.3136\times {10}^{-8}$	$9.6377\times {10}^{-8}$
80	320	$3.1391\times {10}^{-9}$	$2.1830\times {10}^{-9}$	$2.6902\times {10}^{-9}$	$6.0103\times {10}^{-9}$
160	1280	$1.9617\times {10}^{-10}$	$1.3642\times {10}^{-10}$	$1.6812\times {10}^{-10}$	$3.7559\times {10}^{-10}$
320	5120	$1.2261\times {10}^{-11}$	$8.5261\times {10}^{-12}$	$1.0507\times {10}^{-11}$	$2.3474\times {10}^{-11}$

Table 9. Absolute values of the errors in approximating $p(t)$.

$x_i$
M	N	0.2	0.4	0.6	$0.8$
40	80	$5.0456\times {10}^{-5}$	$5.8778\times {10}^{-5}$	$5.9484\times {10}^{-5}$	$5.0371\times {10}^{-5}$
80	320	$3.1704\times {10}^{-6}$	$3.6714\times {10}^{-6}$	$3.7152\times {10}^{-6}$	$3.1437\times {10}^{-6}$
160	1280	$1.9805\times {10}^{-7}$	$2.2930\times {10}^{-7}$	$2.3224\times {10}^{-7}$	$1.9652\times {10}^{-7}$
320	5120	$1.2888\times {10}^{-8}$	$1.3480\times {10}^{-8}$	$1.4167\times {10}^{-8}$	$1.2226\times {10}^{-8}$

Table 10. Errors obtained in approximating $u(x,1)$ and $p(t)$.

M	N	$E_{\infty }(h,\mathit{\tau })$	$F_{\infty }(h,\mathit{\tau })$
40	80	$9.63772527\times {10}^{-8}$	$6.03303129\times {10}^{-5}$
80	320	$6.01039494\times {10}^{-9}$	$3.76885527\times {10}^{-6}$
160	1280	$3.75599260\times {10}^{-10}$	$2.35594598\times {10}^{-7}$
320	5120	$2.34763250\times {10}^{-11}$	$1.66652096\times {10}^{-8}$

Table 11. Comparison of absolute error in approximating $u(x,1)$ with $h=\frac{1}{50},\mathit{\tau }=0.001$.

$x_i$	Exact value	MOL [20]	Present method
0.10	$-0.00668827$	$5.76430077\times {10}^{-9}$	$2.8836\times {10}^{-10}$
0.20	$-0.01291635$	$4.86355500\times {10}^{-9}$	$4.7905\times {10}^{-10}$
0.30	$-0.01827602$	$3.57758127\times {10}^{-9}$	$5.0098\times {10}^{-10}$
0.40	$-0.02245485$	$1.91489006\times {10}^{-9}$	$3.3019\times {10}^{-10}$
0.50	$-0.02526554$	$0$	$0$
0.60	$-0.02665683$	$1.94571320\times {10}^{-9}$	$4.0129\times {10}^{-10}$
0.70	$-0.02670603$	$3.64833393\times {10}^{-9}$	$7.4437\times {10}^{-10}$
0.80	$-0.02559572$	$4.83831276\times {10}^{-9}$	$8.8099\times {10}^{-10}$
0.90	$-0.02358009$	$5.30474325\times {10}^{-9}$	$6.6972\times {10}^{-10}$

As we see the numerical solutions are in good agreement with the exact solutions. Tables 8 and 9 show the absolute error obtained in approximating $u(x,1)$ and $p(t)$ for some points.

Table 10 shows the $E_{\infty }(h,\mathit{\tau })$ and $F_{\infty }(h,\mathit{\tau })$ errors of the difference scheme, respectively.

Table 12. Comparison of absolute error in approximating $p(t)$ with $h=\frac{1}{50},\mathit{\tau }=0.001$.

t	Exact value	MOL [20]	Present method
0.10	$-1.03000000$	$1.60042767\times {10}^{-3}$	$7.3556\times {10}^{-7}$
0.20	$-1.12000000$	$2.31799154\times {10}^{-6}$	$7.2429\times {10}^{-7}$
0.30	$-1.27000000$	$8.39331809\times {10}^{-5}$	$6.9548\times {10}^{-7}$
0.40	$-1.48000000$	$2.34966456\times {10}^{-4}$	$6.7260\times {10}^{-7}$
0.50	$-1.75000000$	$3.42279236\times {10}^{-3}$	$6.7260\times {10}^{-7}$
0.60	$-2.08000000$	$2.21312062\times {10}^{-3}$	$6.6262\times {10}^{-7}$
0.70	$-2.47000000$	$1.07885240\times {10}^{-3}$	$6.6771\times {10}^{-7}$
0.80	$-2.92000000$	$3.06771160\times {10}^{-4}$	$6.8867\times {10}^{-7}$
0.90	$-3.43000000$	$5.62716894\times {10}^{-4}$	$7.2583\times {10}^{-7}$

Figure 4. Errors obtained in approximating $u(x,1)$ (left panel) and $p(t)$ (right panel) with $h=1/50$ and $\mathit{\tau }=0.001$.

Figure 5. Error versus increasing $M$ with $\mathit{\tau }=0.0001$ (left panel) and versus imcreasing $N$ with $h=0.01$ (right panel).

In Tables 11 and 12, we compare the numerical results of the proposed method with MOL method [20] when $h=\frac{1}{50}$ and $▵t=0.001$. As we see the present method has better results. Figure 4 presents the errors obtained in approximating $u(x,1)$ (left panel) and $p(t)$ (right panel) with $h=1/50$ and $\mathit{\tau }=0.001$.

Table 13. Errors, computational orders and CPU time in Test problem 2 for $u(x,1)$.

h	$\frac{1}{10}$	$\frac{1}{20}$	$\frac{1}{40}$	$\frac{1}{80}$
Error (with $\mathit{\tau }=0.0001$)	$1.7005\times {10}^{-7}$	$1.0565\times {10}^{-8}$	$6.6499\times {10}^{-10}$	$4.7338\times {10}^{-11}$
C-Order	$-$	$4.0086$	$3.9898$	$3.8123$
CPU time (s)	$0.638048$	$1.776574$	$3.368969$	$9.513341$
$\mathit{\tau }$	$\frac{1}{60}$	$\frac{1}{120}$	$\frac{1}{240}$	$\frac{1}{480}$
Error (with $h=0.01$)	$1.7043\times {10}^{-7}$	$4.2502\times {10}^{-8}$	$1.0630\times {10}^{-8}$	$2.6696\times {10}^{-9}$
C-Order	$-$	$2.0036$	$1.9994$	$1.9934$
CPU time (s)	$0.098085$	$0.169225$	$0.347135$	$0.682694$

Table 14. Errors at different times for some positions with $h=1/40$ and $\mathit{\tau }=1/100$.

T	$x=0.2$	$x=0.4$	$x=0.6$
0.1	$3.2970\times {10}^{-7}$	$2.3141\times {10}^{-7}$	$2.9037\times {10}^{-7}$
0.3	$2.9148\times {10}^{-7}$	$2.3256\times {10}^{-7}$	$2.9148\times {10}^{-7}$
0.5	$2.8319\times {10}^{-7}$	$1.9841\times {10}^{-7}$	$2.4793\times {10}^{-7}$
0.7	$1.7095\times {10}^{-7}$	$1.1953\times {10}^{-7}$	$1.4881\times {10}^{-7}$
0.9	$6.6029\times {10}^{-8}$	$4.6033\times {10}^{-8}$	$5.6999\times {10}^{-8}$

Figure 6. A noise ($\mathit{ϵ}randn(size(\mathbf{E}))$) in $E(t)$ (left panel) and resulting absolute error in approximating $u$($x$,1) (right panel) for Test problem 2 with $h=1/40$, $\mathit{\tau }=1/100$ and $\mathit{ϵ}=0.01$.

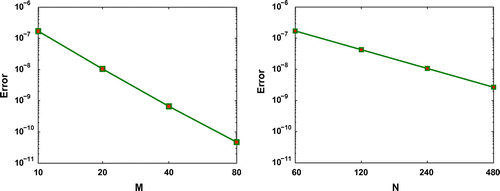
To investigate the order of method numerically, in Figure 5 we plot the error versus $N$ with $M$ fixed and vice versa, where the log-log scaling is used for the axes. The slope of the error curves show the order of accuracy of proposed method. To more clarify the results, we calculate the computational orders (denoted by C-Order) with the following formula$$C-Order=\frac{log\left(\frac{E_1}{E_2}\right)}{log\left(\frac{h_1}{h_2}\right)},$$in which $E_1$ and $E_2$ are errors correspond to grids with mesh size $h_1$ and $h_2$, respectively. Table 13 presents the computational orders and CPU time in Test problem 2 for $u(x,1)$.

Table 13 shows the fourth and second order of accuracy of method in space and time components, respectively. In Table 14, we present the resulting error at different times for some positions with $h=1/40$ and $\mathit{\tau }=1/100$ for Test problem 2.

Figure 7. A noise ($\mathit{ϵ}randn(size(\mathbf{E}))$) in $E(t)$ (left panel) and resulting absolute error in approximating $u$($x$,1) (right panel) for Test problem 2 with $h=1/40$, $\mathit{\tau }=1/100$ and $\mathit{ϵ}=0.1$.

We show the noise in $E(t)$ and resulting error in approximate solution with $h=1/40$, $\mathit{\tau }=1/100$ and $\mathit{ϵ}=0.01$ in Figure 6 and $\mathit{ϵ}=0.1$ in Figure 7 for Test problem 2. As we see, the proposed method produces satisfactory results and is stable respect to noise in the $E(t)$.

5 Conclusion

In this paper we introduced a high order scheme for determining unknown control parameter and unknown solution of parabolic inverse problem with overspecification at a point in the spatial domain. In the proposed numerical scheme we replaced the space derivative with a fourth-order compact finite difference. We proved the stability and convergence of proposed scheme and showed that the convergence order is $\mathcal{O}({\mathit{\tau }}^2+h^4)$. Numerical results corroborate the theoretical results and high accuracy of proposed scheme in comparison with the other methods in the literature. Also we investigated the effect of noise on the data and obtained satisfactory results with new method.

Acknowledgements

The authors would like to thank the five referees and the associate editor for the careful reading of the paper and the thoughtful comments and suggestions, which have considerably improved the quality of the paper.

Notes

The authors are also thankful to the University of Kashan for the financial support [grant number 364989/1] of this work.