A nonlinear integral equation method for the inverse scattering problem by sound-soft rough surfaces

Abstract

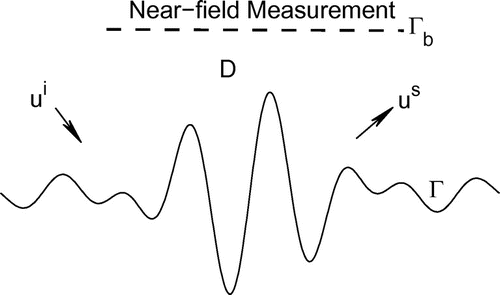
In this paper, we consider the two-dimensional (2D) inverse acoustic scattering by a sound-soft, infinite rough surface. Our approach to this problem is based on the nonlinear integral equation method which was developed by Kress and Rundell for bounded obstacles. By using multiple frequency data, we derive a stable and accurate reconstruction method to image the profile of the rough surface. Numerical experiments are presented to illustrate the effectiveness of the inversion method.

Keywords:

• Inverse scattering
• rough surface
• sound-soft
• nonlinear integral equation
• multiple frequency

AMS Subject Classifications:

• 65R32
• 35J05
• 78A46
• 45Q05

1 Introduction

In this paper, we study the 2D Dirichlet boundary value problem for the Helmholtz equation $△u+k^{2}u=0$ in a nonlocally perturbed half-plane. The Dirichlet boundary problem models time-harmonic acoustic scattering by a sound-soft, infinite rough surface as well as electromagnetic wave propagation over outdoor ground, sea surfaces or optical grating.

Figure 1. Geometrical setting of the scattering problem.

As in Figure 1, let the scattering surface $\mathrm{\Gamma }$ be the graph of some function $f$, i.e.$$\begin{array}{c}\hfill \mathrm{\Gamma }:=\{x=(x_1,x_2)\in {\mathbb{R}}^2:x_2=f(x_1)\},\end{array}$$and let the space above $\mathrm{\Gamma }$ be denoted by $D$, i.e.$$\begin{array}{c}\hfill D:=\{x=(x_1,x_2)\in {\mathbb{R}}^2:x_2>f(x_1)\}.\end{array}$$Whenever we wish to express the dependence of $\mathrm{\Gamma }$ and $D$ on the boundary function $f$, we write ${\mathrm{\Gamma }}_f$ for $\mathrm{\Gamma }$ and $D_f$ for $D$. Let $u^i$ be the incident field and $u^s$ be the scattered field. The total field $u:=u^i+u^s$ satisfies the Helmholtz equation in $D$, and vanishes on $\mathrm{\Gamma }$ for a sound-soft surface. In order to ensure the uniqueness of the solution, we assume that $u^s$ satisfies some radiation condition along with the following growth condition in the $x_2$-direction: for some $a\in \mathbb{R}$1.1 $$\begin{array}{c}\hfill \underset{x\in D}{sup}{x}_2^a|u^s(x)|<+\infty .\end{array}$$1.1 In this paper, $u^s$ is required to satisfy the upward propagating radiation condition (UPRC) [1]: for some $h>f_{+}:={sup}_{x_1\in \mathbb{R}}f(x_1)\text{and}\mathit{\varphi }\in L^{\infty }({\mathrm{\Gamma }}_h)$1.2 $$\begin{array}{c}\hfill u^s(x)=2{\int }_{{\mathrm{\Gamma }}_h}\frac{\mathit{\partial }\mathrm{\Phi }(x,y)}{\mathit{\partial }{y}_2}\mathit{\varphi }(y)ds(y),x\in U_h,\end{array}$$1.2 where ${\mathrm{\Gamma }}_h:=\{x=(x_1,x_2)\in {\mathbb{R}}^2|x_2=h\}$ and $U_h:=\{x=(x_1,x_2)\in {\mathbb{R}}^2|x_2>h\}$. The properties of UPRC are shown in Theorem 2.9 of [1].

Here, we need a function space $BC(V):=\{\mathit{\phi }(x):\mathit{\phi }(x)\text{is bounded and continuous on V}\}$ for $V\subset {\mathbb{R}}^n$$(n=1,2)$, which is a Banach space under the norm ${||\mathit{\phi }||}_{\infty ,V}:={sup}_{x\in V}|\mathit{\phi }(x)|$. The above problem of scattering by an infinite sound-soft rough surface can now be formulated as the following Dirichlet boundary value problem (DP) for the scattered field $u^s$: given $g=-u^i\in BC(\mathrm{\Gamma })$, determine $u^s\in C^2(D)\cap C(\overline{D})$ such that:

(1)	$u^s$ is a solution of the Helmholtz equation $▵u^s+k^2{u}^s=0\text{in}D;$
(2)	$u^s=g\text{on}\mathrm{\Gamma };$
(3)	$u^s$ satisfies (1.11.1 $$\begin{array}{c}\hfill \underset{x\in D}{sup}{x}_2^a|u^s(x)|<+\infty .\end{array}$$1.1 );
(4)	$u^s$ satisfies the UPRC (1.21.2 $$\begin{array}{c}\hfill u^s(x)=2{\int }_{{\mathrm{\Gamma }}_h}\frac{\mathit{\partial }\mathrm{\Phi }(x,y)}{\mathit{\partial }{y}_2}\mathit{\varphi }(y)ds(y),x\in U_h,\end{array}$$1.2 ).

Many authors have studied the well-posedness of (DP) via integral equation methods, see Refs. [2–6]. For example in [6], the authors represented the scattered field $u^s$ in the form of a combined double- and single-layer potential with a parameter, then reduced the problem (DP) to a boundary integral equation in $\mathbb{R}$, by the generalized Fredholm theory established by Chandler-Wilde and Zhang in [7, 8], and further obtained the well-posedness of the boundary integral equation in $BC(\mathbb{R})$ under some assumption with respect to the parameter in the potential. The unique solvability of the boundary integral equation in $BC(\mathbb{R})$ has been extended to the $L^p$ spaces for $1\le p\le \infty$, for details see [9]. For the numerical solution of the boundary integral equation, we use the Nyström method established by Meier et al. [10] where the stability and convergence of the method is also established.

The inverse scattering problem we are concerned with is: given the incident field $u^i$ and the near-field $u^s$ on some open subset $S\subset D$, determine the scattering surface $\mathrm{\Gamma }$ which causes such a near-field on $S$.

Chandler-Wilde and Ross studied the inverse problem for scattering by infinite surfaces in a lossy medium $(\mathfrak{I}k>0)$ in [2] where they imposed the following growth condition on $u^s$: $|u^s(x)|\le Cexp(\mathit{\theta }|x|)$ for some $C>0$ and $\mathit{\theta }<\mathfrak{I}k$. Under the growth condition, they proved that the inverse problem has at most one solution.

For numerical investigation of the inverse problem, many authors obtained the accurate reconstructions by a variety of methods. For global rough surface, Burkard and Potthast studied the inverse problem in ${\mathbb{R}}^3$ via the Kirsch-Kress scheme [11] and developed a time-domain probe method for rough surface reconstruction in ${\mathbb{R}}^3$,[12] and Lines used Point Source Method to reconstruct perfectly conducting unbounded rough surfaces when the incident field is a time-harmonic point source in [13]. An extension of the Point Source Method is also given in [13] when the incident field is not necessarily time-harmonic. For local rough surface, Bao and Lin [14] developed a stable and convergent reconstruction algorithm by multiple frequency measurements of near-field, and Zhang and Zhang [15] proposed a novel integral equation formulation defined on a bounded curve and obtained an accurate reconstruction of the profile from multiple frequency far-field data. The main ideas of employing multiple frequency data include overcoming the ill-posedness of the inverse problem and increasing resolution limited by Rayleigh’s criteria. For more related work on multiple frequency data, we refer the readers to [16–18] and the references therein. In this paper, our attention is restricted to the reconstruction of a global sound-soft rough surface by multiple frequency near-field data, corresponding to incident plane waves and point sources.

For solving the inverse scattering problem, there are many iterative methods, for example Newton-type iterations. The derivatives occurring in the iterative process can be obtained through associated boundary value problems.[19] For simplicity, in [20] Kress and Rundell developed an iterative method named nonlinear integral equations in which the derivatives can be explicitly expressed in terms of integral operators rather than boundary value problems. This reduces the computational costs. Recently, nonlinear integral equation method is very popular. Ivanyshyn and Johansson used it to reconstruct the shape of a planar acoustically sound-soft obstacle in [21]. By the same method, Ivanyshyn and Kress reconstructed the surface impedance function of a three-dimensional acoustic scatterer with a known shape in [22]. Furthermore, in [23] they studied the inverse boundary value problems for inclusions and cracks via the method. For the 2D inverse electrical impedance problem in the case of piecewise constant conductivities, Eckel and Kress reconstructed the shape and conductivities accurately with a finite number of Cauchy pairs in [24]. To the best of our knowledge, there is no paper to study the method for rough surface scattering. Therefore, the main purpose of this paper is to extend the nonlinear integral equation method to rough surface scattering.

The paper is organized as follows. In Section 2, we focus on the well-posedness of the direct scattering problem. This is followed by the study of the Nyström method in Section 3. After describing the nonlinear integral equation method for the inverse scattering problem in Section 4, we conclude with several numerical experiments in Section 5.

2 An integral equation formulation of the direct problem

In this section, we propose an integral equation formulation developed in [6], and establish the corresponding unique solvability in $BC(\mathrm{\Gamma })$. For detailed discussions, we refer to [6].

For two positive constants $c_1$, $c_2$, we define $B$ by$$\begin{array}{c}\hfill B=B(c_1,c_2):=\{f\in C^2(\mathbb{R})|f(s)\ge c_1,s\in {\mathbb{R}\text{and}\Vert f\Vert }_{C^2(\mathbb{R})}\le c_2\}.\end{array}$$Let the rough surface function $f\in B$ with $f_{-}:={inf}_{x_1\in \mathbb{R}}f(x_1)>0$. We consider two different kinds of incoming waves in this paper. One is an time-harmonic acoustic plane wave $u^i(x)=e^{ikx·d}$, where $k$ is the wave number satisfying  $\mathfrak{R}k>0$ and $\mathfrak{I}k\ge 0$, and $d$ is the incident direction given by $d=(-cos\mathit{\theta },-sin\mathit{\theta })$ with the incident angle $0\le \mathit{\theta }\le \mathit{\pi }$. The other is a sum of several point sources $u^i(x)={\sum }_{j=-n}^n\mathrm{\Phi }(x,z_j)$, where $z_j(j=-n,\dots ,n)$ is the location of the point source, and for $x,z\in {\mathbb{R}}^2,x\ne z$, $\mathrm{\Phi }(x,z):=\frac{i}{4}{H}_0^{(1)}(k|x-z|)$ is the free-space Green’s function for Helmholtz equation while $H_0^{(1)}(y)$ is the Hankel function of the first kind of order zero for $y\in {\mathbb{R}}^2$.

When $u^i(x)=e^{ikx·d}$, from [6] we can look for the solution to the problem (DP) in the form of a combined double- and single-layer potential2.1 $$\begin{array}{c}\hfill u^s(x)={\int }_{\mathrm{\Gamma }}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in D,\end{array}$$2.1 for some $\mathit{\psi }\in BC(\mathrm{\Gamma })$, where $G(x,y):=\mathrm{\Phi }(x,y)-\mathrm{\Phi }(x,y^{\prime })$ is the Dirichlet Green’s function for $▵+k^2$ in the upper half-plane $U_0$, $y=(y_1,y_2),y^{\prime }=(y_1,-y_2)$, $\mathit{\eta }\ne 0$ is an arbitrary complex number to be fixed later and $\mathit{\nu }(y)$ denotes the normal vector at $y\in \mathrm{\Gamma }$ pointing out of $D$.

When $u^i(x)={\sum }_{j=-n}^n\mathrm{\Phi }(x,z_j)$, instead of (2.32.3 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{\mathrm{\Gamma }}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in \mathrm{\Gamma }.\end{array}$$2.3 ) we will find a solution in the following form [25]:2.2 $$\begin{array}{c}\hfill u^s(x)=-\sum _{j=-n}^n\mathrm{\Phi }(x,z_j^{\ast })+{\int }_{\mathrm{\Gamma }}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in D,\end{array}$$2.2 where $z=(z_1,z_2),z^{\ast }=(z_1,\mathit{\lambda }-z_2)$, and $\mathit{\lambda }=\frac{2\mathit{\pi }}{k}$ denotes the wave length. We represent the solution $u^s$ in the form of (2.32.3 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{\mathrm{\Gamma }}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in \mathrm{\Gamma }.\end{array}$$2.3 ), then we can obtain the following theorem (Theorem 3.2 in [6]):

Theorem 2.1

The combined double- and single-layer potential (2.32.3 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{\mathrm{\Gamma }}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in \mathrm{\Gamma }.\end{array}$$2.3 ) satisfies the problem (DP) with $a=-\frac{1}{2}$, provided $\mathit{\psi }\in BC(\mathrm{\Gamma })$ satisfies the boundary integral equation2.3 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{\mathrm{\Gamma }}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in \mathrm{\Gamma }.\end{array}$$2.3

Remark 2.2

It is easy to see that $g(x)=-e^{ikx·d},x\in \mathrm{\Gamma }$ in the case of (2.32.3 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{\mathrm{\Gamma }}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in \mathrm{\Gamma }.\end{array}$$2.3 ). Similarly, for the case of (2.42.4 $$\begin{array}{c}\hfill \mathit{\kappa }(s,t):=2[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\sqrt{1+{[f^{\prime }(t)]}^2}s,t\in \mathbb{R},s\ne t.\end{array}$$2.4 ), we can get (2.52.5 $$\begin{array}{c}\hfill (K\tilde{\mathit{\psi }})(s):={\int }_{\mathbb{R}}\mathit{\kappa }(s,t)\tilde{\mathit{\psi }}(t)dt,s\in \mathbb{R}.\end{array}$$2.5 ) with $g(x)={\sum }_{j=-n}^n[\mathrm{\Phi }(x,z_j)-\mathrm{\Phi }(x,z_j^{\ast })]$, a sum of Dirichlet Green functions. This implies that $\mathit{\psi }(x)=O(|x{|}^{-\frac{3}{2}})$ as $|x|\to \infty$ for $x\in \mathrm{\Gamma }$, which is the advantage of the new form (2.42.4 $$\begin{array}{c}\hfill \mathit{\kappa }(s,t):=2[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\sqrt{1+{[f^{\prime }(t)]}^2}s,t\in \mathbb{R},s\ne t.\end{array}$$2.4 ). We may choose suitable point source positions $z_j$ to let $z_j^{\ast }$ below $\mathrm{\Gamma }$. Then the form (2.42.4 $$\begin{array}{c}\hfill \mathit{\kappa }(s,t):=2[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\sqrt{1+{[f^{\prime }(t)]}^2}s,t\in \mathbb{R},s\ne t.\end{array}$$2.4 ) satisfies the condition (3) of the problem (DP) with $a=-\frac{1}{2}$.

For $x,y\in \mathrm{\Gamma }$, we denote $x=(s,f(s)),y=(t,f(t))$. Then we can represent the boundary integral Equation (2.52.5 $$\begin{array}{c}\hfill (K\tilde{\mathit{\psi }})(s):={\int }_{\mathbb{R}}\mathit{\kappa }(s,t)\tilde{\mathit{\psi }}(t)dt,s\in \mathbb{R}.\end{array}$$2.5 ) in $BC(\mathbb{R})$ by defining$$\begin{array}{c}\hfill \tilde{\mathit{\psi }}(s):=\mathit{\psi }(s,f(s))\in BC(\mathbb{R}),\tilde{g}(s):=g(s,f(s))\in BC(\mathbb{R}),s\in \mathbb{R},\end{array}$$and the integral kernel $\mathit{\kappa }$:2.4 $$\begin{array}{c}\hfill \mathit{\kappa }(s,t):=2[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\sqrt{1+{[f^{\prime }(t)]}^2}s,t\in \mathbb{R},s\ne t.\end{array}$$2.4 With the kernel, we can rewrite the integral operator in (2.52.5 $$\begin{array}{c}\hfill (K\tilde{\mathit{\psi }})(s):={\int }_{\mathbb{R}}\mathit{\kappa }(s,t)\tilde{\mathit{\psi }}(t)dt,s\in \mathbb{R}.\end{array}$$2.5 ) in the simple form:2.5 $$\begin{array}{c}\hfill (K\tilde{\mathit{\psi }})(s):={\int }_{\mathbb{R}}\mathit{\kappa }(s,t)\tilde{\mathit{\psi }}(t)dt,s\in \mathbb{R}.\end{array}$$2.5 We will denote $K$ by $K_f$ to express the dependence of the rough surface $f$. Then (2.52.5 $$\begin{array}{c}\hfill (K\tilde{\mathit{\psi }})(s):={\int }_{\mathbb{R}}\mathit{\kappa }(s,t)\tilde{\mathit{\psi }}(t)dt,s\in \mathbb{R}.\end{array}$$2.5 ) becomes:2.6 $$\begin{array}{c}\hfill (I-K_f)\tilde{\mathit{\psi }}=-2\tilde{g}\end{array}$$2.6 where $I$ is the identity operator. For the solvability of (2.82.6 $$\begin{array}{c}\hfill (I-K_f)\tilde{\mathit{\psi }}=-2\tilde{g}\end{array}$$2.6 ) in $BC(\mathbb{R})$, we have the following theorem (Theorem 3.4 in [6]):

Theorem 2.3

Let $\mathfrak{R}(\overline{\mathrm{k}}\mathit{\eta })>0$. Then for all $f\in B$ the integral operator $I-K_f:BC(\mathbb{R})\to BC(\mathbb{R})$ is bijective (and so boundedly invertible) with$$\begin{array}{c}\hfill \underset{f\in B}{sup}\Vert {(I-K_f)}^{-1}\Vert <+\infty \end{array}$$Thus, the integral Equations (2.52.5 $$\begin{array}{c}\hfill (K\tilde{\mathit{\psi }})(s):={\int }_{\mathbb{R}}\mathit{\kappa }(s,t)\tilde{\mathit{\psi }}(t)dt,s\in \mathbb{R}.\end{array}$$2.5 ) and (2.82.6 $$\begin{array}{c}\hfill (I-K_f)\tilde{\mathit{\psi }}=-2\tilde{g}\end{array}$$2.6 ) have exactly one solution for every $f\in B$ and $g\in BC(\mathrm{\Gamma })$, with$$\begin{array}{c}\hfill {\Vert \mathit{\psi }\Vert }_{\infty ,\mathrm{\Gamma }}=\Vert \tilde{\mathit{\psi }}{\Vert }_{\infty }\le C\Vert \tilde{g}{\Vert }_{\infty }=C{\Vert g\Vert }_{\infty ,\mathrm{\Gamma }}\end{array}$$for some constant $C>0$ depending only on $B$ and $k$.

3 The Nyström method for the direct problem

For the numerical solution of the boundary integral Equation (2.82.6 $$\begin{array}{c}\hfill (I-K_f)\tilde{\mathit{\psi }}=-2\tilde{g}\end{array}$$2.6 ), we use the Nyström method based on appropriately weighted numerical quadratures on an equidistant mesh. Colton and Kress used it to obtain the numerical solution of the scattering problem for bounded obstacles in [26]. Meier et al. developed a Nyström method for the scattering problem by rough surfaces and diffraction gratings in [10], where they established stability and convergence of this method and proved that the convergence rates depend on the smoothness of components of the integral kernel. For details of some results in this section, we refer to [10].

In order to introduce the Nyström method, we define some function spaces and integral operators. We denote by $B{C}^n({\mathbb{R}}^m)$ the Banach space of all functions whose derivatives up to order $n$ are bounded and continuous on ${\mathbb{R}}^m$. Furthermore, we define$$\begin{array}{c}\hfill C_{0,\mathit{\pi }}^n({\mathbb{R}}^2):=\{a\in B{C}^n({\mathbb{R}}^2):a(s,t)=0,|s-t|\ge \mathit{\pi }\},\end{array}$$which is a closed subspace of $B{C}^n({\mathbb{R}}^2)$. In addition, let$$\begin{array}{c}\hfill B{C}_p^n(\mathbb{R}):=\{\mathit{\psi }\in B{C}^n{(\mathbb{R}):\Vert \mathit{\psi }\Vert }_{B{C}_p^n(\mathbb{R})}:=\underset{m=0,1,\dots ,n}{sup}{\Vert w_p{\mathit{\psi }}^{(m)}\Vert }_{\infty }<\infty \}\end{array}$$with the weight $w_p(t):={(1+|t|)}^p$ and$$\begin{array}{c}\hfill B{C}_p^n({\mathbb{R}}^2):=\{a\in B{C}^n({\mathbb{R}}^2){:\Vert a\Vert }_{B{C}_p^n({\mathbb{R}}^2)}:=\underset{j,k=0,\dots ,n,j+k\le n}{sup}{\Vert {\tilde{w}}_p{\mathit{\partial }}_1^j{\mathit{\partial }}_2^{k}a\Vert }_{\infty }<\infty \}\end{array}$$with the weight ${\tilde{w}}_p(s,t):=w_p(s-t)$.

Next, we define the improper integral operator $Q:BC(\mathbb{R})\to BC(\mathbb{R})$ by$$\begin{array}{c}\hfill (Q\mathit{\mu })(s):=\frac{1}{2\mathit{\pi }}{\int }_0^{2\mathit{\pi }}ln(4{sin}^2\frac{s-t}{2})\mathit{\mu }(t)dt,s\in \mathbb{R}.\end{array}$$In numerical quadrature formula, we replace $\mathit{\mu }$ by ${\mathit{\mu }}_N$ which is the unique trigonometric polynomial with the interpolation property ${\mathit{\mu }}_N(t_j)=\mathit{\mu }(t_j):={\mathit{\mu }}_j,t_j=\frac{j\mathit{\pi }}{N},j=0,1,\dots ,2N-1$. ${\mathit{\mu }}_N$ can be explicitly expressed by:$$\begin{array}{c}\hfill {\mathit{\mu }}_N(t)=\frac{{\mathit{\alpha }}_0}{2}+\sum _{k=1}^{N-1}({\mathit{\alpha }}_{k}cos(kt)+{\mathit{\beta }}_{k}sin(kt))+\frac{{\mathit{\alpha }}_N}{2}cos(Nt),\end{array}$$where the coefficients are given by$$\begin{array}{cc}\hfill {\mathit{\alpha }}_k& =\frac{1}{N}\sum _{j=0}^{2N-1}{\mathit{\mu }}_{j}cos(k{t}_j),k=0,1,\dots ,N,\hfill \\ \hfill {\mathit{\beta }}_k& =\frac{1}{N}\sum _{j=0}^{2N-1}{\mathit{\mu }}_{j}sin(k{t}_j),k=1,2,\dots ,N-1.\hfill \end{array}$$Then from [27], we approximate $Q\mathit{\mu }$ by $Q_N\mathit{\mu }$ which is defined by3.1 $$\begin{array}{c}\hfill Q_N\mathit{\mu }(s):=Q{\mathit{\mu }}_N(s)=\sum _{j=0}^{2N-1}{R}_j^{(N)}(s)\mathit{\mu }(t_j),\end{array}$$3.1 where$$\begin{array}{c}\hfill R_j^{(N)}(s)=-\frac{1}{N}\left\{{\displaystyle \sum _{m=1}^{N-1}\frac{1}{m}cosm(s-t_j)+\frac{1}{2N}cosN(s-t_j)}\right\},\end{array}$$for $j=0,\dots ,2N-1.$ In order to calculate the integral in (2.82.6 $$\begin{array}{c}\hfill (I-K_f)\tilde{\mathit{\psi }}=-2\tilde{g}\end{array}$$2.6 ), we introduce the next integral:$$\begin{array}{c}\hfill I\mathit{\omega }:={\int }_{-\infty }^{+\infty }\mathit{\omega }(t)dt\end{array}$$where $\mathit{\omega }\in B{C}_p^n(\mathbb{R})$, for some $p>1$ and $n\in {\mathbb{N}}_0:=\mathbb{N}\cup \{0\}$. By the trapezium rule, we approximate the integral by3.2 $$\begin{array}{c}\hfill I_h\mathit{\omega }:=h\sum _{j\in \mathbb{Z}}\mathit{\omega }(jh).\end{array}$$3.2 From [10], we know that this approximation converges rapidly as $h\to 0$.

In the Nyström method, the kernel $\mathit{\kappa }(s,t)$ in (2.72.5 $$\begin{array}{c}\hfill (K\tilde{\mathit{\psi }})(s):={\int }_{\mathbb{R}}\mathit{\kappa }(s,t)\tilde{\mathit{\psi }}(t)dt,s\in \mathbb{R}.\end{array}$$2.5 ) is required to be the following form:3.3 $$\begin{array}{c}\hfill \mathit{\kappa }(s,t)=\frac{1}{2\mathit{\pi }}A(s,t)ln(4{sin}^2\frac{s-t}{2})+B(s,t),s,t\in \mathbb{R},s\ne t.\end{array}$$3.3 Here $A(s,t)\in C_{0,\mathit{\pi }}^n({\mathbb{R}}^2)$ and $B(s,t)\in B{C}_p^n({\mathbb{R}}^2)$ for some $p>1$. Then we can approximate (2.72.5 $$\begin{array}{c}\hfill (K\tilde{\mathit{\psi }})(s):={\int }_{\mathbb{R}}\mathit{\kappa }(s,t)\tilde{\mathit{\psi }}(t)dt,s\in \mathbb{R}.\end{array}$$2.5 ) by using (3.93.1 $$\begin{array}{c}\hfill Q_N\mathit{\mu }(s):=Q{\mathit{\mu }}_N(s)=\sum _{j=0}^{2N-1}{R}_j^{(N)}(s)\mathit{\mu }(t_j),\end{array}$$3.1 ) and (3.103.2 $$\begin{array}{c}\hfill I_h\mathit{\omega }:=h\sum _{j\in \mathbb{Z}}\mathit{\omega }(jh).\end{array}$$3.2 ).

Note that$$\begin{array}{cc}\hfill r& :=r(s,t)=|x-y|=\sqrt{{(s-t)}^2+{(f(s)-f(t))}^2},\hfill \\ \hfill r^{\prime }& :=r^{\prime }(s,t)=|x-y^{\prime }|=\sqrt{{(s-t)}^2+{(f(s)+f(t))}^2}.\hfill \end{array}$$With $H_0^{(1){}^{\prime }}=-H_1^{(1)}$, we have$$\begin{array}{cc}\hfill \mathit{\kappa }(s,t)& =2[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\sqrt{1+{[f^{\prime }(t)]}^2}\hfill \\ \hfill & =\frac{ik{H}_1^{(1)}(kr)}{2r}[(s-t)f^{\prime }(t)+f(t)-f(s)]\hfill \\ \hfill & -\frac{ik{H}_1^{(1)}(k{r}^{\prime })}{2r^{\prime }}[(s-t)f^{\prime }(t)+f(t)+f(s)]\hfill \\ \hfill & +i\mathit{\eta }[\frac{i}{2}{H}_0^{(1)}(kr)-\frac{i}{2}{H}_0^{(1)}(k{r}^{\prime })]\sqrt{1+{[f^{\prime }(t)]}^2}\hfill \\ \hfill & :=i\mathit{\eta }M(s,t)+L(s,t)+S(s,t),\hfill \end{array}$$where$$\begin{array}{cc}& M(s,t):=\frac{i}{2}{H}_0^{(1)}(kr)\sqrt{1+{[f^{\prime }(t)]}^2},\hfill \\ \hfill & L(s,t):=\frac{ik{H}_1^{(1)}(kr)}{2r}[(s-t)f^{\prime }(t)+f(t)-f(s)],\hfill \\ \hfill & S(s,t):=-\frac{ik{H}_1^{(1)}(k{r}^{\prime })}{2r^{\prime }}[(s-t)f^{\prime }(t)+f(t)+f(s)]+\frac{\mathit{\eta }}{2}{H}_0^{(1)}(k{r}^{\prime })\sqrt{1+{[f^{\prime }(t)]}^2}.\hfill \end{array}$$Here $M(s,t)$ and $L(s,t)$ have logarithmic singularity at $s=t$, and $S(s,t)$ is continuous at $s=t$. We split the kernels $M(s,t)$ and $L(s,t)$ into$$\begin{array}{cc}& M(s,t):=M_1(s,t)ln|s-t|+M_2(s,t),\hfill \\ \hfill & L(s,t):=L_1(s,t)ln|s-t|+L_2(s,t),\hfill \end{array}$$where$$\begin{array}{cc}& M_1(s,t):=-\frac{1}{\mathit{\pi }}{J}_0(kr)\sqrt{1+{[f^{\prime }(t)]}^2},\hfill \\ \hfill & M_2(s,t):=M(s,t)-M_1(s,t)ln|s-t|,\hfill \\ \hfill & L_1(s,t):=-\frac{k{J}_1(kr)}{\mathit{\pi }r}[f^{\prime }(t)(s-t)+f(t)-f(s)],\hfill \\ \hfill & L_2(s,t):=L(s,t)-L_1(s,t)ln|s-t|.\hfill \end{array}$$In particular, using ${lim}_{z\to 0}{J}_0(z)=1$ and ${lim}_{z\to 0}(H_0^{(1)}(z)-\frac{2i}{\mathit{\pi }}{J}_0(z)lnz)=\frac{2i}{\mathit{\pi }}(C-ln2)+1$ where $C$ denotes Euler’s constant, we can deduce the diagonal terms$$\begin{array}{cc}& M_1(s,s)=-\frac{1}{\mathit{\pi }}\sqrt{1+{[f^{\prime }(s)]}^2},\hfill \\ \hfill & M_2(s,s)=\{\frac{i}{2}-\frac{C}{\mathit{\pi }}-\frac{1}{2\mathit{\pi }}ln\frac{k^2\{1+{[f^{\prime }(s)]}^2\}}{4}\}\sqrt{1+{[f^{\prime }(s)]}^2}.\hfill \end{array}$$Using ${lim}_{z\to 0}\frac{J_1(z)}{z}=\frac{1}{2}$ and $H_{\mathit{\nu }}^{(1,2)}(x)\approx \mp i(\frac{2}{x}{)}^{\mathit{\nu }}\frac{\mathrm{\Gamma }(\mathit{\nu })}{\mathit{\pi }},x\to 0,\mathit{\nu }>0$ (see (5.16.3) in [28]), where $\mathrm{\Gamma }(\mathit{\nu })$ denotes the gamma function, we can obtain the diagonal terms$$\begin{array}{cc}& L_1(s,s)=0,L_2(s,s)=L(s,s)=-\frac{f^{″}(s)}{2\mathit{\pi }\{1+{[f^{\prime }(s)]}^2\}},\hfill \\ \hfill & S(s,s)=-\frac{ik}{2}{H}_1^{(1)}(2kf(s))+\frac{\mathit{\eta }}{2}{H}_0^{(1)}(2kf(s))\sqrt{1+{[f^{\prime }(s)]}^2}.\hfill \end{array}$$Split off the logarithmic singularity, the kernels $M_1(s,t)$, $M_2(s,t)$, $L_1(s,t)$ and $L_2(s,t)$ turn out to be analytic. Set$$\begin{array}{cc}\hfill a^{\ast }(s,t)& :=i\mathit{\eta }{M}_1(s,t)+L_1(s,t),\hfill \\ \hfill b^{\ast }(s,t)& :=i\mathit{\eta }{M}_2(s,t)+L_2(s,t)+S(s,t)\hfill \end{array}$$for any $n\in \mathbb{N}$, then3.4 $$\begin{array}{c}\hfill \mathit{\kappa }(s,t)=a^{\ast }(s,t)ln|s-t|+b^{\ast }(s,t).\end{array}$$3.4 Now we have written $\mathit{\kappa }(s,t)$ in the form (3.123.4 $$\begin{array}{c}\hfill \mathit{\kappa }(s,t)=a^{\ast }(s,t)ln|s-t|+b^{\ast }(s,t).\end{array}$$3.4 ). In order to obtain (3.113.3 $$\begin{array}{c}\hfill \mathit{\kappa }(s,t)=\frac{1}{2\mathit{\pi }}A(s,t)ln(4{sin}^2\frac{s-t}{2})+B(s,t),s,t\in \mathbb{R},s\ne t.\end{array}$$3.3 ), our approach is to express $A(s,t)$, $B(s,t)$ by $a^{\ast }(s,t)$, $b^{\ast }(s,t)$ using Theorem 2.1 in [10]. Above all, we introduce a cut-off function $\mathit{\chi }(s)\in C_0^{\infty }(\mathbb{R})$ satisfying that (1) $0\le \mathit{\chi }(s)\le 1,s\in \mathbb{R};$ (2) $\mathit{\chi }(s)=0,|s|\ge \mathit{\pi };$ (3) $\mathit{\chi }(s)=1,|s|\le 1;$ (4) $\mathit{\chi }(-s)=\mathit{\chi }(s),s\in \mathbb{R}.$ In calculation, we let$$\begin{array}{c}\hfill \mathit{\chi }(s)=\left\{\begin{array}{cc}1,\hfill & |s|\le 1,\hfill \\ {\left[1,+,exp,\left(\frac{1}{\mathit{\pi }-|s|},+,\frac{1}{1-|s|}\right)\right]}^{-1},\hfill & 1<|s|<\mathit{\pi },\hfill \\ 0,\hfill & \mathit{\pi }\le |s|.\hfill \end{array}\right.\end{array}$$With $\mathit{\chi }(s)$ and (2.6), (2.7) in [10], $A(s,t)$ and $B(s,t)$ are given by:$$\begin{array}{cc}& A(s,t):=\mathit{\pi }{a}^{\ast }(s,t)\mathit{\chi }(s-t),s\ne t,\hfill \\ \hfill & B(s,t):=a^{\ast }(s,t)[ln|s-t|(1-\mathit{\chi }(s-t))-\mathit{\chi }(s-t)ln\left(\frac{sin(\frac{s-t}{2})}{\frac{s-t}{2}}\right)]+b^{\ast }(s,t),s\ne t,\hfill \end{array}$$with the diagonal terms$$\begin{array}{cc}\hfill A(s,s)& =\mathit{\pi }[i\mathit{\eta }{M}_1(s,s)+L_1(s,s)]\mathit{\chi }(0)=-i\mathit{\eta }\sqrt{1+{[f^{\prime }(s)]}^2},\hfill \\ \hfill B(s,s)& =b^{\ast }(s,s)=i\mathit{\eta }{M}_2(s,s)+L_2(s,s)+S(s,s)\hfill \\ \hfill & =i\mathit{\eta }\{\frac{i}{2}-\frac{C}{\mathit{\pi }}-\frac{1}{2\mathit{\pi }}ln\frac{k^2\{1+{[f^{\prime }(s)]}^2\}}{4}\}\sqrt{1+{[f^{\prime }(s)]}^2}-\frac{f^{″}(s)}{2\mathit{\pi }[1+{[f^{\prime }(s)]}^2]}\hfill \\ \hfill & +\frac{\mathit{\eta }}{2}{H}_0^{(1)}(2kf(s))\sqrt{1+{[f^{\prime }(s)]}^2}-\frac{ik}{2}{H}_1^{(1)}(2kf(s)).\hfill \end{array}$$By Theorem 4.3 and Theorem 2.1 in [10], we can deduce that when the rough surface function $f\in B$, $A(s,t)\in C_{0,\mathit{\pi }}^0({\mathbb{R}}^2)$ and $B(s,t)\in B{C}_{\frac{3}{2}}^0({\mathbb{R}}^2)$. Therefore, the integral operator $K$ can be divided into two parts as:$$\begin{array}{c}\hfill K\tilde{\mathit{\psi }}(s)=K^A\tilde{\mathit{\psi }}(s)+K^B\tilde{\mathit{\psi }}(s),\end{array}$$where$$\begin{array}{c}\hfill K^A\tilde{\mathit{\psi }}(s):=\frac{1}{2\mathit{\pi }}{\int }_{\mathbb{R}}ln(4{sin}^2\frac{s-t}{2})A(s,t)\tilde{\mathit{\psi }}(t)dt,K^B\tilde{\mathit{\psi }}(s):={\int }_{\mathbb{R}}B(s,t)\tilde{\mathit{\psi }}(t)dt.\end{array}$$For $s\in \mathbb{R}$, define the period extension operator $E_s:BC(\mathbb{R})\to L^{\infty }(\mathbb{R})$ by$$\begin{array}{cc}& E_s\mathit{\varphi }(t)=\mathit{\varphi }(t),s-\mathit{\pi }\le t<s+\mathit{\pi },\hfill \\ \hfill & E_s\mathit{\varphi }(t+2\mathit{\pi })=E_s\mathit{\varphi }(t),t\in \mathbb{R}.\hfill \end{array}$$Due to the facts that $A(s,t)\in C_{0,\mathit{\pi }}^0({\mathbb{R}}^2)$ and $ln(4{sin}^2(\frac{s-t}{2}))E_s(A(s,·)\tilde{\mathit{\psi }})(t)$ is $2\mathit{\pi }$ period function with respect to $t$, it can be obtained that$$\begin{array}{cc}\hfill K^A\tilde{\mathit{\psi }}(s)& =\frac{1}{2\mathit{\pi }}{\int }_{\mathbb{R}}ln\left(4,{sin}^2,\left(\frac{s-t}{2}\right)\right)A(s,t)\tilde{\mathit{\psi }}(t)dt\hfill \\ \hfill & =\frac{1}{2\mathit{\pi }}{\int }_{s-\mathit{\pi }}^{s+\mathit{\pi }}ln\left(4,{sin}^2,\left(\frac{s-t}{2}\right)\right)A(s,t)\tilde{\mathit{\psi }}(t)dt\hfill \\ \hfill & =\frac{1}{2\mathit{\pi }}{\int }_{s-\mathit{\pi }}^{s+\mathit{\pi }}ln\left(4,{sin}^2,\left(\frac{s-t}{2}\right)\right)E_s(A(s,·)\tilde{\mathit{\psi }})(t)dt\hfill \\ \hfill & =\frac{1}{2\mathit{\pi }}{\int }_0^{2\mathit{\pi }}ln\left(4,{sin}^2,\left(\frac{s-t}{2}\right)\right)E_s(A(s,·)\tilde{\mathit{\psi }})(t)dt.\hfill \\ \hfill \end{array}$$By (3.93.1 $$\begin{array}{c}\hfill Q_N\mathit{\mu }(s):=Q{\mathit{\mu }}_N(s)=\sum _{j=0}^{2N-1}{R}_j^{(N)}(s)\mathit{\mu }(t_j),\end{array}$$3.1 ) and (3.103.2 $$\begin{array}{c}\hfill I_h\mathit{\omega }:=h\sum _{j\in \mathbb{Z}}\mathit{\omega }(jh).\end{array}$$3.2 ), we define $K_N^A$ and $K_N^B$ as$$\begin{array}{cc}& K_N^A\tilde{\mathit{\psi }}(s)=\sum _{j=0}^{2N-1}{R}_j^{(N)}(s)(E_s(A(s,·)\tilde{\mathit{\psi }}))(t_j)=\sum _{j\in \mathbb{Z}}{R}_j^{(N)}(s)A(s,t_j)\tilde{\mathit{\psi }}(t_j),\hfill \\ \hfill & K_N^B\tilde{\mathit{\psi }}(s)=I_{\frac{\mathit{\pi }}{N}}(B(s,·)\tilde{\mathit{\psi }})=\frac{\mathit{\pi }}{N}\sum _{j\in \mathbb{Z}}B(s,t_j)\tilde{\mathit{\psi }}(t_j).\hfill \end{array}$$In the Nystr$\ddot{\text{o}}$m method, we approximate $K=K^A+K^B$ by $K_N:=K_N^A+K_N^B$. Clearly,$$\begin{array}{c}\hfill K_N\tilde{\mathit{\psi }}(s)=\sum _{j\in \mathbb{Z}}{\mathit{\alpha }}_j^{(N)}(s)\tilde{\mathit{\psi }}(t_j),s\in \mathbb{R},\end{array}$$where ${\mathit{\alpha }}_j^{(N)}(s):=R_j^{(N)}(s)A(s,t_j)+\frac{\mathit{\pi }}{N}B(s,t_j)$. Then the integral Equation (2.82.6 $$\begin{array}{c}\hfill (I-K_f)\tilde{\mathit{\psi }}=-2\tilde{g}\end{array}$$2.6 ) is replaced by the approximating equation:3.5 $$\begin{array}{c}\hfill \tilde{\mathit{\psi }}(s)-\sum _{j\in \mathbb{Z}}{\mathit{\alpha }}_j^{(N)}(s)\tilde{\mathit{\psi }}(t_j)=-2\tilde{g}(s),s\in \mathbb{R}.\end{array}$$3.5

Remark 3.1

In [10], the authors established the stability analysis of the Nyström method. It depends crucially on the error estimates in Theorem 3.3 which establish the convergence of $K_N\mathit{\varphi }$ to $K\mathit{\varphi }$. Besides, the convergence of the method is also proved. Here we omit the detailed results.

The multiple frequency data used in all examples in Section 5 are obtained by solving (3.133.5 $$\begin{array}{c}\hfill \tilde{\mathit{\psi }}(s)-\sum _{j\in \mathbb{Z}}{\mathit{\alpha }}_j^{(N)}(s)\tilde{\mathit{\psi }}(t_j)=-2\tilde{g}(s),s\in \mathbb{R}.\end{array}$$3.5 ) through the collocation method. Here we define parameters used in all examples in Section 5. Let the incident direction $d=(0,-1)$ when the incident wave is the plane wave. While the point sources as the incident wave we set $z_j=(-20+0.5j,2)$ in (2.42.4 $$\begin{array}{c}\hfill \mathit{\kappa }(s,t):=2[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\sqrt{1+{[f^{\prime }(t)]}^2}s,t\in \mathbb{R},s\ne t.\end{array}$$2.4 ), $j=0,1,\dots ,80$, a total of 81 point sources, and $z_j^{\ast }$ is the symmetry point of $z_j$ with respect to the plane $x_2=-5$. Furthermore, let $\mathit{\eta }=k$ in (2.32.3 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{\mathrm{\Gamma }}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in \mathrm{\Gamma }.\end{array}$$2.3 ) to guarantee that the condition $\mathfrak{R}(\overline{k}\mathit{\eta })>0$ holds in Theorem 2.3. When solving (3.133.5 $$\begin{array}{c}\hfill \tilde{\mathit{\psi }}(s)-\sum _{j\in \mathbb{Z}}{\mathit{\alpha }}_j^{(N)}(s)\tilde{\mathit{\psi }}(t_j)=-2\tilde{g}(s),s\in \mathbb{R}.\end{array}$$3.5 ), we set the truncated interval as $(-16\mathit{\pi },16\mathit{\pi })$ and put 10 equidistant nodes in each wave length $\mathit{\lambda }=\frac{2\mathit{\pi }}{k}$, and then the step length $htol=\frac{\mathit{\lambda }}{10}=\frac{\mathit{\pi }}{N}$ with $N=5k$. Let $s_j=-cuttol+j·htol$ replace $s$ in (3.133.5 $$\begin{array}{c}\hfill \tilde{\mathit{\psi }}(s)-\sum _{j\in \mathbb{Z}}{\mathit{\alpha }}_j^{(N)}(s)\tilde{\mathit{\psi }}(t_j)=-2\tilde{g}(s),s\in \mathbb{R}.\end{array}$$3.5 ), $j=0,1,2,3,\dots ,2cuttol/htol$. After obtaining the density $\mathit{\psi }$ from (3.133.5 $$\begin{array}{c}\hfill \tilde{\mathit{\psi }}(s)-\sum _{j\in \mathbb{Z}}{\mathit{\alpha }}_j^{(N)}(s)\tilde{\mathit{\psi }}(t_j)=-2\tilde{g}(s),s\in \mathbb{R}.\end{array}$$3.5 ), we use the trapezoidal quadrature formula to calculate the scattered field $u^s$ on the receiving plane by (2.32.3 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{\mathrm{\Gamma }}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in \mathrm{\Gamma }.\end{array}$$2.3 ) for incident plane waves and (2.42.4 $$\begin{array}{c}\hfill \mathit{\kappa }(s,t):=2[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\sqrt{1+{[f^{\prime }(t)]}^2}s,t\in \mathbb{R},s\ne t.\end{array}$$2.4 ) for incident point sources. We put the receiving points on the plane $x_2=b$ from $-cutb=-8\mathit{\pi }$ to $cutb=8\mathit{\pi }$ with step length $hb=0.05\mathit{\pi }$, a total of $Nb=321$ equidistant nodes. Unless otherwise stated we let $b=1.65$.

4 Nonlinear integral equations for the inverse problem

The inverse scattering problem we are considering consists of reconstructing the rough surface ${\mathrm{\Gamma }}_f$ from the measured data $u^b(x):=u^s{(x)|}_{{\mathrm{\Gamma }}_b}$, $b>f_{+}$, corresponding to the incident field $u^i(x)=e^{ikx·d}$ or $u^i(x)={\sum }_{j=-n}^n\mathrm{\Phi }(x,z_j)$. In this paper, we will solve the inverse scattering problem via the nonlinear integral equation method. The main idea of the method is to prove the equivalence between the inverse scattering problem and an integral scheme. Firstly, we derive the integral scheme: from Section 2, we know that the density $\mathit{\psi }$ in (2.32.3 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{\mathrm{\Gamma }}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in \mathrm{\Gamma }.\end{array}$$2.3 ) or (2.42.4 $$\begin{array}{c}\hfill \mathit{\kappa }(s,t):=2[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\sqrt{1+{[f^{\prime }(t)]}^2}s,t\in \mathbb{R},s\ne t.\end{array}$$2.4 ) can be solved from4.1 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in {\mathrm{\Gamma }}_f.\end{array}$$4.1 Then the scattered field $u^s$ on ${\mathrm{\Gamma }}_b$ can be reformulated with the known density $\mathit{\psi }$ as4.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 Here $g(x)=-e^{ikx·d},\mathit{\gamma }(x)=0$ when $u^i(x)=e^{ikx·d}$ and $g(x)={\sum }_{j=-n}^n(\mathrm{\Phi }(x,z_j)-\mathrm{\Phi }(x,z_j^{\ast })),\mathit{\gamma }(x)=-{\sum }_{j=-n}^n\mathrm{\Phi }(x,z_j^{\ast })$ when $u^i(x)={\sum }_{j=-n}^n\mathrm{\Phi }(x,z_j)$. With the integral schemes (4.144.1 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in {\mathrm{\Gamma }}_f.\end{array}$$4.1 ) and (4.154.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 ), we can immediately state the following equivalence theorem.

Theorem 4.1

Assume the rough surface ${\mathrm{\Gamma }}_f$ can be uniquely determined by the near-field $u^s{|}_{{\mathrm{\Gamma }}_b}$. Then for a given near-field $u^b(x):=u^s{(x)|}_{{\mathrm{\Gamma }}_b}$, the boundary ${\mathrm{\Gamma }}_f$ is a solution of the inverse scattering problem if and only if the pair $({\mathrm{\Gamma }}_f,\mathit{\psi })$ solves the integral scheme (4.144.1 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in {\mathrm{\Gamma }}_f.\end{array}$$4.1 ) and (4.154.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 ).

Proof

If the pair $({\mathrm{\Gamma }}_f,\mathit{\psi })$ solves the integral scheme (4.144.1 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in {\mathrm{\Gamma }}_f.\end{array}$$4.1 ) and (4.154.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 ), we define:$$\begin{array}{c}\hfill u^s(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in D_f.\end{array}$$In view of (4.144.1 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in {\mathrm{\Gamma }}_f.\end{array}$$4.1 ), it leads to $u^s(x)=g(x)$ on ${\mathrm{\Gamma }}_f$. Then $u^s(x)$ is the solution to the problem (DP). Because of (4.154.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 ) and the assumption we can deduce that the boundary ${\mathrm{\Gamma }}_f$ is a solution to the inverse scattering problem.

Conversely, for a given near-field $u^b(x)$, we assume that ${\mathrm{\Gamma }}_f$ is a solution to the inverse scattering problem. Then the solution to the problem (DP) is$$\begin{array}{c}\hfill u^s(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in D_f,\end{array}$$where $\mathit{\psi }$ solves (4.144.1 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in {\mathrm{\Gamma }}_f.\end{array}$$4.1 ). From the uniqueness of the problem (DP), it can be obtained that (4.154.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 ) holds. Therefore, the theorem is completed.

With the equivalence Theorem 4.1, our treatment of the inverse scattering problem is to solve the integral schemes (4.144.1 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in {\mathrm{\Gamma }}_f.\end{array}$$4.1 ) and (4.154.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 ). We denote the right-hand side of (4.154.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 ) as $F[f,\mathit{\psi }](x)$. It is easy to see that $F[f,\mathit{\psi }](x)$ is nonlinear with respect to $f$. For a fixed $\mathit{\psi }$, finding $f$ from (4.154.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 ) requires a linearization of (4.154.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 ). We assume that the linearization of (4.154.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 ) at $f$ with respect to the direction $h$ reads4.3 $$\begin{array}{c}\hfill F[f,\mathit{\psi }](x)+(F^{\prime }[f,\mathit{\psi }]h)(x)=u^b(x),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.3 The formulations of $F[f,\mathit{\psi }](x)$ and $(F^{\prime }[f,\mathit{\psi }]h)(x)$ will be given in the Appendix 1.

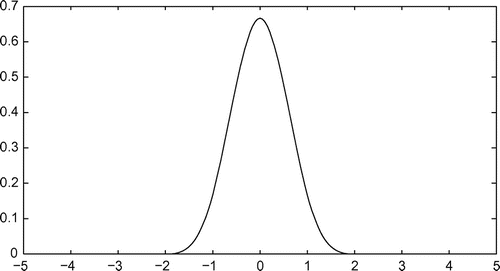
Further analysis of the linearized Equation (4.164.3 $$\begin{array}{c}\hfill F[f,\mathit{\psi }](x)+(F^{\prime }[f,\mathit{\psi }]h)(x)=u^b(x),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.3 ) requires us to choose parameterizations for functions in $B$ defined in Section 2. Since the cubic B-spline function ${\mathrm{\Omega }}_3(t)$ is twice continuously differentiable and compactly supported, we express the rough surface function $f\in B$ and the updated function $h\in B$ as a linear combination of cubic B-spline functions, i.e.4.4 $$\begin{array}{cc}\hfill f(t)& =d+p{\mathrm{\Omega }}_3\left(\frac{t}{q}\right)+\sum _{n=1}^{N_1}\left[a_n,{\mathrm{\Omega }}_3,\left(\frac{t-n·l}{q}\right),+,b_n,{\mathrm{\Omega }}_3,\left(\frac{t+n·l}{q}\right)\right],\hfill \end{array}$$4.4 4.5 $$\begin{array}{cc}\hfill h(t)& =d^h+p^h{\mathrm{\Omega }}_3\left(\frac{t}{q}\right)+\sum _{n=1}^{N_1}\left[a_n^h,{\mathrm{\Omega }}_3,\left(\frac{t-n·l}{q}\right),+,b_n^h,{\mathrm{\Omega }}_3,\left(\frac{t+n·l}{q}\right)\right]\hfill \end{array}$$4.5 for some positive constants $q$ and $l$. Here ${\mathrm{\Omega }}_3(t)$ is a piecewise function given by:$$\begin{array}{c}\hfill {\mathrm{\Omega }}_3(t)=\left\{\begin{array}{cc}\frac{1}{2}{|t|}^3-t^2+\frac{2}{3},\hfill & |t|\le 1,\hfill \\ -\frac{1}{6}{|t|}^3+t^2-2|t|+\frac{4}{3},\hfill & 1<|t|<2,\hfill \\ 0,\hfill & |t|\ge 2.\hfill \end{array}\right.\end{array}$$The graph of ${\mathrm{\Omega }}_3(t)$ is shown in Figure 2.

Figure 2. $\mathrm{C}ubicB-splinefunction$.

Define $dp={(d,p,a_1,\dots ,a_m,b_1,\dots ,b_m)}^T$, $d{p}^h={(d^h,p^h,a_1^h,\dots ,a_m^h,b_1^h,\dots ,b_m^h)}^T$ and denote the receiving points on ${\mathrm{\Gamma }}_b$ by $x=x^{(i)}:=(-cutb+i·hb,b),i=1,2,\dots ,Nb$. With given $f$ in the form (4.174.4 $$\begin{array}{cc}\hfill f(t)& =d+p{\mathrm{\Omega }}_3\left(\frac{t}{q}\right)+\sum _{n=1}^{N_1}\left[a_n,{\mathrm{\Omega }}_3,\left(\frac{t-n·l}{q}\right),+,b_n,{\mathrm{\Omega }}_3,\left(\frac{t+n·l}{q}\right)\right],\hfill \end{array}$$4.4 ), by substituting $x=x^{(i)}$ and (4.174.4 $$\begin{array}{cc}\hfill f(t)& =d+p{\mathrm{\Omega }}_3\left(\frac{t}{q}\right)+\sum _{n=1}^{N_1}\left[a_n,{\mathrm{\Omega }}_3,\left(\frac{t-n·l}{q}\right),+,b_n,{\mathrm{\Omega }}_3,\left(\frac{t+n·l}{q}\right)\right],\hfill \end{array}$$4.4 ), (4.184.5 $$\begin{array}{cc}\hfill h(t)& =d^h+p^h{\mathrm{\Omega }}_3\left(\frac{t}{q}\right)+\sum _{n=1}^{N_1}\left[a_n^h,{\mathrm{\Omega }}_3,\left(\frac{t-n·l}{q}\right),+,b_n^h,{\mathrm{\Omega }}_3,\left(\frac{t+n·l}{q}\right)\right]\hfill \end{array}$$4.5 ) into (4.164.3 $$\begin{array}{c}\hfill F[f,\mathit{\psi }](x)+(F^{\prime }[f,\mathit{\psi }]h)(x)=u^b(x),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.3 ), (4.164.3 $$\begin{array}{c}\hfill F[f,\mathit{\psi }](x)+(F^{\prime }[f,\mathit{\psi }]h)(x)=u^b(x),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.3 ) reduces to the finite linear system:4.6 $$\begin{array}{c}\hfill Jd{p}^h=r,\end{array}$$4.6 where $r$ is a column vector with elements $r_i:=u^b(x^{(i)})-F[f,\mathit{\psi }](x^{(i)}),i=1,\dots ,Nb,$ and $J={(J_{ij})}_{Nb\times (2N_1+2)}$ is a matrix with elements $J_{ij}:=F^{\prime }[f,\mathit{\psi }]h_j(x^{(i)}),i=1,\dots ,Nb,j=1,\dots ,2N_1+2$ with$$\begin{array}{c}\hfill h_j(t)=\left\{\begin{array}{cc}1,\hfill & j=1,\hfill \\ {\mathrm{\Omega }}_3(\frac{t}{q}),\hfill & j=2,\hfill \\ {\mathrm{\Omega }}_3\left(\frac{t-(j-2)·l}{q}\right),\hfill & 3\le j\le N_1+2,\hfill \\ {\mathrm{\Omega }}_3\left(\frac{t+(j-N_1-2)·l}{q}\right),\hfill & N_1+3\le j\le 2N_1+2.\hfill \end{array}\right.\end{array}$$The kernel of the integral operator in (4.154.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 ) is smooth, and therefore the inversion is severely ill-posed. The linearized Equation (4.164.3 $$\begin{array}{c}\hfill F[f,\mathit{\psi }](x)+(F^{\prime }[f,\mathit{\psi }]h)(x)=u^b(x),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.3 ) inherits the ill-posedness. In order to deal with this difficulty, we use the Tikhonov regularization to solve (4.164.3 $$\begin{array}{c}\hfill F[f,\mathit{\psi }](x)+(F^{\prime }[f,\mathit{\psi }]h)(x)=u^b(x),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.3 ) with the corresponding regularization parameter $\mathit{\alpha }$. With regularization, the Equation (4.194.6 $$\begin{array}{c}\hfill Jd{p}^h=r,\end{array}$$4.6 ) leads to:4.7 $$\begin{array}{c}\hfill (J^{\ast }J+\mathit{\alpha }I)d{p}^h=J^{\ast }r.\end{array}$$4.7

Remark 4.2

In (4.204.7 $$\begin{array}{c}\hfill (J^{\ast }J+\mathit{\alpha }I)d{p}^h=J^{\ast }r.\end{array}$$4.7 ), $J$ is a complex matrix and $r$ is a complex vector. We use $[\mathfrak{R}J;\mathfrak{I}J]$ and $[\mathfrak{R}r;\mathfrak{I}r]$ instead of $J$ and $r$ in order to obtain a real vector $dp$ in (4.204.7 $$\begin{array}{c}\hfill (J^{\ast }J+\mathit{\alpha }I)d{p}^h=J^{\ast }r.\end{array}$$4.7 ).

Before introducing the iterative algorithm based on the nonlinear integral equation, we define the relative error $\mathit{\epsilon }(k,f_r)$. Let $f_r$ denote the reconstructed rough surface. For a fixed wave number $k$ and the measured data $u_k^b(x)=u_k^s{(x)|}_{{\mathrm{\Gamma }}_b}$ corresponding to the exact rough surface $f_e$, we denote the corresponding scattered field on the receiving points by $u_{k,f_r}^b(x)$ and define the relative error $\mathit{\epsilon }(k,f_r)$ for the reconstructed rough surface $f_r$ by$$\begin{array}{c}\hfill \mathit{\epsilon }(k,f_r):=\frac{||u_{k,f_r}^b(x)-u_k^b(x){||}_2}{||u_k^b(x){||}_2}.\end{array}$$For a fixed wave number $k$, the iterative algorithm to solve the integral schemes (4.144.1 $$\begin{array}{c}\hfill \mathit{\psi }(x)=2{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)-2g(x),x\in {\mathrm{\Gamma }}_f.\end{array}$$4.1 ) and (4.154.2 $$\begin{array}{c}\hfill u^b(x)=\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.2 ) is as follows. Assume that using Algorithm 4.1 we can obtain the reconstruction of the rough surface $f_k$ for the fixed $k$ and the corresponding relative error $\mathit{\epsilon }(k,f_k)$. With the iterative algorithm for a fixed wave number, we can give the iterative algorithm for multiple frequency near-field data as follows. Given the tolerance ${\mathit{\epsilon }}_0\in (0,1)$, the initial guess $f_0$ (in this paper let $f_0$ be a constant function) and the constant $\mathit{\rho }\in (0,1)$, we propose the nonlinear integral equation iteration algorithm:

5 Numerical examples

In the final section, we present some numerical experiments to exhibit the effectiveness of the nonlinear integral equation method described in Section 4.

In all examples, we set the regularization parameter ${\mathit{\alpha }}_m(k_j)={\Vert u_{f_m(k_j)}^b-u^b(k_j)\Vert }_2^{\frac{1}{4}}$ in (4.204.7 $$\begin{array}{c}\hfill (J^{\ast }J+\mathit{\alpha }I)d{p}^h=J^{\ast }r.\end{array}$$4.7 ). For the relative noise level $\mathit{\delta }$, the perturbed data are constructed in the following way$$\begin{array}{c}\hfill u_{\mathit{\delta }}^b(k_j)=u^b(k_j)+\mathit{\delta }\frac{\Vert u^b(k_j){\Vert }_2}{{\Vert \mathit{\lambda }\Vert }_2}\mathit{\lambda },\text{for}j=1,2,\dots ,n,\end{array}$$where $\mathit{\lambda }={\mathit{\lambda }}_1+i{\mathit{\lambda }}_2$ with ${\mathit{\lambda }}_1,{\mathit{\lambda }}_2\in N(0,1)$ normally distributed. In all figures, we denote the exact rough surface by solid (blue) lines, the initial guess by dash-dot (black) lines and the reconstructed rough surface by dashed (red) lines.

Example 1

For the first example, we consider the reconstruction of a rough surface which is approximately local and parameterized by5.1 $$\begin{array}{c}\hfill f(t)=0.6+0.2exp(-0.16t^2)-0.4exp(-0.25{(t+8)}^2)+0.5exp(-0.49{(t-10)}^2)\end{array}$$5.1 with different width and different amplitude. We set $q=0.5$, $l=0.5$ and $N_1=80$ in (4.174.4 $$\begin{array}{cc}\hfill f(t)& =d+p{\mathrm{\Omega }}_3\left(\frac{t}{q}\right)+\sum _{n=1}^{N_1}\left[a_n,{\mathrm{\Omega }}_3,\left(\frac{t-n·l}{q}\right),+,b_n,{\mathrm{\Omega }}_3,\left(\frac{t+n·l}{q}\right)\right],\hfill \end{array}$$4.4 ) and (4.184.5 $$\begin{array}{cc}\hfill h(t)& =d^h+p^h{\mathrm{\Omega }}_3\left(\frac{t}{q}\right)+\sum _{n=1}^{N_1}\left[a_n^h,{\mathrm{\Omega }}_3,\left(\frac{t-n·l}{q}\right),+,b_n^h,{\mathrm{\Omega }}_3,\left(\frac{t+n·l}{q}\right)\right]\hfill \end{array}$$4.5 ). We implement the experiments with $k=1,3,5,7,9,11,13,15$ for incident plane waves and $k=1,3,5,7$ for incident point sources. Due to the limitation of space, for plane wave incidence, we only show the reconstructions results from exact data and from $10\%$ noisy data when $k=1,9,15$ in Figures 3 and 4, while for incident point sources we only show the results for $k=1,3,7$ in Figures 5 and 6. We can see the reconstructions for incident plane waves and point sources are both very accurate even with $10\%$ noise added.

Figure 3. Reconstruction of (5.215.1 $$\begin{array}{c}\hfill f(t)=0.6+0.2exp(-0.16t^2)-0.4exp(-0.25{(t+8)}^2)+0.5exp(-0.49{(t-10)}^2)\end{array}$$5.1 ) from exact data for incident plane wave with $\mathit{\epsilon }=0.10$, $\mathit{\rho }=0.90$ and $k=1,9,15$.

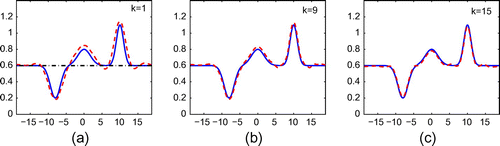
Figure 4. Reconstruction of (5.215.1 $$\begin{array}{c}\hfill f(t)=0.6+0.2exp(-0.16t^2)-0.4exp(-0.25{(t+8)}^2)+0.5exp(-0.49{(t-10)}^2)\end{array}$$5.1 ) from 10% noisy data for incident plane wave with $\mathit{\epsilon }=0.15$, $\mathit{\rho }=0.90$ and $k=1,9,15$.

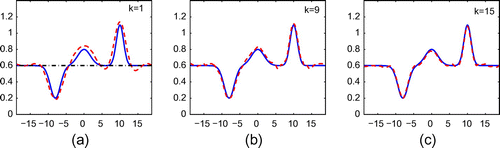
Figure 5. Reconstructions of (5.215.1 $$\begin{array}{c}\hfill f(t)=0.6+0.2exp(-0.16t^2)-0.4exp(-0.25{(t+8)}^2)+0.5exp(-0.49{(t-10)}^2)\end{array}$$5.1 ) from exact data for incident point sources with $\mathit{\epsilon }=0.15$, $\mathit{\rho }=0.90$ and $k=1,3,7$.

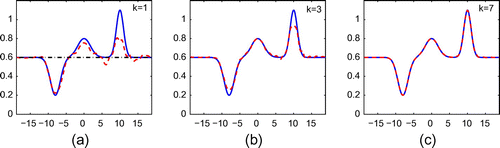
Figure 6. Reconstruction of (5.215.1 $$\begin{array}{c}\hfill f(t)=0.6+0.2exp(-0.16t^2)-0.4exp(-0.25{(t+8)}^2)+0.5exp(-0.49{(t-10)}^2)\end{array}$$5.1 ) from 10% noisy data for incident point sources with $\mathit{\epsilon }=0.20$, $\mathit{\rho }=0.90$ and $k=1,3,7$.

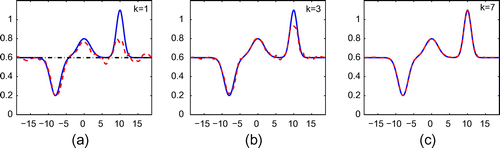
Figure 7. Reconstruction of (5.225.2 $$\begin{array}{c}\hfill f(t)=0.6+0.2sin(2t)+0.3sin(6t).\end{array}$$5.2 ) from exact data for incident plane wave with $\mathit{\epsilon }=0.40$, $\mathit{\rho }=0.90$ and $k=3,5,11$.

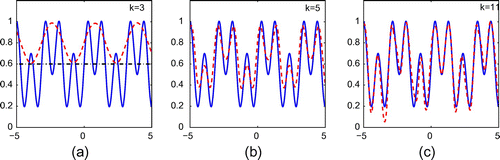
Figure 8. Reconstruction of (5.225.2 $$\begin{array}{c}\hfill f(t)=0.6+0.2sin(2t)+0.3sin(6t).\end{array}$$5.2 ) from 10% noisy data for incident plane wave with $\mathit{\epsilon }=0.40$, $\mathit{\rho }=0.95$ and $k=3,5,11$.

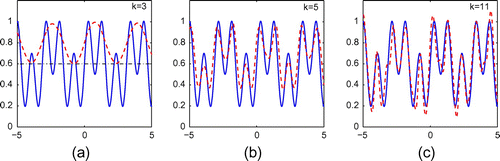
Figure 9. Reconstruction of (5.225.2 $$\begin{array}{c}\hfill f(t)=0.6+0.2sin(2t)+0.3sin(6t).\end{array}$$5.2 ) from exact data for incident point sources with $\mathit{\epsilon }=0.20$, $\mathit{\rho }=0.95$ and $k=3,7,11$.

Figure 10. Reconstruction of (5.225.2 $$\begin{array}{c}\hfill f(t)=0.6+0.2sin(2t)+0.3sin(6t).\end{array}$$5.2 ) from 10% noisy data for incident point sources with $\mathit{\epsilon }=0.20$, $\mathit{\rho }=0.95$ and $k=3,7,11$.

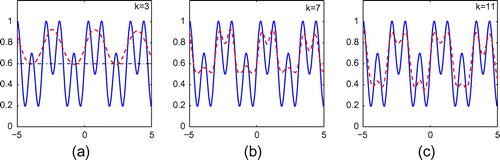
Figure 11. Reconstruction of (5.235.3 $$\begin{array}{c}\hfill f(t)=1-0.2cos(0.01t^2)exp(-sin(t)).\end{array}$$5.3 ) from exact data for incident plane wave with $\mathit{\epsilon }=0.60$, $\mathit{\rho }=0.90$ and $k=3,7,11$.

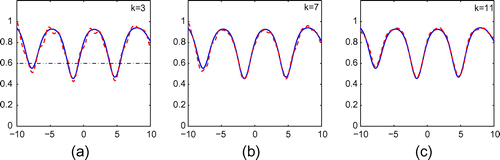
Figure 12. Reconstruction of (5.235.3 $$\begin{array}{c}\hfill f(t)=1-0.2cos(0.01t^2)exp(-sin(t)).\end{array}$$5.3 ) from exact data for incident plane wave with $\mathit{\epsilon }=0.60$, $\mathit{\rho }=0.90$ and $k=3,7,11$ when the measurements were taken at $x_2=2.50$.

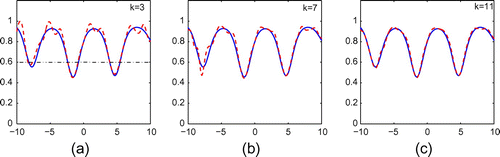
Figure 13. Reconstruction of (5.235.3 $$\begin{array}{c}\hfill f(t)=1-0.2cos(0.01t^2)exp(-sin(t)).\end{array}$$5.3 ) from exact data for incident plane wave with $\mathit{\epsilon }=0.60$, $\mathit{\rho }=0.90$ and $k=3,7,11$ when the measurements were taken at $x_2=3.50$.

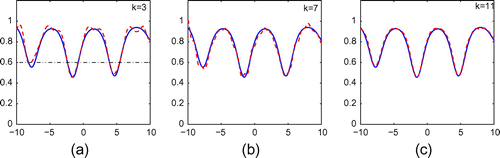
Figure 14. Reconstruction of (5.235.3 $$\begin{array}{c}\hfill f(t)=1-0.2cos(0.01t^2)exp(-sin(t)).\end{array}$$5.3 ) from 10% noisy data for incident plane wave with $\mathit{\epsilon }=0.60$, $\mathit{\rho }=0.90$ and $k=3,7,11$.

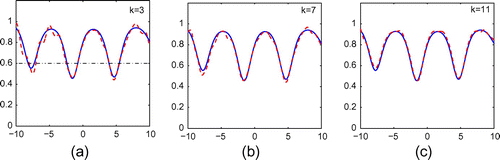
Figure 15. Reconstruction of (5.235.3 $$\begin{array}{c}\hfill f(t)=1-0.2cos(0.01t^2)exp(-sin(t)).\end{array}$$5.3 ) from exact data for incident point sources with $\mathit{\epsilon }=0.30$, $\mathit{\rho }=0.90$ and $k=3,7,11$.

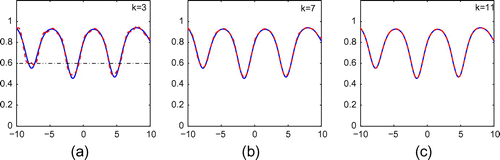
Figure 16. Reconstruction of (5.235.3 $$\begin{array}{c}\hfill f(t)=1-0.2cos(0.01t^2)exp(-sin(t)).\end{array}$$5.3 ) from exact data for incident point sources with $\mathit{\epsilon }=0.30$, $\mathit{\rho }=0.90$ and $k=3,7,11$ when the measurements were taken at $x_2=2.50$.

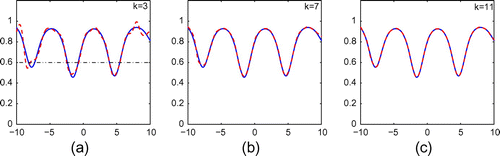
Figure 17. Reconstruction of (5.235.3 $$\begin{array}{c}\hfill f(t)=1-0.2cos(0.01t^2)exp(-sin(t)).\end{array}$$5.3 ) from exact data for incident point sources with $\mathit{\epsilon }=0.30$, $\mathit{\rho }=0.90$ and $k=3,7,11$ when the measurements were taken at $x_2=3.50$.

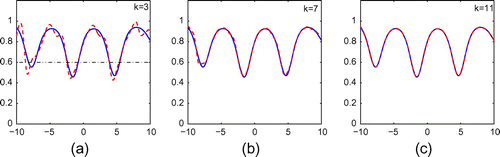
Figure 18. Reconstruction of (5.235.3 $$\begin{array}{c}\hfill f(t)=1-0.2cos(0.01t^2)exp(-sin(t)).\end{array}$$5.3 ) from 10% noisy data for incident point sources with $\mathit{\epsilon }=0.30$, $\mathit{\rho }=0.90$ and $k=3,7,11$.

Example 2

In the second example, we attempt to reconstruct a nonlocally rough surface which is periodic with the parameterization5.2 $$\begin{array}{c}\hfill f(t)=0.6+0.2sin(2t)+0.3sin(6t).\end{array}$$5.2 We let $q=0.25$, $l=0.25$ and $N_1=160$ in (4.174.4 $$\begin{array}{cc}\hfill f(t)& =d+p{\mathrm{\Omega }}_3\left(\frac{t}{q}\right)+\sum _{n=1}^{N_1}\left[a_n,{\mathrm{\Omega }}_3,\left(\frac{t-n·l}{q}\right),+,b_n,{\mathrm{\Omega }}_3,\left(\frac{t+n·l}{q}\right)\right],\hfill \end{array}$$4.4 ) and (4.184.5 $$\begin{array}{cc}\hfill h(t)& =d^h+p^h{\mathrm{\Omega }}_3\left(\frac{t}{q}\right)+\sum _{n=1}^{N_1}\left[a_n^h,{\mathrm{\Omega }}_3,\left(\frac{t-n·l}{q}\right),+,b_n^h,{\mathrm{\Omega }}_3,\left(\frac{t+n·l}{q}\right)\right]\hfill \end{array}$$4.5 ). We implement the experiments at $k=3,5,7,9,11$. Because of the limited space, we only present the results from exact data and from $10\%$ noisy data for incident plane waves for $k=3,5,11$ in Figures 7 and 8. The reconstruction results for point sources are presented in Figures 9 and 10 when $k=3,7,11$. 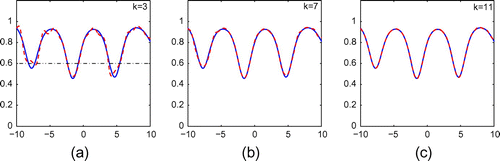From the figures in this example, it can be seen that the algorithm works well for nonlocally rough surfaces when the incoming wave is a plane wave, but the reconstruction is not good enough when the incoming wave is point sources. We attempt to increase the wave numbers in Figures 9 and 10, but the reconstruction is not improved very much.

Example 3

In the last example, we test our algorithm on a rough surface which is nonlocal and nonperiodic, and formulated by5.3 $$\begin{array}{c}\hfill f(t)=1-0.2cos(0.01t^2)exp(-sin(t)).\end{array}$$5.3 We let $q=0.5$, $l=0.5$ and $N_1=80$ in (4.174.4 $$\begin{array}{cc}\hfill f(t)& =d+p{\mathrm{\Omega }}_3\left(\frac{t}{q}\right)+\sum _{n=1}^{N_1}\left[a_n,{\mathrm{\Omega }}_3,\left(\frac{t-n·l}{q}\right),+,b_n,{\mathrm{\Omega }}_3,\left(\frac{t+n·l}{q}\right)\right],\hfill \end{array}$$4.4 ) and (4.184.5 $$\begin{array}{cc}\hfill h(t)& =d^h+p^h{\mathrm{\Omega }}_3\left(\frac{t}{q}\right)+\sum _{n=1}^{N_1}\left[a_n^h,{\mathrm{\Omega }}_3,\left(\frac{t-n·l}{q}\right),+,b_n^h,{\mathrm{\Omega }}_3,\left(\frac{t+n·l}{q}\right)\right]\hfill \end{array}$$4.5 ) and implement the experiments with $k=3,5,7,9,11$. Due to the limitation of space, we only show a part of results. For plane wave incidence, we show the reconstruction results from the exact measurement data and from $10\%$ noisy data at $k=3,7,11$ and $x_2=1.65$ in Figures 11 and 14. In order to see the effect of our algorithm at different measurement heights, we also present the reconstruction results by using the exact scattering data measured at different heights $x_2=2.5$ and $x_2=3.5$ in Figures 12 and 13. For incident point sources, the results from the exact data and from $10\%$ noisy data with $k=3,7,11$ and $x_2=1.65$ are presented in Figures 15 and 18. The reconstruction results from the exact data at the heights $x_2=2.5$ and $x_2=3.5$ are given in Figures 16 and 17. As we can see from the figures, the reconstructions are very accurate, especially when $k=11$. Even $10\%$ noise is added to the measurements, the reconstructed surfaces still agree well with the exact one. Furthermore, when the measurement height is within a reasonable range, smaller measurement heights (that is, the measurement place is closer to the exact surface) give better results in both cases of incident plane waves and point sources with a single wave number. However, the effect of measurement height is weak when using multiple frequency data.

Through the examples in this section we can see that the nonlinear integral equation method works well for the problem of inverse scattering by sound-soft rough surfaces. For locally rough surface and gently rough surface, we obtain satisfactory results whether the incident field is plane waves or point sources. However, for the nonlocally rough surfaces with considerable oscillations, the reconstruction results for incident plane waves are better than that for incident point sources.

Acknowledgements

The authors would like to thank Prof. Bo Zhang, Dr. Jiaqing Yang and Dr. Haiwen Zhang for the valuable discussions. The authors also thank the referees for their constructive comments and suggestions which helped improve the paper.

Additional information

Funding

This work was partly supported by the NNSF of China [grant number 11071244], [grant number 61379093]. Guanying Sun was also supported by the Starting Research Fund from North China University of Technology.

Appendix 1.

In this appendix, we give the formulations of $F[f,\mathit{\psi }](x)$ and $(F^{\prime }[f,\mathit{\psi }]h)(x)$ in (4.164.3 $$\begin{array}{c}\hfill F[f,\mathit{\psi }](x)+(F^{\prime }[f,\mathit{\psi }]h)(x)=u^b(x),x\in {\mathrm{\Gamma }}_b.\end{array}$$4.3 ).$$\begin{array}{cc}\hfill F[f,\mathit{\psi }](x)& =\mathit{\gamma }(x)+{\int }_{{\mathrm{\Gamma }}_f}[\frac{\mathit{\partial }G(x,y)}{\mathit{\partial }\mathit{\nu }(y)}+i\mathit{\eta }G(x,y)]\mathit{\psi }(y)ds(y)\hfill \\ \hfill & =\mathit{\gamma }(x)+{\int }_{\mathbb{R}}\{\frac{i{k}^2}{4}\frac{H_1^{(1)}(k|x-y|)}{k|x-y|}[(x_1-y_1)f^{\prime }(y_1)+f(y_1)-x_2]\hfill \\ \hfill & -\frac{i{k}^2}{4}\frac{H_1^{(1)}(k|x^{\prime }-y|)}{k|x^{\prime }-y|}[(x_1-y_1)f^{\prime }(y_1)+f(y_1)+x_2]\hfill \\ \hfill & -\frac{1}{4}\mathit{\eta }[H_0^{(1)}(k|x-y|)-H_0^{(1)}(k|x^{\prime }-y|)]\sqrt{1+{[f^{\prime }(y_1)]}^2}\}\mathit{\psi }(y)d{y}_1,x\in {\mathrm{\Gamma }}_b.\hfill \end{array}$$The Fréchet derivative of $F[f,\mathit{\psi }](x)$ at $f$ with respect to the direction $h$ can be obtained by differentiating the kernel with respect to $f$ (see [29]). Therefore, the derivative is given by:$$\begin{array}{c}\hfill F^{\prime }[f,\mathit{\psi }]h(x)=Y_1+Y_2+Y_3+Y_4\text{for}h\in B,\end{array}$$where$$\begin{array}{cc}\hfill Y_1& =\frac{k^{2}i}{4}{\int }_{\mathbb{R}}\{\frac{H_1^{(1)}(k|x-y|)}{k|x-y|}-\frac{H_1^{(1)}(k|x^{\prime }-y|)}{k|x^{\prime }-y|}\hfill \\ \hfill & -\frac{H_2^{(1)}(k|x-y|)}{{|x-y|}^2}(f(y_1)-x_2)[(x_1-y_1)f^{\prime }(y_1)+f(y_1)-x_2]\hfill \\ \hfill & +\frac{H_2^{(1)}(k|x^{\prime }-y|)}{|x^{\prime }{-y|}^2}(f(y_1)+x_2)[(x_1-y_1)f^{\prime }(y_1)+f(y_1)+x_2]\}\mathit{\psi }(y_1)h(y_1)d{y}_1,\hfill \\ \hfill Y_2& =\frac{k\mathit{\eta }}{4}{\int }_{\mathbb{R}}[\frac{H_1^{(1)}(k|x-y|)}{|x-y|}(f(y_1)-x_2)\hfill \\ \hfill & -\frac{H_1^{(1)}(k|x^{\prime }-y|)}{|x^{\prime }-y|}(f(y_1)+x_2)]\sqrt{1+{[f^{\prime }(y_1)]}^2}\mathit{\psi }(y_1)h(y_1)d{y}_1,\hfill \\ \hfill Y_3& =\frac{\mathit{\eta }}{4}{\int }_{\mathbb{R}}[-H_0^{(1)}(k|x-y|)+H_0^{(1)}(k|x^{\prime }-y|)]\frac{f^{\prime }(y_1)\mathit{\psi }(y_1)}{\sqrt{1+{[f^{\prime }(y_1)]}^2}}{h}^{\prime }(y_1)d{y}_1,\hfill \\ \hfill Y_4& =\frac{k^{2}i}{4}{\int }_{\mathbb{R}}[\frac{H_1^{(1)}(k|x-y|)}{k|x-y|}-\frac{H_1^{(1)}(k|x^{\prime }-y|)}{k|x^{\prime }-y|}](x_1-y_1)\mathit{\psi }(y_1)h^{\prime }(y_1)d{y}_1.\hfill \end{array}$$