Interval uncertainty analysis of elastic bimodular truss structures

Abstract

Two numerical models are presented for the interval uncertainty analysis of elastic bimodular truss structures. The first one is for the intervals estimation of displacements when constitutive parameters are interval variables, and the second one is for the intervals estimation of unknown constitutive parameters when there exists an interval uncertainty in the measurement. Based on a smoothed FE model, an interval relationship between displacements and bimodular parameters is put forward using Taylor series expansion and interval arithmetic, two deterministic formulae are derived to estimate the uncertain interval bounds of displacements, and a two-step strategy is developed to estimate the intervals of elastic bimodular constitutive parameters as well. Numerical comparisons are provided to verify the proposed approach and the advantage/shortcomings of the proposed approach is discussed.

Keywords:

• interval
• bimodulus
• uncertainty
• bounds estimation
• identification
• truss structure

1. Introduction

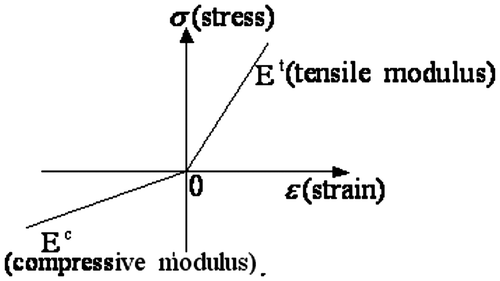
There exists many natural and synthetic bimodular materials, such as fibre-reinforced glass, plastics, porcelain, rock, bone, concrete, and composites. Additionally, some structures, such as solar sails, inflatable antennae and membrane optics, exhibit a notable difference between their compressive and tensile resistances. The major character of these materials is that their elastic moduli are different in tension and compression. The stress–strain relationship of this kind of material is usually described via a bilinear model,[1] as shown in Figure 1, where a slope discontinuity can be observed at the origin.

Figure 1. Stress–strain relationship of bimodular materials.

The bimodular problem has been catching eyes of a number of researchers, and there are a number of literatures concerned with the solutions of bimodular problems which are difficult to acquire analytically in general. Recently, K. Khan et al. presented a new constitutive model for bimodular-laminated structures [2] and carried out a numerical investigation on the non-linear forced vibration of bimodular-laminated composite plates.[3] In 2011, Zhang et al. not only presented a detailed summary on the history of bimodular problems with related research activities, but also converted the bimodular problem into a standard complementary quadratic programming problem, which can be solved without a pre-assumption of stress states and the stiffness matrices update as conventional iterative techniques required. Consequently, they developed an efficient parametric variational principle-based finite element method.[4] Later Zhang et al. extended their approach into the 2D dynamic bimodular analysis and static analysis of bimodular truss and tensegrity structures.[5,6] However, all the previous work on the bimodular problem seems to be carried out under a deterministic framework, i.e. based on deterministic mathematical models with precisely defined parameters. Unfortunately, constitutive parameters, boundary conditions and loads, presented via the experimental data, measurements, statistical analysis, and expert knowledge, more or less contain uncertainty. This uncertainty will result in uncertain results, and necessitates to take into account.[7,8] The ability to include non-deterministic properties is of great value for a design engineer. It enables realistic reliability assessment that incorporates the uncertain aspects of the design. Furthermore, the design can be optimized for robust behaviour under varying external influences. Non-deterministic approaches are gaining momentum in the field of numerical modelling techniques.[9]

This paper focuses on the numerical modelling of bimodular truss structure with a kind of uncertainty, i.e. interval uncertainty which means that uncertainties are introduced as interval values, i.e. the values are known to lie between two values, but the exact values are unknown. The interval description on the uncertainty is realistic or natural,[10] and only needs the bounds of changes of the uncertain parameters, instead of the uncertainty distribution inside their definition ranges or some other prior knowledge as probabilistic and fuzzy models required.[10] The ‘supermarket’ of interval uncertainty analysis is quite large, a series of new products are made by I. Elishakoff et al. such as ‘parameterized intervals’ and ‘new anti-optimization modelling’.[11,12] In comparison with the study on the interval uncertainty problems in structural engineering and some other engineering aspects,[13] the bimodular problem with interval uncertainty is inadequately concerned, to the best of authors knowledge, there seems no report directly related with this issue.

This paper mainly relates with two issues, one is the intervals estimation of displacements when constitutive parameters are interval variables, and another is the intervals estimation of unknown constitutive parameters when there exists an interval uncertainty in the measurement. In Section 3, in virtue of a smooth function technique and FEM, a numerical model is developed to estimate the lower and upper bounds of the uncertain intervals of displacements using Taylor series expansion and interval arithmetic. In Section 4，a two-step strategy is presented to estimate interval bounds of elastic bimodulus when the measurements of displacement are interval variables. In Section 5, numerical tests are carried out to verify the proposed approaches.

2. A smoothed FE model of elastic bimodular truss structures

For ith rod in an elastic bimodular truss structure, the constitutive equation is described by [1](1) $${\mathit{\sigma }}_i=\left\{\begin{array}{cc}{E}^{+}{\mathit{\epsilon }}_i,\hfill & {\mathit{\epsilon }}_i>0\hfill \\ E^{-}{\mathit{\epsilon }}_i,\hfill & {\mathit{\epsilon }}_i<0\hfill \end{array}\right.$$(1)

where subscript i refers to ith rod, ${\mathit{\sigma }}_i$ and ${\mathit{\epsilon }}_i$ stands for the stress and strain, respectively, $E^{+}$and E⁻ refer to the tensile and compressive moduli, respectively.

Equation (1(1) $${\mathit{\sigma }}_i=\left\{\begin{array}{cc}{E}^{+}{\mathit{\epsilon }}_i,\hfill & {\mathit{\epsilon }}_i>0\hfill \\ E^{-}{\mathit{\epsilon }}_i,\hfill & {\mathit{\epsilon }}_i<0\hfill \end{array}\right.$$(1) ) can be smoothed utilizing a smooth function technique [14](2) $${\mathit{\sigma }}_i({\mathit{\epsilon }}_i)=\frac{1}{p}[E^{+}ln(1+e^{p{\mathit{\epsilon }}_i})-E^{-}ln(1+e^{-p{\mathit{\epsilon }}_i})]$$(2)

where p stands for a smoothing constant.

Equation (2) is not reasonable because ${\mathit{\sigma }}_i\ne 0$ when ${\mathit{\epsilon }}_i=0$, thereby it is further improved by [15](3) $${\mathit{\sigma }}_i=\frac{d{\mathit{\sigma }}_i}{d{\mathit{\epsilon }}_i}{\mathit{\epsilon }}_i=\frac{d_i({\mathit{\epsilon }}_i)}{l_i}[{\begin{array}{cc}cos{\mathit{\alpha }}_i& sin\mathit{\alpha }\end{array}}_i]\left(\begin{array}{cc}{u}_m\hfill & -u_n\hfill \\ v_m\hfill & -v_n\hfill \end{array}\right)$$(3) (4) $$d_i=E^{+}\left(\frac{e^{p{\mathit{\epsilon }}_i}}{1+e^{p{\mathit{\epsilon }}_i}}\right)+E^{-}\left(\frac{e^{-p{\mathit{\epsilon }}_i}}{1+e^{-p{\mathit{\epsilon }}_i}}\right)$$(4) (5) $$u_x^i=u_m-u_n$$(5) (6) $$u_y^i=v_m-v_n$$(6)

where α_i is the angle between the axis of ith rod and X axis of the global coordinate system, subscripts m and n refer to the nodal numbers of two ends, respectively. u_m, v_m, u_n and v_n stand for the displacements of two ends along the X and Y directions of global coordinate system.

In virtue of the virtual work principle, a smoothed FE equation can be derived [15](7) $$\mathit{K}(E^{+},E^{-},\mathit{u})\mathit{u}=\mathit{P}$$(7)

where $\mathit{u}$ is the general nodal vector of displacement, $\mathit{K}$ stands for the general stiffness matrix and $\mathit{P}$ denotes the vector of general nodal force.

The stiffness matrix of ith rod is given by(8) $$[k^i]=\left[\begin{array}{cc}{k}_i& -k_i\\ -k_i& k_i\end{array}\right]$$(8) (9) $$k_i={[k]}_{2\times 2}$$(9) (10) $$k_{11}=\frac{A_i}{l_i}{d}_i{cos}^2{\mathit{\alpha }}_i$$(10) (11) $$k_{12}=k_{21}=\frac{A_i}{l_i}{d}_{i}cos{\mathit{\alpha }}_{i}sin{\mathit{\alpha }}_i$$(11) (12) $$k_{22}=\frac{A_i}{l_i}{d}_i{sin}^2{\mathit{\alpha }}_i$$(12)

where A_i and l_i refer to the cross-sectional area and length of ith rod, respectively.

Equation (5(5) $$u_x^i=u_m-u_n$$(5) ) is non-linear, and can be solved by the Newton-Raphson algorithm in the following iterative process [15]$${\mathit{u}}^{(k+1)}={\mathit{u}}^{(k)}-{\mathit{R}}^{\prime }{({\mathit{u}}^{(k)})}^{-1}\mathit{R}({\mathit{u}}^{(k)})$$$$\mathit{R}({\mathit{u}}^{(k)})=\mathit{K}({\mathit{u}}^{(k)}){\mathit{u}}^{(k)}-\mathit{P}$$(13) $${\mathit{R}}^{\prime }({\mathit{u}}^{(k)})=\left[\begin{array}{cccc}\frac{\mathit{\partial }{R}_1(u^{(k)})}{\mathit{\partial }{u}_1}& \frac{\mathit{\partial }{R}_1(u^{(k)})}{\mathit{\partial }{u}_2}& \cdots & \frac{\mathit{\partial }{R}_1(u^{(k)})}{\mathit{\partial }{u}_n}\\ \frac{\mathit{\partial }{R}_2(u^{(k)})}{\mathit{\partial }{u}_1}& \frac{\mathit{\partial }{R}_2(u^{(k)})}{\mathit{\partial }{u}_2}& \cdots & \frac{\mathit{\partial }{R}_2(u^{(k)})}{\mathit{\partial }{u}_n}\\ ⋮& ⋮& ⋮& ⋮\\ \frac{\mathit{\partial }{R}_n(u^{(k)})}{\mathit{\partial }{u}_1}& \frac{\mathit{\partial }{R}_n(u^{(k)})}{\mathit{\partial }{u}_2}& \cdots & \frac{\mathit{\partial }{R}_n(u^{(k)})}{\mathit{\partial }{u}_n}\end{array}\right]$$(13)

where superscript k refers to kth iterative step.

The detailed contribution of $[k^i]$ to $\mathit{R}$ and ${\mathit{R}}^{\prime }$ can be obtained via Equations (10)–(12), for instance, the contribution to $R_{2m-1}$ is $k_{11}{u}_m+k_{12}{v}_m-k_{11}{u}_n-k_{12}{v}_n$, and the contribution to $\frac{\mathit{\partial }{R}_{2m-1}}{\mathit{\partial }{u}_m}$ is(14) $$k_{11}+(u_m-u_n)\frac{\mathit{\partial }{k}_{11}}{\mathit{\partial }{u}_m}+(v_m-v_n)\frac{\mathit{\partial }{k}_{12}}{\mathit{\partial }{u}_m}=k_{11}+(u_m-u_n)p\left[E^{+}\frac{e^{P{\mathit{\epsilon }}_i}}{{(1+e^{P{\mathit{\epsilon }}_i})}^2}-E^{-}\frac{e^{-P{\mathit{\epsilon }}_i}}{{(1+e^{-P{\mathit{\epsilon }}_i})}^2}\right]{cos}^2{\mathit{\alpha }}_i\frac{\mathit{\partial }{\mathit{\epsilon }}_i}{\mathit{\partial }{u}_m}\frac{A}{l}+(v_m-v_n)p\left[E^{+}\frac{e^{P{\mathit{\epsilon }}_i}}{{(1+e^{P{\mathit{\epsilon }}_i})}^2}-E^{-}\frac{e^{-P{\mathit{\epsilon }}_i}}{{(1+e^{-P{\mathit{\epsilon }}_i})}^2}\right]cos{\mathit{\alpha }}_{i}sin{\mathit{\alpha }}_i\frac{\mathit{\partial }{\mathit{\epsilon }}_i}{\mathit{\partial }{u}_m}\frac{A}{l}$$(14)

3. Interval estimation of forward problem

This section presents a numerical model to tackle with the forward interval bimodular problem.

We assume that both $E^{+}$ and E⁻ are interval variables, and are described by ${\mathit{E}}^I=[E^{+I},E^{-I}]$(15) $$E^{+I}=E^{+c}+\mathrm{\Delta }{E}^{+I}$$(15) (16) $$E^{-I}=E^{-c}+\mathrm{\Delta }{E}^{-I}$$(16) (17) $$\mathbf{\Delta }{\mathit{E}}^{+I}=\mathbf{\Delta }{\mathit{E}}^{+}·\mathit{e}$$(17) (18) $$\mathbf{\Delta }{E}^{-I}=\mathbf{\Delta }{E}^{-}·\mathit{e}$$(18)

where E^+c/E^−c and $\mathrm{\Delta }{E}^{+}\ge 0$/$\mathrm{\Delta }{E}^{-}\ge 0$ refer to the central values and radius of intervals, respectively, $\mathit{e}=[-1,1]$

Therefore, Equation (7(7) $$\mathit{K}(E^{+},E^{-},\mathit{u})\mathit{u}=\mathit{P}$$(7) ) becomes(19) $$\mathit{K}(E^{+I},E^{-I},{\mathit{u}}^I){\mathit{u}}^I=\mathit{P}$$(19) (20) $${\mathit{u}}^{\mathit{I}}={\mathit{u}}^c+\mathrm{\Delta }{\mathit{u}}^{\mathit{I}},$$(20)

where $\mathrm{\Delta }{\mathit{u}}^{\mathit{I}}=\mathrm{\Delta }\mathit{u}\mathit{e}$, ${\mathit{u}}^c$ and $\mathrm{\Delta }\mathit{u}\ge 0$ refer to the central value and radius of ${\mathit{u}}^{\mathit{I}}$.

As a matter of fact, there are number of techniques to estimate the interval of ${\mathit{u}}^{\mathit{I}}$, such as interval arithmetic approach, the optimization approach, combinatorial methods and perturbation techniques, etc. In a comprehensive review given by David et al. [9], the main principles, strengths and shortcomings of the two fundamental classes of interval approaches, i.e. interval arithmetic and the optimization approaches, are discussed. The interval arithmetic approach is the most straightforward strategy for the solution of systems of interval equations, and is appealing for its inherent high computational efficiency. But it may encounter an impasse due to its inability to keep track of the dependency between uncertainty-affected quantities, equations, sub-results and final results. The optimization approach is non-intrusive in nature, and is a generic strategy for performing interval analysis. However, its price for accurate interval results comes as a high computational cost. Taylor series expansion method, catalogued in the pool of perturbation techniques, is an effective and convenient tool to deal with forward interval problems when interval quantities width is relatively small.[16] Generally, it is less accurate, but more computationally economic than optimization and combinatorial methods.[17] For the inverse interval problem involved in this paper, since the solution of forward problem is continually required in an iterative process, Taylor series expansion method is more efficient than the optimization and combinatorial approaches in terms of computational expense. On the other hand, it seems difficult and complicated to analyse and deal with the uncertain parameter dependency that is necessary for accurate interval results with the interval arithmetic approach. With all the above considerations, Taylor series expansion method is employed in this paper.

In the vicinity of ${\mathit{E}}^c=[E^{+c},E^{-c}]$,(21) $$\mathit{E}={\mathit{E}}^c+\mathit{\delta }{\mathit{E}}^c=[E^{+c},E^{-c}]+[\mathit{\delta }{E}^{+},\mathit{\delta }{E}^{-}]$$(21)

where(22) $$|\mathit{\delta }{E}^{+}|\le \mathrm{\Delta }{E}^{+}$$(22) (23) $$|\mathit{\delta }{E}^{-}|\le \mathrm{\Delta }{E}^{-}$$(23)

Using first-order Taylor expansion, $\mathit{u}$ can be approximated by(24) $$\mathit{u}(\mathit{E})=\mathit{u}({\mathit{E}}^{\mathit{c}}+\mathit{\delta }E)=\mathit{u}({\mathit{E}}^{\mathit{c}})+\sum _{j=1}^2\frac{\mathit{\partial }\mathit{u}({\mathit{E}}^{\mathit{c}})}{\mathit{\partial }{\mathit{E}}_j}\mathit{\delta }{E}_j={\mathit{u}}^{\mathit{c}}+\mathit{\delta }\mathit{u}$$(24)

where subscript j = 1 refers to E⁺, j = 2 refers to E⁻, respectively.(25) $$\mathit{K}({\mathit{E}}^{\mathit{c}},\mathit{u}({\mathit{E}}^{\mathit{c}}))\mathit{u}({\mathit{E}}^{\mathit{c}})=\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}}){\mathit{u}}^{\mathit{c}}=\mathit{P}$$(25) (26) $$\frac{\mathit{\partial }\mathit{u}({\mathit{E}}^{\mathit{c}})}{\mathit{\partial }{\mathit{E}}_j}=-{\left[\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})+\frac{\mathit{\partial }\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})}{\mathit{\partial }\mathit{u}}{\mathit{u}}^{\mathit{c}}\right]}^{-1}\left[\frac{\mathit{\partial }\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})}{\mathit{\partial }{\mathit{E}}_j}{\mathit{u}}^{\mathit{c}}\right]$$(26)

For the lth component of $\mathit{u}$, the lower and upper bounds can be estimated by(27) $${\underline{\mathit{u}}}_l={\mathit{u}}_{{}^{\mathit{l}}}^{\mathit{c}}-\sum _{j=1}^2\left|\frac{\mathit{\partial }\mathit{u}{({\mathit{E}}^{\mathit{c}})}_l}{\mathit{\partial }{\mathit{E}}_j}\right|\mathrm{\Delta }{E}_j={\mathit{u}}_l^{\mathit{c}}-\sum _{j=1}^2{\left|{\left[\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})+\frac{\mathit{\partial }\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})}{\mathit{\partial }\mathit{u}}{\mathit{u}}^{\mathit{c}}\right]}^{-1}\left[\frac{\mathit{\partial }\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})}{\mathit{\partial }{\mathit{E}}_j}{\mathit{u}}^{\mathit{c}}\right]\right|}_l\mathrm{\Delta }{E}_j$$(27) (28) $${\overline{\mathit{u}}}_l={\mathit{u}}_{{}^{\mathit{l}}}^{\mathit{c}}+\sum _{j=1}^2\left|\frac{\mathit{\partial }\mathit{u}{({\mathit{E}}^{\mathit{c}})}_l}{\mathit{\partial }{\mathit{E}}_j}\right|\mathrm{\Delta }{E}_j={\mathit{u}}_l^{\mathit{c}}+\sum _{j=1}^2{\left|{\left[{\mathit{K}\mathbf{(}\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})+\frac{\mathit{\partial }\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})}{\mathit{\partial }\mathit{u}}{\mathit{u}}^{\mathit{c}}\right]}^{-1}\left[\frac{\mathit{\partial }\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})}{\mathit{\partial }{\mathit{E}}_j}{\mathit{u}}^{\mathit{c}}\right]\right|}_l\mathrm{\Delta }{E}_j$$(28)

When ${\mathit{u}}^{\mathit{c}}$ is obtained via Equation (25(26) $$\frac{\mathit{\partial }\mathit{u}({\mathit{E}}^{\mathit{c}})}{\mathit{\partial }{\mathit{E}}_j}=-{\left[\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})+\frac{\mathit{\partial }\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})}{\mathit{\partial }\mathit{u}}{\mathit{u}}^{\mathit{c}}\right]}^{-1}\left[\frac{\mathit{\partial }\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})}{\mathit{\partial }{\mathit{E}}_j}{\mathit{u}}^{\mathit{c}}\right]$$(26) ), all items at the right side of Equations (26)–(27) are determined; therefore, the bounds estimation of ${\mathit{u}}^{\mathit{I}}$ can be realized.

4. Interval estimation of inverse problem

This section presents a numerical model to solve the inverse interval bimodular problem.

The inverse problem here is mainly an issue to identify intervals of unknown constitutive parameters when measurement uncertainty is described by interval variables.

Assume ${\mathit{u}}^{*}$ is the vector of measured displacements, and is described by(29) $${\mathit{u}}^{*}={\mathit{u}}^{{\mathit{c}}^{*}}+\mathrm{\Delta }{\mathit{u}}^{*}\mathit{e}$$(29) (30) $${\mathit{u}}^{{\mathit{c}}^{*}}=\frac{1}{2}({\overline{\mathit{u}}}^{*}+{\underline{\mathit{u}}}^{*})$$(30) (31) $$\mathrm{\Delta }{\mathit{u}}^{*}=\frac{1}{2}({\overline{\mathit{u}}}^{*}-{\underline{\mathit{u}}}^{*})$$(31)

where ${\overline{\mathit{u}}}^{*}$ and ${\underline{\mathit{u}}}^{*}$ stand for the upper and lower bounds of ${\mathit{u}}^{*}$, respectively.

The interval identification of $\mathit{E}$ can be realized via two steps

Step 1. The identification of ${\mathit{E}}^c=[E^{+c},E^{-c}]$(32) $$\text{Let}\mathit{\phi }=[E^{+c},E^{-c}]$$(32)

$\mathit{\phi }$ can be determined via a minimizing process defined by(33) $$\left\{\begin{array}{c}min\prod (\mathit{\phi })=\frac{1}{2}{(\mathit{L}\mathit{u}(\mathit{\phi })-{\mathit{u}}^{{\mathit{c}}^{*}})}^T(\mathit{L}\mathit{u}(\mathit{\phi })-{\mathit{u}}^{{\mathit{c}}^{*}})=\frac{1}{2}{\mathit{S}}^{\mathit{T}}\mathit{S}\hfill \\ \text{s.t.}\mathit{K}(\mathit{\phi },u(\mathit{\phi }))\mathit{u}(\mathit{\phi })=\mathit{P}\hfill \end{array}\right.$$(33)

where L is a matrix mapping the topologic relationship between $\mathit{u}$ and ${\mathit{u}}^{*}$.

The above minimization can be realized via the Gauss–Newton algorithm in the following iterative process [15](34) $${\mathit{\phi }}^{\mathit{m}+1}={\mathit{\phi }}^{\mathit{m}}+\mathrm{\Delta }\mathit{\phi }$$(34) (35) $$({\mathit{G}}^{\mathit{T}}\mathit{G})\mathrm{\Delta }\mathit{\phi }={\mathit{G}}^{\mathit{T}}\mathit{S}$$(35) (36) $$\mathit{G}=\frac{\mathit{\partial }\mathit{u}}{\mathit{\partial }\mathit{\phi }}=-{\left(\mathit{K}+\frac{\mathit{\partial }\mathit{K}}{\mathit{\partial }\mathit{u}}\mathit{u}\right)}^{-1}\frac{\mathit{\partial }\mathit{K}}{\mathit{\partial }\mathit{\phi }}\mathit{u}$$(36)

Iteration stops if $\Vert \mathrm{\Delta }\mathit{\phi }\Vert \le \mathit{\beta }$

where $\mathit{\beta }$ refers to an error tolerance.

Regarding to $\frac{\mathit{\partial }\mathit{K}}{\mathit{\partial }\mathit{\phi }}$, the contribution of ith rod is(37) $$\frac{\mathit{\partial }{k}_{11}}{\mathit{\partial }{E}^{+}}=\frac{A_i}{l_i}·cos{\mathit{\alpha }}_i^2·\frac{e^{p{\mathit{\epsilon }}_i}}{1+e^{p{\mathit{\epsilon }}_i}}$$(37) (38) $$\frac{\mathit{\partial }{k}_{11}}{\mathit{\partial }{E}^{-}}=\frac{A_i}{l_i}·cos{\mathit{\alpha }}_i^2·\frac{e^{-p{\mathit{\epsilon }}_i}}{1+e^{-p{\mathit{\epsilon }}_i}}$$(38) (39) $$\frac{\mathit{\partial }{k}_{12}}{\mathit{\partial }{E}^{+}}=\frac{\mathit{\partial }{k}_{21}}{\mathit{\partial }{E}^{+}}=\frac{A_i}{l_i}·cos{\mathit{\alpha }}_{i}sin·{\mathit{\alpha }}_i\frac{e^{p{\mathit{\epsilon }}_i}}{1+e^{p{\mathit{\epsilon }}_i}}$$(39) (40) $$\frac{\mathit{\partial }{k}_{12}}{\mathit{\partial }{E}^{-}}=\frac{\mathit{\partial }{k}_{21}}{\mathit{\partial }{E}^{-}}=\frac{A_i}{l_i}·cos{\mathit{\alpha }}_i·sin·{\mathit{\alpha }}_i\frac{e^{-p{\mathit{\epsilon }}_i}}{1+e^{-p{\mathit{\epsilon }}_i}}$$(40) (41) $$\frac{\mathit{\partial }{k}_{22}}{\mathit{\partial }{E}^{+}}=\frac{A_i}{l_i}·sin{\mathit{\alpha }}_i^2·\frac{e^{p{\mathit{\epsilon }}_i}}{1+e^{p{\mathit{\epsilon }}_i}}$$(41) (42) $$\frac{\mathit{\partial }{k}_{22}}{\mathit{\partial }{E}^{-}}=\frac{A_i}{l_i}·sin{\mathit{\alpha }}_i^2·\frac{e^{-p{\mathit{\epsilon }}_i}}{1+e^{-p{\mathit{\epsilon }}_i}}$$(42)

Step 2

When $E^{\mathit{c}}$ is obtained, ${[\mathrm{\Delta }{E}^{+},\mathrm{\Delta }{E}^{-}]}^T$can be determined using a least square method [18](43) $$\left[\begin{array}{c}\mathrm{\Delta }{E}^{+}\hfill \\ \mathrm{\Delta }{E}^{-}\hfill \end{array}\right]={\left(\left[\begin{array}{c}{\mathit{L}}^{\mathit{T}}{\mathit{Q}}_1^{\mathit{T}}\\ {\mathit{L}}^{\mathit{T}}{\mathit{Q}}_2^{\mathit{T}}\end{array}\right][{\mathit{L}\mathit{Q}}_1,{\mathit{L}\mathit{Q}}_2]\right)}^{-1}\left[\begin{array}{c}{\mathit{L}}^{\mathit{T}}{\mathit{Q}}_1^{\mathit{T}}\hfill \\ {\mathit{L}}^{\mathit{T}}{\mathit{Q}}_2^{\mathit{T}}\hfill \end{array}\right]\mathrm{\Delta }{\mathit{u}}^{*}$$(43)

where(44) $$[Q_I]=\left|{\left[\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})+\frac{\mathit{\partial }\mathit{K}}{\mathit{\partial }\mathit{u}}{\mathit{u}}^{\mathit{c}}\right]}^{-1}\left[\frac{\mathit{\partial }\mathit{K}({\mathit{E}}^{\mathit{c}},{\mathit{u}}^{\mathit{c}})}{\mathit{\partial }{\mathit{E}}_j}{\mathit{u}}^{\mathit{c}}\right]\right|.(i=1,2)$$(44)

The effect of noisy data is taken into account in the form(45) $${\underline{\mathit{u}}}_n^{*}=(1+\mathit{\delta }\mathit{\varsigma }){\underline{\mathit{u}}}^{*}$$(45) (46) $${\overline{\mathit{u}}}_{\mathit{n}}^{*}=(1+\mathit{\delta }\mathit{\varsigma }){\overline{\mathit{u}}}^{*}$$(46)

where ${\underline{\mathit{u}}}_n^{*}$ and ${\overline{\mathit{u}}}_{\mathit{n}}^{*}$ represent the vectors of lower and upper bounds of measured or stimulated displacement containing the noisy data, ς is a random variable between −0.5 and 0.5 and δ refers to a noisy level.

5. Numerical verification and discussions

For simplicity, all the computing parameters are assumed dimensionless.

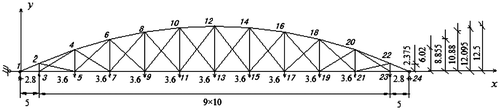
Example 1 considers a truss structure as shown in Figure 2, where E⁺ ∊ [1.16, 1.20] × 10⁸, E⁻ ∊ [2.08, 2.12] × 10⁸ and P = 1 × 10⁸. In terms of central value and radius of ${\mathit{u}}^{\mathit{I}}=[\underline{\mathit{u}},\overline{\mathit{u}}]$, Table 1 exhibits a comparison of intervals given by the proposed method and the combinatorial method.[19]

Figure 2. An elastic bimodulus truss structure.

Table 1. A comparison of intervals.

Displacement	${\mathit{u}}^{\mathit{c}}$	$\mathrm{\Delta }\mathit{u}$	${\mathit{u}}_{\mathit{r}}^{\mathit{c}}$	$\mathrm{\Delta }{\mathit{u}}_{\mathit{r}}$	$\frac{{\mathit{u}}^{\mathit{c}}}{{\mathit{u}}_{\mathit{r}}^{\mathit{c}}}$ (%)	$\frac{\mathbf{\Delta }\mathit{u}}{{\mathbf{\Delta }\mathit{u}}_{\mathit{r}}}$ (%)
u1	0.00E+00	0.00E+00	0.00E+00	0.00E+00	0.0000	0.0000
v1	0.00E+00	0.00E+00	0.00E+00	0.00E+00	0.0000	0.0000
u2	1.01E−05	1.44E−07	1.01E−05	1.44E−07	0.0179	0.0260
v2	−2.39E−05	3.30E−07	−2.39E−05	3.30E−07	0.0209	0.0264
u3	1.69E−06	2.87E−08	1.70E−06	2.87E−08	0.0295	0.0264
v3	−2.39E−05	3.29E−07	−2.39E−05	3.29E−07	0.0188	0.0173
u4	1.65E−05	2.41E−07	1.65E−05	2.41E−07	0.0242	0.0278
v4	−4.56E−05	6.28E−07	−4.56E−05	6.28E−07	0.0208	0.0167
u5	4.54E−06	7.37E−08	4.54E−06	7.37E−08	0.0275	0.0250
v5	−4.56E−05	6.27E−07	−4.56E−05	6.27E−07	0.0197	0.0233
u6	1.89E−05	2.81E−07	1.89E−05	2.81E−07	0.0212	0.0156
v6	−5.97E−05	8.23E−07	−5.97E−05	8.24E−07	0.0209	0.0234
u7	7.41E−06	1.20E−07	7.41E−06	1.20E−07	0.0277	0.0257
v7	−5.97E−05	8.22E−07	−5.97E−05	8.22E−07	0.0201	0.0198
u8	1.90E−05	2.91E−07	1.90E−05	2.91E−07	0.0263	0.0330
v8	−6.88E−05	9.51E−07	−6.88E−05	9.51E−07	0.0211	0.0209
u9	1.03E−05	1.69E−07	1.03E−05	1.69E−07	0.0339	0.0350
v9	−6.88E−05	9.48E−07	−6.88E−05	9.49E−07	0.0211	0.0253
u10	1.79E−05	2.83E−07	1.79E−05	2.83E−07	0.0280	0.0173
v10	−7.40E−05	1.02E−06	−7.40E−05	1.02E−06	0.0203	0.0225
u11	1.32E−05	2.17E−07	1.32E−05	2.17E−07	0.0264	0.0354
v11	−7.40E−05	1.02E−06	−7.40E−05	1.02E−06	0.0203	0.0216
u12	1.62E−05	2.66E−07	1.62E−05	2.66E−07	0.0278	0.0255
v12	−7.57E−05	1.05E−06	−7.57E−05	1.05E−06	0.0198	0.0210
u13	1.62E−05	2.66E−07	1.62E−05	2.66E−07	0.0278	0.0255
v13	−7.57E−05	1.04E−06	−7.57E−05	1.04E−06	0.0205	0.0192
u14	1.45E−05	2.60E−07	1.45E−05	2.60E−07	0.0277	0.0419
v14	−7.40E−05	1.02E−06	−7.40E−05	1.02E−06	0.0203	0.0225
u15	1.91E−05	3.15E−07	1.91E−05	3.16E−07	0.0288	0.0345
v15	−7.40E−05	1.02E−06	−7.40E−05	1.02E−06	0.0203	0.0216
u16	1.33E−05	2.80E−07	1.33E−05	2.80E−07	0.0300	0.0161
v16	−6.88E−05	9.51E−07	−6.88E−05	9.51E−07	0.0211	0.0209
u17	2.20E−05	3.64E−07	2.20E−05	3.64E−07	0.0250	0.0349
v17	−6.88E−05	9.48E−07	−6.88E−05	9.49E−07	0.0211	0.0253
u18	1.34E−05	3.08E−07	1.34E−05	3.08E−07	0.0335	0.0340
v18	−5.97E−05	8.23E−07	−5.97E−05	8.24E−07	0.0209	0.0234
u19	2.49E−05	4.12E−07	2.49E−05	4.12E−07	0.0261	0.0291
v19	−5.97E−05	8.22E−07	−5.97E−05	8.22E−07	0.0201	0.0198
u20	1.58E−05	3.50E−07	1.58E−05	3.50E−07	0.0285	0.0246
v20	−4.56E−05	6.28E−07	−4.56E−05	6.28E−07	0.0208	0.0167
u21	2.78E−05	4.59E−07	2.78E−05	4.59E−07	0.0288	0.0213
v21	−4.56E−05	6.27E−07	−4.56E−05	6.27E−07	0.0197	0.0232
u22	2.23E−05	4.11E−07	2.23E−05	4.11E−07	0.0314	0.0269
v22	−2.39E−05	3.30E−07	−2.39E−05	3.30E−07	0.0209	0.0263
u23	3.06E−05	5.04E−07	3.06E−05	5.04E−07	0.0277	0.0323
v23	−2.39E−05	3.29E−07	−2.39E−05	3.29E−07	0.0188	0.0173
u24	3.23E−05	5.33E−07	3.23E−05	5.33E−07	0.0278	0.0255
v24	0.00E+00	0.00E+00	0.00E+00	0.00E+00	0.0000	0.0000

In Table 1, $u_r^c=(u_{max}+u_{min})/2$, $\mathrm{\Delta }{\mathit{u}}_{\mathit{r}}=(u_{max}-u_{min})/2$, $u_{max}$ and $u_{min}$ refer to the maximum and minimum values of displacement among the solutions given by the combinatorial method with four set combinations of constitutive parameters, i.e.

[1.16, 2.08] × 10⁸; [1.16, 2.12] × 10⁸;

[1.20, 2.08] × 10⁸; [1.20, 2.12] × 10⁸.

Example 2 consider an identification problem to estimate ${\mathit{E}}^{\mathit{c}}$ and $\mathrm{\Delta }\mathit{E}$ for the structure shown in the Example 1, ${\mathit{u}}^{*}$ is given by Equations (23)–(25) with actual values of ${\mathit{E}}^{\mathit{c}}$ and $\mathrm{\Delta }\mathit{E}$, i.e. E^c= [1.20 × 10⁸, 5.00 × 10⁸], and ΔE = [4.00 × 10⁷, 1.00 × 10⁸], respectively. We tried several different arrangements of sampling points randomly, which seemed to have no impact on the identification results. Some of these results are presented in Tables 2–5 with different δ.

Table 2. Numerical comparison of E^c and ΔE (24 sampling points (1–24)).

δ	1%		3%		5%
E^c obtained by the proposed approach	1.20E+08	4.96E+08	1.20E+08	5.04E+08	1.19E+08	5.05E+08
Relative error of E^c (%)	0.00%	−0.80%	0.00%	0.80%	−0.83%	1.00%
ΔE obtained by the proposed approach	4.00E+07	9.92E+07	3.97E+07	1.01E+08	3.95E+07	1.03E+08
Relative error of ΔE (%)	0.00%	−0.80%	−0.75%	1.00%	−1.25%	3.00%

Table 3. Numerical comparison of E^c and ΔE (10 sampling points (1, 2, 5, 8, 11,14, 17, 20, 23, 24)).

δ	1%		3%		5%
E^c obtained by the proposed approach	1.20E+08	5.02E+08	1.20E+08	4.90E+08	1.21E+08	5.11E+08
Relative error of E^c (%)	0.00%	0.40%	0.00%	−2.00%	0.83%	2.20%
ΔE obtained by the proposed approach	4.00E+07	9.98E+07	4.02E+07	1.01E+08	3.98E+07	9.80E+07
Relative error of ΔE (%)	0.00%	−0.20%	0.50%	1.00%	−0.50%	−2.00%

Table 4. Numerical comparison of E^c and ΔE (7 sampling points (1, 3, 8, 13, 18, 23, 24)).

δ	1%		3%		5%
E^c obtained by the proposed approach	1.21E+08	5.00E+08	1.21E+08	4.94E+08	1.22E+08	5.08E+08
Relative error of E^c (%)	0.83%	0.00%	0.83%	−1.20%	1.67%	1.60%
ΔE obtained by the proposed approach	3.99E+07	1.01E+08	4.02E+07	9.79E+07	3.96E+07	1.02E+08
Relative error of ΔE (%)	−0.25%	1.00%	0.50%	−2.10%	−1.00%	2.00%

Table 5. Numerical comparison of E^c and ΔE (5 sampling points (1, 4, 11, 18, 24)).

δ	1%		3%		5%
E^c obtained by the proposed approach	1.19E+08	5.01E+08	1.21E+08	5.06E+08	1.21E+08	4.90E+08
Relative error of E^c (%)	−0.83%	0.20%	0.83%	1.20%	0.83%	−2.00%
ΔE obtained by the proposed approach	4.00E+07	1.00E+08	3.99E+07	1.00E+08	4.00E+07	9.89E+07
Relative error of ΔE (%)	0.00%	0.00%	−0.25%	0.00%	0.00%	−1.10%

The numerical framework is constructed on the basis of Taylor series expansion method that not only provides a deterministic platform to estimate intervals, but also an easy gain of derivatives of displacements with respect to constitutive parameters. These derivatives are absolutely necessary for solving both the forward and inverse problems. As exhibited in the numerical tests, the Taylor series expansion-based solutions for either forward or inverse problems are satisfactory. As shown Table 1, in comparison with the combinatorial method that was considered as the most accurate method for solving interval system of equations,[19] the maximum relative error of intervals estimation for displacements is less than 0.05%. For the solution of an inverse problem, the maximum relative error is 3%, as shown in Tables 2^{Table 3Table 4}–5.

6. Conclusions and discussion

This paper attempts to develop numerical models for the interval uncertainty analysis of elastic bimodular truss structures, the major contribution includes

1. Present a numerical framework to estimate interval uncertainty in the bimodular truss structure, forward and backward. Thereby, the intervals estimation of displacements can be given when constitutive parameters are interval variables, and the intervals estimation of unknown constitutive parameters can be realized when there exists an interval uncertainty in the measurement. Due to the insufficient concern about the bimodular problem with interval uncertainty, the work presented may kick-off the study on this issue.

2. Develop a Taylor series expansion-based numerical model to solve inverse interval bimodular problems. Frankly, Taylor series expansion is basically not new, and has been employed in some structural analysis with interval variables. However, it is new to deal with bimodular problems with interval uncertainty, forward and inverse particularly.

3. Provide numerical verifications for the proposed models, forward and inverse.

Because the proposed approach is based on Taylor series expansion that is available when interval quantities width is relatively small, the interval size has to be taken into account in the application. The sharpness of Taylor series expansion-based solution deteriorates with the increase in the interval quantities’ width. In this case, optimization and combinatorial methods are more proper option to gain more accurate results, but need more computational expense, particularly the cost of solving inverse problems may increase significantly. On the other hand, due to the lack of actual uncertainty information either from experiment or industry more efforts for the further model V&V are required. In addition to the numerical verification similar to this paper, the experiment-based verification is particularly required.

Funding

The authors acknowledge the support from NSF’s [grant number 10421002], [grant number 10772035], [grant number 10721062], [grant number 11072043] and NKBRP [2010CB832703].