Reconstruction of scatterers with four different boundary conditions by T-matrix method

Abstract

This paper introduces a general inversion method to simultaneously reconstruct scatterers with different boundary conditions such as Dirichlet, Neumann, Robin, and transmission boundaries without a priori information on their locations, shapes, or physical properties. The forward scattering of mixed scatterers is modeled by a unified framework of T-matrix method, while the objective function considered in the inverse problem is solved by a subspace-based optimization method. The unknowns are T-matrix coefficients, from which the types of boundary conditions of scatterers are identified. Numerical examples show that this method is able to recover not only the shapes of scatterers but also their physical properties and parameters.

Keywords:

• inverse scattering
• T-matrix method
• four boundary conditions
• subspace based optimization

AMS Subject Classifications:

• 65N21
• 65N20
• 78M16
• 78M50

1 Introduction

Inverse scattering is a kind of widely used technique to determine characteristics of scatterers such as their locations, shapes and material properties from measured scattered field. Various inverse scattering methods [1–4] have been proposed and widely applied in geological exploration, through wall imaging and remote sensing et al. To the best of our knowledge, most known inverse scattering methods are designed with particular prior information on physical properties of the unknown scatterers. For example, the scatterer should be known as dielectric medium [5–7] or perfect electric conductor (PEC) a priori.[8–11] However, in practical problems, the individual targets to be reconstructed are possible to have different boundary conditions (BCs) simultaneously such as Dirichlet, transmission or Robin et al. This is one of the main motivations of the current study.

It should be indicated that there are already some qualitative inverse scattering methods like linear sampling method [12, 13] that can retrieve shapes of scatterers with mixed BCs. However, this qualitative method can not further classify the physical characteristics of scatterers. Therefore, there is a demand to develop a quantitative method to solve such problems. It is well known that this is a challenging task. There are two main difficulties to be overcome, i.e. finding a uniform framework to model the scattering phenomenon of different types of scatterers and developing criteria to further classify their physical properties.

For this aim, recently, we have introduced a T-matrix method [14] to simultaneously retrieve dielectric and PEC scatterers without any prior information. The T-matrix method is a conventional method to solve scattering problems. It was firstly introduced by Waterman [15] and further developed by Chew and Wang [16], Otto and Chew [17, 18], Lin and Chew [19]. Before,[14] the original T-matrix inversion method was thought to work with a known boundary type of scatterers. In T-matrix method, scatterers are firstly divided into a set of subunits. Then both the incident and scattered fields are expanded on each subunit as functions of multipoles. The coefficients of scattered field are related to that of the incident field through T-matrix which is determined from BCs. Different properties of scatterers own different T-matrices.[20] This property makes the T-matrix method become a good candidate to model scattering phenomenon of mixed boundary scatterers.

In [14], both monopole and dipole terms were employed in the multipole expansion but only the monopole term exists in most original T-matrix inversions. This is because there exists magnitude difference between dielectric and PEC T-matrix coefficients. Therefore, it can ensure the accuracy of dielectric-PEC mixed boundaries scattering. The PEC was differentiated from dielectric scatterers by the recovered zeroth-order T-matrix coefficient, i.e. the coefficient of monopole term. It has been shown that this classification criterion works well to distinguish dielectric scatterers (even lossy) from PEC.

In this paper, we further extend our work in [14] to a more general case. Four types of BCs including Dirichlet, Neumann, impedance and transmission boundaries are considered simultaneously. It covers most commonly used BCs in electromagnetic or acoustic wave scattering problems. To the best of authors’ knowledge, this is the first paper to discuss a quantitative inversion method to retrieve scatterers with four types of BCs. The scattering phenomenon of mixed boundary scatterers is still modeled in a T-matrix framework. The boundary types of recovered scatterers can be classified according to the different characteristics of T-matrix coefficients. Compared with [14], the problem considered in this paper is more challenging and complicated for the following two reasons: (1) Obviously it is much more difficult to classify four boundary conditions than two; (2) Some boundary conditions exhibit similarities under certain conditions. For example, scatterer with impedance boundary can only be conditionally differentiated from that with Dirichlet or Neumann boundary due to their close relation on physical properties. New classification criterion should be provided to do so. Finally, as seen, T-matrix method is a pixel based inversion method. We will discuss about the uniqueness of T-matrix method for recovering the scatterers with mixed boundaries.

The structure of this paper is as follows. In Section 2, the forward scattering model with T-matrix method is introduced. Then the inverse scattering method based on subspace based optimization is discussed in Section 3. Numerical examples are shown in Section 4. Finally, conclusions are made in Section 5.

2 The forward scattering problem and T-matrix method

2.1 The governing equations of forward scattering problem

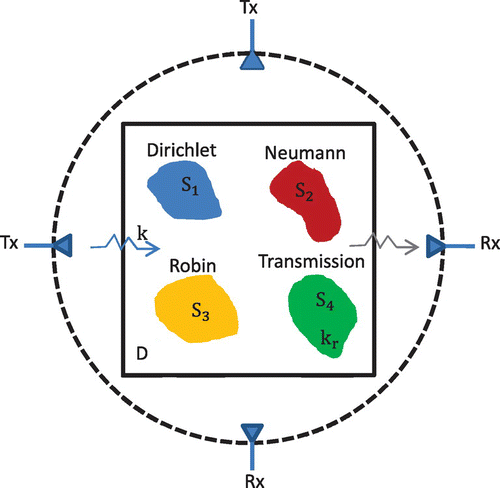
The forward scattering problem aims to solve the scattered field due to presence of scatterers illuminated by a sequence of incident waves. In this paper, we consider only two dimensional scattering problems. The domain of interest $D$ is supposed to be bounded, where nonmagnetic scatters with different types of BCs are inside, as shown in Figure 1. Suppose there are a total of $N_{inc}$ plane waves at a single frequency (wavenumber is $k$) illuminated evenly from transmitters (Tx) outside $D$. For each incidence, the scattered fields are measured by $N_r$ receivers (Rx) located at ${\overline{r}}_q,q=1,2,\dots ,N_r$ as depicted in Figure 1.

We first briefly introduce the governing equations of two dimensional forward scattering problem with different BCs. For a given incidence, the total field $u(x,y)$ outside scatterers satisfies1 $$\begin{array}{c}\hfill {\mathrm{\nabla }}^{2}u+k^{2}u=0,\mathrm{i}n{\mathbb{R}}^2\backslash S\end{array}$$1 where $k=2\mathit{\pi }/\mathit{\lambda }$ is the wavenumber of incident wave in the background medium, $\mathit{\lambda }$ is the wavelength of incident wave and $S=\bigcup S_j$ is the total boundary of all scatterers.

Figure 1. Sketch of scattering problem with mixed boundary conditions.

The scattered field can be determined once we know the BCs which reflect intrinsic characteristics of scatterers. Four kinds of BCs, namely, Dirichlet, Neumann, Robin and transmission conditions will be considered simultaneously. In electromagnetics, they correspond to PEC, PMC, impedance and dielectric scatterers, respectively. While in acoustics, they correspond to sound soft, sound hard, impedance and transmission scatterers.

Take the four scatterers in Figure 1 for example. The first scatterer owns Dirichlet BC that satisfies2 $$\begin{array}{c}\hfill u=0,\mathrm{o}n\mathit{\partial }{S}_1.\end{array}$$2 The second scatterer satisfies Neumann BC3 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }n}=0,\mathrm{o}n\mathit{\partial }{S}_2\end{array}$$3 where $n$ is the normal direction of the scatterer boundary.

The third one satisfies Robin BC4 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }n}+i\mathit{\eta }ku=0,\mathrm{o}n\mathit{\partial }{S}_3\end{array}$$4 where $\mathit{\eta }>0$ is the impedance.

The fourth scatterer has transmission BC that is5 $$\begin{array}{c}\hfill {u|}_{\mathit{\partial }{S}_4^{-}}{=u|}_{\mathit{\partial }{S}_4^{+}},\frac{\mathit{\partial }u}{\mathit{\partial }n}{{|}_{\mathit{\partial }{S}_4^{-}}=\mathit{\zeta }\frac{\mathit{\partial }u}{\mathit{\partial }n}|}_{\mathit{\partial }{S}_4^{+}}.\end{array}$$5 For electromagnetic waves with transverse (with respect to the z-axis) magnetic ($T{M}_z$) polarization, $\mathit{\zeta }$ is equal to $1.$ For acoustic wave, $\mathit{\zeta }$ can be other values. For the transmission BC, the total field inside scatterer satisfies6 $$\begin{array}{c}\hfill {\mathrm{\nabla }}^{2}u+k_r^{2}u=0,\mathrm{i}n{S}_4\end{array}$$6 where $k_r$ is the wavenumber inside the scatterer.

2.2 The T-matrix method of forward scattering problem

In this section, we briefly introduce the T-matrix method to solve the governing equations in Section 2.1. More details about T-matrix method can be found in [14] and references therein.

For a single small scatterer, the T-matrix relates the multipole expansion coefficients of the incident field to those of its scattered field. Suppose there is a standalone cylindrical scatterer whose center is located at ${\overline{C}}_0=(r_0,{\mathit{\theta }}_0)$ and its $M$th order T-matrix is given as $\overline{\overline{T}}=diag([T_m]),m=-M,\dots ,M$ with $M$ as the truncation number of multipoles. Suppose the observation point is at $\overline{t}$ under the global coordinate. The cylindrical scatterer is illuminated by an incident field, which can be represented by the multipole expansion as $Rg{\overline{\mathrm{\Psi }}}^t(k,{\overline{t}}^{\prime })·{\overline{e}}_0={\sum }_{-M}^{M}Rg{[\mathrm{\Psi }(k,{\overline{t}}^{\prime })]}_m·{[{\overline{e}}_0]}_m$, where ${\overline{t}}^{\prime }=\overline{t}-{\overline{C}}_0=({\mathit{\rho }}_0,{\mathit{\varphi }}_0)$ is under the local coordinate of the current scatterer at ${\overline{C}}_0$. Here $Rg$ indicates the regular part of Hankel function and ${[{\overline{\mathrm{\Psi }}}^t(k,{\overline{t}}^{\prime })]}_m=H_m^{(1)}(k{\mathit{\rho }}_0)e^{im{\mathit{\varphi }}_0},m=-M,\dots ,M$. ${\overline{e}}_0$ is the multiple expansion coefficients of the incident filed. For a plane wave, ${\overline{e}}_0$ has explicit form which can be found in [14, 21]. Both the vectors $\overline{\mathrm{\Psi }}$ and ${\overline{e}}_0$ have dimension $2M+1$. According to the definition of T-matrix, the scattered field can be written by $u^{sca}\left(\overline{t}\right)={\sum }_{-M}^M{[\mathrm{\Psi }(k,{\overline{t}}^{\prime })]}_m·T_m·{[{\overline{e}}_0]}_m$. The examples of calculating the $T_m$ will be introduced in Section 2.3.

Next, we derive the scattering equation using the T-matrix representation for general scatterers. Suppose the domain of interest $D$ is discretized into $N$ subunits and each subunit is small enough which can be well approximated by a circle of the same area. And the center of each circle is at ${\overline{C}}_i=(r_{0,i},{\mathit{\theta }}_{0,i}),i=1,2,\dots ,N$ under the global coordinate. The field at $\overline{t}$ (also under a global coordinate) outside all scatterers can be represented by the multipole expansion and addition theorem as [21]7 $$\begin{array}{c}\hfill u^{tot}\left(\overline{t}\right)=Rg{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·{\overline{e}}_i+\sum _{j=1}^N{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_j^{\prime }\right)·{\overline{a}}_j,i=1,2,\dots ,N\end{array}$$7 where the first term of right hand side is the incident field on the $i$th subunit and the second term is the scattered field from all the subunits. Here ${\overline{t}}_i^{\prime }=\overline{t}-{\overline{C}}_i=({\mathit{\rho }}_i,{\mathit{\varphi }}_i),i=1,2,\dots ,N$ is under the local coordinate of the $i$th subunit. The vectors ${\overline{a}}_j,j=1,2,\dots ,N$ also have a dimension $2M+1$ and they are referred as the vectors of amplitude of the induced multipoles.

The total incident field on the $i$th subunit can be further expressed as the summation of the background incident field and the multiple scattered fields from other subunits. Therefore, we can split Equation (77 $$\begin{array}{c}\hfill u^{tot}\left(\overline{t}\right)=Rg{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·{\overline{e}}_i+\sum _{j=1}^N{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_j^{\prime }\right)·{\overline{a}}_j,i=1,2,\dots ,N\end{array}$$7 ) into the total incident field (the first two terms in Equation (88 $$\begin{array}{c}\hfill u^{tot}\left(\overline{t}\right)=Rg{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·{\overline{e}}_i+\sum _{j=1,j\ne i}^N{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_j^{\prime }\right)·{\overline{a}}_j+{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·{\overline{a}}_i,i=1,2,\dots ,N.\end{array}$$8 )) onto the $i$th subunit and the scattered field off it8 $$\begin{array}{c}\hfill u^{tot}\left(\overline{t}\right)=Rg{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·{\overline{e}}_i+\sum _{j=1,j\ne i}^N{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_j^{\prime }\right)·{\overline{a}}_j+{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·{\overline{a}}_i,i=1,2,\dots ,N.\end{array}$$8 As known, the translational addition theorem enables one to represent the scattered field from other scatterers as a form of the incident field to one scatterer. Namely, there is9 $$\begin{array}{c}\hfill {\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_j^{\prime }\right)=Rg{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·{\overline{\overline{\mathit{\alpha }}}}_{ij},\end{array}$$9 where ${\overline{\overline{\mathit{\alpha }}}}_{ij}$ is the translational matrix given in [22]. The substitution of Equation (99 $$\begin{array}{c}\hfill {\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_j^{\prime }\right)=Rg{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·{\overline{\overline{\mathit{\alpha }}}}_{ij},\end{array}$$9 ) into Equation (88 $$\begin{array}{c}\hfill u^{tot}\left(\overline{t}\right)=Rg{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·{\overline{e}}_i+\sum _{j=1,j\ne i}^N{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_j^{\prime }\right)·{\overline{a}}_j+{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·{\overline{a}}_i,i=1,2,\dots ,N.\end{array}$$8 ) yields10 $$\begin{array}{c}\hfill u^{tot}\left(\overline{t}\right)=Rg{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·\left[{\overline{e}}_i,+,\sum _{j=1,j\ne i}^N,{\overline{\overline{\mathit{\alpha }}}}_{ij},·,{\overline{a}}_j\right]+{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·{\overline{a}}_i,i=1,2,\dots ,N.\end{array}$$10 The first term in Equation (1010 $$\begin{array}{c}\hfill u^{tot}\left(\overline{t}\right)=Rg{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·\left[{\overline{e}}_i,+,\sum _{j=1,j\ne i}^N,{\overline{\overline{\mathit{\alpha }}}}_{ij},·,{\overline{a}}_j\right]+{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{t}}_i^{\prime }\right)·{\overline{a}}_i,i=1,2,\dots ,N.\end{array}$$10 ) means the total incident field on the $i$th subunit and the second term means the scattered field off it. Thus, from the definition of the T-matrix, we easily obtain,11 $$\begin{array}{c}\hfill {\overline{a}}_i={\overline{\overline{T}}}_i·\left[{\overline{e}}_i,+,\sum _{j=1,j\ne i}^N,{\overline{\overline{\mathit{\alpha }}}}_{ij},·,{\overline{a}}_j\right].\end{array}$$11 Combining Equation (1111 $$\begin{array}{c}\hfill {\overline{a}}_i={\overline{\overline{T}}}_i·\left[{\overline{e}}_i,+,\sum _{j=1,j\ne i}^N,{\overline{\overline{\mathit{\alpha }}}}_{ij},·,{\overline{a}}_j\right].\end{array}$$11 ) on all subunits into one matrix equation, we have12 $$\begin{array}{c}\hfill \overline{a}=\overline{\overline{O}}·\left[\overline{e},-,\overline{\overline{A}},·,\overline{a}\right]\end{array}$$12 where ${[\overline{\overline{O}}]}_{ii}={\overline{\overline{T}}}_i$ and zero off-diagonal, ${[\overline{\overline{A}}]}_{ij}=-{\overline{\overline{\mathit{\alpha }}}}_{ij}$ for $i\ne j$ and zero otherwise, ${[\overline{a}]}_i={\overline{a}}_i$ and ${[\overline{e}]}_i={\overline{e}}_i.$

The scattered field $u^{sca}$ at the receiver position ${\overline{r}}_q(q=1,2,\dots ,N_r)$ under global coordinate can be obtained by13 $$\begin{array}{c}\hfill u^{sca}({\overline{r}}_q)=\sum _{j=1}^N{\overline{\mathrm{\Psi }}}^t\left(k,,,{\overline{r}}_j^{\prime }\right)·{\overline{a}}_j\end{array}$$13 where ${\left[{\overline{\mathrm{\Psi }}}^t,(k,{\overline{r}}_{j^{\prime }})\right]}_m=H_m^{(1)}(k{r}_j)e^{im{\mathit{\psi }}_j}$ with $m\in [-M,M]$, and ${\overline{r}}_j^{\prime }={\overline{r}}_q-{\overline{C}}_j=\left(r_j,,,{\mathit{\psi }}_j\right)$ is the local-coordinate representation of the receiver where the origin of the coordinate system is placed at the center of the $j$th subunit.

Combining the $N_r$ equations for all the receivers into one matrix equation, we have14 $$\begin{array}{c}\hfill {\overline{u}}^{sca}={\overline{\overline{\mathrm{\Psi }}}}^t·\overline{a}.\end{array}$$14 Equations (1212 $$\begin{array}{c}\hfill \overline{a}=\overline{\overline{O}}·\left[\overline{e},-,\overline{\overline{A}},·,\overline{a}\right]\end{array}$$12 ) and (1414 $$\begin{array}{c}\hfill {\overline{u}}^{sca}={\overline{\overline{\mathrm{\Psi }}}}^t·\overline{a}.\end{array}$$14 ) are referred to as the state equation and the field equation, respectively. For each incident field, the two unknowns $\overline{a}$ and ${\overline{u}}^{sca}$ can be obtained by solving these two equations together. Then all scattered fields ${\{{\overline{u}}_j^{sca}\}}_{j=1}^{N_{inc}}$ are measured and will be used in inversion.

2.3 The T-matrix coefficients and their asymptotic properties at $kR\approx 0$

As known, the T-matrix coefficients are determined from boundary conditions. We briefly introduce the derivations here for the easy understanding of readers. For more details, please refer to [20] and references therein. All the derivations are under assumption that the scatterer is circular and homogeneous. Suppose the radius of circular scatterer is $R$.

First the plane wave $u^{inc}=e^{-ikrcos(\mathit{\varphi })}$ can be represented as15 $$\begin{array}{c}\hfill u^{inc}=\sum _{m=-\infty }^{\infty }{J}_m(kr)e^{im(\mathit{\varphi }-1/2\mathit{\pi })}.\end{array}$$15 The outgoing wave $u_1$ needs to satisfy the radiation condition at infinity and therefore can be represented as16 $$\begin{array}{c}\hfill u_1=\sum _{m=-\infty }^{\infty }{b}_m{H}_m^{(1)}(kr)e^{im(\mathit{\varphi }-1/2\mathit{\pi })}.\end{array}$$16 Inside the scatterer, the field $u_2$ should be bounded at $r=0$ and it is expanded as17 $$\begin{array}{c}\hfill u_2=\sum _{m=-\infty }^{\infty }{c}_m{J}_m(k_{r}r)e^{im(\mathit{\varphi }-1/2\mathit{\pi })}.\end{array}$$17 By substituting the above filed expansions into boundary conditions (22 $$\begin{array}{c}\hfill u=0,\mathrm{o}n\mathit{\partial }{S}_1.\end{array}$$2 ), (33 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }n}=0,\mathrm{o}n\mathit{\partial }{S}_2\end{array}$$3 ), (44 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }n}+i\mathit{\eta }ku=0,\mathrm{o}n\mathit{\partial }{S}_3\end{array}$$4 ) and (55 $$\begin{array}{c}\hfill {u|}_{\mathit{\partial }{S}_4^{-}}{=u|}_{\mathit{\partial }{S}_4^{+}},\frac{\mathit{\partial }u}{\mathit{\partial }n}{{|}_{\mathit{\partial }{S}_4^{-}}=\mathit{\zeta }\frac{\mathit{\partial }u}{\mathit{\partial }n}|}_{\mathit{\partial }{S}_4^{+}}.\end{array}$$5 ) at $r=R$, the corresponding T-matrix coefficients ${\left[\overline{\overline{T}}\right]}_m\equiv b_m$ are obtained. It should be indicated that $u_2$ is not required in the Dirichlet and Impedance boundary conditions. For these two boundary conditions, the total field is $u=u^{inc}+u_1$.

Therefore, the $m$th order of T-matrix coefficients for Dirichlet BC in Equation (22 $$\begin{array}{c}\hfill u=0,\mathrm{o}n\mathit{\partial }{S}_1.\end{array}$$2 ) is18 $$\begin{array}{c}\hfill {\left[\overline{\overline{T}}\right]}_m=-\frac{J_m(kR)}{H_m^{(1)}(kR)}.\end{array}$$18 The $m$th order of T-matrix coefficients of Neumann BC in Equation (33 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }n}=0,\mathrm{o}n\mathit{\partial }{S}_2\end{array}$$3 ) is19 $$\begin{array}{c}\hfill {\left[\overline{\overline{T}}\right]}_m=-\frac{J_m^{\prime }(kR)}{H_m^{{(1)}^{\prime }}(kR)}.\end{array}$$19 The $m$th order of T-matrix coefficients of Robin BC in Equation (44 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }n}+i\mathit{\eta }ku=0,\mathrm{o}n\mathit{\partial }{S}_3\end{array}$$4 ) is20 $$\begin{array}{c}\hfill {\left[\overline{\overline{T}}\right]}_m=-\frac{i\mathit{\eta }{J}_m(kR)+J_m^{\prime }(kR)}{i\mathit{\eta }{H}_m^{(1)}(kR)+H_m^{{(1)}^{\prime }}(kR)}.\end{array}$$20 It can be noticed that the coefficients of T-matrix for scatterers with Dirichlet and Neumann BCs can also be obtained form Equation (2020 $$\begin{array}{c}\hfill {\left[\overline{\overline{T}}\right]}_m=-\frac{i\mathit{\eta }{J}_m(kR)+J_m^{\prime }(kR)}{i\mathit{\eta }{H}_m^{(1)}(kR)+H_m^{{(1)}^{\prime }}(kR)}.\end{array}$$20 ) by taking $\mathit{\eta }=\infty$ and $\mathit{\eta }=0$, respectively.

Finally, the $m$th order of T-matrix coefficients of scatterer with transmission BC in Equation (55 $$\begin{array}{c}\hfill {u|}_{\mathit{\partial }{S}_4^{-}}{=u|}_{\mathit{\partial }{S}_4^{+}},\frac{\mathit{\partial }u}{\mathit{\partial }n}{{|}_{\mathit{\partial }{S}_4^{-}}=\mathit{\zeta }\frac{\mathit{\partial }u}{\mathit{\partial }n}|}_{\mathit{\partial }{S}_4^{+}}.\end{array}$$5 ) is21 $$\begin{array}{c}\hfill {\left[\overline{\overline{T}}\right]}_m=\frac{\mathit{\zeta }{k}_r{J}_m(kR)J_m^{\prime }(k_{r}R)-k{J}_m(k_{r}R)J_m^{\prime }(kR)}{k{H}_m^{{(1)}^{\prime }}(kR)J_m(k_{r}R)-\mathit{\zeta }{k}_r{J}_m^{\prime }(k_{r}R)H_m^{(1)}(kR)}.\end{array}$$21 The T-matrix coefficient in Equation (2121 $$\begin{array}{c}\hfill {\left[\overline{\overline{T}}\right]}_m=\frac{\mathit{\zeta }{k}_r{J}_m(kR)J_m^{\prime }(k_{r}R)-k{J}_m(k_{r}R)J_m^{\prime }(kR)}{k{H}_m^{{(1)}^{\prime }}(kR)J_m(k_{r}R)-\mathit{\zeta }{k}_r{J}_m^{\prime }(k_{r}R)H_m^{(1)}(kR)}.\end{array}$$21 ) is consistent with the results in [14] where $\mathit{\zeta }=1$ and $k_r=k\sqrt{{\mathit{ϵ}}_r}$ with ${\mathit{ϵ}}_r$ as the relative permittivity of scatterer.

Practical scatterers with arbitrary shape and inhomogeneous physical parameters need to be discretized into several subunits which are small enough. Therefore, each subunit is assumed to be homogeneous and can be approximated by an equivalent circular subunit with radius $R$. Then the T-matrix coefficients derived above for circular scatterer can be used as a good approximation.

Table 1. The asymptotic expansions of $T_0$ for small $kR$.

BC	$\mathrm{R}e(T_0)$	$\mathrm{I}m(T_0)$
Dirichlet	$-\frac{{\mathit{\pi }}^2}{4{(ln(kR))}^2}$	$\frac{\mathit{\pi }}{2ln(kR)}$
Neumann	$-\frac{1}{16}{\mathit{\pi }}^2{(kR)}^4$	$-\frac{1}{4}\mathit{\pi }{(kR)}^2$
Robin	$-\frac{\mathit{\eta }\mathit{\pi }}{2}kR$	$\frac{{\mathit{\eta }}^2\mathit{\pi }}{2}ln(kR){(kR)}^2$
Transmission	$-\frac{{\mathit{\pi }}^2}{16}{(\mathit{\zeta }{k}_r^2-k^2)}^2{R}^4$	$\frac{1}{4}(\mathit{\zeta }{k}_r^2-k^2)\mathit{\pi }{R}^2$

Because each subunit is small enough to ensure the validity of the T-matrix coefficients, it is necessary to understand the asymptotic property of $T_0$ when $kR$ is small enough. Under the assumption that $kR$ approaches to zero, the asymptotic expansions of $T_0$ for different types of scatterers are summarized in Table 1.

3 Inversion algorithm

In this section, we first introduce the inversion algorithm with a subspace based optimization (SOM).[7] Then the criterion to classify different BCs is discussed.

3.1 Subspace based optimization

Suppose the singular value decomposition of ${\overline{\overline{\mathrm{\Psi }}}}^t$ is ${\overline{\overline{\mathrm{\Psi }}}}^t·{\overline{v}}_j={\mathit{\lambda }}_j{\overline{u}}_j.$ Therefore, for one incident field, the vector $\overline{a}$ can be represented by22 $$\begin{array}{c}\hfill \overline{a}={\overline{a}}^{det}+\overline{\overline{V}}·\overline{c}\end{array}$$22 where ${\overline{a}}^{det}={\sum }_{j=1}^L\frac{{\overline{u}}_j^H·{\overline{u}}^{sca}}{{\mathit{\lambda }}_j}{\overline{v}}_j$ and $\overline{\overline{V}}$ is composed by the rest (excluding the first $L$) of right singular vectors. Here the value of $L$ can be chosen according to the rules given in [7, 23].

For one incident field, the cost functional is built according to (1212 $$\begin{array}{c}\hfill \overline{a}=\overline{\overline{O}}·\left[\overline{e},-,\overline{\overline{A}},·,\overline{a}\right]\end{array}$$12 ) and (1414 $$\begin{array}{c}\hfill {\overline{u}}^{sca}={\overline{\overline{\mathrm{\Psi }}}}^t·\overline{a}.\end{array}$$14 ) as23 $$\begin{array}{c}\hfill f(\overline{a},\overline{\overline{O}})={∥{\overline{u}}^{sca},-,{\overline{\overline{\mathrm{\Psi }}}}^t,·,\overline{a}∥}^2/{∥{\overline{u}}^{sca}∥}^2+{∥\overline{a},-,\overline{\overline{O}},·,[,\overline{e},-,\overline{\overline{A}},·,\overline{a},]∥}^2/{∥\overline{e}∥}^2.\end{array}$$23 The unknowns are the multipole expansion coefficient $\overline{a}$ and T-matrix coefficients $\overline{\overline{O}}$.

The cost functional (2323 $$\begin{array}{c}\hfill f(\overline{a},\overline{\overline{O}})={∥{\overline{u}}^{sca},-,{\overline{\overline{\mathrm{\Psi }}}}^t,·,\overline{a}∥}^2/{∥{\overline{u}}^{sca}∥}^2+{∥\overline{a},-,\overline{\overline{O}},·,[,\overline{e},-,\overline{\overline{A}},·,\overline{a},]∥}^2/{∥\overline{e}∥}^2.\end{array}$$23 ) is reformulated under the framework of subspace optimization method which is found to significantly speed up the convergence and make the algorithm perform robustly in the presence of noise.[5–7] So we have24 $$\begin{array}{c}\hfill f\left(\overline{c},,,\overline{\overline{O}}\right)={∥{\overline{\overline{\mathrm{\Psi }}}}^t,·,{\overline{a}}^{det},+,{\overline{\overline{\mathrm{\Psi }}}}^t,·,\overline{\overline{V}},·,\overline{c},-,{\overline{u}}^{sca}∥}^2/{∥{\overline{u}}^{sca}∥}^2+{∥\overline{\overline{D}},·,\overline{c},-,\overline{b}∥}^2/{∥{\overline{a}}^{det}∥}^2\end{array}$$24 where $\overline{\overline{D}}=(\overline{\overline{V}}+\overline{\overline{O}}·\overline{\overline{A}}·\overline{\overline{V}})·\overline{c}$ and $\overline{b}=\overline{\overline{O}}·(\overline{e}-\overline{\overline{A}}·{\overline{a}}^{det})-{\overline{a}}^{det}.$

When all $N_{inc}$ incidences are considered, the total cost function can be written as25 $$\begin{array}{c}\hfill {\mathrm{\Delta }}^{tot}\left({\overline{c}}_j,,,\overline{\overline{O}}\right)=\frac{1}{2}\sum _{j=1}^{N_{inc}}f\left({\overline{c}}_j,,,\overline{\overline{O}}\right).\end{array}$$25 The variables ${\overline{c}}_j$ and $\overline{\overline{O}}$ in Equation (2525 $$\begin{array}{c}\hfill {\mathrm{\Delta }}^{tot}\left({\overline{c}}_j,,,\overline{\overline{O}}\right)=\frac{1}{2}\sum _{j=1}^{N_{inc}}f\left({\overline{c}}_j,,,\overline{\overline{O}}\right).\end{array}$$25 ) can be updated alternatively during the optimization process.

Before next step, we want to clarify some concerns about the uniqueness of T-matrix inversion for scatterers with mixed boundaries. It is known that the uniqueness of inverse scattering problem for a single type boundary condition has been well established by mathematicians.[24] However, to the best knowledge of the authors, there is little information known for retrieving scatterers with four different boundary conditions simultaneously. And this is out of the scope of our paper to theoretically prove its uniqueness. Since the T-matrix coefficient of a given scatterer, regardless of boundary condition, is unique, we simply suppose here that the T-matrix solution for mixed type inverse scattering problem is also unique. Therefore, we will mainly focus on the numerical discussion about the capability of T-matrix method to solve such problems.

After obtaining the T-matrix coefficients $\overline{\overline{O}}$ by optimization, we can further determine other parameters of scatterers. For scatterer with Robin BC, the impedance can be further obtained as26 $$\begin{array}{c}\hfill \mathit{\eta }=-\frac{i}{k}\frac{T_{0}k{H}_1^{(1)}(kR)+k{J}_1(kR)}{T_0{H}_0^{(1)}(kR)+J_0(kR)}.\end{array}$$26 For scatterer with transmission boundary, the recovered wavenumber of scatterer can be obtained as27 $$\begin{array}{c}\hfill k_r={\left(\frac{4\mathrm{I}m(T_0)}{\mathit{\pi }{R}^2},+,k^2\right)}^{\frac{1}{2}}.\end{array}$$27 For electromagnetic scattering problem, the relative permittivity of dielectric scatterer can be further obtained from Equation (2727 $$\begin{array}{c}\hfill k_r={\left(\frac{4\mathrm{I}m(T_0)}{\mathit{\pi }{R}^2},+,k^2\right)}^{\frac{1}{2}}.\end{array}$$27 ) as28 $$\begin{array}{c}\hfill {\mathit{ϵ}}_r=1+4\frac{\mathrm{I}m(T_0)}{\mathit{\pi }{(kR)}^2}.\end{array}$$28 After getting the T-matrix coefficients $\overline{\overline{O}}$ and other related parameters, the next task is to classify the types of scatterers which is introduced in next section.

3.2 The criterion to classify different scatterers

In this section, we introduce the criterion to classify different scatterers. Theoretically, both $T_0$ and $T_1$ can be used in the classification. However, the magnitude of $T_1$ is usually much smaller than that of $T_0$ and it leads to the inaccuracy of the recovered $T_1$. Therefore, in this paper, only $T_0$ and its related variables $f(T_0)$ are used in the classification criterion. Here $f(T_0)$ means related parameter derived from $T_0.$ For example, $f(T_0)$ can be $\mathit{\eta }(T_0)$ or ${\mathit{ϵ}}_r(T_0)$.

Before we introduce the exact classification criterion, some assumptions and hints are given first:

(1)	It is known that the Dirichlet and Neumann BCs have close relation to Robin boundary if $\mathit{\eta }=\infty$ or $\mathit{\eta }=0$. Therefore, the impedance $\mathit{\eta }$ in Equation (44 $$\begin{array}{c}\hfill \frac{\mathit{\partial }u}{\mathit{\partial }n}+i\mathit{\eta }ku=0,\mathrm{o}n\mathit{\partial }{S}_3\end{array}$$4 ) is supposed to be neither too large (acts like Dirichlet BC) nor too small (acts like Neumann BC).
(2)	In this paper, we only consider the case of $k_r>k$ for scatterers with transmission boundary. In electromagnetics, it means the dielectric scatterer has positive contrast. For the case of $k_r<k$, it can be treated in a similar way and is not discussed here.
(3)	The order of $T_0$ for Dirichlet and Neumann scatterers is only dependent on the wavenumber of incident wave and the size of discrete grid. Therefore, it is known a priori before inversion. This information can be used in the classification.
(4)	For the purpose of proving the concept, here we only consider the case of $\mathit{\zeta }=1$ for transmission BC. For other values of $\mathit{\zeta }$, we can discuss for case of $\mathit{\zeta }>1$ and $\mathit{\zeta }<1$, and the result will not be shown here.

Table 2. The order and sign of asymptotic expressions of $T_0$ when $kR$ is small.

20.5cmBC	$\mathrm{R}e(T_0)$		$\mathrm{I}m(T_0)$
	Order	Sign	Order	Sign
Dirichlet	${\displaystyle O\left(\frac{1}{{(ln(R))}^2}\right)}$	$-$	${\displaystyle O\left(\frac{1}{ln(R)}\right)}$	$-$
Neumann	$O(R^4)$	$-$	$O(R^2)$	$-$
Robin	$O(R)$	$-$	$O(R^{2}ln(R))$	$-$
Transmission	$O(R^4)$	$-$	$O(R^2)$	$+$

Table 3. The characteristics of impedance and permittivity obtained from $T_0$ for different scatterers when $kR$ is small.

BC	Impedance $(\mathit{\eta })$	Permittivity $({\mathit{ϵ}}_r)$
Dirichlet	infinite	${\mathit{ϵ}}_r=1+\frac{2}{ln(kR){(kR)}^2}<0$
Neumann	zero	${\mathit{ϵ}}_r=0$$(O(R^2))$
Robin	finite	${\mathit{ϵ}}_r=1+2{\mathit{\eta }}^{2}ln(kR)<0$
Transmission	$\mathit{\eta }=0$$(O(R))$	${\mathit{ϵ}}_r>1$

Based on the asymptotic expressions of $T_0$ in Table 1, their orders and signs are listed in Table 2. The characteristics of $\mathit{\eta }(T_0)$ (by (2626 $$\begin{array}{c}\hfill \mathit{\eta }=-\frac{i}{k}\frac{T_{0}k{H}_1^{(1)}(kR)+k{J}_1(kR)}{T_0{H}_0^{(1)}(kR)+J_0(kR)}.\end{array}$$26 )) and ${\mathit{ϵ}}_r(T_0)$ (by (2828 $$\begin{array}{c}\hfill {\mathit{ϵ}}_r=1+4\frac{\mathrm{I}m(T_0)}{\mathit{\pi }{(kR)}^2}.\end{array}$$28 )) are listed in Table 3. The classification criterion for different scatterers are summarized as follows based on information from Tables 2 and 3:

(1)	Classify the imaginary part of $\mathrm{I}m(T_0)$. Pixels with $\mathrm{I}m(T_0)>0$ are classified to be part of scatterer with transmission boundary.
(2)	The rest pixels with $\mathrm{I}m(T_0)<0$ include scatterers with possibly Dirichlet, Neumann or Robin boundary conditions. They are further classified by $\mathit{\eta }(T_0)$ and ${\mathit{ϵ}}_r(T_0)$. Pixels with $\mathit{\eta }(T_0)$ and ${\mathit{ϵ}}_r(T_0)$ both close to zero are seen as part of Neumann scatterer.
(3)	For the remaining pixels with $\mathrm{I}m(T_0)<0,$ if $\mathit{\eta }(T_0)$ is very large, it is most possible to be a part of Dirichlet scatterer. Otherwise, it’s seen as part of a Robin scatterer.

It should be indicated that the asymptotic expansions in Table 3 are only valid under assumption that $kR$ is sufficiently small. In practical computation, the discrete grid may not be so small. For example, the $\mathit{\eta }(T_0)$ of scatterer with transmission boundary has order $O(R)$. When $R$ is not small enough, the real part of $\mathit{\eta }$ for transmission boundary can be some finite value which is easier to be confused with Robin BC etc. In that case, we also need to consider the imaginary part of $\mathit{\eta }$ which is one order smaller that its real part. These characteristics can all be helpful in actual classification. Finally, we need to be aware that it is difficult to differentiate the Dirichlet scatterers from the Robin ones. This is because the reconstructed $\mathit{\eta }(T_0)$ is always finite for Dirichlet scatterer in practice.

4 Numerical simulations

In this section, the proposed method is tested through a lot of numerical examples. Firstly, the experimental configuration is introduced. The wavenumber of incident wave in background medium is $k=2\mathit{\pi }.$ It means the wavelength of incident wave in background medium is $\mathit{\lambda }=1$. The domain of interest for all the numerical examples is square of size $2\mathit{\lambda }\times 2\mathit{\lambda }$. The domain is discretized into $N=35\times 35$ square subunits by default unless other declaration. $N_{inc}=10$ plane incident waves are used to evenly illuminate the domain around a circle. $N_r=30$ receivers are symmetrically placed around a circle of radius $5\mathit{\lambda }$. The synthetic data is calculated by T-matrix method with $M=2$ and $10\%$ additive Gaussian white noise is contaminated in the scattered field. In the inverse problem, $M=1$ is chosen as the truncation number of the multipoles. The results of $M=0$ (only monopole) is chosen to compute initial guess. The iteration steps with $M=0$ is $20$, while that for $M=1$ (both monopole and dipole) is 200.

Four examples will be tested by the T-matrix method. There is no prior information about the number and physical characteristics of all the scatterers. As discussed before, exact $T_0$ as well as the reconstructed ${\tilde{T}}_0$, $\tilde{\mathit{\eta }}$ and ${\widetilde{\mathit{ϵ}}}_r$ (hereafter the ‘tilde’ symbol indicates the reconstructed value) will be plotted for each example.

4.1 Example 1

The first example is introduced to verify the validity of the proposed T-matrix method and show its resolution with complicated scatterers.

The scatterers are supposed to compose an Austria-like profile. Two circles and one ring are considered simultaneously. The two circles are of radius $0.1\mathit{\lambda }$ and their center locations are at $(-0.7,0.7)\mathit{\lambda }$ and $(0.7,0.7)\mathit{\lambda }$, respectively. The center of the ring is at $(0,-0.3)\mathit{\lambda }$. Its inner radius is $0.3\mathit{\lambda }$ and its outer radius is $0.6\mathit{\lambda }$. The left circle has Dirichlet boundary, while the right circle has Neumann boundary. The ring has transmission boundary with $k_r=\sqrt{2}k$.

We have run this example with $N=35\times 35$ and $N=65\times 65$, respectively. Firstly, the reconstructed results of Example 1 with $N=35\times 35$ are shown in Figure 2. As discussed before, the key point to classify scatterers with mixed BCs lies in the accuracy of the recovered $T_0$ because the other two variables $\mathit{\eta }$ and $\mathit{ϵ}$ are both obtained from $T_0$. From Figure 2, it can be seen that both the real and imaginary parts of $T_0$ are well reconstructed. Then according to the criterion introduced in Section 3.2, we firstly identify the dielectric scatterer by the imaginary part of $T_0$. It can be seen that the ring is a dielectric scatterer with transmission boundary condition and the relative permittivity is approximate to be 2. Since the imaginary parts of the other two circular scatterers are negative, they are classified as Dirichlet, Neumann or Robin boundary. Then based on the results that the $\tilde{\mathit{\eta }}$ and $\widetilde{\mathit{ϵ}}$ are close to zero, it is concluded that the right small circle is a Neumann-boundary like scatterer. Finally, the left small circle is most possibly to be a Dirichlet-boundary like scatterer because its reconstructed $\tilde{\mathit{\eta }}$ is positive and large.

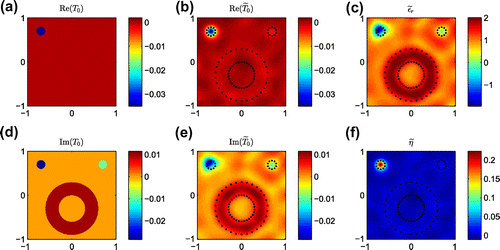
Furthermore, we run this example again with dense grid at $N=65\times 65$. This is to verify the accuracy of the above results, for both the synthetic measurements and the inversion results of T-matrix method at $N=35\times 35$. It is noted that synthetic measurements obtained at $N=35\times 35$ are quite similar as that at $N=65\times 65$. The average relative error ($\frac{\Vert {\overline{\overline{u}}}_{35}^{sca}-{\overline{\overline{u}}}_{65}^{sca}{\Vert }_F}{\Vert {\overline{\overline{u}}}_{65}^{sca}{\Vert }_F}\times 100\%$) between them is $4.41\%$ which is quite small and therefore we take $N=35\times 35$ as default discretization number. Correspondingly, the inversion results obtained at $N=65\times 65$ are shown in Figure 3. It can be seen the results are quite similar as that obtained at $N=35\times 35$. All scatterers are clearly reconstructed and classified. It should be noted that the T-matrix values are dependent on the circular size, which is controlled by discretization size and therefore are different from Figure 2.

Figure 2. Inversion results of Example 1 ($N=35\times 35$) with $10\%$ Gaussian white noise. (a) Exact real part of $T_0$; (b) Reconstructed real part of ${\tilde{T}}_0$; (c) Reconstructed relative permittivity ${\widetilde{\mathit{ϵ}}}_r$; (d) Exact imaginary part of $T_0$; (e) Reconstructed imaginary part of ${\tilde{T}}_0$; (f) Reconstructed impedance $\tilde{\mathit{\eta }}$.

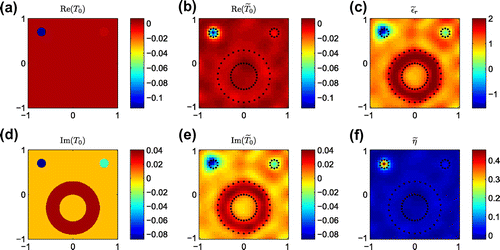
Figure 3. Inversion results of Example 1 ($N=65\times 65$) with $10\%$ Gaussian white noise. (a) Exact real part of $T_0$; (b) Reconstructed real part of ${\tilde{T}}_0$; (c) Reconstructed relative permittivity ${\widetilde{\mathit{ϵ}}}_r$; (d) Exact imaginary part of $T_0$; (e) Reconstructed imaginary part of ${\tilde{T}}_0$; (f) Reconstructed impedance $\tilde{\mathit{\eta }}$.

Both the results of Example 1 with different grid sizes show that the T-matrix method own good resolution to recover scatterers with complex shapes and mixed boundary conditions. Since the grid size at $N=35\times 35$ is small enough, we will test all the other examples hereafter with this grid configuration.

4.2 Example 2

The second example is to further test the robustness of T-matrix method to retrieve scatterers with complicated shapes. There are three scatterers, i.e. two circles together with one rectangle. The two circles are of radius $0.1\mathit{\lambda }$ and their center locations are at $(-0.5,0.7)\mathit{\lambda }$ and $(0.5,0.7)\mathit{\lambda }$, respectively. The center of the rectangle is at $(0,0)\mathit{\lambda }$ with width as $1.2\mathit{\lambda }$ and height as $0.5\mathit{\lambda }.$ The upper left circle has Dirichlet boundary, while the upper right circle owns Neumann boundary. The rectangle has transmission boundary with $k_r=\sqrt{2}k$. The distances between all scatterers are much closer than Example 1 and therefore is thought more difficult to solve.

Figure 4. Inversion results of Example 2 with $10\%$ Gaussian white noise. (a) Exact real part of $T_0$; (b) Reconstructed real part of ${\tilde{T}}_0$; (c) Reconstructed relative permittivity ${\widetilde{\mathit{ϵ}}}_r$; (d) Exact imaginary part of $T_0$; (e) Reconstructed imaginary part of ${\tilde{T}}_0$; (f) Reconstructed impedance $\tilde{\mathit{\eta }}$.

Figure 5. Convergence curves of Examples $1$ and $2$ with $M=1$.

The reconstructed results of this example are shown in Figure 4. From the recovered real and imaginary parts of $T_0$ as well as the ${\widetilde{\mathit{ϵ}}}_r$, it can be seen the rectangle has transmission boundary condition and the relative permittivity is approximate to be 2. Furthermore, similar as Example 1, the left circle is a Dirichlet-boundary like scatterer and the right circle is a Neumann-boundary like scatterer. Finally, the convergence curves of the first two examples are shown in Figure 5. It can be seen the T-matrix method converges smoothly to its final solutions. This example further shows that the proposed T-matrix method is stable to retrieve mixed-type scatterers with complex shapes.

4.3 Example 3

The third example aims to evaluate the capability of the T-matrix method to classify all the four kinds of scatterers.

In this example, there are four circles with equal radius $0.15\mathit{\lambda }$ and their centers are located at $(-0.65,0.65)\mathit{\lambda }$, $(0.65,0.65)\mathit{\lambda }$, $(-0.65,-0.65)\mathit{\lambda }$ and $(0.65,-0.65)\mathit{\lambda }$, respectively. The center of interested domain is at $(0,0)\mathit{\lambda }.$ The upper left circle is a scatterer with Dirichlet boundary. The upper right one owns Neumann boundary. The lower left one has transmission boundary condition and $k_r=\sqrt{2}k.$ The last lower right one has impedance boundary condition and $\mathit{\eta }=1/\mathit{\pi }.$

Figure 6. Inversion results of Example $3$ with $10\%$ Gaussian white noise. (a) Exact real part of $T_0$; (b) Reconstructed real part of ${\tilde{T}}_0$; (c) Reconstructed relative permittivity ${\widetilde{\mathit{ϵ}}}_r$; (d) Exact imaginary part of $T_0$; (e) Reconstructed imaginary part of ${\tilde{T}}_0$; (f) Reconstructed impedance $\tilde{\mathit{\eta }}$.

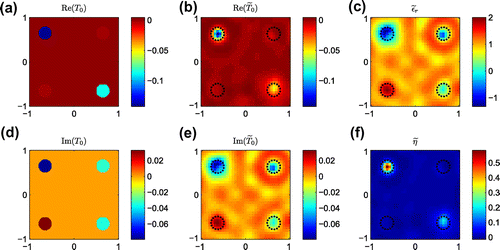
Figure 7. Inversion results of Example $4$ with $10\%$ Gaussian white noise. (a) Exact real part of $T_0$; (b) Reconstructed real part of ${\tilde{T}}_0$; (c) Reconstructed relative permittivity ${\widetilde{\mathit{ϵ}}}_r$; (d) Exact imaginary part of $T_0$; (e) Reconstructed imaginary part of ${\tilde{T}}_0$; (f) Reconstructed impedance $\tilde{\mathit{\eta }}$.

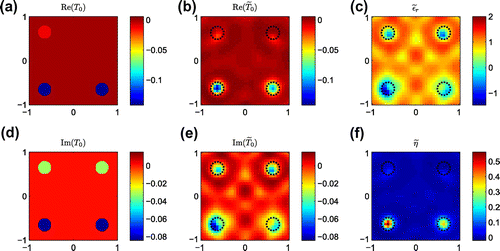
The results are shown in Figure 6. According to the inversion results and the criterion introduced in Section 3.2, we firstly identify the dielectric scatterer by the imaginary part of $T_0.$ It can be seen that the lower left circle is dielectric scatterer with transmission boundary condition. Since the imaginary parts of the other three scatterers are negative, they are classified as Dirichlet, Neumann or Robin boundary. From the values of ${\tilde{T}}_0,$$\tilde{\mathit{\eta }}$ and ${\widetilde{\mathit{ϵ}}}_r$, the boundary condition of the upper right scatterer can be classified as Neumann type. For the left two scatterers, it can be seen their impedances are obviously positive values, especially the upper left one. Therefore, this scatterer is most possibly to satisfy Dirichlet BC, while the lower right one can be Robin BC. As we discussed before, it’s not easy to classify these two kinds of scatterers clearly because the recovered impedance for scatterer with Dirichlet boundary is always finite.

4.4 Example 4

The fourth example is to illustrate the limitation or difficulty of the proposed T-matrix method to classify the Dirichlet or Neumann scatterers with the Robin ones due to their close physical relations.

Suppose there are four circles with the same shapes and locations but different boundary conditions as example 3. The upper left circle has Robin BC and $\mathit{\eta }=\frac{1}{10\mathit{\pi }}$. The upper right one has Neumann BC ($\mathit{\eta }=0$). The lower left one has Dirichlet BC ($\mathit{\eta }=\infty$). And the fourth one has Robin BC with $\mathit{\eta }=\frac{10}{\mathit{\pi }}.$ Theoretically, the upper two scatterers own similar scattering behavior while the scattered field of the last two scatterers are nearly the same. This is determined by their physical relations and it means that classification of these scatterers with each other is not easy or impossible. The results in Figure 7 verify this conclusion. It can be seen in Figure 7 that the locations and shapes of all scatterers are successfully recovered. And all the four scatterers can be clearly divided into two groups (group 1: the upper two scatterers; group 2: the lower two scatterers) by the values of $T_0$ and its related ${\widetilde{\mathit{ϵ}}}_r$ and $\tilde{\mathit{\eta }}$. But as expected, it’s difficult to further identify the physical properties of the two scatterers within a group. This is the reason why we add assumption on $\mathit{\eta }$ for Robin BC in Section 3.2.

5 Conclusions

In this paper, we have introduced a T-matrix method to simultaneously reconstruct the scatterers with different BCs like Dirichlet, Neumann, Robin, and transmission boundaries without any prior information. The numerical results show that the introduced method is a good inversion framework for scatterers with different boundary conditions. The locations and shapes of all scatterers are well reconstructed while their physical characteristics are further classified by the zeroth order coefficients of T-matrix and other related parameters. We also indicate that the current classification criterion still has some limitations for classifying scatterers with similar BCs. This is mainly due to the close physical properties of scatterers. Since both monopole and dipole terms are employed in the current inversion, the computational cost is larger than the conventional method of moment. Further work can be done on accelerating the convergence and reducing the computational cost of the proposed algorithm.

Additional information

Funding

This work was supported by the Singapore Temasek Defence Systems Institute under [grant number TDSI/10-005/1A].