A wavelet multiscale-adaptive homotopy method for the inverse problem of nonlinear diffusion equation

Abstract

This article considers a permeability estimation problem of nonlinear diffusion equation within multiphase porous media flow. By combining the wavelet multiscale method with the adaptive homotopy method, we shall design a joint inversion method called the wavelet multiscale-adaptive homotopy method. And the adaptive homotopy method provides a simple manner to adapt computational refinement to the choice of the homotopy parameters. Numerical experiments show that the proposed algorithm is globally convergent, computationally efficient, and has the anti-noise and de-noising abilities.

Keywords:

• wavelet
• adaptive homotopy method
• regularization
• inversion of nonlinear diffusion equation
• permeability

AMS Subject Classifications:

• 35R30
• 65H20
• 65M32
• 65T60
• 76S05

1 Introduction

The inverse problems of the multiphase porous media flow equations such as nonlinear diffusion equation play a key role in reservoir simulation. The effectiveness of the traditional linearized inversion methods like quasi-Newton or Gauss–Newton strongly depends on the choice of a good initial value, because the problems are intrinsically nonlinear and ill-posed.

Recently, wavelet has been recognized as a powerful new mathematical tool and has been applied to inverse problems in order to solve the above defect and improve computational efficiency.[1] Donoho constructed the nonlinear wavelet method for recovery of signals, densities and spectra from indirect and noisy data,[2] and the wavelet-vaguelette decomposition for nonlinear solution of the linear inverse problems.[3] Wavelet can also been seen as a kind of multiscale method because of its properties of adaptability and localization.[4] As a recently developed inversion strategy, wavelet multiscale method has a worldwide reputation for speeding up convergence, enhancing stability of inversion, avoiding impact of local minimum, and by which we can find the global minimum. The last few years have witnessed an intense activity and interest in the application of the wavelet multiscale inversion approach. Liu [5] showed that the wavelet multiscale method could be applied to the distributed parameter estimation of the one-dimensional elliptical equation. Fu and Han [6, 7] applied the wavelet multiscale method to the velocity estimation of a two-dimensional acoustic wave equation. Zhang et al. developed the wavelet multiscale method for the porosity inversion of fluid-saturated porous media,[8] the porosity inversion of one-dimensional two-phase medium[9] and the multiparameter inversion of fluid-saturated porous medium.[10] And further development about the wavelet multiscale method for the porosity inversion of fluid-saturated porous media has been done by He and Han [11]. Ding et al. [12] considered the wavelet multiscale method to solve the problem of estimating the conductivity in Maxwell equations. These results show that the performance of iterative inversion methods is much better when there exists the wavelet multiscale technology.

Figure 1. Simulation geometry with the locations of producer points and injector points.

Homotopy method provides an ideal tool for solving the inverse problems due to its widely convergent property.[13] It is very interesting to apply the homotopy method to solve the inverse problems of differential equations. There is a large amount of literature about the homotopy method for the parameter estimation recently. The homotopy method has been used to solve the parameter estimation problem of two-phase viscoelastic media,[14] the parameter estimation problem of an elliptical equation,[15] the parameter estimation problem of a two-dimensional acoustic wave equation,[16, 17] the well-log constraint waveform inversion,[18–20] the reconstruction of mountain surface[21] and the PEM estimation of ARMAX models.[22] All these works testified that the homotopy method is effective for the inverse problems, especially the parameter estimation problems.

For the nonlinear diffusion equation inversion, both the wavelet multiscale method [23] and the adaptive homotopy method [24] have been proven to be effective. However, these two methods all have some limitations on practice. In reality, it may be doubtful whether the global minimum will be obtained when either of the above two inversion methods is used singly to solve the inverse problem of nonlinear diffusion equation. The major reason is that we cannot obtain the global minimum using the homotopy method when there are many local minima in the corresponding objective function; and we cannot obtain the global minimum at the longest scale using the wavelet multiscale method, because the objective function may also be nonconvex. Thus, a natural idea is to make the combination of these two methods, but how to combine these two methods into one is still a great challenge. The novelty of this article is to combine these two methods into one method effectively by means of using wavelet to implement decompositions, taking the regularized Gauss–Newton method as the basic inversion method at every scale except the longest one, and using the adaptive homotopy method to find the global minimum at the longest scale. This hybrid inversion strategy, named by the wavelet multiscale-adaptive homotopy method, has not only a larger region of convergence than the wavelet multiscale method but also less computational cost than the adaptive homotopy method.

Figure 2. The errors of numerical solution and ground truth with respect to the iteration numbers with different initial values in Example 5.1: (a) the initial value is 0.17; (b) the initial value is 2.45; (c) the initial value is 4.15; (d) the initial value is 6.58.

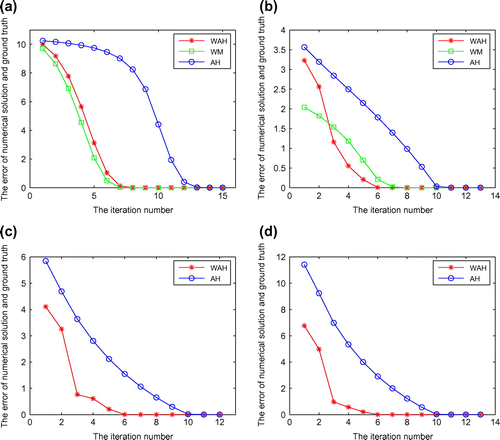
Figure 3. The numerical solutions with respect to the iteration numbers with the initial value 0.17 at some grid points in Example 5.1: (a) the grid point is (1/8, 1/8); (b) the grid point is (1/8, 7/8); (c) the grid point is (7/8, 1/8); (d) the grid point is (7/8, 7/8).

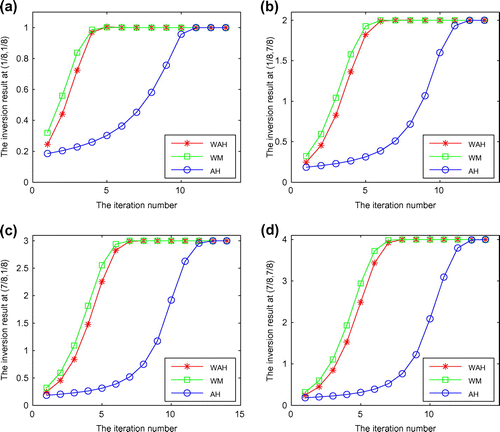
Figure 4. The numerical solutions with respect to the iteration numbers with the initial value 2.45 at some grid points in Example 5.1: (a) the grid point is (1/8, 1/8); (b) the grid point is (1/8, 7/8); (c) the grid point is (7/8, 1/8); (d) the grid point is (7/8, 7/8).

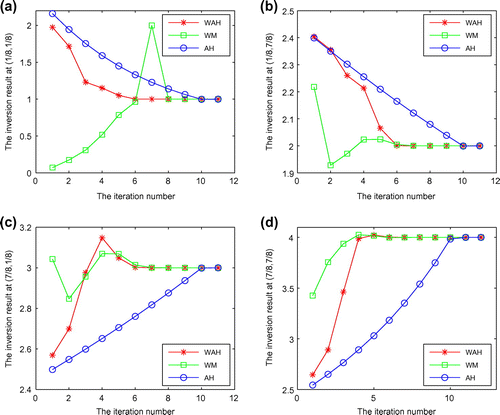
Figure 5. The true model based on (2.22.2 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(\mathrm{\nabla }u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.2 ) and inversion results $q^{\ast }$ with the noise level $\mathit{ϵ}=0.05$ in Example 5.2: (a) the true model based on (2.22.2 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(\mathrm{\nabla }u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.2 ); (b) the inversion result $q^{\ast }$ for $N(\mathrm{\nabla }u)=1+{0.1|\mathrm{\nabla }u|}^2$; (c) the inversion result $q^{\ast }$ for $N(\mathrm{\nabla }u)=1/(1-0.1|\mathrm{\nabla }u{|}^2)$.

Figure 6. The true model based on (2.12.1 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.1 ) and inversion results $q^{\ast }$ with the noise level $\mathit{ϵ}=0.05$ in Example 5.3: (a) the true model based on (2.12.1 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.1 ); (b) the inversion result $q^{\ast }$ for $N(u)=u^4-u^3+u^2-u+1$; (c) the inversion result $q^{\ast }$ for $N(u)=u^4+u^3+u^2+u+1$.

In this article, a wavelet multiscale-adaptive homotopy method is designed by effectively combining the wavelet multiscale method with the adaptive homotopy method in the inversion process. And the article is organized as follows. In Section 2, we give a brief description of the mathematical model of the inverse problem of nonlinear diffusion equation. In Section 3, we present the adaptive homotopy method, whose adaptive property provides a simple manner to adapt computational refinements to the choice of the homotopy parameters. In Section 4, we present the proposed wavelet multiscale-adaptive homotopy method in detail and describe how this algorithm can be carried out by combining the wavelet multiscale method with the adaptive homotopy method. In Section 5, we provide some numerical experiments. Finally, some conclusions are obtained.

2 Mathematical model

The inverse problem of nonlinear diffusion equation intends to identify the permeability model which minimizes the discrepancy between computed and observation data. The computed data are generated by the following nonlinear diffusion equation:2.1 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.1 or2.2 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(\mathrm{\nabla }u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.2 with the boundary condition2.3 $$\begin{array}{c}\hfill u(\mathbf{x},t)=0,(\mathbf{x},t)\in \mathit{\partial }\mathrm{\Omega }\times (0,T),\end{array}$$2.3 and the initial condition2.4 $$\begin{array}{c}\hfill u(\mathbf{x},0)=u_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$2.4 where $q(\mathbf{x})$ is the permeability at $\mathbf{x}$ in the medium, $N$ is a positive nonlinear function of $u$ or $\mathrm{\nabla }u$, $s(\mathbf{x},t)$ is the piecewise smooth source function, and $\mathrm{\Omega }$ can be any bounded domain in ${\mathbb{R}}^d$, $d\ge 1$, with piecewise smooth boundary $\mathit{\partial }\mathrm{\Omega }$.

Equation (2.12.1 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.1 ) or (2.22.2 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(\mathrm{\nabla }u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.2 ) with conditions (2.32.3 $$\begin{array}{c}\hfill u(\mathbf{x},t)=0,(\mathbf{x},t)\in \mathit{\partial }\mathrm{\Omega }\times (0,T),\end{array}$$2.3 ) and (2.42.4 $$\begin{array}{c}\hfill u(\mathbf{x},0)=u_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$2.4 ) form the forward problem of nonlinear diffusion equation. If the permeability $q(\mathbf{x})$ is known, the observation data $u_{obs}({\mathbf{x}}^d,t)$, $d=1,2,\dots ,D$, $t\in (0,T)$ can be calculated from Equation (2.12.1 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.1 ) or (2.22.2 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(\mathrm{\nabla }u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.2 ) with conditions (2.32.3 $$\begin{array}{c}\hfill u(\mathbf{x},t)=0,(\mathbf{x},t)\in \mathit{\partial }\mathrm{\Omega }\times (0,T),\end{array}$$2.3 ) and (2.42.4 $$\begin{array}{c}\hfill u(\mathbf{x},0)=u_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$2.4 ) by using some numerical method. But in practice, the permeability $q(\mathbf{x})$ is not known. What is known is only some observation data $u_{obs}$. We can reconstruct the unknown permeability $q(\mathbf{x})$ from Equation (2.12.1 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.1 ) or (2.22.2 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(\mathrm{\nabla }u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.2 ) with conditions (2.32.3 $$\begin{array}{c}\hfill u(\mathbf{x},t)=0,(\mathbf{x},t)\in \mathit{\partial }\mathrm{\Omega }\times (0,T),\end{array}$$2.3 ), (2.42.4 $$\begin{array}{c}\hfill u(\mathbf{x},0)=u_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$2.4 ) and observation data $u_{obs}$. Then, Equation (2.12.1 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.1 ) or (2.22.2 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(\mathrm{\nabla }u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.2 ) with conditions (2.32.3 $$\begin{array}{c}\hfill u(\mathbf{x},t)=0,(\mathbf{x},t)\in \mathit{\partial }\mathrm{\Omega }\times (0,T),\end{array}$$2.3 ), (2.42.4 $$\begin{array}{c}\hfill u(\mathbf{x},0)=u_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$2.4 ) and observation data $u_{obs}$ form the model of the inverse problem of nonlinear diffusion equation.

The identification process is carried out in a manner that the computed data $u$ match the observation data $u_{obs}$, optimally. A measure of the discrepancy between computed and observation data can be obtained by using the norm2.5 $$\begin{array}{c}\hfill K(q)={\int }_0^T\sum _{d=1}^D\frac{1}{2}{(u({\mathbf{x}}^d,t)-u_{obs}({\mathbf{x}}^d,t))}^{2}dt,\end{array}$$2.5 where $u({\mathbf{x}}^d,t)$, $d=1,2,\dots ,D$, $t\in (0,T)$ are the computed data at the observation points. The permeability field $q(\mathbf{x})$, which minimizes Equation (2.52.5 $$\begin{array}{c}\hfill K(q)={\int }_0^T\sum _{d=1}^D\frac{1}{2}{(u({\mathbf{x}}^d,t)-u_{obs}({\mathbf{x}}^d,t))}^{2}dt,\end{array}$$2.5 ), is the wanted solution to this inverse problem.

It is obvious that the solution of the forward problem (Equation (2.12.1 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.1 ) or (2.22.2 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(\mathrm{\nabla }u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.2 ) with conditions (2.32.3 $$\begin{array}{c}\hfill u(\mathbf{x},t)=0,(\mathbf{x},t)\in \mathit{\partial }\mathrm{\Omega }\times (0,T),\end{array}$$2.3 ) and (2.42.4 $$\begin{array}{c}\hfill u(\mathbf{x},0)=u_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$2.4 )) depends nonlinearly on the permeability field $q(\mathbf{x})$. From the observation data $u_{obs}$, with giving the definition of the nonlinear operator of $K(q)$ in (2.52.5 $$\begin{array}{c}\hfill K(q)={\int }_0^T\sum _{d=1}^D\frac{1}{2}{(u({\mathbf{x}}^d,t)-u_{obs}({\mathbf{x}}^d,t))}^{2}dt,\end{array}$$2.5 ) as follows$$\begin{array}{cc}\hfill E(q)& \equiv (u(q;{\mathbf{x}}^1,t)-u_{obs}({\mathbf{x}}^1,t),u(q;{\mathbf{x}}^2,t)-u_{obs}({\mathbf{x}}^2,t),\hfill \\ \hfill & \dots ,u(q;{\mathbf{x}}^D,t)-u_{obs}({\mathbf{x}}^D,t){)}^{\top },t\in (0,T),\hfill \end{array}$$the inverse problem of nonlinear diffusion equation can be reduced to find an epsilon-solution $q^{\ast }$ such that2.6 $$\begin{array}{c}\hfill E(q^{\ast })=\mathbf{0},\end{array}$$2.6 where $\mathbf{0}$ denotes the $D$-dimensional zero vector. It is worth noting that the epsilon-solution $q^{\ast }$ is uniform in $t$ because the permeability function $q(\mathbf{x})$ is only space-dependent.

The nonlinear operator Equation (2.62.6 $$\begin{array}{c}\hfill E(q^{\ast })=\mathbf{0},\end{array}$$2.6 ) is a parameter estimation problem, which is a kind of typical ill-posed problem. Its ill-posedness is mainly reflected in the following three aspects (see also [25, 26]): (I) there may be no model that exactly fits the data, so the solution may not exist; (II) if exact solutions do exist, they may not be unique, because there may be many models that adequately fit the data; (III) the process of computing an inverse solution can be, and often is, extremely unstable in that a small change in measurement can lead to an enormous change in the estimated model.

3 Adaptive homotopy method

Because the nonlinear operator Equation (2.62.6 $$\begin{array}{c}\hfill E(q^{\ast })=\mathbf{0},\end{array}$$2.6 ) is a nonlinear and ill-posed problem, the Tikhonov regularization needs to be introduced. Instead of directly solving (2.62.6 $$\begin{array}{c}\hfill E(q^{\ast })=\mathbf{0},\end{array}$$2.6 ), we consider the optimal problem3.1 $$\begin{array}{c}\hfill min\{\Vert E(q){\Vert }^2+\mathit{\alpha }\Vert q-q^0{\Vert }^2\},\end{array}$$3.1 where $\Vert ·\Vert$ is the Euclid norm, $\mathit{\alpha }$ is the regularization parameter and $q^0$ is a prior estimate of the solution $q^{\ast }$. The iteratively regularized Gauss–Newton method can be used to find the minimum3.2 $$\begin{array}{cc}& q^{k+1}=q^k-{[E^{\prime }{(q^k)}^{\ast }{E}^{\prime }(q^k)+\mathit{\alpha }I]}^{-1}·[E^{\prime }{(q^k)}^{\ast }E(q^k)+\mathit{\alpha }(q^k-q^0)],k=0,1,2,\dots \hfill \end{array}$$3.2

Remark 3.1

The specific expressions of the operators $E^{\prime }(q^k)$ and $E^{\prime }{(q^k)}^{\ast }$ are given in numerical form. The practical problems are usually solved numerically after a space discretization, so when $\mathrm{\Omega }$ is discretized into $G$ units, $q$ can be expressed as a $G$-dimensional vector, and then $E(q)$ is transformed into a nonlinear vector-valued function. In this case, $E^{\prime }(q^k)$ is the Jacobian matrix of $E(q)$ at the point $q^k$, and $E^{\prime }{(q^k)}^{\ast }$ is the transpose of the Jacobian matrix $E^{\prime }(q^k)$.

This iteratively regularized Gauss–Newton method has fast convergence speed and good stability; however, it is as local convergent as the other iterative methods. To overcome this weakness, let us use the homotopy method to solve (3.13.1 $$\begin{array}{c}\hfill min\{\Vert E(q){\Vert }^2+\mathit{\alpha }\Vert q-q^0{\Vert }^2\},\end{array}$$3.1 ).

It is easy to see that the corresponding Euler equation to the optimal problem (3.13.1 $$\begin{array}{c}\hfill min\{\Vert E(q){\Vert }^2+\mathit{\alpha }\Vert q-q^0{\Vert }^2\},\end{array}$$3.1 ) is3.3 $$\begin{array}{c}\hfill E^{\prime }{(q)}^{\ast }E(q)+\mathit{\alpha }(q-q^0)=0.\end{array}$$3.3 Here the fixed point homotopy method is considered to solve (3.33.3 $$\begin{array}{c}\hfill E^{\prime }{(q)}^{\ast }E(q)+\mathit{\alpha }(q-q^0)=0.\end{array}$$3.3 ):3.4 $$\begin{array}{c}\hfill H(q,\mathit{\beta })=\mathit{\beta }[E^{\prime }{(q)}^{\ast }E(q)+\mathit{\alpha }(q-q^0)]+(1-\mathit{\beta })(q-q^0)=0,\end{array}$$3.4 where $\mathit{\beta }\in [0,1]$ is the homotopy parameter.

In order to derive $q^{\ast }$, we divide $[0,1]$ into $0={\mathit{\beta }}_0<{\mathit{\beta }}_1<\cdots <{\mathit{\beta }}_W=1$, and for $\mathit{\beta }={\mathit{\beta }}_w$, use the iterative method similar to (3.23.2 $$\begin{array}{cc}& q^{k+1}=q^k-{[E^{\prime }{(q^k)}^{\ast }{E}^{\prime }(q^k)+\mathit{\alpha }I]}^{-1}·[E^{\prime }{(q^k)}^{\ast }E(q^k)+\mathit{\alpha }(q^k-q^0)],k=0,1,2,\dots \hfill \end{array}$$3.2 ) to solve (3.43.4 $$\begin{array}{c}\hfill H(q,\mathit{\beta })=\mathit{\beta }[E^{\prime }{(q)}^{\ast }E(q)+\mathit{\alpha }(q-q^0)]+(1-\mathit{\beta })(q-q^0)=0,\end{array}$$3.4 ) in sequence from $w=1$ to $w=W$. When $\mathit{\beta }=0$, the solution of $H(q,0)=0$ is $q^0$, which is known. Thus, it can be taken as the initial guess of the next equation. That means $q^0$ is the initial guess of the whole computation. Assume that the solution $q^{w-1}$ of the $(w-1)$th equation has already been derived. Then, $q^{w-1}$ can be taken as the initial guess of the $w$th equation. All this leads up to the following iterative formula3.5 $$\begin{array}{cc}\hfill q_{k+1}^w& =q_k^w-{[{\mathit{\beta }}_w{E}^{\prime }{(q_k^w)}^{\ast }{E}^{\prime }(q_k^w)+(\mathit{\alpha }{\mathit{\beta }}_w+(1-{\mathit{\beta }}_w))I]}^{-1}\hfill \\ \hfill & ·\left[{\mathit{\beta }}_w,E^{\prime },{(q_k^w)}^{\ast },E,(q_k^w),+,(\mathit{\alpha }{\mathit{\beta }}_w+(1-{\mathit{\beta }}_w)),(q_k^w-q^0)\right],k=0,1,\dots ,w_m,\hfill \\ \hfill q_0^w& =q^{w-1},q^w=q_{w_m+1}^w,w=1,2,\dots ,W.\hfill \end{array}$$3.5 If ${\mathit{\beta }}_w=\frac{w}{W}$, $w=0,1,\dots ,W$ by an isometric division and $w_m=0$, then (3.53.5 $$\begin{array}{cc}\hfill q_{k+1}^w& =q_k^w-{[{\mathit{\beta }}_w{E}^{\prime }{(q_k^w)}^{\ast }{E}^{\prime }(q_k^w)+(\mathit{\alpha }{\mathit{\beta }}_w+(1-{\mathit{\beta }}_w))I]}^{-1}\hfill \\ \hfill & ·\left[{\mathit{\beta }}_w,E^{\prime },{(q_k^w)}^{\ast },E,(q_k^w),+,(\mathit{\alpha }{\mathit{\beta }}_w+(1-{\mathit{\beta }}_w)),(q_k^w-q^0)\right],k=0,1,\dots ,w_m,\hfill \\ \hfill q_0^w& =q^{w-1},q^w=q_{w_m+1}^w,w=1,2,\dots ,W.\hfill \end{array}$$3.5 ) becomes a more simple iterative formula3.6 $$\begin{array}{cc}\hfill q^w& =q^{w-1}-{\left[\frac{w}{W},E^{\prime },{\left(q^{w-1}\right)}^{\ast },E^{\prime },\left(q^{w-1}\right),+,\left(\frac{\mathit{\alpha }w}{W},+,\left(1,-,\frac{w}{W}\right)\right),I\right]}^{-1}\hfill \\ \hfill & ·\left[\frac{w}{W},E^{\prime },{\left(q^{w-1}\right)}^{\ast },E,\left(q^{w-1}\right),+,\left(\frac{\mathit{\alpha }w}{W},+,\left(1,-,\frac{w}{W}\right)\right),(q^{w-1}-q^0)\right],\hfill \\ \hfill w& =1,2,\dots ,W.\hfill \end{array}$$3.6 The iterative result $q^W$ of Equation (3.63.6 $$\begin{array}{cc}\hfill q^w& =q^{w-1}-{\left[\frac{w}{W},E^{\prime },{\left(q^{w-1}\right)}^{\ast },E^{\prime },\left(q^{w-1}\right),+,\left(\frac{\mathit{\alpha }w}{W},+,\left(1,-,\frac{w}{W}\right)\right),I\right]}^{-1}\hfill \\ \hfill & ·\left[\frac{w}{W},E^{\prime },{\left(q^{w-1}\right)}^{\ast },E,\left(q^{w-1}\right),+,\left(\frac{\mathit{\alpha }w}{W},+,\left(1,-,\frac{w}{W}\right)\right),(q^{w-1}-q^0)\right],\hfill \\ \hfill w& =1,2,\dots ,W.\hfill \end{array}$$3.6 ) can be taken as the initial guess of Equation (3.23.2 $$\begin{array}{cc}& q^{k+1}=q^k-{[E^{\prime }{(q^k)}^{\ast }{E}^{\prime }(q^k)+\mathit{\alpha }I]}^{-1}·[E^{\prime }{(q^k)}^{\ast }E(q^k)+\mathit{\alpha }(q^k-q^0)],k=0,1,2,\dots \hfill \end{array}$$3.2 ). Then iterate repeatedly using (3.23.2 $$\begin{array}{cc}& q^{k+1}=q^k-{[E^{\prime }{(q^k)}^{\ast }{E}^{\prime }(q^k)+\mathit{\alpha }I]}^{-1}·[E^{\prime }{(q^k)}^{\ast }E(q^k)+\mathit{\alpha }(q^k-q^0)],k=0,1,2,\dots \hfill \end{array}$$3.2 ) until the solution $q^{\ast }$ is obtained. Thus, formulae (3.63.6 $$\begin{array}{cc}\hfill q^w& =q^{w-1}-{\left[\frac{w}{W},E^{\prime },{\left(q^{w-1}\right)}^{\ast },E^{\prime },\left(q^{w-1}\right),+,\left(\frac{\mathit{\alpha }w}{W},+,\left(1,-,\frac{w}{W}\right)\right),I\right]}^{-1}\hfill \\ \hfill & ·\left[\frac{w}{W},E^{\prime },{\left(q^{w-1}\right)}^{\ast },E,\left(q^{w-1}\right),+,\left(\frac{\mathit{\alpha }w}{W},+,\left(1,-,\frac{w}{W}\right)\right),(q^{w-1}-q^0)\right],\hfill \\ \hfill w& =1,2,\dots ,W.\hfill \end{array}$$3.6 ) and (3.23.2 $$\begin{array}{cc}& q^{k+1}=q^k-{[E^{\prime }{(q^k)}^{\ast }{E}^{\prime }(q^k)+\mathit{\alpha }I]}^{-1}·[E^{\prime }{(q^k)}^{\ast }E(q^k)+\mathit{\alpha }(q^k-q^0)],k=0,1,2,\dots \hfill \end{array}$$3.2 ) can constitute a stable and globally convergent method for the inverse problem of nonlinear diffusion equation.

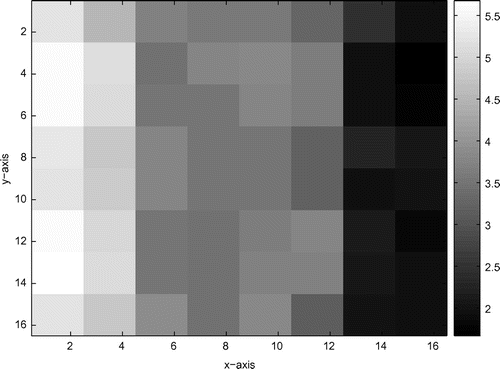
Figure 7. The true model based on (2.12.1 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.1 ) in Example 5.4.

Figure 8. The inversion result $q^{\ast }$ at the original scale with the noise level $\mathit{ϵ}=0.01$ in Example 5.4.

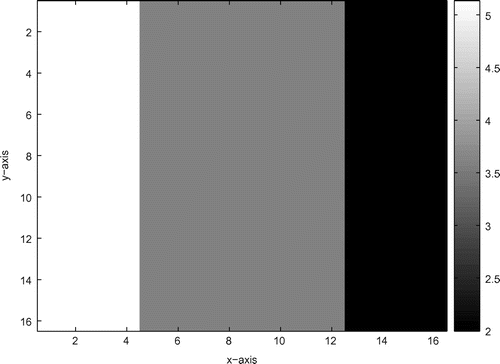
Figure 9. The true model based on (2.22.2 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(\mathrm{\nabla }u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.2 ) in Example 5.5.

Figure 10. The inversion result $q^{\ast }$ at the original scale with the noise level $\mathit{ϵ}=0.01$ in Example 5.5.

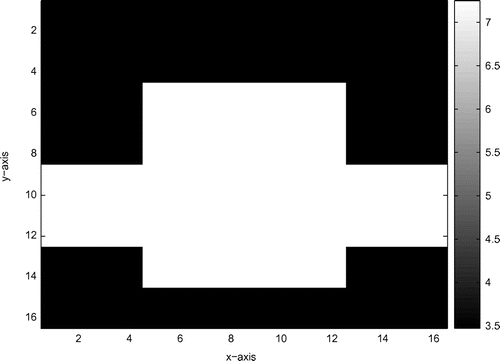
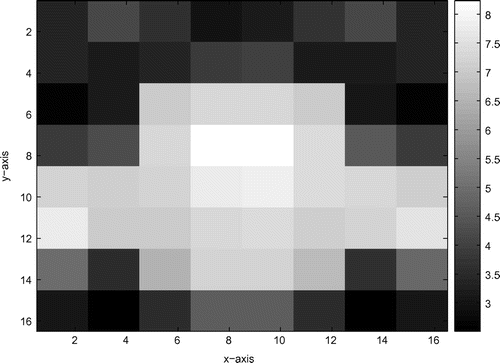
Figure 11. The true model based on (2.12.1 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.1 ) in Example 5.6.

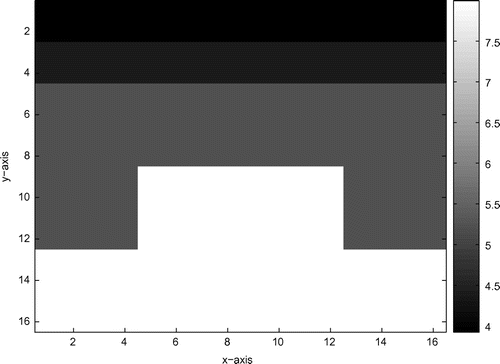
Figure 12. The inversion results $q^{\ast }$ with the noise level $\mathit{ϵ}=0.04$ in Example 5.6: (a) the inversion result $q^{\ast }$ at scale 1; (b) the inversion result $q^{\ast }$ at scale 0.

As is well known, the homotopy parameters ${\mathit{\beta }}_w=\frac{w}{W}$, $w=0,1,\dots ,W$ play a leading role in the inversion process. A great deal of calculation is needed when $W$ is too large, and the solution $q^{\ast }$ may be lost when $W$ is too small. Therefore, a modified homotopy method is proposed to solve this dilemma. At the end of each iteration, the control value $\mathit{\tau }$ is used to control the step length of the homotopy parameters $d=\frac{1}{W}$ by comparing $\frac{\Vert q^w-q^{w-1}\Vert }{\Vert q^{w-1}-q^{w-2}\Vert }$ and $\mathit{\tau }$. Here the control value $\mathit{\tau }$ is often chosen by the heuristic method. If $\frac{\Vert q^w-q^{w-1}\Vert }{\Vert q^{w-1}-q^{w-2}\Vert }<\mathit{\tau }$, then double the step length of the homotopy parameters $d$; otherwise let $d$ be half of the original value. Because this algorithm can adaptively choose the homotopy parameters ${\mathit{\beta }}_w$, it is named the adaptive homotopy method (see [24]).

4 Wavelet multiscale-adaptive homotopy method

The bottleneck restricting the development of the inversion theory of nonlinear diffusion equation in reservoir simulation is the existence of numerous local minimum in the objective function, and it is one of the most difficult problems for the theory and application. The wavelet multiscale inversion has an impressive ability to improve this difficult problem because of its decomposition of inverse problem by scale. After the decomposition, the long scale components contain little varying features because at long scales the number of local minimum is enormously reduced and those that remain are further apart from each other. Consequently, the application of the adaptive homotopy method at the longest scale component will be more likely (than at other short scale components) to find the global minimum or at least a local minimum that is in the neighbourhood of the global minimum, even if the minimum of the longest scale component is not unique. The solution of the longest scale component is such a good approximation of the global minimum of the second longest scale component that it can be taken as the initial guess of the second optimization problem. Therefore, the solution obtained from the longest scale component is then recursively refined in this way.

This thesis attempts to use wavelet to implement decompositions, to take the iteratively regularized Gauss–Newton method as the basic inversion method at every scale except the longest one, and to use the adaptive homotopy method to find the global minimum or its approximation at the longest scale. This new joint inversion method can be named the wavelet multiscale-adaptive homotopy method. It is as numerically stable and computationally efficient as the wavelet multiscale method, and as globally convergent as the adaptive homotopy method. Most important of all, this new joint inversion method has not only a larger region of convergence than the wavelet multiscale method but also less computational complexity than the adaptive homotopy method.

Algorithm 4.1 (Wavelet multiscale-adaptive homotopy algorithm)

5 Numerical experiments

Some numerical experiments with the proposed algorithm for the permeability estimation are shown in this section. The test problem is$$\begin{array}{cc}& u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u,\mathrm{\nabla }u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\hfill \\ \hfill & u(\mathbf{x},t)=0,(\mathbf{x},t)\in \mathit{\partial }\mathrm{\Omega }\times (0,T),\hfill \\ \hfill & u(\mathbf{x},0)=u_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\hfill \end{array}$$with several choices for the nonlinear function $N$. Here $\mathrm{\Omega }=[0,1]\times [0,1]$, $T=0.6$, $u_0(\mathbf{x})=0$ and the source function is$$s(\mathbf{x},t)=g(t)\left[\sum _{i=1}^{16},\mathit{\delta },(\mathbf{x}-{\mathbf{x}}^i),-,4,\sum _{p=1}^4,\mathit{\delta },(\mathbf{x}-{\mathbf{x}}^p)\right],$$where $g(t)=1.6sin(80\mathit{\pi }t)exp(-80\mathit{\pi }(t/2))$, $\mathit{\delta }(·)$ is the Dirac $\mathit{\delta }$-function, and ${\mathbf{x}}^i$, ${\mathbf{x}}^p$ 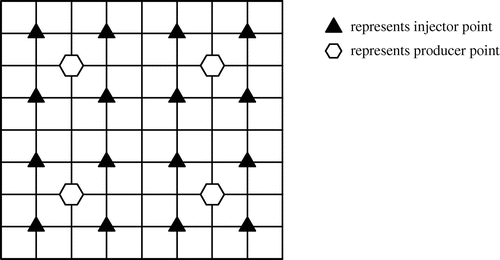are the injector points and producer points, respectively. Figure 1 shows the exact locations of injector points and producer points in simulation geometry, and we place 16 receivers in each injector point simultaneously, which means that $D=16$. For an exact $u_{obs}(\mathbf{x},t)$, its discrete noisy version is$$u_{obs}^{\mathit{ϵ}}=u_{obs}+\mathit{ϵ}·randn(size(u_{obs})),$$the function ‘$randn(·)$’ generates arrays of random numbers whose elements are normally distributed with mean 0, variance ${\mathit{\sigma }}^2=1$, and $\mathit{ϵ}$ indicates the noise level.

In all examples, the temporal step length $\mathrm{\Delta }t=0.02$ and the principle for choosing the regularization parameter $\mathit{\alpha }$ is mainly based on the popular heuristic regularization parameter choice method. In the first three examples, the spatial step length $\mathrm{\Delta }x=\mathrm{\Delta }y=1/8$, and the true permeability, $q(\mathbf{x})$, is piecewise constant$$q(\mathbf{x})=\left\{\begin{array}{cc}{q}_1^c,\hfill & \left\}\right\}x\in [0,0.5]\times [0,0.5],\hfill \\ q_2^c,\hfill & \left\}\right\}x\in [0,0.5]\times [0.5,1],\hfill \\ q_3^c,\hfill & \left\}\right\}x\in [0.5,1]\times [0,0.5],\hfill \\ q_4^c,\hfill & \left\}\right\}x\in [0.5,1]\times [0.5,1].\hfill \end{array}\right.$$The results seem to be best when the regularization parameter is chosen by $\mathit{\alpha }=0$. As pointed out in [29], the reason for this is that the dimension is relatively small in the first three examples. In the last three examples, the spatial step length $\mathrm{\Delta }x=\mathrm{\Delta }y=1/16$, the regularization parameter $\mathit{\alpha }={10}^{-12}$ and the complex permeability models will specifically be described. Except for Examples 5.2 and 5.5 which are based on the partial differential equation in (2.22.2 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(\mathrm{\nabla }u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.2 ), all the examples are based on the partial differential equation in (2.12.1 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.1 ).

The longest scale J of wavelet decomposition, the control value $\mathit{\tau }$ and initial step length of the homotopy parameters $d$ in the adaptive homotopy method are, respectively, set at 3, 1 and 0.1. The iteratively regularized Gauss–Newton method (3.23.2 $$\begin{array}{cc}& q^{k+1}=q^k-{[E^{\prime }{(q^k)}^{\ast }{E}^{\prime }(q^k)+\mathit{\alpha }I]}^{-1}·[E^{\prime }{(q^k)}^{\ast }E(q^k)+\mathit{\alpha }(q^k-q^0)],k=0,1,2,\dots \hfill \end{array}$$3.2 ) is terminated when the modification is equal to or less than ${10}^{-4}$. It is worth mentioning that the wavelet is not used for denoising in this paper, hence the threshold [30] is not needed to be considered. Here, the wavelet is used mainly as the accelerating convergence technique, so the wavelet order is set at 3 (see [23]).

Example 5.1

In the first example, the ground truth is $q_i^c=i$, $i=1,\dots ,4$, and we respectively use the wavelet multiscale-adaptive homotopy method (WAH), wavelet multiscale method (WM) in [23], adaptive homotopy method (AH) in [24]. The nonlinear function $N$ is $N(u)=u^2+u+1$, and the initial guess value $q^0$ is given as a constant.

To compare the performance of WAH, WM and AH, the errors of the numerical solutions and the ground truth vs. the iteration numbers with different initial values 0.17, 2.45, 4.15 and 6.58 are plotted in Figure 2. Meanwhile, the specific data in Figure 2(a)–(d) are listed in Tables 1–4, respectively. It can be seen from Tables 3 and 4 that WM is divergent after the first iteration, so the green line about WM cannot be obtained in Figure 2(c) and (d). To compare the performance of WAH, WM and AH with respect to spatial domain, the numerical solutions vs. the iteration numbers with the initial values 0.17 and 2.45 at some grid points are plotted in Figures 3 and 4, respectively. The grid points in Figure 3(a)–(d) are, respectively, (1/8, 1/8), (1/8, 7/8), (7/8, 1/8) and (7/8, 7/8), where the ground truths are respectively 1, 2, 3 and 4, and the same grid points are chosen in Figure 4. Furthermore, for the permeability values are from range of 0 to 10 in reality, the required iteration numbers of WAH, WM and AH are given in Table 5 with different initial values 0.17, 2.45, 4.15, 6.58, 8.23 and 9.99. It indicates that when the initial guess value is poor (i.e. the cases of 4.15, 6.58, 8.23 and 9.99), there is no convergence by WM, while for WAH and AH, the convergence can be achieved. It is shown that WAH has a larger region of convergence than WM. In Table 6, the absolute computational times of WAH, WM and AH are given. It can be seen that WAH has less computational cost than AH. Therefore, one can conclude that the wavelet multiscale-adaptive homotopy method is globally convergent and computationally efficient from Figures 2–4 and Tables 5 and 6.

Table 1. The errors of numerical solution and ground truth by WAH, WM and AH with the initial value 0.17 in Example 5.1.

Iteration number	WAH	WM	AH
1	10.0039	9.7011	10.2474
2	9.1854	8.6512	10.1695
3	7.7769	6.9255	10.0695
4	5.6471	4.5503	9.9362
5	3.1213	2.0821	9.7486
6	1.0361	0.4841	9.4676
7	0.1289	0.0296	9.0165
8	0.0021	$1.1705\times {10}^{-4}$	8.2459
9	$2.6095\times {10}^{-7}$	$2.4680\times {10}^{-8}$	6.8729
10	$5.7368\times {10}^{-11}$	$5.6682\times {10}^{-12}$	4.4157
11	$1.3339\times {10}^{-14}$	$7.5187\times {10}^{-16}$	1.9299
12	$1.4239\times {10}^{-15}$	$1.1123\times {10}^{-15}$	0.4075
13	$9.7081\times {10}^{-16}$	$8.8817\times {10}^{-16}$	0.0203
14	$7.2875\times {10}^{-16}$	$6.1328\times {10}^{-16}$	$4.8887\times {10}^{-5}$
15	$7.4638\times {10}^{-16}$	$4.9649\times {10}^{-16}$	$1.0874\times {10}^{-8}$

Table 2. The errors of numerical solution and ground truth by WAH, WM and AH with the initial value 2.45 in Example 5.1.

Iteration number	WAH	WM	AH
1	3.2287	2.0417	3.5632
2	2.5617	1.8221	3.1935
3	1.1558	1.5371	2.8413
4	0.5521	1.1836	2.4964
5	0.2077	0.6964	2.1467
6	0.0039	0.2145	1.7830
7	$3.2263\times {10}^{-6}$	0.0211	1.3972
8	$8.3792\times {10}^{-10}$	$2.4191\times {10}^{-4}$	0.9818
9	$2.4202\times {10}^{-13}$	$1.3159\times {10}^{-7}$	0.5289
10	$1.4201\times {10}^{-15}$	$9.2188\times {10}^{-11}$	0.0319
11	$1.0793\times {10}^{-15}$	$6.4001\times {10}^{-14}$	$1.2034\times {10}^{-4}$
12	$1.3798\times {10}^{-15}$	$2.0261\times {10}^{-15}$	$2.6732\times {10}^{-8}$
13	$1.2429\times {10}^{-15}$	$1.1633\times {10}^{-15}$	$6.9694\times {10}^{-12}$

Table 3. The errors of numerical solution and ground truth by WAH, WM and AH with the initial value 4.15 in Example 5.1.

Iteration number	WAH	WM	AH
1	4.1052	12.9611	5.8474
2	3.2551	$\infty$	4.6877
3	0.7618	$\infty$	3.6352
4	0.6079	$\infty$	2.8049
5	0.2067	$\infty$	2.1178
6	0.0041	$\infty$	1.5461
7	$3.2381\times {10}^{-6}$	$\infty$	1.0642
8	$8.3425\times {10}^{-10}$	$\infty$	0.6526
9	$2.3170\times {10}^{-13}$	$\infty$	0.2967
10	$1.6043\times {10}^{-15}$	$\infty$	0.0153
11	$1.3068\times {10}^{-15}$	$\infty$	$4.2494\times {10}^{-5}$
12	$1.6677\times {10}^{-15}$	$\infty$	$2.6573\times {10}^{-8}$

Table 4. The errors of numerical solution and ground truth by WAH, WM and AH with the initial value 6.58 in Example 5.1.

Iteration number	WAH	WM	AH
1	6.7614	47.6033	11.4152
2	4.9733	$\infty$	9.2323
3	0.9618	$\infty$	6.9785
4	0.5663	$\infty$	5.3391
5	0.2092	$\infty$	4.0014
6	0.0041	$\infty$	2.9099
7	$3.3133\times {10}^{-6}$	$\infty$	1.9987
8	$8.5869\times {10}^{-10}$	$\infty$	1.2243
9	$2.3371\times {10}^{-13}$	$\infty$	0.5554
10	$2.2577\times {10}^{-15}$	$\infty$	0.0307
11	$1.2000\times {10}^{-15}$	$\infty$	$9.9211\times {10}^{-5}$
12	$2.0861\times {10}^{-15}$	$\infty$	$4.7145\times {10}^{-8}$
13	$1.1922\times {10}^{-15}$	$\infty$	$2.6898\times {10}^{-11}$

Table 5. The required iteration numbers by WAH, WM and AH in Example 5.1.

Initial value	WAH	WM	AH
0.17	10	10	15
2.45	8	10	13
4.15	8	No convergence	12
6.58	8	No convergence	13
8.23	10	No convergence	13
9.99	10	No convergence	13

Table 6. The required CPU times (in seconds) by WAH, WM and AH in Example 5.1.

Initial value	WAH	WM	AH
0.17	14.73	14.39	22.17
2.45	11.82	15.02	18.84
4.15	11.78	No convergence	16.93
6.58	11.93	No convergence	18.78
8.23	14.30	No convergence	18.87
9.99	14.51	No convergence	18.86

Example 5.2

In this example, $q_1^c=q_4^c=3$, $q_2^c=q_3^c=5$, and we use WAH. The nonlinear functions $N$ are respectively $N(\mathrm{\nabla }u)=1+{0.1|\mathrm{\nabla }u|}^2$ and $N(\mathrm{\nabla }u)=1/(1-0.1|\mathrm{\nabla }u{|}^2)$, $q^0\equiv 5$, and the Gaussian noise level $\mathit{ϵ}=0.05$. The true model based on (2.22.2 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(\mathrm{\nabla }u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.2 ) and inversion results $q^{\ast }$ are shown in Figure 5, and the relative $l^2$ errors for $N(\mathrm{\nabla }u)=1+{0.1|\mathrm{\nabla }u|}^2$ and $N(\mathrm{\nabla }u)=1/(1-0.1|\mathrm{\nabla }u{|}^2)$ are 0.0148 and 0.0104, respectively.

Example 5.3

In oil reservoirs the permeability usually has greatly large jumps, so we use WAH with $q_1^c=9$, $q_2^c=1$, $q_3^c=2$, $q_4^c=10$ in this example. The nonlinear functions $N$ are respectively $N(u)=u^4-u^3+u^2-u+1$ and $N(u)=u^4+u^3+u^2+u+1$, $q^0\equiv 5$, and the Gaussian noise level $\mathit{ϵ}=0.05$. The true model based on (2.12.1 $$\begin{array}{c}\hfill u_t-\mathrm{\nabla }·(q(\mathbf{x})N(u)\mathrm{\nabla }u)=s(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times (0,T),\end{array}$$2.1 ) and inversion results $q^{\ast }$ are shown in Figure 6, and the relative $l^2$ errors for $N(u)=u^4-u^3+u^2-u+1$ and $N(u)=u^4+u^3+u^2+u+1$ are 0.0115 and 0.0121, respectively.

It can be seen from these Examples 5.2 and 5.3 that the wavelet multiscale-adaptive homotopy method is effective for the different $N$-functions, even if $N$ is highly nonlinear. Moreover, in Example 5.3, the traditional iteration methods such as Newton type is not convergent when the initial guess value is given as an arbitrary constant. Hence, we conclude that the wavelet multiscale-adaptive homotopy method is not only effective, and even necessary for reservoir simulation.

Example 5.4

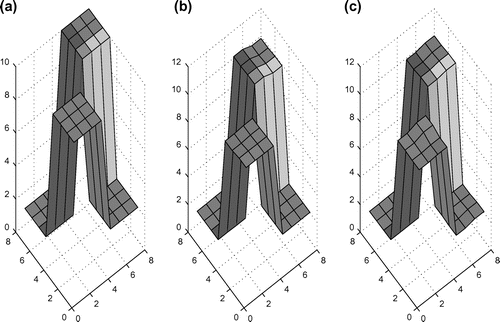
In this example, a vertical stratified medium containing two interfaces shown in Figure 7 is considered. The nonlinear function $N(u)=u^4+u^3+u^2+u+1$, initial guess value $q^0\equiv 5$ and $\mathit{ϵ}=0.01$. Figure 8 shows the inversion result at the original scale, which is obtained by WAH. Starting from the same initial guess value, WM is not convergent; and AH is also convergent, but takes about 146.53% CPU time of WAH.

Example 5.5

In this example, we consider the model of one anomalous body in a homogeneous medium with a permeability of 3.44. The anomalous body has the permeability of 7.28. The nonlinear function $N(\mathrm{\nabla }u)=1+{0.1|\mathrm{\nabla }u|}^2$, initial guess value $q^0\equiv 5$ and $\mathit{ϵ}=0.01$. This model and its inversion result at the original scale obtained by WAH are respectively shown in Figures 9 and 10. Starting from the same initial guess value, WM is not convergent; and AH is also convergent, but takes about 139.76% CPU time of WAH.

Example 5.6

In this example, we consider a complex and inhomogeneous model, which has the permeability of 3.89, 4.39, 5.23 and 8.03 from top to bottom. The nonlinear function $N(u)=u^2+u+1$, initial guess value $q^0\equiv 5$, and $\mathit{ϵ}=0.04$. This model and its inversion results at scale 1 and scale 0 obtained by WAH are respectively shown in Figures 11 and 12. The relative $l^2$ errors for the inversion results at scale 1 and scale 0 are respectively equal to 0.0588 and 0.0607.

It can be seen from these Examples 5.4–5.6 that even though the model is large scale and complicated, the wavelet multiscale-adaptive homotopy method still is globally convergent, computationally efficient, and has the anti-noise ability. From Examples 5.4 and 5.5, we can see that the wavelet multiscale-adaptive homotopy method still has a larger region of convergence than the wavelet multiscale method and less computational cost than the adaptive homotopy method for the large-scale and complicated models. In addition, in Example 5.6, the inversion result at scale 1 is better than the one at scale 0. Hence, we can easily conclude that if the observation data are strongly noisy, the wavelet multiscale-adaptive homotopy method will eliminate noise to a certain degree. This is due to the good de-noising performance of wavelet.

6 Conclusions

For the inverse problem of nonlinear diffusion equation within multiphase porous media flow, we have designed a wavelet multiscale-adaptive homotopy method which combines the advantages of wavelet multiscale method and adaptive homotopy method, and realized the numerical inversion of permeability parameter of two-dimensional nonlinear diffusion equation in reservoir simulation. The results of numerical experiments demonstrate the effectiveness of the proposed method. All the inverse problems in reservoir simulation have similar difficulties of nonlinearity and ill-posedness, so we are certain that the proposed method will have a great influence on the development of practical solutions to the permeability estimation problems in the multiphase porous media flow equations.

Acknowledgements

The authors wish to thank the referees for their valuable comments which helped us to improve the present paper.

Additional information

Funding

This work was supported by the National Natural Science Foundation of China [grant number 11101109], [grant number 11271102], the Natural Science Foundation of Hei-long-jiang Province of China [grant number A201107] and SRF for ROCS, SEM.