A new inverse problem for the determination of textile fabrics thickness

Abstract

This paper deals with a new inverse problem of estimating textile fabrics thickness based on a one-dimensional steady-state heat and moisture transfer model. First, we give an existence and uniqueness theorem for the solution to the heat and moisture transfer problem in the Banach space. Then we present an inverse problem for the determination of textile fabrics thickness and formulate the inverse problem as an optimization problem with maximum probability, according to the requirement of heat-moisture comfort of clothing. Moreover, considering that the objective function of the proposed optimization problem may not be continuous and the points achieving maximum value may not be unique, we proceed to recast this inverse problem as a minimum norm with a maximum probability constraint problem. Finally, we use a static penalty method to convert the constrained problem into an equivalent unconstrained minimization problem and obtain the solution for the optimization problem by a stochastic search method known as particle swarm optimization algorithm. Numerical experiments show that our new model and its equivalent transformation is quite acceptable, and the proposed numerical method is valid and robust.

Keywords:

• inverse problems
• heat and moisture transfer
• textile fabric
• thickness determination
• optimization algorithm

AMS Subject Classifications:

• 34A55
• 80A23
• 80M50

The notation used in the paper is defined as follows:

Nomenclature
$x$	=	distance from the inner covering fabric (m)
$L$	=	thickness of the fabric batting (m)
$T$	=	temperature (K)
$T_0$	=	temperature of the surface next to the human body (K)
$T_L$	=	temperature of the surrounding air (K)
$p_v$	=	water vapour pressure (Pa)
$p_{v,L}$	=	water vapour pressure of the surrounding air (Pa)
$m_v$	=	mass flux of water vapour $(\text{kg}{\text{m}}^{-2}{\text{s}}^{-1})$
$m_{v,0}$	=	mass flux of water vapour of the surface next to the human body$(\text{kg}{\text{m}}^{-2}{\text{s}}^{-1})$
$r$	=	radius of cylindrical pore (m)
$R_{to}$	=	heat transfer resistance of textile material $(\text{K}{\text{m}}^2{\text{w}}^{-1})$
$h_t$	=	the convective heat transfer coefficient $(\text{w}{\text{K}}^{-1}{\text{m}}^{-2})$
$k_1,k_2$	=	constants which are related with molecular weight and gas constant
$RH$	=	relative humidity
$P_{\mathrm{sat}}$	=	saturated water vapour pressure at temperature $T$ (Pa)

Greek symbols
$\mathit{\lambda }$	=	latent heat of sorption and condensation of water vapour (J ${\mathrm{kg}}^{-1}$)
$\mathit{\kappa }$	=	effective thermal conductivity of the porous batting $(\text{w}{\text{m}}^{-1}{\text{K}}^{-1})$
$\mathit{\tau }$	=	effective tortuosity of the textile
$\mathit{\epsilon }$	=	porosity of textile surface (%)
$\mathrm{\Gamma }$	=	rate of condensation $(\text{kg}{\text{m}}^{-3}{\text{s}}^{-1})$

1 Introduction

Clothing has served a variety of social purposes. The primary function of clothing is to improve the comfort of the wearer. In hot climates, clothing provides protection from sunburn or wind damage, while in cold climates its thermal insulation properties are generally more important. On this account, happiness and health of humans largely depends on clothing. The main effect of clothing will be the influence on the heat and moisture exchange between the skin and the environment. An understanding of the heat and moisture transfer in clothing system has developed over the past few decades. Henry [1] developed one of the first theories of coupled heat and moisture transfer through clothing considering accumulation effects. Shitzer and Chato [2] studied the heat and mass transfer of the air-clothing-skin system, where the heat and mass transfer in the system was considered as a steady-state problem in a one-dimensional model composed of five layers. Jones [3] and Li and Holcombe [4] introduced dynamic models of heat and moisture characteristics in interaction with two node human thermoregulation model of Gagge et al. [5], respectively. Fan et al. [6, 7], Fan and Wen [8] developed more general dynamic models in textile materials. Min et al. [9] set up a mathematical model to simulate the heat and moisture transfer from skin to environment through fabrics by including heat radiation between surfaces and the surface diffusion along fibres. Wu and Fan [10] and Wissler and Havenith [11] presented mathematical models for heat and moisture transport through multi-layer clothing, respectively.

Heat-moisture comfort refers to the condition of the mind which expresses satisfaction with the heat and moisture environment. The heat-moisture comfort indices have been developed with the help of coupled heat and moisture transfer equations designed to predict heat-moisture comfort. The heat-moisture comfort feeling of the human body is influenced by various parameters. The three main factors are: environmental climate, clothing and physical activity. Clothing factors such as thickness of material, clothing insulation value, type of material, volume of air enclosed in the fibres, resistance to diffusion of water vapour, layers of clothing, body fit, air permeability, etc influence the thermal and moisture comfort. A considerable amount of research has been done in order to ascertain the influence of various factors of clothing on comfort, the interested readers may refer to some articles [12–16] for further understanding.

The direct heat and moisture transfer problems consist of determining the temperature and moisture distribution within the fabrics when the boundary and initial conditions, physical properties and geometric parameters are known. In contrast, the inverse heat and moisture transfer problems consider the identification of boundary and initial conditions, physical properties and geometric parameters by given measurements. These inverse problems are beneficial for the development of advanced textile materials to protect against harmful environmental stresses including the climatic conditions.

Only few works have been done on the inverse problems in textile material design. Xu et al. [17, 18] studied the inverse heat and moisture transfer problems based on a one-dimensional steady-state model of heat and moisture transfer through parallel cylinder pore textiles for estimation of material thickness and type. Xu and Ge [19] also presented an inverse problem of textile thickness determination based on a heat and moisture transfer model with phase change in porous textile materials. Numerical methods and simulations for the heat and moisture transport in porous textile materials have been studied in their papers. However, the authors haven’t explored the existence and uniqueness analysis for the heat and moisture transfer problem, and the according inverse problems are formulated as unconstrained minimization problems by choosing the ideal relative humidity of the surface close to skin as a fixed percentage, for example 50%, and the numerical treatment for that inverse problem is mainly applied by the direct search methods: Hooke–Jeeves (H–J) algorithm and Golden-Section (G-S) method.

In this paper, based on some assumptions, we establish an existence and uniqueness result for the solution to the heat and moisture transfer problem. Considering that, the ideal relative humility in the inverse heat and moisture transfer problems can vary from 40 to 60%, we design a new maximum probability optimization model for the inverse heat and moisture transfer problem, and then we recast this inverse problem as a minimum norm with a maximum probability constraint problem. We transform the proposed constrained problem into an equivalent unconstrained problem by the static penalty method, and then adopt the particle swarm optimization algorithm to obtain the approximate solution for the new optimization problem. Three representative fabrics are selected for our model and algorithm testification. The numerical results show that our new optimization model is quite reasonable and the proposed algorithm is quite robust.

This paper is organized as follows. In Section 2, the heat and moisture transfer problem based on a steady-state model is described and solved. The Banach fixed-point theorem is applied to prove the existence and uniqueness of a solution of the direct problem considered. In Section 3, an inverse problem of thickness determination for textile fabric and its transformation into a constrained optimization problem are presented. An overview of the particle swarm optimization (PSO) algorithm is also illustrated in this part. The numerical examples including the noise perturbation for the optimization problem are discussed in Section 4. Section 5 ends the paper by making some conclusions.

2 The direct heat and moisture transfer problem

We first introduce the direct problem for the heat and moisture transfer problem. And then we give an existence and uniqueness theorem for the solution to the above problem. Finally, we illustrate the finite difference method for solving it.

2.1 The direct problem

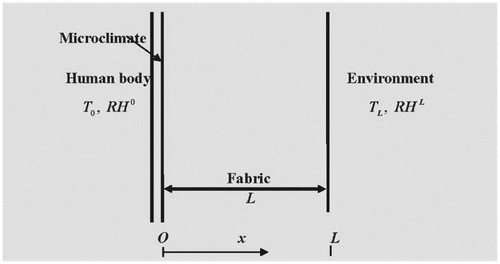
Let us consider a system that consists of human skin, fabric and environment as shown in Figure 1. Considering that the fabric may be distributed uniformly and the mass and heat influx may uniformly fall on the fabric as well. Furthermore, assuming that the distribution of temperature, water vapour pressure and mass flux of water vapour proliferation within the fabric are all steady as the time changes.

Figure 1. Schematic diagram of the body-fabric-environment system.

Mass flux of water vapour proliferation within the parallel cylindrical pore can be represented as1 $$\begin{array}{c}\hfill m_v(x)=-k_1\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}·\frac{p_v(x)}{T^{3/2}(x)}·\frac{d{p}_v(x)}{dx}.\end{array}$$1 Combining the Equation (11 $$\begin{array}{c}\hfill m_v(x)=-k_1\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}·\frac{p_v(x)}{T^{3/2}(x)}·\frac{d{p}_v(x)}{dx}.\end{array}$$1 ) with the mass conservation law, the energy conservation law and the rate of condensation equation, one obtains a one-dimensional model of the coupled heat and mass transfer problem through parallel cylinder pore textiles as follows [20] :2 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{k}_1\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}·\frac{p_v(x)}{T^{3/2}(x)}·\frac{d{p}_v(x)}{dx}+m_v(x)=0,\hfill \\ \frac{d{m}_v(x)}{dx}+\mathrm{\Gamma }(x)=0,\hfill \\ \mathit{\kappa }(x)\frac{d^{2}T(x)}{d{x}^2}+\mathit{\lambda }\mathrm{\Gamma }(x)=0,\hfill \\ \mathrm{\Gamma }(x)=-k_2\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}(p_{\mathrm{sat}}(T(x))-p_v(x))\frac{1}{\sqrt{T(x)}},\hfill \end{array}\right.0<x<L,\end{array}$$2 which subjected to the following boundary conditions:3 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{T(x)|}_{x=0}=T_0,\hfill \\ {T(x)|}_{x=L}=T_L,\hfill \\ m_v{(x)|}_{x=0}=m_{v,0},\hfill \\ p_v{(x)|}_{x=L}=p_{v,L},\hfill \end{array}\right.\end{array}$$3 where the saturation vapour pressure is related to temperature by:4 $$\begin{array}{c}\hfill p_{\mathrm{sat}}(T)=100\times e^{18.956-\frac{4030}{(T-273.15)+235}}.\end{array}$$4 Our model is based on the assumptions listed below.

(1)	The inner pore structure of the fabric is assumed to be parallel cylinder, and there are no voids in the pores.
(2)	The fibrous porous batting is isotropic and homogeneous in fibre arrangement and material properties.
(3)	The air and vapour are continuous and treated as ideal gases.
(4)	Volume changes of the fibres due to changing moisture and water content are neglected.

In Equation (22 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{k}_1\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}·\frac{p_v(x)}{T^{3/2}(x)}·\frac{d{p}_v(x)}{dx}+m_v(x)=0,\hfill \\ \frac{d{m}_v(x)}{dx}+\mathrm{\Gamma }(x)=0,\hfill \\ \mathit{\kappa }(x)\frac{d^{2}T(x)}{d{x}^2}+\mathit{\lambda }\mathrm{\Gamma }(x)=0,\hfill \\ \mathrm{\Gamma }(x)=-k_2\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}(p_{\mathrm{sat}}(T(x))-p_v(x))\frac{1}{\sqrt{T(x)}},\hfill \end{array}\right.0<x<L,\end{array}$$2 ), the parameters $\mathit{\epsilon }(x),r(x),\mathit{\tau }(x),\mathit{\kappa }(x)$ may be assumed to be constants for a uniform fibrous batting, and can be assumed to be variables for nonuniform fibrous batting. The problem defined by Equation (22 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{k}_1\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}·\frac{p_v(x)}{T^{3/2}(x)}·\frac{d{p}_v(x)}{dx}+m_v(x)=0,\hfill \\ \frac{d{m}_v(x)}{dx}+\mathrm{\Gamma }(x)=0,\hfill \\ \mathit{\kappa }(x)\frac{d^{2}T(x)}{d{x}^2}+\mathit{\lambda }\mathrm{\Gamma }(x)=0,\hfill \\ \mathrm{\Gamma }(x)=-k_2\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}(p_{\mathrm{sat}}(T(x))-p_v(x))\frac{1}{\sqrt{T(x)}},\hfill \end{array}\right.0<x<L,\end{array}$$2 ) is called a direct problem in which the interior temperature $T(x)$ should be determined when the physical properties and boundary conditions (33 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{T(x)|}_{x=0}=T_0,\hfill \\ {T(x)|}_{x=L}=T_L,\hfill \\ m_v{(x)|}_{x=0}=m_{v,0},\hfill \\ p_v{(x)|}_{x=L}=p_{v,L},\hfill \end{array}\right.\end{array}$$3 ) are known. In the next section, we will prove the existence and uniqueness of solution $T(x)$ to the direct problem by Banach fixed-point theorem.

2.2 Theoretical result for the direct problem

Let ${\displaystyle A(x)=\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}}$ and ${\displaystyle k_3=\frac{\mathit{\kappa }}{\mathit{\lambda }}}$. We decouple the ordinary differential Equation (22 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{k}_1\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}·\frac{p_v(x)}{T^{3/2}(x)}·\frac{d{p}_v(x)}{dx}+m_v(x)=0,\hfill \\ \frac{d{m}_v(x)}{dx}+\mathrm{\Gamma }(x)=0,\hfill \\ \mathit{\kappa }(x)\frac{d^{2}T(x)}{d{x}^2}+\mathit{\lambda }\mathrm{\Gamma }(x)=0,\hfill \\ \mathrm{\Gamma }(x)=-k_2\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}(p_{\mathrm{sat}}(T(x))-p_v(x))\frac{1}{\sqrt{T(x)}},\hfill \end{array}\right.0<x<L,\end{array}$$2 ) to obtain the following two-point boundary value problem of nonlinear integral-differential equation:5 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\sqrt{T}\frac{d^{2}T}{d{x}^2}=\frac{k_2}{k_3}A(x)[p_{\mathrm{sat}}(T(x))-\sqrt{p_v^2(L)+2{\int }_x^L\frac{T^{3/2}(s)}{k_{1}A(s)}[k_3{T}^{\prime }(s)+C_1]ds}],\hfill \\ T(0)=T_0,T(L)=T_L,\hfill \end{array}\right.\end{array}$$5 where $C_1=m_v(0)-k_3{T}^{\prime }(0).$

The two-point boundary value problem (55 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\sqrt{T}\frac{d^{2}T}{d{x}^2}=\frac{k_2}{k_3}A(x)[p_{\mathrm{sat}}(T(x))-\sqrt{p_v^2(L)+2{\int }_x^L\frac{T^{3/2}(s)}{k_{1}A(s)}[k_3{T}^{\prime }(s)+C_1]ds}],\hfill \\ T(0)=T_0,T(L)=T_L,\hfill \end{array}\right.\end{array}$$5 ) can be rewritten as$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle {\left(p_{\mathrm{sat}},(T(x)),-,\frac{k_3}{k_{2}A(x)},\sqrt{T},T^{″}\right)}^2-2{\int }_x^L\frac{T^{\frac{3}{2}}(s)}{k_{1}A(s)}\left[k_3,T^{\prime },(s),+,C_1\right]ds-p_v^2(L)=0,}\hfill \\ {\displaystyle T(0)=T_0,T(L)=T_L,}\hfill \end{array}\right.\end{array}$$where $0<x<L$.

Before we present our main theorem, some basic assumptions are given as follows:

(1)	$T_L\le T(x)\le T_0.$
(2)	$T(x)$ belongs to $C^2[0,L]$, i.e. there exists a constant $M>0$, such that$$\begin{array}{c}\hfill {∥,T∥}_{C^2[0,L]}\le M.\end{array}$$
(3)	There exist constants $N_1,N_2>0,$ such that$$\begin{array}{c}\hfill \left|\frac{k_3}{k_2·A(x)}\right|\le N_1,\left|\frac{1}{k_1·A(x)}\right|\le N_2,0<x<L.\end{array}$$
(4)	There exists a constant $P>0,$ such that$$\begin{array}{c}\hfill \left|p_{\mathrm{sat}},(T)\right|<P.\end{array}$$

Let $r$ be a real constant. Define an operator $\mathbf{B}:C^2[0,L]\to C[0,L]$ as follows:$$\begin{array}{cc}\hfill \mathbf{B}(T(x))& =T(x)+r{\left(p_{\mathrm{sat}},(T(x)),-,\frac{k_3}{k_{2}A(x)},\sqrt{T},T^{″}\right)}^2\hfill \\ \hfill & -2r{\int }_x^L\frac{T^{\frac{3}{2}}(s)}{k_{1}A(s)}\left[k_3,T^{\prime },(s),+,C_1\right]ds-r{p}_v^2(L).\hfill \end{array}$$Now we state our main result.

Theorem 3.1

Assume (1)–(4) hold and the constant $r$ satisfies$$\begin{array}{c}\hfill |r|<min\left\{\frac{1-L}{dL+2L{k}_3{N}_2{M}^{\frac{3}{2}}},,,\frac{1}{2(P+N_1{M}^{\frac{3}{2}})N_1{M}^{\frac{1}{2}}}\right\},\end{array}$$where$$\begin{array}{c}\hfill d=2\left(P,+,N_1,M^{\frac{3}{2}}\right)\left(P,+,\frac{1}{2},N_1,M^{\frac{1}{2}}\right)+3L{N}_2{M}^{\frac{1}{2}}\left(C_1,+,k_3,M\right).\end{array}$$Then there exists a unique solution $T(x)$ in the space $C^2[0,L]$ such that6 $$\begin{array}{c}\hfill T(x)=\mathbf{B}(T(x)).\end{array}$$6

Proof

For any $T_1(x),T_2(x)\in C^2[0,L]$, we have$$\begin{array}{cc}& \mathbf{B}(T_1(x))-\mathbf{B}(T_2(x))\hfill \\ \hfill & =T_1-T_2+r\left[{\left(p_{\mathrm{sat}},(T_1),-,\frac{k_3}{k_{2}A(x)},\sqrt{T_1},T_1^{″}\right)}^2,-,{\left(p_{\mathrm{sat}},(T_2),-,\frac{k_3}{k_{2}A(x)},\sqrt{T_2},T_2^{″}\right)}^2\right]\hfill \\ \hfill & -2r\left[{\int }_x^L,\frac{T_1^{\frac{3}{2}}(s)}{k_{1}A(s)},\left[k_3,T_1^{\prime },(s),+,C_1\right],d,s,-,{\int }_x^L,\frac{T_2^{\frac{3}{2}}(s)}{k_{1}A(s)},\left[k_3,T_2^{\prime },(s),+,C_1\right],d,s\right].\hfill \end{array}$$ By the assumption (11 $$\begin{array}{c}\hfill m_v(x)=-k_1\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}·\frac{p_v(x)}{T^{3/2}(x)}·\frac{d{p}_v(x)}{dx}.\end{array}$$1 ) and mean value theorem of differentials, we get$$\begin{array}{cc}\hfill \left|p_{\mathrm{sat}},(T_1),-,p_{\mathrm{sat}},(T_2)\right|& =100\times e^{18.956-\frac{4030}{(\mathit{\xi }-273.15)+235}}\frac{4030}{{(\mathit{\xi }-38.15)}^2}\times |T_1-T_2|\hfill \\ \hfill & \le P\Vert T_1-T_2{\Vert }_{C[0,L]}.\hfill \end{array}$$where $\mathit{\xi }$ lies between $T_1$ and $T_2.$

In terms of the above basic assumptions (22 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{k}_1\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}·\frac{p_v(x)}{T^{3/2}(x)}·\frac{d{p}_v(x)}{dx}+m_v(x)=0,\hfill \\ \frac{d{m}_v(x)}{dx}+\mathrm{\Gamma }(x)=0,\hfill \\ \mathit{\kappa }(x)\frac{d^{2}T(x)}{d{x}^2}+\mathit{\lambda }\mathrm{\Gamma }(x)=0,\hfill \\ \mathrm{\Gamma }(x)=-k_2\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}(p_{\mathrm{sat}}(T(x))-p_v(x))\frac{1}{\sqrt{T(x)}},\hfill \end{array}\right.0<x<L,\end{array}$$2 ) and (33 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{T(x)|}_{x=0}=T_0,\hfill \\ {T(x)|}_{x=L}=T_L,\hfill \\ m_v{(x)|}_{x=0}=m_{v,0},\hfill \\ p_v{(x)|}_{x=L}=p_{v,L},\hfill \end{array}\right.\end{array}$$3 ) and some classic inequalities, we obtain the following estimates$$\begin{array}{cc}& {∥,{\left(p_{\mathrm{sat}},(T_1),-,\frac{k_3}{k_{2}A(x)},\sqrt{T_1},T_1^{″}\right)}^2,-,{\left(p_{\mathrm{sat}},(T_2),-,\frac{k_3}{k_{2}A(x)},\sqrt{T_2},T_2^{″}\right)}^2∥}_{C[0,L]}\hfill \\ \hfill & =∥,\left(p_{\mathrm{sat}},(T_1),+,p_{\mathrm{sat}},(T_2),-,\frac{k_3}{k_{2}A(x)},\left(\sqrt{T_1},T_1^{″},+,\sqrt{T_2},T_2^{″}\right)\right)\hfill \\ \hfill & {\times ,\left(p_{\mathrm{sat}},(T_1),-,p_{\mathrm{sat}},(T_2),-,\frac{k_3}{k_{2}A(x)},\left(\sqrt{T_1},T_1^{″},-,\sqrt{T_2},T_2^{″}\right)\right)∥}_{C[0,L]}\hfill \\ \hfill & \le 2\left(P,+,N_1,M^{\frac{3}{2}}\right)\left[P\Vert ,T_1,-,T_2,{\Vert }_{C[0,L]},+,N_1,{∥,\sqrt{T_1},\left(T_1^{″},-,T_2^{″}\right),+,\left(\sqrt{T_1},-,\sqrt{T_2}\right),T_2^{″}∥}_{C[0,L]}\right]\hfill \\ \hfill & \le 2\left(P,+,N_1,M^{\frac{3}{2}}\right)\left[P\Vert ,T_1,-,T_2,{\Vert }_{C[0,L]},+,N_1,M^{\frac{1}{2}},\left(\Vert ,T_1^{″},-,T_2^{″},{\Vert }_{C[0,L]},+,\frac{1}{2},{\Vert T_1-T_2\Vert }_{C[0,L]}\right)\right],\hfill \end{array}$$and$$\begin{array}{cc}& {∥,{\int }_x^L,\frac{T_1^{\frac{3}{2}}(s)}{k_{1}A(s)},\left[k_3,T_1^{\prime },(s),+,C_1\right],d,s,-,{\int }_x^L,\frac{T_2^{\frac{3}{2}}(s)}{k_{1}A(s)},\left[k_3,T_2^{\prime },(s),+,C_1\right],d,s∥}_{C[0,L]}\hfill \\ \hfill & \le {∥,{\int }_x^L,\frac{C_1}{k_{1}A(s)},\left[T_1^{\frac{3}{2}},(s),-,T_2^{\frac{3}{2}},(s)\right],d,s∥}_{C[0,L]}\hfill \\ \hfill & +{∥,{\int }_x^L,\frac{k_3}{k_{1}A(s)},\left[T_1^{\frac{3}{2}},(s),T_1^{\prime },(s),-,T_2^{\frac{3}{2}},(s),T_2^{\prime },(s)\right],d,s∥}_{C[0,L]}\hfill \\ \hfill & \le |C_1|N_2{∥,{\int }_x^L,\left[\frac{T_1(s)-T_2(s)}{\sqrt{T_1(s)}+\sqrt{T_2(s)}},(T_1(s)+\sqrt{T_1(s)T_2(s)}+T_2(s))\right],d,s∥}_{C[0,L]}\hfill \\ \hfill & +k_3{N}_2{∥,{\int }_x^L,\left[(T_1^{\frac{3}{2}}(s)-T_2^{\frac{3}{2}}(s)),T_1^{\prime },(s),+,T_2^{\frac{3}{2}},(s),(T_1^{\prime }(s)-T_2^{\prime }(s))\right],d,s∥}_{C[0,L]}\hfill \\ \hfill & \le \frac{3}{2}L{N}_2{M}^{\frac{1}{2}}\left(C_1,+,k_3,M\right)\Vert T_1-T_2{\Vert }_{C[0,L]}+L{k}_3{N}_2{M}^{\frac{3}{2}}{\Vert T_1^{\prime }-T_2^{\prime }\Vert }_{C[0,L]}.\hfill \end{array}$$Therefore, we have$$\begin{array}{cc}& \Vert \mathbf{B}(T_1(x))-\mathbf{B}(T_2(x)){\Vert }_{C[0,L]}\hfill \\ \hfill & \le \left|1,+,|r|,\left[2,\left(P,+,N_1,M^{\frac{3}{2}}\right),(P+\frac{1}{2}{N}_1{M}^{\frac{1}{2}}),+,3,L,N_2,M^{\frac{1}{2}},\left(C_1,+,k_3,M\right)\right]\right|\hfill \\ \hfill & \Vert T_1-T_2{\Vert }_{C[0,L]}+2|r|L{k}_3{N}_2{M}^{\frac{3}{2}}{\Vert T_1^{\prime }-T_2^{\prime }\Vert }_{C[0,L]}\hfill \\ \hfill & +2|r|\left(P,+,N_1,M^{\frac{3}{2}}\right)N_1{M}^{\frac{1}{2}}{\Vert T_1^{″}-T_2^{″}\Vert }_{C[0,L]}\hfill \\ \hfill & \le \left[(1+|r|d)L+2|r|L,k_3,N_2,M^{\frac{3}{2}}\right]{\Vert T_1^{\prime }-T_2^{\prime }\Vert }_{C[0,L]}\hfill \\ \hfill & +2|r|\left(P,+,N_1,M^{\frac{3}{2}}\right)N_1{M}^{\frac{1}{2}}{\Vert T_1^{″}-T_2^{″}\Vert }_{C[0,L]}\hfill \\ \hfill & <\Vert T_1-T_2{\Vert }_{C^2[0,L]}.\hfill \end{array}$$By the Banach fixed-point theorem, there exists a unique solution $T(x)$ in the $C^2[0,L]$ space such that$$T(x)=\mathbf{B}(T(x)).$$which completes the proof.$\square$

Under the same assumptions as that in Theorem 3.1, we conclude that there exists a unique solution to the direct problem (55 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\sqrt{T}\frac{d^{2}T}{d{x}^2}=\frac{k_2}{k_3}A(x)[p_{\mathrm{sat}}(T(x))-\sqrt{p_v^2(L)+2{\int }_x^L\frac{T^{3/2}(s)}{k_{1}A(s)}[k_3{T}^{\prime }(s)+C_1]ds}],\hfill \\ T(0)=T_0,T(L)=T_L,\hfill \end{array}\right.\end{array}$$5 ).

2.3 The finite difference method to solve the direct problem

The direct problem can be solved by discretizing the above equations with the finite difference method. Let $h=\frac{L}{N}$ be the step length in space coordinates, and $\{0=x_0<x_1<\cdots <x_N=L\}$ denote partitions of $[0,L]$. The finite difference approximation for the differential equation of (55 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\sqrt{T}\frac{d^{2}T}{d{x}^2}=\frac{k_2}{k_3}A(x)[p_{\mathrm{sat}}(T(x))-\sqrt{p_v^2(L)+2{\int }_x^L\frac{T^{3/2}(s)}{k_{1}A(s)}[k_3{T}^{\prime }(s)+C_1]ds}],\hfill \\ T(0)=T_0,T(L)=T_L,\hfill \end{array}\right.\end{array}$$5 ) may be written in the form$$\begin{array}{c}\hfill \begin{array}{c}\sqrt{T_i}\frac{T_i-2T_{i-1}+T_{i-2}}{h^2}=\frac{k_{2}A(x_i)}{k_3}[p_{\mathrm{sat}}(T_i)-\sqrt{p_{v,L}^2+2\sum _{j=i}^{N-1}\frac{T_{j+1}^{3/2}}{k_{1}A(x_j)}[k_3\frac{T_{j+1}-T_j}{h}+C_1]h}],\hfill \\ i=N-1,N-2,\dots ,2,\hfill \end{array}\end{array}$$and7 $$\begin{array}{c}\hfill \sqrt{T_N}\frac{T_N-2T_{N-1}+T_{N-2}}{h^2}=\frac{k_2}{k_3}A(x_N)[p_{\mathrm{sat}}(T_N)-p_{v,L}],i=N,\end{array}$$7 where $T_i$ is the approximate value of $T(x_i)$.

Using $T_0$ and $T_L$, we approximate$$\begin{array}{ccc}\hfill T_1& \approx \hfill & \hfill T_0-\frac{T_0-T_L}{N},\\ \hfill T_{N-1}& \approx \hfill & \hfill T_0-\frac{(T_0-T_L)(N-1)}{N},\\ \hfill T^{\prime }(0)& \approx \hfill & \hfill \frac{T_1-T_0}{h}.\\ \hfill \end{array}$$Using $T_{N-1},\dots ,T_1$, we find8 $$\begin{array}{c}\hfill p_{v,0}=\sqrt{p_{v,L}^2+2\sum _{j=0}^{N-1}\frac{T_{j+1}^{3/2}}{k_{1}A(x_j)}\left[k_3,\frac{T_{j+1}-T_j}{h},+,C_1\right]h},\end{array}$$8 and the relative humidity at the boundary next to the human body9 $$\begin{array}{c}\hfill R{H}^0=\frac{p_{v,0}}{p_{\mathrm{sat}}(T_0)}=\frac{\sqrt{p_{v,L}^2+2\sum _{j=0}^{N-1}\frac{T_{j+1}^{3/2}}{k_{1}A(x_j)}\left[k_3,\frac{T_{j+1}-T_j}{h},+,C_1\right]h}}{100·e^{(18.956-\frac{4030}{(T_0-273.16)+235})}}.\end{array}$$9

3 The inverse heat and moisture transfer problem of determining textile fabrics thickness

In this section, we introduce a new inverse heat and moisture transfer problem and the corresponding PSO algorithm.

3.1 Formulation of the inverse problem of thickness determination of textile fabrics

If the parameters such as thickness, radius of cylindrical pore, conductivity and porosity are given in the Equation (22 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{k}_1\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}·\frac{p_v(x)}{T^{3/2}(x)}·\frac{d{p}_v(x)}{dx}+m_v(x)=0,\hfill \\ \frac{d{m}_v(x)}{dx}+\mathrm{\Gamma }(x)=0,\hfill \\ \mathit{\kappa }(x)\frac{d^{2}T(x)}{d{x}^2}+\mathit{\lambda }\mathrm{\Gamma }(x)=0,\hfill \\ \mathrm{\Gamma }(x)=-k_2\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}(p_{\mathrm{sat}}(T(x))-p_v(x))\frac{1}{\sqrt{T(x)}},\hfill \end{array}\right.0<x<L,\end{array}$$2 ), combining with the boundary conditions (33 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{T(x)|}_{x=0}=T_0,\hfill \\ {T(x)|}_{x=L}=T_L,\hfill \\ m_v{(x)|}_{x=0}=m_{v,0},\hfill \\ p_v{(x)|}_{x=L}=p_{v,L},\hfill \end{array}\right.\end{array}$$3 ), one obtains the temperature and moisture distribution within the fabrics, which is the direct problem. But if any one or more parameters are unknown, it turns into an inverse problem. In what follows, we assume that the other parameters are known except for the textiles thickness $L$.

The heat and moisture comfort indices can be used as an additional information to determine the unknown parameter. Huang [21] showed that when the temperature of microclimate, which is located between the skin surface and the inner surface of fabric, varies from 31 to ${33}^{\circ }$C, the relative humidity from 40 to 60% and the wind speed from 0.1 to 0.4 m s${}^{-1}$, the human body feels comfortable. By using these comfort indices, the inverse problem can be recast as an optimization problem.

3.2 Minimum norm with maximum probability constraint problem

Suppose $T_{min}^L$ and $T_{max}^L$ are minimum and maximum average temperature at a particular place during a particular period, respectively. $R{H}_{min}^L$ and $R{H}_{max}^L$ are minimum and maximum average relative humidity, respectively. We discretize the intervals $[T_{min}^L,T_{max}^L]$ and $[R{H}_{min}^L,R{H}_{max}^L]$ into a series of $N_1$, $N_2$ cells, namely$$\left[T_{min}^L,,,T_{max}^L\right]=\bigcup _{j=1}^{N_1}\left[T_{j-1}^L,,,T_j^L\right],\left[R,H_{min}^L,,,R,H_{max}^L\right]=\bigcup _{j=1}^{N_2}\left[R,H_{j-1}^L,,,R,H_j^L\right],$$thus we obtain $(N_1+1)\times (N_2+1)$ combinations about the environmental temperature and relative humidity$$\left(T_i^L,,,,R,H_j^L\right),i=0,1,\dots ,N_1,j=0,1,\dots ,N_2.$$If $(T_i^L,R{H}_j^L)$ is given, we can obtain the according relative humility of the surface close to skin calculated from direct problem, denoted by $R{H}_{i,j}^0,$ which vary from different $i$ and $j$. Suppose $P(L)$ be the probability of an event that $R{H}_{i,j}^0\in [40\%,60\%],\text{for all}i\in N_1,j\in N_2,$ where the thickness of fabric is $L$. We want to find the optimal thickness, which has the maximum probability to make the human body feels comfortable, i.e. the maximum probability of value $R{H}_{i,j}^0$ lies in [40%, 60%]. We obtain the following maximum optimization problem:10 $$\begin{array}{c}\hfill \text{maximize}P(L).\end{array}$$10 The objective function $P(L)$ may not be continuous and its points achieve maximum value may not be unique. Let $0<M\le 1$ be the maximum value of $P(L)$. Considering that the thinner fabric the better the human body feels. Therefore, the original optimization problem (1010 $$\begin{array}{c}\hfill \text{maximize}P(L).\end{array}$$10 ) can be modified as the following constrained minimization problem11 $$\begin{array}{c}\hfill \text{minimize}L,\end{array}$$11 12 $$\begin{array}{c}\hfill \text{s.t.}P(L)=M.\end{array}$$12 This objective function is linear and combined with the nonlinear constraint. Suppose $L^{\ast }$ be the solution to this constrained optimization problem, then we call it as a minimum norm with maximum probability constraint problem in textile fabric.

The static penalty method [22] can be used to transform a constrained problem into an unconstrained problem. For this method, the constraints are placed into the objective function via a penalty parameter in a way that penalizes any violation of the constraints. Using static penalty method, the constrained problem can be replaced by the following unconstrained problem13 $$\begin{array}{c}\hfill \text{minimize}L+\text{K}\times [M-P(L)],\end{array}$$13 where $K$ is a large positive constant. We can intuitively see that an optimal solution to the above problem must have $P(L)$ very close to $M$, because otherwise a large penalty $\text{K}\times [M-P(L)]$ will be incurred.

Due to the existence of probability function $P(L)$, the objective function of the optimization problem (1313 $$\begin{array}{c}\hfill \text{minimize}L+\text{K}\times [M-P(L)],\end{array}$$13 ) may not be continuous. Conventional optimization technique such as gradient based algorithm are not good enough to solve the problems involving the probability function because it depends on first and second derivatives of the objective function. Thus, it’s important to find an appropriate method for solving such a complicate problem. In what follows, we use a stochastic method known as particle swarm optimization algorithm to solve the above optimization problem. The advantages of the PSO algorithm is its capability in searching for the global optimum and no computation of the complicated gradients.

3.3 Particle swarm optimization

The PSO method [23–26] is an efficient technique for solving many complex optimization problems which are nonlinear, nondifferentiable and multi-modal. It is becoming very popular because of its simplicity of implementation as well as ability to swiftly converge to a good solution. It does not require any gradient information of the function to be optimized and uses only primitive mathematical operators.

In PSO, the set of particles is called a swarm. A swarm consists of N particles moving around in a D-dimensional search space. The position of the ith particle can be represented by$$L_i=(L_{i_1},L_{i_2},\dots ,L_{i_D}).$$The velocity for the ith particle can be written as$$\begin{array}{c}\hfill ▵L_i=(▵L_{i_1},▵L_{i_2},\dots ,▵L_{i_D}).\end{array}$$The positions and velocities of the particles are confined within $[X_{min},X_{max}]$ and $[V_{min},V_{max}]$, respectively. Each particle coexists and evolves simultaneously based on knowledge shared with neighbouring particles, and it makes use of its own memory and knowledge gained by the swarm as a whole to find the best solution. The best previously encountered position of the $i$th particle is denoted its individual best position$$L_i^p=(L_{i_1}^p,L_{i_2}^p,\dots ,L_{i_D}^p),$$a value called $p_i^{\mathrm{best}}$. The best value of the all individual $p_i^{\mathrm{best}}$ values is denoted the global best position$$L_i^g=(L_{i_1}^g,L_{i_2}^g,\dots ,L_{i_D}^g)$$and called $g^{\mathrm{best}}$. The PSO process is initialized with a population of random particles, and the algorithm then executes a search for optimal solutions by continuously updating generations. At each generation, the position and velocity of the ith particle are updated by $p_i^{\mathrm{best}}$ and $g^{\mathrm{best}}$ in the swarm. The update equations can be formulated as:14 $$\begin{array}{cc}& ▵L_i^{\mathrm{new}}=w\times ▵L_i^{\mathrm{old}}+c_1\times r_1\times (p_i^{\mathrm{best}}-L_i^{\mathrm{old}})+c_2\times r_2\times (g_i^{\mathrm{best}}-L_i^{\mathrm{old}}),\hfill \end{array}$$14 15 $$\begin{array}{cc}& L_i^{\mathrm{new}}=L_i^{\mathrm{old}}+▵L_i^{\mathrm{new}},\hfill \end{array}$$15 where $r_1$ and $r_2$ are random numbers between $[0,1]$, and $c_1$ and $c_2$ are acceleration constants, which control how far a particle will move in a single generation. Velocities $▵L_i^{\mathrm{new}}$ and $▵L_i^{\mathrm{old}}$ denote the velocities of the new and old particle, respectively. $L_i^{\mathrm{old}}$ is the current particle position, and $L_i^{\mathrm{new}}$ is the new, updated particle position. The inertia weight w controls the impact of the previous velocity of a particle on its current one.

The typical pseudo-code of the PSO process is shown below.

The algorithm only requires fitness function for each of the particle, without assumption such as continuity and differentiability, which makes it very useful for a discontinuous function.

4 Numerical examples and discussion

We select three representative fabrics: wool, polyester and polypropylene fibre for the proposed optimization problem (1313 $$\begin{array}{c}\hfill \text{minimize}L+\text{K}\times [M-P(L)],\end{array}$$13 ). In the model, the parameters $\mathit{\epsilon },r,\mathit{\tau }$ and $\mathit{\kappa }$ for these three kinds of fabrics are listed in Table 1. The parameters used in the study are taken as$$\begin{array}{c}\hfill k_1=0.00006,k_2=0.00007\text{and}\mathit{\lambda }=2260\text{kJ/kg}.\end{array}$$The boundary conditions next to skin are$$\begin{array}{c}\hfill m_{v,0}=3.3084\times {10}^{-5}\text{kg}/({\text{m}}^2·\text{s})\text{and}{T}_0=305.16\text{K}.\end{array}$$The numbers of grid points $N_1,N_2$ are all taken as 30.

The parameters in PSO are set as $N=20,c_1=c_2=1.4962,w=0.7298,$ and the penalty parameter $K={10}^{12}.$

Table 1. Physical properties of fabrics used in the simulation.

Material	Wool	Polyester	Polypropylene fibre
r	$1\times {10}^{-5}$	$1\times {10}^{-5}$	$1\times {10}^{-5}$
$\mathit{\epsilon }$	0.915	0.88	0.87
$\mathit{\tau }$	1.2	1.2	1.2
$\mathit{\kappa }$	0.052	0.084	0.071

We chose two different combination of the temperature and humidity in the environment for the numerical calculation.

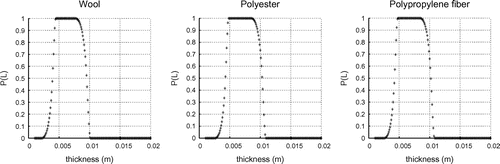
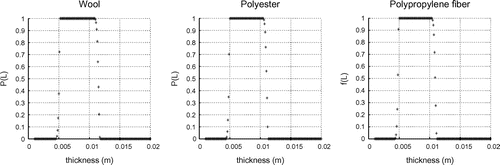
• Case 1   The temperature and humidity in the environment are assumed to $T_L\in [275.15\mathrm{K},285.15\mathrm{K}]$ and $R{H}^L\in [40\%,90\%];$

• Case 2   The temperature and humidity in the environment are assumed to $T_L\in [265.15\mathrm{K},275.15\mathrm{K}]$ and $R{H}^L\in [30\%,85\%].$

In Figures 2 and 3, we plot the objective function $P(L)$ with exact measurements for wool, polyester and polypropylene fibre in Cases 1 and 2, respectively.

Figure 2. The graph of function $P(L)$ for three kinds of fabrics in Case 1 with exact measurements.

Figure 3. The graph of function $P(L)$ for three kinds of fabrics in Case 2 with exact measurements.

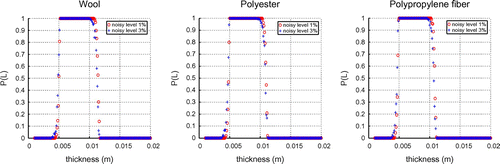
It can be seen from Figures 2 and 3 that thickness of textile fabric have significant implication for heat-moisture comfort, as it means, too thin or too thick of a textile fabric will make human feeling uncomfortable.

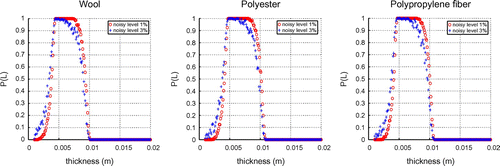
In order to compare the results involving random measurement noise, we add a uniform distribution uncorrelated errors. The simulated inexact measurement data ${\overline{T}}_i^L,{\overline{RH}}_j^L$ can be expressed as$$\begin{array}{c}\hfill {\overline{T}}_i^L=T_i^L[1+\mathit{\delta }·\text{rand(i)}],{\overline{RH}}_j^L=R{H}_j^L[1+\mathit{\delta }·\text{rand(j)}],i=1,2,\dots ,N_1,j=1,2,\dots ,N_2.\end{array}$$ where $T_i^L,R{H}_j^L$ are the exact data, and $\mathit{\delta }$ is the noise level. In Figures 4 and 5, we plot the objective function L with the noisy measurements $\mathit{\delta }=1\%$ and $\mathit{\delta }=3\%$ for wool, polyester and polypropylene fibre in Cases 1 and 2, respectively.

Figure 4. The graph of function $P(L)$ for three kinds of fabrics in Case 1 with noisy measurements.

Figure 5. The graph of function $P(L)$ for three kinds of fabrics in Case 2 with noisy measurements.

Table 2. Estimated results with different $\mathit{\delta }$ for three kinds of fabrics in Case 1.

Material	Wool		Polyester		Polypropylene fibre
	$L^{\ast }$ (m)	$P(L^{\ast })$	$L^{\ast }$ (m)	$P(L^{\ast })$	$L^{\ast }$ (m)	$P(L^{\ast })$
$\mathit{\delta }=0$	0.0044289	1	0.0047775	1	0.0047232	1
$\mathit{\delta }=1\%$	0.0044037	1	0.0047341	1	0.0047112	1
$\mathit{\delta }=3\%$	0.0043679	0.9968783	0.0047104	0.9979188	0.0046479	1

Table 3. Estimated results with different $\mathit{\delta }$ for three kinds of fabrics in Case 2.

Material	Wool		Polyester		Polypropylene fibre
	$L^{\ast }$ (m)	$P(L^{\ast })$	$L^{\ast }$ (m)	$P(L^{\ast })$	$L^{\ast }$ (m)	$P(L^{\ast })$
$\mathit{\delta }=0$	0.0051998	1	0.0050009	1	0.0049441	1
$\mathit{\delta }=1\%$	0.0051819	1	0.0049978	1	0.0049283	1
$\mathit{\delta }=3\%$	0.0051937	1	0.0050000	1	0.0049254	1

Except for the number of particles, the computational time involved in the PSO method mainly depends on the structure of proposed optimization function. To obtain a global minima for the optimization problem (1313 $$\begin{array}{c}\hfill \text{minimize}L+\text{K}\times [M-P(L)],\end{array}$$13 ), in each run of the PSO searching, one needs to solve $30\times 30$ direct problems, each direct problem is composed by the nonlinear integral-differential Equation (55 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\sqrt{T}\frac{d^{2}T}{d{x}^2}=\frac{k_2}{k_3}A(x)[p_{\mathrm{sat}}(T(x))-\sqrt{p_v^2(L)+2{\int }_x^L\frac{T^{3/2}(s)}{k_{1}A(s)}[k_3{T}^{\prime }(s)+C_1]ds}],\hfill \\ T(0)=T_0,T(L)=T_L,\hfill \end{array}\right.\end{array}$$5 ) with different boundary conditions. Thus, the computational time normally needs about 1 h in our PC computer. Tables 2 and 3 show the estimated results with different noise levels $\mathit{\delta }$ for three kinds of fabrics by the PSO algorithm in Cases 1 and 2, respectively. It is noted that the thickness of textile fabric changes with the environment conditions.

5 Conclusions

We present a new inverse problem that can determine the unknown thickness based on a minimum norm with the maximum probability constraint optimization problem. Comparing with the existing inverse problem to determine textile fabrics thickness, the new constrained optimization model is more reasonable and practical, which provides an effective way to study the inverse problems of heat and moisture transport in porous textile materials.

We adopt PSO algorithm to solve the proposed optimization problem. The advantages of this stochastic search method is that it does not require the gradient computation and the choice of initial guess. The numerical results is in relatively good agreement with the values as shown in Figures 2–5. We can verify that the results in Tables 2 and 3 are the minimum norm solutions with maximum probability by direct computation. Therefore, one can conclude that the PSO is stable to deal with this inverse problem even with small noisy measurements and the proposed new optimization is theoretically well-founded.

Further works in the future are still needed. One is to establish the stability result on the solution to the strong nonlinearity boundary value problem (22 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{k}_1\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}·\frac{p_v(x)}{T^{3/2}(x)}·\frac{d{p}_v(x)}{dx}+m_v(x)=0,\hfill \\ \frac{d{m}_v(x)}{dx}+\mathrm{\Gamma }(x)=0,\hfill \\ \mathit{\kappa }(x)\frac{d^{2}T(x)}{d{x}^2}+\mathit{\lambda }\mathrm{\Gamma }(x)=0,\hfill \\ \mathrm{\Gamma }(x)=-k_2\frac{\mathit{\epsilon }(x)r(x)}{\mathit{\tau }(x)}(p_{\mathrm{sat}}(T(x))-p_v(x))\frac{1}{\sqrt{T(x)}},\hfill \end{array}\right.0<x<L,\end{array}$$2 ) and (33 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{T(x)|}_{x=0}=T_0,\hfill \\ {T(x)|}_{x=L}=T_L,\hfill \\ m_v{(x)|}_{x=0}=m_{v,0},\hfill \\ p_v{(x)|}_{x=L}=p_{v,L},\hfill \end{array}\right.\end{array}$$3 ), and the other is to adopt our maximum probability constraint technique to other inverse heat and moisture transfer problems, especially for the inverse problem considering fabric composed of multiple layers.

Acknowledgements

The authors kindly acknowledge the help of the anonymous referees in improving the readability of the paper.

Additional information

Funding

The research is supported by the grant from National Natural Science Foundation of China No. 11071221, the grant from Natural Science Foundation of Zhejiang Province No. LQ12A01024, LY14A010033 and the grant from Zhejiang Top Priority Discipline of Textile Science and Engineering & Engineering Research Center of Clothing Technology of Zhejiang Province No 2013KF10.