Inversion of top of atmospheric reflectance values by conic multivariate adaptive regression splines

Abstract

Spatial technologies offer high flexibility to handle substantial amount of spatial data and wide range of modelling capabilities. Remotely sensed data are the most significant data source used in spatial technologies. However, it is often associated with uncertainties due to atmospheric effects (i.e. absorption and scattering by atmospheric gases and aerosols). Methods based on rigorous treatment of radiative transfer models still have some drawbacks in the inversion of top of atmospheric reflectance values to surface reflectance values on large numbers of satellite images. In this paper, our aim is to represent a more flexible (adaptive) approach for the regional atmospheric correction by employing nonparametric regression splines within the frame of inverse problems and modern techniques of continuous optimization. To achieve this objective, atmospheric correction models obtained through conic multivariate adaptive regression splines, which is an alternative method to multivariate adaptive regression splines by constructing a penalized residual sum of squares as a Tikhonov regularization problem, are applied on a set of satellite images in order to convert the top of atmospheric reflectance values into surface reflectance values. The results are compared with the ones obtained by both multivariate adaptive regression splines and a radiative transfer-based method.

Keywords:

• MARS
• CMARS
• conic quadratic programming
• remote sensing
• atmospheric correction
• radiative transfer

1. Introduction

1.1. Significance of atmospheric correction in remote sensing

Since the day it emerged (namely, in the 1960s), Geographical Information Systems (GIS), together with the parallel developments in Remote Sensing (RS) technologies, have been offering unique capabilities for editing, managing, analysing and automating different kinds of spatial data that provides valuable information required for decision-making.[1]

These technologies have been extensively employed in diverse areas of science and engineering studies such as global warming,[2] sustainable management of natural resources,[3] emergency response systems for natural events,[4] and weather and climate modelling,[5] financial and environmental analysis of investments in energy markets,[6] real estate business,[7] urban development planning,[8] agriculture,[9] farming industry and rural area management,[10,11] and oil and mining industry.[12,13]

Remotely sensed image data have been used as a primary information source in spatial technologies. However, a fundamental problem in RS is the perturbations on surface reflectance data due to absorption and scattering by atmospheric gases and molecules.[14] So, in order to guarantee correct analysis and interpretation of remotely sensed images, the reflectance values of the image pixels must accurately represent the ground surface reflectance values. Failure to correct for the atmospheric effects can inevitably lead to different surface reflectance values, and will definitely have a significant effect on any conclusions drawn from such data. This issue is particularly important in the evaluation of long time series, over which the atmospheric parameters do not remain constant.[15]

1.2. A brief remark on radiative transfer models

Numerous methods and algorithms based on Radiative Transfer (RT) models have been proposed by various authors in order to remove atmospheric effects from images taken by sensors with different technical specs and operational objectives.[16–18]

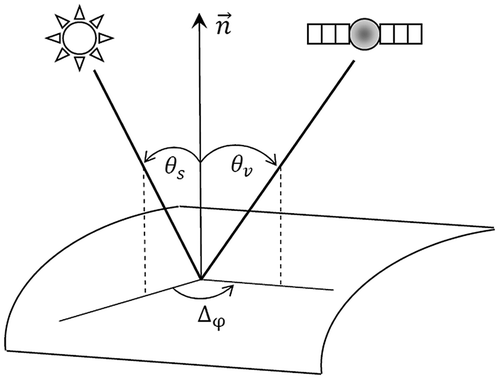
Generally speaking, the goal of RT-based correction schemes is to remove the influence of the atmosphere by modifying Top Of Atmospheric (TOA) reflectance measurement recorded by a sensor. Aerosol and water vapour content (uWV) of the atmosphere have a substantial effect on atmospheric absorption and scattering. Besides, the View Zenith Angle (VZA) and Solar Zenith Angle (SZA) also play a crucial role in determining the effects of the atmosphere (Figure 1). When the zenith angle is far from nadir, then the ray path travelled by the photon through the atmosphere gets larger, which increases the probability of an absorption or scattering event in turn.[15,19]

Figure 1. Geometry of the problem (θ_s: SZA, θ_v: VZA, Δ_φ: Relative azimuth).

Even though no atmospheric correction scheme can completely nullify the effects of the atmosphere, the RT in clear atmosphere is now well understood and a significant amount of work has been done in improving the accuracy and quality of correction algorithms.[20]

However, we should emphasize that the high accuracy available with detailed RT models may not actually be reached when working over large areas, due to unknown atmospheric parameters. For large areas and long time periods, these models still need faster methods in order to derive surface reflectances and to retrieve atmospheric parameters.

Additionally, in images, acquired by instruments with high temporal resolution and large field of view, each pixel has a different observational geometry and each atmospheric parameter has to be calculated for each pixel. Hence, it is highly costly and time consuming to employ models based on a rigorous treatment of the RT problem, like Second Simulation of a Satellite Signal in the Solar Spectrum (6S),[21] for the atmospheric correction of bulk numbers of such satellite images in real time.

The Simplified Model for Atmospheric Correction (SMAC) was first introduced nearly two decades ago as an alternative approach to tackle these problems. It is based on the parameterization of detailed RT models.[22] Despite its age and lower level of accuracy as compared to 6S, it is still a preferred atmospheric correction tool for many research groups due to its high speed.[15]

1.3. Nonparametric regression splines with continuous optimization and conic quadratic programming

In our paper, we, for the first time ever, adjust, refine and employ the new regression and classification tool of data mining, Conic Multivariate Adaptive Regression Splines (CMARS),[23] on a subject of RS. Developed as an alternative approach to Multivariate Adaptive Regression Splines (MARS),[24] CMARS converts the second stage of the MARS algorithm (i.e. the backward step) into a Tikhonov Regularization (TR) problem based on Penalized Residual Sum of Squares (PRSS) approach and solves the problem through Conic Quadratic Programming (CQP).

In each dimension of the input variables in CMARS algorithm, a piecewise linear ‘zig-zag’ function is built up, where the linear parts represent and approximate the data over whole intervals. The aim in the regularization of the CMARS approach by addressing first- and second-order derivatives is to obtain ‘easy’ models. This regularization is turned into the language of a CQP model by penalization.

The components of the unknown parameters’ vector are forced to be 0 or, as much as possible, be nearby to vanish, which also implies that the smallest possible number of ‘significant’ coefficients is aimed in CMARS. MARS follows this goal through an ‘index’ called Generalized Cross-Validation (GCV); however, in CMARS, integrated framework of conic and global optimization is employed to reach this goal.

A second class of parameters is the penalty parameters or, equivalently, upper bounds of the complexity. These parameters are already reduced by just single values, per class of variables, and no longer individually per basis functions (BFs), and this means a strong reduction of the entire numbers of parameters, too. Actually, this work on the number of parameters can also be considered as a model selection.[25]

1.3.1. Advantage of using splines

The use of spline functions offer great advantages, in general, and in the context of our modelling in RS, as will be explained now compactly [25]:

• Splines, from the perspective of just one dimension (input variable), are ‘piecewise polynomials’. If only polynomials are used, then they would usually converge to plus or minus infinity when the absolute values of the (input) variables grow large. Since real-life processes stay in bounded margins (even if these bounds may be very large) generally, polynomials would need to have a high degree to oscillate sufficiently in order to remain within some reasonable margin. However, with high-degree polynomials it is hard and costly to work, in particular, as the real-life challenges are multivariate, which may need multiplications and, hence, a rapid increase in degree of the occurring multivariate splines. Using splines however permits us, in every dimension, to keep the degree of the polynomial ‘pieces’ very low. Splines are indeed quite ‘flexible’ and sufficiently ‘elastic’ in order to approximate complex and high-dimensional data structures. So, they are often called ‘smoothing splines’, since they ‘smoothly’ approximate discrete data.

• The splines of CMARS are more ‘smooth’ even in the sense that their oscillation is kept under control via a penalization of their integrals of squared first- and, especially, second-order derivatives, i.e. their complexity. Then the integrals are discretized, and a programme of TR is obtained and represented in the form of CQP.

• The multivariate splines of CMARS are multiplication products of ‘zig-zagging’, piecewise linear functions of degree 1 (or 0), and it can be carefully determined how many dimensions to include into the process of multiplications of those one-dimensional splines in order to prevent the complexity of our model from becoming too high. Let us recall that reducing the complexity can also be expressed as an increase in stability.

• Those multiplications are an expression of the fact that there are input variables, which are dependent and, together in groups, contributing to an explanation of response variable by those explanatory input variables.

• Finally, differently from the use of ‘stiff’ model formulas, which are motivated by the tradition in science, and in our paper recalled by the formulas (1)–(4), our approach by CMARS is very adaptive and is getting into the data-set with its particular subsets and characteristics of shape.

1.4. Our motive and objective

With this paper, we recommend our adaptive tool for regression and classification, CMARS, to be used in the area of RS, especially, as an alternative to traditional formula-based approaches who have their scientific origins in the natural sciences, especially, in physics. However, we very much respect and appreciate those formulas as they represent important relations between essential, natural dimensions, though on a certain level of abstraction and, sometimes, simplification. Our CMARS approach of learning and modelling is based on both the empirical data and the mathematics of applied probability and, especially, optimization theory, whereby accuracy becomes compromised with complexity. But we herewith do also deliver formulas again, as in the traditional approaches; the formulas now are our CMARS models.

In order to accomplish our goals in this study, CMARS is applied to build a model for the atmospheric correction of a MODerate-resolution Imaging Spectroradiometer (MODIS) image data-set. We also employ MARS for the same purpose, since it has many successful applications in economy, technology and many other branches of science where complex relationships among variables are modelled.[26–28] The atmospheric correction models obtained through CMARS and MARS algorithms are applied on 24 MODIS images, half of which was taken over the Alps region and the other half was taken over Turkey. Atmospherically corrected surface reflectance values for the same areas are also obtained by SMAC algorithm. Then, the results are compared against the surface reflectance values of MODIS Level 2G products,[29] which are already corrected for the atmospheric effects via 6S, and the results are given in terms of both Root-Mean-Square Error (RMSE) and correlation coefficient (r) values.

2. 6S and SMAC methods

Atmospheric correction algorithms have evolved a lot during the last three decades, starting from the empirical line method to the recent RT-based algorithms; however, we do not intend to cover all these methods in a comprehensive manner. Instead, 6S and SMAC methods are briefly introduced based on [22,30,31].

2.1. 6S

The 6S is a computer code that can accurately simulate the surface reflectance values measured by satellite or airborne platforms of land or sea surfaces in the visible and near infrared, which is strongly affected by the presence of the atmosphere along the sun-ground target-sensor path, and its first version was introduced in the late 1990s. As an RT-based correction algorithm, the latest vector version of 6S code (6SV) is the basic code employed for the atmospheric correction of MODIS Level 1B land surface reflectance products,[32] and it has been extensively tested.

The algorithm requires seven input variables: TOA reflectance (i.e. apparent reflectance value of the ground target recorded by the sensor at the top of atmosphere, which is attenuated by the atmospheric effects), SZA, VZA and relative azimuth between the sun and the satellite direction (Δ_φ) (as shown in Figure 1), Atmospheric Optical Depth (AOD), uWV and Ozone (uO₃) content. Here, AOD accounts for the degree to which aerosols prevent the transmission of solar radiation by absorption or scattering of light along the sun-ground target-sensor path, whereas uWV and uO₃ consider the effect of atmospheric gaseous absorption.

The atmospherically corrected surface reflectance value of a target pixel, ${\mathit{\rho }}_s$, is then given by(1) $${\mathit{\rho }}_s\left({\mathit{\theta }}_s,{\mathit{\theta }}_v,{\mathrm{\Delta }}_{\mathit{\phi }}\right):=\frac{{\mathit{\rho }}_s^{\prime }}{1+S{\mathit{\rho }}_s^{\prime }},$$(1)

with(2) $${\mathit{\rho }}_s^{\prime }:=\frac{\frac{{\mathit{\rho }}_{TOA}\left({\mathit{\theta }}_s,{\mathit{\theta }}_v,{\mathrm{\Delta }}_{\mathit{\phi }}\right)}{T_G}-{\mathit{\rho }}_a\left({\mathit{\theta }}_s,{\mathit{\theta }}_v,{\mathrm{\Delta }}_{\mathit{\phi }}\right)}{T_{{\mathit{\theta }}_s}{T}_{{\mathit{\theta }}_v}}.$$(2)

Here, ${\mathit{\theta }}_s$, ${\mathit{\theta }}_v$ and ${\mathrm{\Delta }}_{\mathit{\phi }}$ are SZA, VZA and relative azimuth between the sun and the satellite, respectively, $S$ is the spherical albedo of the atmosphere (i.e. the ratio of reflected radiation from the surface to incident radiation upon it over all sun angles), and ${\mathit{\rho }}_{TOA}$ denotes the TOA reflectance. $T_G$ denotes the gaseous transmission, $T_{{\mathit{\theta }}_s}$ and $T_{{\mathit{\theta }}_v}$ are the total downward and upward atmospheric transmittances, respectively, and finally, ${\mathit{\rho }}_a$ is the atmospheric reflectance. Values of AOD, uWV and uO₃ are internally used by the algorithm to calculate the parameters related with the atmospheric scattering and gaseous absorption processes as mentioned above.

2.2. Simplified model for atmospheric correction

Real-time atmospheric correction of large data-sets collected by sensors with high-temporal resolution via detailed RT codes, like 6SV, is operationally impractical. So, SMAC was proposed as an alternative method about two decades ago. Even though 6SV and SMAC operate in a similar manner, the former is based on the rigorous treatment of the RT problem. SMAC employs the simplified forms of the formulas used in 6SV to calculate the process variables. This leads to reduced complexity and quick atmospheric correction on a large data-set. However, since SMAC does not include many components that are modelled within 6SV in a more complex manner, the accuracy of the atmospheric correction is degraded, as compared to 6SV.

Apart from a series of predefined coefficients that depends on the RS instrument, SMAC requires the same input variables as in 6S. Then, the corrected surface reflectance is expressed as(3) $${\mathit{\rho }}_s\left({\mathit{\theta }}_s,{\mathit{\theta }}_v,{\mathrm{\Delta }}_{\mathit{\phi }}\right):=\frac{{{\mathit{\rho }}^{\prime }}_s}{T_G{T}_{{\mathit{\theta }}_s}{T}_{{\mathit{\theta }}_v}+S{\mathit{\rho }}^{\prime }},$$(3)

with(4) $${\mathit{\rho }}_s^{\prime }:={\mathit{\rho }}_{TOA}\left({\mathit{\theta }}_s,{\mathit{\theta }}_v,{\mathrm{\Delta }}_{\mathit{\phi }}\right)-T_G{\mathit{\rho }}_a\left({\mathit{\theta }}_s,{\mathit{\theta }}_v,{\mathrm{\Delta }}_{\mathit{\phi }}\right).$$(4)

Despite its age and lower level of accuracy, SMAC approach is still used by many research groups and projects, since it can perform an atmospheric correction in a short time. In addition, when new sensors are introduced, only the band-specific coefficients need to be updated while the routines remain the same. Additionally, SMAC is available as a free and open-source code. This means that it can easily be implemented in an operational data preprocessing computer and can be modified according to user requirements, which is another attractive feature of SMAC algorithm that makes it still popular.

3. Basic overview on MARS and CMARS

In this section, the reader can find the fundamentals of MARS and CMARS based on [23,24,33,34].

3.1. Multivariate adaptive regression splines

Nonparametric regression and classification techniques are mostly the key data mining tools in explaining real-life problems and natural phenomena where many effects often exhibit a nonlinear behaviour. As a form of regression analysis, MARS is a nonparametric regression technique widely used in data mining and estimation theory in order to built flexible regression models for high-dimensional nonlinear data. In MARS model building, piecewise linear BFs are fitted in such a way that additive and interactive effects of the predictors are taken into account to determine the response variable.

MARS uses two stages when building up regression model, namely, the forward and the backward step algorithms. In forward step, BFs are added up until the highest level of complexity is reached. Since the first step creates an over-fit model, preferred and eventual model is obtained by the elimination of BFs in backward step. Selection of BFs is data-based and specific to the problem in MARS, which makes it an adaptive regression procedure suitable for solving high-dimensional problems.

MARS uses expansions of the truncated piecewise linear BFs of the form ${\left(\pm \left(x_j-\mathit{\tau }\right)\right)}_{+}$, where $x_j$ is the jth component of p-dimensional variable x, and $\mathit{\tau }$ is the associated knot location of $x_j$. The ‘ ± ’ symbol indicates that only the positive or the negative parts are used, respectively, and $x$, $\mathit{\tau }\in \mathbb{R}$.

The relation between input and response in general model is expressed as(5) $$Y=f(\mathit{x})+\mathit{\epsilon },$$(5)

where Y is a response variable, $\mathit{x}={\left(x_1,x_2,\dots ,x_p\right)}^T$is a vector of predictors and $\mathit{\epsilon }$ is the error term in the observation with zero mean. MARS builds reflected pairs for each input $x_j\left(j=1,2,\dots ,p\right)$ with p-dimensional knots ${\mathit{\tau }}_i={\left({\mathit{\tau }}_{i,1},{\mathit{\tau }}_{i,2},\dots ,{\mathit{\tau }}_{i,p}\right)}^T$at each input data vectors ${\overline{\mathit{x}}}_i={\left({\overline{x}}_{i,1},{\overline{x}}_{i,2},\dots ,{\overline{x}}_{i,p}\right)}^T$of that input $i=1,2,\dots ,N$. Then, the collection of BFs is:(6) $$C:=\left\{{\left(x_j-\mathit{\tau }\right)}_{+},{\left(\mathit{\tau }-x_j\right)}_{+},\mathit{\tau }\in \left\{x_{1,j},x_{2,j},\dots ,x_{N,j}\right\}\left(j\in \left\{1,2,\dots ,p\right\}\right)\right\},$$(6)

where N is the total number of observations, p is the dimension of the input space. In order to reach spline fitting in higher dimensions, the tensor products of univariate spline functions are employed, leading to multivariate spline BFs in the following form:(7) $$B_m\left({\mathit{x}}^m\right):=\prod _{j=1}^{K_m}{\left[s_{{\mathit{\kappa }}_j^m}.\left(x_{{\mathit{\kappa }}_j^m}-{\mathit{\tau }}_{{\mathit{\kappa }}_j^m}\right)\right]}_{+},$$(7)

where K_m is the interaction degree of the mth BF and x^m denotes the vector of independent variables contributing to the mth BF. Furthermore, $x_{{\mathit{\kappa }}_j^m}$ is the corresponding input variable of the kth truncated linear function in the mth BF, the corresponding knot value for the variable $x_{{\mathit{\kappa }}_j^m}$ is given by ${\mathit{\tau }}_{{\mathit{\kappa }}_j^m}$, and finally $s_{{\mathit{\kappa }}_j^m}\in \left\{\pm 1\right\}$.

The forward and the backward step algorithms of MARS are used for the estimation of model function $f(\mathit{x}).$ In the forward step, the use of functions from the set C and their products are allowed to represent interaction, which generates a maximal model that overfits the data. The initial model is in the following form:(8) $$f(\mathit{x})={\mathit{\beta }}_0+\sum _{m=1}^M{\mathit{\beta }}_m{B}_m\left({\mathit{x}}^m\right),$$(8)

where $B_m$ is either a function or product of two or more functions from the set C. The number of BFs in the current model is indicated by M, and ${\mathit{\beta }}_0$ is the intercept.

In order to compare the possible BFs, a Lack-Of-Fit (LOF) criterion is used. For generating an estimated best model ${\widehat{f}}_{\mathit{\alpha }}$ with the optimal value $\mathit{\alpha }$, where $\mathit{\alpha }$ represents some complexity of the estimation, MARS algorithm first adds BFs and products of the BFs in the forward step. Then, the least significant ones are deleted in the backward step. To find the value for $\mathit{\alpha }$, MARS uses GCV indicating the LOF and it is given as $GCV(\mathit{\alpha }):={\sum }_{i=1}^N{(y_i-{\widehat{f}}_{\mathit{\alpha }}({\mathit{x}}_i))}^2/{(1-Q(\mathit{\alpha })/N)}^2$. Here, N is the number of sample observations, $Q\left(\mathit{\alpha }\right)=u+dK$ with K representing the number of knots which are selected in forward step. The number of linearly independent functions in the model is given by u, and d denotes a cost for each BF optimization. While a larger $Q\left(\mathit{\alpha }\right)$ value creates a smaller model with less number of BFs, a smaller $Q\left(\mathit{\alpha }\right)$ value generates a larger model with more BFs. Using the LOF criterion, the best model is chosen according to backward step that minimizes GCV.

3.2. Conic multivariate adaptive regression splines

CMARS has been developed as an alternative method to MARS by utilizing statistical learning, inverse problems and multiobjective optimization theories. Instead of applying backward step of MARS, PRSS with the BFs is built up during forward step. Then, penalty terms are added to the least squares estimation to control the LOF. This introduces a different approach to the complexity and the stability of the problem.

PRSS summed up during the forward step of MARS has the following form:(9) $$PRSS:=\sum _{i=1}^N{\left(y_i-f\left({\overline{\mathit{x}}}_i\right)\right)}^2+\sum _{m=1}^{M_{max}}{\mathit{\phi }}_m\sum _{\begin{array}{c}\left|\mathit{\delta }\right|=1\\ \mathit{\delta }={\left({\mathit{\delta }}_1,{\mathit{\delta }}_2\right)}^T\end{array}}^2\sum _{\begin{array}{c}r<s\\ r,s\in V_m\end{array}}\underset{Q_m}{\int }{\mathit{\lambda }}_m^2{\left[G_{r,s}^{\mathit{\delta }}{B}_m\left({\mathit{h}}^m\right)\right]}^{2}d{\mathit{h}}^m.$$(9)

Here, $V_m:=\left\{{\mathit{\kappa }}_j^m\left|j=1,2,\dots ,K_m\right.\right\}$ denotes the variable set related with the mth BF, and ${\mathit{h}}_m={\left(h_{m_1},h_{m_2},\dots ,h_{m_{K_m}}\right)}^T$ is the vector of variables contributing to the mth BF. Furthermore, ${\mathit{\phi }}_m⩾0$ are penalty parameters, and Q_m are suitable integration domains $\left(m=1,2,\dots ,M_{\text{max}}\right).$ Finally, $G_{r,s}^{\mathit{\delta }}{B}_m({\mathit{h}}^m):=({\mathit{\partial }}^{\mathit{\delta }}{B}_m/{\mathit{\partial }}^{{\mathit{\delta }}_1}{h}_r^m{\mathit{\partial }}^{{\mathit{\delta }}_2}{h}_s^m)({\mathit{h}}^m)$ for $\mathit{\delta }={\left({\mathit{\delta }}_1,{\mathit{\delta }}_2\right)}^T$, $\left|\mathit{\delta }\right|:={\mathit{\delta }}_1+{\mathit{\delta }}_2$, where ${\mathit{\delta }}_1,{\mathit{\delta }}_2\in \left\{0,1\right\}$.

The trade-off between accuracy and complexity in this optimization problem is established through the penalties ${\mathit{\phi }}_m$, and the PRSS can be approximated as a TR problem by rearranging (9) as:(10) $$PRSS\approx ||\mathit{y}-\mathit{B}(\tilde{\mathit{g}})\mathit{\lambda }{||}_2^2+\sum _{m=1}^{M_{\text{max}}}{\mathit{\phi }}_m\sum _{i=1}^{{(N+1)}^{K_m}}{L}_{im}^2{\mathit{\lambda }}_m^2=||\mathit{y}-\mathit{B}(\tilde{\mathit{g}})\mathit{\lambda }{||}_2^2+{\mathit{\phi }}_1||{\mathit{L}}_1{\mathit{\lambda }}_1{||}_2^2+{\mathit{\phi }}_2||{\mathit{L}}_2{\mathit{\lambda }}_2{||}_2^2+\dots +{\mathit{\phi }}_{M_{max}}||{\mathit{L}}_{M_{max}}{\mathit{\lambda }}_{M_{max}}{||}_2^2,$$(10)

where, $\mathit{y}:={\left(y_1,y_2,\dots ,y_n\right)}^T$is the vector of responses, $\mathit{B}(\tilde{\mathit{g}})={(\mathit{B}({\tilde{\mathit{g}}}_1),\mathit{B}({\tilde{\mathit{g}}}_2),\dots ,\mathit{B}({\tilde{\mathit{g}}}_N))}^T$ is an $\left(N\times \left(M_{max}+1\right)\right)$-matrix, ${\sum }_{i=1}^N{\left(y_i-{\mathit{\lambda }}^T\mathit{B}({\tilde{\mathit{g}}}_i)\right)}^2={\left(\mathit{y}-\mathit{B}({\tilde{\mathit{g}}}_i)\mathit{\lambda }\right)}^T(\mathit{y}-\mathit{B}({\tilde{\mathit{g}}}_i)\mathit{\lambda })={||\mathit{y}-\mathit{B}(\stackrel{\mathbf{~}}{\mathit{g}})\mathit{\lambda }||}_2^2$, and ${\mathit{L}}_m:={\left(L_{1m},L_{2m},\dots ,L_{{(N+1)}^{K_m}m}\right)}^T(m=1,2,\dots ,M_{max})$ with$$L_{im}:={\left[\left(\sum _{\begin{array}{c}\left|\mathit{\delta }\right|=1\hfill \\ \mathit{\delta }={({\mathit{\delta }}_1,{\mathit{\delta }}_2)}^T\hfill \end{array}}^2\sum _{\begin{array}{c}r<s\hfill \\ r,s\in V(m)\hfill \end{array}}{\left[G_{r,s}^{\mathit{\delta }}{B}_m({\widehat{\mathit{x}}}_i^m)\right]}^2\right)\mathrm{\Delta }{\widehat{\mathit{x}}}_i^m\right]}^{1/2}.$$

Although a finite sequence of the trade-off or penalty parameters $\mathit{\phi }={({\mathit{\phi }}_1,{\mathit{\phi }}_2,\dots ,{\mathit{\phi }}_{M_{\text{max}}})}^T$ exists, the expression in (10) is still not a TR problem with a single parameter. Therefore, a uniform penalization by taking the same $\mathit{\phi }$ for each derivative term is applied, and approximation to PRSS may be rewritten as follows:(11) $$PRSS\approx ||\mathit{y}-\mathit{B}\left(\tilde{\mathit{g}}\right)\mathit{\lambda }{||}_2^2+{\mathit{\phi }||\mathit{L}\mathit{\lambda }||}_2^2,$$(11)

where $\mathit{L}$ is a diagonal $\left(\left(M_{\text{max}}+1\right)\times \left(M_{\text{max}}+1\right)\right)$-matrix and $\mathit{\lambda }$ denotes an $\left(\left(M_{max}+1\right)\times 1\right)$-parameter vector estimated through the data points. The PRSS problem turns into a classical TR problem with $\mathit{\phi }>0,\mathit{\phi }={\mathit{\varphi }}^2$ for some $\mathit{\varphi }\in \mathbb{R}$. A brief introductory to TR can be found in Appendix 1.

The TR problem in (11) can be treated by CQP with a convenient choice of bound $\tilde{Z}\in \mathbb{R}$:(12) $$\begin{array}{c}\underset{h,\mathit{\lambda }}{\text{minimize}}h,\hfill \\ \text{subject to}||\mathit{y}-\mathit{B}\left(\tilde{\mathit{g}}\right)\mathit{\lambda }{||}_2\le h,{||\mathit{L}\mathit{\lambda }||}_2\le \sqrt{\tilde{Z}}.\hfill \end{array}$$(12)

At this point, one has to note that a careful learning process must be followed in order to obtain the values of bound $\tilde{Z}$. By applying the modern methods of continuous optimization, the CQP can be written in this basic notation:(13) $$\begin{array}{c}\underset{\mathit{x}}{\text{minimize}}{\mathit{c}}^T\mathit{x},\hfill \\ \text{subject to}||{\mathit{g}}_i-{\mathit{G}}_i\mathit{x}{||}_2\le {\mathit{p}}_i^T\mathit{x}-q_i\left(1,2,\dots ,k\right).\hfill \end{array}$$(13)

The parametrical upper bound $\tilde{Z}$ in the second constraint of the CQP and the penalty parameter $\mathit{\phi }$ in the PRSS are linked, and the value for $\mathit{\phi }$ can be obtained via TR. It should also be emphasized that the high importance of the goal of numerical precision (accuracy) as a core target inside of the trade-off stated above. At this point, it is also of value to mention that the issue of non-differentiability is handled by choosing the knots of the splines in each coordinate nearby to but not identical with the data points; by this way, there is no problem in the evaluation of the splines at the data points. Additionally, during the integration of the squared first- and second-order partial derivatives of the BFs of the model in the ‘complexity part’ of the optimization problem, the ‘set of non-differentiability’ is of measure zero.

4. Methodology

4.1. Data-set and retrieval of necessary parameters

The MODIS instrument capture daily data in 36 spectral bands ranging in wavelength from 0.4 to 14.4 μm at varying spatial resolutions (bands 1 and 2: 250 m, bands 3–7: 500 m, bands 8–36: 1000 m) in order to investigate earth’s global dynamics such as radiation budget, cloud cover and atmosphere. MODIS Level 2G surface reflectance product comprises the atmospherically corrected surface reflectance values for the first seven bands, and the vector version of 6S (6SV) is the basic correction algorithm behind this product. The algorithm takes the TOA reflectance values from MODIS Level 1B product, and makes a series of corrections for the absorption and scattering by atmospheric gases and molecules. It also takes into account the coupling between atmospheric and surface bi-directional reflectance function and adjacency effect.

Another product family of MODIS is the Level 3 daily atmospheric product,[35] from which AOD, uWV and uO₃ can be retrieved in order to be employed as input in SMAC. All these features make MODIS an attractive and convenient platform for this study.

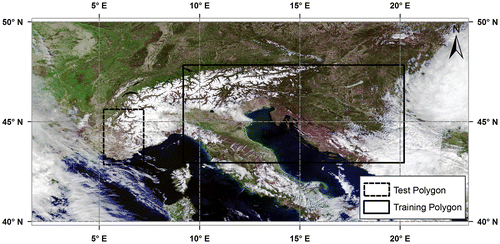
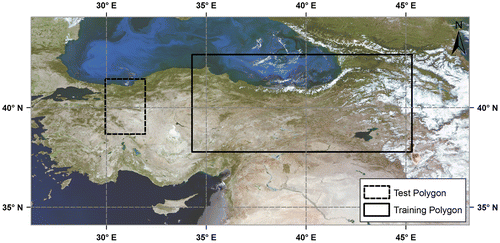
Twenty-four MODIS images taken by Terra satellite are selected as data-set. Half of the images are over Alps region (Figure 2) and the other half is over Turkey (Figure 3). Detailed information about the data-set can be found in Table 1. At this point, we emphasize that all the calculations and operations are performed on the 4th reflective solar band (0.545–0.565 μm).

Figure 2. Alps (A11: 6 November 2002).

Figure 3. Turkey (T7: 16 July 2012).

Table 1. TOA reflectance statistics for training and testing sets of Alps (A) and Turkey (T).

Data set	Date	Training set (area: 483,000 km^2)				Testing set (area: 53,700 km^2)
		Min	Max	Mean	Standard deviation	Min	Max	Mean	Standard deviation
A1	13.01.2006	0.023006	0.515043	0.111236	0.066780	0.021848	0.540773	0.065938	0.062607
A2	03.02.2005	0.021381	0.612208	0.187324	0.084896	0.027219	0.570827	0.052124	0.038957
A3	10.03.2002	0.036336	0.634253	0.123546	0.098884	0.052459	0.591130	0.093768	0.061479
A4	22.04.2005	0.037909	0.815975	0.117174	0.118288	0.045157	0.045157	0.132936	0.154975
A5	03.05.2003	0.043902	0.831254	0.120384	0.080038	0.042749	0.893523	0.157483	0.158453
A6	04.06.2007	0.051815	0.984628	0.409352	0.252784	0.039096	1.039224	0.231790	0.193401
A7	01.07.2007	0.041622	0.617155	0.103806	0.064886	0.051844	1.010623	0.176865	0.142061
A8	06.08.2008	0.052038	1.018599	0.134000	0.123403	0.042518	0.904316	0.135226	0.100786
A9	03.09.2001	0.044417	0.730243	0.122082	0.094248	0.031365	0.680813	0.107640	0.108413
A10	11.10.2001	0.024596	0.706770	0.082712	0.059985	0.020154	0.623411	0.059328	0.039499
A11	06.11.2002	0.023207	0.499682	0.115683	0.112962	0.019956	0.730805	0.087927	0.099035
A12	06.12.2003	0.019304	0.497581	0.112805	0.082715	0.020898	0.559915	0.074968	0.08527
T1	22.01.2007	0.022460	0.438156	0.072725	0.072429	0.018987	0.531954	0.063973	0.061618
T2	08.02.2004	0.030369	0.494759	0.072528	0.057265	0.025595	0.571422	0.076824	0.080169
T3	22.03.2009	0.041930	0.767917	0.174026	0.149042	0.038070	0.834106	0.171948	0.146781
T4	13.04.2008	0.074651	0.735924	0.161762	0.105837	0.046226	0.833497	0.152259	0.119837
T5	16.05.2011	0.046915	0.763972	0.100172	0.076170	0.038706	0.747831	0.107228	0.077950
T6	17.06.2003	0.056582	0.981983	0.147624	0.110149	0.077487	0.923808	0.211551	0.138608
T7	16.07.2012	0.044871	0.627486	0.097143	0.029799	0.055703	0.398507	0.100335	0.030883
T8	01.08.2005	0.036527	0.909753	0.229990	0.175922	0.036824	0.891506	0.135249	0.094953
T9	26.09.2009	0.040853	0.783761	0.104974	0.093539	0.033658	0.743776	0.098932	0.056643
T10	18.10.2002	0.035435	0.173049	0.068862	0.021872	0.032394	0.123435	0.061462	0.015683
T11	02.11.2010	0.033515	0.279079	0.057913	0.017563	0.024014	0.507661	0.056879	0.033940
T12	18.12.2006	0.024390	0.443912	0.060216	0.038547	0.025587	0.446532	0.073266	0.034281

TOA reflectance values are retrieved from MODIS Level 1B product, which comprises the 3rd, 4th, 5th, 6th and 7th reflective solar bands at 500 m spatial resolution. Atmospheric parameters required to perform atmospheric correction through SMAC algorithm (i.e. AOD, uWV and uO3) are obtained from MODIS Level 3 daily atmospheric product.

The results obtained by MARS, CMARS and SMAC methods are tested against MODIS Level 2G product. The atmospheric correction algorithm used in this product is based on 6SV method. 6SV has been seriously cross-checked with other complex correction algorithms and has given highly accurate results under various conditions; therefore, it is preferred as a reference in the comparison of the results.

For data processing and modelling, a computer with an Intel Core i5 M430 2.27 GHz processor and 8 GB DDR3 1333 MHz RAM is used.

4.2. MARS & CMARS model training

In the model training phase, for each region (i.e. Alps and Turkey), a training polygon with fixed dimension (i.e. rectangular in shape with an area of 483,000 km²), which includes all basic land-cover types, is drawn on each image. In each training polygon, 5000 points are randomly generated, and for each point, TOA reflectance value and atmospherically corrected surface reflectance value are extracted from MODIS Level 1B and MODIS Level 2G products, respectively, together with the corresponding geographic longitude and latitude. As seen in Table 1, each month appears once in the data-set. So, month value of the image, from which the corresponding model training parameters are retrieved, is also written in that point data file. In the next step, the training data from each of the training polygons are combined in a single text file, which results in 60,000 data points on aggregate for each region.

In MARS model building, $\mathit{x}={\left(\mathit{\eta },\mathit{\varphi },\mathit{\rho },\mathit{\zeta }\right)}^T$is the vector of predictor variables, where $\mathit{\eta }$ and $\mathit{\varphi }$ represent the geographic latitude and longitude, respectively, $\mathit{\rho }$ is the TOA reflectance value, and $\mathit{\zeta }$ is the month indicator ($\mathit{\zeta }=1,2,\dots ,12$). The observation equation for MARS is given by $y_i=\text{SRef}\left({\mathit{x}}_i\right)+{\mathit{\epsilon }}_i(i=1,2,\dots ,N)$, where $y_i$ is the atmospherically corrected surface reflectance (i.e. response) obtained from MODIS Level 2G product at ${\mathit{x}}_i={\left({\mathit{\eta }}_i,{\mathit{\varphi }}_i,{\mathit{\rho }}_i,{\mathit{\zeta }}_i\right)}^T$ with a measurement error ${\mathit{\epsilon }}_i$. $\text{SRef}$ is the function that gives the surface reflectance predicted by MARS, and $N$ is the total number of observations.

Since MARS algorithm allows users to define model-building dimensions such as maximal number of terms, the degree of interaction among predictor variables, different settings are applied, and the model that gives the minimum GCV value and the maximum adjusted R² [36] value are chosen. All settings in the model training are given in Table 2. Salford Systems MARS^® Version 3 [37] is used for MARS model building.

Table 2. Settings for MARS model training.

	Alps	Turkey
Number of basis functions	40	40
Degree of interaction	3	2
GCV	0.00575	0.00274
R^2	0.9175	0.8938
Adjusted R^2	0.9174	0.8937

In CMARS, BFs, which are considered for the formulation of PRSS in the form of a CQP problem, are created by using MARS^®. Next, CMARS model is obtained by running a MATLAB code. Then, the CQP problem is solved by using MOSEK^TM software.[38]

5. Results

After constructing MARS and CMARS models for each region through the training phase, the obtained models are tested on each image in the data-set. For testing, both models are applied on a predefined area with a size of 53,700 km² on each image. In addition to MARS and CMARS models, SMAC algorithm is also employed (Figure 4). Then, the surface reflectance values produced by MARS, CMARS and SMAC algorithms for each test area are compared with the ones given by MODIS Level 2G product in terms of RMSE and r (Table 3). Details about the processing times can be found in Table 4.

Figure 4. Test area images for A11 (6 November 2002): (a) CMARS, (b) MARS, (c) SMAC and (d) MODIS Level 2G.

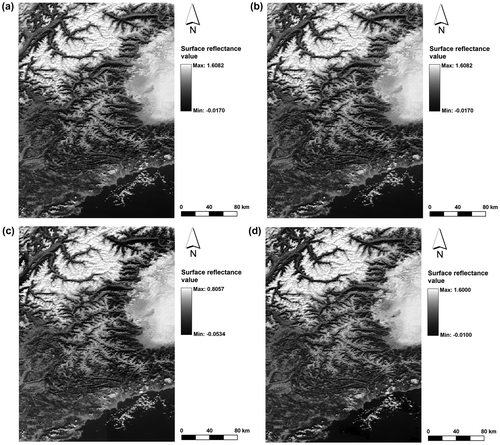
Table 3. Comparison of results for Alps (A) and Turkey (T).

Data set	RMSE			r
	SMAC	MARS	CMARS	SMAC	MARS	CMARS
A1	0.1868	0.0999	0.0998	0.7092	0.9341	0.9342
A2	0.1182	0.0495	0.0494	0.8230	0.8715	0.8717
A3	0.1183	0.0411	0.0411	0.9179	0.9511	0.9511
A4	0.1087	0.0959	0.0958	0.7914	0.8192	0.8194
A5	0.0848	0.0774	0.0774	0.9232	0.9414	0.9414
A6	0.0801	0.0793	0.0793	0.9337	0.9531	0.9532
A7	0.0887	0.0827	0.0827	0.9159	0.9324	0.9325
A8	0.0699	0.0649	0.0649	0.9062	0.9114	0.9114
A9	0.0691	0.0613	0.0613	0.8550	0.8789	0.8789
A10	0.0715	0.0421	0.0421	0.6870	0.7240	0.7240
A11	0.1942	0.1037	0.1037	0.6599	0.7258	0.7259
A12	0.2755	0.1360	0.1360	0.8162	0.8522	0.8523
T1	0.1232	0.0701	0.0701	0.7633	0.7837	0.7839
T2	0.1237	0.0622	0.0620	0.8144	0.8710	0.8712
T3	0.0941	0.0649	0.0639	0.8769	0.8911	0.8917
T4	0.0705	0.0583	0.0583	0.9310	0.9520	0.9521
T5	0.0578	0.0570	0.0567	0.8164	0.8270	0.8274
T6	0.0670	0.0660	0.0651	0.9251	0.9531	0.9582
T7	0.0233	0.0121	0.0113	0.9410	0.9735	0.9744
T8	0.0724	0.0706	0.0702	0.6838	0.6903	0.6954
T9	0.0726	0.0536	0.0533	0.8606	0.8703	0.8732
T10	0.0558	0.0162	0.0155	0.7920	0.8656	0.8667
T11	0.0779	0.0338	0.0320	0.7355	0.8846	0.8884
T12	0.1520	0.0316	0.0308	0.8893	0.9806	0.9823

Table 4. Processing times (in seconds) of SMAC, MARS and CMARS for Alps (A) and Turkey (T).

Data set	SMAC		MARS		CMARS
	Training	Testing	Training	Testing	Training	Testing
A1		24		32		233
A2		27		34		241
A3		23		32		239
A4		25		33		243
A5		24		35		241
A6	N/A	26	57	37	1148	237
A7		28		32		246
A8		24		38		244
A9		24		33		238
A10		25		35		240
A11		23		33		242
A12		24		36		239
T1		25		33		243
T2		23		36		229
T3		27		36		233
T4		24		35		231
T5		25		32		239
T6	N/A	24	59	37	1183	242
T7		24		34		238
T8		26		34		234
T9		23		31		241
T10		24		34		232
T11		25		33		238
T12		26		35		240

It is evident that CMARS (and MARS) outperforms the traditional RT-based approach SMAC according to the results given in terms of both RMSE and r (Table 3). The processing time for the CMARS in the training phase is evidently much longer than the MARS (Table 4); however, it must be noted that MARS has already been in the statistical learning and data mining community for more than two decades, and it is available as a standalone and sophisticated software package, whereas different software packages (i.e. MARS^®, MATLAB^® and MOSEK^TM) have to be used for the time being in order to obtain the CMARS model, which naturally increases the processing time.

The average processing time of MARS (34 s) in the testing phase is almost comparable with that of SMAC (25 s). Although the average testing time for CMARS (238 s) is longer than the other two models, it still seems acceptable and competitive for this kind of huge and complex real-life data. As new refinements are made on CMARS, improvement on the processing time will be achieved.

Here, we would also like to emphasize our respect and appreciation to MARS, and we regard CMARS as an additional offer to be considered in different applied contexts, but not as a total replacement of MARS. However, we should further mention that CMARS proposes a ‘model-based’ approach on controlling the complexity, in the form of TR which is very well established in engineering and realized by us in the form of CQP together with its efficient Interior Point Methods, and by this a remarkable support is gained from the more model-based methods of calculus and of modern mathematics in general, in particular, through state-of-the-art continuous optimization theory. Moreover, via the trade-off between precision and complexity, CMARS lets us open our investigations to real-world challenges which include noise in the response (output) variable, namely, to the Theory of Inverse Problems, to Data Mining and to Statistical Learning.

Since we are interested in the multi-criteria antagonism (trade-off) between accuracy and stability (stability may be called as small complexity), this trade-off, keeping the complexity under ‘control’, is realized by us through CMARS in different ways: (i) restraining the discretized integral of first- and second-order derivatives of the BFs within some margin or ‘tolerance’ (under a chosen and prescribed upper bound), and (ii) using modern optimization theory (model-based approach) for a more integrated approach of both the forward and the backward step, which we have in MARS. By this, we are closer also to exploiting the ‘power’ of differential and integral calculus and to future developments in this calculus and in optimization theory. In future, we can also do modifications and elaborations by new and forthcoming principles and techniques of discretization.[25]

Moreover, with CMARS we are now ‘hosted’ in optimization theory and its scientific community; furthermore, we even have a promise of future benefiting from Robust Optimization, which we can apply through the robust counterpart of CMARS, Robust CMARS (RCMARS).[39] It will additionally permit to imply into our modelling the uncertainty in the input variables, which is typical for real-life problems also.

When we insert CMARS or RCMARS into Generalized Partial Linear Models (GPLM), which means linear models from linear regression or logistic regression are combined with a nonlinear model (i.e. (C)MARS), we obtain CGPLM and RCGPLM.[40] All these generalizations of CMARS have been applied to data-sets from various applied fields and led to very good results as compared with MARS, and we intend to apply them at our subject from RS.

Another specific feature of CMARS when viewed within the RS perspective regarding our particular problem, CMARS stays ‘longer’ model-based than MARS since it offers a more direct and intriguing comparison with the traditional ‘formulas’ of RS, which are originated from physics and other natural sciences, where functional relationships between variables are assumed. CMARS permits this by its interactive and adaptive ‘functional model’, which is supported by optimization and applied mathematics and can learn under different forms of uncertainty.

6. Conclusions and outlook

In this paper, we try to shed light onto the areas of data mining and optimization within a real-life perspective by taking the unique advantages of spline functions. Natural phenomena and real-life problems often exhibit a nonparametric and multivariate behaviour, in which the curse of dimensionality may easily prevail. This means, controlled successive multiplications may sometimes be inevitable and useful to represent the multi-dimensional interaction of the model.

High dimensional and complex data-sets can be wisely handled with the inherent smoothing characteristic of splines. As illustrated in our case, splines applied in CMARS are even made smoother through TR and CQP, and enable us to adaptively penetrate into our complex and large data-set.

For this particular problem, it has been shown that our CMARS has absolutely equal effectiveness as MARS as seen from RMSE and r values given in Table 3; on the other hand, MARS still performs well and gives satisfactory results on the data-set. This has already been expected because that is what MARS was designed for: to overcome large and complex data. Although MARS seems to perform much better than CMARS in terms of processing time, it should be noted that three software packages have to be used successively for CMARS modelling, but even so, the processing times for CMARS are still in acceptable margin for this kind of RS data.

As our study showed us, CMARS (and MARS) can be employed as an alternative tool for atmospheric correction, and can also be used for other problems associated with earth sciences. By integrating the dynamical progress of scientific advances in modern continuous optimization with the spatial technologies, we can enhance our understanding of the value of spatial data and its inherent structure to reach better modelling capabilities in GIS and RS.

Our further studies in the area of RS will definitely concentrate on the new applications of CMARS, and RCMARS, which will be considered as another new and powerful data mining tool in order to cope with the uncertainties in our huge data-set by applying the principles of robust optimization.

Appendix 1. Tikhonov regularization

TR is the most common and well-known form to make ill-posed problems regular and stable.[41] Tikhonov solution can be expressed easily in terms of the Singular Value Decomposition (SVD) of the coefficient matrix A of regarded linear systems of equations $\mathit{A}\mathit{x}-\mathit{b},$ where A is an ill-conditioned $(N\times m)$-matrix. The standard approach to approximately solve this system of equations is known as Least Square Estimation. It seeks to minimize the residual ${||\mathit{A}\mathit{x}-\mathit{b}||}_2^2$. To solve different kinds of TR problem, we use SVD to have a solution that minimizes the objective function including ${||\mathit{x}||}_2$. However, in many cases, it is preferred to achieve a solution that minimizes some other measure of x, such as the norm of first- or second-order derivatives. They are, in approximate sense, given by first- or second-order difference quotients of x, considered as a function that is evaluated at the points k and k + 1. These difference quotients approximate those derivatives; altogether, they are comprised by products Lx of x with matrices L. These matrices represent the discrete differential operators of first- and second-order, respectively. Hereby, the optimization problem is in the following form:(14) $$\underset{\mathit{x}}{\text{minimize}}{||\mathit{A}\mathit{x}-\mathit{b}||}_2^2+{\mathit{\lambda }}^2{||\mathit{L}\mathit{x}||}_2^2.$$(14)

Generally, Equation (14) consists of high-order TR problems, and generalized SVD is used to solve them. In many situations, to obtain a solution which minimizes some other measure x, the norm of the first- or second-derivative is preferred.