A Newton-type method for solving an inverse Sturm-Liouville problem

Abstract

A Newton-type method is proposed for the recovery of the unknown coefficient function in the canonical Sturm-Liouville differential equation from two spectral data. Specifically, the two spectral data will be used to produce two Cauchy data, which in turn will serve as the input in a non-linear equation whose unknown is the coefficient function in the canonical Sturm-Liouville differential equation. This non-linear equation is to be solved numerically by the Newton method. Each Newton iterate requires that a Goursat-Cauchy boundary value problem be solved numerically. The Fréchet differentiability of the non-linear map is also discussed in the present paper. The numerical implementation of the Newton method for this inverse Sturm-Liouville problem is illustrated with examples, and it will be compared with a quasi-Newton method, and with a variational method discussed in previous literature. The numerical examples show that the Newton method needs fewer iterates to recover the true coefficient function than the quasi-Newton method. The Newton method is comparable with the variational method in terms of accuracy and number of iterates when the boundary parameters are given, and it requires a much smaller number of iterates than the variational method, when the boundary parameters are reconstructed from the available spectra.

Keywords:

• second order hyperbolic partial differential equation
• inverse Sturm-Liouville problem
• Goursat boundary value problem
• Cauchy boundary value problem
• Newton-type method

AMS Subject Classifications:

• 35L20
• 35P99

1 Introduction

The goal of the paper is to develop a Newton-type method for solving numerically a class of inverse Sturm-Liouville problems: reconstruction of the potential (coefficient) function in the canonical Sturm-Liouville differential equation from two spectra. The potential reconstruction from two spectra is further beneficial to other inverse spectral problems (e.g. solving inverse Sturm-Liouville problems by multiple spectra). For solving numerically inverse Sturm-Liouville problems by three spectra, see for instance [1–3].

In practice, the Sturm-Liouville differential equation arises from the infinitesimal, vertical vibration of an elastic string of negligible weight and the constraints on the string give rise to the boundary conditions that accompany the differential equation (e.g. [3, Chapter 2 and the beginning of Section 5.2]).

While a quasi-Newton method was proposed in [4], the present work distinguishes itself from previous literature in the following aspects. We introduce intuitively the formula for the Fréchet derivative of the map in the non-linear equation we wish to solve. We then prove rigorously that the proposed formula satisfies the requirements of the Fréchet derivative. The non-linear map that we propose is different from that of [4, p.166]. Another essential difference between the present paper and [4] is that our method calls for updating the inverse of the Fréchet derivative operator at each step in the process, whereas the quasi-Newton method in [4] does not update the inverse of the Fréchet derivative, but rather uses the inverse of the Fréchet derivative operator at zero in each stage of the iteration process. Using the inverse of the Fréchet derivative operator at the current iterate to produce the next iterate (i.e. the Newton method) results in fewer iterates needed to reconstruct the true potential function than the quasi-Newton method, as the examples in Section 6 indicate.

Our Newton-type method is also different from the variational method of [5, 6]. Compared with our approach, where the two sequences of eigenvalues are used to produce two Cauchy data, and these data are the information the Newton’s method uses directly, the approach of [5, 6] is to directly use the two sequences of eigenvalues. Specifically, the method in [5, 6] constructs a weighted least-squares functional that quantifies the distance between the two given sequences of eigenvalues of a potential function that is to be reconstructed and the two counterpart sequences of eigenvalues of a trial potential. It is shown in [5, 6] that the only extrema of the functional are global minimum points, and thus, the steepest descent method used to minimize the least-squares functional will generate an estimate of the global minimum point, i.e. an estimate of the true potential function. In [5], the parameters in the boundary conditions are given, and they are used in the construction of the functional gradient. In [6], the boundary parameters are reconstructed along with the potential function, which is a more realistic case, but the method therein requires a large number of iterates (hundreds and even thousands) to converge. The Newton method we propose, works well (i.e. low number of iterates and small relative/absolute error) in both cases: given the Robin boundary parameter H, and estimated H, because the only place these parameters are needed is in the construction of the Cauchy data which is done outside of the Newton algorithm. In both cases, the mean of the true potential function that is needed in the construction of the Cauchy data is estimated from the eigenvalues.

In the remainder of the paper, we shall provide the background of the inverse Sturm-Liouville problem by two spectra (Section 2), the description and details of our Newton-type method (Sections 3–5), the numerical results (Section 6), and the proof of an auxiliary result (Appendix 1).

2 Preliminaries

The canonical Sturm-Liouville equation on the interval $[0,a]$ is the second-order linear ordinary differential equation:2.1 $$\begin{array}{c}\hfill -u^{″}(x)+q(x)u(x)=\mathit{\lambda }u(x),0<\mathrm{x}<\mathrm{a}.\end{array}$$2.1 Here, the function $q(x)$ is called the coefficient function or potential function. Equation (2.12.1 $$\begin{array}{c}\hfill -u^{″}(x)+q(x)u(x)=\mathit{\lambda }u(x),0<\mathrm{x}<\mathrm{a}.\end{array}$$2.1 ) is accompanied by two boundary conditions (one per end-point). Then two types of problems arise:

• the direct Sturm-Liouville problem: given $q(x)$, find the eigenpairs $\{\mathit{\lambda },u(x)\}$ of (2.12.1 $$\begin{array}{c}\hfill -u^{″}(x)+q(x)u(x)=\mathit{\lambda }u(x),0<\mathrm{x}<\mathrm{a}.\end{array}$$2.1 ) with the accompanying boundary conditions. It has been proved in literature that if $q\in L^2(0,a)$ is real-valued, then the eigenvalues $\mathit{\lambda }$ are real, distinct, countably many, tending to infinity, and satisfying an asymptotic formula specific to the type of boundary conditions under consideration, and that the normalized eigenfunctions ${\displaystyle \frac{u(x)}{{∥u∥}_2}}$ are real-valued and form an orthonormal basis of $L^2(0,a)$ (i.e. orthonormal and complete sequence). See Section 4.3 of [7], and also [8–10].

• the inverse Sturm-Liouville problem: given two spectral data, find the coefficient function $q(x)$. Note that the two spectral data are not the set of eigenpairs $\{\mathit{\lambda },u(x)\}$, since otherwise, even with one eigenpair, the problem would become trivial (i.e. knowing one pair $\{\mathit{\lambda },u(x)\}$, the coefficient $q(x)$ will be immediately found from (2.12.1 $$\begin{array}{c}\hfill -u^{″}(x)+q(x)u(x)=\mathit{\lambda }u(x),0<\mathrm{x}<\mathrm{a}.\end{array}$$2.1 )). Rather, the two spectral data can be either two sequences of eigenvalues (one sequence corresponding to one pair of boundary conditions, and the other sequence corresponding to another pair of boundary conditions of different type than the first pair, or of the same type but with different boundary parameters), or one sequence of eigenvalues and one sequence of norming constants, or one sequence of eigenvalues and partial information about the potential function (e.g. symmetric with respect to the midpoint of the interval $[0,a]$).

To illustrate the idea that two spectral data produce two Cauchy data, we chose to discuss the case of two sequences of eigenvalues. Let ${\{{\mathit{\lambda }}_n\}}_{n\ge 1}$ be the sequence of eigenvalues for the Dirichlet eigenvalue problem (2.12.1 $$\begin{array}{c}\hfill -u^{″}(x)+q(x)u(x)=\mathit{\lambda }u(x),0<\mathrm{x}<\mathrm{a}.\end{array}$$2.1 ) and (2.22.2 $$\begin{array}{cc}\hfill u(0)& =0=u(a),\hfill \end{array}$$2.2 ). Let ${\{{\mathit{\mu }}_n\}}_{n\ge 1}$ be the sequence of eigenvalues for the Dirichlet–Robin eigenvalue problem (2.12.1 $$\begin{array}{c}\hfill -u^{″}(x)+q(x)u(x)=\mathit{\lambda }u(x),0<\mathrm{x}<\mathrm{a}.\end{array}$$2.1 ) and (2.32.3 $$\begin{array}{cc}\hfill u(0)& =0=u^{\prime }(a)+Hu(a),\hfill \end{array}$$2.3 ), where the Dirichlet and the Dirichlet–Robin boundary conditions are, respectively:2.2 $$\begin{array}{cc}\hfill u(0)& =0=u(a),\hfill \end{array}$$2.2 2.3 $$\begin{array}{cc}\hfill u(0)& =0=u^{\prime }(a)+Hu(a),\hfill \end{array}$$2.3 where H is a real number. Then, ${\mathit{\lambda }}_n$’s are the zeros of the characteristic function for the eigenvalue problem (2.12.1 $$\begin{array}{c}\hfill -u^{″}(x)+q(x)u(x)=\mathit{\lambda }u(x),0<\mathrm{x}<\mathrm{a}.\end{array}$$2.1 ) and (2.22.2 $$\begin{array}{cc}\hfill u(0)& =0=u(a),\hfill \end{array}$$2.2 ), and ${\mathit{\mu }}_n$’s are the zeros of the characteristic function for the eigenvalue problem (2.12.1 $$\begin{array}{c}\hfill -u^{″}(x)+q(x)u(x)=\mathit{\lambda }u(x),0<\mathrm{x}<\mathrm{a}.\end{array}$$2.1 ) and (2.32.3 $$\begin{array}{cc}\hfill u(0)& =0=u^{\prime }(a)+Hu(a),\hfill \end{array}$$2.3 ), as discussed in [7, p.135 and 144 of Section 4.3]. The reader can also refer to Section 3.2.5 of [3], Appendix A of [11], and Section 2 of [1] for full details on the equivalence between being an eigenvalue (Dirichlet, Dirichlet–Neumann and respectively Dirichlet–Robin) and being a zero of the corresponding characteristic function. That means that:2.4 $$\begin{array}{cc}\hfill S(a;q,{\mathit{\lambda }}_n)& =0,\text{for}n\ge 1,\hfill \end{array}$$2.4 2.5 $$\begin{array}{cc}\hfill S^{\prime }(a;q,{\mathit{\mu }}_n)+HS(a;q,{\mathit{\mu }}_n)& =0,\text{for}n\ge 1,\hfill \end{array}$$2.5 where $S(·;q,\mathit{\lambda })$ denotes the weak solution (i.e. in $H^2(0,a)$) of the initial value problem: (2.12.1 $$\begin{array}{c}\hfill -u^{″}(x)+q(x)u(x)=\mathit{\lambda }u(x),0<\mathrm{x}<\mathrm{a}.\end{array}$$2.1 ) along with the initial conditions2.6 $$\begin{array}{c}\hfill u(0)=0,u^{\prime }(0)=1.\end{array}$$2.6 The notation $S(·;q,\mathit{\lambda })$ is meant to be suggestive, as when $q(x)=0$, the solution to (2.12.1 $$\begin{array}{c}\hfill -u^{″}(x)+q(x)u(x)=\mathit{\lambda }u(x),0<\mathrm{x}<\mathrm{a}.\end{array}$$2.1 ) and (2.62.6 $$\begin{array}{c}\hfill u(0)=0,u^{\prime }(0)=1.\end{array}$$2.6 ) is ${\displaystyle \frac{sin(\sqrt{\mathit{\lambda }}·)}{\sqrt{\mathit{\lambda }}}}$. It has been proved in the theory of direct Sturm-Liouville problems (see for example [7, Theorem 4.18 and Example 4.19, p.154–157]) that $S(·;q,\mathit{\lambda })$ has the integral representation:2.7 $$\begin{array}{c}\hfill S(x;q,\mathit{\lambda })=\frac{sin(\sqrt{\mathit{\lambda }}x)}{\sqrt{\mathit{\lambda }}}+{\int }_0^x\mathcal{K}(x,t;q)\frac{sin(\sqrt{\mathit{\lambda }}t)}{\sqrt{\mathit{\lambda }}}dt,0\le x\le a.\end{array}$$2.7 Here $\mathcal{K}(x,t;q)$ is the weak solution in the triangle ${\mathrm{\Delta }}_0:=\left\{(x,t)\in {\mathbb{R}}^2:0<t<x<a\right\}$ (see Figure 1) of the Goursat problem:2.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8

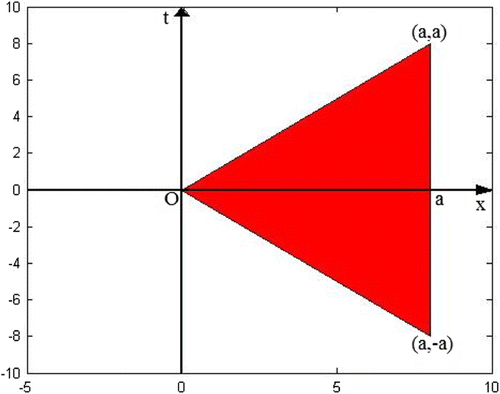
Figure 1. The domain of the problem (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ).

Differentiating (2.72.7 $$\begin{array}{c}\hfill S(x;q,\mathit{\lambda })=\frac{sin(\sqrt{\mathit{\lambda }}x)}{\sqrt{\mathit{\lambda }}}+{\int }_0^x\mathcal{K}(x,t;q)\frac{sin(\sqrt{\mathit{\lambda }}t)}{\sqrt{\mathit{\lambda }}}dt,0\le x\le a.\end{array}$$2.7 ) with respect to $x$ and using the first boundary condition of (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ) we obtain:2.9 $$\begin{array}{cc}\hfill S^{\prime }(x;q,\mathit{\lambda })& =cos(\sqrt{\mathit{\lambda }}x)+\left(\frac{1}{2}{\int }_0^{x}q(s)ds\right)\frac{sin(\sqrt{\mathit{\lambda }}x)}{\sqrt{\mathit{\lambda }}}\hfill \\ \hfill & +{\int }_0^x{\mathcal{K}}_x(x,t;q)\frac{sin(\sqrt{\mathit{\lambda }}t)}{\sqrt{\mathit{\lambda }}}dt,0\le x\le a.\hfill \end{array}$$2.9 Based on (2.72.7 $$\begin{array}{c}\hfill S(x;q,\mathit{\lambda })=\frac{sin(\sqrt{\mathit{\lambda }}x)}{\sqrt{\mathit{\lambda }}}+{\int }_0^x\mathcal{K}(x,t;q)\frac{sin(\sqrt{\mathit{\lambda }}t)}{\sqrt{\mathit{\lambda }}}dt,0\le x\le a.\end{array}$$2.7 ) and (2.92.9 $$\begin{array}{cc}\hfill S^{\prime }(x;q,\mathit{\lambda })& =cos(\sqrt{\mathit{\lambda }}x)+\left(\frac{1}{2}{\int }_0^{x}q(s)ds\right)\frac{sin(\sqrt{\mathit{\lambda }}x)}{\sqrt{\mathit{\lambda }}}\hfill \\ \hfill & +{\int }_0^x{\mathcal{K}}_x(x,t;q)\frac{sin(\sqrt{\mathit{\lambda }}t)}{\sqrt{\mathit{\lambda }}}dt,0\le x\le a.\hfill \end{array}$$2.9 ) we can write the systems of Equations (2.42.4 $$\begin{array}{cc}\hfill S(a;q,{\mathit{\lambda }}_n)& =0,\text{for}n\ge 1,\hfill \end{array}$$2.4 ) and (2.52.5 $$\begin{array}{cc}\hfill S^{\prime }(a;q,{\mathit{\mu }}_n)+HS(a;q,{\mathit{\mu }}_n)& =0,\text{for}n\ge 1,\hfill \end{array}$$2.5 ) in the equivalent form:2.10 $$\begin{array}{c}\hfill sin(\sqrt{{\mathit{\lambda }}_n}a)+{\int }_0^a\mathcal{K}(a,t;q)sin(\sqrt{{\mathit{\lambda }}_n}t)dt=0,n\ge 1\end{array}$$2.10 and respectively2.11 $$\begin{array}{cc}& \sqrt{{\mathit{\mu }}_n}cos(\sqrt{{\mathit{\mu }}_n}a)+\left(\frac{a[q]}{2}+H\right)sin(\sqrt{{\mathit{\mu }}_n}a)\hfill \\ \hfill & +{\int }_0^a\left({\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)\right)sin(\sqrt{{\mathit{\mu }}_n}t)dt=0,n\ge 1,\hfill \end{array}$$2.11 where ${\displaystyle [q]:=\frac{1}{a}{\int }_0^{a}q(s)ds}$. The unknowns in (2.102.10 $$\begin{array}{c}\hfill sin(\sqrt{{\mathit{\lambda }}_n}a)+{\int }_0^a\mathcal{K}(a,t;q)sin(\sqrt{{\mathit{\lambda }}_n}t)dt=0,n\ge 1\end{array}$$2.10 ) and (2.112.11 $$\begin{array}{cc}& \sqrt{{\mathit{\mu }}_n}cos(\sqrt{{\mathit{\mu }}_n}a)+\left(\frac{a[q]}{2}+H\right)sin(\sqrt{{\mathit{\mu }}_n}a)\hfill \\ \hfill & +{\int }_0^a\left({\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)\right)sin(\sqrt{{\mathit{\mu }}_n}t)dt=0,n\ge 1,\hfill \end{array}$$2.11 ) are the functions$$\begin{array}{c}t\in [0,a]\to \mathcal{K}(a,t;q)\hfill \\ t\in [0,a]\to {\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q).\hfill \end{array}$$Expanding them in Fourier series and inserting these Fourier series in (2.102.10 $$\begin{array}{c}\hfill sin(\sqrt{{\mathit{\lambda }}_n}a)+{\int }_0^a\mathcal{K}(a,t;q)sin(\sqrt{{\mathit{\lambda }}_n}t)dt=0,n\ge 1\end{array}$$2.10 ) and (2.112.11 $$\begin{array}{cc}& \sqrt{{\mathit{\mu }}_n}cos(\sqrt{{\mathit{\mu }}_n}a)+\left(\frac{a[q]}{2}+H\right)sin(\sqrt{{\mathit{\mu }}_n}a)\hfill \\ \hfill & +{\int }_0^a\left({\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)\right)sin(\sqrt{{\mathit{\mu }}_n}t)dt=0,n\ge 1,\hfill \end{array}$$2.11 ), respectively, we obtain two linear systems with the Fourier coefficients being the unknowns. Hence, the functions$$\mathcal{K}(a,t;q),\text{and}{\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)$$will be determined through their Fourier coefficients. Then the Cauchy data$$\mathcal{K}(a,t;q),\text{and}{\mathcal{K}}_x(a,t;q)$$will be immediately obtained. We want to add here that the bases functions of the Fourier series representations must be chosen carefully to insure numerical accuracy in the Cauchy data when constructing them from the eigenvalues. An idea on how to choose the bases functions is provided by (2.102.10 $$\begin{array}{c}\hfill sin(\sqrt{{\mathit{\lambda }}_n}a)+{\int }_0^a\mathcal{K}(a,t;q)sin(\sqrt{{\mathit{\lambda }}_n}t)dt=0,n\ge 1\end{array}$$2.10 ) and (2.112.11 $$\begin{array}{cc}& \sqrt{{\mathit{\mu }}_n}cos(\sqrt{{\mathit{\mu }}_n}a)+\left(\frac{a[q]}{2}+H\right)sin(\sqrt{{\mathit{\mu }}_n}a)\hfill \\ \hfill & +{\int }_0^a\left({\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)\right)sin(\sqrt{{\mathit{\mu }}_n}t)dt=0,n\ge 1,\hfill \end{array}$$2.11 ), the known properties of $\mathcal{K}(x,t;q)$, and the asymptotic formulas of the eigenvalues ${\mathit{\lambda }}_n$’s and ${\mathit{\mu }}_n$’s.

It is known in literature (see [8, p.256], or [10, Theorem 1 (p.29), Theorem 2 (p.30), Theorem 4 (p.35)], or [7, Lemma 4.7 (p.135–136) and formula (4.25) on p.139], and rescale $[0,1]$ to $[0,a]$ by the change of variables $x=a·s$, with $s\in [0,1]$) that the Dirichlet spectrum of the potential function $q\in L_{\mathbb{R}}^2(0,a)$ is a sequence of real, simple eigenvalues, increasing, and satisfying the asymptotic formula:2.12 $$\begin{array}{c}\hfill {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+[q]+r_n,\text{for}n\ge 1,\end{array}$$2.12 where ${\{r_n\}}_{n\ge 1}$ is an $l_2$ sequence of real numbers (i.e. ${\displaystyle \sum _{n=1}^{\infty }{r}_n^2<\infty }$).

It is also known (see [8, p.255] and rescale $[0,1]$ to $[0,a]$) that the Dirichlet–Robin spectrum of the potential function $q\in L_{\mathbb{R}}^2(0,a)$ and boundary parameter $H\in \mathbb{R}$ is a sequence of real, simple eigenvalues, increasing, and satisfying the asymptotic formula:2.13 $$\begin{array}{c}\hfill {\mathit{\mu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}\right)}^2+[q]+2\frac{H}{a}+s_n,\text{for}n\ge 1,\end{array}$$2.13 where ${\{s_n\}}_{n\ge 1}$ is an $l_2$ sequence of real numbers. It follows from (2.122.12 $$\begin{array}{c}\hfill {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+[q]+r_n,\text{for}n\ge 1,\end{array}$$2.12 ) and (2.132.13 $$\begin{array}{c}\hfill {\mathit{\mu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}\right)}^2+[q]+2\frac{H}{a}+s_n,\text{for}n\ge 1,\end{array}$$2.13 ) that2.14 $$\begin{array}{c}\hfill \sqrt{{\mathit{\lambda }}_n}=\frac{n\mathit{\pi }}{a}+\mathcal{O}\left(\frac{1}{n}\right)\text{and}\sqrt{{\mathit{\mu }}_n}=\frac{(n-\frac{1}{2})\mathit{\pi }}{a}+\mathcal{O}\left(\frac{1}{n}\right),\end{array}$$2.14 from which we infer that for $n$ sufficiently large,2.15 $$\begin{array}{c}\hfill sin(\sqrt{{\mathit{\lambda }}_n}t)\approx sin\left(\frac{n\mathit{\pi }}{a}t\right)\text{and}sin(\sqrt{{\mathit{\mu }}_n}t)\approx sin\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}t\right).\end{array}$$2.15 Noting from (2.102.10 $$\begin{array}{c}\hfill sin(\sqrt{{\mathit{\lambda }}_n}a)+{\int }_0^a\mathcal{K}(a,t;q)sin(\sqrt{{\mathit{\lambda }}_n}t)dt=0,n\ge 1\end{array}$$2.10 ) and (2.112.11 $$\begin{array}{cc}& \sqrt{{\mathit{\mu }}_n}cos(\sqrt{{\mathit{\mu }}_n}a)+\left(\frac{a[q]}{2}+H\right)sin(\sqrt{{\mathit{\mu }}_n}a)\hfill \\ \hfill & +{\int }_0^a\left({\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)\right)sin(\sqrt{{\mathit{\mu }}_n}t)dt=0,n\ge 1,\hfill \end{array}$$2.11 ) that the functions$$\begin{array}{ccc}\mathcal{K}(a,t;q)\hfill & \text{is integrated against}\hfill & sin(\sqrt{{\mathit{\lambda }}_n}t),\hfill \\ {\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)\hfill & \text{is integrated against}\hfill & sin(\sqrt{{\mathit{\mu }}_n}t),\hfill \end{array}$$formula (2.152.15 $$\begin{array}{c}\hfill sin(\sqrt{{\mathit{\lambda }}_n}t)\approx sin\left(\frac{n\mathit{\pi }}{a}t\right)\text{and}sin(\sqrt{{\mathit{\mu }}_n}t)\approx sin\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}t\right).\end{array}$$2.15 ) suggests considering the bases functions2.16 $$\begin{array}{c}\hfill {\{sin\left(\frac{n\mathit{\pi }}{a}t\right)\}}_{n\ge 1}\text{and}{\{sin\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}t\right)\}}_{n\ge 1}.\end{array}$$2.16 They are orthogonal bases of $L^2(0,a)$ as seen from [12, Example 2(d1), p.308–309] with $L=a$, and the Appendix of [1] with $b=a$, respectively. The orthogonality of the functions in (2.162.16 $$\begin{array}{c}\hfill {\{sin\left(\frac{n\mathit{\pi }}{a}t\right)\}}_{n\ge 1}\text{and}{\{sin\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}t\right)\}}_{n\ge 1}.\end{array}$$2.16 ), along with (2.152.15 $$\begin{array}{c}\hfill sin(\sqrt{{\mathit{\lambda }}_n}t)\approx sin\left(\frac{n\mathit{\pi }}{a}t\right)\text{and}sin(\sqrt{{\mathit{\mu }}_n}t)\approx sin\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}t\right).\end{array}$$2.15 ) make it easier for (2.102.10 $$\begin{array}{c}\hfill sin(\sqrt{{\mathit{\lambda }}_n}a)+{\int }_0^a\mathcal{K}(a,t;q)sin(\sqrt{{\mathit{\lambda }}_n}t)dt=0,n\ge 1\end{array}$$2.10 ) and (2.112.11 $$\begin{array}{cc}& \sqrt{{\mathit{\mu }}_n}cos(\sqrt{{\mathit{\mu }}_n}a)+\left(\frac{a[q]}{2}+H\right)sin(\sqrt{{\mathit{\mu }}_n}a)\hfill \\ \hfill & +{\int }_0^a\left({\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)\right)sin(\sqrt{{\mathit{\mu }}_n}t)dt=0,n\ge 1,\hfill \end{array}$$2.11 ) to be solved numerically, as their coefficient-matrices will be almost diagonal. Another reason to choose the bases functions (2.162.16 $$\begin{array}{c}\hfill {\{sin\left(\frac{n\mathit{\pi }}{a}t\right)\}}_{n\ge 1}\text{and}{\{sin\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}t\right)\}}_{n\ge 1}.\end{array}$$2.16 ) is that$$\mathcal{K}(a,t;q)\text{and}{\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)$$are zero at $t=0$, as inferred from the second boundary condition of (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ). The same is true for the functions in (2.162.16 $$\begin{array}{c}\hfill {\{sin\left(\frac{n\mathit{\pi }}{a}t\right)\}}_{n\ge 1}\text{and}{\{sin\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}t\right)\}}_{n\ge 1}.\end{array}$$2.16 ) at $t=0$. Also,$${\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)$$is not zero at $t=a$, and neither ${\displaystyle sin\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}t\right)}$ are. From the first boundary condition of (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ) and the discussion above, we see that the best Fourier series representations are:2.17 $$\begin{array}{cc}\hfill \mathcal{K}(a,t;q)& =\frac{[q]}{2}t+\sum _{m=1}^{\infty }{\mathit{\alpha }}_{m}sin\left(\frac{m\mathit{\pi }}{a}t\right)\hfill \end{array}$$2.17 2.18 $$\begin{array}{cc}\hfill {\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)& =\sum _{m=1}^{\infty }{\mathit{\beta }}_{m}sin\left(\frac{(m-\frac{1}{2})\mathit{\pi }}{a}t\right).\hfill \end{array}$$2.18 We mention here that we do not need ${\mathcal{K}}_t(a,t;q)$ for our numerical method/algorithm. However, since$${\mathcal{K}}_t(a,t;q)=\frac{d}{dt}\left(\mathcal{K}(a,t;q)\right),$$${\mathcal{K}}_t(a,t;q)$ can be obtained numerically in one of these two ways. The first way is to apply a divided difference scheme to the just calculated $\mathcal{K}(a,t;q)$. Specifically,$$\left\{\begin{array}{c}{\mathcal{K}}_t(a,t_{N_t};q)=\frac{\mathcal{K}(a,t_{N_t};q)-\mathcal{K}(a,t_{N_t-1};q)}{dt}\hfill \\ {\mathcal{K}}_t(a,t_j;q)=\frac{\mathcal{K}(a,t_{j+1};q)-\mathcal{K}(a,t_{j-1};q)}{2dt},\text{for}j=N_t-1,N_t-2,\dots ,3,2\hfill \\ {\mathcal{K}}_t(a,t_1;q)=\frac{\mathcal{K}(a,t_2;q)-\mathcal{K}(a,t_1;q)}{dt}.\hfill \end{array}\right.$$Here, $N_t$ is the number of partition points in $t$-direction. The second way is to take advantage of the integration by parts formula in (2.102.10 $$\begin{array}{c}\hfill sin(\sqrt{{\mathit{\lambda }}_n}a)+{\int }_0^a\mathcal{K}(a,t;q)sin(\sqrt{{\mathit{\lambda }}_n}t)dt=0,n\ge 1\end{array}$$2.10 ), and the two boundary conditions of (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ) with $x=a$:2.19 $$\begin{array}{c}\hfill 0=sin(\sqrt{{\mathit{\lambda }}_n}a)-\frac{a[q]}{2}·\frac{cos(\sqrt{{\mathit{\lambda }}_n}a)}{\sqrt{{\mathit{\lambda }}_n}}+{\int }_0^a{\mathcal{K}}_t(a,t;q)·\frac{cos(\sqrt{{\mathit{\lambda }}_n}t)}{\sqrt{{\mathit{\lambda }}_n}}dt,n\ge 1.\\ \hfill \end{array}$$2.19 From (2.192.19 $$\begin{array}{c}\hfill 0=sin(\sqrt{{\mathit{\lambda }}_n}a)-\frac{a[q]}{2}·\frac{cos(\sqrt{{\mathit{\lambda }}_n}a)}{\sqrt{{\mathit{\lambda }}_n}}+{\int }_0^a{\mathcal{K}}_t(a,t;q)·\frac{cos(\sqrt{{\mathit{\lambda }}_n}t)}{\sqrt{{\mathit{\lambda }}_n}}dt,n\ge 1.\\ \hfill \end{array}$$2.19 ) and (2.142.14 $$\begin{array}{c}\hfill \sqrt{{\mathit{\lambda }}_n}=\frac{n\mathit{\pi }}{a}+\mathcal{O}\left(\frac{1}{n}\right)\text{and}\sqrt{{\mathit{\mu }}_n}=\frac{(n-\frac{1}{2})\mathit{\pi }}{a}+\mathcal{O}\left(\frac{1}{n}\right),\end{array}$$2.14 ), and the fact that$$\{1\}\cup {\{cos\left(\frac{n\mathit{\pi }}{a}t\right)\}}_{n\ge 1}$$is an orthogonal basis of $L^2(0,a)$ (see [12, Example 2(c1), pg 308–309] with $L=a$), we can write the Fourier series representation of ${\mathcal{K}}_t(a,t;q)$ as2.20 $$\begin{array}{c}\hfill {\mathcal{K}}_t(a,t;q)={\mathit{\gamma }}_0+\sum _{m=1}^{\infty }{\mathit{\gamma }}_{m}cos\left(\frac{m\mathit{\pi }}{a}t\right).\end{array}$$2.20 Note that the bases functions ${\{sin\left(\frac{n\mathit{\pi }}{a}t\right)\}}_{n\ge 1}$ are not beneficial, because they are zero at $t=0$ and $t=a$, whereas ${\mathcal{K}}_t(a,t;q)$ need not be so.

3 The Newton method for the inverse two spectra problem

Now we can describe the proposed Newton method for recovering the potential function $q(x)$ from two spectra. Let us take for illustration two sequences of eigenvalues. To be specific, we take ${\{{\mathit{\lambda }}_n\}}_{n\ge 1}$ - the Dirichlet eigenvalues and ${\{{\mathit{\mu }}_n\}}_{n\ge 1}$ - the Dirichlet–Robin eigenvalues. Note that for another pair of spectral data, the difference in the way $q(x)$ is reconstructed resides only in the manner the pair of Cauchy data is extracted from the given pair of spectral data, the Newton method remaining basically the same. Note also that in practice, only finitely many of the ${\mathit{\lambda }}_n$’s and ${\mathit{\mu }}_n$’s are available. So, we can assume that only $\{{\mathit{\lambda }}_i|i=1,2,\dots ,N_1\}$ and $\{{\mathit{\mu }}_i|i=1,2,\dots ,N_2\}$ are known. Write Fourier series expansions for the functions $\tilde{f}(t)$ and $\tilde{h}(t)$ and insert them, respectively, into the systems:3.1 $$\begin{array}{cc}& sin(\sqrt{{\mathit{\lambda }}_i}a)+{\int }_0^a\tilde{f}(t)sin(\sqrt{{\mathit{\lambda }}_i}t)dt=0,i=1,2,\dots ,N_1,\hfill \end{array}$$3.1 3.2 $$\begin{array}{cc}& \sqrt{{\mathit{\mu }}_i}cos(\sqrt{{\mathit{\mu }}_i}a)+\left(\frac{aC}{2}+H\right)sin(\sqrt{{\mathit{\mu }}_i}a)\hfill \\ \hfill & +{\int }_0^a\tilde{h}(t)sin(\sqrt{{\mathit{\mu }}_i}t)dt=0,i=1,2,\dots ,N_2,\hfill \end{array}$$3.2 where $C$ and H are real numbers that can be estimated from the eigenvalues ${\mathit{\lambda }}_n$’s and ${\mathit{\mu }}_n$’s. Precisely, due to the asymptotic formulas of the eigenvalues (2.122.12 $$\begin{array}{c}\hfill {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+[q]+r_n,\text{for}n\ge 1,\end{array}$$2.12 ) and (2.132.13 $$\begin{array}{c}\hfill {\mathit{\mu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}\right)}^2+[q]+2\frac{H}{a}+s_n,\text{for}n\ge 1,\end{array}$$2.13 ), we can write:3.3 $$\begin{array}{cc}\hfill [q]& =\underset{n\to \infty }{lim}\left({\mathit{\lambda }}_n-{\left(\frac{n\mathit{\pi }}{a}\right)}^2\right),\hfill \end{array}$$3.3 3.4 $$\begin{array}{cc}\hfill [q]+\frac{2H}{a}& =\underset{n\to \infty }{lim}\left({\mathit{\mu }}_n-{\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right).\hfill \end{array}$$3.4 Since $C$ is expected to match $[q]$, we take3.5 $$\begin{array}{c}\hfill C=\underset{n\to \infty }{lim}\left({\mathit{\lambda }}_n-{\left(\frac{n\mathit{\pi }}{a}\right)}^2\right),\end{array}$$3.5 and hence3.6 $$\begin{array}{c}\hfill \frac{aC}{2}+H=\frac{a}{2}·\underset{n\to \infty }{lim}\left({\mathit{\mu }}_n-{\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right).\end{array}$$3.6 Bearing in mind (2.172.17 $$\begin{array}{cc}\hfill \mathcal{K}(a,t;q)& =\frac{[q]}{2}t+\sum _{m=1}^{\infty }{\mathit{\alpha }}_{m}sin\left(\frac{m\mathit{\pi }}{a}t\right)\hfill \end{array}$$2.17 ) and (2.182.18 $$\begin{array}{cc}\hfill {\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)& =\sum _{m=1}^{\infty }{\mathit{\beta }}_{m}sin\left(\frac{(m-\frac{1}{2})\mathit{\pi }}{a}t\right).\hfill \end{array}$$2.18 ), we write the Fourier series (actually, truncated Fourier series) of $\tilde{f}(t)$ and $\tilde{h}(t)$ as follows:3.7 $$\begin{array}{cc}\hfill \tilde{f}(t)& =\frac{C}{2}t+\sum _{j=1}^{N_1}{\mathit{\alpha }}_{j}sin\left(\frac{j\mathit{\pi }}{a}t\right),\hfill \end{array}$$3.7 3.8 $$\begin{array}{cc}\hfill \tilde{h}(t)& =\sum _{j=1}^{N_2}{\mathit{\beta }}_{j}sin\left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a}t\right).\hfill \end{array}$$3.8 Solve the newly obtained linear systems (3.13.1 $$\begin{array}{cc}& sin(\sqrt{{\mathit{\lambda }}_i}a)+{\int }_0^a\tilde{f}(t)sin(\sqrt{{\mathit{\lambda }}_i}t)dt=0,i=1,2,\dots ,N_1,\hfill \end{array}$$3.1 ) and (3.23.2 $$\begin{array}{cc}& \sqrt{{\mathit{\mu }}_i}cos(\sqrt{{\mathit{\mu }}_i}a)+\left(\frac{aC}{2}+H\right)sin(\sqrt{{\mathit{\mu }}_i}a)\hfill \\ \hfill & +{\int }_0^a\tilde{h}(t)sin(\sqrt{{\mathit{\mu }}_i}t)dt=0,i=1,2,\dots ,N_2,\hfill \end{array}$$3.2 ) for the Fourier coefficients ${\{{\mathit{\alpha }}_j\}}_{j=1}^{N_1}$ and ${\{{\mathit{\beta }}_j\}}_{j=1}^{N_2}$ of $\tilde{f}(t)$ and $\tilde{h}(t)$, respectively. Then we need to determine $q(x)$ such that the functions$$\begin{array}{ccc}\mathcal{K}(a,t;q)\hfill & \text{matches the Cauchy datum}\hfill & \tilde{f}(t)\hfill \\ {\mathcal{K}}_x(a,t;q)\hfill & \text{matches the Cauchy datum}\hfill & \tilde{g}(t):=\tilde{h}(t)-H·\tilde{f}(t),\hfill \end{array}$$where $\mathcal{K}(x,t;q)$ solves the Goursat problem (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ). In other words, we need to solve the non-linear equation3.9 $$\begin{array}{c}\hfill F(q)=\{\tilde{f}(t),\tilde{g}(t)\}\end{array}$$3.9 for the unknown function $q(x)$, where the map $F$ is defined by3.10 $$\begin{array}{c}\hfill L_{\mathbb{R}}^2(0,a)\ni q\to F(q):=\{\mathcal{K}(a,t;q),{\mathcal{K}}_x(a,t;q)\}\in H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)\end{array}$$3.10 with $\mathcal{K}(x,t;q)$ being the weak solution to the Goursat problem (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ). The non-linear Equation (3.93.9 $$\begin{array}{c}\hfill F(q)=\{\tilde{f}(t),\tilde{g}(t)\}\end{array}$$3.9 ) is equivalent to the equation3.11 $$\begin{array}{c}\hfill F(q)-\{\tilde{f}(t),\tilde{g}(t)\}=0.\end{array}$$3.11 Letting $G(q):=F(q)-\{\tilde{f}(t),\tilde{g}(t)\}$, the Newton method applied to (3.113.11 $$\begin{array}{c}\hfill F(q)-\{\tilde{f}(t),\tilde{g}(t)\}=0.\end{array}$$3.11 ) reads:$$\left\{\begin{array}{c}\text{pick initial guess}{q}_0\hfill \\ \text{calculate}{q}_{n+1}\text{from}0-G(q_n)=G^{\prime }(q_n)(q_{n+1}-q_n),\text{for}n=0,1,2,\dots ,\hfill \end{array}\right.$$which can be written equivalently based on the definition of $G$ and (3.103.10 $$\begin{array}{c}\hfill L_{\mathbb{R}}^2(0,a)\ni q\to F(q):=\{\mathcal{K}(a,t;q),{\mathcal{K}}_x(a,t;q)\}\in H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)\end{array}$$3.10 ) as3.12 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\text{pick initial guess}{q}_0\hfill \\ \text{calculate}{q}_{n+1}\text{from}\{\tilde{f}(t)-\mathcal{K}(a,t;q_n),\tilde{g}(t)-{\mathcal{K}}_x(a,t;q_n)\}\hfill \\ =F^{\prime }(q_n)(q_{n+1}-q_n),\text{for}n=0,1,2,\dots .\hfill \end{array}\right.\end{array}$$3.12 In order for (3.123.12 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\text{pick initial guess}{q}_0\hfill \\ \text{calculate}{q}_{n+1}\text{from}\{\tilde{f}(t)-\mathcal{K}(a,t;q_n),\tilde{g}(t)-{\mathcal{K}}_x(a,t;q_n)\}\hfill \\ =F^{\prime }(q_n)(q_{n+1}-q_n),\text{for}n=0,1,2,\dots .\hfill \end{array}\right.\end{array}$$3.12 ) to be usable, the map $F$ must be proven to be Fréchet differentiable, and the formula for its Fréchet derivative must be found. We shall also need to find the inverse of the Fréchet derivative operator.

Prior to working towards these goals, we mention that ${\tilde{f}}^{\prime }(t)$, although not needed for our algorithm (but needed for quasi-Newton), can be constructed numerically by following the model of ${\mathcal{K}}_t(a,t;q)$ (see the paragraph between (2.182.18 $$\begin{array}{cc}\hfill {\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)& =\sum _{m=1}^{\infty }{\mathit{\beta }}_{m}sin\left(\frac{(m-\frac{1}{2})\mathit{\pi }}{a}t\right).\hfill \end{array}$$2.18 ) and (2.202.20 $$\begin{array}{c}\hfill {\mathcal{K}}_t(a,t;q)={\mathit{\gamma }}_0+\sum _{m=1}^{\infty }{\mathit{\gamma }}_{m}cos\left(\frac{m\mathit{\pi }}{a}t\right).\end{array}$$2.20 )). Specifically, either apply a divided difference scheme to the just calculated $\tilde{f}(t)$, or else write3.13 $$\begin{array}{c}\hfill {\tilde{f}}^{\prime }(t)={\mathit{\gamma }}_0+\sum _{j=1}^{N_1-1}{\mathit{\gamma }}_{j}cos\left(\frac{j\mathit{\pi }}{a}t\right),\end{array}$$3.13 and insert it into the system3.14 $$\begin{array}{c}\hfill \sqrt{{\mathit{\lambda }}_i}sin(\sqrt{{\mathit{\lambda }}_i}a)-\frac{aC}{2}·cos(\sqrt{{\mathit{\lambda }}_i}a)+{\int }_0^a{\tilde{f}}^{\prime }(t)·cos(\sqrt{{\mathit{\lambda }}_i}t)dt=0,i=1,2,\dots N_1,\end{array}$$3.14 to solve for the Fourier coefficients ${\{{\mathit{\gamma }}_j\}}_{j=0}^{N_1-1}$ of ${\tilde{f}}^{\prime }(t)$.

4 The Fréchet differentiability of the map $F$

For $q\in L_{\mathbb{R}}^2(0,a)$, the Fréchet derivative operator $F^{\prime }(q)$ must be a linear bounded operator from $L_{\mathbb{R}}^2(0,a)$ into $H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)$ such that:4.1 $$\begin{array}{c}\hfill \frac{{∥F(q+\mathit{\delta }q)-F(q)-F^{\prime }(q)(\mathit{\delta }q)∥}_{H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)}}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}}\to 0,\text{when}{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\to 0.\end{array}$$4.1 We shall work step-by-step to find a natural choice for $F^{\prime }(q)(\mathit{\delta }q)$, then we shall prove that the proposed formula for $F^{\prime }(q)(\mathit{\delta }q)$ satisfies (4.14.1 $$\begin{array}{c}\hfill \frac{{∥F(q+\mathit{\delta }q)-F(q)-F^{\prime }(q)(\mathit{\delta }q)∥}_{H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)}}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}}\to 0,\text{when}{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\to 0.\end{array}$$4.1 ), and also that $F^{\prime }(q)$ is a linear and bounded operator between the previously indicated spaces of functions. Due to (3.103.10 $$\begin{array}{c}\hfill L_{\mathbb{R}}^2(0,a)\ni q\to F(q):=\{\mathcal{K}(a,t;q),{\mathcal{K}}_x(a,t;q)\}\in H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)\end{array}$$3.10 ), we have that4.2 $$\begin{array}{c}\hfill F(q+\mathit{\delta }q)-F(q)=\{\mathcal{K}(a,t;q+\mathit{\delta }q)-\mathcal{K}(a,t;q),{\mathcal{K}}_x(a,t;q+\mathit{\delta }q)-{\mathcal{K}}_x(a,t;q)\},\end{array}$$4.2 where $\mathcal{K}(x,t;q)$ solves (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ), and $\mathcal{K}(x,t;q+\mathit{\delta }q)$ solves (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ) with $q(x)+\mathit{\delta }q(x)$ in place of $q(x)$. Letting$$\tilde{\mathcal{K}}(x,t):=\mathcal{K}(x,t;q+\mathit{\delta }q)-\mathcal{K}(x,t;q),$$we see that $\tilde{\mathcal{K}}(x,t)$ satisfies4.3 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\tilde{\mathcal{K}}}_{xx}(x,t)-{\tilde{\mathcal{K}}}_{tt}(x,t)-q(x)\tilde{\mathcal{K}}(x,t)=\mathit{\delta }q(x)\mathcal{K}(x,t;q+\mathit{\delta }q),\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \tilde{\mathcal{K}}(x,x)=\frac{1}{2}{\int }_0^x\mathit{\delta }q(s)ds,\hfill & 0\le x\le a\hfill \\ \tilde{\mathcal{K}}(x,0)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.3 Due to the continuous dependence of $\mathcal{K}(x,t;q)$ on $q$ (see Theorem 4.15(b) in [7, p.147]), and based on (4.34.3 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\tilde{\mathcal{K}}}_{xx}(x,t)-{\tilde{\mathcal{K}}}_{tt}(x,t)-q(x)\tilde{\mathcal{K}}(x,t)=\mathit{\delta }q(x)\mathcal{K}(x,t;q+\mathit{\delta }q),\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \tilde{\mathcal{K}}(x,x)=\frac{1}{2}{\int }_0^x\mathit{\delta }q(s)ds,\hfill & 0\le x\le a\hfill \\ \tilde{\mathcal{K}}(x,0)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.3 ) and (4.24.2 $$\begin{array}{c}\hfill F(q+\mathit{\delta }q)-F(q)=\{\mathcal{K}(a,t;q+\mathit{\delta }q)-\mathcal{K}(a,t;q),{\mathcal{K}}_x(a,t;q+\mathit{\delta }q)-{\mathcal{K}}_x(a,t;q)\},\end{array}$$4.2 ), a natural choice for $F^{\prime }(q)(\mathit{\delta }q)$ is4.4 $$\begin{array}{c}\hfill F^{\prime }(q)(\mathit{\delta }q):=\{\mathcal{K}(a,t;q,\mathit{\delta }q),{\mathcal{K}}_x(a,t;q,\mathit{\delta }q)\},\end{array}$$4.4 where $\mathcal{K}(x,t;q,\mathit{\delta }q)$ satisfies4.5 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q,\mathit{\delta }q)-{\mathcal{K}}_{tt}(x,t;q,\mathit{\delta }q)-q(x)\mathcal{K}(x,t;q,\mathit{\delta }q)=\mathit{\delta }q(x)\mathcal{K}(x,t;q),\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q,\mathit{\delta }q)=\frac{1}{2}{\int }_0^x\mathit{\delta }q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q,\mathit{\delta }q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.5 The proposed formula (4.44.4 $$\begin{array}{c}\hfill F^{\prime }(q)(\mathit{\delta }q):=\{\mathcal{K}(a,t;q,\mathit{\delta }q),{\mathcal{K}}_x(a,t;q,\mathit{\delta }q)\},\end{array}$$4.4 ) would be correct if we prove that (4.14.1 $$\begin{array}{c}\hfill \frac{{∥F(q+\mathit{\delta }q)-F(q)-F^{\prime }(q)(\mathit{\delta }q)∥}_{H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)}}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}}\to 0,\text{when}{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\to 0.\end{array}$$4.1 ) is satisfied. Letting4.6 $$\begin{array}{c}\hfill W(x,t):=\tilde{\mathcal{K}}(x,t)-\mathcal{K}(x,t;q,\mathit{\delta }q),\end{array}$$4.6 formula (4.14.1 $$\begin{array}{c}\hfill \frac{{∥F(q+\mathit{\delta }q)-F(q)-F^{\prime }(q)(\mathit{\delta }q)∥}_{H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)}}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}}\to 0,\text{when}{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\to 0.\end{array}$$4.1 ) will be equivalent to:4.7 $$\begin{array}{c}\hfill \frac{{∥W(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_t(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_x(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2}\to 0,\text{when}{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\to 0.\end{array}$$4.7 Based on (4.34.3 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\tilde{\mathcal{K}}}_{xx}(x,t)-{\tilde{\mathcal{K}}}_{tt}(x,t)-q(x)\tilde{\mathcal{K}}(x,t)=\mathit{\delta }q(x)\mathcal{K}(x,t;q+\mathit{\delta }q),\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \tilde{\mathcal{K}}(x,x)=\frac{1}{2}{\int }_0^x\mathit{\delta }q(s)ds,\hfill & 0\le x\le a\hfill \\ \tilde{\mathcal{K}}(x,0)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.3 ) and (4.54.5 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q,\mathit{\delta }q)-{\mathcal{K}}_{tt}(x,t;q,\mathit{\delta }q)-q(x)\mathcal{K}(x,t;q,\mathit{\delta }q)=\mathit{\delta }q(x)\mathcal{K}(x,t;q),\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q,\mathit{\delta }q)=\frac{1}{2}{\int }_0^x\mathit{\delta }q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q,\mathit{\delta }q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.5 ), $W(x,t)$ satisfies the boundary value problem:4.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{W}_{xx}(x,t)-W_{tt}(x,t)-q(x)W(x,t)=\mathit{\delta }q(x)\tilde{\mathcal{K}}(x,t),\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ W(x,x)=0,\hfill & 0\le x\le a\hfill \\ W(x,0)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.8

Figure 2. The extended domain $\mathrm{\Delta }:=\left\{(x,t)\in {\mathbb{R}}^2:0<|t|<x<a\right\}$.

In preparation for dealing with (4.74.7 $$\begin{array}{c}\hfill \frac{{∥W(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_t(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_x(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2}\to 0,\text{when}{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\to 0.\end{array}$$4.7 ) we make some remarks. Let ${\mathcal{K}}^{ext}(x,t;q)$ be the odd extension in $t$-variable of $\mathcal{K}(x,t;q)$ from ${\mathrm{\Delta }}_0$ to $\mathrm{\Delta }:=\left\{(x,t)\in {\mathbb{R}}^2:0<|t|<x<a\right\}$ (see Figure 2), i.e.$${\mathcal{K}}^{ext}(x,t;q):=\left\{\begin{array}{cc}\mathcal{K}(x,t;q),\hfill & \text{if}(x,t)\in {\mathrm{\Delta }}_0\hfill \\ -\mathcal{K}(x,-t;q),\hfill & \text{if}(x,t)\in \mathrm{\Delta }\backslash {\mathrm{\Delta }}_0.\hfill \end{array}\right.$$Then based on (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ) and the fact that $(x,t)\in \mathrm{\Delta }\backslash {\mathrm{\Delta }}_0$ is the same as $(x,-t)\in {\mathrm{\Delta }}_0$, one can easily show that ${\mathcal{K}}^{ext}(x,t;q)$ will satisfy the boundary value problem:4.9 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{Z}}_{xx}(x,t)-{\mathcal{Z}}_{tt}(x,t)-q(x)\mathcal{Z}(x,t)=0,\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ \mathcal{Z}(x,x)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{Z}(x,-x)=-\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.9 Conversely, if $\mathcal{Z}(x,t)$ satisfies (4.94.9 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{Z}}_{xx}(x,t)-{\mathcal{Z}}_{tt}(x,t)-q(x)\mathcal{Z}(x,t)=0,\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ \mathcal{Z}(x,x)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{Z}(x,-x)=-\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.9 ), then so will $\mathcal{Y}(x,t):=-\mathcal{Z}(x,-t)$ do, as one can easily check because $(x,-t)\in \mathrm{\Delta }$ at the same time $(x,t)\in \mathrm{\Delta }$. Due to the uniqueness of solution to the boundary value problem (4.94.9 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{Z}}_{xx}(x,t)-{\mathcal{Z}}_{tt}(x,t)-q(x)\mathcal{Z}(x,t)=0,\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ \mathcal{Z}(x,x)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{Z}(x,-x)=-\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.9 ), it follows that the two solutions coincide, i.e. $\mathcal{Z}(x,t)=\mathcal{Y}(x,t)$, for all $(x,t)\in \mathrm{\Delta }$ from which we get $\mathcal{Z}(x,t)=-\mathcal{Z}(x,-t)$, for all $(x,t)\in \mathrm{\Delta }$. This further implies that $\mathcal{Z}(x,0)=0$, and so the restriction of $\mathcal{Z}(x,t)$ to ${\mathrm{\Delta }}_0$ will satisfy (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ). Since the solution to (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ) is unique, it follows that ${\mathcal{Z}|}_{{\mathrm{\Delta }}_0}=\mathcal{K}(·,·;q)$. Thus, we proved that (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ) and (4.94.9 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{Z}}_{xx}(x,t)-{\mathcal{Z}}_{tt}(x,t)-q(x)\mathcal{Z}(x,t)=0,\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ \mathcal{Z}(x,x)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{Z}(x,-x)=-\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.9 ) are equivalent. Therefore, we shall regard $\mathcal{K}(x,t;q)$ as its own odd extension in variable $t$ from ${\mathrm{\Delta }}_0$ to $\mathrm{\Delta }$. Thus, $\mathcal{K}(x,t;q)$ is an odd function in $t$ and satisfies (4.94.9 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{Z}}_{xx}(x,t)-{\mathcal{Z}}_{tt}(x,t)-q(x)\mathcal{Z}(x,t)=0,\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ \mathcal{Z}(x,x)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{Z}(x,-x)=-\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.9 ). The same will be true for $\mathcal{K}(x,t;q+\mathit{\delta }q)$ with $q(x)+\mathit{\delta }q(x)$ replacing $q(x)$ in (4.94.9 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{Z}}_{xx}(x,t)-{\mathcal{Z}}_{tt}(x,t)-q(x)\mathcal{Z}(x,t)=0,\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ \mathcal{Z}(x,x)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{Z}(x,-x)=-\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.9 ). Then $\tilde{\mathcal{K}}(x,t)$, $\mathcal{K}(x,t;q,\mathit{\delta }q)$, $W(x,t)$ can also be regarded as their own odd extensions in $t$-variable. They will satisfy, respectively,4.10 $$\begin{array}{cc}& \left\{\begin{array}{cc}{\tilde{\mathcal{K}}}_{xx}(x,t)-{\tilde{\mathcal{K}}}_{tt}(x,t)-q(x)\tilde{\mathcal{K}}(x,t)=\mathit{\delta }q(x)\mathcal{K}(x,t;q+\mathit{\delta }q),\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ \tilde{\mathcal{K}}(x,\pm x)=\pm \frac{1}{2}{\int }_0^x\mathit{\delta }q(s)ds,\hfill & 0\le x\le a,\hfill \end{array}\right.\hfill \end{array}$$4.10 4.11 $$\begin{array}{cc}& \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q,\mathit{\delta }q)-{\mathcal{K}}_{tt}(x,t;q,\mathit{\delta }q)-q(x)\mathcal{K}(x,t;q,\mathit{\delta }q)=\mathit{\delta }q(x)\mathcal{K}(x,t;q),\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ \mathcal{K}(x,\pm x;q,\mathit{\delta }q)=\pm \frac{1}{2}{\int }_0^x\mathit{\delta }q(s)ds,\hfill & 0\le x\le a,\hfill \end{array}\right.\hfill \end{array}$$4.11 4.12 $$\begin{array}{cc}& \left\{\begin{array}{cc}{W}_{xx}(x,t)-W_{tt}(x,t)-q(x)W(x,t)=\mathit{\delta }q(x)\tilde{\mathcal{K}}(x,t),\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ W(x,\pm x)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\hfill \end{array}$$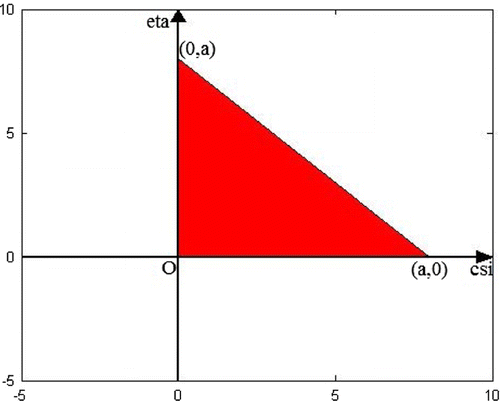4.12 Making the change of independent variables $\mathrm{\Delta }\ni (x,t)\leftrightarrow (\mathit{\xi },\mathit{\eta })\in D$, given by4.13 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\xi }:=\frac{x+t}{2}\hfill \\ \mathit{\eta }:=\frac{x-t}{2}\hfill \end{array}\right.\end{array}$$4.13

Figure 3. The transformed domain $D:=\left\{(\mathit{\xi },\mathit{\eta })\in {\mathbb{R}}^2:0<\mathit{\xi }<a,0<\mathit{\eta }<a,0<\mathit{\xi }+\mathit{\eta }<a\right\}$.

and letting $w(\mathit{\xi },\mathit{\eta }):=W(x,t)$, $Q(\mathit{\xi },\mathit{\eta }):=q(x)$, $\mathit{\delta }Q(\mathit{\xi },\mathit{\eta }):=\mathit{\delta }q(x)$, $\tilde{k}(\mathit{\xi },\mathit{\eta }):=\tilde{\mathcal{K}}(x,t)$, we have that$$D:=\left\{(\mathit{\xi },\mathit{\eta })\in {\mathbb{R}}^2:0<\mathit{\xi }<a,0<\mathit{\eta }<a,0<\mathit{\xi }+\mathit{\eta }<a\right\},$$(see Figure 3) and (4.124.12 $$\begin{array}{cc}& \left\{\begin{array}{cc}{W}_{xx}(x,t)-W_{tt}(x,t)-q(x)W(x,t)=\mathit{\delta }q(x)\tilde{\mathcal{K}}(x,t),\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ W(x,\pm x)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\hfill \end{array}$$4.12 ) is transformed into:4.14 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{w}_{\mathit{\xi }\mathit{\eta }}(\mathit{\xi },\mathit{\eta })-Q(\mathit{\xi },\mathit{\eta })w(\mathit{\xi },\mathit{\eta })=\mathit{\delta }Q(\mathit{\xi },\mathit{\eta })\tilde{k}(\mathit{\xi },\mathit{\eta }),\hfill & (\mathit{\xi },\mathit{\eta })\in D,\hfill \\ w(\mathit{\xi },0)=0,\hfill & 0\le \mathit{\xi }\le a,\hfill \\ w(0,\mathit{\eta })=0,\hfill & 0\le \mathit{\eta }\le a.\hfill \end{array}\right.\end{array}$$4.14 One can show that the problem (4.144.14 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{w}_{\mathit{\xi }\mathit{\eta }}(\mathit{\xi },\mathit{\eta })-Q(\mathit{\xi },\mathit{\eta })w(\mathit{\xi },\mathit{\eta })=\mathit{\delta }Q(\mathit{\xi },\mathit{\eta })\tilde{k}(\mathit{\xi },\mathit{\eta }),\hfill & (\mathit{\xi },\mathit{\eta })\in D,\hfill \\ w(\mathit{\xi },0)=0,\hfill & 0\le \mathit{\xi }\le a,\hfill \\ w(0,\mathit{\eta })=0,\hfill & 0\le \mathit{\eta }\le a.\hfill \end{array}\right.\end{array}$$4.14 ) is equivalent to:4.15 $$\begin{array}{cc}\hfill w(\mathit{\xi },\mathit{\eta })& ={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })w({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime }\hfill \\ \hfill & +{\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}\mathit{\delta }Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })\tilde{k}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.15 Now we can define an operator$$C(\overline{D})\ni w\to T[w]\in C(\overline{D}),$$given by4.16 $$\begin{array}{c}\hfill T[w](\mathit{\xi },\mathit{\eta }):={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })w({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\end{array}$$4.16 The fact that $T$ is well defined (i.e. $T[w]\in C(\overline{D})$, for each $w\in C(\overline{D})$) can be verified by the Lebesgue Dominated Convergence theorem (see [13, Theorem 16, p.91]) applied to the sequence of functions4.17 $$\begin{array}{c}\hfill {\left\{Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })w({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime }){\mathit{\chi }}_{[0,{\mathit{\xi }}_n]\times [0,{\mathit{\eta }}_n]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })\right\}}_{n\ge 1},\end{array}$$4.17 where ${\mathit{\chi }}_{[0,{\mathit{\xi }}_n]\times [0,{\mathit{\eta }}_n]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })$ is the characteristic function of the rectangle $[0,{\mathit{\xi }}_n]\times [0,{\mathit{\eta }}_n]$, and $({\mathit{\xi }}_n,{\mathit{\eta }}_n)\to (\mathit{\xi },\mathit{\eta })$ in $\overline{D}$, as $n\to \infty$. See Figure 4 for some details of the proof.

Figure 4. The position of $({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })$ relative to the quadrants formed by the horizontal and vertical lines through $(\mathit{\xi },\mathit{\eta })$ determines the value $0$ or $1$ of ${\mathit{\chi }}_{[0,{\mathit{\xi }}_n]\times [0,{\mathit{\eta }}_n]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })$ and ${\mathit{\chi }}_{[0,\mathit{\xi }]\times [0,\mathit{\eta }]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })$. Specifically, Upper-Left: ${\mathit{\chi }}_{[0,{\mathit{\xi }}_n]\times [0,{\mathit{\eta }}_n]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })=0={\mathit{\chi }}_{[0,\mathit{\xi }]\times [0,\mathit{\eta }]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })$, for all $n$ large enough; Upper-Right: ${\mathit{\chi }}_{[0,{\mathit{\xi }}_n]\times [0,{\mathit{\eta }}_n]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })=0={\mathit{\chi }}_{[0,\mathit{\xi }]\times [0,\mathit{\eta }]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })$, for all $n$ large enough; Lower-Left: ${\mathit{\chi }}_{[0,{\mathit{\xi }}_n]\times [0,{\mathit{\eta }}_n]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })=1={\mathit{\chi }}_{[0,\mathit{\xi }]\times [0,\mathit{\eta }]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })$, for all $n$ large enough; Lower-Right: ${\mathit{\chi }}_{[0,{\mathit{\xi }}_n]\times [0,{\mathit{\eta }}_n]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })=0={\mathit{\chi }}_{[0,\mathit{\xi }]\times [0,\mathit{\eta }]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })$, for all $n$ large enough. This is so because $({\mathit{\xi }}_n,{\mathit{\eta }}_n)\to (\mathit{\xi },\mathit{\eta })$, as $n\to \infty$, making ${\mathit{\xi }}_n$ stay much closer to $\mathit{\xi }$ than ${\mathit{\xi }}^{\prime }$ stays, and ${\mathit{\eta }}_n$ stay much closer to $\mathit{\eta }$ than ${\mathit{\eta }}^{\prime }$ stays, for all $n$ large enough. So, $|{\mathit{\chi }}_{[0,{\mathit{\xi }}_n]\times [0,{\mathit{\eta }}_n]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })-{\mathit{\chi }}_{[0,\mathit{\xi }]\times [0,\mathit{\eta }]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })|=0$, for all $n\ge N=N(\mathit{\xi },\mathit{\eta },{\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })$, and all $({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })\in \overline{D}$, except maybe for those $({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })$ in $\overline{D}$ located on the horizontal and vertical line segments through $(\mathit{\xi },\mathit{\eta })$. But these line segments have Lebesgue measure zero, and so we proved that the sequence (4.174.17 $$\begin{array}{c}\hfill {\left\{Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })w({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime }){\mathit{\chi }}_{[0,{\mathit{\xi }}_n]\times [0,{\mathit{\eta }}_n]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })\right\}}_{n\ge 1},\end{array}$$4.17 ) converges to $Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })w({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime }){\mathit{\chi }}_{[0,\mathit{\xi }]\times [0,\mathit{\eta }]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })$ a.e. in $({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })\in \overline{D}$. Also, all terms of (4.174.17 $$\begin{array}{c}\hfill {\left\{Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })w({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime }){\mathit{\chi }}_{[0,{\mathit{\xi }}_n]\times [0,{\mathit{\eta }}_n]}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })\right\}}_{n\ge 1},\end{array}$$4.17 ) are dominated by $|Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })|·{∥w∥}_{C(\overline{(}D))}$, which can be easily proven to belong to $L_{\mathbb{R}}^1(D)$.

The linearity of $T$ follows from the linearity of the double integral. The boundedness of $T$ is proven as follows. From (4.164.16 $$\begin{array}{c}\hfill T[w](\mathit{\xi },\mathit{\eta }):={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })w({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\end{array}$$4.16 ) and (4.134.13 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\xi }:=\frac{x+t}{2}\hfill \\ \mathit{\eta }:=\frac{x-t}{2}\hfill \end{array}\right.\end{array}$$4.13 ), and the Cauchy-Schwartz inequality we have4.18 $$\begin{array}{cc}\hfill |T[w](\mathit{\xi },\mathit{\eta })|& \le {∥w∥}_{C(\overline{D})}\sqrt{\mathit{\xi }\mathit{\eta }}·\sqrt{a}·{∥q∥}_{L_{\mathbb{R}}^2(0,a)},\text{for all}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.18 Taking ${\displaystyle \underset{(\mathit{\xi },\mathit{\eta })\in \overline{D}}{sup}}$ in (4.184.18 $$\begin{array}{cc}\hfill |T[w](\mathit{\xi },\mathit{\eta })|& \le {∥w∥}_{C(\overline{D})}\sqrt{\mathit{\xi }\mathit{\eta }}·\sqrt{a}·{∥q∥}_{L_{\mathbb{R}}^2(0,a)},\text{for all}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.18 ) we obtain:4.19 $$\begin{array}{c}\hfill {∥T[w]∥}_{C(\overline{D})}\le a\sqrt{a}{∥q∥}_{L_{\mathbb{R}}^2(0,a)}{∥w∥}_{C(\overline{D})}.\end{array}$$4.19 Thus, the boundedness of the operator $T$ is established:$${∥T∥}_{\mathcal{B}(C(\overline{D}))}\le a\sqrt{a}{∥q∥}_{L_{\mathbb{R}}^2(0,a)}.$$Next, we shall find an upper bound for ${∥T^n∥}_{\mathcal{B}(C(\overline{D}))}$, for $n=1,2,3,\dots$. Using $T^2[w](\mathit{\xi },\mathit{\eta })=T[T[w]](\mathit{\xi },\mathit{\eta })$, (4.164.16 $$\begin{array}{c}\hfill T[w](\mathit{\xi },\mathit{\eta }):={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })w({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\end{array}$$4.16 ) with $w$ replaced by $T[w]$, (4.184.18 $$\begin{array}{cc}\hfill |T[w](\mathit{\xi },\mathit{\eta })|& \le {∥w∥}_{C(\overline{D})}\sqrt{\mathit{\xi }\mathit{\eta }}·\sqrt{a}·{∥q∥}_{L_{\mathbb{R}}^2(0,a)},\text{for all}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.18 ) and (4.134.13 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\xi }:=\frac{x+t}{2}\hfill \\ \mathit{\eta }:=\frac{x-t}{2}\hfill \end{array}\right.\end{array}$$4.13 ), and the Cauchy-Schwartz inequality we find:4.20 $$\begin{array}{cc}\hfill |T^2[w](\mathit{\xi },\mathit{\eta })|& \le {∥w∥}_{C(\overline{D})}·{(\sqrt{a})}^2·{∥q∥}_{L_{\mathbb{R}}^2(0,a)}^2·\frac{\mathit{\xi }\mathit{\eta }}{2},\text{for all}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.20 Based on (4.184.18 $$\begin{array}{cc}\hfill |T[w](\mathit{\xi },\mathit{\eta })|& \le {∥w∥}_{C(\overline{D})}\sqrt{\mathit{\xi }\mathit{\eta }}·\sqrt{a}·{∥q∥}_{L_{\mathbb{R}}^2(0,a)},\text{for all}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.18 ) and (4.204.20 $$\begin{array}{cc}\hfill |T^2[w](\mathit{\xi },\mathit{\eta })|& \le {∥w∥}_{C(\overline{D})}·{(\sqrt{a})}^2·{∥q∥}_{L_{\mathbb{R}}^2(0,a)}^2·\frac{\mathit{\xi }\mathit{\eta }}{2},\text{for all}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.20 ), we propose the following estimate which can be proven by induction on $n$ with similar calculations as the ones in (4.204.20 $$\begin{array}{cc}\hfill |T^2[w](\mathit{\xi },\mathit{\eta })|& \le {∥w∥}_{C(\overline{D})}·{(\sqrt{a})}^2·{∥q∥}_{L_{\mathbb{R}}^2(0,a)}^2·\frac{\mathit{\xi }\mathit{\eta }}{2},\text{for all}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.20 ):4.21 $$\begin{array}{c}\hfill |T^n[w](\mathit{\xi },\mathit{\eta })|\le {∥w∥}_{C(\overline{D})}·{(\sqrt{a})}^n·{∥q∥}_{L_{\mathbb{R}}^2(0,a)}^n·\frac{{(\sqrt{\mathit{\xi }\mathit{\eta }})}^n}{n!},\text{for all}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\end{array}$$4.21 Taking ${\displaystyle \underset{(\mathit{\xi },\mathit{\eta })\in \overline{D}}{sup}}$ in (4.214.21 $$\begin{array}{c}\hfill |T^n[w](\mathit{\xi },\mathit{\eta })|\le {∥w∥}_{C(\overline{D})}·{(\sqrt{a})}^n·{∥q∥}_{L_{\mathbb{R}}^2(0,a)}^n·\frac{{(\sqrt{\mathit{\xi }\mathit{\eta }})}^n}{n!},\text{for all}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\end{array}$$4.21 ), we have that4.22 $$\begin{array}{c}\hfill {∥T^n[w]∥}_{C(\overline{D})}\le \frac{{(a\sqrt{a})}^n}{n!}{∥q∥}_{L_{\mathbb{R}}^2(0,a)}^n{∥w∥}_{C(\overline{D})},\end{array}$$4.22 and so4.23 $$\begin{array}{c}\hfill {∥T^n∥}_{\mathcal{B}(C(\overline{D}))}\le \frac{{(a\sqrt{a})}^n}{n!}{∥q∥}_{L_{\mathbb{R}}^2(0,a)}^n.\end{array}$$4.23 Formula (4.234.23 $$\begin{array}{c}\hfill {∥T^n∥}_{\mathcal{B}(C(\overline{D}))}\le \frac{{(a\sqrt{a})}^n}{n!}{∥q∥}_{L_{\mathbb{R}}^2(0,a)}^n.\end{array}$$4.23 ) implies that ${\displaystyle {∥T^n∥}_{\mathcal{B}(C(\overline{D}))}^{\frac{1}{n}}\le \frac{a\sqrt{a}{∥q∥}_{L_{\mathbb{R}}^2(0,a)}}{\sqrt[n]{n!}}}$, for $n=1,2,3,\dots$. Since ${\displaystyle \underset{n\to \infty }{lim}\frac{1}{\sqrt[n]{n!}}=0}$, it follows that for some $m$ large enough, ${\displaystyle {∥T^m∥}_{\mathcal{B}(C(\overline{D}))}^{\frac{1}{m}}<1}$. Thus, by Lemma 1 of Appendix 1 we infer that $I-T$ is an invertible linear operator on $C(\overline{D})$ with a bounded inverse. This fact together with (4.154.15 $$\begin{array}{cc}\hfill w(\mathit{\xi },\mathit{\eta })& ={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })w({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime }\hfill \\ \hfill & +{\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}\mathit{\delta }Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })\tilde{k}({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.15 ), and similar calculations to those in (4.184.18 $$\begin{array}{cc}\hfill |T[w](\mathit{\xi },\mathit{\eta })|& \le {∥w∥}_{C(\overline{D})}\sqrt{\mathit{\xi }\mathit{\eta }}·\sqrt{a}·{∥q∥}_{L_{\mathbb{R}}^2(0,a)},\text{for all}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.18 ) imply that:4.24 $$\begin{array}{cc}\hfill {∥w∥}_{C(\overline{D})}& \le a\sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·{∥\tilde{\mathcal{K}}∥}_{C(\overline{\mathrm{\Delta }})}·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}.\hfill \end{array}$$4.24 Then using the definition of the $L^2$-norm, the fact that $W(x,t)$ is odd in $t$, and the fact that ${\int }_{-a}^{a}U(t)dt=2{\int }_0^{a}U(t)dt$, for $U(t)=even$, formula (4.244.24 $$\begin{array}{cc}\hfill {∥w∥}_{C(\overline{D})}& \le a\sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·{∥\tilde{\mathcal{K}}∥}_{C(\overline{\mathrm{\Delta }})}·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}.\hfill \end{array}$$4.24 ), and the Cauchy-Schwartz inequality, we obtain:4.25 $$\begin{array}{c}\hfill {∥W(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2\le a^4{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}^2·{∥\tilde{\mathcal{K}}∥}_{C(\overline{\mathrm{\Delta }})}^2·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2.\end{array}$$4.25 By (4.134.13 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\xi }:=\frac{x+t}{2}\hfill \\ \mathit{\eta }:=\frac{x-t}{2}\hfill \end{array}\right.\end{array}$$4.13 ) and $w(\mathit{\xi },\mathit{\eta }):=W(x,t)$ we have:4.26 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{W}_x(a,t)=\frac{1}{2}{w}_{\mathit{\xi }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)+\frac{1}{2}{w}_{\mathit{\eta }}\left(\frac{a+t}{2},\frac{a-t}{2}\right),-a\le t\le a\hfill \\ W_t(a,t)=\frac{1}{2}{w}_{\mathit{\xi }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)-\frac{1}{2}{w}_{\mathit{\eta }}\left(\frac{a+t}{2},\frac{a-t}{2}\right),-a\le t\le a.\hfill \end{array}\right.\end{array}$$4.26 Due to (4.264.26 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{W}_x(a,t)=\frac{1}{2}{w}_{\mathit{\xi }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)+\frac{1}{2}{w}_{\mathit{\eta }}\left(\frac{a+t}{2},\frac{a-t}{2}\right),-a\le t\le a\hfill \\ W_t(a,t)=\frac{1}{2}{w}_{\mathit{\xi }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)-\frac{1}{2}{w}_{\mathit{\eta }}\left(\frac{a+t}{2},\frac{a-t}{2}\right),-a\le t\le a.\hfill \end{array}\right.\end{array}$$4.26 ), the odd/even of $W(x,t)$, $W_x(x,t)$, $W_t(x,t)$ in $t$, the fact that ${∥U∥}_{L_{\mathbb{R}}^2(-a,a)}^2=2{∥U∥}_{L_{\mathbb{R}}^2(0,a)}^2$, for $U(-t)=\pm U(t)$, and the fact that ${\Vert u\pm v\Vert }^2\le (\Vert u\Vert +{\Vert v\Vert )}^2$, we write:4.27 $$\begin{array}{c}\hfill {∥W_x(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2\le \frac{a}{4}·{\left(\begin{array}{cc}sup|w_{\mathit{\xi }}(\mathit{\xi },\mathit{\eta })|+\hfill & sup|w_{\mathit{\eta }}(\mathit{\xi },\mathit{\eta })|\hfill \\ (\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill & (\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill \\ \mathit{\xi }+\mathit{\eta }=a\hfill & \mathit{\xi }+\mathit{\eta }=a\hfill \end{array}\right)}^2,\end{array}$$4.27 4.28 $$\begin{array}{c}\hfill {∥W_t(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2\le \frac{a}{4}·{\left(\begin{array}{cc}sup|w_{\mathit{\xi }}(\mathit{\xi },\mathit{\eta })|+\hfill & sup|w_{\mathit{\eta }}(\mathit{\xi },\mathit{\eta })|\hfill \\ (\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill & (\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill \\ \mathit{\xi }+\mathit{\eta }=a\hfill & \mathit{\xi }+\mathit{\eta }=a\hfill \end{array}\right)}^2.\end{array}$$4.28 Using the PDE of (4.144.14 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{w}_{\mathit{\xi }\mathit{\eta }}(\mathit{\xi },\mathit{\eta })-Q(\mathit{\xi },\mathit{\eta })w(\mathit{\xi },\mathit{\eta })=\mathit{\delta }Q(\mathit{\xi },\mathit{\eta })\tilde{k}(\mathit{\xi },\mathit{\eta }),\hfill & (\mathit{\xi },\mathit{\eta })\in D,\hfill \\ w(\mathit{\xi },0)=0,\hfill & 0\le \mathit{\xi }\le a,\hfill \\ w(0,\mathit{\eta })=0,\hfill & 0\le \mathit{\eta }\le a.\hfill \end{array}\right.\end{array}$$4.14 ) along with the first and respectively second boundary condition of (4.144.14 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{w}_{\mathit{\xi }\mathit{\eta }}(\mathit{\xi },\mathit{\eta })-Q(\mathit{\xi },\mathit{\eta })w(\mathit{\xi },\mathit{\eta })=\mathit{\delta }Q(\mathit{\xi },\mathit{\eta })\tilde{k}(\mathit{\xi },\mathit{\eta }),\hfill & (\mathit{\xi },\mathit{\eta })\in D,\hfill \\ w(\mathit{\xi },0)=0,\hfill & 0\le \mathit{\xi }\le a,\hfill \\ w(0,\mathit{\eta })=0,\hfill & 0\le \mathit{\eta }\le a.\hfill \end{array}\right.\end{array}$$4.14 ), we obtain:4.29 $$\begin{array}{cc}\hfill w_{\mathit{\xi }}(\mathit{\xi },\mathit{\eta })& ={\int }_0^{\mathit{\eta }}Q(\mathit{\xi },{\mathit{\eta }}^{\prime })w(\mathit{\xi },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }+{\int }_0^{\mathit{\eta }}\mathit{\delta }Q(\mathit{\xi },{\mathit{\eta }}^{\prime })\tilde{k}(\mathit{\xi },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D},\hfill \end{array}$$4.29 4.30 $$\begin{array}{cc}\hfill w_{\mathit{\eta }}(\mathit{\xi },\mathit{\eta })& ={\int }_0^{\mathit{\xi }}Q({\mathit{\xi }}^{\prime },\mathit{\eta })w({\mathit{\xi }}^{\prime },\mathit{\eta })d{\mathit{\xi }}^{\prime }+{\int }_0^{\mathit{\xi }}\mathit{\delta }Q({\mathit{\xi }}^{\prime },\mathit{\eta })\tilde{k}({\mathit{\xi }}^{\prime },\mathit{\eta })d{\mathit{\xi }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.30 Next, for an arbitrary but fixed $(\mathit{\xi },\mathit{\eta })\in \overline{D}$ such that $\mathit{\xi }+\mathit{\eta }=a$, we have based on (4.294.29 $$\begin{array}{cc}\hfill w_{\mathit{\xi }}(\mathit{\xi },\mathit{\eta })& ={\int }_0^{\mathit{\eta }}Q(\mathit{\xi },{\mathit{\eta }}^{\prime })w(\mathit{\xi },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }+{\int }_0^{\mathit{\eta }}\mathit{\delta }Q(\mathit{\xi },{\mathit{\eta }}^{\prime })\tilde{k}(\mathit{\xi },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D},\hfill \end{array}$$4.29 ), (4.244.24 $$\begin{array}{cc}\hfill {∥w∥}_{C(\overline{D})}& \le a\sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·{∥\tilde{\mathcal{K}}∥}_{C(\overline{\mathrm{\Delta }})}·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}.\hfill \end{array}$$4.24 ) and (4.134.13 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\xi }:=\frac{x+t}{2}\hfill \\ \mathit{\eta }:=\frac{x-t}{2}\hfill \end{array}\right.\end{array}$$4.13 ), the definitions of $Q(\mathit{\xi },\mathit{\eta })$, $\mathit{\delta }Q(\mathit{\xi },\mathit{\eta })$, $\tilde{k}(\mathit{\xi },\mathit{\eta })$ (see right after (4.134.13 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\xi }:=\frac{x+t}{2}\hfill \\ \mathit{\eta }:=\frac{x-t}{2}\hfill \end{array}\right.\end{array}$$4.13 )), and the Cauchy-Schwartz inequality, that:4.31 $$\begin{array}{cc}\hfill |w_{\mathit{\xi }}(\mathit{\xi },\mathit{\eta })|& \le \sqrt{a}·{∥\tilde{\mathcal{K}}∥}_{C(\overline{\mathrm{\Delta }})}·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\hfill \\ \hfill & ·\left(a\sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·{∥q∥}_{L_{\mathbb{R}}^2(0,a)}+1\right).\hfill \end{array}$$4.31 Thus,4.32 $$\begin{array}{cc}\hfill \underset{\begin{array}{c}(\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill \\ \mathit{\xi }+\mathit{\eta }=a\hfill \end{array}}{sup}|w_{\mathit{\xi }}(\mathit{\xi },\mathit{\eta })|& \le \sqrt{a}·{∥\tilde{\mathcal{K}}∥}_{C(\overline{\mathrm{\Delta }})}·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\hfill \\ \hfill & ·\left(a\sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·{∥q∥}_{L_{\mathbb{R}}^2(0,a)}+1\right),\hfill \end{array}$$4.32 and similarly,4.33 $$\begin{array}{cc}\hfill \underset{\begin{array}{c}(\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill \\ \mathit{\xi }+\mathit{\eta }=a\hfill \end{array}}{sup}|w_{\mathit{\eta }}(\mathit{\xi },\mathit{\eta })|& \le \sqrt{a}·{∥\tilde{\mathcal{K}}∥}_{C(\overline{\mathrm{\Delta }})}·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\hfill \\ & ·\left(a\sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·{∥q∥}_{L_{\mathbb{R}}^2(0,a)}+1\right).\hfill \end{array}$$4.33 By (4.254.25 $$\begin{array}{c}\hfill {∥W(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2\le a^4{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}^2·{∥\tilde{\mathcal{K}}∥}_{C(\overline{\mathrm{\Delta }})}^2·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2.\end{array}$$4.25 ), (4.274.27 $$\begin{array}{c}\hfill {∥W_x(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2\le \frac{a}{4}·{\left(\begin{array}{cc}sup|w_{\mathit{\xi }}(\mathit{\xi },\mathit{\eta })|+\hfill & sup|w_{\mathit{\eta }}(\mathit{\xi },\mathit{\eta })|\hfill \\ (\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill & (\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill \\ \mathit{\xi }+\mathit{\eta }=a\hfill & \mathit{\xi }+\mathit{\eta }=a\hfill \end{array}\right)}^2,\end{array}$$4.27 ), (4.284.28 $$\begin{array}{c}\hfill {∥W_t(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2\le \frac{a}{4}·{\left(\begin{array}{cc}sup|w_{\mathit{\xi }}(\mathit{\xi },\mathit{\eta })|+\hfill & sup|w_{\mathit{\eta }}(\mathit{\xi },\mathit{\eta })|\hfill \\ (\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill & (\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill \\ \mathit{\xi }+\mathit{\eta }=a\hfill & \mathit{\xi }+\mathit{\eta }=a\hfill \end{array}\right)}^2.\end{array}$$4.28 ), (4.324.32 $$\begin{array}{cc}\hfill \underset{\begin{array}{c}(\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill \\ \mathit{\xi }+\mathit{\eta }=a\hfill \end{array}}{sup}|w_{\mathit{\xi }}(\mathit{\xi },\mathit{\eta })|& \le \sqrt{a}·{∥\tilde{\mathcal{K}}∥}_{C(\overline{\mathrm{\Delta }})}·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\hfill \\ \hfill & ·\left(a\sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·{∥q∥}_{L_{\mathbb{R}}^2(0,a)}+1\right),\hfill \end{array}$$4.32 ), (4.334.33 $$\begin{array}{cc}\hfill \underset{\begin{array}{c}(\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill \\ \mathit{\xi }+\mathit{\eta }=a\hfill \end{array}}{sup}|w_{\mathit{\eta }}(\mathit{\xi },\mathit{\eta })|& \le \sqrt{a}·{∥\tilde{\mathcal{K}}∥}_{C(\overline{\mathrm{\Delta }})}·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\hfill \\ & ·\left(a\sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·{∥q∥}_{L_{\mathbb{R}}^2(0,a)}+1\right).\hfill \end{array}$$4.33 ), we have:4.34 $$\begin{array}{cc}& \frac{{∥W(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_t(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_x(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2}\hfill \\ \hfill & \le a^2·\mathbf{A}·{∥\mathcal{K}(·,·;q+\mathit{\delta }q)-\mathcal{K}(·,·;q)∥}_{C({\overline{\mathrm{\Delta }}}_0)}^2\hfill \\ \hfill & \text{because}\mathcal{K}(x,t;q+\mathit{\delta }q)\text{and}\mathcal{K}(x,t;q)\text{are odd in}t.\hfill \end{array}$$4.34 In (4.344.34 $$\begin{array}{cc}& \frac{{∥W(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_t(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_x(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2}\hfill \\ \hfill & \le a^2·\mathbf{A}·{∥\mathcal{K}(·,·;q+\mathit{\delta }q)-\mathcal{K}(·,·;q)∥}_{C({\overline{\mathrm{\Delta }}}_0)}^2\hfill \\ \hfill & \text{because}\mathcal{K}(x,t;q+\mathit{\delta }q)\text{and}\mathcal{K}(x,t;q)\text{are odd in}t.\hfill \end{array}$$4.34 ), we used ${∥\mathcal{K}(·,·;q+\mathit{\delta }q)-\mathcal{K}(·,·;q)∥}_{C(\overline{\mathrm{\Delta }})}={∥\mathcal{K}(·,·;q+\mathit{\delta }q)-\mathcal{K}(·,·;q)∥}_{C({\overline{\mathrm{\Delta }}}_0)}$. The quantity $\mathbf{A}$ in (4.344.34 $$\begin{array}{cc}& \frac{{∥W(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_t(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_x(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2}\hfill \\ \hfill & \le a^2·\mathbf{A}·{∥\mathcal{K}(·,·;q+\mathit{\delta }q)-\mathcal{K}(·,·;q)∥}_{C({\overline{\mathrm{\Delta }}}_0)}^2\hfill \\ \hfill & \text{because}\mathcal{K}(x,t;q+\mathit{\delta }q)\text{and}\mathcal{K}(x,t;q)\text{are odd in}t.\hfill \end{array}$$4.34 ) is:$$\mathbf{A}=a^2·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}^2+2·{\left(a\sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·{∥q∥}_{L_{\mathbb{R}}^2(0,a)}+1\right)}^2.$$Thus, (4.344.34 $$\begin{array}{cc}& \frac{{∥W(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_t(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_x(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2}\hfill \\ \hfill & \le a^2·\mathbf{A}·{∥\mathcal{K}(·,·;q+\mathit{\delta }q)-\mathcal{K}(·,·;q)∥}_{C({\overline{\mathrm{\Delta }}}_0)}^2\hfill \\ \hfill & \text{because}\mathcal{K}(x,t;q+\mathit{\delta }q)\text{and}\mathcal{K}(x,t;q)\text{are odd in}t.\hfill \end{array}$$4.34 ) shows that (4.74.7 $$\begin{array}{c}\hfill \frac{{∥W(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_t(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_x(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2}\to 0,\text{when}{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\to 0.\end{array}$$4.7 ) is satisfied, because ${∥\mathcal{K}(·,·;q+\mathit{\delta }q)-\mathcal{K}(·,·;q)∥}_{C({\overline{\mathrm{\Delta }}}_0)}\to 0$, as ${∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\to 0$ (see Theorem 4.15(b) in [7, p.147]). Hence, (4.14.1 $$\begin{array}{c}\hfill \frac{{∥F(q+\mathit{\delta }q)-F(q)-F^{\prime }(q)(\mathit{\delta }q)∥}_{H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)}}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}}\to 0,\text{when}{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\to 0.\end{array}$$4.1 ) is satisfied, because as mentioned previously (4.74.7 $$\begin{array}{c}\hfill \frac{{∥W(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_t(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥W_x(a,·)∥}_{L_{\mathbb{R}}^2(0,a)}^2}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2}\to 0,\text{when}{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\to 0.\end{array}$$4.7 ) is equivalent to (4.14.1 $$\begin{array}{c}\hfill \frac{{∥F(q+\mathit{\delta }q)-F(q)-F^{\prime }(q)(\mathit{\delta }q)∥}_{H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)}}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}}\to 0,\text{when}{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\to 0.\end{array}$$4.1 ).

In order to completely validate formula (4.44.4 $$\begin{array}{c}\hfill F^{\prime }(q)(\mathit{\delta }q):=\{\mathcal{K}(a,t;q,\mathit{\delta }q),{\mathcal{K}}_x(a,t;q,\mathit{\delta }q)\},\end{array}$$4.4 ) as the definition of the Fréchet derivative for the map $F$, in addition to proving (4.14.1 $$\begin{array}{c}\hfill \frac{{∥F(q+\mathit{\delta }q)-F(q)-F^{\prime }(q)(\mathit{\delta }q)∥}_{H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)}}{{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}}\to 0,\text{when}{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}\to 0.\end{array}$$4.1 ), we also need to show that for a fixed $q\in L_{\mathbb{R}}^2(0,a)$, $F^{\prime }(q)(\mathit{\delta }q)$ is linear and bounded in $\mathit{\delta }q\in L_{\mathbb{R}}^2(0,a)$. The linearity follows from the fact that the boundary value problem (4.54.5 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q,\mathit{\delta }q)-{\mathcal{K}}_{tt}(x,t;q,\mathit{\delta }q)-q(x)\mathcal{K}(x,t;q,\mathit{\delta }q)=\mathit{\delta }q(x)\mathcal{K}(x,t;q),\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q,\mathit{\delta }q)=\frac{1}{2}{\int }_0^x\mathit{\delta }q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q,\mathit{\delta }q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.5 ) can be easily proven to be linear in $\mathit{\delta }q(x)$ via the uniqueness of its solution $\mathcal{K}(x,t;q,\mathit{\delta }q)$.

For the boundedness of $F^{\prime }(q)$ we proceed as follows. For a fixed $q\in L_{\mathbb{R}}^2(0,a)$, the function $\mathcal{K}(x,t;q)$ will be determined from (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ), so it will be known. Then recall that (4.54.5 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q,\mathit{\delta }q)-{\mathcal{K}}_{tt}(x,t;q,\mathit{\delta }q)-q(x)\mathcal{K}(x,t;q,\mathit{\delta }q)=\mathit{\delta }q(x)\mathcal{K}(x,t;q),\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q,\mathit{\delta }q)=\frac{1}{2}{\int }_0^x\mathit{\delta }q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q,\mathit{\delta }q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$4.5 ) is equivalent to (4.114.11 $$\begin{array}{cc}& \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q,\mathit{\delta }q)-{\mathcal{K}}_{tt}(x,t;q,\mathit{\delta }q)-q(x)\mathcal{K}(x,t;q,\mathit{\delta }q)=\mathit{\delta }q(x)\mathcal{K}(x,t;q),\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ \mathcal{K}(x,\pm x;q,\mathit{\delta }q)=\pm \frac{1}{2}{\int }_0^x\mathit{\delta }q(s)ds,\hfill & 0\le x\le a,\hfill \end{array}\right.\hfill \end{array}$$4.11 ) with the understanding that $\mathcal{K}(x,t;q,\mathit{\delta }q)$ and $\mathcal{K}(x,t;q)$ in (4.114.11 $$\begin{array}{cc}& \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q,\mathit{\delta }q)-{\mathcal{K}}_{tt}(x,t;q,\mathit{\delta }q)-q(x)\mathcal{K}(x,t;q,\mathit{\delta }q)=\mathit{\delta }q(x)\mathcal{K}(x,t;q),\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ \mathcal{K}(x,\pm x;q,\mathit{\delta }q)=\pm \frac{1}{2}{\int }_0^x\mathit{\delta }q(s)ds,\hfill & 0\le x\le a,\hfill \end{array}\right.\hfill \end{array}$$4.11 ) are actually the odd extensions in variable $t$ of the originals $\mathcal{K}(x,t;q,\mathit{\delta }q)$ and $\mathcal{K}(x,t;q)$ from ${\mathrm{\Delta }}_0$ to $\mathrm{\Delta }$. By the change of independent variables (4.134.13 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\xi }:=\frac{x+t}{2}\hfill \\ \mathit{\eta }:=\frac{x-t}{2}\hfill \end{array}\right.\end{array}$$4.13 ), and letting4.35 $$\begin{array}{c}\hfill v(\mathit{\xi },\mathit{\eta }):=\mathcal{K}(x,t;q,\mathit{\delta }q)\text{and}k(\mathit{\xi },\mathit{\eta }):=\mathcal{K}(x,t;q),\end{array}$$4.35 the problem (4.114.11 $$\begin{array}{cc}& \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q,\mathit{\delta }q)-{\mathcal{K}}_{tt}(x,t;q,\mathit{\delta }q)-q(x)\mathcal{K}(x,t;q,\mathit{\delta }q)=\mathit{\delta }q(x)\mathcal{K}(x,t;q),\hfill & (x,t)\in \mathrm{\Delta }\hfill \\ \mathcal{K}(x,\pm x;q,\mathit{\delta }q)=\pm \frac{1}{2}{\int }_0^x\mathit{\delta }q(s)ds,\hfill & 0\le x\le a,\hfill \end{array}\right.\hfill \end{array}$$4.11 ) takes the equivalent form:4.36 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{v}_{\mathit{\xi }\mathit{\eta }}(\mathit{\xi },\mathit{\eta })-q(\mathit{\xi }+\mathit{\eta })v(\mathit{\xi },\mathit{\eta })=\mathit{\delta }q(\mathit{\xi }+\mathit{\eta })k(\mathit{\xi },\mathit{\eta }),\hfill & (\mathit{\xi },\mathit{\eta })\in D\hfill \\ v(\mathit{\xi },0)=\frac{1}{2}{\int }_0^{\mathit{\xi }}\mathit{\delta }q(s)ds,\hfill & 0\le \mathit{\xi }\le a\hfill \\ v(0,\mathit{\eta })=-\frac{1}{2}{\int }_0^{\mathit{\eta }}\mathit{\delta }q(s)ds,\hfill & 0\le \mathit{\eta }\le a.\hfill \end{array}\right.\end{array}$$4.36 In turn,  (4.364.36 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{v}_{\mathit{\xi }\mathit{\eta }}(\mathit{\xi },\mathit{\eta })-q(\mathit{\xi }+\mathit{\eta })v(\mathit{\xi },\mathit{\eta })=\mathit{\delta }q(\mathit{\xi }+\mathit{\eta })k(\mathit{\xi },\mathit{\eta }),\hfill & (\mathit{\xi },\mathit{\eta })\in D\hfill \\ v(\mathit{\xi },0)=\frac{1}{2}{\int }_0^{\mathit{\xi }}\mathit{\delta }q(s)ds,\hfill & 0\le \mathit{\xi }\le a\hfill \\ v(0,\mathit{\eta })=-\frac{1}{2}{\int }_0^{\mathit{\eta }}\mathit{\delta }q(s)ds,\hfill & 0\le \mathit{\eta }\le a.\hfill \end{array}\right.\end{array}$$4.36 ) is equivalent to4.37 $$\begin{array}{cc}\hfill v(\mathit{\xi },\mathit{\eta })& ={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}q({\mathit{\xi }}^{\prime }+{\mathit{\eta }}^{\prime })v({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime }+{\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}\mathit{\delta }q({\mathit{\xi }}^{\prime }+{\mathit{\eta }}^{\prime })k({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime }\hfill \\ \hfill & +\frac{1}{2}{\int }_0^{\mathit{\xi }}\mathit{\delta }q({\mathit{\xi }}^{\prime })d{\mathit{\xi }}^{\prime }-\frac{1}{2}{\int }_0^{\mathit{\eta }}\mathit{\delta }q({\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.37 We also have:4.38 $$\begin{array}{cc}\hfill v_{\mathit{\xi }}(\mathit{\xi },\mathit{\eta })& ={\int }_0^{\mathit{\eta }}q(\mathit{\xi }+{\mathit{\eta }}^{\prime })v(\mathit{\xi },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }+{\int }_0^{\mathit{\eta }}\mathit{\delta }q(\mathit{\xi }+{\mathit{\eta }}^{\prime })k(\mathit{\xi },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }+\frac{1}{2}·\mathit{\delta }q(\mathit{\xi }),\text{for}(\mathit{\xi },\mathit{\eta })\in D\hfill \\ \hfill \end{array}$$4.38 4.39 $$\begin{array}{cc}\hfill v_{\mathit{\eta }}(\mathit{\xi },\mathit{\eta })& ={\int }_0^{\mathit{\xi }}q({\mathit{\xi }}^{\prime }+\mathit{\eta })v({\mathit{\xi }}^{\prime },\mathit{\eta })d{\mathit{\xi }}^{\prime }+{\int }_0^{\mathit{\xi }}\mathit{\delta }q({\mathit{\xi }}^{\prime }+\mathit{\eta })k({\mathit{\xi }}^{\prime },\mathit{\eta })d{\mathit{\xi }}^{\prime }-\frac{1}{2}·\mathit{\delta }q(\mathit{\eta }),\text{for}(\mathit{\xi },\mathit{\eta })\in D.\hfill \\ \hfill \end{array}$$4.39 By (4.164.16 $$\begin{array}{c}\hfill T[w](\mathit{\xi },\mathit{\eta }):={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })w({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\end{array}$$4.16 ) and (4.374.37 $$\begin{array}{cc}\hfill v(\mathit{\xi },\mathit{\eta })& ={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}q({\mathit{\xi }}^{\prime }+{\mathit{\eta }}^{\prime })v({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime }+{\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}\mathit{\delta }q({\mathit{\xi }}^{\prime }+{\mathit{\eta }}^{\prime })k({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime }\hfill \\ \hfill & +\frac{1}{2}{\int }_0^{\mathit{\xi }}\mathit{\delta }q({\mathit{\xi }}^{\prime })d{\mathit{\xi }}^{\prime }-\frac{1}{2}{\int }_0^{\mathit{\eta }}\mathit{\delta }q({\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\hfill \end{array}$$4.37 ), and the fact that $I-T$ is invertible in $\mathcal{B}(C(\overline{D}))$ as shown previously, we write:4.40 $$\begin{array}{c}\hfill v={(I-T)}^{-1}[u],\end{array}$$4.40 where4.41 $$\begin{array}{cc}\hfill u(\mathit{\xi },\mathit{\eta })& :={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}\mathit{\delta }q({\mathit{\xi }}^{\prime }+{\mathit{\eta }}^{\prime })k({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime }\hfill \\ \hfill & +\frac{1}{2}{\int }_0^{\mathit{\xi }}\mathit{\delta }q({\mathit{\xi }}^{\prime })d{\mathit{\xi }}^{\prime }-\frac{1}{2}{\int }_0^{\mathit{\eta }}\mathit{\delta }q({\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill \end{array}$$4.41 It follows that $u\in C(\overline{D})$ because the first term in (4.414.41 $$\begin{array}{cc}\hfill u(\mathit{\xi },\mathit{\eta })& :={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}\mathit{\delta }q({\mathit{\xi }}^{\prime }+{\mathit{\eta }}^{\prime })k({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime }\hfill \\ \hfill & +\frac{1}{2}{\int }_0^{\mathit{\xi }}\mathit{\delta }q({\mathit{\xi }}^{\prime })d{\mathit{\xi }}^{\prime }-\frac{1}{2}{\int }_0^{\mathit{\eta }}\mathit{\delta }q({\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill \end{array}$$4.41 ) can be proven to belong to $C(\overline{D})$ by the Lebesgue Dominated Convergence theorem (similar arguments to those we justified that the right hand side of (4.164.16 $$\begin{array}{c}\hfill T[w](\mathit{\xi },\mathit{\eta }):={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}Q({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })w({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}.\end{array}$$4.16 ) lies in $C(\overline{D})$), and the second and last terms in (4.414.41 $$\begin{array}{cc}\hfill u(\mathit{\xi },\mathit{\eta })& :={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}\mathit{\delta }q({\mathit{\xi }}^{\prime }+{\mathit{\eta }}^{\prime })k({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime }\hfill \\ \hfill & +\frac{1}{2}{\int }_0^{\mathit{\xi }}\mathit{\delta }q({\mathit{\xi }}^{\prime })d{\mathit{\xi }}^{\prime }-\frac{1}{2}{\int }_0^{\mathit{\eta }}\mathit{\delta }q({\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill \end{array}$$4.41 ) are $H^1(0,a)$ since $\mathit{\delta }q\in L_{\mathbb{R}}^2(0,a)$, so they are $AC[0,a]$, and so continuous in $\mathit{\xi }$ and respectively in $\mathit{\eta }$. Also, from (4.414.41 $$\begin{array}{cc}\hfill u(\mathit{\xi },\mathit{\eta })& :={\int }_0^{\mathit{\xi }}{\int }_0^{\mathit{\eta }}\mathit{\delta }q({\mathit{\xi }}^{\prime }+{\mathit{\eta }}^{\prime })k({\mathit{\xi }}^{\prime },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }d{\mathit{\xi }}^{\prime }\hfill \\ \hfill & +\frac{1}{2}{\int }_0^{\mathit{\xi }}\mathit{\delta }q({\mathit{\xi }}^{\prime })d{\mathit{\xi }}^{\prime }-\frac{1}{2}{\int }_0^{\mathit{\eta }}\mathit{\delta }q({\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime },\text{for}(\mathit{\xi },\mathit{\eta })\in \overline{D}\hfill \end{array}$$4.41 ) and (4.134.13 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\xi }:=\frac{x+t}{2}\hfill \\ \mathit{\eta }:=\frac{x-t}{2}\hfill \end{array}\right.\end{array}$$4.13 ) whose Jacobian is ${\displaystyle -\frac{1}{2}}$, and the Cauchy-Schwartz inequality we get:4.42 $$\begin{array}{cc}\hfill {∥u∥}_{C(\overline{D})}& \le \sqrt{a}·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}·\left(a·{∥\mathcal{K}(·,·;q)∥}_{C(\overline{\mathrm{\Delta }}0)}+1\right).\hfill \end{array}$$4.42 Formulas (4.404.40 $$\begin{array}{c}\hfill v={(I-T)}^{-1}[u],\end{array}$$4.40 ) and (4.424.42 $$\begin{array}{cc}\hfill {∥u∥}_{C(\overline{D})}& \le \sqrt{a}·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}·\left(a·{∥\mathcal{K}(·,·;q)∥}_{C(\overline{\mathrm{\Delta }}0)}+1\right).\hfill \end{array}$$4.42 ) imply that4.43 $$\begin{array}{c}\hfill {∥v∥}_{C(\overline{D})}\le \sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·\left(a·{∥\mathcal{K}(·,·;q)∥}_{C(\overline{\mathrm{\Delta }}0)}+1\right)·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}.\end{array}$$4.43 From (4.44.4 $$\begin{array}{c}\hfill F^{\prime }(q)(\mathit{\delta }q):=\{\mathcal{K}(a,t;q,\mathit{\delta }q),{\mathcal{K}}_x(a,t;q,\mathit{\delta }q)\},\end{array}$$4.4 ), (4.354.35 $$\begin{array}{c}\hfill v(\mathit{\xi },\mathit{\eta }):=\mathcal{K}(x,t;q,\mathit{\delta }q)\text{and}k(\mathit{\xi },\mathit{\eta }):=\mathcal{K}(x,t;q),\end{array}$$4.35 ), (4.134.13 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathit{\xi }:=\frac{x+t}{2}\hfill \\ \mathit{\eta }:=\frac{x-t}{2}\hfill \end{array}\right.\end{array}$$4.13 ), and the fact that $\mathcal{K}(x,t;q,\mathit{\delta }q)$ is odd in $t$ variable (and thus ${\mathcal{K}}_x(x,t;q,\mathit{\delta }q)$ is odd in $t$, whereas ${\mathcal{K}}_t(x,t;q,\mathit{\delta }q)$ is even in $t$), and letting ${\displaystyle \mathcal{N}:={∥F^{\prime }(q)(\mathit{\delta }q)∥}_{H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)}}$ we write that:4.44 $$\begin{array}{cc}\hfill {\mathcal{N}}^2& ={∥\mathcal{K}(a,·;q,\mathit{\delta }q)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥{\mathcal{K}}_t(a,·;q,\mathit{\delta }q)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥{\mathcal{K}}_x(a,·;q,\mathit{\delta }q)∥}_{L_{\mathbb{R}}^2(0,a)}^2\hfill \\ \hfill & \le \frac{1}{2}·{∥v\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2}^2\hfill \\ \hfill & +\frac{1}{4}·{\left({∥v_{\mathit{\xi }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2}+{∥v_{\mathit{\eta }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2}\right)}^2.\hfill \\ \hfill \end{array}$$4.44 In (4.444.44 $$\begin{array}{cc}\hfill {\mathcal{N}}^2& ={∥\mathcal{K}(a,·;q,\mathit{\delta }q)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥{\mathcal{K}}_t(a,·;q,\mathit{\delta }q)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥{\mathcal{K}}_x(a,·;q,\mathit{\delta }q)∥}_{L_{\mathbb{R}}^2(0,a)}^2\hfill \\ \hfill & \le \frac{1}{2}·{∥v\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2}^2\hfill \\ \hfill & +\frac{1}{4}·{\left({∥v_{\mathit{\xi }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2}+{∥v_{\mathit{\eta }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2}\right)}^2.\hfill \\ \hfill \end{array}$$4.44 ), ${∥·∥}_{L_{\mathbb{R}}^2}$ means ${∥·∥}_{L_{\mathbb{R}}^2(-a,a)}$, and we used ${∥U∥}_{L_{\mathbb{R}}^2(-a,a)}^2=2{∥U∥}_{L_{\mathbb{R}}^2(0,a)}^2$, for $U(-t)=\pm U(t)$. By (4.434.43 $$\begin{array}{c}\hfill {∥v∥}_{C(\overline{D})}\le \sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·\left(a·{∥\mathcal{K}(·,·;q)∥}_{C(\overline{\mathrm{\Delta }}0)}+1\right)·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}.\end{array}$$4.43 ) we have:4.45 $$\begin{array}{cc}& {∥v\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2(-a,a)}^2\hfill \\ \hfill & \le 2a^2·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}^2·{\left(a·{∥\mathcal{K}(·,·;q)∥}_{C(\overline{\mathrm{\Delta }}0)}+1\right)}^2·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2.\hfill \\ \hfill \end{array}$$4.45 Then, by (4.384.38 $$\begin{array}{cc}\hfill v_{\mathit{\xi }}(\mathit{\xi },\mathit{\eta })& ={\int }_0^{\mathit{\eta }}q(\mathit{\xi }+{\mathit{\eta }}^{\prime })v(\mathit{\xi },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }+{\int }_0^{\mathit{\eta }}\mathit{\delta }q(\mathit{\xi }+{\mathit{\eta }}^{\prime })k(\mathit{\xi },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }+\frac{1}{2}·\mathit{\delta }q(\mathit{\xi }),\text{for}(\mathit{\xi },\mathit{\eta })\in D\hfill \\ \hfill \end{array}$$4.38 ), and with the understanding that in what follows ${∥·∥}_{L_{\mathbb{R}}^2}$ means ${∥·∥}_{L_{\mathbb{R}}^2(-a,a)}$ we write:4.46 $$\begin{array}{cc}\hfill {∥v_{\mathit{\xi }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2}& \le \sqrt{{\int }_{-a}^a{\left({\int }_0^{\frac{a-t}{2}}\left|q(\frac{a+t}{2}+{\mathit{\eta }}^{\prime })v(\frac{a+t}{2},{\mathit{\eta }}^{\prime })\right|d{\mathit{\eta }}^{\prime }\right)}^{2}dt}\hfill \\ \hfill & +\frac{1}{2}·\sqrt{{\int }_{-a}^a{\left|\mathit{\delta }q(\frac{a+t}{2})\right|}^{2}dt}\hfill \\ \hfill & +\sqrt{{\int }_{-a}^a{\left({\int }_0^{\frac{a-t}{2}}\left|\mathit{\delta }q(\frac{a+t}{2}+{\mathit{\eta }}^{\prime })k(\frac{a+t}{2},{\mathit{\eta }}^{\prime })\right|d{\mathit{\eta }}^{\prime }\right)}^{2}dt}\hfill \\ \hfill \end{array}$$4.46 Next, by the change of variable ${\mathit{\eta }}^{\prime }\leftrightarrow x^{\prime }$, with ${\displaystyle x^{\prime }:=\frac{a+t}{2}+{\mathit{\eta }}^{\prime }}$ in the first and third terms, and the change of variable $t\leftrightarrow s$, with ${\displaystyle s:=\frac{a+t}{2}}$ in the second term in (4.464.46 $$\begin{array}{cc}\hfill {∥v_{\mathit{\xi }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2}& \le \sqrt{{\int }_{-a}^a{\left({\int }_0^{\frac{a-t}{2}}\left|q(\frac{a+t}{2}+{\mathit{\eta }}^{\prime })v(\frac{a+t}{2},{\mathit{\eta }}^{\prime })\right|d{\mathit{\eta }}^{\prime }\right)}^{2}dt}\hfill \\ \hfill & +\frac{1}{2}·\sqrt{{\int }_{-a}^a{\left|\mathit{\delta }q(\frac{a+t}{2})\right|}^{2}dt}\hfill \\ \hfill & +\sqrt{{\int }_{-a}^a{\left({\int }_0^{\frac{a-t}{2}}\left|\mathit{\delta }q(\frac{a+t}{2}+{\mathit{\eta }}^{\prime })k(\frac{a+t}{2},{\mathit{\eta }}^{\prime })\right|d{\mathit{\eta }}^{\prime }\right)}^{2}dt}\hfill \\ \hfill \end{array}$$4.46 ), and using (4.434.43 $$\begin{array}{c}\hfill {∥v∥}_{C(\overline{D})}\le \sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·\left(a·{∥\mathcal{K}(·,·;q)∥}_{C(\overline{\mathrm{\Delta }}0)}+1\right)·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}.\end{array}$$4.43 ), we write:4.47 $$\begin{array}{c}\hfill {∥v_{\mathit{\xi }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2(-a,a)}\le \mathit{\alpha }·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}.\end{array}$$4.47 We also used the fact that $k(\mathit{\xi },\mathit{\eta }):=\mathcal{K}(x,t;q)$. The constant $\mathit{\alpha }$ in (4.474.47 $$\begin{array}{c}\hfill {∥v_{\mathit{\xi }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2(-a,a)}\le \mathit{\alpha }·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}.\end{array}$$4.47 ) is:4.48 $$\begin{array}{cc}\hfill \mathit{\alpha }& :=\sqrt{2}·[a\sqrt{a}·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}·\left(a·{∥\mathcal{K}(·,·;q)∥}_{C(\overline{\mathrm{\Delta }}0)}+1\right)·{∥q∥}_{L_{\mathbb{R}}^2(0,a)}\hfill \\ \hfill & +\left(a·{∥\mathcal{K}(·,·;q)∥}_{C({\overline{\mathrm{\Delta }}}_0)}+\frac{1}{2}\right)].\hfill \end{array}$$4.48 With similar calculations, but using (4.394.39 $$\begin{array}{cc}\hfill v_{\mathit{\eta }}(\mathit{\xi },\mathit{\eta })& ={\int }_0^{\mathit{\xi }}q({\mathit{\xi }}^{\prime }+\mathit{\eta })v({\mathit{\xi }}^{\prime },\mathit{\eta })d{\mathit{\xi }}^{\prime }+{\int }_0^{\mathit{\xi }}\mathit{\delta }q({\mathit{\xi }}^{\prime }+\mathit{\eta })k({\mathit{\xi }}^{\prime },\mathit{\eta })d{\mathit{\xi }}^{\prime }-\frac{1}{2}·\mathit{\delta }q(\mathit{\eta }),\text{for}(\mathit{\xi },\mathit{\eta })\in D.\hfill \\ \hfill \end{array}$$4.39 ) in place of (4.384.38 $$\begin{array}{cc}\hfill v_{\mathit{\xi }}(\mathit{\xi },\mathit{\eta })& ={\int }_0^{\mathit{\eta }}q(\mathit{\xi }+{\mathit{\eta }}^{\prime })v(\mathit{\xi },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }+{\int }_0^{\mathit{\eta }}\mathit{\delta }q(\mathit{\xi }+{\mathit{\eta }}^{\prime })k(\mathit{\xi },{\mathit{\eta }}^{\prime })d{\mathit{\eta }}^{\prime }+\frac{1}{2}·\mathit{\delta }q(\mathit{\xi }),\text{for}(\mathit{\xi },\mathit{\eta })\in D\hfill \\ \hfill \end{array}$$4.38 ) we obtain:4.49 $$\begin{array}{c}\hfill {∥v_{\mathit{\eta }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2(-a,a)}\le \mathit{\alpha }·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}.\end{array}$$4.49 Finally, using (4.454.45 $$\begin{array}{cc}& {∥v\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2(-a,a)}^2\hfill \\ \hfill & \le 2a^2·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}^2·{\left(a·{∥\mathcal{K}(·,·;q)∥}_{C(\overline{\mathrm{\Delta }}0)}+1\right)}^2·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2.\hfill \\ \hfill \end{array}$$4.45 ),  (4.474.47 $$\begin{array}{c}\hfill {∥v_{\mathit{\xi }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2(-a,a)}\le \mathit{\alpha }·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}.\end{array}$$4.47 ) and (4.494.49 $$\begin{array}{c}\hfill {∥v_{\mathit{\eta }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2(-a,a)}\le \mathit{\alpha }·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}.\end{array}$$4.49 ) in (4.444.44 $$\begin{array}{cc}\hfill {\mathcal{N}}^2& ={∥\mathcal{K}(a,·;q,\mathit{\delta }q)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥{\mathcal{K}}_t(a,·;q,\mathit{\delta }q)∥}_{L_{\mathbb{R}}^2(0,a)}^2+{∥{\mathcal{K}}_x(a,·;q,\mathit{\delta }q)∥}_{L_{\mathbb{R}}^2(0,a)}^2\hfill \\ \hfill & \le \frac{1}{2}·{∥v\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2}^2\hfill \\ \hfill & +\frac{1}{4}·{\left({∥v_{\mathit{\xi }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2}+{∥v_{\mathit{\eta }}\left(\frac{a+t}{2},\frac{a-t}{2}\right)∥}_{L_{\mathbb{R}}^2}\right)}^2.\hfill \\ \hfill \end{array}$$4.44 ), we obtain:4.50 $$\begin{array}{cc}& {∥F^{\prime }(q)(\mathit{\delta }q)∥}_{H_{\mathbb{R}}^1(0,a)\times L_{\mathbb{R}}^2(0,a)}^{2}MYAMP]\le \left[a^2·{∥{(I-T)}^{-1}∥}_{\mathcal{B}(C(\overline{D}))}^2·{\left(a·{∥\mathcal{K}(·,·;q)∥}_{C(\overline{\mathrm{\Delta }}0)}+1\right)}^2+{\mathit{\alpha }}^2\right]·{∥\mathit{\delta }q∥}_{L_{\mathbb{R}}^2(0,a)}^2.\hfill \end{array}$$4.50 Thus, the boundedness of $F^{\prime }(q)$ is proven.

5 The inverse of the Fréchet derivative operator $F^{\prime }(q)$

The inverse of the Fréchet derivative $F^{\prime }(q)$ is needed in (3.123.12 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\text{pick initial guess}{q}_0\hfill \\ \text{calculate}{q}_{n+1}\text{from}\{\tilde{f}(t)-\mathcal{K}(a,t;q_n),\tilde{g}(t)-{\mathcal{K}}_x(a,t;q_n)\}\hfill \\ =F^{\prime }(q_n)(q_{n+1}-q_n),\text{for}n=0,1,2,\dots .\hfill \end{array}\right.\end{array}$$3.12 ) to calculate the Newton iterates $q_n(x)$. An analytical formula for the inverse of $F^{\prime }(q)$ is difficult to find. However, we only need to solve (3.123.12 $$\begin{array}{c}\hfill \left\{\begin{array}{c}\text{pick initial guess}{q}_0\hfill \\ \text{calculate}{q}_{n+1}\text{from}\{\tilde{f}(t)-\mathcal{K}(a,t;q_n),\tilde{g}(t)-{\mathcal{K}}_x(a,t;q_n)\}\hfill \\ =F^{\prime }(q_n)(q_{n+1}-q_n),\text{for}n=0,1,2,\dots .\hfill \end{array}\right.\end{array}$$3.12 ) numerically. Specifically, we shall do this as follows:

(1)	Obtain the Cauchy data $\tilde{f}(t)$ and $\tilde{g}(t)$ as described in Section 3.
(2)	Pick an initial guess $q_0(x)$ (it can be the zero function).
(3)	With the current iterate $q_n(x)$ calculate numerically $\mathcal{K}(x,t;q_n)$, ${\mathcal{K}}_x(x,t;q_n)$ and ${\mathcal{K}}_t(x,t;q_n)$ for all $(x,t)$ grid points of the domain ${\mathrm{\Delta }}_0$. Section 6.1 of [3] provides the details on how to calculate the solution $\mathcal{K}(x,t;q)$ of (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ), together with the first-order partial derivatives ${\mathcal{K}}_x(x,t;q)$ and ${\mathcal{K}}_t(x,t;q)$ at the grid points $(x,t)$ on the vertical boundary $x=a$ of the domain ${\mathrm{\Delta }}_0$, but the method described therein can be adjusted easily to all grid points of ${\mathrm{\Delta }}_0$.
(4)	Solve $\{\tilde{f}(t)-\mathcal{K}(a,t;q_n),\tilde{g}(t)-{\mathcal{K}}_x(a,t;q_n)\}=F^{\prime }(q_n)(\mathit{\delta }{q}_n)$ for $\mathit{\delta }{q}_n(x)$. This functional equation is equivalent via (4.44.4 $$\begin{array}{c}\hfill F^{\prime }(q)(\mathit{\delta }q):=\{\mathcal{K}(a,t;q,\mathit{\delta }q),{\mathcal{K}}_x(a,t;q,\mathit{\delta }q)\},\end{array}$$4.4 ) to solving the following Goursat-Cauchy boundary value problem in ${\mathrm{\Delta }}_0$:5.1 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{K}}_{xx}(x,t;q_n,\mathit{\delta }{q}_n)-{\mathcal{K}}_{tt}(x,t;q_n,\mathit{\delta }{q}_n)-q_n(x)\mathcal{K}(x,t;q_n,\mathit{\delta }{q}_n)\hfill \\ =\mathit{\delta }{q}_n(x)\mathcal{K}(x,t;q_n),\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q_n,\mathit{\delta }{q}_n)=\frac{1}{2}{\int }_0^x\mathit{\delta }{q}_n(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q_n,\mathit{\delta }{q}_n)=0,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(a,t;q_n,\mathit{\delta }{q}_n)=\tilde{f}(t)-\mathcal{K}(a,t;q_n),\hfill & 0\le t\le a\hfill \\ {\mathcal{K}}_x(a,t;q_n,\mathit{\delta }{q}_n)=\tilde{g}(t)-{\mathcal{K}}_x(a,t;q_n),\hfill & 0\le t\le a.\hfill \end{array}\right.\end{array}$$5.1 Note that (5.15.1 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{K}}_{xx}(x,t;q_n,\mathit{\delta }{q}_n)-{\mathcal{K}}_{tt}(x,t;q_n,\mathit{\delta }{q}_n)-q_n(x)\mathcal{K}(x,t;q_n,\mathit{\delta }{q}_n)\hfill \\ =\mathit{\delta }{q}_n(x)\mathcal{K}(x,t;q_n),\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q_n,\mathit{\delta }{q}_n)=\frac{1}{2}{\int }_0^x\mathit{\delta }{q}_n(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q_n,\mathit{\delta }{q}_n)=0,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(a,t;q_n,\mathit{\delta }{q}_n)=\tilde{f}(t)-\mathcal{K}(a,t;q_n),\hfill & 0\le t\le a\hfill \\ {\mathcal{K}}_x(a,t;q_n,\mathit{\delta }{q}_n)=\tilde{g}(t)-{\mathcal{K}}_x(a,t;q_n),\hfill & 0\le t\le a.\hfill \end{array}\right.\end{array}$$5.1 ) has two unknowns: $\mathcal{K}(x,t;q_n,\mathit{\delta }{q}_n)$ and $\mathit{\delta }{q}_n(x)$. We refer to [11] for how to solve numerically the Goursat-Cauchy boundary value problem in the triangle ${\mathrm{\Delta }}_0$.
(5)	Set $q_{n+1}(x):=q_n(x)+\mathit{\delta }{q}_n(x)$, for all $x$-grid points in $[0,a]$.
(6)	Repeat steps 3, 4, 5 until the relative error ${\displaystyle \frac{{∥q_{n+1}-q_n∥}_2}{{∥q_n∥}_2}}$ becomes smaller than a desired tolerance.
(7)	The last Newton iterate will be a numerical estimate of the true potential function $q(x)$.

6 Numerical results and discussion

To observe how efficient our Newton-type method is in recovering the coefficient function $q(x)$ from two sequences of eigenvalues, we started with a known $q(x)$, on a chosen interval $[0,a]$, and a known Robin parameter H, then passed them to MATSLISE [14] and obtained $\{{\mathit{\lambda }}_i|i=1,2,\dots ,N_1\}$ (Dirichlet eigenvalues) and $\{{\mathit{\mu }}_i|i=1,2,\dots ,N_2\}$ (Dirichlet–Robin eigenvalues), for the desired values of $N_1$ and $N_2$. Then continued as outlined in Section 5. Note that Sections 2 and 3 not only provide a way of constructing the Cauchy data $\mathcal{K}(a,t;q)$, ${\mathcal{K}}_x(a,t;q)$, ${\mathcal{K}}_t(a,t;q)$ from ${\{{\mathit{\lambda }}_i\}}_{i=1}^{N_1}$, ${\{{\mathit{\mu }}_i\}}_{i=1}^{N_2}$, $[q]$, H, but also indicate how $[q]$ and H can be estimated from the two eigenvalue sequences (see (3.53.5 $$\begin{array}{c}\hfill C=\underset{n\to \infty }{lim}\left({\mathit{\lambda }}_n-{\left(\frac{n\mathit{\pi }}{a}\right)}^2\right),\end{array}$$3.5 ) and (3.63.6 $$\begin{array}{c}\hfill \frac{aC}{2}+H=\frac{a}{2}·\underset{n\to \infty }{lim}\left({\mathit{\mu }}_n-{\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right).\end{array}$$3.6 )). The numerical solution obtained via the implementation of the Newton algorithm in MATLAB codes is plotted together with the original $q(x)$ on the same plot, for comparison. We also passed the two eigenvalue sequences to the quasi-Newton MATLAB code and displayed the original $q(x)$ along with the numerical one on the same plot. The two types of plots (i.e. quasi-Newton and Newton) are featured side-by-side in Figures 5 and 8 – 12 for the examples of $q(x)$ given below. We included on each picture

• the number of iterates performed by the method used to produce that plot.

• the relative error between the last two iterates (as defined in item 6 of Section 5). The stopping criterion for each method was a relative error smaller than ${10}^{-8}$ between two successive iterates.

• the $L^2$-error of the last iterate with respect to the original (true) $q(x)$.

Figure 5. Reconstruction of $q(x)$ in Example 1; quasi-Newton (left) – Newton (right); exact Cauchy data supplied (top) - estimated Cauchy data supplied (bottom). When estimating the Cauchy data, we did not assume H, neither $[q]$, nor $q(a)$ known. The Robin parameters H and $[q]$ were recovered from the two eigenvalue sequences, and $q(a)$ was not estimated by $[q]$. Rather we used (3.83.8 $$\begin{array}{cc}\hfill \tilde{h}(t)& =\sum _{j=1}^{N_2}{\mathit{\beta }}_{j}sin\left(\frac{(j-\frac{1}{2})\mathit{\pi }}{a}t\right).\hfill \end{array}$$3.8 ), and not (6.76.7 $$\begin{array}{c}\hfill \tilde{h}(t)=\frac{\tilde{C}}{a}t+\sum _{j=1}^{N_2}{\mathit{\delta }}_{j}sin\left(\frac{j\mathit{\pi }}{a}t\right).\end{array}$$6.7 ).

Figure 6. The comparison of the analytical Cauchy data to the numerical Cauchy data corresponding to $q(x)$ of Example 1. The numerical Cauchy data were produced from the first $N_1=21$ Dirichlet eigenvalues ($\mathit{\lambda }$’s), and the first $N_2=12$ Dirichlet–Robin eigenvalues ($\mathit{\mu }$’s). The impedance parameter in the Robin boundary condition is $H=2$. To produce these three panels, the exact value of $q(a)$ was neither passed as an input argument, nor estimated by $[q]$ (a possible gross estimate, though the only one available), and the exact value of H was only used by MATSLISE to yield the two eigenvalue sequences. Once these two sequences become available, they were used to estimate the mean of $q(x)$ and H (see (3.53.5 $$\begin{array}{c}\hfill C=\underset{n\to \infty }{lim}\left({\mathit{\lambda }}_n-{\left(\frac{n\mathit{\pi }}{a}\right)}^2\right),\end{array}$$3.5 ) and (3.63.6 $$\begin{array}{c}\hfill \frac{aC}{2}+H=\frac{a}{2}·\underset{n\to \infty }{lim}\left({\mathit{\mu }}_n-{\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right).\end{array}$$3.6 )), which in turn served to the construction of the three Cauchy data, as presented in Sections 2 and 3.

Example 1

The potential function ${\displaystyle q^{\ast }(x)=\frac{2}{{(c+x)}^2}}$, where $c$ is a real constant, is special in the sense that we are able to solve analytically the Goursat problem (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ) by separating the variables $x$ and $t$, i.e. write $\mathcal{K}(x,t;q^{\ast })=\mathit{\varphi }(x)\mathit{\psi }(t)$. We obtained:$$\mathcal{K}(x,t;q^{\ast })=\frac{1}{c}·\frac{t}{c+x},\text{for}(x,t)\in {\mathrm{\Delta }}_0.$$Thus, we have the Cauchy data that correspond to this $q^{\ast }(x)$ (i.e. $\{\mathcal{K}(a,t;q^{\ast }),{\mathcal{K}}_x(a,t;q^{\ast })\}=F(q^{\ast })$) in analytical form. Applying the Newton method to the non-linear equation$$F(q)=\{\tilde{f}(t),\tilde{g}(t)\}$$with6.1 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \tilde{f}(t):=\mathcal{K}(a,t;q^{\ast })=\frac{1}{c}·\frac{t}{c+a}}\hfill \\ {\displaystyle \tilde{g}(t):={\mathcal{K}}_x(a,t;q^{\ast })=\frac{1}{c}·\frac{-t}{{(c+a)}^2},}\hfill \end{array}\right.\end{array}$$6.1 the hope is that the numerical solution is close to the actual solution, $q^{\ast }(x)$. And they are indeed so, if either quasi-Newton or Newton method is employed, as seen in the top two panels of Figure 5. However, the Newton method requires fewer iterates to converge than the quasi-Newton. Note that the quasi-Newton method uses the Cauchy data6.2 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \tilde{g}(t):={\mathcal{K}}_x(a,t;q^{\ast })=\frac{1}{c}·\frac{-t}{{(c+a)}^2}}\hfill \\ {\displaystyle {\tilde{f}}^{\prime }(t):={\mathcal{K}}_t(a,t;q^{\ast })=\frac{1}{c}·\frac{1}{c+a},}\hfill \end{array}\right.\end{array}$$6.2 instead of (6.16.1 $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \tilde{f}(t):=\mathcal{K}(a,t;q^{\ast })=\frac{1}{c}·\frac{t}{c+a}}\hfill \\ {\displaystyle \tilde{g}(t):={\mathcal{K}}_x(a,t;q^{\ast })=\frac{1}{c}·\frac{-t}{{(c+a)}^2},}\hfill \end{array}\right.\end{array}$$6.1 ). We also ran the two MATLAB codes (quasi-Newton and Newton) with the appropriate Cauchy data for each code, but they are now constructed from the two sets of eigenvalues, rather than being the exact Cauchy data. The results can be seen in the bottom two panels of Figure 5. We are also including the figures that display the comparison of the analytical and numerical (i.e. constructed from the two spectra) Cauchy data corresponding to the above-mentioned $q^{\ast }(x)$. See Figure 6.

• Example 1, exact Cauchy data: the comparison Newton versus quasi-Newton for$$\begin{array}{cc}\hfill q(x)& =\frac{2}{{(c+x)}^2}\text{on}[0,a],\text{with}c=5\text{and}a=2.8.\hfill \\ \hfill & \text{The impedance parameter is}H=2.\hfill \end{array}$$ We supplied to both MATLAB codes (i.e. Newton and quasi-Newton) the exact (i.e. analytical) Cauchy data.

• Example 1, estimated Cauchy data: the comparison Newton versus quasi-Newton for$$\begin{array}{cc}\hfill q(x)& =\frac{2}{{(c+x)}^2}\text{on}[0,a],\text{with}c=5\text{and}a=2.8.\hfill \\ \hfill & \text{The impedance parameter is}H=2.\hfill \end{array}$$ We constructed the two Cauchy data required by each method from the eigenvalues. We used the first $N_1=21$ Dirichlet eigenvalues ($\mathit{\lambda }$’s), and the first $N_2=12$ Dirichlet–Robin eigenvalues ($\mathit{\mu }$’s). In MATSLISE, we took a tolerance of ${10}^{-9}$ and ${10}^{-8}$ for calculating the Dirichlet and the Dirichlet–Robin eigenvalues, respectively.

We now discuss Figures 5 and 6. First of all, the reason the top two panels of Figure 5 seem identical is that the absolute (relative) errors in the quasi-Newton and Newton code-outputs are very small when the exact Cauchy data were supplied to these codes, and so the numerical solution cannot be distinguished from the true $q(x)$ in either case (quasi-Newton or Newton). Similarly, when the estimated Cauchy data were supplied (bottom two panels), the numerical solution of the Newton code behaves almost the same as the one of the quasi-Newton code, because their absolute (relative) errors are almost the same.

Secondly, we see in these figures that when the exact Cauchy data were supplied to the Newton or quasi-Newton MATLAB codes, the reconstruction of the true potential function of Example 1 is very good: an $L^2$-error between the last iterate and the true $q(x)$ of order ${10}^{-10}$ for the Newton case, and of order ${10}^{-6}$ for the quasi-Newton case. When the estimated Cauchy data were supplied, the reconstruction was possible, but not with such high accuracy as for the exact Cauchy data. This is an indication that both codes are efficient, and the efforts must be focused on obtaining the Cauchy data more accurately.

The top and bottom panels of Figure 6 indicate that the Cauchy data $\tilde{f}(t)$ and ${\tilde{f}}^{\prime }(t)$ (they are expected to match $\mathcal{K}(a,t;q)$, and respectively ${\mathcal{K}}_t(a,t;q)$ - see Section 3) are effectively constructed from the two eigenvalue sequences. The middle panel of Figure 6 features the Cauchy datum $\tilde{g}(t)$ (expected to match ${\mathcal{K}}_x(a,t;q)$ – see Section 3). We see that at the left end $t=0$ of the interval $[0,a]$, it fits the true ${\mathcal{K}}_x(a,t;q)$, but at the right end $t=a$ is inaccurate. This is reminiscent of the Fourier series representation (2.182.18 $$\begin{array}{cc}\hfill {\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)& =\sum _{m=1}^{\infty }{\mathit{\beta }}_{m}sin\left(\frac{(m-\frac{1}{2})\mathit{\pi }}{a}t\right).\hfill \end{array}$$2.18 ) we had for$${\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q).$$Recall from Section 2, that (2.182.18 $$\begin{array}{cc}\hfill {\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)& =\sum _{m=1}^{\infty }{\mathit{\beta }}_{m}sin\left(\frac{(m-\frac{1}{2})\mathit{\pi }}{a}t\right).\hfill \end{array}$$2.18 ) was our best choice within the available information (i.e. the two eigenvalue sequences). However, if in addition to the two eigenvalue sequences, the value $q(a)$ were known, we would have chosen to represent the function6.3 $$\begin{array}{c}\hfill {\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)-\tilde{C}·\frac{t}{a},\end{array}$$6.3 (with $\tilde{C}$ chosen conveniently - see below), relative to the orthogonal basis of functions in $L_{\mathbb{R}}^2(0,a)$6.4 $$\begin{array}{c}\hfill {\left\{sin\left(\frac{m\mathit{\pi }}{a}t\right)\right\}}_{m=1,2,\dots }.\end{array}$$6.4 This is a better representation than (2.182.18 $$\begin{array}{cc}\hfill {\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)& =\sum _{m=1}^{\infty }{\mathit{\beta }}_{m}sin\left(\frac{(m-\frac{1}{2})\mathit{\pi }}{a}t\right).\hfill \end{array}$$2.18 ) (and it turns out that it eliminates the discrepancy at $t=a$ for $\tilde{g}(t)={\mathcal{K}}_x(a,t;q)$ - see the bottom two panels of Figure 7), because both the function (6.36.3 $$\begin{array}{c}\hfill {\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)-\tilde{C}·\frac{t}{a},\end{array}$$6.3 ) and the basis functions (6.46.4 $$\begin{array}{c}\hfill {\left\{sin\left(\frac{m\mathit{\pi }}{a}t\right)\right\}}_{m=1,2,\dots }.\end{array}$$6.4 ) are equal to zero at $t=0$, and $t=a$, by the second boundary condition of (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ) and by our choice of $\tilde{C}$, respectively. We choose $\tilde{C}$ to make the function (6.36.3 $$\begin{array}{c}\hfill {\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)-\tilde{C}·\frac{t}{a},\end{array}$$6.3 ) zero at $t=a$. That means6.5 $$\begin{array}{c}\hfill \tilde{C}={\mathcal{K}}_x(a,a;q)+H\mathcal{K}(a,a;q).\end{array}$$6.5 Using the first boundary condition of (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ), we can manipulate further (6.56.5 $$\begin{array}{c}\hfill \tilde{C}={\mathcal{K}}_x(a,a;q)+H\mathcal{K}(a,a;q).\end{array}$$6.5 ) as:6.6 $$\begin{array}{c}\hfill \tilde{C}=\left(\frac{q(a)}{2}-{\mathcal{K}}_t(a,a;q)\right)+H·\frac{a[q]}{2}=\frac{1}{2}·\left(q(a)+a·C·H\right)-{\tilde{f}}^{\prime }(a),\end{array}$$6.6 because as mentioned in Section 3, $C$ is expected to be $[q]$ and $\tilde{f}(t)$ is expected to match $\mathcal{K}(a,t;q)$. Thus, when $q(a)$ is known, we shall calculate numerically $\tilde{f}(t)$ and ${\tilde{f}}^{\prime }(t)$ as outlined in Section 3, obtain $\tilde{C}$ via (6.66.6 $$\begin{array}{c}\hfill \tilde{C}=\left(\frac{q(a)}{2}-{\mathcal{K}}_t(a,a;q)\right)+H·\frac{a[q]}{2}=\frac{1}{2}·\left(q(a)+a·C·H\right)-{\tilde{f}}^{\prime }(a),\end{array}$$6.6 ), then write a truncated Fourier series for (6.36.3 $$\begin{array}{c}\hfill {\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)-\tilde{C}·\frac{t}{a},\end{array}$$6.3 ) relative to the orthogonal basis (6.46.4 $$\begin{array}{c}\hfill {\left\{sin\left(\frac{m\mathit{\pi }}{a}t\right)\right\}}_{m=1,2,\dots }.\end{array}$$6.4 ). Bearing in mind that $\tilde{h}(t)$ is expected to match ${\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)$ (see Section 3), we shall obtain6.7 $$\begin{array}{c}\hfill \tilde{h}(t)=\frac{\tilde{C}}{a}t+\sum _{j=1}^{N_2}{\mathit{\delta }}_{j}sin\left(\frac{j\mathit{\pi }}{a}t\right).\end{array}$$6.7 Then continue as outlined in Section 3. If $q(a)$ is unknown, we can either estimate it by $[q]$, a possible gross estimate but the only one available, and then follow the steps above, or we can go ahead with the procedure described in Section 3 to construct numerically the three Cauchy data.

As mentioned at the end of Section 1, the Newton method (and also the quasi-Newton method) works as well in the case of estimated H as in the case of known H (see Figures 8 and 9), because the only place H is needed is in the construction of the Cauchy data, and this is done outside of the Newton (and quasi-Newton) algorithm. The case of constructing the Cauchy data when H is estimated from the eigenvalues was presented in Section 3. Therein, an estimate of H was derived from (3.63.6 $$\begin{array}{c}\hfill \frac{aC}{2}+H=\frac{a}{2}·\underset{n\to \infty }{lim}\left({\mathit{\mu }}_n-{\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right).\end{array}$$3.6 ), and an estimate of $[q]$ from (3.53.5 $$\begin{array}{c}\hfill C=\underset{n\to \infty }{lim}\left({\mathit{\lambda }}_n-{\left(\frac{n\mathit{\pi }}{a}\right)}^2\right),\end{array}$$3.5 ). Specifically, we took numerically6.8 $$\begin{array}{cc}\hfill C& ={\mathit{\lambda }}_{N_1}-{\left(\frac{N_1\mathit{\pi }}{a}\right)}^2,\hfill \end{array}$$6.8 6.9 $$\begin{array}{cc}\hfill \frac{aC}{2}+H& =\frac{a}{2}·\left({\mathit{\mu }}_{N_2}-{\left(\frac{(N_2-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right),\hfill \end{array}$$6.9 where the first $N_1$ Dirichlet eigenvalues $\mathit{\lambda }$’s, and the first $N_2$ Dirichlet–Robin eigenvalues $\mathit{\mu }$’s are available. If H is known, (6.96.9 $$\begin{array}{cc}\hfill \frac{aC}{2}+H& =\frac{a}{2}·\left({\mathit{\mu }}_{N_2}-{\left(\frac{(N_2-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right),\hfill \end{array}$$6.9 ) gives us a second estimate for $[q]$:6.10 $$\begin{array}{c}\hfill C=\left({\mathit{\mu }}_{N_2}-{\left(\frac{(N_2-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right)-\frac{2H}{a}.\end{array}$$6.10 Which of (6.86.8 $$\begin{array}{cc}\hfill C& ={\mathit{\lambda }}_{N_1}-{\left(\frac{N_1\mathit{\pi }}{a}\right)}^2,\hfill \end{array}$$6.8 ) or (6.106.10 $$\begin{array}{c}\hfill C=\left({\mathit{\mu }}_{N_2}-{\left(\frac{(N_2-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right)-\frac{2H}{a}.\end{array}$$6.10 ) to take for an estimate of $[q]$, when H is known? There are some options:

• either (6.86.8 $$\begin{array}{cc}\hfill C& ={\mathit{\lambda }}_{N_1}-{\left(\frac{N_1\mathit{\pi }}{a}\right)}^2,\hfill \end{array}$$6.8 ) or (6.106.10 $$\begin{array}{c}\hfill C=\left({\mathit{\mu }}_{N_2}-{\left(\frac{(N_2-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right)-\frac{2H}{a}.\end{array}$$6.10 );

• a weighted average of (6.86.8 $$\begin{array}{cc}\hfill C& ={\mathit{\lambda }}_{N_1}-{\left(\frac{N_1\mathit{\pi }}{a}\right)}^2,\hfill \end{array}$$6.8 ) and (6.106.10 $$\begin{array}{c}\hfill C=\left({\mathit{\mu }}_{N_2}-{\left(\frac{(N_2-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right)-\frac{2H}{a}.\end{array}$$6.10 ):6.11 $$\begin{array}{c}\hfill C=\frac{N_1}{N_1+N_2}·\left[{\mathit{\lambda }}_{N_1}-{\left(\frac{N_1\mathit{\pi }}{a}\right)}^2\right]+\frac{N_2}{N_1+N_2}·\left[\left({\mathit{\mu }}_{N_2}-{\left(\frac{(N_2-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right)-\frac{2H}{a}\right];\end{array}$$6.11

• take (6.86.8 $$\begin{array}{cc}\hfill C& ={\mathit{\lambda }}_{N_1}-{\left(\frac{N_1\mathit{\pi }}{a}\right)}^2,\hfill \end{array}$$6.8 ), if $N_1>N_2$; take (6.106.10 $$\begin{array}{c}\hfill C=\left({\mathit{\mu }}_{N_2}-{\left(\frac{(N_2-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right)-\frac{2H}{a}.\end{array}$$6.10 ), if $N_2>N_1$; and take (6.116.11 $$\begin{array}{c}\hfill C=\frac{N_1}{N_1+N_2}·\left[{\mathit{\lambda }}_{N_1}-{\left(\frac{N_1\mathit{\pi }}{a}\right)}^2\right]+\frac{N_2}{N_1+N_2}·\left[\left({\mathit{\mu }}_{N_2}-{\left(\frac{(N_2-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right)-\frac{2H}{a}\right];\end{array}$$6.11 ), if $N_1=N_2$.

The reason for the last option is that the asymptotics (2.122.12 $$\begin{array}{c}\hfill {\mathit{\lambda }}_n={\left(\frac{n\mathit{\pi }}{a}\right)}^2+[q]+r_n,\text{for}n\ge 1,\end{array}$$2.12 ) and (2.132.13 $$\begin{array}{c}\hfill {\mathit{\mu }}_n={\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}\right)}^2+[q]+2\frac{H}{a}+s_n,\text{for}n\ge 1,\end{array}$$2.13 ) give better estimates, the larger $n$ is. We went through extensive numerical experimentation with all these possibilities. It turned out that (6.86.8 $$\begin{array}{cc}\hfill C& ={\mathit{\lambda }}_{N_1}-{\left(\frac{N_1\mathit{\pi }}{a}\right)}^2,\hfill \end{array}$$6.8 ) yields the best accuracy in all three Cauchy data $\mathcal{K}(a,t;q)$, ${\mathcal{K}}_x(a,t;q)$, ${\mathcal{K}}_t(a,t;q)$. This is not at all surprising, because even when H was estimated and nothing was done regarding $q(a)$ (see Section 3), the use of (6.86.8 $$\begin{array}{cc}\hfill C& ={\mathit{\lambda }}_{N_1}-{\left(\frac{N_1\mathit{\pi }}{a}\right)}^2,\hfill \end{array}$$6.8 ) generated the numerical $\mathcal{K}(a,t;q)$ and ${\mathcal{K}}_t(a,t;q)$ with high accuracy, as seen in the top and bottom panels of Figure 6.

To conclude the discussion about the important parameters for the Cauchy data, we need to say a few words about the combination ${\displaystyle \frac{aC}{2}+H}$. In addition to $C$ needed in (3.13.1 $$\begin{array}{cc}& sin(\sqrt{{\mathit{\lambda }}_i}a)+{\int }_0^a\tilde{f}(t)sin(\sqrt{{\mathit{\lambda }}_i}t)dt=0,i=1,2,\dots ,N_1,\hfill \end{array}$$3.1 ) to produce the Cauchy datum $\tilde{f}(t)=\mathcal{K}(a,t;q)$, we also need the combination ${\displaystyle \frac{aC}{2}+H}$ in (3.23.2 $$\begin{array}{cc}& \sqrt{{\mathit{\mu }}_i}cos(\sqrt{{\mathit{\mu }}_i}a)+\left(\frac{aC}{2}+H\right)sin(\sqrt{{\mathit{\mu }}_i}a)\hfill \\ \hfill & +{\int }_0^a\tilde{h}(t)sin(\sqrt{{\mathit{\mu }}_i}t)dt=0,i=1,2,\dots ,N_2,\hfill \end{array}$$3.2 ) to produce the auxiliary datum $\tilde{h}(t)={\mathcal{K}}_x(a,t;q)+H\mathcal{K}(a,t;q)$. If H is unknown, we would use (6.96.9 $$\begin{array}{cc}\hfill \frac{aC}{2}+H& =\frac{a}{2}·\left({\mathit{\mu }}_{N_2}-{\left(\frac{(N_2-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right),\hfill \end{array}$$6.9 ) derivable from (3.43.4 $$\begin{array}{cc}\hfill [q]+\frac{2H}{a}& =\underset{n\to \infty }{lim}\left({\mathit{\mu }}_n-{\left(\frac{(n-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right).\hfill \end{array}$$3.4 ), as there is nothing else available. If H is known, we can use directly ${\displaystyle \frac{aC}{2}+H}$, by plugging in (6.86.8 $$\begin{array}{cc}\hfill C& ={\mathit{\lambda }}_{N_1}-{\left(\frac{N_1\mathit{\pi }}{a}\right)}^2,\hfill \end{array}$$6.8 ) for $C$, and the given value for H. It turned out through numerical experimentation that this latter estimate gives better accuracy in the Cauchy datum $\tilde{g}(t)={\mathcal{K}}_x(a,t;q)$ than (6.96.9 $$\begin{array}{cc}\hfill \frac{aC}{2}+H& =\frac{a}{2}·\left({\mathit{\mu }}_{N_2}-{\left(\frac{(N_2-\frac{1}{2})\mathit{\pi }}{a}\right)}^2\right),\hfill \end{array}$$6.9 ). The panels of Figure 7 display the comparison between the exact (true) and the numerical Cauchy datum ${\mathcal{K}}_x(a,t;q)$ for all possible combinations $(H,q(a))$:

• H estimated; H known

• $q(a)$ neither known nor estimated; $q(a)$ estimated with $[q]$; $q(a)$ known.

The comparison of the numerical $\mathcal{K}(a,t;q)$ and ${\mathcal{K}}_t(a,t;q)$ to the exact (true) ones respectively, remains the same for all these combinations of $(H,q(a))$ as it was featured in the top and bottom panels of Figure 6, for which reason we have not displayed them again.

Figures 8 and 9 feature the comparison between the exact (true) and the numerical potential function $q(x)$ when the Cauchy data constructed in each case of $(H,q(a))$ from the two eigenvalue sequences were supplied to the quasi-Newton and Newton codes. Note that for Figure 8 when H is estimated, the panels quasi-Newton and Newton for the case $q(a)$ unknown and not estimated that we obtained by running our MATLAB codes are the same as the bottom two panels of Figure 5, for which reason we have not included them in Figure 8. Also, for Figure 9 when H is given, the panels quasi-Newton and Newton for the case of given $q(a)$ that we obtained by running our MATLAB codes are similar to the top two panels of Figure 5, for which reason we have not displayed them in Figure 9. The only significant difference between these two pairs of panels resides in the errors of the numerical potential (i.e. the last iterate) with respect to the original (true) $q(x)$. These errors are of order ${10}^{-3}$ for the quasi-Newton and Newton panels when H and $q(a)$ are given, and of order ${10}^{-6}$, ${10}^{-10}$ as seen in the top two panels of Figure 5. These computer-codes outputs demonstrate the power of our Newton-type method (and of the quasi-Newton method), as the coefficient function $q(x)$ was high accurately reconstructed when the inputs (here the two Cauchy data) were supplied more accurately to the Newton (respectively, quasi-Newton) MATLAB codes. Indeed, as the panels of Figures 6 and 7 illustrate, the best accuracy in the Cauchy data $\mathcal{K}(a,t;q)$, ${\mathcal{K}}_x(a,t;q)$, ${\mathcal{K}}_t(a,t;q)$ was achieved when H and $q(a)$ were known.

In most cases (i.e. for the most $q(x)$’s), the Goursat problem (2.82.8 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mathcal{K}}_{xx}(x,t;q)-{\mathcal{K}}_{tt}(x,t;q)-q(x)\mathcal{K}(x,t;q)=0,\hfill & (x,t)\in {\mathrm{\Delta }}_0\hfill \\ \mathcal{K}(x,x;q)=\frac{1}{2}{\int }_0^{x}q(s)ds,\hfill & 0\le x\le a\hfill \\ \mathcal{K}(x,0;q)=0,\hfill & 0\le x\le a.\hfill \end{array}\right.\end{array}$$2.8 ) cannot be solved in closed form, so analytical formulas for the Cauchy data will not be possible. Thus, we must construct the Cauchy data numerically, from the available eigenvalues. Then we shall pass them to the quasi-Newton or Newton codes to produce the numerical potential functions. We are also including the following examples to illustrate the effectiveness of Newton as compared to quasi-Newton [4] and to the variational method.[5, 6]

Figure 7. The comparison analytical – numerical Cauchy datum ${\mathcal{K}}_x(a,t)$ corresponding to $q(x)$ of Example 1. The Robin boundary parameter $H=2$ is: estimated from the two spectra (left) – given (right). The exact value $q(a)$ of the true potential at the right end of the interval is: unknown and not estimated (first row); estimated with $[q]$ (second row); given (third row).

Figure 8. Reconstruction of $q(x)$ in Example 1, estimated Cauchy data. Here $H=2$ is estimated from the two spectra; quasi-Newton (left) – Newton (right); unknown and not estimated $q(a)$ (first row) – estimated $q(a)$ with $[q]$ (second row) – given $q(a)$ (third row). Note that the two panels that were supposed to be on the first row (i.e. unknown and not estimated $q(a)$) are the same as the bottom two panels of Figure 5, and so they were not displayed here again.

Figure 9. Reconstruction of $q(x)$ in Example 1, estimated Cauchy data. Here $H=2$ is given; quasi-Newton (left) – Newton (right); unknown and not estimated $q(a)$ (first row) - estimated $q(a)$ with $[q]$ (second row) – given $q(a)$ (third row). Note that the two panels that were supposed to be on the third row (i.e. given $q(a)$) are similar to the top two panels of Figure 5 – see Section 6 for details – for which reason they were not displayed here.

Figure 10. Reconstruction of $q(x)$ in Example 2, estimated Cauchy data. Here $H=-1/3$ is estimated from the two spectra; quasi-Newton (left) – Newton (right); unknown and not estimated $q(a)$ (first row) – estimated $q(a)$ with $[q]$ (second row) – given $q(a)$ (third row). The clustering of the iterates for the Newton panels is an indication that the Newton method converges faster than the quasi-Newton method.

Figure 11. Reconstruction of $q(x)$ in Example 2, estimated Cauchy data. Here $H=-1/3$ is given; quasi-Newton (left) – Newton (right); unknown and not estimated $q(a)$ (first row) – estimated $q(a)$ with $[q]$ (second row) – given $q(a)$ (third row). The clustering of the iterates for the Newton panels is an indication that the Newton method converges faster than the quasi-Newton method.

Figure 12. Reconstruction of $q(x)$ in Example 3, estimated Cauchy data. Here $H=0$ is estimated from the two spectra; quasi-Newton (left) – Newton (right); unknown and not estimated $q(a)$ (first row) – estimated $q(a)$ with $[q]$ (second row) – given $q(a)$ (third row). We mention that the counterpart panels for the case of given H that we obtained by running the quasi-Newton and Newton MATLAB codes are similar to these presented here in terms of plot-shape, number of iterates, and errors, for which reason we have not displayed them in a new figure. This fact indicates that the Newton method works, in terms of the number of iterates and errors, equally well when the boundary parameter H is estimated, as when it is given. The same is true for the quasi-Newton method.

Example 2

Reconstruction of the more complicated potential6.12 $$\begin{array}{c}\hfill q(x)=\left\{\begin{array}{cc}sin\left(\frac{x}{5}-\frac{\mathit{\pi }}{12}\right)+2,\hfill & \text{for}0<x<\frac{\mathit{\pi }}{3}\hfill \\ cos\left(\frac{5\mathit{\pi }}{6}-3x\right),\hfill & \text{for}\frac{\mathit{\pi }}{3}<x<\frac{\mathit{\pi }}{2}\hfill \\ e^{-x+2},\hfill & \text{for}\frac{\mathit{\pi }}{2}<x<\frac{2\mathit{\pi }}{3}.\hfill \end{array}\right.\end{array}$$6.12 The impedance parameter in the Robin boundary condition is $H=-1/3$. The Cauchy data are estimated from the first $N_1=11$ Dirichlet eigenvalues ($\mathit{\lambda }$’s), and the first $N_2=13$ Dirichlet–Robin eigenvalues ($\mathit{\mu }$’s). The MATSLISE tolerance was set at ${10}^{-9}$ and ${10}^{-7}$, respectively, when calculating the two types of eigenvalues. As Figures 10 and 11 illustrate, the quasi-Newton method requires over 60 iterates to converge, whereas the proposed Newton method requires only 6 iterates (or an order of magnitude smaller).

Example 3

Reconstruction of6.13 $$\begin{array}{c}\hfill q(x)=75.16x^6-176.44x^5+129.35x^4-30.67x^3+2.6x^2+0.001x,\text{for}x\in [0,1].\end{array}$$6.13 The impedance parameter in the Robin boundary condition is $H=0$. The Cauchy data are estimated from the first $N_1=30$ Dirichlet eigenvalues ($\mathit{\lambda }$’s), and the first $N_2=30$ Dirichlet–Robin eigenvalues ($\mathit{\mu }$’s). The MATSLISE tolerance was set at ${10}^{-13}$ and ${10}^{-15}$, respectively, when calculating the two types of eigenvalues. See Figure 12. This example was also considered in [4, 5]. We took $H=0$, $[0,a]=[0,1]$ and the first $30$ eigenvalues of each type, in order to match the default setting of [5], where $\mathit{\alpha }=\mathit{\beta }=0$, ${\displaystyle \mathit{\gamma }=\frac{\mathit{\pi }}{2}}$. Our Newton-type method recovered $q(x)$ in $4$ iterates in both situations: estimated Robin boundary parameter H, and given H. The least squares functional method [5] recovered $q(x)$ in $3$ iterates for the case of given boundary parameters $\mathit{\alpha }=\mathit{\beta }=0$ and ${\displaystyle \mathit{\gamma }=\frac{\mathit{\pi }}{2}}$. However, results are not available in [5], nor in [6] about the case when the boundary parameters $\mathit{\alpha }=\mathit{\beta }=0$, ${\displaystyle \mathit{\gamma }=\frac{\mathit{\pi }}{2}}$ are not supplied as input data. The $L^2$-error between the last iterate and the exact (true) $q(x)$ is $4.8·{10}^{-3}$ and $4.4·{10}^{-3}$ for the Newton method when $q(a)$ is neither known nor estimated and H is estimated (upper-right panel of Figure 12) and respectively when H is given (panel not included as it is similar to its counterpart for the case H estimated), and it is $2.7·{10}^{-3}$ for the least squares functional method when the boundary parameters $\mathit{\alpha },\mathit{\beta },\mathit{\gamma }$ are given. Overall, the Newton method and the least squares functional method are comparable, in the sense that the number of iterates and the absolute errors have the same order of magnitude. Within the same order of magnitude, the least squares functional method holds a slight advantage in this example.

The counterpart panels of those in Figure 12 for the case of given H that we obtained by running the quasi-Newton and Newton MATLAB codes are similar (in plot-shape, number of iterates, errors) to the panels in Figure 12, and so they were not displayed. This fact indicates that the Newton (and also the quasi-Newton) method works, in terms of the number of iterates and errors, as well when the boundary parameter H is estimated as when H is given.

We note here that a variant of the least squares functional method [5] is discussed in [6] where in addition to recovering the potential function, the boundary parameters are recovered as well. However, the default setting in [5]: $\mathit{\alpha }=\mathit{\beta }=0$, ${\displaystyle \mathit{\gamma }=\frac{\mathit{\pi }}{2}}$, where $\mathit{\alpha },\mathit{\beta },\mathit{\gamma }$ are the parameters in the two pairs of boundary conditions:6.14 $$\begin{array}{c}\hfill u(0)cos\mathit{\alpha }+u^{\prime }(0)sin\mathit{\alpha }=0,u(1)cos\mathit{\beta }+u^{\prime }(1)sin\mathit{\beta }=0,\end{array}$$6.14 and respectively6.15 $$\begin{array}{c}\hfill u(0)cos\mathit{\alpha }+u^{\prime }(0)sin\mathit{\alpha }=0,u(1)cos\mathit{\gamma }+u^{\prime }(1)sin\mathit{\gamma }=0,\end{array}$$6.15 does not fall into the setting of [6], where the two pairs of boundary conditions considered are:6.16 $$\begin{array}{c}\hfill h_{0}u(0)+u^{\prime }(0)=0,h_{1}u(1)+u^{\prime }(1)=0,\end{array}$$6.16 and respectively6.17 $$\begin{array}{c}\hfill h_{0}u(0)+u^{\prime }(0)=0,h_{2}u(1)+u^{\prime }(1)=0.\end{array}$$6.17 In the least squares functional method, the reconstruction of (6.136.13 $$\begin{array}{c}\hfill q(x)=75.16x^6-176.44x^5+129.35x^4-30.67x^3+2.6x^2+0.001x,\text{for}x\in [0,1].\end{array}$$6.13 ) from the first $30$ eigenvalues of (6.166.16 $$\begin{array}{c}\hfill h_{0}u(0)+u^{\prime }(0)=0,h_{1}u(1)+u^{\prime }(1)=0,\end{array}$$6.16 )-type with $h_0=h_1=3$, and the first $30$ eigenvalues of (6.176.17 $$\begin{array}{c}\hfill h_{0}u(0)+u^{\prime }(0)=0,h_{2}u(1)+u^{\prime }(1)=0.\end{array}$$6.17 )-type with $h_0=3$, $h_2=0$, along with the reconstruction of the boundary parameters $h_0$, $h_1$, $h_2$ was achieved in $1887$ iterates with an accuracy of $0.0387$ in the potential function. As mentioned before, the Newton method needs only four iterates to achieve an accuracy of $4.8·{10}^{-3}$, although the reconstructed boundary parameters are of a different type. Also, to increase the speed of convergence in the method of [6], the trial potential must be set to zero several times and restart the process. It is concluded in [6] that determining at which iterates the trial potential must be set to zero is an open theoretical matter.

In all of the above examples, we required that both quasi-Newton and Newton methods stop when a relative error smaller than ${10}^{-8}$ is attained between two successive iterates. Also, for both methods, we used a partition of $[0,a]$ with $101$ equally spaced nodes in $x$-direction, and therefore $51$ equally spaced nodes in $t$-direction.

7 Summary and conclusions

This paper investigates a different method for solving inverse Sturm-Liouville problems by two spectra. The method is Newton-type, in the sense that a non-linear equation that involves the solution $q(x)$ of the inverse spectral problem is solved numerically by the Newton iterative method. The non-linear map in question is a functional that maps $q(x)$ into the pair of functions $\{\mathcal{K}(a,t;q),{\mathcal{K}}_x(a,t;q)\}$, where $\mathcal{K}(x,t;q)$ is the solution in a triangular domain to the Goursat problem that corresponds to $q(x)$. ($\mathcal{K}(x,t;q)$ is also known as the Gelfand-Levitan-Marchenko kernel that corresponds to $q(x)$.) Each Newton iterate requires that a Goursat-Cauchy boundary value problem be solved numerically, the details of which can be found in [11]. The Fréchet differentiability of the non-linear map we used was proven rigorously in Section 4.

We illustrated with examples how the Newton method works in the case of the two spectra being two sequences of eigenvalues: Dirichlet type and Dirichlet–Robin type. The advantages of this method are that it recovers the true potential function of the canonical Sturm-Liouville equation with about the same accuracy as the quasi-Newton and the least squares methods, in fewer iterates than the quasi-Newton and comparable number of iterates as the least squares method when the boundary parameter is given as input datum. However, the Newton method recovers the true potential function with about the same efficiency (i.e. low number of iterates, and approximately the same accuracy) in both situations: given Robin boundary parameter H, and estimated H from the available spectra, whereas the least squares functional method needs a large number of iterates (hundreds or even thousands) in the more realistic case when the boundary parameters are not given and must be recovered. For the Newton method, the mean of the true potential function was estimated from the eigenvalues in both situations: given H, and estimated H.

Acknowledgements

I would like to thank Dr. Paul E. Sacks of Iowa State University for helpful discussions on the general topic of numerical reconstructions for inverse Sturm-Liouville problems.

Appendix 1

We conclude with the following result used in Section 4.

Lemma 1

Let $T\in \mathcal{B}(X)$ (i.e. $T$ is a linear bounded operator on the Banach space $X$ over $\mathbb{R}$ or $\mathbb{C}$) be such that ${∥T^m∥}_{\mathcal{B}(X)}^{1/m}<1$, for some $m\in \{1,2,3,\dots \}$. Then the series ${\displaystyle \sum _{j=0}^{\infty }{T}^j}$ converges in $\mathcal{B}(X)$, $I-T$ is invertible, andA1 $$\begin{array}{c}\hfill {(I-T)}^{-1}=\sum _{j=0}^{\infty }{T}^j.\end{array}$$A1

Proof

Let $\mathit{\rho }$ be a real number such that ${∥T^m∥}_{\mathcal{B}(X)}^{1/m}<\mathit{\rho }<1$ (possible since ${∥T^m∥}_{\mathcal{B}(X)}^{1/m}<1$). Then ${∥T^m∥}_{\mathcal{B}(X)}<{\mathit{\rho }}^m<1$. Let us denote byA2 $$\begin{array}{c}\hfill S_k:=\sum _{j=0}^k{T}^j\text{and}{R}_k:=\sum _{j=k+1}^{\infty }{T}^j\end{array}$$A2 the partial sum and respectively the remainder sum of order $k$ ($k=0,1,2,3,\dots$) of the series ${\displaystyle \sum _{j=0}^{\infty }{T}^j}$. Choose $k=0,1,2,3\dots$ and fix it. By the remainder theorem we can write $k=n·m+r$, for some unique $n\in \mathbb{N}$ and $r\in \{0,1,\dots ,m-1\}$. Then,A3 $$\begin{array}{cc}\hfill R_k& =\left(T^{n·m+(r+1)}+\dots +T^{n·m+(m-1)}\right)\hfill \\ \hfill & +\left(T^{(n+1)·m}+T^{(n+1)·m+1}+\dots +T^{(n+1)·m+(m-1)}\right)+\dots .\hfill \end{array}$$A3 From (A3A3 $$\begin{array}{cc}\hfill R_k& =\left(T^{n·m+(r+1)}+\dots +T^{n·m+(m-1)}\right)\hfill \\ \hfill & +\left(T^{(n+1)·m}+T^{(n+1)·m+1}+\dots +T^{(n+1)·m+(m-1)}\right)+\dots .\hfill \end{array}$$A3 ), using $||U+V||\le ||U||+||V||$; $||UV||\le ||U||·||V||$, for $U,V\in \mathcal{B}(X)$, and ${∥T^m∥}_{\mathcal{B}(X)}<{\mathit{\rho }}^m<1$:A4 $$\begin{array}{cc}\hfill ||R_k||& \le {\left({\mathit{\rho }}^m\right)}^n·\left(||T^{r+1}||+\dots +||T^{m-1}||\right)+{\left({\mathit{\rho }}^m\right)}^{n+1}·\left(1+||T||+\dots +||T^{m-1}||\right)\hfill \\ \hfill & +{\left({\mathit{\rho }}^m\right)}^{n+2}·\left(1+||T||+\dots +||T^{m-1}||\right)+\dots \hfill \\ \hfill & ={\left({\mathit{\rho }}^m\right)}^n·\left(||T^{r+1}||+\dots +||T^{m-1}||\right)+{\left({\mathit{\rho }}^m\right)}^{n+1}·\frac{1}{1-{\mathit{\rho }}^m}·\left(1+||T||+\dots +||T^{m-1}||\right).\hfill \\ \hfill \end{array}$$A4 If we let $k\to \infty$ in (A4A4 $$\begin{array}{cc}\hfill ||R_k||& \le {\left({\mathit{\rho }}^m\right)}^n·\left(||T^{r+1}||+\dots +||T^{m-1}||\right)+{\left({\mathit{\rho }}^m\right)}^{n+1}·\left(1+||T||+\dots +||T^{m-1}||\right)\hfill \\ \hfill & +{\left({\mathit{\rho }}^m\right)}^{n+2}·\left(1+||T||+\dots +||T^{m-1}||\right)+\dots \hfill \\ \hfill & ={\left({\mathit{\rho }}^m\right)}^n·\left(||T^{r+1}||+\dots +||T^{m-1}||\right)+{\left({\mathit{\rho }}^m\right)}^{n+1}·\frac{1}{1-{\mathit{\rho }}^m}·\left(1+||T||+\dots +||T^{m-1}||\right).\hfill \\ \hfill \end{array}$$A4 ), so $n\to \infty$ because $k=n·m+r$, we obtain that $||R_k||\to 0$. Thus, we proved that the series ${\displaystyle \sum _{j=0}^{\infty }{T}^j}$ is convergent in $\mathcal{B}(X)$. Let $S:={\sum }_{j=0}^{\infty }{T}^j.$ It follows by (A2A2 $$\begin{array}{c}\hfill S_k:=\sum _{j=0}^k{T}^j\text{and}{R}_k:=\sum _{j=k+1}^{\infty }{T}^j\end{array}$$A2 ) and $k=n·m+r$ that,A5 $$\begin{array}{cc}\hfill ||S·(I-T)-I||& \le ||(S-S_k)·(I-T)||+||S_k·(I-T)-I||\hfill \\ \hfill & =||R_k·(I-T)||+||-T^{k+1}||\le ||R_k||·||I-T||+{\left({\mathit{\rho }}^m\right)}^n·||T^{r+1}||.\hfill \end{array}$$A5 Letting $k\to \infty$, so $n\to \infty$ since $k=n·m+r$ in (A5A5 $$\begin{array}{cc}\hfill ||S·(I-T)-I||& \le ||(S-S_k)·(I-T)||+||S_k·(I-T)-I||\hfill \\ \hfill & =||R_k·(I-T)||+||-T^{k+1}||\le ||R_k||·||I-T||+{\left({\mathit{\rho }}^m\right)}^n·||T^{r+1}||.\hfill \end{array}$$A5 ), we obtain that $||S·(I-T)-I||=0$. This implies that $S·(I-T)=I$. Similarly, one can show that $(I-T)·S=I$. Hence we proved that $I-T$ is invertible and$${(I-T)}^{-1}=S:=\sum _{j=0}^{\infty }{T}^j\in \mathcal{B}(X).$$$\square$