Reconstruction of the complex refractive index in nonlinear phase contrast tomography

Abstract

A new nonlinear method to reconstruct the complex refractive index distribution with in-line phase tomography measurements is presented. The inverse problem is regularized with the Tikhonov smoothing $L_2$ norm of the index. The original nonlinear iterative approach is based on the Fréchet derivative of the intensity recorded at a single propagation distance and on a Simultaneous Algebraic Reconstruction technique. The reconstruction method requires no a priori knowledge about the materials. The algorithm is successfully applied to some simulated data with noise.

Keywords:

• inverse problems
• phase retrieval
• X-ray imaging

AMS Subject Classifications:

• 65J22
• 65J20
• 65K10

1 Introduction

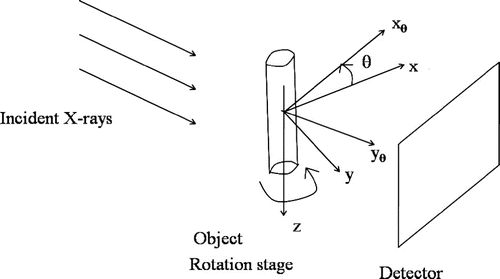
X-ray microtomography is a very useful imaging technique in material science [1] and medical imaging.[2–6] Yet, its sensitivity is now largely improved for soft tissues within dense materials with phase contrast imaging obtained with third-generation synchrotrons. X-ray in-line phase tomography is based on a coupling of tomography and phase retrieval to reconstruct the real part of the refractive index.[7, 8] For coherent X-rays, phase contrast can be achieved by letting the beam propagate in the free space after interaction with the object and by recording the intensity for one or several propagation distances and for several projection angles (Figure 1). The relationship between the phase shift induced by a sample and the intensity recorded at a given sample-to-detector distance relies on the Fresnel diffraction theory.[9–12] Several linear algorithms have been proposed for the phase retrieval from the Fresnel diffraction patterns [1, 10, 13–18] valid under some restrictive assumptions. More recently, some nonlinear approaches have been developed [12, 19, 20] that improve the reconstruction results.

Figure 1. Experimental set-up in propagation-based phase contrast tomography from a single propagation-based phase contrast image per projection showing the coordinate system.

In order to reconstruct the refractive index in phase contrast tomography, the prior that the ratio of the imaginary to the real part of the complex refractive index is piecewise constant can be included.[8, 11, 21] If the attenuation image can be measured, it is possible to use a scaled version of this image to construct an a prior knowledge of the phase for multimaterial objects.[8, 11] A linear algorithm has also been proposed for multimaterial objects to recover the distance travelled in each material and the real and complex part of the refractive index.[21, 22]

All these schemes rely on restrictive assumptions and formulate the phase contrast tomography as a linear inverse problem. The reconstruction images obtained need improvements. The simultaneous nonlinear reconstruction of the real and of the imaginary part of the index from noisy intensity measurements for different projection angles in in-line phase tomography has not been theoretically investigated. The coupling of phase retrieval with tomography sets an ill-posed nonlinear inverse problem. Several regularization methods can be investigated. In this work, we investigate the functional properties of the direct operator and we present new reconstruction results obtained for a single propagation distance with a nonlinear Tikhonov regularization scheme coupled with Simultaneous Algebraic Reconstruction technique.

An extensive comparison with the linear state of the art algorithms in the literature on experimental data is beyond the scope of this study. The new nonlinear reconstruction method is tested on a simulated multi-material object, with an object of a given material embedded in a matrix of a second material. In this case, the complex refractive index takes two distinct values.

We first study the direct problem of the image formation. Then we investigate the functional properties of the direct intensity operator and detail the nonlinear Tikhonov regularization method used. The numerical results obtained with a coupling of a modified Landweber method with Simultaneous Algebraic Reconstruction techniques (ART) on noisy simulated multimaterial data are presented and discussed before concluding remarks.

2 The direct problem of the image formation

In the following, we will consider a monochromatic, coherent, parallel X-ray beam. The real and imaginary parts of the complex refractive index to be reconstructed, denoted as $\mathit{\delta }$ and $\mathit{\beta }$ are defined on a 3D bounded domain ($\mathrm{\Sigma }$) with spatial coordinates $(x,y,z)$. For the sake of simplicity, we assume that $\mathrm{\Sigma }$ is the cartesian product ${\mathrm{\Sigma }}_x\times {\mathrm{\Sigma }}_y\times {\mathrm{\Sigma }}_z$ of bounded intervals on the coordinate axes. We denote $(x_{\mathit{\theta }},y_{\mathit{\theta }},z)$ be the rotated spatial coordinate system for an angle $\mathit{\theta }$ around the z axis (Figure 1).

2.1 The Fresnel intensity

The optical properties of an object interacting with coherent X-rays of wavelength $\mathit{\lambda }$ are related to its complex refractive index given by:1 $$\begin{array}{c}\hfill n(x,y,z)=1-\mathit{\delta }(x,y,z)+i\mathit{\beta }(x,y,z)\end{array}$$1 where $\mathit{\delta }$ is the refractive index decrement and $\mathit{\beta }$ is the absorption index for the spatial coordinates $(x,y,z)$ in the object domain.[23] For a fixed projection angle $\mathit{\theta }$, thin objects and straight line propagation of the beam along the $y_{\mathit{\theta }}$ direction, this interaction can be described by a transmittance function $T$ of the coordinates $X_{\mathit{\theta }}=(x_{\mathit{\theta }},z)$:2 $$\begin{array}{c}\hfill T_{\mathit{\theta }}[\mathit{\delta },\mathit{\beta }](X_{\mathit{\theta }})=exp(-B_{\mathit{\theta }}[\mathit{\beta }](X_{\mathit{\theta }})+i{\mathit{\phi }}_{\mathit{\theta }}[\mathit{\delta }](X_{\mathit{\theta }}))=a_{\mathit{\theta }}(X_{\mathit{\theta }})exp(i{\mathit{\phi }}_{\mathit{\theta }}[\mathit{\delta }](X_{\mathit{\theta }})),\end{array}$$2 where $a_{\mathit{\theta }}[\mathit{\beta }](X_{\mathit{\theta }})$ is the absorption and ${\mathit{\phi }}_{\mathit{\theta }}[\mathit{\delta }](X)$ the phase shift induced by the object for the projection angle $\mathit{\theta }$.[8] The phase and the negative logarithm of the absorption, $B_{\mathit{\theta }}[\mathit{\beta }](X)=-\text{log}(a_{\mathit{\theta }}[\mathit{\beta }](X))$, are the projections of the absorption index and refraction index, respectively:3 $$\begin{array}{cc}\hfill B_{\mathit{\theta }}[\mathit{\beta }](X_{\mathit{\theta }})& =\frac{2\mathit{\pi }}{\mathit{\lambda }}\int \mathit{\beta }(y_{\mathit{\theta }},X_{\mathit{\theta }})\mathrm{d}{y}_{\mathit{\theta }}\hfill \end{array}$$3 4 $$\begin{array}{cc}\hfill {\mathit{\phi }}_{\mathit{\theta }}[\mathit{\delta }](X_{\mathit{\theta }})& =\frac{2\mathit{\pi }}{\mathit{\lambda }}\int (1-\mathit{\delta }(y_{\mathit{\theta }},X_{\mathit{\theta }}))\mathrm{d}{y}_{\mathit{\theta }}\hfill \end{array}$$4 where $y_{\mathit{\theta }}$ is the propagation direction of the X-rays. In the framework of the Fresnel diffraction theory, the intensity detected at a distance $D$ after the sample is given by the squared modulus of the 2D convolution between the transmittance $T_{\mathit{\theta }}$ and the Fresnel propagator $P_D$ for a distance $D$ downstream of the object [8, 11, 24]:5 $$\begin{array}{c}\hfill I_{D,\mathit{\theta }}[\mathit{\delta },\mathit{\beta }]={|T_{\mathit{\theta }}[\mathit{\delta },\mathit{\beta }]\times P_D|}^2\end{array}$$5 where6 $$\begin{array}{c}\hfill P_D(X_{\mathit{\theta }})=\frac{1}{i\mathit{\lambda }D}exp\left(i\frac{\mathit{\pi }}{\mathit{\lambda }D}{|X_{\mathit{\theta }}|}^2\right).\end{array}$$6 The intensity $I_D$ operator can thus be considered as a nonlinear function of $\mathit{\delta }$ and $\mathit{\beta }$.

2.2 The coupling with Radon projection operator

The direct intensity operator can be rewritten with the Radon projection operator. We first summarize some properties of this projection operator.[25] Let $\mathrm{\Omega }\subset {\mathbb{R}}^2$ be a bounded open domain, the mathematical model for 2D tomography is the Radon transform $R$ which maps a function $f\in L^1(\mathrm{\Omega })$ to its line integrals.

Definition 2.1

Let $L(\mathit{\theta },x_{\mathit{\theta }})$ the line defined by $L(\mathit{\theta },x_{\mathit{\theta }})=\{y_{\mathit{\theta }}{\overline{\mathit{\theta }}}^{\ast }+x_{\mathit{\theta }}\overline{\mathit{\theta }}:y_{\mathit{\theta }}\in \mathbb{R}\}$, with $\overline{\mathit{\theta }}=(cos(\mathit{\theta }),sin(\mathit{\theta }))$ and ${\overline{\mathit{\theta }}}^{\ast }=(-sin(\mathit{\theta }),cos(\mathit{\theta }))$, $Ra$ the range of the Radon transform and $Z=[0,\mathit{\pi }]\times Ra$, the Radon transform for $f\in L^1(\mathrm{\Omega })$ is defined by:7 $$\begin{array}{c}\hfill Rf(\mathit{\theta },x_{\mathit{\theta }})=R_{\mathit{\theta }}f(x_{\mathit{\theta }})={\int }_{t\in L(\mathit{\theta },x_{\mathit{\theta }})\cap \mathrm{\Omega }}f(t)\mathrm{d}t\end{array}$$7

Proposition 2.2

Let $g\in L^1([0,\mathit{\pi }]\times \mathbb{R})$ and $\overline{U}=(x,y)$, the adjoint $R^{\ast }$ of $R$ is given by:8 $$\begin{array}{c}\hfill R^{\ast }g(\overline{U})={\int }_0^{\mathit{\pi }}g(\mathit{\theta },\overline{U}.\overline{\mathit{\theta }})\mathrm{d}\mathit{\theta }\end{array}$$8

Proof

The proof can be found in [25].$\square$

For parallel beam projection, with a beam parallel to the $X=(x,y)$ plane, $f\in L^1(\mathrm{\Sigma })$ and $L(\mathit{\theta },x_{\mathit{\theta }},z)$ the $L(\mathit{\theta },x_{\mathit{\theta }})$ line for the coordinate $z$.9 $$\begin{array}{c}\hfill Rf(\mathit{\theta },x_{\mathit{\theta }},z)=R_{\mathit{\theta }}f(x_{\mathit{\theta }})={\int }_{t\in L(\mathit{\theta },x_{\mathit{\theta }},z)\cap \mathrm{\Sigma }}f(t)\mathrm{d}t\end{array}$$9

Definition 2.3

Let $g\in L^1([0,\mathit{\pi }]\times \mathbb{R})$, and the one-dimensional Fourier $F_p(g)(\mathit{\theta },\mathit{\tau })$ defined by $F_p(g)(\mathit{\theta },\mathit{\tau })=\frac{1}{\sqrt{2\mathit{\pi }}}{\int }_{\mathbb{R}}{exp}^{-i\mathit{\tau }p}g(\mathit{\theta },p)\mathrm{d}p$. Let $s\in \mathbb{R}$, the Sobolev space on $[0,\mathit{\pi }]\times \mathbb{R}$ denoted as $H^{0,s}([0,\mathit{\pi }]\times \mathbb{R})$, is the set of all distributions g on ($[0,\mathit{\pi }]\times \mathbb{R})$ such that the Fourier transform $F_p(g)$ is a function and such that the Sobolev norm of g, ${\Vert g\Vert }_{H^{0,s}(Z)}^2$, is finite.[25] The norm ${\Vert g\Vert }_{H^{0,s}(Z)}^2$ is defined as:10 $$\begin{array}{c}\hfill {\Vert g\Vert }_{H^{0,s}(Z)}={\int }_0^{\mathit{\pi }}{\int }_{\mathbb{R}}{(1+|\mathit{\tau }|}^2{)}^s{|F_p(g)(\mathit{\theta },\mathit{\tau })|}^{2}d\mathit{\tau }\mathrm{d}\mathit{\theta }\end{array}$$10

The Radon operator is a smoothing operator as detailed in the following proposition.

Proposition 2.4

Let $f$ be a distribution with a compact support, then the following bound holds for $s\ge 0$:11 $$\begin{array}{c}\hfill {\Vert R(f)\Vert }_{H^{0,s+1/2}(Z)}\le C{\Vert f\Vert }_{H^s({\mathbb{R}}^2)}\end{array}$$11 where the constant $C$ depend on the size of the support, and $H^s({\mathbb{R}}^2)$ is the classical Sobolev space of order s of functions such that all partial derivatives of f of order up to s are square integrable.

Proof

The proof of this proposition can be found in  [25].$\square$

It is now possible to use the mapping properties of the Radon transform in the context of phase contrast tomography and in an Hilbert spaces framework.

Proposition 2.5

Let $R{a}_z$ be range of the Radon operator for the height z, the operators $B=R[\mathit{\beta }]:L^2(\mathrm{\Sigma })\to L^2([0,\mathit{\pi }]\times {\mathrm{\Sigma }}_z\times \cup R{a}_z)$ is continuous. The same result is true for the operator $\mathit{\phi }=R[\mathit{\delta }]$.

Proof

For $s>0$, $H_0^s({\mathbb{R}}^2)$ is continuously embedded in $L^2({\mathbb{R}}^2)$ and thus for compactly supported functions, there is a positive constant $C_1$ such that:12 $$\begin{array}{c}\hfill {\Vert f\Vert }_{H^s({\mathbb{R}}^2)}\le C_1{\Vert f\Vert }_{L^2({\mathbb{R}}^2)}\end{array}$$12 Using Equation 1111 $$\begin{array}{c}\hfill {\Vert R(f)\Vert }_{H^{0,s+1/2}(Z)}\le C{\Vert f\Vert }_{H^s({\mathbb{R}}^2)}\end{array}$$11 , there exists a positive constant $C$ such that:13 $$\begin{array}{c}\hfill {\Vert R(f)\Vert }_{H^{0,0}(Z)}\le {\Vert R(f)\Vert }_{H^{0,1/2}(Z)}\le C{\Vert f\Vert }_{L_2({\mathbb{R}}^2)}\end{array}$$13 In an Hilbert spaces context, the Radon transform is thus a linear continuous operator from $L^2({\mathbb{R}}^2)$ to $L^2(Z)$. For parallel beam projection, let $R{a}_z$ be range of the Radon operator for the height z. For each value of z, the Radon operator is continuous from $L^2({\mathrm{\Sigma }}_x\times {\mathrm{\Sigma }}_y)$ to $L^2([0,\mathit{\pi }]\times R{a}_z)$. By integration on the variable $z$, the operator $B=R[\mathit{\beta }]:L^2(\mathrm{\Sigma })\to L^2([0,\mathit{\pi }]\times {\mathrm{\Sigma }}_z\times \cup R{a}_z)$ is continuous. The same result is holds for the operator $\mathit{\phi }=R[\mathit{\delta }]$.$\square$

With the Radon projection operator, Equations 33 $$\begin{array}{cc}\hfill B_{\mathit{\theta }}[\mathit{\beta }](X_{\mathit{\theta }})& =\frac{2\mathit{\pi }}{\mathit{\lambda }}\int \mathit{\beta }(y_{\mathit{\theta }},X_{\mathit{\theta }})\mathrm{d}{y}_{\mathit{\theta }}\hfill \end{array}$$3 and 44 $$\begin{array}{cc}\hfill {\mathit{\phi }}_{\mathit{\theta }}[\mathit{\delta }](X_{\mathit{\theta }})& =\frac{2\mathit{\pi }}{\mathit{\lambda }}\int (1-\mathit{\delta }(y_{\mathit{\theta }},X_{\mathit{\theta }}))\mathrm{d}{y}_{\mathit{\theta }}\hfill \end{array}$$4 can be rewritten:14 $$\begin{array}{cc}\hfill B_{\mathit{\theta }}[\mathit{\beta }](X_{\mathit{\theta }})& =\frac{2\mathit{\pi }}{\mathit{\lambda }}R[\mathit{\beta }](\mathit{\theta },X_{\mathit{\theta }})\hfill \end{array}$$14 15 $$\begin{array}{cc}\hfill {\mathit{\phi }}_{\mathit{\theta }}[\mathit{\delta }](X_{\mathit{\theta }})& =\frac{2\mathit{\pi }}{\mathit{\lambda }}R[1-\mathit{\delta }](\mathit{\theta },X_{\mathit{\theta }})\hfill \end{array}$$15 Let $M$ the multiplication operator, $F_D$ the convolution with $P_D$ and $\mathit{\psi }:L^2({\mathrm{\Sigma }}_z\times \cup R{a}_z)\times L^2({\mathrm{\Sigma }}_z\times \cup R{a}_z)\to L^2({\mathrm{\Sigma }}_z\times \cup R{a}_z)$ defined by $\mathit{\psi }(B,\mathit{\varphi })=exp(-B)exp(i\mathit{\varphi })$. With the above-defined operators and Equations 22 $$\begin{array}{c}\hfill T_{\mathit{\theta }}[\mathit{\delta },\mathit{\beta }](X_{\mathit{\theta }})=exp(-B_{\mathit{\theta }}[\mathit{\beta }](X_{\mathit{\theta }})+i{\mathit{\phi }}_{\mathit{\theta }}[\mathit{\delta }](X_{\mathit{\theta }}))=a_{\mathit{\theta }}(X_{\mathit{\theta }})exp(i{\mathit{\phi }}_{\mathit{\theta }}[\mathit{\delta }](X_{\mathit{\theta }})),\end{array}$$2 , 55 $$\begin{array}{c}\hfill I_{D,\mathit{\theta }}[\mathit{\delta },\mathit{\beta }]={|T_{\mathit{\theta }}[\mathit{\delta },\mathit{\beta }]\times P_D|}^2\end{array}$$5 , 1313 $$\begin{array}{c}\hfill {\Vert R(f)\Vert }_{H^{0,0}(Z)}\le {\Vert R(f)\Vert }_{H^{0,1/2}(Z)}\le C{\Vert f\Vert }_{L_2({\mathbb{R}}^2)}\end{array}$$13 and 1414 $$\begin{array}{cc}\hfill B_{\mathit{\theta }}[\mathit{\beta }](X_{\mathit{\theta }})& =\frac{2\mathit{\pi }}{\mathit{\lambda }}R[\mathit{\beta }](\mathit{\theta },X_{\mathit{\theta }})\hfill \end{array}$$14 , we obtain:

Proposition 2.6

The nonlinear intensity operator $I_D:L^2(\mathrm{\Sigma })\times L^2(\mathrm{\Sigma })\to L^2([0,\mathit{\pi }]\times {\mathbb{R}}^2)$ admits the following decomposition, for $(\mathit{\theta },X_{\mathit{\theta }})\in [0,\mathit{\pi }]\times {\mathbb{R}}^2$:16 $$\begin{array}{ccc}\hfill I_D[\mathit{\delta },\mathit{\beta }](\mathit{\theta },X_{\mathit{\theta }})& =I_{D,\mathit{\theta }}[\mathit{\delta },\mathit{\beta }](X_{\mathit{\theta }})MYAMP]=\hfill & \hfill M(F_D\circ \mathit{\psi },\overline{F_D\circ \mathit{\psi }})\left(\frac{2\mathit{\pi }}{\mathit{\lambda }}{R}_{\mathit{\theta }}[\mathit{\beta }](X_{\mathit{\theta }}),\frac{2\mathit{\pi }}{\mathit{\lambda }}{R}_{\mathit{\theta }}[1-\mathit{\delta }](X_{\mathit{\theta }})\right)\end{array}$$16

3 The Fréchet derivative of the Fresnel intensity operator and its adjoint

The minimization of the regularization functional can be performed with iterative methods and it is useful to calculate the Fréchet derivative of the intensity operator and its adjoint.

Proposition 3.1

Let $T_{\mathit{\theta }}[{\mathit{\beta }}_k,{\mathit{\delta }}_k]=exp(-B_{\mathit{\theta }}[{\mathit{\beta }}_k]-i{\mathit{\phi }}_{\mathit{\theta }}[{\mathit{\delta }}_k])$, the Fréchet derivative of the operator $I_D[{\mathit{\beta }}_k,{\mathit{\delta }}_k]$ at the point $({\mathit{\beta }}_k,{\mathit{\delta }}_k)$ is the operator $I_D^{\prime }[{\mathit{\beta }}_k,{\mathit{\delta }}_k]:$$L^2(\mathrm{\Sigma })\times L^2(\mathrm{\Sigma })\to L^2([0,\mathit{\pi }]\times {\mathbb{R}}^2)$ defined by:17 $$\begin{array}{c}\hfill I_{D,\mathit{\theta }}^{\prime }[{\mathit{\beta }}_k,{\mathit{\delta }}_k]({\mathit{ϵ}}_1,{\mathit{ϵ}}_2)=\frac{4\mathit{\pi }}{\mathit{\lambda }}\mathrm{Real}\{[((-R_{\mathit{\theta }}[{\mathit{ϵ}}_1]-i{R}_{\mathit{\theta }}[{\mathit{ϵ}}_2])T_{\mathit{\theta }}[{\mathit{\beta }}_k,{\mathit{\delta }}_k])\ast P_D][\overline{T_{\mathit{\theta }}[{\mathit{\beta }}_k,{\mathit{\delta }}_k]}\ast \overline{P_D}]\}\end{array}$$17

Proof

The Fréchet derivative can be calculated with the decomposition given Equation 1313 $$\begin{array}{c}\hfill {\Vert R(f)\Vert }_{H^{0,0}(Z)}\le {\Vert R(f)\Vert }_{H^{0,1/2}(Z)}\le C{\Vert f\Vert }_{L_2({\mathbb{R}}^2)}\end{array}$$13 and follows from the chain rule. The operators $R_{\mathit{\theta }}$ and $F_D$ are linear and continuous operators and they are identical to their Fréchet derivatives. The Fréchet derivative of the operator $I_{D,\mathit{\theta }}$ at the point $({\mathit{\beta }}_k,{\mathit{\delta }}_k)$ is given for $({\mathit{ϵ}}_1,{\mathit{ϵ}}_2)\in L^2(\mathrm{\Sigma })\times L^2(\mathrm{\Sigma })$ by:18 $$\begin{array}{c}\hfill I_{D,\mathit{\theta }}^{\prime }[{\mathit{\beta }}_k,{\mathit{\delta }}_k]({\mathit{ϵ}}_1,{\mathit{ϵ}}_2)=M(A,\overline{F_D\circ \mathit{\psi }(B_{\mathit{\theta }}[{\mathit{\beta }}_k],{\mathit{\varphi }}_{\mathit{\theta }}[{\mathit{\beta }}_k])})+\text{conjugate terms}\end{array}$$18 with $A=F_D\circ (-\frac{2\mathit{\pi }}{\mathit{\lambda }}\mathit{\psi }(B_{\mathit{\theta }}[{\mathit{\beta }}_k],{\mathit{\varphi }}_{\mathit{\theta }}[{\mathit{\delta }}_k])R_{\mathit{\theta }}[{\mathit{ϵ}}_1])+F_D\circ (-i\frac{2\mathit{\pi }}{\mathit{\lambda }}\mathit{\psi }(B_{\mathit{\theta }}[{\mathit{\beta }}_k],{\mathit{\varphi }}_{\mathit{\theta }}[{\mathit{\delta }}_k])R_{\mathit{\theta }}[{\mathit{ϵ}}_2])$.$\square$

Proposition 3.2

The adjoint $I_D^{\prime }{[{\mathit{\beta }}_k,{\mathit{\delta }}_k]}^{\ast }:L^2([0,\mathit{\pi }]\times {\mathbb{R}}^2)\to L^2(\mathrm{\Sigma })\times L^2(\mathrm{\Sigma })$ is thus defined by $I_D^{\prime }{[{\mathit{\beta }}_k,{\mathit{\delta }}_k]}^{\ast }(w)=\frac{4\mathit{\pi }}{\mathit{\lambda }}Real(v_1,v_2)$ with:19a $$\begin{array}{c}\hfill v_1[w](X_{\mathit{\theta }})=R_{\mathit{\theta }}^{\ast }\{[-w(T_{\mathit{\theta }}[{\mathit{\beta }}_k,{\mathit{\delta }}_k]\ast P_D)]\ast \overline{P_D}\}(X_{\mathit{\theta }})\{\overline{T_{\mathit{\theta }}[{\mathit{\beta }}_k,{\mathit{\delta }}_k](X_{\mathit{\theta }})}\}\end{array}$$19a 19b $$\begin{array}{c}\hfill v_2[w](X_{\mathit{\theta }})=R_{\mathit{\theta }}^{\ast }\{[(w(T_{\mathit{\theta }}[{\mathit{\beta }}_k,{\mathit{\delta }}_k]\ast P_D)]\ast \overline{P_D}\}(X_{\mathit{\theta }})\{i\overline{T_{\mathit{\theta }}[{\mathit{\beta }}_k,{\mathit{\delta }}_k](X_{\mathit{\theta }})}\}\end{array}$$19b

Proof

This proposition follows from the definition of the Hilbert space adjoint of the Fresnel diffraction intensity Fréchet derivative defined for all $w\in L^2([0,\mathit{\pi }]\times {\mathbb{R}}^2)$, and for all ${\mathit{ϵ}}_1,{\mathit{ϵ}}_2\in L^2{(\mathrm{\Sigma })}^2$ by:20 $$\begin{array}{c}\hfill {⟨w,I_D^{\prime }[\mathit{\beta },\mathit{\delta }]({\mathit{ϵ}}_1,{\mathit{ϵ}}_2)⟩}_{L_2}={⟨I_D^{\prime }{[\mathit{\beta },\mathit{\delta }]}^{\ast }w,({\mathit{ϵ}}_1,{\mathit{ϵ}}_2)⟩}_{L_2\times L_2}\end{array}$$20 $\square$

4 Nonlinear Tikhonov regularization for phase contrast tomography

4.1 Nonlinear Tikhonov regularization

Our aim is thus to estimate the two components $(\mathit{\beta },\mathit{\delta })$, from the noisy intensity $I_{{\mathit{\delta }}_n}$ measurements such that21 $$\begin{array}{c}\hfill \Vert I-I_{{\mathit{\delta }}_n}{\Vert }_{L_2}\le {\mathit{\delta }}_n\end{array}$$21 where $I$ is the noise free intensity data, and ${\mathit{\delta }}_n$ the noise level.

The Radon operator and the convolution by the Fresnel operator are compact operators. Our inverse problem is ill-posed and must be regularized. In order to obtain stable solutions, we have used a nonlinear Tikhonov regularization, which is a widely used approach for solving nonlinear inverse problems in a stable way. The aim of the nonlinear Tikhonov regularization is to minimize the functional $J_{\mathit{\alpha },I_{{\mathit{\delta }}_n}}$ of the two components $(\mathit{\delta },\mathit{\beta })$:22 $$\begin{array}{c}\hfill J_{\mathit{\alpha }}[\mathit{\delta },\mathit{\beta }]=\frac{1}{2}\Vert I_{D,\mathit{\theta }}[\mathit{\delta },\mathit{\beta }]-I_{{\mathit{\delta }}_n}{\Vert }_{L^2}^2+\frac{\mathit{\alpha }}{2}{\Vert \mathit{\delta }\Vert }_{L^2}^2+\frac{\mathit{\alpha }}{2}{\Vert \mathit{\beta }\Vert }_{L^2}^2\end{array}$$22 where $\mathit{\alpha }>0$ is a regularization parameter. In the following, we will make use of the stability and convergence result of Engl et al. [26–28] for regularization methods in Hilbert spaces. We first detail the functional properties of the forward intensity operator for phase tomography.

Proposition 4.1

The Fresnel intensity operator $I_D:L^2(\mathrm{\Sigma })\times L^2(\mathrm{\Sigma })\to L^2([0,\mathit{\pi }]\times {\mathbb{R}}^2)$ is continuous, weakly sequentially closed and Fréchet differentiable with a Lipschitz continuous Fréchet derivative on its domain.

Proof

In [20], it was shown that the operator $I_D(B,\mathit{\phi })$ is continuous, weakly sequentially closed and Fréchet differentiable with a Lipschitz continuous Fréchet derivative on its domain. In Section 2, it was shown that the Radon operator $R$ is linear and continuous between well-defined Hilbert spaces and thus the former properties are satisfied for $I_D[\mathit{\beta },\mathit{\delta }]:L^2(\mathrm{\Sigma })\times L^2(\mathrm{\Sigma })\to L^2([0,\mathit{\pi }]\times {\mathbb{R}}^2)$.$\square$

Assume that a minimum norm solution $u^{+}$ exists with $I_D(u^{+})=I$, then the following convergence and stability results hold:

Theorem 4.2

Assume $I_k\to I_{\mathit{\delta }}$, and $u_k\in argmin(J_{\mathit{\alpha },I_k})$ for all k. Then $(u_k)$ has a convergent subsequence. Every convergent subsequence converges to a minimizer of $J_{\mathit{\alpha },I_{\mathit{\delta }}}$.

Theorem 4.3

Assume that $\mathit{\alpha }$ satisfies $\mathit{\alpha }(\mathit{\delta })\to 0$ and $\frac{{\mathit{\delta }}^2}{\mathit{\alpha }(\mathit{\delta })}\to 0$ as $\mathit{\delta }\to 0$. Let $({\mathit{\delta }}_k)$ be a sequence of positive numbers converging to 0 such that the data satisfy $\Vert I-I_k\Vert \le {\mathit{\delta }}_k$. Let $u_k\in argmin(J_{\mathit{\alpha }({\mathit{\delta }}_k),I_k})$. Then $(u_k)$ has a convergent subsequence. The limit is a $u^{\ast }$-minimal norm solution .

Proof

The operator $I_D$ is continuous and weakly sequentially closed and the result follows from the classical Tikhonov regularization in Hilbert spaces.[27, 28]$\square$

Some convergence rate can also be derived under suitable source conditions.[27, 28]

4.2 Implementation of the nonlinear regularization method

In order to minimize the Tikhonov regularization functional, many iterative methods have been investigated based on Landweber or Gauss–Newton approaches.[27, 28] In the field of discrete ART for tomography, several schemes have been studied which are some variants of the Landweber methods.[25, 29, 30] In this work, we use a variant of the Landweber method and of the Simultaneous Algebraic Reconstruction Technique where the update is performed per projection angle.

The first order optimality condition for the minimization of the regularization functional can be written:23 $$\begin{array}{c}\hfill I_D^{\prime }{[\mathit{\beta },\mathit{\delta }]}^{\ast }(I_D[\mathit{\beta },\mathit{\delta }]-I_{{\mathit{\delta }}_n})+\mathit{\alpha }(\mathit{\beta },\mathit{\delta })=0\end{array}$$23

Table 1. Values of the $\mathit{\delta }$ and $\mathit{\mu }$ values for the materials in the object, for 24 keV X-rays, from http://henke.lbl.gov/optical_constants.

Material	$\mathit{\delta }({10}^{-7})$	$\mathit{\mu }({\mathrm{m}}^{-1})$
PMMA	4.628	41.2
Al	9.396	502.6

Figure 2. Horizontal section of the true $\mathit{\beta }$ and $\mathit{\delta }$ maps.

Figure 3. Horizontal section of the initial blurred $\mathit{\beta }$ and $\mathit{\delta }$ maps.

Figure 4. Section of the reconstructed $\mathit{\beta }$ and $\mathit{\delta }$ maps for a PPSNR of 24 dB.

Figure 5. Diagonal profiles of the $\mathit{\beta }$ map:intial map (blue), true map (red), reconstructed map (Black) (PPSNR $=$ 24 dB).

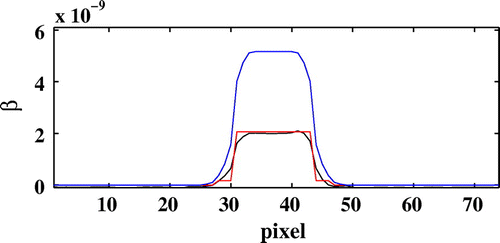
Figure 6. Diagonal profiles of the $\mathit{\delta }$ map:intial map (blue), true map (red), reconstructed map (black) (PPSNR $=$ 24 dB).

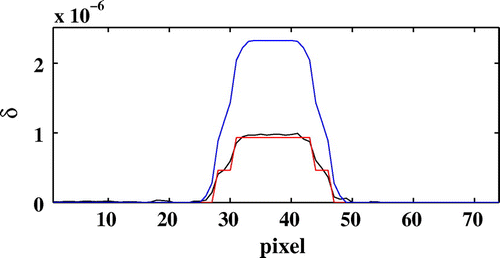
Figure 7. Evolution of the partial data term corresponding to the selected projection angle as a function of the iterations number without noise (full line) and with noise (dotted line) for a $\mathrm{PPSNR}=24$ dB.

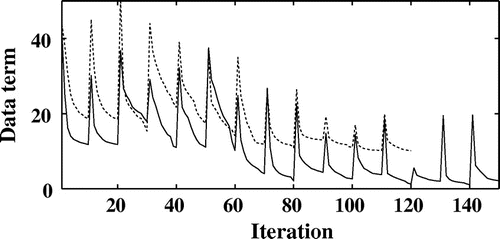
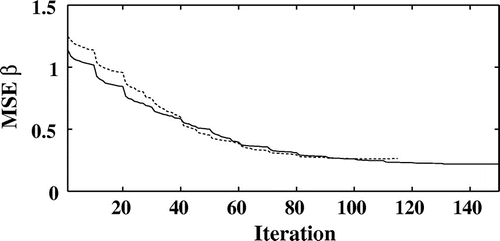
Figure 8. Evolution of the normalized mean square error on $\mathit{\delta }$ as a function of the iterations number without noise (full line) and with noise (dotted line) for a PPSNR $=$ 24 dB.

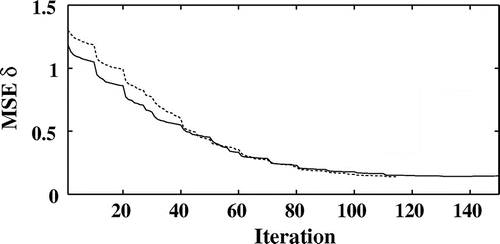
Figure 9. Evolution of the normalized mean square error on $\mathit{\beta }$ as a function of the iterations number without noise (full line) and with noise (dotted line) for a PPSNR $=$ 24 dB.

The update formula in our Landweber type method becomes:24 $$\begin{array}{c}\hfill ({\mathit{\beta }}_{k+1},{\mathit{\delta }}_{k+1})=({\mathit{\beta }}_k,{\mathit{\delta }}_k)-{\mathit{\tau }}_k(I_D{[{\mathit{\beta }}_k,{\mathit{\delta }}_k]}^{\ast }(I_D[{\mathit{\beta }}_k,{\mathit{\delta }}_k]-I_{{\mathit{\delta }}_n})+\mathit{\alpha }({\mathit{\beta }}_k,{\mathit{\delta }}_k))\end{array}$$24 In our implementation, to avoid large data storage, one projection angle is first iteratively chosen at random for the calculation of the adjoint of the Radon projection operator. The step length parameter ${\mathit{\tau }}_k$ is chosen with a backtracking strategy in order to obtain the best decrease of the Tikhonov’s functional along the descent direction $d_k$, with $d_k=(I_D{[{\mathit{\beta }}_k,{\mathit{\delta }}_k]}^{\ast }(I_D[{\mathit{\beta }}_k,{\mathit{\delta }}_k]-I_{{\mathit{\delta }}_n})+\mathit{\alpha }({\mathit{\beta }}_k,{\mathit{\delta }}_k))$. This type of method has been used for linear ill-posed problems.[31] It corresponds to a modification of the standard Landweber method where the step length is constant. In the nonlinear case, the convergence results are established for a small constant step length.[32] Yet, in our simulations the best numerical results were achieved with an optimized descent parameter. The choice of the regularization parameter $\mathit{\alpha }$ and the stopping index of the iterations $k^{\ast }$ are based on the Morozov’s discrepancy principle.[27] The regularization parameter is chosen such that the discrepancy term satisfy the condition:25 $$\begin{array}{c}\hfill \Vert I_D[\mathit{\beta },\mathit{\delta }]-I_{{\mathit{\delta }}_n}{\Vert }_2\le c{\mathit{\delta }}_n\end{array}$$25 for a constant $c\ge 1$.

5 Results and discussion

5.1 Simulation details

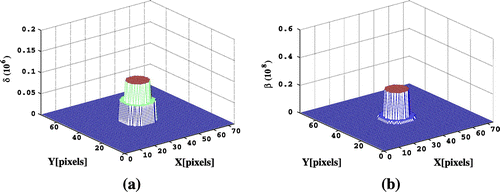
The nonlinear regularization method used for the recovery of the real and imaginary part of the refraction index has been tested on simulated data with an homogeneous material embedded in another one. The simulated object consists of an Al cylinder of $20\mathrm{\mu }\mathrm{m}$ in diameter and $110\mathrm{\mu }\mathrm{m}$ in height embedded in another Poly(methyl-methacrylate ($C_5{H}_8{O}_2$) cylinder with diameter $30\mathrm{\mu }\mathrm{m}$. Let $\mathit{\mu }=\frac{4\mathit{\pi }\mathit{\beta }}{\mathit{\lambda }}$, the $\mathit{\delta }$ and $\mathit{\mu }$ values for the materials in the object, for 24 keV X-rays, are listed in Table 1. The $\mathit{\beta }$ and $\mathit{\delta }$ values were discretized on a regular grid with a pixel size of $1.5\mathrm{\mu }\mathrm{m}$. The cylinders are included in a rectangular volume of size $N_1\times N_1\times N_2$ with $N_1=74$ and $N_2=109$ used for the simulations. Horizontal sections of the original $\mathit{\delta }$ and $\mathit{\beta }$ maps to be retrieved are displayed in Figure 2.

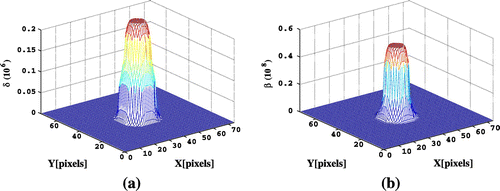
The discrete approximation of the Radon transform is the projection operator implemented in the Mablab Toolbox. The nonlinear algorithm was implemented with 400 projections angles. The Fresnel diffraction image was simulated with a hard X-ray beam of wavelength $\mathit{\lambda }=0.5166\mathrm{\AA }$ (24 keV) at one sample-to-detector distances $D=100\mathrm{mm}$. An initialization index map was obtained by smoothing the true index map. Horizontal sections of the initial $\mathit{\delta }$ and $\mathit{\beta }$ functions are displayed in Figure 3. The intensity data were corrupted with additive Gaussian white noise with a peak-to-peak signal-to-noise ratio (PPSNR) between 0 and 24 dB.

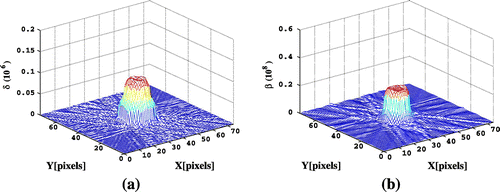
5.2 Results

Figure 4 displays the horizontal section of the real and imaginary part of the reconstructed index map for a PPSNR of 24 dB. The diagonal profiles for this section for $\mathit{\delta }$ and $\mathit{\beta }$ are compared in Figures 5 and 6. The reconstruction errors have been significantly reduced. Similar results are obtained for the other sections. The evolution of the partial data term $\Vert I_{D,\mathit{\theta }}-I_{{\mathit{\delta }}_n,\mathit{\theta }}\Vert$ corresponding to the selected projection angle $\mathit{\theta }$ is displayed as a function of the number of iterations in Figure 7 without noise and for a PPSNR of 24 dB. Let ${\mathit{\delta }}^{\ast }$ and ${\mathit{\beta }}^{\ast }$ be the real and imaginary parts of the complex refractive index to be retrieved. In order to have a more quantitative information about the convergence of the method, the evolution of the normalized least square error using the $L_2(\mathrm{\Sigma })$ norm $\Vert {\mathit{\delta }}^{\ast }{-\mathit{\delta }\Vert }_2/{\Vert {\mathit{\delta }}^{\ast }\Vert }_2$ and $\Vert {\mathit{\beta }}^{\ast }{-\mathit{\beta }\Vert }_2/{\Vert {\mathit{\beta }}^{\ast }\Vert }_2$ is displayed as a function of the number of iterations without noise on the projections and for a PPSNR of 24 dB on Figures 8 and 9. The normalized mean square errors on the two components of the refractive index are much decreased. It should be noted that the method developed does not require any a priori knowledge about the complex refractive index of the material and a priori about the total projected thickness of the sample for each orientation contrary to the other approaches found in the literature.[8, 11, 21, 22] Others regularization schemes and prior information may be introduced in the object domain.

6 Conclusion

In this work, we have investigated the new nonlinear inverse problem associated to the reconstruction of the real and complex part of the refractive index in phase contrast tomography. The functional properties of the direct operator are investigated. The regularization scheme investigated is a classical nonlinear Tikhonov scheme. Our iterative algorithm to minimize the regularization functional is based on the use of the adjoint of the Fréchet derivative of the intensity operator, a modified Landweber method and the Simultaneous Algebraic Reconstruction technique. The proposed regularization method is tested on a multimaterial phantom. The reconstruction errors are much decreased. The proposed nonlinear method will be compared with other algorithms in future studies. This method opens promising perspectives to process experimental data in various applications.