Recovery of a space-dependent vector source in thermoelastic systems

Abstract

In this contribution, an inverse problem of determining a space-dependent vector source in a thermoelastic system of type-I, type-II and type-III is studied using information from a supplementary measurement at a fixed time. These thermoelastic systems consist of two equations that are coupled: a parabolic equation for the temperature $\mathit{\theta }$ and a vectorial hyperbolic equation for the displacement $\mathbf{u}$. In this latter one, the source is unknown, but solely space dependent. A spacewise-dependent additional measurement at the final time ensures that the inverse problem corresponding with each type of thermoelasticity has a unique solution when a damping term $\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)$ (with $\mathbf{g}$ componentwise strictly monotone increasing) is present in the hyperbolic equation. Despite the ill-posed nature of these inverse problems, a stable iterative algorithm is proposed to recover the unknown source in the case that $\mathbf{g}$ is also linear. This method is based on a sequence of well-posed direct problems, which are numerically solved at each iteration, step by step, using the finite element method. The instability of the inverse source problem is overcome by stopping the iterations at the first iteration for which the discrepancy principle is satisfied. Numerical results support the theoretically obtained results.

Keywords:

• thermoelasticity
• inverse problems
• iterative regularization
• discrepancy principle
• finite element method

1 Introduction

Thermoelasticity is the change in the size and shape of a solid object as the temperature of that object fluctuates. A material that is elastic expands when heated and contracts when cooled. There are mathematical systems established that describe how the shape of an object changes when there are fluctuations in the temperature. More specifically, a thermoelastic system consists of two equations that are coupled: a parabolic equation for the temperature and a vectorial hyperbolic equation for the displacement. In [1], three theories of thermoelasticity each with a corresponding system are developed: type-I, type-II and type-III thermoelasticities. The first type is based on Fourier’s law to describe the heat conduction in the body. This theory has the shortcoming that a thermal disturbance at one point of the body is instantly felt everywhere (infinite speed of propagation phenomena). This is physically not acceptable for materials with memory and is overcome by taking memory effects into account in the models for type-II and type-III thermoelasticities. The main difference between type-II and type-III is that in type-II thermoelasticity, the heat conduction is independent of the present values of the temperature gradient, see also [2, 3]. A topic of great interest is the recovery of unknown (vector or heat) sources in thermoelastic systems from additional measurements.

In this contribution, an inverse problem of determining a space-dependent source in a thermoelastic system of type-III using information from a supplementary measurement at a given single instant of time is studied. The mathematical setting is the following. An isotropic and homogeneous thermoelastic body occupying an open and bounded domain $\mathrm{\Omega }\subset {\mathbb{R}}^d,d⩾1,$ with Lipschitz continuous boundary $\mathrm{\Gamma }$ is considered. Let $Q_T=\mathrm{\Omega }\times (0,T)$ and ${\mathrm{\Sigma }}_T=\mathrm{\Gamma }\times (0,T)$ for a given final time $T>0$. The convolution product of a kernel $k$ and a function $\mathit{\theta }$ is denoted with the sign ‘$\star$’$$\left(k,\star ,\mathit{\theta }\right)(\mathbf{x},t):={\int }_0^{t}k(t-s)\mathit{\theta }(\mathbf{x},s)\mathrm{d}s,(\mathbf{x},t)\in Q_T.$$The following thermoelastic system of type-III describing the elastic and thermal behaviour in $\mathrm{\Omega }$ is discussed:1 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{f}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \end{array}\right)\end{array}$$1 with initial conditions:2 $$\begin{array}{c}\hfill \mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_0(\mathbf{x}),{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_1(\mathbf{x}),\mathit{\theta }(\mathbf{x},0)={\overline{\mathit{\theta }}}_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$2 where the unknown vector source $\mathbf{f}$ is of the form3 $$\begin{array}{c}\hfill \mathbf{f}(\mathbf{x},t)=\mathbf{p}(\mathbf{x})+\mathbf{r}(\mathbf{x},t),(\mathbf{x},t)\in Q_T,\end{array}$$3 with the vector fields $\mathbf{r}$ known and $\mathbf{p}$ unknown. The heat source $h$ is known. Here, $\mathbf{u}={\left(u_1,,,\dots ,,,u_d\right)}^{\mathsf{T}}$ and $\mathit{\theta }$ denote, respectively, the displacement and the temperature difference from the reference value (in Kelvin) of the solid elastic material at the location $\mathbf{x}$ and time $t$. The Lamé parameters $\mathit{\alpha }$ and $\mathit{\beta }$, the coupling (absorbing) coefficient $\mathit{\gamma }$ and the thermal coefficient $\mathit{\rho }$ are assumed to be positive constants because the medium is supposed to be isotropic homogeneous. The goal of this paper is to determine the spatial vector function $\mathbf{p}(\mathbf{x})$ by an additional measurement (the condition of final overdetermination)4 $$\begin{array}{c}\hfill {\mathbf{u}}_T(\mathbf{x}):=\mathbf{u}(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega }.\end{array}$$4 This means that the displacement is measured at the final time. The kernel function (also called relaxation function) $k\in C^2([0,T])$ decays to zero as time goes to infinity. Moreover, it is assumed that$$k^{\prime }(t)\not\equiv 0\text{and}{(-1)}^j{k}^{(j)}(t)⩾0,$$with $j=0,1,2$ denoting the order of the derivative. These assumptions imply that $k$ is strongly positive definite [4, Corollary $7.2.1$]. This is equivalent with the existence of a positive constant $C_0$ independent of $T$ such that [4, Lemma $7.2.2$], [5]$${\int }_0^T\mathit{\varphi }(t)(k\star \mathit{\varphi })(t)\mathrm{d}t⩾C_0{\int }_0^T{\left(k,\star ,\mathit{\varphi }\right)}^2(t)\mathrm{d}t,\forall T>0,\forall \mathit{\varphi }\in L_{\mathrm{l}oc}^1(\mathrm{\Omega }).$$These assumptions on the kernel $k$ are natural, because usually $k$ takes the form [6]$$k(t)=aexp(-bt),t>0,$$with $a$ and $b$, two positive constants. Note that a damping term $\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)=\left(g_1,({\mathit{\partial }}_t\mathbf{u}),,,\dots ,,\right)$$\left(g_d,({\mathit{\partial }}_t\mathbf{u})\right)$ is added in the hyperbolic equation in comparison with the classic thermoelasticity system, $g_i:{\mathbb{R}}^d\to \mathbb{R},i=1,\dots ,d$. This term is also considered in [4, Chapter $9$], [7, 8]. Moreover, this term is essential to establish the uniqueness of a solution to the inverse problem, see Theorem 2.1.

Recently, inverse source problems related to the classic thermoelastic system have been studied by several authors. Without taking memory effects into account, i.e. $k\equiv 0$ and $\mathit{\rho }\ne 0$, Bellassoued and Yamamoto [9] investigated an inverse heat source problem for type-I thermoelasticity. The main subject of their paper is the inverse problem of determining the heat source $h(\mathbf{x})$ instead of the vector source $\mathbf{p}(\mathbf{x})$. This is done by measuring ${\mathit{u}}_{|\mathit{\omega }\times (0,T)}$ and $\mathit{\theta }(·,t_0)$, where $\mathit{\omega }$ is a subdomain of $\mathrm{\Omega }$ such that $\mathrm{\Gamma }\subset \mathit{\partial }\mathit{\omega }$ and $t_0\in (0,T)$. They do not need data of $\mathbf{u}(·,t_0)$ over the whole domain $\mathrm{\Omega }$. Using a Carleman estimate, a Hölder stability for the inverse source problem is proved, which implies the uniqueness of the inverse source problem. Wu and Liu [10] studied an inverse source problem of determining $\mathbf{p}(\mathbf{x})$ for type-II thermoelasticity, i.e. $k\ne 0$ and $\mathit{\rho }=0$. Based on a Carleman estimate, again a Hölder stability for the inverse source problem has been established from a displacement measurement ${\mathbf{u}}_{|\mathit{\omega }\times (0,T)}$ provided that $\mathbf{p}$ is known in a neighbourhood ${\mathit{\omega }}_0$ of $\mathrm{\Gamma }$. Note that there is no temperature measurement needed. In both contributions, no numerical scheme is provided to recover the unknown source. From now on, consider the most general situation that $k\ne 0$ and $\mathit{\rho }\ne 0$, i.e. type-III thermoelasticity. As mentioned before, the goal of this contribution is to determine $\mathbf{p}(\mathbf{x})$ from the additional final in time measurement (44 $$\begin{array}{c}\hfill {\mathbf{u}}_T(\mathbf{x}):=\mathbf{u}(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega }.\end{array}$$4 ). The uniqueness of a solution to problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{f}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \end{array}\right)\end{array}$$1 ) is proved using a variational approach instead of using a Carleman estimate. One of the key assumptions is that $\mathbf{g}$ is componentwise strictly monotone increasing. Unfortunately, this inverse problem is ill-posed since small errors present in any practical measurements give rise to large errors into the solutions. However, in the case that $\mathbf{g}$ is also linear, a stable iterative algorithm is proposed to recover the unknown source. This method is based on a sequence of well-posed direct problems, which are numerically solved at each iteration step using the finite element method. The instability of this inverse source problem is overcome by stopping the iterations using the discrepancy principle.[11] This scheme is of the Landweber–Friedman type and is similar to that of Johansson and Lesnic for the heat conduction equation.[12] This procedure is also used for the heat conduction equation with time-dependent coefficients in [13].

The remainder of this paper is organized as follows. The uniqueness of a solution to the inverse problem under consideration is established in Section 2 under the assumption that $\mathbf{g}$ is componentwise strictly monotone increasing ($\mathbf{g}$ can be linear or non-linear). In Section 3, a convergent and stable algorithm is proposed for the recovery of the unknown vector source in the case that $\mathbf{g}$ is also linear. Finally, some numerical experiments are developed in Section 4.

2 Uniqueness

Using Green’s formulas, the following coupled variational formulation for (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{f}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \end{array}\right)\end{array}$$1 ) is obtained: find $⟨\mathbf{u},\mathit{\theta },\mathbf{p}⟩\in {\mathbf{H}}_0^1(\mathrm{\Omega })\times H_0^1(\mathrm{\Omega })\times {\mathbf{L}}_2(\mathrm{\Omega })$ such that5 $$\begin{array}{cc}\hfill \left({\mathit{\partial }}_{tt},\mathbf{u},,,\mathit{\phi }\right)+\left(\mathbf{g},\left({\mathit{\partial }}_t,\mathbf{u}\right),,,\mathit{\phi }\right)+\mathit{\alpha }\left(\mathrm{\nabla },\mathbf{u},,,\mathrm{\nabla },\mathit{\phi }\right)+\mathit{\beta }\left(\mathrm{\nabla },·,\mathbf{u},,,\mathrm{\nabla },·,\mathit{\phi }\right)+\mathit{\gamma }\left(\mathrm{\nabla },\mathit{\theta },,,\mathit{\phi }\right)& =\left(\mathbf{p},+,\mathbf{r},,,\mathit{\phi }\right)\hfill \end{array}$$5 6 $$\begin{array}{cc}\hfill {\displaystyle \left({\mathit{\partial }}_t,\mathit{\theta },,,\mathit{\psi }\right)+\mathit{\rho }\left(\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\psi }\right)+\left(k,\star ,\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\psi }\right)-\mathit{\gamma }\left({\mathit{\partial }}_t,\mathbf{u},,,\mathrm{\nabla },\mathit{\psi }\right)}& {\displaystyle =\left(h,,,\mathit{\psi }\right),}\hfill \end{array}$$6 for all $\mathit{\phi }\in {\mathbf{H}}_0^1(\mathrm{\Omega })$ and $\mathit{\psi }\in H_0^1(\mathrm{\Omega })$. The spacewise-dependent measurement (44 $$\begin{array}{c}\hfill {\mathbf{u}}_T(\mathbf{x}):=\mathbf{u}(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega }.\end{array}$$4 ) ensures that the inverse problem has a unique solution. This is stated in the following theorem.

Theorem 2.1

(Uniqueness). Let $\overline{}\}{u}_0,\overline{}\}{u}_1,{\mathit{\xi }}_T\in {\mathbf{L}}_2(\mathrm{\Omega })$, ${\overline{\mathit{\theta }}}_0\in L_2(\mathrm{\Omega })$ and ${\mathbf{g}}^{\prime }>\mathbf{0}$ componentwise. Then there exists at most one triplet $⟨\mathbf{u},\mathit{\theta },\mathbf{p}⟩\in {\mathbf{H}}_0^1(\mathrm{\Omega })\times H_0^1(\mathrm{\Omega })\times {\mathbf{L}}_2(\mathrm{\Omega })$ such that problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{f}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \end{array}\right)\end{array}$$1 ) together with the condition (44 $$\begin{array}{c}\hfill {\mathbf{u}}_T(\mathbf{x}):=\mathbf{u}(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega }.\end{array}$$4 ) hold.

Proof

Suppose that there are two solutions $⟨{\mathbf{u}}_1,{\mathit{\theta }}_1,{\mathbf{p}}_1⟩$ and $⟨{\mathbf{u}}_2,{\mathit{\theta }}_2,{\mathbf{p}}_2⟩$ to (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{f}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \end{array}\right)\end{array}$$1 )–(44 $$\begin{array}{c}\hfill {\mathbf{u}}_T(\mathbf{x}):=\mathbf{u}(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega }.\end{array}$$4 ). Subtract, equation by equation, the variational formulation (55 $$\begin{array}{cc}\hfill \left({\mathit{\partial }}_{tt},\mathbf{u},,,\mathit{\phi }\right)+\left(\mathbf{g},\left({\mathit{\partial }}_t,\mathbf{u}\right),,,\mathit{\phi }\right)+\mathit{\alpha }\left(\mathrm{\nabla },\mathbf{u},,,\mathrm{\nabla },\mathit{\phi }\right)+\mathit{\beta }\left(\mathrm{\nabla },·,\mathbf{u},,,\mathrm{\nabla },·,\mathit{\phi }\right)+\mathit{\gamma }\left(\mathrm{\nabla },\mathit{\theta },,,\mathit{\phi }\right)& =\left(\mathbf{p},+,\mathbf{r},,,\mathit{\phi }\right)\hfill \end{array}$$5 ) and (66 $$\begin{array}{cc}\hfill {\displaystyle \left({\mathit{\partial }}_t,\mathit{\theta },,,\mathit{\psi }\right)+\mathit{\rho }\left(\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\psi }\right)+\left(k,\star ,\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\psi }\right)-\mathit{\gamma }\left({\mathit{\partial }}_t,\mathbf{u},,,\mathrm{\nabla },\mathit{\psi }\right)}& {\displaystyle =\left(h,,,\mathit{\psi }\right),}\hfill \end{array}$$6 ) corresponding with the solution $⟨{\mathbf{u}}_2,{\mathit{\theta }}_2,{\mathbf{p}}_2⟩$ from the variational formulation for $⟨{\mathbf{u}}_1,{\mathit{\theta }}_1,{\mathbf{p}}_1⟩$. Set $\mathbf{u}={\mathbf{u}}_1-{\mathbf{u}}_2$, $\mathbf{p}={\mathbf{p}}_1-{\mathbf{p}}_2$ and $\mathit{\theta }={\mathit{\theta }}_1-{\mathit{\theta }}_2$. Then is $\mathbf{u}(\mathbf{x},0)=\mathbf{0}$, $\mathbf{u}(\mathbf{x},T)=\mathbf{0}$, ${\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\mathbf{0}$ and $\mathit{\theta }(\mathbf{x},0)=0$. Then, we obtain7 $$\begin{array}{cc}\hfill \left({\mathit{\partial }}_{tt},\mathbf{u},,,\mathit{\phi }\right)+\left(\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_1\right),-,\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_2\right),,,\mathit{\phi }\right)+\mathit{\alpha }\left(\mathrm{\nabla },\mathbf{u},,,\mathrm{\nabla },\mathit{\phi }\right)+\mathit{\beta }\left(\mathrm{\nabla },·,\mathbf{u},,,\mathrm{\nabla },·,\mathit{\phi }\right)& \hfill \\ \hfill +\mathit{\gamma }\left(\mathrm{\nabla },\mathit{\theta },,,\mathit{\phi }\right)& =\left(\mathbf{p},,,\mathit{\phi }\right)\hfill \end{array}$$7 8 $$\begin{array}{cc}\hfill {\displaystyle \left({\mathit{\partial }}_t,\mathit{\theta },,,\mathit{\psi }\right)+\mathit{\rho }\left(\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\psi }\right)+\left(k,\star ,\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\psi }\right)-\mathit{\gamma }\left({\mathit{\partial }}_t,\mathbf{u},,,\mathrm{\nabla },\mathit{\psi }\right)}& {\displaystyle =0,}\hfill \end{array}$$8 for all $\mathit{\phi }\in {\mathbf{H}}_0^1(\mathrm{\Omega })$ and $\mathit{\psi }\in H_0^1(\mathrm{\Omega })$. First, we prove that $\mathbf{u}=\mathbf{0}$ and $\mathit{\theta }=0$. Afterwards, we show that $\mathbf{p}=\mathbf{0}$. Therefore, in the first part of the proof, we should get rid of $\mathbf{p}$. This can be done in a simple way. The main idea is$${\displaystyle {\int }_0^T\mathbf{p}(\mathbf{x})·{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},t)\mathrm{d}t=\mathbf{p}(\mathbf{x})·\mathbf{u}(\mathbf{x},T)-\mathbf{p}(\mathbf{x})·\mathbf{u}(\mathbf{x},0)=0.}$$Indeed, putting $\mathit{\phi }={\mathit{\partial }}_t\mathbf{u}$ in (77 $$\begin{array}{cc}\hfill \left({\mathit{\partial }}_{tt},\mathbf{u},,,\mathit{\phi }\right)+\left(\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_1\right),-,\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_2\right),,,\mathit{\phi }\right)+\mathit{\alpha }\left(\mathrm{\nabla },\mathbf{u},,,\mathrm{\nabla },\mathit{\phi }\right)+\mathit{\beta }\left(\mathrm{\nabla },·,\mathbf{u},,,\mathrm{\nabla },·,\mathit{\phi }\right)& \hfill \\ \hfill +\mathit{\gamma }\left(\mathrm{\nabla },\mathit{\theta },,,\mathit{\phi }\right)& =\left(\mathbf{p},,,\mathit{\phi }\right)\hfill \end{array}$$7 ) and integrating in time over $(0,T)$ gives9 $$\begin{array}{c}\hfill \frac{1}{2}{∥{\mathit{\partial }}_t\mathbf{u}(T)∥}^2+{\int }_0^T\left(\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_1\right),-,\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_2\right),,,{\mathit{\partial }}_t,{\mathbf{u}}_1,-,{\mathit{\partial }}_t,{\mathbf{u}}_2\right)+\mathit{\gamma }{\int }_0^T\left(\mathrm{\nabla },\mathit{\theta },,,{\mathit{\partial }}_t,\mathbf{u}\right)=0,\end{array}$$9 because $\mathbf{u}(\mathbf{x},0)=\mathbf{u}(\mathbf{x},T)={\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\mathbf{0}$. Taking $\mathit{\psi }=\mathit{\theta }$ in (88 $$\begin{array}{cc}\hfill {\displaystyle \left({\mathit{\partial }}_t,\mathit{\theta },,,\mathit{\psi }\right)+\mathit{\rho }\left(\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\psi }\right)+\left(k,\star ,\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\psi }\right)-\mathit{\gamma }\left({\mathit{\partial }}_t,\mathbf{u},,,\mathrm{\nabla },\mathit{\psi }\right)}& {\displaystyle =0,}\hfill \end{array}$$8 ) yields10 $$\begin{array}{c}\hfill \frac{{∥\mathit{\theta }(T)∥}^2}{2}+\mathit{\rho }{\int }_0^T{∥\mathrm{\nabla }\mathit{\theta }∥}^2+{\int }_0^T\left(k,\star ,\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\theta }\right)-\mathit{\gamma }{\int }_0^T\left({\mathit{\partial }}_t,\mathbf{u},,,\mathrm{\nabla },\mathit{\theta }\right)=0,\end{array}$$10 due to $\mathit{\theta }(\mathbf{x},0)=0$. Now, adding (99 $$\begin{array}{c}\hfill \frac{1}{2}{∥{\mathit{\partial }}_t\mathbf{u}(T)∥}^2+{\int }_0^T\left(\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_1\right),-,\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_2\right),,,{\mathit{\partial }}_t,{\mathbf{u}}_1,-,{\mathit{\partial }}_t,{\mathbf{u}}_2\right)+\mathit{\gamma }{\int }_0^T\left(\mathrm{\nabla },\mathit{\theta },,,{\mathit{\partial }}_t,\mathbf{u}\right)=0,\end{array}$$9 ) and (1010 $$\begin{array}{c}\hfill \frac{{∥\mathit{\theta }(T)∥}^2}{2}+\mathit{\rho }{\int }_0^T{∥\mathrm{\nabla }\mathit{\theta }∥}^2+{\int }_0^T\left(k,\star ,\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\theta }\right)-\mathit{\gamma }{\int }_0^T\left({\mathit{\partial }}_t,\mathbf{u},,,\mathrm{\nabla },\mathit{\theta }\right)=0,\end{array}$$10 ) implies11 $$\begin{array}{cc}& \frac{1}{2}{∥{\mathit{\partial }}_t\mathbf{u}(T)∥}^2+{\int }_0^T\left(\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_1\right),-,\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_2\right),,,{\mathit{\partial }}_t,{\mathbf{u}}_1,-,{\mathit{\partial }}_t,{\mathbf{u}}_2\right)\hfill \\ \hfill & +\frac{{∥\mathit{\theta }(T)∥}^2}{2}+\mathit{\rho }{\int }_0^T{∥\mathrm{\nabla }\mathit{\theta }∥}^2+{\int }_0^T\left(k,\star ,\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\theta }\right)=0.\hfill \end{array}$$11 The strongly positive definiteness of $k$ implies that$${\displaystyle {\int }_0^T\left(k,\star ,\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\theta }\right)⩾C_0{\int }_0^T{∥k\star \mathrm{\nabla }\mathit{\theta }∥}^2.}$$Thus, from (1111 $$\begin{array}{cc}& \frac{1}{2}{∥{\mathit{\partial }}_t\mathbf{u}(T)∥}^2+{\int }_0^T\left(\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_1\right),-,\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_2\right),,,{\mathit{\partial }}_t,{\mathbf{u}}_1,-,{\mathit{\partial }}_t,{\mathbf{u}}_2\right)\hfill \\ \hfill & +\frac{{∥\mathit{\theta }(T)∥}^2}{2}+\mathit{\rho }{\int }_0^T{∥\mathrm{\nabla }\mathit{\theta }∥}^2+{\int }_0^T\left(k,\star ,\mathrm{\nabla },\mathit{\theta },,,\mathrm{\nabla },\mathit{\theta }\right)=0.\hfill \end{array}$$11 ), it follows that$${∥{\mathit{\partial }}_t\mathbf{u}(T)∥}^2+{\int }_0^T\left(\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_1\right),-,\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_2\right),,,{\mathit{\partial }}_t,{\mathbf{u}}_1,-,{\mathit{\partial }}_t,{\mathbf{u}}_2\right)=0$$and12 $$\begin{array}{c}\hfill {∥\mathit{\theta }(T)∥}^2+\mathit{\rho }{\int }_0^T{∥\mathrm{\nabla }\mathit{\theta }∥}^2+{\int }_0^T{∥k\star \mathrm{\nabla }\mathit{\theta }∥}^2=0.\end{array}$$12 Due to the fact that $\mathit{\theta }=0$ on $\mathit{\partial }\mathrm{\Omega }$, we deduce that$$\mathit{\theta }=0\text{a.e. in}{Q}_T.$$Here, we can also see why the damping term is necessary. Without this term, we would only have that $∥{\mathit{\partial }}_t\mathbf{u}(T)∥=0$, which gives no guarantee that $\mathbf{u}=\mathbf{0}$. Employing the fact that the vector field $\mathbf{g}$ is componentwise strictly monotone increasing, we get that ${\mathbf{u}}_t=\mathbf{0}$, i.e. $\mathbf{u}$ is constant in time. Therefore,$$\mathbf{u}(\mathbf{x},0)=\mathbf{0}\Rightarrow \mathbf{u}(\mathbf{x},t)=\mathbf{0}\text{in}{Q}_T.$$Putting the obtained information in (77 $$\begin{array}{cc}\hfill \left({\mathit{\partial }}_{tt},\mathbf{u},,,\mathit{\phi }\right)+\left(\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_1\right),-,\mathbf{g},\left({\mathit{\partial }}_t,{\mathbf{u}}_2\right),,,\mathit{\phi }\right)+\mathit{\alpha }\left(\mathrm{\nabla },\mathbf{u},,,\mathrm{\nabla },\mathit{\phi }\right)+\mathit{\beta }\left(\mathrm{\nabla },·,\mathbf{u},,,\mathrm{\nabla },·,\mathit{\phi }\right)& \hfill \\ \hfill +\mathit{\gamma }\left(\mathrm{\nabla },\mathit{\theta },,,\mathit{\phi }\right)& =\left(\mathbf{p},,,\mathit{\phi }\right)\hfill \end{array}$$7 ) gives$$\left(\mathbf{p},,,\mathit{\phi }\right)=0,\forall \mathit{\phi }\in {\mathbf{H}}_0^1(\mathrm{\Omega }).$$From this, we conclude that $\mathbf{p}=\mathbf{0}$ in ${\mathbf{L}}_2(\mathrm{\Omega })$.$\square$

Remark 2.2

From this theorem follows also immediately the uniqueness to the inverse problem corresponding with type-I thermoelasticity ($k=0,\mathit{\rho }\ne 0$). For type-II thermoelasticity ($\mathit{\rho }=0,k\ne 0$), the proof of uniqueness of a solution is less straightforward. Then (1212 $$\begin{array}{c}\hfill {∥\mathit{\theta }(T)∥}^2+\mathit{\rho }{\int }_0^T{∥\mathrm{\nabla }\mathit{\theta }∥}^2+{\int }_0^T{∥k\star \mathrm{\nabla }\mathit{\theta }∥}^2=0.\end{array}$$12 ) becomes$${∥\mathit{\theta }(T)∥}^2+{\int }_0^T{∥k\star \mathrm{\nabla }\mathit{\theta }∥}^2=0.$$Therefore, ${\displaystyle {\int }_0^{t}k(t-s)\mathrm{\nabla }\mathit{\theta }(\mathbf{x},s)\mathrm{d}s=0}$ for all $t\in [0,T]$ and $\mathbf{x}\in \mathrm{\Omega }$. Hence, since the Laplace transform is one-to-one, it is clear that $\mathrm{\nabla }\mathit{\theta }=0$ in $Q_T$. The uniqueness of a solution follows from $\mathit{\theta }=0$ on $\mathit{\partial }\mathrm{\Omega }$.

Remark 2.3

In fact, to prove the uniqueness of a solution in the case of type-III thermoelasticity, it is sufficient that the kernel $k$ is positive definite instead of strongly positive definite. But, the strongly positive definiteness of $k$ is immediately considered because under this assumption, the unicity of a solution to the inverse problem is valid for all types of thermoelasticities, as mentioned in Remark 2.2.

Remark 2.4

The main trick of the proof is not applicable if the heat source $h(\mathbf{x})$ should be unknown, i.e. ${\int }_0^{T}h(\mathbf{x})\mathit{\theta }(\mathbf{x},t)\mathrm{d}t\ne 0$.

Remark 2.5

The uniqueness of the solution can also be obtained for more general coefficients. For instance, for$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathrm{\nabla }·(\mathit{\alpha }(\mathbf{x})\mathrm{\nabla }\mathbf{u})-\mathrm{\nabla }\left(\mathit{\beta },(,\mathbf{x},),\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{f}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathrm{\nabla }·(\mathit{\rho }(\mathbf{x})\mathrm{\nabla }\mathit{\theta })-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \end{array}\right)\end{array}$$the following assumptions have to be satisfied$$0⩽\mathit{\alpha }(\mathbf{x})<{\mathit{\alpha }}_1,0⩽\mathit{\beta }(\mathbf{x})<{\mathit{\beta }}_1\text{and}0<{\mathit{\rho }}_0<\mathit{\rho }(\mathbf{x})<{\mathit{\rho }}_1.$$

3 Reconstruction of the source term in a linear case

From now on, it is assumed that $\mathbf{g}$ is linear. Then, the principle of linear superposition is applicable on problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{f}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \end{array}\right)\end{array}$$1 )–(44 $$\begin{array}{c}\hfill {\mathbf{u}}_T(\mathbf{x}):=\mathbf{u}(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega }.\end{array}$$4 ). The solution $⟨\mathbf{u},\mathit{\theta },\mathbf{p}⟩$ is given by $⟨{\mathbf{u}}_1+{\mathbf{u}}_2,{\mathit{\theta }}_1+{\mathit{\theta }}_2,\mathbf{p}⟩$, where $⟨{\mathbf{u}}_1,{\mathit{\theta }}_1,\mathbf{p}⟩$ is a solution to13 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{p}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =0}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)={\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\mathbf{0},\mathit{\theta }(\mathbf{x},0)\hfill & =0\hfill & \mathbf{x}\in \mathrm{\Omega };\hfill \end{array}\right)\end{array}$$13 and $⟨{\mathbf{u}}_2,{\mathit{\theta }}_2⟩$ is solving14 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{r}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_0(\mathbf{x}),{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_1(\mathbf{x}),\mathit{\theta }(\mathbf{x},0)\hfill & ={\overline{\mathit{\theta }}}_0(\mathbf{x})\hfill & \mathbf{x}\in \mathrm{\Omega }.\hfill \end{array}\right)\end{array}$$14 First, the well posedness of problem (1414 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{r}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_0(\mathbf{x}),{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_1(\mathbf{x}),\mathit{\theta }(\mathbf{x},0)\hfill & ={\overline{\mathit{\theta }}}_0(\mathbf{x})\hfill & \mathbf{x}\in \mathrm{\Omega }.\hfill \end{array}\right)\end{array}$$14 ) is discussed. Rivera and Qin [14] proved the global existence and uniqueness of solutions to problem (1414 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{r}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_0(\mathbf{x}),{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_1(\mathbf{x}),\mathit{\theta }(\mathbf{x},0)\hfill & ={\overline{\mathit{\theta }}}_0(\mathbf{x})\hfill & \mathbf{x}\in \mathrm{\Omega }.\hfill \end{array}\right)\end{array}$$14 ) in one dimension when $\mathbf{r}\equiv \mathbf{0}\equiv \mathbf{g}$ and $h=0$. In the same situation, a more dimensional case for type-III thermoelasticity is studied in [15]. The following lemma summarizes the available results. For a more general setting, see also [16–18].

Lemma 3.1

   

(i)

Assume that $\mathbf{r}\in L_2([0,T],{\mathbf{L}}_2(\mathrm{\Omega }))$, $h\in L_2([0,T],L_2(\mathrm{\Omega }))$, $\overline{}\}{u}_0(\mathbf{x})\in {\mathbf{H}}_0^1(\mathrm{\Omega })$, $\overline{}\}{u}_1(\mathbf{x})\in {\mathbf{L}}_2(\mathrm{\Omega })$, ${\overline{\mathit{\theta }}}_0\in L_2(\mathrm{\Omega })$, ${\mathbf{g}}^{\prime }>\mathbf{0}$ and $|\mathbf{g}(s)|⩽C(1+|s|)$ a.e. in $\mathbb{R}$. Then (1414 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{r}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_0(\mathbf{x}),{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_1(\mathbf{x}),\mathit{\theta }(\mathbf{x},0)\hfill & ={\overline{\mathit{\theta }}}_0(\mathbf{x})\hfill & \mathbf{x}\in \mathrm{\Omega }.\hfill \end{array}\right)\end{array}$$14 ), has a unique solution $⟨\mathbf{u},\mathit{\theta }⟩$ such that$$\begin{array}{cc}\hfill \mathbf{u}& \in C([0,T],{\mathbf{H}}_0^1(\mathrm{\Omega })),{\mathit{\partial }}_t\mathbf{u}\in C([0,T],{\mathbf{L}}_2(\mathrm{\Omega })),\hfill \\ \hfill \mathit{\theta }& \in C([0,T],L_2(\mathrm{\Omega }))\cap L_2((0,T),H_0^1(\mathrm{\Omega })).\hfill \end{array}$$

(ii)

Assume that $\mathbf{r}(0)\in {\mathbf{L}}_2(\mathrm{\Omega })$, $h(0)\in L_2(\mathrm{\Omega })$, ${\mathit{\partial }}_t\mathbf{r}\in L_2([0,T],{\mathbf{L}}_2(\mathrm{\Omega }))$, ${\mathit{\partial }}_{t}h\in L_2([0,T],L_2(\mathrm{\Omega }))$, $\overline{}\}{u}_0\in {\mathbf{H}}^2(\mathrm{\Omega })\cap {\mathbf{H}}_0^1(\mathrm{\Omega })$, $\overline{}\}{u}_1\in {\mathbf{H}}^1(\mathrm{\Omega })$, ${\overline{\mathit{\theta }}}_0\in H^2(\mathrm{\Omega })\cap H_0^1(\mathrm{\Omega })$ and $\mathbf{0}<{\mathbf{g}}^{\prime }(s)⩽\mathbf{C}$ a.e. in $\mathbb{R}$. Then (1414 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{r}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_0(\mathbf{x}),{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_1(\mathbf{x}),\mathit{\theta }(\mathbf{x},0)\hfill & ={\overline{\mathit{\theta }}}_0(\mathbf{x})\hfill & \mathbf{x}\in \mathrm{\Omega }.\hfill \end{array}\right)\end{array}$$14 ), has a unique solution $⟨\mathbf{u},\mathit{\theta }⟩$ such that$$\begin{array}{cc}\hfill \mathbf{u}& \in C^1([0,T],{\mathbf{H}}_0^1(\mathrm{\Omega })),{\mathit{\partial }}_{tt}\mathbf{u}\in C([0,T],{\mathbf{L}}_2(\mathrm{\Omega })),\hfill \\ \hfill \mathit{\theta }& \in C([0,T],H_0^1(\mathrm{\Omega })),{\mathit{\theta }}_t\in C([0,T],L_2(\mathrm{\Omega })).\hfill \end{array}$$ In the special situation that $\overline{}\}{u}_0(\mathbf{x})=\mathbf{0}$, $\overline{}\}{u}_1(\mathbf{x})=\mathbf{0}$, ${\overline{\mathit{\theta }}}_0=0$, $h=0$ and $\mathbf{r}=\mathbf{r}(\mathbf{x})$, the following estimate is valid15 $$\begin{array}{c}\hfill \underset{t\in [0,T]}{max}\left\{{∥\mathrm{\nabla }\mathbf{u}(t)∥}^2,+,{∥\mathrm{\nabla }{\mathit{\partial }}_t\mathbf{u}(t)∥}^2,+,{∥\mathrm{\nabla }\mathit{\theta }(t)∥}^2,+,{∥{\mathit{\partial }}_t\mathit{\theta }(t)∥}^2\right\}⩽C{∥\mathbf{r}∥}^2.\end{array}$$15

In the remainder of the paper, it is assumed that the assumptions of Lemma 3.1(ii) are valid. This is important because only in this situation are the boundary conditions satisfied since $\mathbf{u}(·,t)\in {\mathbf{H}}_0^1(\mathrm{\Omega })$ and $\mathit{\theta }(·,t)\in H_0^1(\mathrm{\Omega })$ for $t\in [0,T]$. Moreover, also the restriction $\mathbf{u}(\mathbf{x},t_0)$ is well defined for $t_0\in [0,T]$. This means, in particular, that the final displacement measurement $\mathbf{u}(\mathbf{x},T)\in {\mathbf{H}}_0^1(\mathrm{\Omega })$ is well defined. Following Theorem 2.1 and Lemma 3.1(ii), the solution $⟨{\mathbf{u}}_1,{\mathit{\theta }}_1,\mathbf{p}⟩$ to problem (1313 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{p}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =0}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)={\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\mathbf{0},\mathit{\theta }(\mathbf{x},0)\hfill & =0\hfill & \mathbf{x}\in \mathrm{\Omega };\hfill \end{array}\right)\end{array}$$13 ) is unique if the additional final measurement is satisfied, i.e.16 $$\begin{array}{c}\hfill {\mathbf{u}}_1(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x})-{\mathbf{u}}_2(\mathbf{x},T)=:{\tilde{\mathit{\xi }}}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$16 where ${\mathbf{u}}_2$ is the solution to problem (1414 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{r}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_0(\mathbf{x}),{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_1(\mathbf{x}),\mathit{\theta }(\mathbf{x},0)\hfill & ={\overline{\mathit{\theta }}}_0(\mathbf{x})\hfill & \mathbf{x}\in \mathrm{\Omega }.\hfill \end{array}\right)\end{array}$$14 ). Note that for given $\mathbf{p}$, problem (1313 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{p}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =0}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)={\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\mathbf{0},\mathit{\theta }(\mathbf{x},0)\hfill & =0\hfill & \mathbf{x}\in \mathrm{\Omega };\hfill \end{array}\right)\end{array}$$13 ) is a special case of problem (1414 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{r}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_0(\mathbf{x}),{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_1(\mathbf{x}),\mathit{\theta }(\mathbf{x},0)\hfill & ={\overline{\mathit{\theta }}}_0(\mathbf{x})\hfill & \mathbf{x}\in \mathrm{\Omega }.\hfill \end{array}\right)\end{array}$$14 ). In the following subsection, an algorithm for the recovery of the unknown source term is proposed.

Remark 3.2

Also, the well posedness of problem (1414 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{r}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_0(\mathbf{x}),{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_1(\mathbf{x}),\mathit{\theta }(\mathbf{x},0)\hfill & ={\overline{\mathit{\theta }}}_0(\mathbf{x})\hfill & \mathbf{x}\in \mathrm{\Omega }.\hfill \end{array}\right)\end{array}$$14 ) can be obtained for more general coefficients. More specific, when the coefficients are space dependent, the following assumptions have to be satisfied$$0<{\mathit{\alpha }}_0<\mathit{\alpha }(\mathbf{x})<{\mathit{\alpha }}_1,0<{\mathit{\beta }}_0<\mathit{\beta }(\mathbf{x})<{\mathit{\beta }}_1,0<{\mathit{\rho }}_0<\mathit{\rho }(\mathbf{x})<{\mathit{\rho }}_1,0<{\mathit{\gamma }}_0<\mathit{\gamma }(\mathbf{x})<{\mathit{\gamma }}_1.$$

3.1 Algorithm for finding the source term

The procedure for the stable reconstruction of the solution $⟨\mathbf{u},\mathit{\theta }⟩$ and the source term $\mathbf{p}$ of problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{f}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \end{array}\right)\end{array}$$1 )–(44 $$\begin{array}{c}\hfill {\mathbf{u}}_T(\mathbf{x}):=\mathbf{u}(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega }.\end{array}$$4 ) is similar to the one presented in [12, 13, 19]. It runs as follows:

(i)	First solve problem (1414 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{r}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_0(\mathbf{x}),{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_1(\mathbf{x}),\mathit{\theta }(\mathbf{x},0)\hfill & ={\overline{\mathit{\theta }}}_0(\mathbf{x})\hfill & \mathbf{x}\in \mathrm{\Omega }.\hfill \end{array}\right)\end{array}$$14 ) and determine the transformed final overdetermination ${\tilde{\mathit{\xi }}}_T(\mathbf{x})$, see Equation (1616 $$\begin{array}{c}\hfill {\mathbf{u}}_1(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x})-{\mathbf{u}}_2(\mathbf{x},T)=:{\tilde{\mathit{\xi }}}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$16 ). Denote the solution by $⟨{\mathbf{u}}_{\ast },{\mathit{\theta }}_{\ast }⟩$
(ii)	Choose an initial guess ${\mathbf{p}}_0\in {\mathbf{L}}_2(\mathrm{\Omega })$. Let $⟨{\mathbf{v}}_0,{\mathit{\zeta }}_0⟩$ be the solution to (1313 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{p}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =0}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)={\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\mathbf{0},\mathit{\theta }(\mathbf{x},0)\hfill & =0\hfill & \mathbf{x}\in \mathrm{\Omega };\hfill \end{array}\right)\end{array}$$13 ) with $\mathbf{p}={\mathbf{p}}_0$.
(iii)	Assume that ${\mathbf{p}}_k$ and $⟨{\mathbf{v}}_k,{\mathit{\zeta }}_k⟩$ have been constructed. Let $⟨{\mathbf{w}}_k,{\mathit{\eta }}_k⟩$ solve (1313 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{p}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =0}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)={\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\mathbf{0},\mathit{\theta }(\mathbf{x},0)\hfill & =0\hfill & \mathbf{x}\in \mathrm{\Omega };\hfill \end{array}\right)\end{array}$$13 ) with $\mathbf{p}(\mathbf{x})={\mathbf{v}}_k(\mathbf{x},T)-{\tilde{\mathit{\xi }}}_T(\mathbf{x})$.
(iv)	Define$${\mathbf{p}}_{k+1}(\mathbf{x})={\mathbf{p}}_k(\mathbf{x})-\mathit{\kappa }{\mathbf{w}}_k(\mathbf{x},T),\mathbf{x}\in \mathrm{\Omega }$$ where $\mathit{\kappa }>0$, and let $⟨{\mathbf{v}}_{k+1},{\mathit{\zeta }}_{k+1}⟩$ solve (1313 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{p}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =0}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)={\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\mathbf{0},\mathit{\theta }(\mathbf{x},0)\hfill & =0\hfill & \mathbf{x}\in \mathrm{\Omega };\hfill \end{array}\right)\end{array}$$13 ) with $\mathbf{p}={\mathbf{p}}_{k+1}$.
(v)	The procedure continues by repeating steps (ii) and (iii) until a desired level of accuracy is achieved, see Sections 3.2 and 3.3. Suppose that the algorithm stopped after $\tilde{k}$ iterations. Denote the corresponding solution by $⟨{\mathbf{v}}_{\tilde{k}},{\mathit{\zeta }}_{\tilde{k}},{\mathbf{p}}_{\tilde{k}}⟩$. Then, the approximating solution to the original problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{f}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \end{array}\right)\end{array}$$1 )–(44 $$\begin{array}{c}\hfill {\mathbf{u}}_T(\mathbf{x}):=\mathbf{u}(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega }.\end{array}$$4 ) is given by $⟨{\mathbf{u}}_{\ast }+{\mathbf{v}}_{\tilde{k}},{\mathit{\theta }}_{\ast }+{\mathit{\zeta }}_{\tilde{k}},{\mathbf{p}}_{\tilde{k}}⟩$.

The problems used in this iterative procedure are well posed, see Lemma 3.1. Moreover, the restrictions of solutions are well defined. The convergence of the procedure is studied in the following subsection.

3.2 Convergence of the proposed algorithm in Section 3.1

Let $⟨\mathbf{v},\mathit{\zeta }⟩$ be the unique solution to (1313 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{p}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =0}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)={\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\mathbf{0},\mathit{\theta }(\mathbf{x},0)\hfill & =0\hfill & \mathbf{x}\in \mathrm{\Omega };\hfill \end{array}\right)\end{array}$$13 ) for given $\mathbf{p}$, see Lemma 3.1. Define the corresponding operator $M(t)\in \mathcal{L}\left({\mathbf{L}}_2,(\mathrm{\Omega }),,,{\mathbf{L}}_2,(\mathrm{\Omega })\right)$ by$$M(t)\mathbf{p}=\mathbf{v}(·,t).$$Finding a solution to the inverse problem is then equivalent to solving the following operator equation17 $$\begin{array}{c}\hfill M(T)\mathbf{p}={\tilde{\mathit{\xi }}}_T.\end{array}$$17 The following theorem shows the convergence of the proposed algorithm in the previous subsection.

Theorem 3.3

Assume that the assumptions of Lemma 3.1(ii) are satisfied and suppose that the relaxation parameter $\mathit{\kappa }$ satisfies $0<\mathit{\kappa }<{∥M(T)∥}^{-2}$. Denote by $⟨\mathbf{u},\mathit{\theta },\mathbf{p}⟩=⟨{\mathbf{u}}_{\ast }+\mathbf{v},{\mathit{\theta }}_{\ast }+\mathit{\zeta },\mathbf{p}⟩$ the unique solution to the original inverse problem (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{f}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \end{array}\right)\end{array}$$1 )–(44 $$\begin{array}{c}\hfill {\mathbf{u}}_T(\mathbf{x}):=\mathbf{u}(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega }.\end{array}$$4 ), where $⟨{\mathbf{u}}_{\ast },{\mathit{\theta }}_{\ast }⟩$ is the solution to problem (1414 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{r}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_0(\mathbf{x}),{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_1(\mathbf{x}),\mathit{\theta }(\mathbf{x},0)\hfill & ={\overline{\mathit{\theta }}}_0(\mathbf{x})\hfill & \mathbf{x}\in \mathrm{\Omega }.\hfill \end{array}\right)\end{array}$$14 ) and $⟨\mathbf{v},\mathit{\zeta },\mathbf{p}⟩$ is solving (1313 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{p}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =0}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathbf{u}(\mathbf{x},0)={\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\mathbf{0},\mathit{\theta }(\mathbf{x},0)\hfill & =0\hfill & \mathbf{x}\in \mathrm{\Omega };\hfill \end{array}\right)\end{array}$$13 )–(1616 $$\begin{array}{c}\hfill {\mathbf{u}}_1(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x})-{\mathbf{u}}_2(\mathbf{x},T)=:{\tilde{\mathit{\xi }}}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$16 ). Let $⟨{\mathbf{v}}_k,{\mathit{\zeta }}_k,{\mathbf{p}}_k⟩$ the $k$th approximation in the iterative algorithm of Section 3.1. Then$$\underset{k\to \infty }{lim}\left\{{∥\mathbf{v}-{\mathbf{v}}_k∥}_{C\left([0,T],,,{\mathbf{H}}_0^1,(\mathrm{\Omega })\right)},+,{∥\mathit{\zeta }-{\mathit{\zeta }}_k∥}_{C\left([0,T],,,H_0^1,(\mathrm{\Omega })\right)}\right\}=0$$and$$\underset{k\to \infty }{lim}\left\{{∥{\mathit{\partial }}_t\mathbf{v}-{\mathit{\partial }}_t{\mathbf{v}}_k∥}_{C\left([0,T],,,{\mathbf{H}}_0^1,(\mathrm{\Omega })\right)},+,{∥{\mathit{\partial }}_t\mathit{\zeta }-{\mathit{\partial }}_t{\mathit{\zeta }}_k∥}_{C\left([0,T],,,L_2,(\mathrm{\Omega })\right)}\right\}=0$$for every function ${\mathbf{p}}_0\in {\mathbf{L}}_2(\mathrm{\Omega })$.

Proof

From the iterative algorithm and the linearity of the operator $M(t)$, it is possible to deduce that$$\begin{array}{cc}\hfill {\mathbf{p}}_{k+1}& ={\mathbf{p}}_k-\mathit{\kappa }{\mathbf{w}}_k(·,T)\hfill \\ \hfill & ={\mathbf{p}}_k-\mathit{\kappa }M(T)\left({\mathbf{v}}_k,(·,T),-,{\tilde{\mathit{\xi }}}_T\right)\hfill \\ \hfill & ={\mathbf{p}}_k-\mathit{\kappa }M(T)\left(M,(T),{\mathbf{p}}_k,-,M,(T),\mathbf{p}\right)\hfill \\ \hfill & ={\mathbf{p}}_k-\mathit{\kappa }M(T)M(T)\left({\mathbf{p}}_k,-,\mathbf{p}\right).\hfill \end{array}$$Therefore,$${\mathbf{p}}_{k+1}-\mathbf{p}=\left(I,-,\mathit{\kappa },M,(,T,),M,(,T,)\right)\left({\mathbf{p}}_k,-,\mathbf{p}\right).$$This is a Landweber–Friedmann iteration scheme for solving the operator Equation (1717 $$\begin{array}{c}\hfill M(T)\mathbf{p}={\tilde{\mathit{\xi }}}_T.\end{array}$$17 ). The standard proof of convergence for Landweber’s iterations is given for $T_2=T_1^{\ast }$ and $T_1\in \mathcal{L}(X,Y)$ with $X$ and $Y$ abstract Hilbert spaces in [20, Theorem $6.1$]. A more general version of the proof of convergence for two not self-adjoint operators $T_1,T_2\in \mathcal{L}(X,Y)$ is given in [21, Theorem 3]. This implies thanks to the assumption $0<\mathit{\kappa }<{∥M(T)∥}^{-2}$ that the sequence ${\mathbf{p}}_k$ converges to $\mathbf{p}$ in ${\mathbf{L}}_2(\mathrm{\Omega })$ for arbitrary ${\mathbf{p}}_0\in {\mathbf{L}}_2(\mathrm{\Omega })$. Inequality (1515 $$\begin{array}{c}\hfill \underset{t\in [0,T]}{max}\left\{{∥\mathrm{\nabla }\mathbf{u}(t)∥}^2,+,{∥\mathrm{\nabla }{\mathit{\partial }}_t\mathbf{u}(t)∥}^2,+,{∥\mathrm{\nabla }\mathit{\theta }(t)∥}^2,+,{∥{\mathit{\partial }}_t\mathit{\theta }(t)∥}^2\right\}⩽C{∥\mathbf{r}∥}^2.\end{array}$$15 ) implies that ${\mathbf{v}}_k\to \mathbf{v}$ and ${\mathit{\zeta }}_k\to \mathit{\zeta }$ in $C\left([0,T],,,{\mathbf{H}}_0^1,(\mathrm{\Omega })\right)$. Furthermore, ${\mathit{\partial }}_t{\mathbf{v}}_k\to {\mathit{\partial }}_t\mathbf{v}$ in $C\left([0,T],,,{\mathbf{H}}_0^1,(\mathrm{\Omega })\right)$ and ${\mathit{\partial }}_t{\mathit{\zeta }}_k\to {\mathit{\partial }}_t\mathit{\zeta }$ in $C\left([0,T],,,L_2,(\mathrm{\Omega })\right)$.$\square$

3.3 Stopping criterion

Reconsider the algorithm given in Section 3.1. There are errors present in each practical experiment. In this contribution, the displacement at the final time is measured to obtain a solution to problems (11 $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}{\displaystyle {\mathit{\partial }}_{tt}\mathbf{u}+\mathbf{g}\left({\mathit{\partial }}_t,\mathbf{u}\right)-\mathit{\alpha }\mathrm{\Delta }\mathbf{u}-\mathit{\beta }\mathrm{\nabla }\left(\mathrm{\nabla },·,\mathbf{u}\right)+\mathit{\gamma }\mathrm{\nabla }\mathit{\theta }}\hfill & {\displaystyle =\mathbf{f}}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ {\displaystyle {\mathit{\partial }}_t\mathit{\theta }-\mathit{\rho }\mathrm{\Delta }\mathit{\theta }-k\star \mathrm{\Delta }\mathit{\theta }+\mathit{\gamma }\mathrm{\nabla }·{\mathit{\partial }}_t\mathbf{u}}\hfill & {\displaystyle =h}\hfill & (\mathbf{x},t)\in Q_T;\hfill \\ \mathbf{u}(\mathbf{x},t)\hfill & =\mathbf{0}\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \\ \mathit{\theta }(\mathbf{x},t)\hfill & =0\hfill & (\mathbf{x},t)\in {\mathrm{\Sigma }}_T;\hfill \end{array}\right)\end{array}$$1 )–(33 $$\begin{array}{c}\hfill \mathbf{f}(\mathbf{x},t)=\mathbf{p}(\mathbf{x})+\mathbf{r}(\mathbf{x},t),(\mathbf{x},t)\in Q_T,\end{array}$$3 ). Therefore, the case is considered when there is some error in the additional measurement (44 $$\begin{array}{c}\hfill {\mathbf{u}}_T(\mathbf{x}):=\mathbf{u}(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega }.\end{array}$$4 ), i.e.18 $$\begin{array}{c}\hfill ∥{\mathit{\xi }}_T-{\mathit{\xi }}_T^e∥⩽e,\end{array}$$18 with $e>0$. This implies that also ${\tilde{\mathit{\xi }}}_T$ is perturbated, see (1616 $$\begin{array}{c}\hfill {\mathbf{u}}_1(\mathbf{x},T)={\mathit{\xi }}_T(\mathbf{x})-{\mathbf{u}}_2(\mathbf{x},T)=:{\tilde{\mathit{\xi }}}_T(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$16 ). The perturbated field is designated analogously by ${\tilde{\mathit{\xi }}}_T^e$. The functions ${\mathbf{p}}_k^e,{\mathbf{v}}_k^e$ and ${\mathit{\zeta }}_k^e$ are obtained using the algorithm with no noise on the initial data (22 $$\begin{array}{c}\hfill \mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_0(\mathbf{x}),{\mathit{\partial }}_t\mathbf{u}(\mathbf{x},0)=\overline{}\}{u}_1(\mathbf{x}),\mathit{\theta }(\mathbf{x},0)={\overline{\mathit{\theta }}}_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\end{array}$$2 ). Note that this latter is a good assumption since the inverse problem is stable with respect to small perturbations in the initial data. The absolute ${\mathbf{L}}^2$-error between this final measurement ${\tilde{\mathit{\xi }}}_T^e$ and the $k$th approximation ${\mathbf{v}}_k^e(·,t)$ at $t=T$ is denoted by19 $$\begin{array}{c}\hfill E_{k,{\mathbf{u}}_T}=∥{\mathbf{v}}_k^e(·,T)-{\tilde{\mathit{\xi }}}_T^e∥.\end{array}$$19 Given the noise level $e$, the discrepancy principle [11] can be used to obtain a stopping criterion for the algorithm [20, Proposition 6.4]. This principle suggests to finish the iterations at the smallest index $k=k(e,\mathit{\kappa })$ for which$$E_{k,{\mathbf{u}}_T}⩽e.$$

4 Numerical experiment

In the numerical experiments, it is assumed that the density, the thermal coefficient, the Lamé parameters and the coupling coefficient are normalized to be one, i.e. $\mathit{\alpha }=\mathit{\beta }=\mathit{\gamma }=\mathit{\rho }=1$. Moreover, for ease of implementation, only the $1$D linear model of type-I thermoelasticity is considered. It is given by: find $⟨u,\mathit{\theta },p⟩$ such that20 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle u_{tt}(x,t)+u_t(x,t)-u_{xx}(x,t)+{\mathit{\theta }}_x(x,t)=p(x)+r(x,t)}\hfill & x\in (0,L),t\in (0,T]\hfill \\ {\mathit{\theta }}_t(x,t)-{\mathit{\theta }}_{xx}(x,t)+u_{xt}(x,t)=h(x,t)\hfill & x\in (0,L),t\in (0,T]\hfill \\ u(0,t)=u(L,t)=\mathit{\theta }(0,t)=\mathit{\theta }(L,t)=0\hfill & t\in (0,T]\hfill \\ u(x,0)={\overline{u}}_0(x),u_t(x,0)={\overline{u}}_1(x),\mathit{\theta }(x,0)={\overline{\mathit{\theta }}}_0(x)\hfill & x\in (0,L)\hfill \end{array}\right)\end{array}$$20 and the final overdetermination condition is satisfied21 $$\begin{array}{c}\hfill u(x,T)={\mathit{\xi }}_T(x),x\in (0,L).\end{array}$$21 The solution to problem (2020 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle u_{tt}(x,t)+u_t(x,t)-u_{xx}(x,t)+{\mathit{\theta }}_x(x,t)=p(x)+r(x,t)}\hfill & x\in (0,L),t\in (0,T]\hfill \\ {\mathit{\theta }}_t(x,t)-{\mathit{\theta }}_{xx}(x,t)+u_{xt}(x,t)=h(x,t)\hfill & x\in (0,L),t\in (0,T]\hfill \\ u(0,t)=u(L,t)=\mathit{\theta }(0,t)=\mathit{\theta }(L,t)=0\hfill & t\in (0,T]\hfill \\ u(x,0)={\overline{u}}_0(x),u_t(x,0)={\overline{u}}_1(x),\mathit{\theta }(x,0)={\overline{\mathit{\theta }}}_0(x)\hfill & x\in (0,L)\hfill \end{array}\right)\end{array}$$20 ) and (2121 $$\begin{array}{c}\hfill u(x,T)={\mathit{\xi }}_T(x),x\in (0,L).\end{array}$$21 ) is recovered by applying the algorithm proposed in Section 3.1. Let $L=T=1$ in all the experiments. The forward mixed problems in this procedure are discretized in time according to the backward Euler method. The timestep for the equidistant time partitioning is chosen to be 0.001. At each timestep, the resulting elliptic mixed problems are solved numerically by the finite element method (FEM) using first-order (P1-FEM) Lagrange polynomials for the space discretization.

In each experiment, the exact solution for $p$ is compared with the numerical solution $p_{\tilde{k}}$ obtained when the algorithm finishes after a finite number of $\tilde{k}$ iterations. The index $\tilde{k}$ is the smallest index $k=k(e,\mathit{\kappa })$ for which $E_{k,{\mathbf{u}}_T}⩽e$ or is the maximum number of iterations when this number is reached. In both experiments, the maximum number of iterations equals 10,000. The finite element library DOLFIN from the FEniCS project is used for the implementation.[22]

4.1 Experiment 1

The exact solution $⟨u,\mathit{\theta },p⟩$ to problem (2020 $$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle u_{tt}(x,t)+u_t(x,t)-u_{xx}(x,t)+{\mathit{\theta }}_x(x,t)=p(x)+r(x,t)}\hfill & x\in (0,L),t\in (0,T]\hfill \\ {\mathit{\theta }}_t(x,t)-{\mathit{\theta }}_{xx}(x,t)+u_{xt}(x,t)=h(x,t)\hfill & x\in (0,L),t\in (0,T]\hfill \\ u(0,t)=u(L,t)=\mathit{\theta }(0,t)=\mathit{\theta }(L,t)=0\hfill & t\in (0,T]\hfill \\ u(x,0)={\overline{u}}_0(x),u_t(x,0)={\overline{u}}_1(x),\mathit{\theta }(x,0)={\overline{\mathit{\theta }}}_0(x)\hfill & x\in (0,L)\hfill \end{array}\right)\end{array}$$20 ) and (2121 $$\begin{array}{c}\hfill u(x,T)={\mathit{\xi }}_T(x),x\in (0,L).\end{array}$$21 ) is prescribed as follows22 $$\begin{array}{cc}\hfill u(x,t)& ={(1+t)}^{2}x(x-1),\hfill \\ \hfill \mathit{\theta }(x,t)& =(1+t)x(1-x),\hfill \\ \hfill p(x)& =x(x-1).\hfill \end{array}$$22 Some simple calculations with the use of this exact solution give the exact data for the numerical experiment$$\begin{array}{cc}\hfill r(x,t)& =2t{x}^2-2t^2-4tx+3x^2-3t-5x-1\hfill \\ \hfill h(x,t)& =4tx-x^2+5x\hfill \\ \hfill {\mathit{\xi }}_1(x)& =4x(x-1)\hfill \\ \hfill {\overline{u}}_0(x)& =x(x-1)\hfill \\ \hfill {\overline{u}}_1(x)& =2x(x-1)\hfill \\ \hfill {\overline{\mathit{\theta }}}_0(x)& =x(1-x).\hfill \end{array}$$For the space discretization, a fixed uniform mesh consisting of 50 intervals is used. In this experiment, an uncorrelated noise is added to the additional condition (2121 $$\begin{array}{c}\hfill u(x,T)={\mathit{\xi }}_T(x),x\in (0,L).\end{array}$$21 ) in order to simulate the errors present in real measurements. The noise is generated randomly with given magnitude $\tilde{e}=1,3$ and 5% and the resulting final measurement is denoted by ${\mathit{\xi }}_T^e(x)$, see also Section 3.3. This gives for (1818 $$\begin{array}{c}\hfill ∥{\mathit{\xi }}_T-{\mathit{\xi }}_T^e∥⩽e,\end{array}$$18 ) that23 $$\begin{array}{c}\hfill ∥{\mathit{\xi }}_T-{\mathit{\xi }}_T^e∥\approx e(\tilde{e})=\left\{\begin{array}{cc}0.0047\hfill & \tilde{e}=1\%\hfill \\ 0.0148\hfill & \tilde{e}=3\%\hfill \\ 0.0222\hfill & \tilde{e}=5\%.\hfill \end{array}\right)\end{array}$$23 According to the discrepancy principle, the algorithm is finished at the smallest index $k=k(e,\mathit{\kappa })$ such that (1919 $$\begin{array}{c}\hfill E_{k,{\mathbf{u}}_T}=∥{\mathbf{v}}_k^e(·,T)-{\tilde{\mathit{\xi }}}_T^e∥.\end{array}$$19 ) is satisfied, see Table 1. The obtained results, see Figure 1, are in accordance with the numerical experiments performed for the heat conduction equation in [12]. As $\mathit{\kappa }$ or $\tilde{e}$ increases, the attainability of the stopping criterion (1919 $$\begin{array}{c}\hfill E_{k,{\mathbf{u}}_T}=∥{\mathbf{v}}_k^e(·,T)-{\tilde{\mathit{\xi }}}_T^e∥.\end{array}$$19 ) becomes faster. In this experiment, the numerical solution $p_{\tilde{k}}$, with $\tilde{k}$ the stopping index, approximates the unknown source better for larger values of $\mathit{\kappa }$. Even for a large amount of noise (5%), an accurate approximation for the source is obtained. Note that the algorithm is divergent for $\mathit{\kappa }>50$.

Table 1. The stopping iteration number $k=k(e,\mathit{\kappa })$ for Experiment 1 given by (1919 $$\begin{array}{c}\hfill E_{k,{\mathbf{u}}_T}=∥{\mathbf{v}}_k^e(·,T)-{\tilde{\mathit{\xi }}}_T^e∥.\end{array}$$19 ), with $e(\tilde{e})$ given by (2323 $$\begin{array}{c}\hfill ∥{\mathit{\xi }}_T-{\mathit{\xi }}_T^e∥\approx e(\tilde{e})=\left\{\begin{array}{cc}0.0047\hfill & \tilde{e}=1\%\hfill \\ 0.0148\hfill & \tilde{e}=3\%\hfill \\ 0.0222\hfill & \tilde{e}=5\%.\hfill \end{array}\right)\end{array}$$23 ).

$\mathit{\kappa }\backslash \tilde{e}$	1%	3%	5%
$1$	$151$	$108$	$107$
$10$	$14$	$10$	$10$
$50$	$3$	$2$	$2$

Figure 1. The exact solution (2424 $$\begin{array}{c}\hfill p(x)=\left\{\begin{array}{cc}0\hfill & \text{for}0⩽x<\frac{1}{3}\hfill \\ 1\hfill & \text{for}\frac{1}{3}⩽x<\frac{2}{3}\hfill \\ 0\hfill & \text{for}\frac{2}{3}<x⩽1\hfill \end{array}\right)\end{array}$$24 ) and the numerical solution for the source (2222 $$\begin{array}{cc}\hfill u(x,t)& ={(1+t)}^{2}x(x-1),\hfill \\ \hfill \mathit{\theta }(x,t)& =(1+t)x(1-x),\hfill \\ \hfill p(x)& =x(x-1).\hfill \end{array}$$22 ) for $\tilde{e}=1\%$ and $\tilde{e}=5\%$ for different values of $\mathit{\kappa }$.

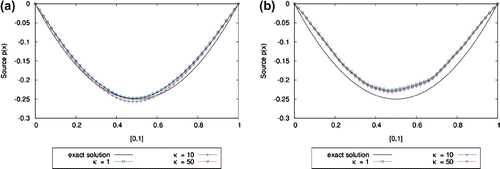
Figure 2. The exact solution (2424 $$\begin{array}{c}\hfill p(x)=\left\{\begin{array}{cc}0\hfill & \text{for}0⩽x<\frac{1}{3}\hfill \\ 1\hfill & \text{for}\frac{1}{3}⩽x<\frac{2}{3}\hfill \\ 0\hfill & \text{for}\frac{2}{3}<x⩽1\hfill \end{array}\right)\end{array}$$24 ) and the numerical solution for the source (2424 $$\begin{array}{c}\hfill p(x)=\left\{\begin{array}{cc}0\hfill & \text{for}0⩽x<\frac{1}{3}\hfill \\ 1\hfill & \text{for}\frac{1}{3}⩽x<\frac{2}{3}\hfill \\ 0\hfill & \text{for}\frac{2}{3}<x⩽1\hfill \end{array}\right)\end{array}$$24 ) for $\tilde{e}=1\%$ and $\mathit{\kappa }=10$.

4.2 Experiment 2

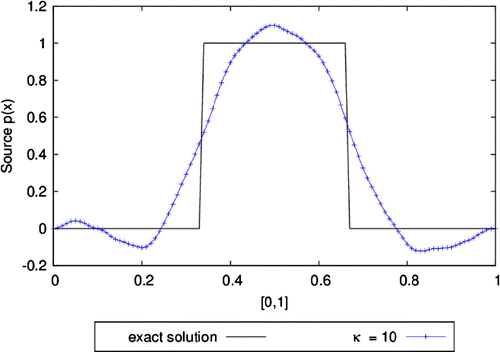
In this experiment, a discontinuous source given by24 $$\begin{array}{c}\hfill p(x)=\left\{\begin{array}{cc}0\hfill & \text{for}0⩽x<\frac{1}{3}\hfill \\ 1\hfill & \text{for}\frac{1}{3}⩽x<\frac{2}{3}\hfill \\ 0\hfill & \text{for}\frac{2}{3}<x⩽1\hfill \end{array}\right)\end{array}$$24 is reconstructed. Since the direct problems in the algorithm for given $p$ do not have an analytical solution, the data (2121 $$\begin{array}{c}\hfill u(x,T)={\mathit{\xi }}_T(x),x\in (0,L).\end{array}$$21 ) is obtained by solving the direct problem using the FEM for $r=h={\overline{u}}_0={\overline{u}}_1={\overline{\mathit{\theta }}}_0=0$. Now, a fixed uniform mesh consisting of $100$ intervals is used for the space discretization. Only a randomly generated noise with magnitude $\tilde{e}=1\%$ is considered on the resulting final measurement. In this experiment, $e(\tilde{e})=0.0048$. The stopping index is equal to $229$ and $1145$ for $\mathit{\kappa }=50$ and $\mathit{\kappa }=10$, respectively. There are more than 10,000 iterations needed for $\mathit{\kappa }=1$. The numerical solution for the source in the case that $\mathit{\kappa }=10$ is given in Figure 2. The approximation is in accordance with the experiment performed in [12] with the same unknown source for only the heat conduction equation. Note that there is a large number of iterations needed to obtain this solution. In the light of this, other stopping criteria were also considered, but they need the same amount of iterations to obtain the same accuracy.

5 Conclusion

In this contribution, the determination of a space-dependent vector source in a thermoelastic system of type-I, type-II and type-III is studied using information from a supplementary measurement at the final time. The uniqueness of a solution is proved when $\mathbf{g}$ is componentwise strictly monotone increasing. A convergent and stable algorithm is developed to approximate the unknown source when $\mathbf{g}$ is also linear. This is demonstrated by numerical experiments.

Acknowledgements

The authors are supported by the IAP P7/02-project of the Belgian Science Policy.