Recover the solute concentration from source measurement and boundary data

Abstract

In this paper, a concentration identification problem of the time fractional inhomogeneous diffusion equation (TFIDE) is investigated. The TFIDE is obtained from the classical diffusion equation by replacing the first-order time derivative by the Caputo fractional derivative of order $\mathit{\alpha }$$(0<\mathit{\alpha }<1)$. Our purpose is to recover the solute concentration from source measurement and boundary data. We show that this problem is severely ill-posed and further apply a convolution-type regularization method to solve it. Convergence estimates are given under a priori bound assumptions for the exact solution. Finally, we provide two numerical examples to confirm our theoretical analysis and show that the corresponding numerical method works effectively.

Keywords:

• time fractional inhomogeneous diffusion equation
• regularization method
• concentration identification problem
• caputo fractional derivative
• convergence estimate
• solute concentration
• Fourier transform

AMS Subject Classifications:

• 65N20
• 65N21

1. Introduction

In recent years, fractional calculus and fractional differential equations have been more and more extensively used in many scientific fields. For example, physical, chemical, biology, mechanical engineering, signal processing and systems identification, electrical, control theory, finance, fractional dynamics and so on, refer to [1–3]. As is known to all, in thermophysics, the normal diffusion obeys Fick (or Fourier) law:$$\begin{array}{c}\hfill J=-\mathit{\kappa }{u}_x,\end{array}$$

where $J$ is diffusion flux, $\mathit{\kappa }$ is diffusion coefficient and $u$ is concentration of substance. Moreover, the normal diffusion can be described quite well by classical diffusion equation (DE) which is derived from Fick law and, in probability theory, it corresponds to Brownian motion (BM). However, there are an increasing number of so-called anomalous diffusion arises in real world, such as the diffusion phenomena occurred in some media with memory and hereditary properties. The anomalous diffusion is not consistent with the classical Fick law, but satisfies what is called time fractional Fick law,[4] i.e.$$\begin{array}{c}\hfill J=-\mathit{\kappa }{·}_0^{RL}{D}_t^{1-\mathit{\alpha }}[u_x],\mathit{\alpha }\in (0,1),\end{array}$$

where ${}_0^{RL}{D}_t^{\mathit{\alpha }}$ is the Riemann–Liouville fractional derivative operator of order $\mathit{\alpha }$ defined by [2](1) $$\begin{array}{ccc}& {}_0^{RL}{D}_t^{\mathit{\alpha }}f(t)=\frac{1}{\mathrm{\Gamma }(1-\mathit{\alpha })}\frac{d}{dt}{\int }_0^t\frac{f(s)}{{(t-s)}^{\mathit{\alpha }}}ds,\hfill & \hfill 0<\mathit{\alpha }<1,\end{array}$$(1)

where $\mathrm{\Gamma }(·)$ is Gamma function. Furthermore, if the function $f$ is continuously differentiable and $f(0)=0$, integration by parts leads to the Caputo fractional derivative of order $\mathit{\alpha }$ :(2) $$\begin{array}{ccc}& {}_0{D}_t^{\mathit{\alpha }}f(t)=\frac{1}{\mathrm{\Gamma }(1-\mathit{\alpha })}{\int }_0^t\frac{f^{\prime }(s)}{{(t-s)}^{\mathit{\alpha }}}ds,\hfill & \hfill 0<\mathit{\alpha }<1.\end{array}$$(2)

Then we get the Caputo time fractional Fick law:$$\begin{array}{c}\hfill J=-\mathit{\kappa }{·}_0{D}_t^{1-\mathit{\alpha }}[u_x],\mathit{\alpha }\in (0,1).\end{array}$$

This general Fick law derives the corresponding time fractional diffusion equation (TFDE), which arises by replacing the standard time partial derivative in the diffusion equation with a time fractional partial derivative and is closely related to fractional Brownian motion.[5] The TFDE is gradually accepted as an important tool for describing anomalous diffusion.[1, 6, 7] About the direct problems for TFDE, i.e. initial value problem and initial boundary value problem, which have been studied extensively in the past few years.[8–18] However, in some practical problems, the boundary data on the whole boundary cannot be obtained. We only know the noisy data on a part of the boundary or at some interior points of the concerned domain, which will lead to some inverse problems, i.e. fractional inverse diffusion problems (FIDP). For the results of FIDP, we can see [19–21]. However, in a practical application, not only does the boundary data need to measure, but also the source term (such as pollution source) need to measure. To the author’s knowledge, there is still not many results of inverse problems for source measurement.

In this article, we consider the following concentration identification problem (CIP) for the time fractional inhomogeneous diffusion equation (TFIDE):(3) $$\begin{array}{c}\hfill {}_0{D}_t^{\mathit{\alpha }}u(x,t)=u_{xx}(x,t)+f(t),0<x<1,t>0,\mathit{\alpha }\in (0,1),\end{array}$$(3)

with the Cauchy condition and initial condition(4) $$\begin{array}{cc}& u(0,t)=g(t),t\ge 0,\hfill \end{array}$$(4) (5) $$\begin{array}{cc}& u_x(0,t)=0,t\ge 0,\hfill \end{array}$$(5) (6) $$\begin{array}{cc}& u(x,0)=0,0<x<1,\hfill \end{array}$$(6)

where $u(x,t)$ is the solute concentration, $f(t)$ is the time-dependent source term and $g(t)$ denotes the solute concentration on left boundary. We will recover the solute concentration $u(x,t)$ in the region $\{(x,t)|0<x\le 1,t>0\}$ from the measurement data of source term $f(t)$ and boundary concentration $g(t)$. Here, we do not need the measurement data of diffusion flux on left boundary, which is different from the Cauchy data measurement in [22]. In fact, it is difficult to measure diffusion flux directly in a practical application.

The CIP for the TFIDE is an inverse problem and is severely ill-posed (see Section 2). That means the solution does not depend continuously on the given data and any small error perturbation in the given data (such as the measurement data of source and boundary) may cause large change of the solution. In this paper, we will present a convolution-type regularization method which is proposed in [23] to construct a stable approximate solution of CIP (3(3) $$\begin{array}{c}\hfill {}_0{D}_t^{\mathit{\alpha }}u(x,t)=u_{xx}(x,t)+f(t),0<x<1,t>0,\mathit{\alpha }\in (0,1),\end{array}$$(3) )–(6(6) $$\begin{array}{cc}& u(x,0)=0,0<x<1,\hfill \end{array}$$(6) ), which is a kind of modify equation method. Namely, we modify the Equation (3(3) $$\begin{array}{c}\hfill {}_0{D}_t^{\mathit{\alpha }}u(x,t)=u_{xx}(x,t)+f(t),0<x<1,t>0,\mathit{\alpha }\in (0,1),\end{array}$$(3) ) as follows:(7) $$\begin{array}{c}\hfill P_{\mathit{\mu }}(t)\ast {[}_0{D}_t^{\mathit{\alpha }}u(x,t)]=u_{xx}(x,t)+f(t),x>0,t>0,\end{array}$$(7)

where $P_{\mathit{\mu }}(t)=\frac{1}{2\mathit{\mu }}{e}^{-\frac{|t|}{\mathit{\mu }}}$, $\mathit{\mu }>0$ play a role of regularization parameter, and ‘$\ast$’ denotes convolution operation.

Our paper is divided into five sections. In Section 2, we explain the ill-posedness of the problem. In Section 3, we propose the regularization method and give some convergence estimates based on a priori assumptions for the exact solution. Numerical results are shown in Section 4. Finally, we give a conclusion in Section 5.

2. Ill-posedness of CIP and two relevant problems

To be able to apply the Fourier transform, we extend all the functions to the whole line $-\infty <t<\infty$ by defining them to be zero for $t<0$. Here, and in the following sections, $\Vert ·\Vert$ denotes the $L_2$ norm, i.e.(8) $$\begin{array}{c}\hfill \Vert f\Vert ={\left({\int }_{\mathbb{R}},{|f(t)|}^2,d,t\right)}^{\frac{1}{2}}.\end{array}$$(8)

The Fourier transform of function $f(t)$ is written as:(9) $$\begin{array}{c}\hfill \widehat{f}(\mathit{\xi })=\frac{1}{\sqrt{2\mathit{\pi }}}{\int }_{-\infty }^{\infty }f(t)e^{-i\mathit{\xi }t}dt,\end{array}$$(9)

and the Laplace transform is defined by(10) $$\begin{array}{c}\hfill \tilde{f}(s)={\int }_0^{\infty }f(t)e^{-st}dt.\end{array}$$(10)

In addition, ${\Vert ·\Vert }_p$ denotes the $H_p$ norm, i.e.(11) $$\begin{array}{c}\hfill {\Vert f\Vert }_p={\left({\int }_{\mathbb{R}},{(1+{\mathit{\xi }}^2)}^p,{|\widehat{f}(\mathit{\xi })|}^2,d,\mathit{\xi }\right)}^{\frac{1}{2}}.\end{array}$$(11)

By the initial condition $u(x,0)=0$, and applying the Laplace transform with respect to $t$ in (3(3) $$\begin{array}{c}\hfill {}_0{D}_t^{\mathit{\alpha }}u(x,t)=u_{xx}(x,t)+f(t),0<x<1,t>0,\mathit{\alpha }\in (0,1),\end{array}$$(3) )–(5(5) $$\begin{array}{cc}& u_x(0,t)=0,t\ge 0,\hfill \end{array}$$(5) ), we get [2](12) $$\begin{array}{cc}& s^{\mathit{\alpha }}\tilde{u}(x,s)={\tilde{u}}_{xx}(x,s)+\tilde{f}(s),\hfill \end{array}$$(12) (13) $$\begin{array}{cc}& \tilde{u}(0,s)=\tilde{g}(s),\hfill \end{array}$$(13) (14) $$\begin{array}{cc}& {\tilde{u}}_x(0,s)=0.\hfill \end{array}$$(14)

Then the solution of (8(8) $$\begin{array}{c}\hfill \Vert f\Vert ={\left({\int }_{\mathbb{R}},{|f(t)|}^2,d,t\right)}^{\frac{1}{2}}.\end{array}$$(8) )–(10(10) $$\begin{array}{c}\hfill \tilde{f}(s)={\int }_0^{\infty }f(t)e^{-st}dt.\end{array}$$(10) ) can easily be given by(15) $$\begin{array}{c}\hfill \tilde{u}(x,s)=\tilde{g}(s)cosh\left(s^{\frac{\mathit{\alpha }}{2}},x\right)+\tilde{f}(s)\frac{1-cosh\left(s^{\frac{\mathit{\alpha }}{2}},x\right)}{s^{\mathit{\alpha }}}.\end{array}$$(15)

Since $f(t)$ and $g(t)$ are vanish for $t<0$, we find the Laplace transform and Fourier transform are related via(16) $$\begin{array}{c}\hfill \tilde{f}(s)=\sqrt{2\mathit{\pi }}\widehat{f}(-is).\end{array}$$(16)

Then, from this relation and (11(11) $$\begin{array}{c}\hfill {\Vert f\Vert }_p={\left({\int }_{\mathbb{R}},{(1+{\mathit{\xi }}^2)}^p,{|\widehat{f}(\mathit{\xi })|}^2,d,\mathit{\xi }\right)}^{\frac{1}{2}}.\end{array}$$(11) ), the solution of (8(8) $$\begin{array}{c}\hfill \Vert f\Vert ={\left({\int }_{\mathbb{R}},{|f(t)|}^2,d,t\right)}^{\frac{1}{2}}.\end{array}$$(8) )–(10(10) $$\begin{array}{c}\hfill \tilde{f}(s)={\int }_0^{\infty }f(t)e^{-st}dt.\end{array}$$(10) ) in frequency domain can be written as:(17) $$\begin{array}{c}\hfill \widehat{u}(x,\mathit{\xi })=\widehat{g}(\mathit{\xi })cosh\left(k,(,\mathit{\xi },),x\right)+\widehat{f}(\mathit{\xi })\frac{1-cosh\left(k,(,\mathit{\xi },),x\right)}{k{(\mathit{\xi })}^2},\end{array}$$(17)

where(18) $$\begin{array}{cc}& k(\mathit{\xi })={(i\mathit{\xi })}^{\frac{\mathit{\alpha }}{2}}={|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}{e}^{i\mathit{\tau }\frac{\mathit{\alpha }\mathit{\pi }}{4}},\mathit{\tau }=sign(\mathit{\xi }),\hfill \end{array}$$(18)

and by (iii) in Lemma 3.1 (see Section 3)$$\begin{array}{c}\hfill \frac{1-cosh\left(k,(,0,),x\right)}{k{(0)}^2}:=\underset{\mathit{\xi }\to 0}{lim}\frac{1-cosh\left(k,(,\mathit{\xi },),x\right)}{k{(\mathit{\xi })}^2}=-\frac{x^2}{2}.\end{array}$$

Note that $k(\mathit{\xi })$ has a positive real part ${|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}$, the small error given by $g(t)$ in the high-frequency components ($|\mathit{\xi }|\to \infty$) will be amplified by the factor $e^{\mathfrak{R}(k(\mathit{\xi }))x}$ ($0<x\le 1$). Moreover, the larger fraction order $\mathit{\alpha }$ is, the larger $e^{\mathfrak{R}(k(\mathit{\xi }))x}$ is, then it causes the higher instability of solution of CIP and this will be reflected in our numerical results (see Section 4). Similarly, the error given by $f(t)$ will also be amplified by the factor $\frac{e^{\mathfrak{R}(k(\mathit{\xi }))x}}{{|\mathit{\xi }|}^{\mathit{\alpha }}}$. Therefore, the CIP is severely ill-posed, we must use some regularization methods to deal with this problem.

Next, we will simply discuss two problems which are related to the CIP for TFIDE. The first one is time fractional homogeneous diffusion problem with non-zero Cauchy data:(19) $$\begin{array}{cc}& {}_0{D}_t^{\mathit{\alpha }}\mathit{\vartheta }(x,t)={\mathit{\vartheta }}_{xx}(x,t),0<x<1,t>0,\hfill \end{array}$$(19) (20) $$\begin{array}{cc}& \mathit{\vartheta }(0,t)=g(t),t\ge 0,\hfill \end{array}$$(20) (21) $$\begin{array}{cc}& {\mathit{\vartheta }}_x(0,t)=0,t\ge 0,\hfill \end{array}$$(21) (22) $$\begin{array}{cc}& \mathit{\vartheta }(x,0)=0,0<x<1.\hfill \end{array}$$(22)

Similarly, we can use Laplace and Fourier transform and get its solution as follows:(23) $$\begin{array}{c}\hfill \widehat{\mathit{\vartheta }}(x,\mathit{\xi })=\widehat{g}(\mathit{\xi })cosh\left(k,(,\mathit{\xi },),x\right).\end{array}$$(23)

The second one is time fractional inhomogeneous diffusion problem with zero Cauchy data:(24) $$\begin{array}{cc}& {}_0{D}_t^{\mathit{\alpha }}\mathit{\varpi }(x,t)={\mathit{\varpi }}_{xx}(x,t)+f(t),0<x<1,t>0,\hfill \end{array}$$(24) (25) $$\begin{array}{cc}& \mathit{\varpi }(0,t)=0,t\ge 0,\hfill \end{array}$$(25) (26) $$\begin{array}{cc}& {\mathit{\varpi }}_x(0,t)=0,t\ge 0,\hfill \end{array}$$(26) (27) $$\begin{array}{cc}& \mathit{\varpi }(x,0)=0,0<x<1.\hfill \end{array}$$(27)

Its solution is given by(28) $$\begin{array}{c}\hfill \widehat{\mathit{\varpi }}(x,\mathit{\xi })=\widehat{f}(\mathit{\xi })\frac{1-cosh\left(k,(,\mathit{\xi },),x\right)}{k{(\mathit{\xi })}^2}.\end{array}$$(28)

It is easy to see that the solution to the CIP (3(3) $$\begin{array}{c}\hfill {}_0{D}_t^{\mathit{\alpha }}u(x,t)=u_{xx}(x,t)+f(t),0<x<1,t>0,\mathit{\alpha }\in (0,1),\end{array}$$(3) )–(6(6) $$\begin{array}{cc}& u(x,0)=0,0<x<1,\hfill \end{array}$$(6) ) $u$ satisfy $u=\mathit{\vartheta }+\mathit{\varpi }$. In order to obtain the convergence estimates of our regularization method, we first give the following a priori bound assumptions:(29) $$\begin{array}{cc}& \Vert \mathit{\vartheta }(1,·)\Vert +\Vert \mathit{\varpi }(1,·)\Vert \le E,\hfill \end{array}$$(29) (30) $$\begin{array}{cc}& {\Vert \mathit{\vartheta }(1,·)\Vert }_p+{\Vert \mathit{\varpi }(1,·)\Vert }_p\le E_p.\hfill \end{array}$$(30)

3. The regularization method and convergence estimates

In order to obtain a stable approximate solution of the CIP (3(3) $$\begin{array}{c}\hfill {}_0{D}_t^{\mathit{\alpha }}u(x,t)=u_{xx}(x,t)+f(t),0<x<1,t>0,\mathit{\alpha }\in (0,1),\end{array}$$(3) )–(6(6) $$\begin{array}{cc}& u(x,0)=0,0<x<1,\hfill \end{array}$$(6) ), we actually solve the following problem:(31) $$\begin{array}{cc}& P_{\mathit{\mu }}(t)\ast {[}_0{D}_t^{\mathit{\alpha }}v(x,t)]=v_{xx}(x,t)+f^{\mathit{\delta }}(t),x>0,t>0,\hfill \end{array}$$(31) (32) $$\begin{array}{cc}& v(0,t)=g^{\mathit{\delta }}(t),t\ge 0,\hfill \end{array}$$(32) (33) $$\begin{array}{cc}& v_x(0,t)=0,t\ge 0,\hfill \end{array}$$(33) (34) $$\begin{array}{cc}& v(x,0)=0,0<x<1,\hfill \end{array}$$(34)

where $\mathit{\mu }$ is a regularization parameter, the measured data $f^{\mathit{\delta }}$ and $g^{\mathit{\delta }}$ satisfy(35) $$\begin{array}{c}\hfill \Vert f^{\mathit{\delta }}-f\Vert \le \mathit{\delta },|g^{\mathit{\delta }}-g\Vert \le \mathit{\delta },\end{array}$$(35)

in which the constant $\mathit{\delta }>0$ is called a error level. We intend to recover the solute concentration $u$ for $0<x\le 1$ from the measured data $f^{\mathit{\delta }}(t)$ and $g^{\mathit{\delta }}(t)$.

Similarly, by the integral transform method, we can obtain the formal solution of problem (27(27) $$\begin{array}{cc}& \mathit{\varpi }(x,0)=0,0<x<1.\hfill \end{array}$$(27) )–(30(30) $$\begin{array}{cc}& {\Vert \mathit{\vartheta }(1,·)\Vert }_p+{\Vert \mathit{\varpi }(1,·)\Vert }_p\le E_p.\hfill \end{array}$$(30) ) as follows:(36) $$\begin{array}{c}\hfill \widehat{v}(x,\mathit{\xi })=\widehat{g^{\mathit{\delta }}}(\mathit{\xi })cosh\left(l,(,\mathit{\xi },),x\right)+\widehat{f^{\mathit{\delta }}}(\mathit{\xi })\frac{1-cosh\left(l,(,\mathit{\xi },),x\right)}{l{(\mathit{\xi })}^2},\end{array}$$(36)

where(37) $$\begin{array}{cc}& l(\mathit{\xi })=\frac{k(\mathit{\xi })}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}=\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}{e}^{i\mathit{\tau }\frac{\mathit{\alpha }\mathit{\pi }}{4}}.\hfill \end{array}$$(37)

Before the main theorems are given, we first prove some auxiliary lemmas.

Lemma 3.1

If $a\ge b\ge 0$, $\mathit{\tau }=sign(\mathit{\xi })$, $\mathit{\xi }\in \mathbb{R}$, then we have(38) $$\begin{array}{cc}& (\mathrm{i})|cosh(a+i\mathit{\tau }b)|\ge \frac{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{2}{e}^a,\hfill \end{array}$$(38) (39) $$\begin{array}{cc}& (\mathrm{i}i)|1-cosh(a+i\mathit{\tau }b)|\ge \left\{\begin{array}{cc}\frac{2b^2}{{\mathit{\pi }}^2}{e}^a,\hfill & 0\le b\le \frac{\mathit{\pi }}{2},\hfill \\ \frac{1-2e^{-\frac{\mathit{\pi }}{2}}}{2}{e}^a,\hfill & b>\frac{\mathit{\pi }}{2};\hfill \end{array}\right.\hfill \end{array}$$(39) (40) $$\begin{array}{cc}& (\mathrm{i}ii)\underset{\mathit{\xi }\to 0}{lim}\frac{1-cosh\left(k,(,\mathit{\xi },),x\right)}{k{(\mathit{\xi })}^2}=-\frac{x^2}{2},0\le x\le 1.\hfill \end{array}$$(40)

Proof

About the proof of (i), we can see [24] and (iii) is obvious.

(ii) Due to the proof is very similar to the one in [22], we omit it.$\square$

Theorem 3.2

Assume that $u$ is the solution of problem (3(3) $$\begin{array}{c}\hfill {}_0{D}_t^{\mathit{\alpha }}u(x,t)=u_{xx}(x,t)+f(t),0<x<1,t>0,\mathit{\alpha }\in (0,1),\end{array}$$(3) )–(6(6) $$\begin{array}{cc}& u(x,0)=0,0<x<1,\hfill \end{array}$$(6) ), whose Fourier transform is given by (13(13) $$\begin{array}{cc}& \tilde{u}(0,s)=\tilde{g}(s),\hfill \end{array}$$(13) ). $v$ is the solution of problem (27(27) $$\begin{array}{cc}& \mathit{\varpi }(x,0)=0,0<x<1.\hfill \end{array}$$(27) )–(30(30) $$\begin{array}{cc}& {\Vert \mathit{\vartheta }(1,·)\Vert }_p+{\Vert \mathit{\varpi }(1,·)\Vert }_p\le E_p.\hfill \end{array}$$(30) ), whose Fourier transform is given by (32(32) $$\begin{array}{cc}& v(0,t)=g^{\mathit{\delta }}(t),t\ge 0,\hfill \end{array}$$(32) ), and the measured data $f^{\mathit{\delta }}$, $g^{\mathit{\delta }}$ satisfy (31(31) $$\begin{array}{cc}& P_{\mathit{\mu }}(t)\ast {[}_0{D}_t^{\mathit{\alpha }}v(x,t)]=v_{xx}(x,t)+f^{\mathit{\delta }}(t),x>0,t>0,\hfill \end{array}$$(31) ).

(1)

If the a priori bound (25(25) $$\begin{array}{cc}& \mathit{\varpi }(0,t)=0,t\ge 0,\hfill \end{array}$$(25) ) holds, and the regularization parameter $\mathit{\mu }$ is selected by(41) $$\begin{array}{c}\hfill \mathit{\mu }=\frac{1}{2{\left(ln,\frac{E}{\mathit{\delta }}\right)}^2}.\end{array}$$(41) Then for every $x\in (0,1)$, we get a convergence estimate(42) $$\begin{array}{c}\hfill \Vert u(x,·)-v(x,·)\Vert \le {\mathit{\epsilon }}_1+{\mathit{\epsilon }}_2,\end{array}$$(42) where ${\mathit{\epsilon }}_1=2max\{e\mathit{\delta },E^x{\mathit{\delta }}^{1-x}\}$, ${\mathit{\epsilon }}_2=Emax\{C_1{\mathit{\mu }}^2,C_2{\mathit{\mu }}^2+C_3{\mathit{\mu }}^4\}$, $C_2=max\{C_4,C_6\}$, $C_3=max\{C_5,C_7\}$, and$$\begin{array}{cc}\hfill C_1& =\frac{4x}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{\left(\frac{1+\frac{4}{\mathit{\alpha }}}{cos\frac{\mathit{\alpha }\mathit{\pi }}{4}(1-x)e}\right)}^{1+\frac{4}{\mathit{\alpha }}},\hfill \\ \hfill C_4& =\frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left({\left(\frac{\frac{4}{\mathit{\alpha }}-2}{cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{4}{\mathit{\alpha }}-2},+,{\left(\frac{\frac{4}{\mathit{\alpha }}-2}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{4}{\mathit{\alpha }}-2}\right.\hfill \\ \hfill & \left.+,2,x,{\left(\frac{\frac{4}{\mathit{\alpha }}-1}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{4}{\mathit{\alpha }}-1}\right),\hfill \\ \hfill C_5& =\frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left({\left(\frac{\frac{8}{\mathit{\alpha }}-2}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{8}{\mathit{\alpha }}-2},+,2,x,{\left(\frac{\frac{8}{\mathit{\alpha }}-2}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{8}{\mathit{\alpha }}-2}\right),\hfill \\ \hfill C_6& =\frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left({\left(\frac{\frac{4}{\mathit{\alpha }}}{cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{4}{\mathit{\alpha }}},+,{\left(\frac{\frac{4}{\mathit{\alpha }}}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{4}{\mathit{\alpha }}}\right.\hfill \\ \hfill & \left.+,2,x,{\left(\frac{\frac{4}{\mathit{\alpha }}+1}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{4}{\mathit{\alpha }}+1}\right),\hfill \\ \hfill C_7& =\frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left({\left(\frac{\frac{8}{\mathit{\alpha }}}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{8}{\mathit{\alpha }}},+,2,x,{\left(\frac{\frac{8}{\mathit{\alpha }}+1}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{8}{\mathit{\alpha }}+1}\right).\hfill \end{array}$$

(2)

If the a priori bound (26(26) $$\begin{array}{cc}& {\mathit{\varpi }}_x(0,t)=0,t\ge 0,\hfill \end{array}$$(26) ) holds, and the regularization parameter $\mathit{\mu }$ is selected by(43) $$\begin{array}{c}\hfill \mathit{\mu }=\frac{1}{2{\left(ln,\left(ln,\frac{E_p}{\mathit{\delta }}\right)\right)}^2}.\end{array}$$(43) Then for $p\ge 2$, $x=1$, we have a convergence estimate(44) $$\begin{array}{c}\hfill \Vert u(1,·)-v(1,·)\Vert \le {\mathit{\epsilon }}_3+{\mathit{\epsilon }}_4,\end{array}$$(44) where ${\mathit{\epsilon }}_3=2max\{e\mathit{\delta },\mathit{\delta }ln\frac{E_p}{\mathit{\delta }}\}$, ${\mathit{\epsilon }}_4=E_{p}max\{{\mathit{\epsilon }}_5,max\{{\mathit{\epsilon }}_6.{\mathit{\epsilon }}_7\}\}$, and$$\begin{array}{cc}\hfill {\mathit{\epsilon }}_5& =\frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}max\{{\mathit{\mu }}^{\frac{p}{2}},{\mathit{\mu }}^{1+\frac{p}{2}-\frac{\mathit{\alpha }}{4}},{\mathit{\mu }}^2\},\hfill \\ \hfill {\mathit{\epsilon }}_6& =\frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}max\{2{\mathit{\mu }}^{\frac{\mathit{\alpha }}{2}+\frac{p}{2}}+3{\mathit{\mu }}^{1+\frac{\mathit{\alpha }}{2}+\frac{p}{2}},4{\mathit{\mu }}^2+{\mathit{\mu }}^{2+\frac{p}{2}+\frac{\mathit{\alpha }}{2}}+2{\mathit{\mu }}^{2+\frac{p}{2}+\frac{\mathit{\alpha }}{4}},\hfill \\ \hfill & 4{\mathit{\mu }}^2+{\mathit{\mu }}^4+2{\mathit{\mu }}^{2+\frac{p}{2}+\frac{\mathit{\alpha }}{4}},4{\mathit{\mu }}^2+3{\mathit{\mu }}^4\},\hfill \\ \hfill {\mathit{\epsilon }}_7& =\frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}max\{2{\mathit{\mu }}^{\frac{p}{2}}+3{\mathit{\mu }}^{1+\frac{p}{2}},2{\mathit{\mu }}^2+2{\mathit{\mu }}^{1+\frac{p}{2}-\frac{\mathit{\alpha }}{4}}+{\mathit{\mu }}^{2+\frac{p}{2}}+2{\mathit{\mu }}^{2+\frac{p}{2}-\frac{\mathit{\alpha }}{4}},\hfill \\ \hfill & 4{\mathit{\mu }}^2+{\mathit{\mu }}^{2+\frac{p}{2}}+2{\mathit{\mu }}^{2+\frac{p}{2}-\frac{\mathit{\alpha }}{4}},4{\mathit{\mu }}^2+{\mathit{\mu }}^4+2{\mathit{\mu }}^{2+\frac{p}{2}-\frac{\mathit{\alpha }}{4}},\hfill \\ \hfill & 4{\mathit{\mu }}^2+3{\mathit{\mu }}^4\}.\hfill \end{array}$$

Proof

(1) From (19(19) $$\begin{array}{cc}& {}_0{D}_t^{\mathit{\alpha }}\mathit{\vartheta }(x,t)={\mathit{\vartheta }}_{xx}(x,t),0<x<1,t>0,\hfill \end{array}$$(19) ) and (24(24) $$\begin{array}{cc}& {}_0{D}_t^{\mathit{\alpha }}\mathit{\varpi }(x,t)={\mathit{\varpi }}_{xx}(x,t)+f(t),0<x<1,t>0,\hfill \end{array}$$(24) ), we obtain(45) $$\begin{array}{c}\hfill \widehat{v}(1,\mathit{\xi })=\widehat{g}(\mathit{\xi })cosh\left(k,(,\mathit{\xi },)\right),\widehat{w}(1,\mathit{\xi })=\widehat{f}(\mathit{\xi })\frac{1-cosh\left(k,(,\mathit{\xi },)\right)}{k{(\mathit{\xi })}^2}.\end{array}$$(45)

Thus, by (13(13) $$\begin{array}{cc}& \tilde{u}(0,s)=\tilde{g}(s),\hfill \end{array}$$(13) ), (25(25) $$\begin{array}{cc}& \mathit{\varpi }(0,t)=0,t\ge 0,\hfill \end{array}$$(25) ), (32(32) $$\begin{array}{cc}& v(0,t)=g^{\mathit{\delta }}(t),t\ge 0,\hfill \end{array}$$(32) ) and using the Parseval theorem, we have$$\begin{array}{cc}& \Vert u(x,·)-v(x,·)\Vert =\Vert \widehat{u}(x,·)-\widehat{v}(x,·)\Vert \hfill \\ \hfill & =∥\widehat{g},cosh,\left(k,x\right),+,\widehat{f},\frac{1-cosh\left(k,x\right)}{k^2},-,\widehat{g^{\mathit{\delta }}},cosh,\left(l,x\right),-,\widehat{f^{\mathit{\delta }}},\frac{1-cosh\left(l,x\right)}{l^2}∥\hfill \\ \hfill & =\Vert \widehat{g}\left(cosh,\left(k,x\right),-,cosh,\left(l,x\right)\right)+\widehat{f}\left(\frac{1-cosh\left(k,x\right)}{k^2},-,\frac{1-cosh\left(l,x\right)}{l^2}\right)\hfill \\ \hfill & +(\widehat{g}-\widehat{g^{\mathit{\delta }}})cosh\left(l,x\right)+(\widehat{f}-\widehat{f^{\mathit{\delta }}})\frac{1-cosh\left(l,x\right)}{l^2}\Vert \hfill \\ \hfill & \le \Vert \widehat{g}cosh\left(k\right)\frac{cosh\left(k,x\right)-cosh\left(l,x\right)}{cosh\left(k\right)}+\widehat{f}\frac{1-cosh\left(k\right)}{k^2}\frac{\frac{1-cosh\left(k,x\right)}{k^2}-\frac{1-cosh\left(l,x\right)}{l^2}}{\frac{1-cosh\left(k\right)}{k^2}}\Vert \hfill \\ \hfill & +\Vert (\widehat{g}-\widehat{g^{\mathit{\delta }}})cosh\left(l,x\right)\Vert +\Vert (\widehat{f}-\widehat{f^{\mathit{\delta }}})\frac{1-cosh\left(l,x\right)}{l^2}\Vert \hfill \\ \hfill & \le max\left\{\underset{\mathit{\xi }\in \mathbb{R}}{sup},A,(\mathit{\xi }),,,,\underset{\mathit{\xi }\in \mathbb{R}}{sup},B,(\mathit{\xi })\right\}·E+\underset{\mathit{\xi }\in \mathbb{R}}{sup}C(\mathit{\xi })·\mathit{\delta }+\underset{\mathit{\xi }\in \mathbb{R}}{sup}D(\mathit{\xi })·\mathit{\delta },\hfill \end{array}$$

where(46) $$\begin{array}{cc}& A(\mathit{\xi })=\left|\frac{cosh(kx)-cosh(lx)}{cosh(k)}\right|,B(\mathit{\xi })=\left|\frac{\frac{1-cosh\left(k,x\right)}{k^2}-\frac{1-cosh\left(l,x\right)}{l^2}}{\frac{1-cosh\left(k\right)}{k^2}}\right|,\hfill \end{array}$$(46) (47) $$\begin{array}{cc}& C(\mathit{\xi })=\left|cosh,(,l,x,)\right|,D(\mathit{\xi })=\left|\frac{1-cosh\left(l,x\right)}{l^2}\right|.\hfill \end{array}$$(47)

Next, we will estimate the four terms of (42(42) $$\begin{array}{c}\hfill \Vert u(x,·)-v(x,·)\Vert \le {\mathit{\epsilon }}_1+{\mathit{\epsilon }}_2,\end{array}$$(42) ) and (43(43) $$\begin{array}{c}\hfill \mathit{\mu }=\frac{1}{2{\left(ln,\left(ln,\frac{E_p}{\mathit{\delta }}\right)\right)}^2}.\end{array}$$(43) ).

(1)	Estimate of $A(\mathit{\xi })$. According to the definition of function $cosh(·)$, we get$$\begin{array}{cc}\hfill 2|cosh(kx)-cosh(lx)|& =|e^{kx}+e^{-kx}-e^{lx}-e^{-lx}|\hfill \\ \hfill & \le |e^{kx}-e^{lx}|+|e^{-kx}-e^{-lx}|\hfill \\ \hfill & =|1-e^{-(k-l)x}|·(|e^{kx}|+|e^{-lx}|).\hfill \end{array}$$ Setting $\mathit{\rho }=k-l={\mathit{\rho }}_1+i{\mathit{\rho }}_2$, by (14(14) $$\begin{array}{cc}& {\tilde{u}}_x(0,s)=0.\hfill \end{array}$$(14) ) and (33(33) $$\begin{array}{cc}& v_x(0,t)=0,t\ge 0,\hfill \end{array}$$(33) ), we obtain$$\begin{array}{cc}\hfill {\mathit{\rho }}_1& ={|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}\left(1,-,\frac{1}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}\right)\hfill \\ \hfill & ={|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}\frac{{\mathit{\mu }}^2{\mathit{\xi }}^2}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}(1+\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2})}\hfill \\ \hfill & \le {|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}{\mathit{\mu }}^2.\hfill \end{array}$$ Similarly,$$\begin{array}{c}\hfill |{\mathit{\rho }}_2{|=|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}sin\frac{\mathit{\alpha }\mathit{\pi }}{4}\left(1,-,\frac{1}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}\right)\le {|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}{\mathit{\mu }}^2.\end{array}$$ Thus,$$\begin{array}{cc}\hfill |1-e^{-(k-l)x}|& =|1-e^{-\mathit{\rho }x}|=|1-e^{-({\mathit{\rho }}_1+i{\mathit{\rho }}_2)x}|\hfill \\ \hfill & \le |e^{-i{\mathit{\rho }}_{2}x}-e^{-({\mathit{\rho }}_1+i{\mathit{\rho }}_2)x}|+|1-e^{-i{\mathit{\rho }}_{2}x}|\hfill \\ \hfill & =|e^{-i{\mathit{\rho }}_{2}x}|·|1-e^{-{\mathit{\rho }}_{1}x}|+\sqrt{{(1-cos({\mathit{\rho }}_{2}x))}^2+{sin}^2({\mathit{\rho }}_{2}x)}\hfill \\ \hfill & =1-e^{-{\mathit{\rho }}_{1}x}+2\left|sin,\frac{{\mathit{\rho }}_{2}x}{2}\right|\hfill \\ \hfill & \le ({\mathit{\rho }}_1+|{\mathit{\rho }}_2|)x\hfill \\ \hfill & \le {2x|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}{\mathit{\mu }}^2\hfill \end{array}$$ According to the above analysis, applying (i) of Lemma 3.1 and Lemma 4.3 in [24], we have$$\begin{array}{cc}\hfill A(\mathit{\xi })& \le \frac{{2x|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}{\mathit{\mu }}^2(|e^{kx}|+|e^{-lx}|)}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}·e^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}}}\hfill \\ \hfill & =\frac{{2x|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}{\mathit{\mu }}^2(e^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}x}+e^{-\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}x}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}})}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}·e^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}}}\hfill \\ \hfill & \le \frac{4x{\mathit{\mu }}^2{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}{e}^{-{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}(1-x)}}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}\hfill \\ \hfill & =\frac{4x{\mathit{\mu }}^2{(|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}{)}^{1+\frac{4}{\mathit{\alpha }}}{e}^{-{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}(1-x)}}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}\hfill \\ \hfill & \le C_1{\mathit{\mu }}^2.\hfill \end{array}$$ where$$\begin{array}{c}\hfill C_1=\frac{4x}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{\left(\frac{1+\frac{4}{\mathit{\alpha }}}{cos\frac{\mathit{\alpha }\mathit{\pi }}{4}(1-x)e}\right)}^{1+\frac{4}{\mathit{\alpha }}}.\end{array}$$
(2)	Estimate of $B(\mathit{\xi })$. By the estimates of ${\mathit{\rho }}_1$ and $|{\mathit{\rho }}_2|$ in 1, we obtain$$\begin{array}{cc}& |l^2{e}^{kx}-k^2{e}^{lx}|=|e^{kx}|·|l^2-k^2{e}^{-(k-l)x}|=|e^{kx}|·|l^2-k^2{e}^{-({\mathit{\rho }}_1+i{\mathit{\rho }}_2)x}|\hfill \\ \hfill & \le |e^{kx}|·(|l^2|·|1-e^{-i{\mathit{\rho }}_{2}x}|+|k^2-l^2|·|e^{-i{\mathit{\rho }}_{2}x}|+|k^2|·|e^{-i{\mathit{\rho }}_{2}x}-e^{-({\mathit{\rho }}_1+i{\mathit{\rho }}_2)x}|)\hfill \\ \hfill & \le |e^{kx}|·(|l^2|·|{\mathit{\rho }}_2|x+|k^2-l^2|+|k^2|·{\mathit{\rho }}_{1}x)\hfill \\ \hfill & \le e^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}xcos\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left({|\mathit{\xi }|}^{2+\mathit{\alpha }},+,2,x,{|\mathit{\xi }|}^{2+\frac{3\mathit{\alpha }}{2}}\right){\mathit{\mu }}^2.\hfill \end{array}$$ Similarly,$$\begin{array}{cc}\hfill |k^2{e}^{-lx}-l^2{e}^{-kx}|& =|e^{-lx}|·|k^2-l^2{e}^{-(k-l)x}|=|e^{-lx}|·|k^2-l^2{e}^{-\mathit{\rho }x}|\hfill \\ \hfill & \le 2e^{-\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}xcos\frac{\mathit{\alpha }\mathit{\pi }}{4}}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}}\left({x|\mathit{\xi }|}^{2+\mathit{\alpha }},+,{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}\right){\mathit{\mu }}^2\hfill \\ \hfill & \le e^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}xcos\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left({|\mathit{\xi }|}^{2+\mathit{\alpha }},+,2,x,{|\mathit{\xi }|}^{2+\frac{3\mathit{\alpha }}{2}}\right){\mathit{\mu }}^2.\hfill \end{array}$$ Thus, setting $b={|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}sin\frac{\mathit{\alpha }\mathit{\pi }}{4}$ in (35(35) $$\begin{array}{c}\hfill \Vert f^{\mathit{\delta }}-f\Vert \le \mathit{\delta },|g^{\mathit{\delta }}-g\Vert \le \mathit{\delta },\end{array}$$(35) ) and applying (ii) of Lemma 3.1 and Lemma 4.3 in [24], if $0<b={|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}sin\frac{\mathit{\alpha }\mathit{\pi }}{4}\le \frac{\mathit{\pi }}{2}$, we have$$\begin{array}{cc}& B(\mathit{\xi })=\left|\frac{\frac{1-cosh\left(k,x\right)}{k^2}-\frac{1-cosh\left(l,x\right)}{l^2}}{\frac{1-cosh\left(k\right)}{k^2}}\right|=\frac{|2(l^2-k^2)+k^2(e^{lx}-e^{-lx})-l^2(e^{kx}-e^{-kx})|}{2|l^2|·|1-cosh\left(k\right)|}\hfill \\ \hfill & \le \frac{2|l^2-k^2|+|k^2{e}^{lx}-l^2{e}^{kx}|+|l^2{e}^{-kx}-k^2{e}^{-lx}|}{2|l^2|·|1-cosh\left(k\right)|}\hfill \\ \hfill & \le \frac{2\frac{{\mathit{\mu }}^2{|\mathit{\xi }|}^{2+\mathit{\alpha }}}{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}+2e^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}xcos\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left({|\mathit{\xi }|}^{2+\mathit{\alpha }},+,2,x,{|\mathit{\xi }|}^{2+\frac{3\mathit{\alpha }}{2}}\right){\mathit{\mu }}^2}{2\frac{{|\mathit{\xi }|}^{\mathit{\alpha }}}{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}·\frac{{2|\mathit{\xi }|}^{\mathit{\alpha }}{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}{{\mathit{\pi }}^2}{e}^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}}}\hfill \\ \hfill & \le \frac{{\mathit{\pi }}^2\left(e^{-{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}},{|\mathit{\xi }|}^{2-\mathit{\alpha }},{\mathit{\mu }}^2,+,e^{-{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}},\left(\left({|\mathit{\xi }|}^{2-\mathit{\alpha }},+,2,x,{|\mathit{\xi }|}^{2-\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^{4-\mathit{\alpha }},+,2,x,{|\mathit{\xi }|}^{4-\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^4\right)\right)}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\hfill \\ \hfill & \le C_4{\mathit{\mu }}^2+C_5{\mathit{\mu }}^4.\hfill \end{array}$$ where$$\begin{array}{cc}\hfill C_4& =\frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left({\left(\frac{\frac{4}{\mathit{\alpha }}-2}{cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{4}{\mathit{\alpha }}-2},+,{\left(\frac{\frac{4}{\mathit{\alpha }}-2}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{4}{\mathit{\alpha }}-2}\right.\hfill \\ \hfill & \left.+,2,x,{\left(\frac{\frac{4}{\mathit{\alpha }}-1}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{4}{\mathit{\alpha }}-1}\right),\hfill \\ \hfill C_5& =\frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left({\left(\frac{\frac{8}{\mathit{\alpha }}-2}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{8}{\mathit{\alpha }}-2},+,2,x,{\left(\frac{\frac{8}{\mathit{\alpha }}-2}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{8}{\mathit{\alpha }}-2}\right).\hfill \end{array}$$ If $b={|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}sin\frac{\mathit{\alpha }\mathit{\pi }}{4}>\frac{\mathit{\pi }}{2}$, similar to above analysis, we get$$\begin{array}{cc}\hfill B(\mathit{\xi })& \le \frac{2\left(e^{-{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}},{|\mathit{\xi }|}^2,{\mathit{\mu }}^2,+,e^{-{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}},\left(\left({|\mathit{\xi }|}^2,+,2,x,{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^4,+,2,x,{|\mathit{\xi }|}^{4+\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^4\right)\right)}{1-2e^{-\frac{\mathit{\pi }}{2}}}\hfill \\ \hfill & \le C_6{\mathit{\mu }}^2+C_7{\mathit{\mu }}^4.\hfill \end{array}$$ where$$\begin{array}{cc}\hfill C_6& =\frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left({\left(\frac{\frac{4}{\mathit{\alpha }}}{cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{4}{\mathit{\alpha }}},+,{\left(\frac{\frac{4}{\mathit{\alpha }}}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{4}{\mathit{\alpha }}}\right.\hfill \\ \hfill & \left.+,2,x,{\left(\frac{\frac{4}{\mathit{\alpha }}+1}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{4}{\mathit{\alpha }}+1}\right),\hfill \\ \hfill C_7& =\frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left({\left(\frac{\frac{8}{\mathit{\alpha }}}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{8}{\mathit{\alpha }}},+,2,x,{\left(\frac{\frac{8}{\mathit{\alpha }}+1}{(1-x)cos\frac{\mathit{\alpha }\mathit{\pi }}{4}e}\right)}^{\frac{8}{\mathit{\alpha }}+1}\right).\hfill \end{array}$$ For $\mathit{\xi }=0$, by the (iii) of Lemma 3.1, it is clear $B(0)=0$. Therefore, we set $C_2=max\{C_4,C_6\}$, $C_3=max\{C_5,C_7\}$, and it follows that$$\begin{array}{cc}\hfill B(\mathit{\xi })& \le C_2{\mathit{\mu }}^2+C_3{\mathit{\mu }}^4.\hfill \end{array}$$
(3)	Estimate of $C(\mathit{\xi })$. Using (33(33) $$\begin{array}{cc}& v_x(0,t)=0,t\ge 0,\hfill \end{array}$$(33) ), we have(48) $$\begin{array}{c}\hfill C(\mathit{\xi })=|cosh(lx)|\le \frac{|e^{lx}|+|e^{-lx}|}{2}\le e^{\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}x}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}}.\end{array}$$(48) Case 1. If $|\mathit{\xi }|\le 1$, then(49) $$\begin{array}{c}\hfill C(\mathit{\xi })\le e^{\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}x}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}}\le e^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}}\le e.\end{array}$$(49) Case 2. If $|\mathit{\xi }|>1$, then(50) $$\begin{array}{c}\hfill C(\mathit{\xi })\le e^{\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}x}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}}\le e^{\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }-1}{2}}x}{\sqrt{2\mathit{\mu }}}}\le e^{\frac{x}{\sqrt{2\mathit{\mu }}}}.\end{array}$$(50) Therefore,(51) $$\begin{array}{c}\hfill C(\mathit{\xi })\le max\{e^{\frac{x}{\sqrt{2\mathit{\mu }}}},e\}.\end{array}$$(51)
(4)	Estimate of $D(\mathit{\xi })$. Applying Taylor formula and triangle inequality, for $\mathit{\xi }\ne 0$, we have$$\begin{array}{cc}\hfill D(\mathit{\xi })& =\left|\frac{1-cosh\left(l,x\right)}{l^2}\right|=\left|\frac{1}{l^2},\underset{n=1}{\overset{\infty }{\mathrm{\Sigma }}},\frac{{(xl)}^{2n}}{(2n)!}\right|=\left|\underset{n=1}{\overset{\infty }{\mathrm{\Sigma }}},\frac{x^{2n}{l}^{2n-2}}{(2n+1)!}\right|\hfill \\ \hfill & \le \underset{n=1}{\overset{\infty }{\mathrm{\Sigma }}}\frac{x^{2n-2}{|l|}^{2n-2}}{(2n-2)!}=cosh(x|l|)\hfill \\ \hfill & \le e^{x|l|}=e^{\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}x}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}}.\hfill \end{array}$$ For $\mathit{\xi }=0$, $D(0):={lim}_{\mathit{\xi }\to 0}\left|\frac{1-cosh\left(l,x\right)}{l^2}\right|=\frac{x^2}{2}\le 1=e^{0x}$. Hence, from (44(44) $$\begin{array}{c}\hfill \Vert u(1,·)-v(1,·)\Vert \le {\mathit{\epsilon }}_3+{\mathit{\epsilon }}_4,\end{array}$$(44) ) to (47(47) $$\begin{array}{cc}& C(\mathit{\xi })=\left|cosh,(,l,x,)\right|,D(\mathit{\xi })=\left|\frac{1-cosh\left(l,x\right)}{l^2}\right|.\hfill \end{array}$$(47) ), we get(52) $$\begin{array}{c}\hfill D(\mathit{\xi })\le max\{e^{\frac{x}{\sqrt{2\mathit{\mu }}}},e\}.\end{array}$$(52) It follows that$$\begin{array}{c}\hfill \Vert u(x,·)-v(x,·)\Vert \le max\{C_1{\mathit{\mu }}^2,C_2{\mathit{\mu }}^2+C_3{\mathit{\mu }}^4\}·E+2max\{e·\mathit{\delta },e^{\frac{x}{\sqrt{2\mathit{\mu }}}}·\mathit{\delta }\}.\end{array}$$ Notice that $\mathit{\mu }$ is given by (37(37) $$\begin{array}{cc}& l(\mathit{\xi })=\frac{k(\mathit{\xi })}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}=\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}{e}^{i\mathit{\tau }\frac{\mathit{\alpha }\mathit{\pi }}{4}}.\hfill \end{array}$$(37) ), we get$$\begin{array}{cc}\hfill \Vert u(x,·)-v(x,·)\Vert & \le 2max\{e\mathit{\delta },E^x{\mathit{\delta }}^{1-x}\}+Emax\{C_1{\mathit{\mu }}^2,C_2{\mathit{\mu }}^2+C_3{\mathit{\mu }}^4\}\hfill \\ \hfill & ={\mathit{\epsilon }}_1+{\mathit{\epsilon }}_2.\hfill \end{array}$$ (2) As in the proof of (1), and using the a priori assumption (26(26) $$\begin{array}{cc}& {\mathit{\varpi }}_x(0,t)=0,t\ge 0,\hfill \end{array}$$(26) ), we obtain$$\begin{array}{cc}& \Vert u(1,·)-v(1,·)\Vert \hfill \\ \hfill & =∥\widehat{g},cosh,\left(k\right),+,\widehat{f},\frac{1-cosh\left(k\right)}{k^2},-,\widehat{g^{\mathit{\delta }}},cosh,\left(l\right),-,\widehat{f^{\mathit{\delta }}},\frac{1-cosh\left(l\right)}{l^2}∥\hfill \\ \hfill & \le ∥{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}},\left(\widehat{g},cosh,\left(k\right),\frac{cosh\left(k\right)-cosh\left(l\right)}{{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}cosh\left(k\right)}\right.\hfill \\ \hfill & \left.+,\widehat{f},\frac{1-cosh\left(k\right)}{k^2},\frac{\frac{1-cosh\left(k\right)}{k^2}-\frac{1-cosh\left(l\right)}{l^2}}{{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}\frac{1-cosh\left(k\right)}{k^2}}\right)∥\hfill \\ \hfill & +\Vert (\widehat{g}-\widehat{g^{\mathit{\delta }}})cosh\left(l\right)\Vert +\Vert (\widehat{f}-\widehat{f^{\mathit{\delta }}})\frac{1-cosh\left(l\right)}{l^2}\Vert \hfill \\ \hfill & \le max\left\{\underset{\mathit{\xi }\in \mathbb{R}}{sup},\tilde{A},(\mathit{\xi }),,,,\underset{\mathit{\xi }\in \mathbb{R}}{sup},\tilde{B},(\mathit{\xi })\right\}·E_p+\underset{\mathit{\xi }\in \mathbb{R}}{sup}\tilde{C}(\mathit{\xi })·\mathit{\delta }+\underset{\mathit{\xi }\in \mathbb{R}}{sup}\tilde{D}(\mathit{\xi })·\mathit{\delta },\hfill \end{array}$$ where(53) $$\begin{array}{cc}& \tilde{A}(\mathit{\xi })=\left|\frac{cosh(k)-cosh(l)}{{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}cosh(k)}\right|,\tilde{B}(\mathit{\xi })=\left|\frac{\frac{1-cosh\left(k\right)}{k^2}-\frac{1-cosh\left(l\right)}{l^2}}{{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}\frac{1-cosh\left(k\right)}{k^2}}\right|,\hfill \end{array}$$(53) (54) $$\begin{array}{cc}& \tilde{C}(\mathit{\xi })=\left|cosh,(,l,)\right|,\tilde{D}(\mathit{\xi })=\left|\frac{1-cosh\left(l\right)}{l^2}\right|.\hfill \end{array}$$(54) By (47(47) $$\begin{array}{cc}& C(\mathit{\xi })=\left|cosh,(,l,x,)\right|,D(\mathit{\xi })=\left|\frac{1-cosh\left(l,x\right)}{l^2}\right|.\hfill \end{array}$$(47) ) and (48(48) $$\begin{array}{c}\hfill C(\mathit{\xi })=|cosh(lx)|\le \frac{|e^{lx}|+|e^{-lx}|}{2}\le e^{\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}x}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}}.\end{array}$$(48) ), it is easy to see(55) $$\begin{array}{c}\hfill \tilde{C}(\mathit{\xi })\le max\{e^{\frac{1}{\sqrt{2\mathit{\mu }}}},e\},\tilde{D}(\mathit{\xi })\le max\{e^{\frac{1}{\sqrt{2\mathit{\mu }}}},e\}.\end{array}$$(55) Next, we will estimate the first term of (49(49) $$\begin{array}{c}\hfill C(\mathit{\xi })\le e^{\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}x}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}}\le e^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}}\le e.\end{array}$$(49) ). Case 1. $|\mathit{\xi }|>{\mathit{\mu }}^{-\frac{1}{2}}$, since(56) $$\begin{array}{c}\hfill |cosh(k)-cosh(l)|\le |cosh(k)|+|cosh(l)|\le 2e^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}},\end{array}$$(56) using (i) of Lemma 3.1, and from $p\ge 2$, we obtain(57) $$\begin{array}{c}\hfill \tilde{A}(\mathit{\xi })\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}\frac{1}{{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}}\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{|\mathit{\xi }|}^{-p}\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{\mathit{\mu }}^{\frac{p}{2}}.\end{array}$$(57) Case 2. $1<|\mathit{\xi }|\le {\mathit{\mu }}^{-\frac{1}{2}}$, similar to the proof of (1), we get(58) $$\begin{array}{c}\hfill \tilde{A}(\mathit{\xi })\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}-p}{\mathit{\mu }}^2.\end{array}$$(58) If $2\le p\le 2+\frac{\mathit{\alpha }}{2}$, note that $|\mathit{\xi }|\le {\mathit{\mu }}^{-\frac{1}{2}}$, (54(54) $$\begin{array}{cc}& \tilde{C}(\mathit{\xi })=\left|cosh,(,l,)\right|,\tilde{D}(\mathit{\xi })=\left|\frac{1-cosh\left(l\right)}{l^2}\right|.\hfill \end{array}$$(54) ) become into(59) $$\begin{array}{c}\hfill \tilde{A}(\mathit{\xi })\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{\mathit{\mu }}^{1+\frac{p}{2}-\frac{\mathit{\alpha }}{4}}.\end{array}$$(59) If $p>2+\frac{\mathit{\alpha }}{2}$, note that $|\mathit{\xi }|>1$, it follows that(60) $$\begin{array}{c}\hfill \tilde{A}(\mathit{\xi })\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{\mathit{\mu }}^2.\end{array}$$(60) Case 3. $|\mathit{\xi }|\le 1$, similar to estimate of (54(54) $$\begin{array}{cc}& \tilde{C}(\mathit{\xi })=\left|cosh,(,l,)\right|,\tilde{D}(\mathit{\xi })=\left|\frac{1-cosh\left(l\right)}{l^2}\right|.\hfill \end{array}$$(54) ), we have(61) $$\begin{array}{c}\hfill \tilde{A}(\mathit{\xi })\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}{\mathit{\mu }}^2\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{\mathit{\mu }}^2.\end{array}$$(61) Finally, we estimate the second term of (49(49) $$\begin{array}{c}\hfill C(\mathit{\xi })\le e^{\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}x}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}}\le e^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}}\le e.\end{array}$$(49) ), which needs to consider three kinds of situations. (I) For $\mathit{\xi }=0$, it is clear that $\tilde{B}(0)=0$. (II) If $0<b={|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}sin\frac{\mathit{\alpha }\mathit{\pi }}{4}\le \frac{\mathit{\pi }}{2}$, we should consider three cases. Case 1. For $|\mathit{\xi }|>{\mathit{\mu }}^{-\frac{1}{2}}$, using (35(35) $$\begin{array}{c}\hfill \Vert f^{\mathit{\delta }}-f\Vert \le \mathit{\delta },|g^{\mathit{\delta }}-g\Vert \le \mathit{\delta },\end{array}$$(35) ) of Lemma 3.1, notice that $p\ge 2$, we obtain$$\begin{array}{cc}\hfill \tilde{B}(\mathit{\xi })& =\frac{|2(l^2-k^2)+k^2(e^l-e^{-l})-l^2(e^k-e^{-k})|}{2|l^2|·|1-cosh\left(k\right)|{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}}\hfill \\ \hfill & \le \frac{2|l^2-k^2|+|k^2{e}^l|+|k^2{e}^{-l}|+|l^2{e}^k|+|l^2{e}^{-k}|}{2|l^2|·|1-cosh\left(k\right)|{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}}\hfill \\ \hfill & \le \frac{2\frac{{\mathit{\mu }}^2{|\mathit{\xi }|}^{2+\mathit{\alpha }}}{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}+4{|\mathit{\xi }|}^{\mathit{\alpha }}{e}^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}}}{2\frac{{|\mathit{\xi }|}^{\mathit{\alpha }}}{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}·\frac{{2|\mathit{\xi }|}^{\mathit{\alpha }}{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}{{\mathit{\pi }}^2}{e}^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}}{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}}\hfill \\ \hfill & \le \frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left({2|\mathit{\xi }|}^{-\mathit{\alpha }-p},+,3,{\mathit{\mu }}^2,{|\mathit{\xi }|}^{2-\mathit{\alpha }-p}\right)\hfill \\ \hfill & \le \frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left(2,{\mathit{\mu }}^{\frac{\mathit{\alpha }}{2}+\frac{p}{2}},+,3,{\mathit{\mu }}^{1+\frac{\mathit{\alpha }}{2}+\frac{p}{2}}\right).\hfill \end{array}$$Case 2. For $1<|\mathit{\xi }|\le {\mathit{\mu }}^{-\frac{1}{2}}$, similar to the proof of (1), we get$$\begin{array}{cc}\hfill \tilde{B}(\mathit{\xi })& \le \frac{{\mathit{\pi }}^2\left(e^{-{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}},{|\mathit{\xi }|}^{2-\mathit{\alpha }},{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^{2-\mathit{\alpha }},+,2,{|\mathit{\xi }|}^{2-\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^{4-\mathit{\alpha }},+,2,{|\mathit{\xi }|}^{4-\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^4\right)}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}}\hfill \\ \hfill & \le \frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left(2,\left({|\mathit{\xi }|}^{2-\mathit{\alpha }-p},+,{|\mathit{\xi }|}^{2-\frac{\mathit{\alpha }}{2}-p}\right),{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^{4-\mathit{\alpha }-p},+,2,{|\mathit{\xi }|}^{4-\frac{\mathit{\alpha }}{2}-p}\right),{\mathit{\mu }}^4\right).\hfill \end{array}$$ If $2\le p\le 4-\mathit{\alpha }$, note that $1<|\mathit{\xi }|\le {\mathit{\mu }}^{-\frac{1}{2}}$, we have$$\begin{array}{c}\hfill \tilde{B}(\mathit{\xi })\le \frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left(4,{\mathit{\mu }}^2,+,{\mathit{\mu }}^{2+\frac{p}{2}+\frac{\mathit{\alpha }}{2}},+,2,{\mathit{\mu }}^{2+\frac{p}{2}+\frac{\mathit{\alpha }}{4}}\right).\end{array}$$ If $4-\mathit{\alpha }<p\le 4-\frac{\mathit{\alpha }}{2}$, it follows that$$\begin{array}{c}\hfill \tilde{B}(\mathit{\xi })\le \frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left(4,{\mathit{\mu }}^2,+,{\mathit{\mu }}^4,+,2,{\mathit{\mu }}^{2+\frac{p}{2}+\frac{\mathit{\alpha }}{4}}\right).\end{array}$$ If $p>4-\frac{\mathit{\alpha }}{2}$, then we get$$\begin{array}{c}\hfill \tilde{B}(\mathit{\xi })\le \frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left(4,{\mathit{\mu }}^2,+,3,{\mathit{\mu }}^4\right).\end{array}$$Case 3. For $|\mathit{\xi }|\le 1$, it follows that$$\begin{array}{cc}\hfill \tilde{B}(\mathit{\xi })& \le \frac{{\mathit{\pi }}^2\left(e^{-{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}},{|\mathit{\xi }|}^{2-\mathit{\alpha }},{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^{2-\mathit{\alpha }},+,2,{|\mathit{\xi }|}^{2-\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^{4-\mathit{\alpha }},+,2,{|\mathit{\xi }|}^{4-\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^4\right)}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}}\hfill \\ \hfill & \le \frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left(2,\left({|\mathit{\xi }|}^{2-\mathit{\alpha }},+,{|\mathit{\xi }|}^{2-\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^{4-\mathit{\alpha }},+,2,{|\mathit{\xi }|}^{4-\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^4\right)\hfill \\ \hfill & \le \frac{{\mathit{\pi }}^2}{2{sin}^2\frac{\mathit{\alpha }\mathit{\pi }}{4}}\left(4,{\mathit{\mu }}^2,+,3,{\mathit{\mu }}^4\right).\hfill \end{array}$$ (III) If $b={|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}sin\frac{\mathit{\alpha }\mathit{\pi }}{4}>\frac{\mathit{\pi }}{2}$, similar to above analysis, we also consider three cases. Case 1. $|\mathit{\xi }|>{\mathit{\mu }}^{-\frac{1}{2}}$, since $p\ge 2$, by (35(35) $$\begin{array}{c}\hfill \Vert f^{\mathit{\delta }}-f\Vert \le \mathit{\delta },|g^{\mathit{\delta }}-g\Vert \le \mathit{\delta },\end{array}$$(35) ), we have$$\begin{array}{cc}\hfill \tilde{B}(\mathit{\xi })& =\frac{|2(l^2-k^2)+k^2(e^l-e^{-l})-l^2(e^k-e^{-k})|}{2|l^2|·|1-cosh\left(k\right)|{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}}\hfill \\ \hfill & \le \frac{2|l^2-k^2|+|k^2{e}^l|+|k^2{e}^{-l})|+|l^2{e}^k|+|l^2{e}^{-k}|}{2|l^2|·|1-cosh\left(k\right)|{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}}\hfill \\ \hfill & \le \frac{2\frac{{\mathit{\mu }}^2{|\mathit{\xi }|}^{2+\mathit{\alpha }}}{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}+4{|\mathit{\xi }|}^{\mathit{\alpha }}{e}^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}}}{2\frac{{|\mathit{\xi }|}^{\mathit{\alpha }}}{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}·\frac{1-2e^{-\frac{\mathit{\pi }}{2}}}{2}{e}^{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}}{(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}}\hfill \\ \hfill & \le \frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left({2|\mathit{\xi }|}^{-p},+,3,{\mathit{\mu }}^2,{|\mathit{\xi }|}^{2-p}\right)\hfill \\ \hfill & \le \frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left(2,{\mathit{\mu }}^{\frac{p}{2}},+,3,{\mathit{\mu }}^{1+\frac{p}{2}}\right).\hfill \end{array}$$Case 2. For $1<|\mathit{\xi }|\le {\mathit{\mu }}^{-\frac{1}{2}}$, refer to the estimate of $B(\mathit{\xi })$ in the case of $b>\frac{\mathit{\pi }}{2}$, we obtain$$\begin{array}{cc}\hfill \tilde{B}(\mathit{\xi })& \le \frac{2\left(e^{-{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}},{|\mathit{\xi }|}^2,{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^2,+,2,{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^4,+,2,{|\mathit{\xi }|}^{4+\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^4\right)}{\left(1,-,2,e^{-\frac{\mathit{\pi }}{2}}\right){(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}}\hfill \\ \hfill & \le \frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left(2,\left({|\mathit{\xi }|}^{2-p},+,{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}-p}\right),{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^{4-p},+,2,{|\mathit{\xi }|}^{4+\frac{\mathit{\alpha }}{2}-p}\right),{\mathit{\mu }}^4\right).\hfill \end{array}$$ If $2\le p\le 2+\frac{\mathit{\alpha }}{2}$, from $1<|\mathit{\xi }|\le {\mathit{\mu }}^{-\frac{1}{2}}$, above estimate becomes into$$\begin{array}{c}\hfill \tilde{B}(\mathit{\xi })\le \frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left(2,{\mathit{\mu }}^2,+,2,{\mathit{\mu }}^{1+\frac{p}{2}-\frac{\mathit{\alpha }}{4}},+,{\mathit{\mu }}^{2+\frac{p}{2}},+,2,{\mathit{\mu }}^{2+\frac{p}{2}-\frac{\mathit{\alpha }}{4}}\right).\end{array}$$ If $2+\frac{\mathit{\alpha }}{2}<p\le 4$, since $1<|\mathit{\xi }|\le {\mathit{\mu }}^{-\frac{1}{2}}$, we get$$\begin{array}{c}\hfill \tilde{B}(\mathit{\xi })\le \frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left(4,{\mathit{\mu }}^2,+,{\mathit{\mu }}^{2+\frac{p}{2}},+,2,{\mathit{\mu }}^{2+\frac{p}{2}-\frac{\mathit{\alpha }}{4}}\right).\end{array}$$ If $4<p\le 4+\frac{\mathit{\alpha }}{2}$, it follows that$$\begin{array}{c}\hfill \tilde{B}(\mathit{\xi })\le \frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left(4,{\mathit{\mu }}^2,+,{\mathit{\mu }}^4,+,2,{\mathit{\mu }}^{2+\frac{p}{2}-\frac{\mathit{\alpha }}{4}}\right).\end{array}$$ If $p>4+\frac{\mathit{\alpha }}{2}$, we obtain$$\begin{array}{c}\hfill \tilde{B}(\mathit{\xi })\le \frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left(4,{\mathit{\mu }}^2,+,3,{\mathit{\mu }}^4\right).\end{array}$$Case 3. $|\mathit{\xi }|\le 1$, it follows that$$\begin{array}{cc}\hfill \tilde{B}(\mathit{\xi })& \le \frac{2\left(e^{-{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}cos\frac{\mathit{\alpha }\mathit{\pi }}{4}},{|\mathit{\xi }|}^2,{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^2,+,2,{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^4,+,2,{|\mathit{\xi }|}^{4+\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^4\right)}{\left(1,-,2,e^{-\frac{\mathit{\pi }}{2}}\right){(1+{\mathit{\xi }}^2)}^{\frac{p}{2}}}\hfill \\ \hfill & \le \frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left(2,\left({|\mathit{\xi }|}^2,+,{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^2,+,\left({|\mathit{\xi }|}^4,+,2,{|\mathit{\xi }|}^{4+\frac{\mathit{\alpha }}{2}}\right),{\mathit{\mu }}^4\right)\hfill \\ \hfill & \le \frac{2}{1-2e^{-\frac{\mathit{\pi }}{2}}}\left(4,{\mathit{\mu }}^2,+,3,{\mathit{\mu }}^4\right).\hfill \end{array}$$ According to above analysis and using (39(39) $$\begin{array}{cc}& (\mathrm{i}i)|1-cosh(a+i\mathit{\tau }b)|\ge \left\{\begin{array}{cc}\frac{2b^2}{{\mathit{\pi }}^2}{e}^a,\hfill & 0\le b\le \frac{\mathit{\pi }}{2},\hfill \\ \frac{1-2e^{-\frac{\mathit{\pi }}{2}}}{2}{e}^a,\hfill & b>\frac{\mathit{\pi }}{2};\hfill \end{array}\right.\hfill \end{array}$$(39) ), we obtain$$\begin{array}{cc}\hfill \Vert u(1,·)-v(1,·)\Vert & \le 2max\left\{e,\mathit{\delta },,,,\mathit{\delta },ln,\frac{E_p}{\mathit{\delta }}\right\}+E_{p}max\left\{{\mathit{\epsilon }}_5,,,,max,\left\{{\mathit{\epsilon }}_6,.,,{\mathit{\epsilon }}_7\right\}\right\},\hfill \\ \hfill & ={\mathit{\epsilon }}_3+{\mathit{\epsilon }}_4.\hfill \end{array}$$$\square$

Remark 3.3

In fact, we can first consider the two problems (15(15) $$\begin{array}{c}\hfill \tilde{u}(x,s)=\tilde{g}(s)cosh\left(s^{\frac{\mathit{\alpha }}{2}},x\right)+\tilde{f}(s)\frac{1-cosh\left(s^{\frac{\mathit{\alpha }}{2}},x\right)}{s^{\mathit{\alpha }}}.\end{array}$$(15) )–(18(18) $$\begin{array}{cc}& k(\mathit{\xi })={(i\mathit{\xi })}^{\frac{\mathit{\alpha }}{2}}={|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}{e}^{i\mathit{\tau }\frac{\mathit{\alpha }\mathit{\pi }}{4}},\mathit{\tau }=sign(\mathit{\xi }),\hfill \end{array}$$(18) ) and (20(20) $$\begin{array}{cc}& \mathit{\vartheta }(0,t)=g(t),t\ge 0,\hfill \end{array}$$(20) )–(23(23) $$\begin{array}{c}\hfill \widehat{\mathit{\vartheta }}(x,\mathit{\xi })=\widehat{g}(\mathit{\xi })cosh\left(k,(,\mathit{\xi },),x\right).\end{array}$$(23) ), respectively, and then derive the convergence estimates of the CIP for the TFIDE, just like that in [22]. But, for simplicity and uniformity, we directly deduce the convergence estimates from the CIP (3(3) $$\begin{array}{c}\hfill {}_0{D}_t^{\mathit{\alpha }}u(x,t)=u_{xx}(x,t)+f(t),0<x<1,t>0,\mathit{\alpha }\in (0,1),\end{array}$$(3) ) to (6(6) $$\begin{array}{cc}& u(x,0)=0,0<x<1,\hfill \end{array}$$(6) ) itself.

Remark 3.4

Noting the $log$-type regularization parameter choice rule (37(37) $$\begin{array}{cc}& l(\mathit{\xi })=\frac{k(\mathit{\xi })}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}=\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}{e}^{i\mathit{\tau }\frac{\mathit{\alpha }\mathit{\pi }}{4}}.\hfill \end{array}$$(37) ) and the $loglog$-type choice rule (39(39) $$\begin{array}{cc}& (\mathrm{i}i)|1-cosh(a+i\mathit{\tau }b)|\ge \left\{\begin{array}{cc}\frac{2b^2}{{\mathit{\pi }}^2}{e}^a,\hfill & 0\le b\le \frac{\mathit{\pi }}{2},\hfill \\ \frac{1-2e^{-\frac{\mathit{\pi }}{2}}}{2}{e}^a,\hfill & b>\frac{\mathit{\pi }}{2};\hfill \end{array}\right.\hfill \end{array}$$(39) ), they also lead to the corresponding convergence estimates ($log$-type and $loglog$-type). Furthermore, above choice rules are independent of the fractional order $\mathit{\alpha }$ and space point $x$. But, in our numerical test (see Section 4), we see the fractional order and space point have big impacts on the numerical accuracy. Thus, the choice rules which depend on the fractional order $\mathit{\alpha }$ and space point $x$ will be considered in our subsequent paper.

Remark 3.5

Since the regularization parameter choice rules (37(37) $$\begin{array}{cc}& l(\mathit{\xi })=\frac{k(\mathit{\xi })}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}=\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}{e}^{i\mathit{\tau }\frac{\mathit{\alpha }\mathit{\pi }}{4}}.\hfill \end{array}$$(37) ) and (39(39) $$\begin{array}{cc}& (\mathrm{i}i)|1-cosh(a+i\mathit{\tau }b)|\ge \left\{\begin{array}{cc}\frac{2b^2}{{\mathit{\pi }}^2}{e}^a,\hfill & 0\le b\le \frac{\mathit{\pi }}{2},\hfill \\ \frac{1-2e^{-\frac{\mathit{\pi }}{2}}}{2}{e}^a,\hfill & b>\frac{\mathit{\pi }}{2};\hfill \end{array}\right.\hfill \end{array}$$(39) ) contain the noise level $\mathit{\delta }$ and a priori bounds, they are called a priori choice rule. But, in a practical application, the noise level and a priori bounds are usually not known, then a posteriori choice rules are popular. For details, refer to [25]. Therefore, we will also consider some a posteriori choice rules in our future works.

4. Numerical examples

In this section, we present and discuss some numerical results obtained by the convolution-type regularization method for two examples. The convergence and stability of the algorithm when using noisy data can be verified. First, the implicit finite difference scheme (IFDS) is used to structure the source data and boundary data. Then, the finite difference solutions will be compared with the regularized solutions given by (32(32) $$\begin{array}{cc}& v(0,t)=g^{\mathit{\delta }}(t),t\ge 0,\hfill \end{array}$$(32) ).

We solve the following mixed boundary value problem by IFDS which is similar to the one in [26](62) $$\begin{array}{cc}& {}_0{D}_t^{\mathit{\alpha }}u=u_{xx}+f(t),0<x<1,0<t<1,\hfill \end{array}$$(62) (63) $$\begin{array}{cc}& u_x(0,t)=0,0\le t\le 1,\hfill \end{array}$$(63) (64) $$\begin{array}{cc}& u(1,t)=\mathit{\varphi }(t),0\le t\le 1,\hfill \end{array}$$(64) (65) $$\begin{array}{cc}& u(x,0)=0,0<x<1,\hfill \end{array}$$(65)

where $\mathit{\varphi }(t)$, $f(t)$ are given boundary value and source function, respectively.

Denote the discrete points in the space interval $[0,1]$ as $x_j=jh$, $j=0,1,2,\dots ,m$ with the space step size $h=1/m$ and the grid points in the time interval $[0,1]$ as $t_n=nk$, $n=0,1,2,\cdots ,s$ where $k=1/s$ represents the time step size. Let $u_j^n$ be the difference approximation to $u(x_j,t_n)$. Then the difference scheme is given as follows:(66) $$\begin{array}{cc}& -\frac{1}{h^2}{u}_{j-1}^1+\left({\mathit{\sigma }}_{\mathit{\alpha },k},+,\frac{2}{h^2}\right)u_j^1-\frac{1}{h^2}{u}_{j+1}^1\hfill \\ \hfill & ={\mathit{\sigma }}_{\mathit{\alpha },k}{u}_j^0+f(k),j=1,2,\dots ,m-1,\hfill \end{array}$$(66)

and for $n=2,3,\dots ,s$,(67) $$\begin{array}{cc}& -\frac{1}{h^2}{u}_{j-1}^n+\left({\mathit{\sigma }}_{\mathit{\alpha },k},+,\frac{2}{h^2}\right)u_j^n-\frac{1}{h^2}{u}_{j+1}^n\hfill \\ \hfill & ={\mathit{\sigma }}_{\mathit{\alpha },k}{u}_j^{n-1}-{\mathit{\sigma }}_{\mathit{\alpha },k}\sum _{i=2}^n{\mathit{\varrho }}_i^{(\mathit{\alpha })}\left(u_j^{n-i+1},-,u_j^{n-i}\right)+f(nk),j=1,2,\dots ,m-1,\hfill \end{array}$$(67)

with boundary conditions(68) $$\begin{array}{c}\hfill \frac{u_1^n-u_0^n}{h}=0,u_m^n=\mathit{\varphi }(nk),n=1,2,\dots ,s\end{array}$$(68)

and initial condition(69) $$\begin{array}{c}\hfill u_j^0=0,j=0,1,2,\dots ,m,\end{array}$$(69)

where ${\mathit{\sigma }}_{\mathit{\alpha },k}=\frac{1}{\mathrm{\Gamma }(1-\mathit{\alpha })}\frac{1}{1-\mathit{\alpha }}\frac{1}{k^{\mathit{\alpha }}}$ and ${\mathit{\varrho }}_i^{(\mathit{\alpha })}=i^{1-\mathit{\alpha }}-{(i-1)}^{1-\mathit{\alpha }}$, $i=1,2,\dots .$

Then the left boundary data (4(4) $$\begin{array}{cc}& u(0,t)=g(t),t\ge 0,\hfill \end{array}$$(4) ) are given by(70) $$\begin{array}{c}\hfill g(t_n)=u(0,t_n)\approx u_0^n,(n=0,1,2,\dots ,s).\end{array}$$(70)

Figure 1. The exact solution and the regularized solution with $\mathit{\alpha }=0.3$.

Figure 2. The exact solution and the regularized solution with $\mathit{\alpha }=0.5$.

Figure 3. The exact solution and the regularized solution with $\mathit{\alpha }=0.7$.

Moreover, the following formulas are used to generate the noisy data(71) $$\begin{array}{cc}& f^{\mathit{\delta }}(t_n)=f(t_n)+\mathit{\delta }·r\text{and}(n),\hfill \end{array}$$(71) (72) $$\begin{array}{cc}& g^{\mathit{\delta }}(t_n)=g(t_n)+\mathit{\delta }·r\text{and}(n),\hfill \end{array}$$(72)

where $t_n=nk$, $n=1,2,\dots ,s$, $f(t_n)$ and $g(t_n)$ are the exact data, $rand(n)$ is a random number uniformly distributed in $[-1,1]$ and the magnitude $\mathit{\delta }$ indicates a noise level. By using the noisy data $(f^{\mathit{\delta }}(t_n),g^{\mathit{\delta }}(t_n))$ generated from (67(67) $$\begin{array}{cc}& -\frac{1}{h^2}{u}_{j-1}^n+\left({\mathit{\sigma }}_{\mathit{\alpha },k},+,\frac{2}{h^2}\right)u_j^n-\frac{1}{h^2}{u}_{j+1}^n\hfill \\ \hfill & ={\mathit{\sigma }}_{\mathit{\alpha },k}{u}_j^{n-1}-{\mathit{\sigma }}_{\mathit{\alpha },k}\sum _{i=2}^n{\mathit{\varrho }}_i^{(\mathit{\alpha })}\left(u_j^{n-i+1},-,u_j^{n-i}\right)+f(nk),j=1,2,\dots ,m-1,\hfill \end{array}$$(67) ) and (68(68) $$\begin{array}{c}\hfill \frac{u_1^n-u_0^n}{h}=0,u_m^n=\mathit{\varphi }(nk),n=1,2,\dots ,s\end{array}$$(68) ), according to (32(32) $$\begin{array}{cc}& v(0,t)=g^{\mathit{\delta }}(t),t\ge 0,\hfill \end{array}$$(32) ), we can get a regularized solution $v$ computed using the Discrete Fourier Transform (DFT). In the numerical examples, we set the time step size $k=\frac{1}{50}$ and the space step size $h=\frac{1}{100}$. For generating the noisy data, we use a noise level $\mathit{\delta }=0.01$. The source function is always given by $f(t)=t(1-t)$, $(0<t<1)$.

In order to test the accuracy of the regularized solution $v$, we use the root mean square error defined as:(73) $$\begin{array}{c}\hfill err(v)=\sqrt{\frac{1}{s}\sum _{n=1}^s{(v(x,t_n)-u(x,t_n))}^2},\end{array}$$(73)

where $x\in [0,1]$ is a fixed space point.

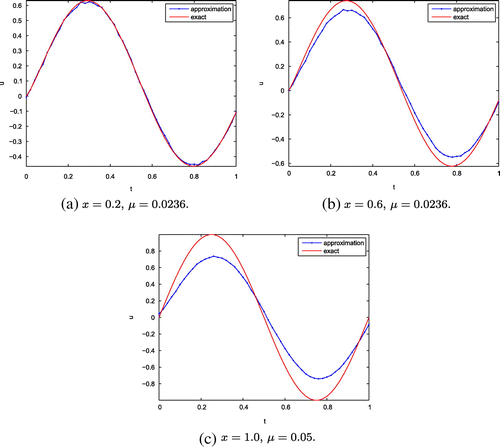
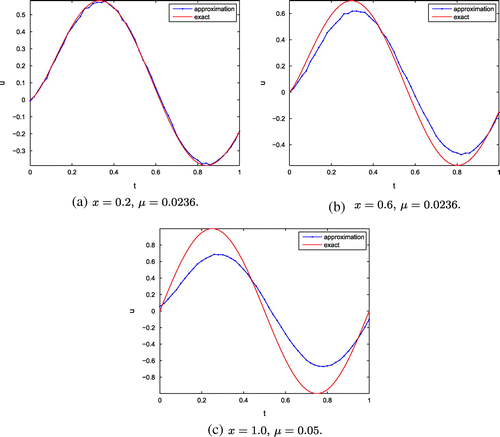
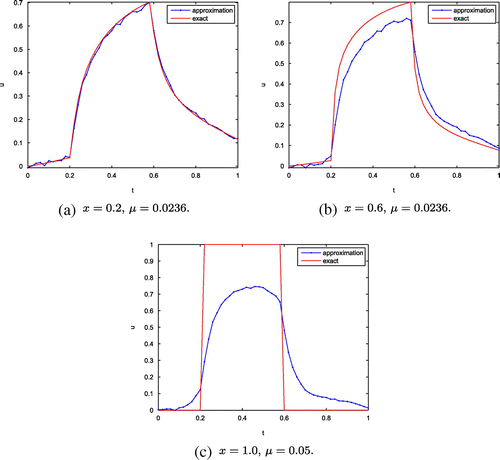
Example 1

(smooth example) Solve the direct problem (58(58) $$\begin{array}{c}\hfill \tilde{A}(\mathit{\xi })\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}-p}{\mathit{\mu }}^2.\end{array}$$(58) )–(61(61) $$\begin{array}{c}\hfill \tilde{A}(\mathit{\xi })\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}{\mathit{\mu }}^2\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{\mathit{\mu }}^2.\end{array}$$(61) ) with(74) $$\begin{array}{c}\hfill \mathit{\varphi }(t)=sin(2\mathit{\pi }t).\end{array}$$(74)

From (13(13) $$\begin{array}{cc}& \tilde{u}(0,s)=\tilde{g}(s),\hfill \end{array}$$(13) ), (19(19) $$\begin{array}{cc}& {}_0{D}_t^{\mathit{\alpha }}\mathit{\vartheta }(x,t)={\mathit{\vartheta }}_{xx}(x,t),0<x<1,t>0,\hfill \end{array}$$(19) ), (24(24) $$\begin{array}{cc}& {}_0{D}_t^{\mathit{\alpha }}\mathit{\varpi }(x,t)={\mathit{\varpi }}_{xx}(x,t)+f(t),0<x<1,t>0,\hfill \end{array}$$(24) ) and (25(25) $$\begin{array}{cc}& \mathit{\varpi }(0,t)=0,t\ge 0,\hfill \end{array}$$(25) ), we know $\Vert u(1,·)\Vert \le \Vert \mathit{\vartheta }(1,·)\Vert +\Vert \mathit{\varpi }(1,·)\Vert \le E$. However, $u(1,t)=sin(2\mathit{\pi }t)$ does not belong to $L^2(\mathbb{R})$, so we can’t find the a priori bound $E$ theoretically. But we will show that, by choosing the a priori bound $E=1$ and getting the regularization parameter $\mathit{\mu }\approx 0.0236$ from (37(37) $$\begin{array}{cc}& l(\mathit{\xi })=\frac{k(\mathit{\xi })}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}=\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}{e}^{i\mathit{\tau }\frac{\mathit{\alpha }\mathit{\pi }}{4}}.\hfill \end{array}$$(37) ) at $x=0.2,0.6$, our method still produce a rational approximation. As for $x=1.0$, we obtain the regularization parameter $\mathit{\mu }=0.05$ by trial and error. Then, we show the numerical results for $\mathit{\alpha }=0.3$ at $x=0.2,0.6,1.0$ in Figure 1, for $\mathit{\alpha }=0.5$ at $x=0.2,0.6,1.0$ are shown in Figure 2 and for $\mathit{\alpha }=0.7$ at $x=0.2,0.6,1.0$ are shown in Figure 3. In Table 1, it illustrates the errors for these various values of fractional order $\mathit{\alpha }$ at different space point $x$.

Table 1. The errors $err(v)$ for various values of fractional order $\mathit{\alpha }$ at various space point $x$, for Example 1.

$\mathit{\alpha }$	$x=0.2$	$x=0.6$	$x=1.0$
$0.3$	0.00840	0.05711	0.18984
$0.5$	0.00983	0.07456	0.24335
$0.7$	0.01319	0.11223	0.31789

Table 2. The errors $err(v)$ for various values of fractional order $\mathit{\alpha }$ at various space point $x$, for Example 2.

$\mathit{\alpha }$	$x=0.2$	$x=0.6$	$x=1.0$
$0.3$	0.00826	0.05641	0.19436
$0.5$	0.00916	0.06896	0.24611
$0.7$	0.01123	0.09539	0.30236

Figure 4. The exact solution and the regularized solution with $\mathit{\alpha }=0.3$.

Figure 5. The exact solution and the regularized solution with $\mathit{\alpha }=0.5$.

Figure 6. The exact solution and the regularized solution with $\mathit{\alpha }=0.7$.

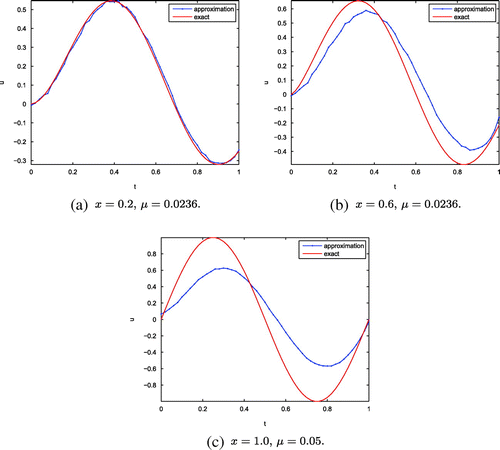
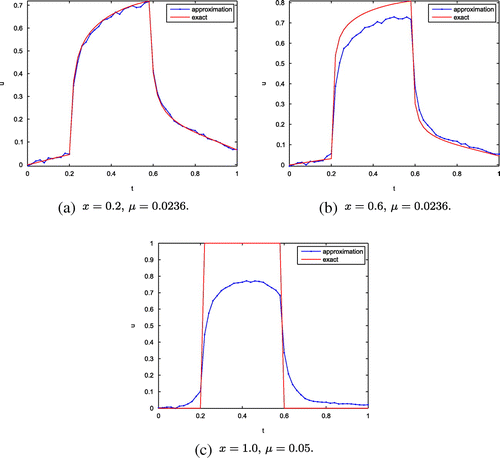
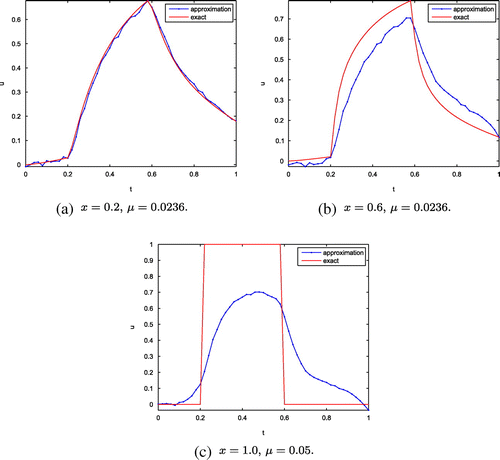
Example 2

(nonsmooth example) In the direct problem (58(58) $$\begin{array}{c}\hfill \tilde{A}(\mathit{\xi })\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}-p}{\mathit{\mu }}^2.\end{array}$$(58) )–(61(61) $$\begin{array}{c}\hfill \tilde{A}(\mathit{\xi })\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{|\mathit{\xi }|}^{2+\frac{\mathit{\alpha }}{2}}{\mathit{\mu }}^2\le \frac{4}{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{\mathit{\mu }}^2.\end{array}$$(61) ), we set(75) $$\begin{array}{c}\hfill \mathit{\varphi }(t)=H(t-0.2)-H(t-0.6),\end{array}$$(75)

where $H(t)$ represents the Heaviside (unit step) function.

Although we can compute $\Vert u(1,·)\Vert$=$\Vert \mathit{\varphi }(·)\Vert =\sqrt{0.4}$, the a priori bound $E$ is still not given by $\Vert u(1,·)\Vert \le \Vert \mathit{\vartheta }(1,·)\Vert +\Vert \mathit{\varpi }(1,·)\Vert \le E$. So similar to Example 1, we also take $E=1$ and obtain the regularization parameter $\mathit{\mu }\approx 0.0236$ by (37(37) $$\begin{array}{cc}& l(\mathit{\xi })=\frac{k(\mathit{\xi })}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}=\frac{{|\mathit{\xi }|}^{\frac{\mathit{\alpha }}{2}}}{\sqrt{1+{\mathit{\mu }}^2{\mathit{\xi }}^2}}{e}^{i\mathit{\tau }\frac{\mathit{\alpha }\mathit{\pi }}{4}}.\hfill \end{array}$$(37) ) at $x=0.2,0.6$. By repeating experiment, we get the regularization parameter $\mathit{\mu }\approx 0.05$ at $x=1.0$. Our method still has good computational effect. Then, we show the numerical results for $\mathit{\alpha }=0.3$ at $x=0.2,0.6,1.0$ in Figure 4, for $\mathit{\alpha }=0.5$ at $x=0.2,0.6,1.0$ are shown in Figure 5 and for $\mathit{\alpha }=0.7$ at $x=0.2,0.6,1.0$ are shown in Figure 6. Moreover, the errors $err(v)$ for these different fractional order at various space point $x$ are presented in Table 2.

From Figures 1–6 and Tables 1 and 2, it can be seen that numerical results near the boundary $x=0$ are better than the ones close to $x=1$. This is consistent with the convergence estimates (38(38) $$\begin{array}{cc}& (\mathrm{i})|cosh(a+i\mathit{\tau }b)|\ge \frac{\sqrt{1-2e^{-\frac{\mathit{\pi }}{2}}}}{2}{e}^a,\hfill \end{array}$$(38) ) and (40(40) $$\begin{array}{cc}& (\mathrm{i}ii)\underset{\mathit{\xi }\to 0}{lim}\frac{1-cosh\left(k,(,\mathit{\xi },),x\right)}{k{(\mathit{\xi })}^2}=-\frac{x^2}{2},0\le x\le 1.\hfill \end{array}$$(40) ). In particular, at $x=1$, (40(40) $$\begin{array}{cc}& (\mathrm{i}ii)\underset{\mathit{\xi }\to 0}{lim}\frac{1-cosh\left(k,(,\mathit{\xi },),x\right)}{k{(\mathit{\xi })}^2}=-\frac{x^2}{2},0\le x\le 1.\hfill \end{array}$$(40) ) gives only $loglog$-type estimate which shows a slow convergence rate. Furthermore, we can see the numerical accuracy becomes worse as the order $\mathit{\alpha }$ of Caputo fractional derivative increases. In fact, as analysis in Section 2, we find the larger fractional order will cause higher instability of solution, and it is reflected naturally in the numerical results. Meanwhile, recalling the definition of ${\mathit{\sigma }}_{\mathit{\alpha },k}$ in IFDS (62(62) $$\begin{array}{cc}& {}_0{D}_t^{\mathit{\alpha }}u=u_{xx}+f(t),0<x<1,0<t<1,\hfill \end{array}$$(62) )–(65(65) $$\begin{array}{cc}& u(x,0)=0,0<x<1,\hfill \end{array}$$(65) ), it is easy to see that the factor ${\mathit{\sigma }}_{\mathit{\alpha },k}$ become singular as fractional order $\mathit{\alpha }$ approaches one. Namely, the IFDS cannot be used for classical diffusion equation ($\mathit{\alpha }=1$). As for $\mathit{\alpha }=1$, we should separately apply standard finite difference scheme (such as Crank-Nicolson scheme). Therefore, our numerical discussion only focus on the case $0<\mathit{\alpha }<1$. In addition, we also find that the convolution-type regularization method applied in both Example 1 (smooth example) and Example 2 (non-smooth example) gives a similar degree of accuracy.

5. Conclusion

In this paper, a convolution-type regularization method is used to solve the CIP for the time fractional inhomogeneous diffusion equation in a strip domain. The convergence estimates have been presented for $0<x\le 1$ under a priori bound assumptions for the exact solution and the suitable choices of the regularization parameter. Finally, the numerical results illustrate our method is effective.

Acknowledgements

The author would like to thank the referees for their very useful suggestions.

Notes

The work described in this paper was supported by the NSF of China (11301168) and Plan for the growth of young teachers of Hunan University (531107040658).