Mathematical modelling and method for solving a parametric identification problem for self-test of measuring devices

Abstract

This paper considers a model describing the dependence of the temperature on the resistance for the self-calibration device. The model represented as a system of equations with non-predetermined parameters. To solve parametric identification problem, the method based on the Tikhonov regularization is proposed. The error estimates of regularized solutions are also obtained. It is proved that these estimates are exact with respect to the order. The obtained results are used for constructing the numerical method which allows to calculate the temperature from resistance measurements with guaranteed accuracy. To model verification and to estimate the stability of the obtained temperature values, computational experiments were carried out. These experiments address both computational and experimental data. Computational results confirm the stability and the efficiency of the proposed method to calculate the temperature values.

Keywords:

• self-test problem
• self-calibration device
• regularization method
• order optimality
• error estimation

AMS Subject Classifications:

• 65F22
• 68W25
• 41A27
• 70Q05
• 78A55

1. Introduction

Many metrology tools such as temperature transducers require a regular monitoring to check for any drift or problems. Self-test for the measuring devices under operating conditions is based on estimation of measured values. At the same time, very often the required values are obtained from the results of indirect measurements that leads to the inverse problem. This paper is devoted to the model describing the dependence of the temperature on the resistances for the temperature transducers. The mathematical model is represented as the system of equations with non-predetermined parameters. Thus, it is necessary to solve the parametric identification problem, to determine the required values via obtained parameters and to estimate the accuracy of these values. We propose a new method for solving the parametric identification problem and a method for determining the required temperature values using the obtained parameters. The method for solving the parametric identification problem is based on Tikhonov regularization with regularization parameter chosen from the modified residual principle.

The regularized algorithms are initially widely used to solve different inverse problems in engineering. Thus, in papers [1–4], the authors applied regularization methods for solving inverse problems of thermal conductivity. Cordier et al. [5], consider a model to a 2D cylinder wake flow where Tikhonov regularization methods of different orders are used to obtain the most efficient solutions. There is a slightly different situation with the metrological problems. Until recently, the most common approach to solving metrology problems has been derived from the least squares approaches. In particular, Forbes [6] has implemented a non-linear least squares solver for sparse-block systems to self-calibration problems in coordinate metrology. Within a relatively short period of a few years, regularization methods have gained an expansion in meteorology. For example, Kunz et al. [7] and Kalivas [8] applied these methods to multidimensional spectroscopic calibration models in optical tomography.

Stability estimates and convergence of the Tikhonov regularization methods are also of great interest. Vasin [9] traced some key points in the development of the variational Tikhonov method and discussed the role which the method has played in inventing other solution methods to ill-posed problems. Lorenz et al. [10] investigated the convergence of the Tikhonov regularization in different spaces. Neubauer et al. [11] and Hofmann and Mathe [12] investigated the convergence speed of Tikhonov regularization methods in Banach spaces with different approaches to the choice of regularization parameters. Haemarik et al. [13] obtained error estimates in a problem with noisy data under different approaches to the regularization parameter choice.

The regularized method proposed in this paper is used for solving the parametric identification problem and it is established that estimates of its solution are exact with respect to the order. This property allows to calculate the required temperature values with guaranteed accuracy for the reasonable exact resistance measurements.

The proposed method was applied to carry out the computational experiment. Computational results confirm the efficiency of the proposed method and indicate the advantages of our approach to calculation of the temperature values. Both the stability and the accuracy of these temperature values were also established. The obtained results provided the basis for the creation of the self-test method for the temperature transducers. This method of solving the self-test problem has been used for the first time.

2. Standard problem model

We consider mathematical aspect the self-test problem for a temperature transducer with two resistance temperature detectors which are made of different metals. The operating principle of the resistance thermometers is based on the dependence of electrical resistance of materials on temperature. This dependence is widely used in actual practice [14] and is expressed as follows [15].

Let $R_1$ and $R_2$ be resistance values of the first thermometer and the second thermometer, respectively. Assume that $R_1$ and $R_2$ were measured for temperature $t$. The relation between temperature and resistance is given as:(1) $$\begin{array}{c}\hfill \frac{R_1}{R_2}=\frac{R_{01}}{R_{02}}\frac{1+a_{1}t+a_2{t}^2+a_4{t}^4+a_6{t}^6}{1+b_{1}t+b_2{t}^2-100b_4{t}^3+b_4{t}^4},\end{array}$$(1)

where $R_{01}$, ${\{a_m\}}_1^6$ are the coefficients of the first resistance and $R_{02}$, ${\{b_m\}}_1^4$ are the coefficients of the second resistance, respectively.

At the same time, resistances $R_1$ and $R_2$ are directly measured values in operation and it is required to calculate temperature values from the measured resistances. The existing methods for obtaining temperature values are developed for each material separately. They contain many special features connected with the measured temperature range, equipment wear and tear, individual device characteristics, etc. In addition, it poses a problem to apply the existing methods for self-test of devices. Hence, it is required to develop a method for calculating temperature values which is uniform for any materials, temperature range, temperature affiliation to the tolerance limits and may be applied for the self-test of devices. The article is devoted to construct this method and to estimate the parameter and temperature errors. These estimates provide the basis for the development of the criteria allowing it to carry out the self-test of device.

3. Statement of the problem

Assume that $n$ resistance measurements were made for each thermometer. Let $R_{1k}$ be the resistance value of the first material and $R_{2k}$ be the resistance value of the second material, measured at temperature $t_k$, $k=\overline{1,n}$.

According to engineer requirements, the mathematical model describing the dependence of temperature on resistances can be represented as the following system:(2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{A}_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=t_k,\hfill \\ B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0=t_k.\hfill \end{array}\right.\end{array}$$(2)

The additional difficulty of self-test problem is that the true values $t_k$ are unknown in operation. It leads to the following equation:(3) $$\begin{array}{c}\hfill A_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0.\end{array}$$(3)

Since a priori information about degrees $m$ and $l$ is unknown, the degrees of the polynomials in left sides of (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{A}_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=t_k,\hfill \\ B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0=t_k.\hfill \end{array}\right.\end{array}$$(2) ) are non-predetermined. Furthermore, instead of the exact $t_k$, we are given temperature values $T_k$ and the allowable temperature error $\mathit{\delta }$. Another important factor connected with solving problem (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{A}_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=t_k,\hfill \\ B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0=t_k.\hfill \end{array}\right.\end{array}$$(2) ) and (3(3) $$\begin{array}{c}\hfill A_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0.\end{array}$$(3) ) is the possible errors of resistance measurements. If the errors are caused by system factors only, we assume that values $R_{1k}$ and $R_{2k}$ are given exactly. Introduce matrices $\overline{P_1}$ and $\overline{P_2}$:(4) $$\begin{array}{c}\hfill \overline{P_1}=\left(\begin{array}{ccccc}{R}_{11}^m& R_{11}^{m-1}& \dots & R_{11}& 1\\ R_{12}^m& R_{12}^{m-1}& \dots & R_{12}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ R_{1n}^m& R_{1n}^{m-1}& \dots & R_{1n}& 1\end{array}\right)\overline{P_2}=\left(\begin{array}{ccccc}{R}_{21}^l& R_{21}^{l-1}& \dots & R_{21}& 1\\ R_{22}^l& R_{22}^{l-1}& \dots & R_{22}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ R_{2n}^l& R_{2n}^{l-1}& \dots & R_{2n}& 1\end{array}\right).\end{array}$$(4)

The exact values of $t_k$ are denoted by $T_0=(t_1,t_2,\dots t_n)$ and values of $T_k$ are denoted by $T_{\mathit{\delta }}=(T_1,T_2,\dots T_n)$. Then vectors $\overline{u}=(A_m,A_{m-1},\dots A_0)$ and $\overline{v}=(B_l,B_{l-1},\dots B_0)$ correspond to coefficients $A_i$ and $B_j$, respectively.

Next, it is required to avoid situation of the insufficient measurements or eliminate the situation of redundant measurements. To do this, we assume that $m>n$ and $l>n$. Then we modify system (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{A}_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=t_k,\hfill \\ B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0=t_k.\hfill \end{array}\right.\end{array}$$(2) ) via eliminating linearly dependent columns from matrices $\overline{P_1}$, $\overline{P_2}$ and respective components of vectors $\overline{u}$, $\overline{v}$. Denote the obtained matrices as $P_1$ and $P_2$, and the obtained vectors as $u$ and $v$. Then system (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{A}_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=t_k,\hfill \\ B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0=t_k.\hfill \end{array}\right.\end{array}$$(2) ) can be expressed as:(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5)

and equation (3(3) $$\begin{array}{c}\hfill A_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0.\end{array}$$(3) ) is transformed to:(6) $$\begin{array}{c}\hfill P_{1}u=P_{2}v.\end{array}$$(6)

It is known that for $T_0$, there exists an exact solution $\{u_0,v_0\}$ to problem (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5) ). However, instead of $T_0$, we are given some approximations $T_{\mathit{\delta }}$ and error level $\mathit{\delta }$ such that deviation of $T_{\mathit{\delta }}$ from $T_0$ does not exceed $\mathit{\delta }$. Using these initial data, it is required to construct a regularized solution $\{u_{{\mathit{\alpha }}_1},v_{{\mathit{\alpha }}_2}\}$ to problem (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5) ) and to estimate its error. Next, using obtained system, it is required to find $T_u=P_1{u}_{{\mathit{\alpha }}_1}$ and $T_v=P_2{v}_{{\mathit{\alpha }}_1}$ and to estimate deviation of $T_u$ and $T_v$ from $T_{\mathit{\delta }}$ and $T_0$. Further, applying equation (6(6) $$\begin{array}{c}\hfill P_{1}u=P_{2}v.\end{array}$$(6) ), we estimate deviation of $T_u$ from $T_v$ and carry out a comparative analysis of obtained temperature errors.

Since system (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5) ) is overdetermined and condition number is rather high we use regularization methods to solve this problem. The physical meaning of the problem allows to consider elements $u,v,T_0,T_{\mathit{\delta }}$ as the elements of non-zero separable Hilbert space $H$, and matrices $P_1$ and $P_2$ as finite-dimensional approximations of linear continuous injective operators.

4. Regularization method

Let $H$ be a separable Hilbert space and operator $A:H\to H$ be a non-zero, linear, bounded, injective operator, whose set of values $R(A)$ is the set everywhere dense in $H$. Let $A^{\ast }$ be operator adjoint to $A$ and for operator $A_1=A^{\ast }A$ holds $Sp(A_1)={[0,\Vert A\Vert }^2]$. We consider the following problem:(7) $$\begin{array}{c}\hfill Ax=f,x,f\in H.\end{array}$$(7)

It is known that for $f_0$, there exists an exact solution $x_0\in M_r$. However, instead of $f_0$, we are given some approximations $f_{\mathit{\delta }}\in H$ and $\mathit{\delta }>0$ such that $\Vert f_{\mathit{\delta }}-f\Vert \le \mathit{\delta }$. Using these initial data, it is required to construct a regularized solution $x_{\mathit{\delta }}^{\mathit{\alpha }}$ to problem (7(7) $$\begin{array}{c}\hfill Ax=f,x,f\in H.\end{array}$$(7) ) and estimate its deviation from the exact solution.

Set $M_r$ is defined as follows. Let ${\overline{S}}_r=\{y:y\in H,\Vert y\Vert \le r\}$ and $B:H\to H$ be a linear bounded operator. Sets of values $R(B)$ and $R(B^{\ast })$ are everywhere dense in $H$. Operator $B_1=B^{\ast }B$ such that $B_1^{\frac{1}{2}}=G(A_1^{\frac{1}{2}})$, where $G(\mathit{\sigma })$ is continuous, strictly increases for $\mathit{\sigma }\in [0,\Vert A\Vert ]$ and $G(0)=0$. Then $M_r=B\overline{S_r}$.

To solve problem (7(7) $$\begin{array}{c}\hfill Ax=f,x,f\in H.\end{array}$$(7) ), we use the approach proposed in [16], according to which the solution to problem (7(7) $$\begin{array}{c}\hfill Ax=f,x,f\in H.\end{array}$$(7) ) is reduced to solving the following variational problem:(8) $$\begin{array}{c}\hfill \underset{x}{inf}\{\Vert Ax-f_{\mathit{\delta }}{\Vert }^2+{\mathit{\alpha }\Vert x\Vert }^2:x\in H\},\mathit{\alpha }>0,\end{array}$$(8)

where $\mathit{\alpha }$ is a regularization parameter. Uniqueness of solution to problem (8(8) $$\begin{array}{c}\hfill \underset{x}{inf}\{\Vert Ax-f_{\mathit{\delta }}{\Vert }^2+{\mathit{\alpha }\Vert x\Vert }^2:x\in H\},\mathit{\alpha }>0,\end{array}$$(8) ) was proved in [17]. This solution is obtained via regularizing operator $J_{\mathit{\alpha }}$, which is defined as follows:(9) $$\begin{array}{c}\hfill J_{\mathit{\alpha }}={(A_1+\mathit{\alpha }E)}^{-1}{A}^{\ast }.\end{array}$$(9)

Then, regularized solution $x_{\mathit{\delta }}^{\mathit{\alpha }}$ of equation (7(7) $$\begin{array}{c}\hfill Ax=f,x,f\in H.\end{array}$$(7) ) has the following form:(10) $$\begin{array}{c}\hfill x_{\mathit{\delta }}^{\mathit{\alpha }}=J_{\mathit{\alpha }}{f}_{\mathit{\delta }}.\end{array}$$(10)

Lemma 4.1

Let function $J_{\mathit{\alpha }}$ be defined by formulas (9(9) $$\begin{array}{c}\hfill J_{\mathit{\alpha }}={(A_1+\mathit{\alpha }E)}^{-1}{A}^{\ast }.\end{array}$$(9) ) then $\Vert J_{\mathit{\alpha }}\Vert \le \frac{1}{2\sqrt{\mathit{\alpha }}}$. For $\mathit{\alpha }\le {\Vert A\Vert }^2$, this relation takes the form of equality.

Proof

From the spectral theorem formulated in [18] and from the properties of operator $B$, we obtain that $\Vert J_{\mathit{\alpha }}{\Vert }^2={sup}_{\mathit{\sigma }\in [0,\Vert A\Vert ]}(\frac{\mathit{\sigma }}{\mathit{\alpha }+{\mathit{\sigma }}^2}{)}^2.$ Since function ${\displaystyle y(\mathit{\sigma })=\frac{\mathit{\sigma }}{\mathit{\alpha }+{\mathit{\sigma }}^2}}$ is continuous and differentiable, we obtain that this function has maximum at point $\mathit{\sigma }=\sqrt{\mathit{\alpha }}$ and in this point, we obtain that $\Vert J_{\mathit{\alpha }}{\Vert }^2=\frac{1}{4\mathit{\alpha }}$. Thus, the lemma is proved. $\square$

To estimate the error of $x_{\mathit{\delta }}^{\mathit{\alpha }}$, we use function $\mathit{\omega }(\mathit{\tau },r)$, which is suggested in [19]:(11) $$\begin{array}{c}\hfill \mathit{\omega }(\mathit{\tau },r)=sup\{\Vert x\Vert :x\in M_r,\Vert Ax\Vert \le \mathit{\tau }\},\end{array}$$(11)

and function $\mathrm{\Delta }(J_{\mathit{\alpha }})$, which is defined by the formula:(12) $$\begin{array}{c}\hfill \mathrm{\Delta }(J_{\mathit{\alpha }})=\underset{x,f_{\mathit{\delta }}}{sup}\{\Vert x-J_{\mathit{\alpha }}{f}_{\mathit{\delta }}\Vert :x\in M_r,\Vert f_{\mathit{\delta }}-Ax\Vert \le \mathit{\delta }\}.\end{array}$$(12)

Note that for many applied problems, it is enough to construct solutions, which error estimates have the same order as the estimates of optimal solution. These solutions are called order-optimal. The basic idea of constructing the order-optimal methods and optimal methods proposed in [20] is as follows. First, more precise below error estimate for the optimal method is obtained. Next, a regularization method is constructed. If its upper error estimate is the same as the below estimate, the method is optimal. If the upper error estimate differs from the below estimate by a multiplicative constant independent of $\mathit{\delta }$, the method is order-optimal. In research, [21] is proved the following estimate for optimal method $F_{\mathit{\delta }}^{opt}$:

Theorem 4.2

Let $F_{\mathit{\delta }}^{opt}$ be an optimal regularization method and $\mathrm{\Delta }(F_{\mathit{\delta }}^{opt})$ be its estimate. Then, the following inequality holds $\mathrm{\Delta }(F_{\mathit{\delta }}^{opt})\ge \frac{1}{2}\mathit{\omega }(\mathit{\delta },r)$ for any $\mathit{\delta }\in (0,{\mathit{\delta }}_0]$.

To estimate $\mathrm{\Delta }(J_{\mathit{\alpha }})$, we define function ${\mathrm{\Delta }}_0(\mathit{\alpha })$ as follows:(13) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\underset{x\in M_r}{sup}\Vert x-J_{\mathit{\alpha }}Ax\Vert .\end{array}$$(13)

Theorem 4.3

Function ${\mathrm{\Delta }}_0(\mathit{\alpha })$ is continuous, bounded and strongly increases.

Proof

From lemma proved in [18], we obtain the existence of a unitary operator $Q$ such that the polar decomposition $B=Q{B}_1^{1/2}$ of the operator $B$ holds. Substitution of polar decomposition into ${\mathrm{\Delta }}_0^2(\mathit{\alpha })$ yields:$${\mathrm{\Delta }}_0^2(\mathit{\alpha })=\underset{\Vert w_0\Vert \le r}{max}\underset{0}{\overset{\Vert A\Vert }{\int }}[\frac{\mathit{\alpha }}{\mathit{\alpha }+{\mathit{\sigma }}^2}{]}^2{G}^2(\mathit{\sigma })d(E_{\mathit{\sigma }}{w}_0,w_0),$$

where $w_0=Q^{-1}{v}_0$ and $\{E_{\mathit{\sigma }}:\mathit{\sigma }\in [0,\Vert A\Vert ]\}$ is the spectral decomposition of $E$ generated by the operator $A_1^{1/2}$. Hence and from the theorem formulated in [18], we obtain:(14) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=r\underset{\mathit{\sigma }\in [0,\Vert A\Vert ]}{max}\frac{\mathit{\alpha }}{\mathit{\alpha }+{\mathit{\sigma }}^2}G(\mathit{\sigma }).\end{array}$$(14)

Next, we show that function ${\mathrm{\Delta }}_0(\mathit{\alpha })$ is continuous for any $\mathit{\alpha }>0$. For arbitrary $\mathit{\alpha }>0$ choose ${\mathit{\beta }}_1>0$ and ${\mathit{\beta }}_2>0$ with ${\mathit{\beta }}_1<\mathit{\alpha }<{\mathit{\beta }}_2$. Consider the function:$${\displaystyle \mathrm{\Phi }(\mathit{\sigma },\mathit{\alpha })=\frac{r\mathit{\alpha }}{\mathit{\alpha }+{\mathit{\sigma }}^2}G(\mathit{\sigma })}$$

which is uniformly continuous at $[0,\Vert A\Vert ]\times [{\mathit{\beta }}_1,{\mathit{\beta }}_2]$. From the properties of function $\mathrm{\Phi }(\mathit{\sigma },\mathit{\alpha })$, it follows that for all $\mathit{\epsilon }>0$ there exists constant $0<\mathit{\rho }<({\mathit{\beta }}_2-{\mathit{\beta }}_1)$ such that the following inequality holds $|{\mathrm{\Delta }}_0({\mathit{\alpha }}_1)-{\mathrm{\Delta }}_0({\mathit{\alpha }}_2)|<\mathit{\epsilon }$ for any ${\mathit{\alpha }}_1,{\mathit{\alpha }}_2$ with $|{\mathit{\alpha }}_1-{\mathit{\alpha }}_2|<\mathit{\rho }$. Thus, function ${\mathrm{\Delta }}_0(\mathit{\alpha })$ is uniformly continuous for any $\mathit{\alpha }\in [{\mathit{\alpha }}_1,{\mathit{\alpha }}_2)$ and, consequently, continuous for any $\mathit{\alpha }\in (0,\infty )$.

Next, we show boundedness of function ${\mathrm{\Delta }}_0(\mathit{\alpha })$. Let us prove that ${\mathrm{\Delta }}_0(\mathit{\alpha })\to 0$ for $\mathit{\alpha }\to 0$. Let ${\mathit{\alpha }}_n\to 0$ and assume the contrary. Suppose that there exists such a constant $d>0$ and subsequence $\{{\mathit{\alpha }}_{n_k}\}$ such that ${\mathrm{\Delta }}_0({\mathit{\alpha }}_{n_k})\ge d$ for all $k$. From the continuity of function $\mathrm{\Phi }(\mathit{\sigma },{\mathit{\alpha }}_{n_k})$ and the Weierstrass theorem, it follows that function $\mathrm{\Phi }(\mathit{\sigma },{\mathit{\alpha }}_{n_k})$ has a maximum in $\widehat{{\mathit{\sigma }}_k}>0$. On the other hand,$$r\frac{{\mathit{\alpha }}_{n_k}}{{\mathit{\alpha }}_{n_k}+{\widehat{{\mathit{\sigma }}_k}}^2}G(\widehat{{\mathit{\sigma }}_k})\le r\frac{{\mathit{\alpha }}_{n_k}}{{\widehat{{\mathit{\sigma }}_k}}^2}G(\Vert A\Vert ).$$

Hence and from (14(14) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=r\underset{\mathit{\sigma }\in [0,\Vert A\Vert ]}{max}\frac{\mathit{\alpha }}{\mathit{\alpha }+{\mathit{\sigma }}^2}G(\mathit{\sigma }).\end{array}$$(14) ), it follows that ${\mathrm{\Delta }}_0({\mathit{\alpha }}_{n_k})\to 0$ for $k\to \infty$. This contradicts relation ${\mathrm{\Delta }}_0({\mathit{\alpha }}_{n_k})\ge d$. Note, that for $\widehat{\mathit{\sigma }}=0$, the convergence ${\mathrm{\Delta }}_0(\mathit{\alpha })\to 0$ is evident.

Assume that $\mathit{\alpha }\to \infty$. From (14(14) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=r\underset{\mathit{\sigma }\in [0,\Vert A\Vert ]}{max}\frac{\mathit{\alpha }}{\mathit{\alpha }+{\mathit{\sigma }}^2}G(\mathit{\sigma }).\end{array}$$(14) ), it follows that ${\mathrm{\Delta }}_0(\mathit{\alpha })\to rG(\Vert A\Vert ).$ Hence and from ${\mathrm{\Delta }}_0(\mathit{\alpha })\to 0$ for $\mathit{\alpha }\to 0$, we obtain the boundedness of function ${\mathrm{\Delta }}_0(\mathit{\alpha })$.

Let us prove the monotony of function ${\mathrm{\Delta }}_0(\mathit{\alpha })$. Consider ${\mathit{\alpha }}_1>{\mathit{\alpha }}_2$. Since function $\mathrm{\Phi }(\mathit{\sigma },\mathit{\alpha })$ is continuous in $[0,\Vert A\Vert ]$, we obtain that there exists ${\mathit{\sigma }}_1$ and ${\mathit{\sigma }}_2\in [0,\Vert A\Vert ]$ such that$${\mathrm{\Delta }}_0({\mathit{\alpha }}_1)=r\frac{{\mathit{\alpha }}_1}{{\mathit{\alpha }}_1+{\mathit{\sigma }}_1^2}G({\mathit{\sigma }}_1),{\mathrm{\Delta }}_0({\mathit{\alpha }}_2)=r\frac{{\mathit{\alpha }}_2}{{\mathit{\alpha }}_2+{\mathit{\sigma }}_2^2}G({\mathit{\sigma }}_2).$$

Assume ${\mathit{\sigma }}_1\ne {\mathit{\sigma }}_2$. From (14(14) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=r\underset{\mathit{\sigma }\in [0,\Vert A\Vert ]}{max}\frac{\mathit{\alpha }}{\mathit{\alpha }+{\mathit{\sigma }}^2}G(\mathit{\sigma }).\end{array}$$(14) ), it follows that ${\displaystyle {\mathrm{\Delta }}_0({\mathit{\alpha }}_1)\ge r\frac{{\mathit{\alpha }}_1}{{\mathit{\alpha }}_1+{\mathit{\sigma }}_2^2}G({\mathit{\sigma }}_2).}$ Hence, we obtain:$$\frac{{\mathit{\alpha }}_1}{{\mathit{\alpha }}_1+{\mathit{\sigma }}_1^2}G({\mathit{\sigma }}_1)-\frac{{\mathit{\alpha }}_2}{{\mathit{\alpha }}_2+{\mathit{\sigma }}_2^2}G({\mathit{\sigma }}_2)>(\frac{{\mathit{\alpha }}_1}{{\mathit{\alpha }}_1+{\mathit{\sigma }}_2^2}-\frac{{\mathit{\alpha }}_2}{{\mathit{\alpha }}_2+{\mathit{\sigma }}_2^2})G({\mathit{\sigma }}_2)>0.$$

If ${\mathit{\sigma }}_1={\mathit{\sigma }}_2$, then the increase of function ${\mathrm{\Delta }}_0(\mathit{\alpha })$ is evident. Thus, the theorem is proved. $\square$

Next, as the regularization parameter $\overline{\mathit{\alpha }}=\mathit{\alpha }(\mathit{\delta })$, we choose the solution of the equation:(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15)

Theorem 4.4

Equation (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ) has a unique solution $\overline{\mathit{\alpha }}(\mathit{\delta })$.

Proof

From Theorem 4.3, we obtain the continuity and strict increase of function ${\mathrm{\Delta }}_0(\mathit{\alpha })$ and for any $\mathit{\alpha }\in (0,\infty )$ it follows:(16) $$\begin{array}{c}\hfill 0\le {\mathrm{\Delta }}_0(\mathit{\alpha })\le rG(\Vert A\Vert ).\end{array}$$(16)

The continuity and strict decrease of function $\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}$ are clearly. Hence and from inequality (16(16) $$\begin{array}{c}\hfill 0\le {\mathrm{\Delta }}_0(\mathit{\alpha })\le rG(\Vert A\Vert ).\end{array}$$(16) ), we obtain the uniqueness of solution to problem (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ) for any $\mathit{\delta }>0$. Thus, the theorem is proved. $\square$

Next, we estimate function ${\mathrm{\Delta }}_0(\overline{\mathit{\alpha }})$ where parameter $\overline{\mathit{\alpha }}$ is chosen from (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ). The following statement holds.

Theorem 4.5

Let $\mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})$ and ${\mathrm{\Delta }}_0(\overline{\mathit{\alpha }})$ be defined by formula (12(12) $$\begin{array}{c}\hfill \mathrm{\Delta }(J_{\mathit{\alpha }})=\underset{x,f_{\mathit{\delta }}}{sup}\{\Vert x-J_{\mathit{\alpha }}{f}_{\mathit{\delta }}\Vert :x\in M_r,\Vert f_{\mathit{\delta }}-Ax\Vert \le \mathit{\delta }\}.\end{array}$$(12) ) and (13(13) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\underset{x\in M_r}{sup}\Vert x-J_{\mathit{\alpha }}Ax\Vert .\end{array}$$(13) ), respectively, parameter $\overline{\mathit{\alpha }}$ is a solution of equation (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ). Then, the following estimate holds:(17) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\overline{\mathit{\alpha }})\le \mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})\le 2{\mathrm{\Delta }}_0(\overline{\mathit{\alpha }}).\end{array}$$(17)

Proof

From (12(12) $$\begin{array}{c}\hfill \mathrm{\Delta }(J_{\mathit{\alpha }})=\underset{x,f_{\mathit{\delta }}}{sup}\{\Vert x-J_{\mathit{\alpha }}{f}_{\mathit{\delta }}\Vert :x\in M_r,\Vert f_{\mathit{\delta }}-Ax\Vert \le \mathit{\delta }\}.\end{array}$$(12) ), it follows that $\mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})={sup}_{x,f_{\mathit{\delta }}}\{\Vert x-J_{\overline{\mathit{\alpha }}}{f}_{\mathit{\delta }}\Vert :x\in M_r,\Vert f_{\mathit{\delta }}-Ax\Vert \le \mathit{\delta }\}.$ Taking into account lemma 4.1 and the relation:$$\Vert x-J_{\overline{\mathit{\alpha }}}{f}_{\mathit{\delta }}\Vert \le \Vert x-J_{\overline{\mathit{\alpha }}}Ax\Vert +\Vert J_{\overline{\mathit{\alpha }}}Ax-J_{\overline{\mathit{\alpha }}}{f}_{\mathit{\delta }}\Vert \le {\mathrm{\Delta }}_0(\overline{\mathit{\alpha }})+\Vert J_{\overline{\mathit{\alpha }}}\Vert \mathit{\delta },$$

we obtain the estimate from above of the values of $\mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})$. Next, we estimate the values of $\mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})$ from below. Since the following estimation holds $\Vert x-J_{\overline{\mathit{\alpha }}}Ax\Vert \ge {\mathrm{\Delta }}_0(\overline{\mathit{\alpha }})-\mathit{\epsilon },$ for any $x\in M_r$ and taking into account the arbitrariness of value $\mathit{\epsilon }$, we obtain below estimate of $\mathrm{\Delta }(J_{\overline{\mathit{\alpha }}}).$ Thus, the theorem is proved. $\square$

The results obtained in Theorems 4.3 and 4.4 provide the basis for constructing the regularization parameter choice procedure. Note that the obtained results can be applied for solving rather a wide range of problems, whose set of solutions generated a strictly increasing function.

5. The error estimate of regularized solution

Let set $M_r$ be defined via function $G(\mathit{\sigma })={\mathit{\sigma }}^p$ and $p>0$. In research [19], it is proved, that in this case for rather small $\mathit{\delta }$ function, $\mathit{\omega }(\mathit{\delta },r)$ satisfies the relation:(18) $$\begin{array}{c}\hfill \mathit{\omega }(\mathit{\delta },r)=r^{1/p+1}{\mathit{\delta }}^{p/p+1}.\end{array}$$(18)

This relation provided the basis for substantiation of the order optimality in the following theorem.

Theorem 5.1

Let $J_{\overline{\mathit{\alpha }}}$ be defined by formula (9(9) $$\begin{array}{c}\hfill J_{\mathit{\alpha }}={(A_1+\mathit{\alpha }E)}^{-1}{A}^{\ast }.\end{array}$$(9) ) parameter, regularization parameter $\overline{\mathit{\alpha }}$ satisfies (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ) and $0<p\le 2$. Then, the following estimate holds:$$\frac{1}{2}[\frac{p}{2-p}{]}^{p/2(p+1)}{r}^{1/p+1}{\mathit{\delta }}^{p/p+1}\le \mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})\le [\frac{p}{2-p}{]}^{p/2(p+1)}{r}^{1/p+1}{\mathit{\delta }}^{p/p+1}.$$

Proof

Applying the arguments as in the proof of Theorem 4.3, we obtain:$${\mathrm{\Delta }}_0(\mathit{\alpha })=r\underset{\mathit{\sigma }\in [0,\Vert A\Vert ]}{max}\frac{\mathit{\alpha }}{\mathit{\alpha }+{\mathit{\sigma }}^2}G(\mathit{\sigma })=\underset{\mathit{\sigma }\in [0,\Vert A\Vert ]}{max}\frac{\mathit{\alpha }}{\mathit{\alpha }+{\mathit{\sigma }}^2}{\mathit{\sigma }}^p.$$

Taking into account the results of Theorem 4.4, we obtain the uniqueness of the solution $\overline{\mathit{\alpha }}$ of equation (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ) for each $\mathit{\delta }$. Thus, to estimate function ${\mathrm{\Delta }}_0^2(\overline{\mathit{\alpha }})$, it is sufficient to estimate the following function:(19) $$\begin{array}{c}\hfill y(\mathit{\sigma })=\frac{\overline{\mathit{\alpha }}}{\overline{\mathit{\alpha }}+{\mathit{\sigma }}^2}{\mathit{\sigma }}^p.\end{array}$$(19)

This function is non-negative, continuous by $\mathit{\sigma }$. Thus, we can use the Weierstrass theorem, according to which there exists $\tilde{\mathit{\sigma }}=\tilde{\mathit{\sigma }}(\overline{\mathit{\alpha }})\in [0,\Vert A\Vert ]$ such that $y(\tilde{\mathit{\sigma }})={max}_{[0,\Vert A\Vert ]}y(\mathit{\sigma })$.

Since $y(\mathit{\sigma })$ is a differentiable function, we obtain that the extremum point coincides either with $\tilde{\mathit{\sigma }}=0$ (but in this case $y(\mathit{\sigma })=0$) or with $\tilde{\mathit{\sigma }}=\sqrt{\frac{p\overline{\mathit{\alpha }}}{2-p}},$ where $p<2$. Using the sufficient condition of the extremum, we obtain that function $y(\mathit{\sigma })$ has a maximum in this point. Substitution of value $\tilde{\mathit{\sigma }}$ into ${\mathrm{\Delta }}_0(\overline{\mathit{\alpha }})$ yields:(20) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\overline{\mathit{\alpha }})=\frac{r}{2}[\frac{p}{2-p}{]}^{p/2}{\overline{\mathit{\alpha }}}^{p/2}.\end{array}$$(20)

From relations (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ), (20(20) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\overline{\mathit{\alpha }})=\frac{r}{2}[\frac{p}{2-p}{]}^{p/2}{\overline{\mathit{\alpha }}}^{p/2}.\end{array}$$(20) ) and taking into account Theorem 4.5, we have:(21) $$\begin{array}{c}\hfill \frac{1}{2}[\frac{p}{2-p}{]}^{p/2(p+1)}{r}^{1/p+1}{\mathit{\delta }}^{p/p+1}\le \mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})\le [\frac{p}{2-p}{]}^{p/2(p+1)}{r}^{1/p+1}{\mathit{\delta }}^{p/p+1}.\end{array}$$(21)

Assume $p=2$ and the regularization parameter $\overline{\mathit{\alpha }}$ satisfies (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ). Then, function $y(\mathit{\sigma })$ defined by (19(19) $$\begin{array}{c}\hfill y(\mathit{\sigma })=\frac{\overline{\mathit{\alpha }}}{\overline{\mathit{\alpha }}+{\mathit{\sigma }}^2}{\mathit{\sigma }}^p.\end{array}$$(19) ) is non-decreasing with respect to $\mathit{\sigma }$ and the function ${\mathrm{\Delta }}_0(\overline{\mathit{\alpha }})$ has the following form:(22) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\overline{\mathit{\alpha }})=\frac{{r\overline{\mathit{\alpha }}\Vert A\Vert }^2}{{\Vert A\Vert }^2+\mathit{\alpha }}.\end{array}$$(22)

From (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ) and (22(22) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\overline{\mathit{\alpha }})=\frac{{r\overline{\mathit{\alpha }}\Vert A\Vert }^2}{{\Vert A\Vert }^2+\mathit{\alpha }}.\end{array}$$(22) ), it follows that $\overline{\mathit{\alpha }}(\mathit{\delta })\ge {(\mathit{\delta }/2r)}^{2/3}$ for rather small $\mathit{\delta }$ and from (22(22) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\overline{\mathit{\alpha }})=\frac{{r\overline{\mathit{\alpha }}\Vert A\Vert }^2}{{\Vert A\Vert }^2+\mathit{\alpha }}.\end{array}$$(22) ), we obtain:(23) $$\begin{array}{c}\hfill C·r^{1/3}{\mathit{\delta }}^{2/3}\le \mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})\le 2^{1/3}·r^{1/3}{\mathit{\delta }}^{2/3},\end{array}$$(23)

where $C\in (0.5;1)$. Thus, the theorem is proved. $\square$

Theorem 5.2

Let $J_{\overline{\mathit{\alpha }}}$ be defined by formula (9(9) $$\begin{array}{c}\hfill J_{\mathit{\alpha }}={(A_1+\mathit{\alpha }E)}^{-1}{A}^{\ast }.\end{array}$$(9) ) parameter, regularization parameter $\overline{\mathit{\alpha }}$ satisfies (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ) and $p>2$. Then the following estimate holds:$$\frac{1}{2}{\Vert A\Vert }^{\frac{p-2}{3}}·r^{1/3}{\mathit{\delta }}^{2/3}\le \mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})\le {\Vert A\Vert }^{\frac{p-2}{3}}·r^{1/3}{\mathit{\delta }}^{2/3}.$$

Proof

For $p>2$ function ${\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{{r\Vert A\Vert }^p\mathit{\alpha }}{{\Vert A\Vert }^2+\mathit{\alpha }}$. From (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ), we have that value of ${\mathrm{\Delta }}_0(\mathit{\alpha })$ may be obtained from the following equation:$${\mathrm{\Delta }}_0{(\mathit{\alpha })}^3+\frac{{\mathit{\delta }}^2}{{4\Vert A\Vert }^2}{\mathrm{\Delta }}_0(\mathit{\alpha })-\frac{{\mathit{\delta }}^2}{4}{\Vert A\Vert }^{p-2}=0.$$

Since the regularization parameter complies with (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ), the solution to the last equation satisfies the following estimate for rather small values of $\mathit{\delta }$:$$\frac{1}{2}{\Vert A\Vert }^{\frac{p-2}{3}}·r^{1/3}{\mathit{\delta }}^{2/3}\le \mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})\le {\Vert A\Vert }^{\frac{p-2}{3}}·r^{1/3}{\mathit{\delta }}^{2/3}.$$

Thus, the theorem is proved. $\square$

Remark

As one of anonymous referees has kindly pointed out to the author, the relation $\mathit{\alpha }\sim {(\mathit{\delta }/r)}^{2/(p+1)}$ is known. Still, the author believes that it makes sense to present the full proof of Theorem 5.1 here, because the above derivation of (21(21) $$\begin{array}{c}\hfill \frac{1}{2}[\frac{p}{2-p}{]}^{p/2(p+1)}{r}^{1/p+1}{\mathit{\delta }}^{p/p+1}\le \mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})\le [\frac{p}{2-p}{]}^{p/2(p+1)}{r}^{1/p+1}{\mathit{\delta }}^{p/p+1}.\end{array}$$(21) ) uses an idea which is different from the well known.

We apply Theorem 5.1 for estimate of the value $\mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})$ in problem (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5) ), (6(6) $$\begin{array}{c}\hfill P_{1}u=P_{2}v.\end{array}$$(6) ). In this Case, $G(\mathit{\sigma })=\mathit{\sigma }$ and the following estimates holds: $\frac{\sqrt{r\mathit{\delta }}}{2}\le \mathrm{\Delta }(J_{\overline{\mathit{\alpha }}})\le \sqrt{r\mathit{\delta }}$. This relation provided the basis for the obtaining coefficient error estimates in system (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5) ) and is applied in calibration of resistance thermometers.

6. Numerical method

We proceed to construct a numerical method for solving problem (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5) ), (6(6) $$\begin{array}{c}\hfill P_{1}u=P_{2}v.\end{array}$$(6) ) based on the suggested regularization method. The solution to the problem subdivided into two parts.

The first part involves getting the polynomial degrees via eliminating linear dependent columns in matrices $\overline{P_1}$ and $\overline{P_2}$. In this case, linear independent columns correspond to non-zero components of vectors $\overline{u}$ and $\overline{v}$ respectively. Ranks $M$ and $L$ of obtained matrices $P_1$ and $P_2$ define the degrees of $m$ and $l$ in system (3(3) $$\begin{array}{c}\hfill A_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0.\end{array}$$(3) ). If ranks of matrices $\overline{P_1}$ and $\overline{P_2}$ are equal to the number of measurements $n$, it testifies that an insufficient number of measurements has been made and additional measurements are required for the successful solving of the self-test problem. Note that while carrying out our research, we used variable data amounts and the similar situation never came about.

Thus, we consider elements $u,v,T_0,T_{\mathit{\delta }}$ as the elements of non-zero separable Hilbert space $H$, and matrices $P_1$ and $P_2$ as finite-dimensional approximations of linear continuous injective operators. The estimate of accuracy for finite-dimensional approximations is one of the goals of future research.

The second part involves using proposed regularizing algorithm for system (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5) ). According to this approach, the regularized solutions $u_{\overline{{\mathit{\alpha }}_1}}$ and $v_{\overline{{\mathit{\alpha }}_2}}$ of the problem (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5) ) are defined by formula (10(10) $$\begin{array}{c}\hfill x_{\mathit{\delta }}^{\mathit{\alpha }}=J_{\mathit{\alpha }}{f}_{\mathit{\delta }}.\end{array}$$(10) ) and regularization parameters $\overline{{\mathit{\alpha }}_1}$ and $\overline{{\mathit{\alpha }}_2}$ are chosen from [15].

Next, we proceed to verification of the result and to estimation the temperature errors. The objective of verification is to ensure that the implementation of the model is correct.

The first step of this procedure involves simulation of the temperature functions $T_u$ and $T_v$ as well as the resistances functions $R((u)$ and $R(v)$. Substituting values $u_{\overline{{\mathit{\alpha }}_1}}$ and $v_{\overline{{\mathit{\alpha }}_2}}$ into (3(3) $$\begin{array}{c}\hfill A_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0.\end{array}$$(3) ), we obtain function $T_u$ and $T_v$. Then, we substitute $T_u$ and $T_v$ in equation (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{A}_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=t_k,\hfill \\ B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0=t_k.\hfill \end{array}\right.\end{array}$$(2) ) and calculate values $R(u)$ and $R(v)$.

The second step of this procedure involves the error estimate. To estimate the error of the resistances, we applied functions:(24) $$\begin{array}{c}\hfill \mathrm{\Delta }(R(u))=\Vert R(u)-R_1\Vert ,\mathrm{\Delta }(R(v))=\Vert R(v)-R_2\Vert .\end{array}$$(24)

The norms in (24(24) $$\begin{array}{c}\hfill \mathrm{\Delta }(R(u))=\Vert R(u)-R_1\Vert ,\mathrm{\Delta }(R(v))=\Vert R(v)-R_2\Vert .\end{array}$$(24) ) conform with the computational technique for the resistance errors used in practice. To estimate the temperature errors, we used system (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5) ) and equation (6(6) $$\begin{array}{c}\hfill P_{1}u=P_{2}v.\end{array}$$(6) ) as well as quantity $\overline{\mathrm{\Delta }}$ which is defined formula:(25) $$\begin{array}{c}\hfill \overline{\mathrm{\Delta }}=∥\sum _{j=0}^M{u}_j{(R{(u)}_k)}^j-\sum _{j=0}^L{v}_j{(R{(v)}_k)}^j∥,k=\overline{1,n}.\end{array}$$(25)

The verification is accepted as successful provided that each value of $\mathrm{\Delta }(R(u))$, $\mathrm{\Delta }(R(v))$ and $\overline{\mathrm{\Delta }}$ both with $\Vert T_u-T_0\Vert$ and $\Vert T_v-T_0\Vert$ are within acceptable limits and then the quantity $u_{\overline{{\mathit{\alpha }}_1}}$, $v_{\overline{{\mathit{\alpha }}_2}}$ complied with the requirements for a solution of the parametric identification problem. The proposed method for solving problem (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{A}_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=t_k,\hfill \\ B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0=t_k.\hfill \end{array}\right.\end{array}$$(2) ), (3(3) $$\begin{array}{c}\hfill A_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0.\end{array}$$(3) ) provided the basis for numerical method. The computational scheme of this method is as follows:

• Determining the polynomial degrees in system (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{A}_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=t_k,\hfill \\ B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0=t_k.\hfill \end{array}\right.\end{array}$$(2) ) via selecting linear independent columns in matrices $\overline{P_1}$ and $\overline{P_2}$ defined by formula (4(4) $$\begin{array}{c}\hfill \overline{P_1}=\left(\begin{array}{ccccc}{R}_{11}^m& R_{11}^{m-1}& \dots & R_{11}& 1\\ R_{12}^m& R_{12}^{m-1}& \dots & R_{12}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ R_{1n}^m& R_{1n}^{m-1}& \dots & R_{1n}& 1\end{array}\right)\overline{P_2}=\left(\begin{array}{ccccc}{R}_{21}^l& R_{21}^{l-1}& \dots & R_{21}& 1\\ R_{22}^l& R_{22}^{l-1}& \dots & R_{22}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ R_{2n}^l& R_{2n}^{l-1}& \dots & R_{2n}& 1\end{array}\right).\end{array}$$(4) ).

• Reducing system (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{A}_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=t_k,\hfill \\ B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0=t_k.\hfill \end{array}\right.\end{array}$$(2) ) to (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5) ). For this, we modify (3(3) $$\begin{array}{c}\hfill A_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0.\end{array}$$(3) ) eliminating linear dependent columns in matrices $\overline{P_1}$ and $\overline{P_2}$. Then we transform components of the vectors $u$ and $v$ respectively.

• Solving system (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5) ). This is done by applying an iterative process based upon (10(10) $$\begin{array}{c}\hfill x_{\mathit{\delta }}^{\mathit{\alpha }}=J_{\mathit{\alpha }}{f}_{\mathit{\delta }}.\end{array}$$(10) ) and (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ). Taking into account results of Theorems 4.3 and 4.4 and equation (15(15) $$\begin{array}{c}\hfill {\mathrm{\Delta }}_0(\mathit{\alpha })=\frac{\mathit{\delta }}{2\sqrt{\mathit{\alpha }}}.\end{array}$$(15) ), we choose certain values of parameters ${\mathit{\alpha }}_1$ and ${\mathit{\alpha }}_1$, and solve system (5(5) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_{1}u=T_{\mathit{\delta }},\hfill \\ P_{2}v=T_{\mathit{\delta }},\hfill \end{array}\right.\end{array}$$(5) ). If quantities of $({\mathrm{\Delta }}_0({\mathit{\alpha }}_k)-\frac{\mathit{\delta }}{2\sqrt{{\mathit{\alpha }}_k}})>0$ attain their minimum we stop the iterative process.

• Calculating values $T_u$, $T_v$, $R(u)$$R(v)$, quantities $\mathrm{\Delta }(R(u))$, $\mathrm{\Delta }(R(v))$ and $\overline{\mathrm{\Delta }}$. The values $T_u$, $T_v$ are obtained via substitution of $u_{\overline{{\mathit{\alpha }}_1}}$, $v_{\overline{{\mathit{\alpha }}_2}}$ in system (2(2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}{A}_m{R}_{1k}^m+A_{m-1}{R}_{1k}^{m-1}+\cdots +A_1{R}_{1k}+A_0=t_k,\hfill \\ B_l{R}_{2k}^l+B_{l-1}{R}_{2k}^{l-1}+\cdots +B_1{R}_{2k}+B_0=t_k.\hfill \end{array}\right.\end{array}$$(2) ). For obtaining values $R(u)$ and $R(v)$, we use equation (1(1) $$\begin{array}{c}\hfill \frac{R_1}{R_2}=\frac{R_{01}}{R_{02}}\frac{1+a_{1}t+a_2{t}^2+a_4{t}^4+a_6{t}^6}{1+b_{1}t+b_2{t}^2-100b_4{t}^3+b_4{t}^4},\end{array}$$(1) ). The quantities of $\mathrm{\Delta }(R(u))$, $\mathrm{\Delta }(R(v))$ and $\overline{\mathrm{\Delta }}$ are calculated according to (24(24) $$\begin{array}{c}\hfill \mathrm{\Delta }(R(u))=\Vert R(u)-R_1\Vert ,\mathrm{\Delta }(R(v))=\Vert R(v)-R_2\Vert .\end{array}$$(24) ) and (25(25) $$\begin{array}{c}\hfill \overline{\mathrm{\Delta }}=∥\sum _{j=0}^M{u}_j{(R{(u)}_k)}^j-\sum _{j=0}^L{v}_j{(R{(v)}_k)}^j∥,k=\overline{1,n}.\end{array}$$(25) ).

• Verifying results. This is done via comparative analysis of $\mathrm{\Delta }(R(u))$, $\mathrm{\Delta }(R(v))$, $\overline{\mathrm{\Delta }}$, $\Vert T_{\mathit{\delta }}-T_0\Vert$, $\Vert T_u-T_0\Vert$, $\Vert T_v-T_0\Vert$, $\Vert T_u-T_{\mathit{\delta }}\Vert$, $\Vert T_v-T_{\mathit{\delta }}\Vert$ with available levels of error.

• Calculating the experimental estimates of the coefficient errors.

To evaluate the effectiveness of the proposed approach, computational experiments were carried out both for the series of model functions and for the experimental data.

7. Computational results

In the experiments, the parametric identification problem was solved, values $T_u$, $T_v$ were obtained and their deviations from model functions $T_{\mathit{\delta }}$ and $T_0$ were determined. The model functions varied from the viewpoint of their affiliation to applicable tolerance limit, which are chosen according to metrological standards. In each series, several recalculations for each function were carried out. The computational experiment includes the following steps:

• Modelling of the initial functions. This stage is implemented when the experimental data are not used as initial and calculation is performed for the model functions. The computational experiment is carried out on $\left[T_1,T_2\right]$ we use the a uniform grid of $(m+1)$ points $T_2-T_1=hm$, and $t_k=T_1+(k-1)h$, $k=\overline{1,(m+1)}$. The values of $T_0$ coincide with the grid point $t_k$. The values of $T_{\mathit{\delta }}$ are simulated at each grid point $t_k$ as evenly distributed random variable in the $[t_k-\mathit{\delta };t_k+\mathit{\delta }]$. Values of $R_{1k}$ and $R_{2k}$ are simulated using equation (1(1) $$\begin{array}{c}\hfill \frac{R_1}{R_2}=\frac{R_{01}}{R_{02}}\frac{1+a_{1}t+a_2{t}^2+a_4{t}^4+a_6{t}^6}{1+b_{1}t+b_2{t}^2-100b_4{t}^3+b_4{t}^4},\end{array}$$(1) ).

• Solving of parametric identification problem with the initial data $T_{\mathit{\delta }}$, $R_{1k}$, $R_{2k}$, $\mathit{\delta }$. To do this, we use the computational scheme based on the regularization method.

• Verifying results. For this purpose, we model $T_u$, $T_v$, $R(u)$, $R(v)$ and calculate the values $\mathrm{\Delta }(R(u))$, $\mathrm{\Delta }(R(v))$, $\overline{\mathrm{\Delta }}$, $\Vert T_{\mathit{\delta }}-T_0\Vert$, $\Vert T_u-T_0\Vert$, $\Vert T_v-T_0\Vert$, $\Vert T_u-T_{\mathit{\delta }}\Vert$, $\Vert T_v-T_{\mathit{\delta }}\Vert$.

• Calculating average values of coefficients and degrees. Computing the experimental estimates of coefficient errors.

The results of the numerical experiment for several model functions and for some experimental data are illustrated in the figures below. Each figure illustrates the graphs of functions $(T_{\mathit{\delta }}-T_0)$, $(T_u-T_0)$ and $(T_v-T_0)$. For the temperature error function, the same notation is used in all figures. The deviation of $T_{\mathit{\delta }}$ from $T_0$ is described by function $(T_{\mathit{\delta }}-T_0)$. The temperature error function for the first device is described by function $(T_u-T_0)$ and for the second device, it corresponds to $(T_v-T_0)$, respectively. Circle-marked lines correspond to applicable tolerance limit for the first resistance thermometer and asterisk-marked lines correspond to applicable tolerance limit for the second resistance thermometer, respectively. We carry out numerical experiment for different temperature ranges, but it is difficult to illustrate the result, when device is out of order. Therefore, in most cases, figures illustrate the graphs of functions in part of temperature range.

Example 1

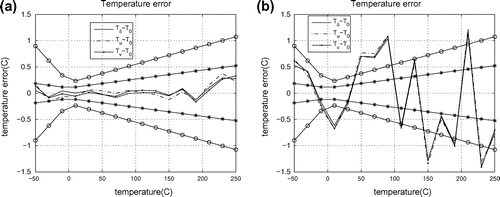
The subject of the performed series of experiments was the model temperature functions provided that both resistance thermometers are in good order and measurement results of both devices are true. Figure 1(a) shows the temperature errors in case when the model functions $T_{\mathit{\delta }}$ were within tolerance limits and Figure 1(b) illustrates the temperature errors in case when model functions $T_{\mathit{\delta }}$ were beyond tolerance limits.

Figure 1. Temperature error functions obtained on the basis of model data and corresponded to the situation when measurement results of both devices are true. (a) Example 1a complies with the situation when the model functions were within tolerance limits and (b) Example 1b corresponds to the situation when $T_{\mathit{\delta }}$ were beyond tolerance limits.

Example 2

This series of experiments corresponded to the situation when one of the devices out of order and values measured by this device are wrong. To simulate it, additive noise was introduced into one of the resistance functions. The quantity additional resistance error is simulated as evenly distributed random value in $[-h;h]$. The level of $h$ is defined arbitrarily. Both Figure 2(a) and 2(b) show the temperature errors in case when $h=0.05$.

Figure 2. Temperature error functions provided that one of resistance thermometers is out of order. The quantity of the additional error is simulated as evenly distributed random value in $[-0.05;0.05]$. Example 2a complies with the situation when first device is out of order. Example 2b corresponds to the same situation for the second device.

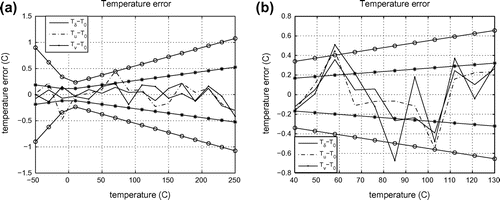
Figure 3. Temperature error functions obtained on the basis of model data and corresponded to the situation when resistance thermometers are out of order. Example 3a corresponds the calculating of the temperature errors which was performed in whole temperature ranges. Example 3b corresponds the similar calculating in one part of temperature range.

Example 3

This series of experiments corresponded to the situation when both resistance thermometers are out of order and the measurement results of both devices were wrong. Simulation of the initial data was carried out in the same manner, that is in the case of the wrong measurements of one device. Figure 3 shows the graphs of temperature errors obtained in different measuring ranges.

Example 4

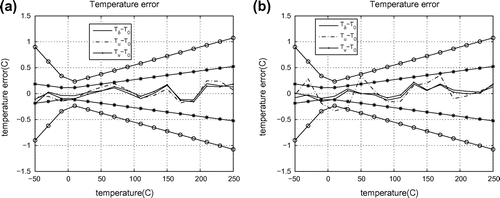
This series used the experimental data. Figure 4(a) shows the temperature errors provided that both resistance thermometers are in order. Figure 4(b) corresponds to the temperature errors provided that the first device is out of order. The temperature error function for this device is described by function $(T_u-T_0)$.

Figure 4. Temperature error functions obtained on the basis of experimental data. Example 4a complies with the situation when the both termometers are in order. Example 4b corresponds the situation when the first device is out of order.

To evaluate the stability of the solutions and estimate the errors in each series of the experiment, we calculated the quantities of basic values. Average values of these quantities obtained in each series of experiments are shown in Table 1.

Table 1. Experimental estimates of temperature deviations.

	Example 1a	Example 1b	Example 2a	Example 2b	Example 3a	Example 4a	Example 4b
$\overline{\mathrm{\Delta }}$	0.1098	0.1100	0.2724	0.3892	0.4020	0.1106	0.3476
$\Vert T_u-T_{\mathit{\delta }}\Vert$	0.1223	0.1227	0.2623	0.1221	0.2879	0.1229	0.2059
$\Vert T_v-T_{\mathit{\delta }}\Vert$	0.0842	0.0843	0.0843	0.2198	0.3507	0.0849	0.0850

The results of the experiments confirm the order-optimality of the proposed regularized method. The approach based on the regularized method allows it to obtain stable solutions to a parametric identification problem and to calculate temperature values with guaranteed accuracy. This property of the solution of the parametric identification problem is confirmed by the theoretical estimates. The results of the experiments show the independence of the temperature errors on temperature ranges and the tolerance limits of the measured temperature under condition that the resistance values are given reasonably exact. This property shows the stability of the measurements and the affiliation of the device to tolerant class.

8. Conclusions

The model describing the dependence of the temperature on the resistances for the self-calibration device is investigated. This model is represented as a system with unknown parameters. The regularization method for solving a parametric identification problem yields approximate solutions with guaranteed accuracy. This estimate is exact with respect to the order. The model verification and the stability of the obtained temperature values were evaluated by a computational experiment both for the series of model functions and for the experimental data. Results of numerical experiments for both model and experimental data are in a good agreement with the theoretical estimates for the proposed regularization method and indicate advantages of our method to calculate temperature values from measured resistances.

The main advantage is possibility to calculate temperature values with guaranteed accuracy only under condition that the resistance values are given reasonably exact. This condition corresponded to the situation when both resistance thermometers are in good order and measurement results of both devices are true. The additional advantage for this method is its independence on temperature ranges and the tolerance limits of the measured temperature. The obtained results provided the basis for creation of the self-test method. It allows to check the condition of metrology for the tools. This method of solving the self-test problem has been used for the first time.

Acknowledgements

The author would like to thank colleagues of the South Ural State University for their support and valuable comments.

Additional information

Funding

This research was supported by Electrical Power Engineering and Electrical Engineering Laboratory, South Ural State University under contract No. 2013243.