Quasi-optimal Tikhonov penalization and parameterization coarseness in space-dependent function estimation

Abstract

The determination of space-dependent functions from boundary measurements or inner pointwise measurements is ill-posed inverse problems that require regularization tools to be stabilized. Among numerous regularization strategies, the Tikhonov penalization is one of the most used in the field of space-dependent function estimation. Its efficient use relies on the Tikhonov parameter value for which search is time consuming although necessary, especially in the field of nonlinear inversion. Other strategies, such as appropriate parameterization, have recently proven to be very efficient to cope with the ill-posedness of such problems. This paper shows that the optimal Tikhonov parameter is almost independent of the mesh used to project the functions to be retrieved. As a consequence, this value should be seeked using a coarse mesh even though reconstructions could further be done on finer meshes. This conclusion is validated by numerical means.

Keywords:

• inverse problem
• Tikhonov regularization
• Gauss–Newton
• finite element parameterization
• ill-posed problems

AMS Subject Classifications:

• 35R30
• 65F22

1. Introduction

The reconstruction of space-dependent functions from pointwise measurements belongs to inverse problems known to be difficult to be solved due to their ill-posed character. More specifically, the reconstruction of maps of radiative properties by illuminating a semi-transparent medium with near infrared radiation and measuring emerging radiation is by definition of the classical optical tomography inverse problem.

From a mathematical point of view, within the diffuse approximation framework in the frequency domain,[1] the geometry ($\mathcal{D}$) being fixed, the total inward flux ($I$) of the amplitude-modulated diffuse source at the frequency $\mathit{\nu }$ being known as well as the speed of light ($c$) in the medium, the knowledge of the space-dependent absorption ($\mathit{\kappa }$) and reduced scattering ($\mathit{\sigma }$) coefficients are sufficient to simulate the photon density distribution ($\mathit{\phi }$) in each location of the computational domain. Such modelling is the forward problem which is known to be well-posed mathematically.

Contrarily, the reconstruction of physical properties from the knowledge of photon density on sensors constitutes an inverse problem. Unfortunately, such a problem is ill-posed in the sense of Hadamard [2]. Hence, regularization must be used to stabilize the solution. Several regularization tools have been introduced in the field of optical tomography in these last decades among which the use of appropriate control space parameterization.[3–6] Dealing with matrix-based inversion, the Tikhonov regularization method, which is a popular method, consists in adding a penalization term to the cost function to be minimized; this method actually relies on a weight parameter that is to be determined very carefully since: (i) under-regularization leads to small cost functions at the end but at the price of highly fluctuating property maps; and (ii) over-regularization leads to stable property maps around priors, leading to biased solutions.[7]

In the following, the optimal Tikhonov parameter, ${\mathit{\vartheta }}^{\ast }$, is defined as the one that minimizes the distance between the actual solution and the noise-free solution. This distance can be computed with $E(\mathit{\vartheta })=\frac{\Vert {\mathit{\gamma }}_{\mathit{\vartheta }}-\overline{\mathit{\gamma }}\Vert }{\Vert \overline{\mathit{\gamma }}\Vert }$, where $\mathit{\vartheta }$ is the Tikhonov parameter, ${\mathit{\gamma }}_{\mathit{\vartheta }}$ is the solution given for the Tikhonov parameter $\mathit{\vartheta }$, $\overline{\mathit{\gamma }}$ is the exact solution and $\Vert ·\Vert$ is a norm. The point is that one cannot, in practice, compute the optimal Tikhonov parameter, $\overline{\mathit{\gamma }}$ being unknown. However, numerous heuristic methods have been introduced to compute quasi-optimal Tikhonov parameters. Some methods use the assumed to be known standard deviation such as in the discrepancy principle.[7, 8] Others [9–11] use less information about the noise properties, such as, for instance, the generalized cross validation (GCV), or even no information about the noise level present in the system, such as the well-known and controversial L-curve. The methods used to find the optimal Tikhonov parameter or at least a quasi-optimal parameter is beyond of the scope of this paper. Moreover, even though methods that do not use error informations are widely used for solving practical problems in various engineering areas, let us recall that in general the L-curve method, for instance, because it does not rely on any noise information, is, as shown by [12, 13], not convergent and introduces a nonremovable bias.

In this paper, the diffuse optical tomography problem is formulated as a nonlinear least squares problem and solved by the Gauss–Newton method. Though this method has been widely used in these last years to solve this inverse problem,[14–19] it is worth mentioning that the Gauss–Newton method is only locally convergent, and this is so, only when the initial guess is not too far from the minimum and the inverse problem is mildly nonlinear.[20] This means that some choices of the initial guess far from the solution lead to inaccurate results whatever the regularization method used. To illustrate this property, the dependence of the accuracy of the numerical solution with respect to the initial guess is discussed in the numerical results section. Although the study of the initial guess of the solution on the convergence of the optimizer is not the main issue of this paper, it should be noted that globally convergent methods, which overcome the major drawback of the Gauss–Newton optimizer, have been developed and applied to the diffuse optical tomography problem.[21–26]

The remainder of the paper will show that the optimal Tikhonov parameter is almost independent of the mesh coarsening used for the parameterization. This assertion is demonstrated theoretically and verified numerically based on two different under-determined inverse problems of space-dependent function estimation: a linear inverse heat conduction problem of flux estimation and a nonlinear diffuse optical tomography problem. The studies are performed on synthetic data and therefore the errors on reconstructions could be calculated. For this reason, one can somehow consider that the proposed approach is heuristic.

Before dealing with the nonlinear inverse problem of diffuse optical tomography (which is the main objective of this paper), a steady-state two-dimensional (2D) inverse heat conduction problem of space-dependent heat flux estimation is dealt with in Section 2. Such inverse problem has recently been studied.[27–30] This space-dependent heat flux estimation problem is highly different from the diffuse optical tomography problem because (i) it deals with a different physics: heat conduction; (ii) measurements are performed within the domain rather than on a boundary; (iii) the heat flux on a boundary is the function to be retrieved rather than physical properties within the medium; and (iv) the forward problem is linear with respect to the coefficients involved in the space-dependent finite element heat flux parameterization. The interest of this first study is above all to illustrate that the quasi-independence of the optimal Tikhonov parameter with the control space parameterization is found in a less heuristic way since only measurement errors are used in the whole process. Indeed, the determination of the Tikhonov parameter can be performed straightforwardly through the knowledge of measurement errors only. In this case, the discrepancy principle is the major recipe to compute the parameters involved in the space-dependent heat flux parameterization. It is known that this method gives satisfactory results and other methods found in the literature may give a Tikhonov parameter closer to the optimal one [9–11], but such consideration is out of the scope of this paper. Moreover, the statement of this article is also validated on this linear inverse problem in the sense of the optimal Tikhonov parameter ${\mathit{\vartheta }}^{\ast }$ previously defined as $argminE(\mathit{\vartheta })$.

Section 3 deals with the nonlinear diffuse optical tomography problem. The forward model of light propagation in a highly diffuse medium is first presented along with the inverse problem settings. First- and second-order cost function derivatives used afterwards in optimization are then detailed. The finite element parameterization of, on the one side, the state and its derivative and, on the other side, the properties to be retrieved, is presented. The optimization is then written down based on the proposed finite dimensional control space. This section then presents the most usual Tikhonov regularization and proves that, under some weak hypothesis, the optimal Tikhonov parameter is quasi-independent of the dimension of the control space. A numerical verification is performed on the nonlinear diffuse optical tomography problem based on the theoretical demonstration.

Overall, the conclusion is that, when dealing with nonlinear inverse problems demanding heavy computational time, the determination of the Tikhonov parameter, whatever the method chosen among those of [31] for instance, should be preferably performed on a highly coarse mesh in order to lower computational time.

2. Space-dependent heat flux estimation

2.1. Problem statement

In this first study, a linear steady-state 2D inverse heat conduction problem is considered to illustrate the quasi-independence of the Tikhonov parameter with mesh coarsening used for the finite element projection of the quantity of interest. In the present case, already studied in different contexts,[27–30] a space-dependent heat flux on a part of the boundary is to be retrieved from pointwise measurements within a bounded domain $\mathcal{D}={[0,1]}^2$. This application is treated first because of its simplicity: as a matter of fact, the response being linear with respect to the input flux,[30] the cost function to be minimized is purely quadratic, and specific tools such as the singular value decomposition coupled with the maximum discrepancy principle [7, 8] can be used to compute straightforwardly a quasi-optimal Tikhonov parameter. In this case, one can speak of ‘Tikhonov parameter found according to the discrepancy principle’. It is shown elsewhere [11] that this quasi-optimal Tikhonov parameter is likely to be close to the optimal one.

Homogeneous steady-state heat conduction without source term but with mixed boundary conditions is described such that:(1) $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}-\mathrm{\Delta }T=0\hfill & & (x_1,x_2)\in \mathcal{D}=]0,1[\times ]0,1[\hfill \\ T=0\hfill & & x_1=0\hfill \\ \mathrm{\nabla }T·\mathbf{n}=0\hfill & & x_2=0\text{and}{x}_2=1\hfill \\ -\mathit{\lambda }\mathrm{\nabla }T·\mathbf{n}=\mathit{\phi }\hfill & & x_1=1\hfill \end{array}\right.\end{array}$$(1)

where $T$ is the temperature, $\mathit{\lambda }$ is the thermal conductivity and $\mathit{\phi }$ is the space-dependent heat flux. The forward problem consists in solving Equation (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}-\mathrm{\Delta }T=0\hfill & & (x_1,x_2)\in \mathcal{D}=]0,1[\times ]0,1[\hfill \\ T=0\hfill & & x_1=0\hfill \\ \mathrm{\nabla }T·\mathbf{n}=0\hfill & & x_2=0\text{and}{x}_2=1\hfill \\ -\mathit{\lambda }\mathrm{\nabla }T·\mathbf{n}=\mathit{\phi }\hfill & & x_1=1\hfill \end{array}\right.\end{array}$$(1) ) for $T$ assuming $\mathit{\lambda }$ and $\mathit{\phi }(x_2)$ are known. In contrast, the inverse problem consists in estimating the space-dependent heat flux $\mathit{\phi }(x_2)$ on the basis of suitable measurement data ${\breve{T}}^l$ in $\mathcal{D}$, under the assumption that the value of $\mathit{\lambda }$ is known.

Let us consider $k$ inner pointwise measurements $(x_1^l,x_2^l)$, $l=1,\dots ,k$. Discrepancies between predictions $T^l=T(x_1^l,x_2^l)$ and associated measurements ${\breve{T}}^l$, $l=1,\dots ,k$, are integrated to the cost function:(2) $$\begin{array}{c}\hfill j_{\mathit{\vartheta }}(\mathit{\phi })=\mathcal{J}(T)+{\mathcal{J}}^{+}(\mathit{\phi })={∥T-\breve{T}∥}_{{\mathbb{R}}^k}^2+\mathit{\vartheta }{∥\mathit{\varphi }∥}_{{\mathbb{R}}^{\mathrm{\Xi }}}^2\end{array}$$(2)

with ${∥a∥}_{{\mathbb{R}}^k}^2={\sum }_{l=1}^k{a}_l^2$ and ${∥a∥}_{{\mathbb{R}}^{\mathrm{\Xi }}}^2={\sum }_{l=1}^{\mathrm{\Xi }}{a}_l^2$. $\mathit{\vartheta }$ is the Tikhonov parameter to be searched according to the noise level $\mathit{ϵ}$. $\mathit{\varphi }$ is the vector obtained after finite element parameterization of the heat flux $\mathit{\phi }$, that is $\mathit{\phi }(x_2)={\sum }_{l=1}^{\mathrm{\Xi }}{\mathrm{\Theta }}_l(x_2)\mathit{\phi }({x_2}_l)={\sum }_{l=1}^{\mathrm{\Xi }}{\mathrm{\Theta }}_l(x_2){\mathit{\varphi }}_l$ where ${\left({\mathrm{\Theta }}_l\right)}_{l=1}^{\mathrm{\Xi }}$ is a finite element basis of $[0,1]$. The singular value decomposition of the matrix $A:\mathit{\varphi }\in {\mathbb{R}}^{\mathrm{\Xi }}\mapsto T\in {\mathbb{R}}^k$ such that $A=W\mathrm{\Lambda }{V}^t$ enables us to rewrite the cost function such that:(3) $$\begin{array}{c}\hfill j_{\mathit{\vartheta }}(\mathit{\xi })={∥\mathrm{\Lambda }\mathit{\xi }-\breve{\mathit{\xi }}∥}_{{\mathbb{R}}^k}^2+\mathit{\vartheta }{∥\mathit{\xi }∥}_{{\mathbb{R}}^{\mathrm{\Xi }}}^2\end{array}$$(3)

where $\mathit{\xi }=V^t\mathit{\varphi }$ and $\breve{\mathit{\xi }}=W^t\breve{T}$. With such a decomposition, the solution of ${\mathit{\xi }}_{\mathit{\vartheta }}^{\ast }=argmin{j}_{\mathit{\vartheta }}(\mathit{\xi })$ is given in terms of singular values of $A$, ${\left({\mathit{\eta }}_i\right)}_{i=1}^{\mathrm{\Xi }}$:(4) $$\begin{array}{c}\hfill {{\mathit{\xi }}_{\mathit{\vartheta }}^{\ast }}_i=\frac{{\mathit{\eta }}_i{\breve{\mathit{\xi }}}_i}{{\mathit{\eta }}_i^2+\mathit{\vartheta }}\forall i=1,\dots ,\mathrm{\Xi }\end{array}$$(4)

On the other hand, the discrepancy principle leads to determine ${\mathit{\xi }}_{\mathit{\vartheta }}^{\ast }$ such that:(5) $$\begin{array}{c}\hfill {∥\mathrm{\Lambda }{\mathit{\xi }}_{\mathit{\vartheta }}^{\ast }-\breve{\mathit{\xi }}∥}_{{\mathbb{R}}^k}^2={\mathit{ϵ}}^2\end{array}$$(5)

where $\mathit{ϵ}$ is the sum of variances of noise on all sensors, i.e. ${\mathit{ϵ}}^2={\sum }_{l=1}^k{\mathit{ϵ}}_l^2$. Combining this latter relationship with Equation (4(4) $$\begin{array}{c}\hfill {{\mathit{\xi }}_{\mathit{\vartheta }}^{\ast }}_i=\frac{{\mathit{\eta }}_i{\breve{\mathit{\xi }}}_i}{{\mathit{\eta }}_i^2+\mathit{\vartheta }}\forall i=1,\dots ,\mathrm{\Xi }\end{array}$$(4) ) leads to determine the quasi-optimal Tikhonov parameter found according to the discrepancy principle, ${\mathit{\vartheta }}_{\text{dp}}^{\ast }$ solution of:(6) $$\begin{array}{c}\hfill R({\mathit{\vartheta }}_{\text{dp}}^{\ast })=\sum _{i=1}^k{\left(\frac{{\mathit{\vartheta }}_{\text{dp}}^{\ast }{\breve{\mathit{\xi }}}_i}{{\mathit{\eta }}_i^2+{\mathit{\vartheta }}_{\text{dp}}^{\ast }}\right)}^2-{\mathit{ϵ}}^2=0\end{array}$$(6)

Figure 1. Distance from the solution to the target $E(\mathit{\vartheta })$ as a function of the Tikhonov parameter $\mathit{\vartheta }$, for three control space dimensions $\mathrm{\Xi }$ equal to $7$, $15$ and $20$. It is seen that ${\mathit{\vartheta }}^{\ast }=argminE(\mathit{\vartheta })$ is independent of $\mathrm{\Xi }$. The quasi-optimal Tikhonov parameter found according to the discrepancy principle has also been added.

2.2. Numerical results

The numerical study shows that the solution of Equation (6(6) $$\begin{array}{c}\hfill R({\mathit{\vartheta }}_{\text{dp}}^{\ast })=\sum _{i=1}^k{\left(\frac{{\mathit{\vartheta }}_{\text{dp}}^{\ast }{\breve{\mathit{\xi }}}_i}{{\mathit{\eta }}_i^2+{\mathit{\vartheta }}_{\text{dp}}^{\ast }}\right)}^2-{\mathit{ϵ}}^2=0\end{array}$$(6) ) is almost independent of the dimension $\mathrm{\Xi }$ used in the parameterization of the flux. To do so, let the synthetic data be generated with the flux $\overline{\mathit{\phi }}(x_2)={\mathit{\phi }}_0\left(sin\left(\frac{\mathit{\pi }{x}_2}{2}\right)-1\right)$, ${\mathit{\phi }}_0=-{10}^4$ W/m${}^2$ and the thermal conductivity $\mathit{\lambda }=30$ W/m K. Five pointwise temperature measurements ($k=5$) are performed at locations $x_1=0.9$, and $x_2=0.1$, $0.3$, $0.5$, $0.7$ and $0.9$. The data are then perturbated according to a Gaussian white noise with variance ${\mathit{ϵ}}_l^2$ ranging from ${10}^{-4}$ to ${10}^{-1}$ K${}^2$, $\forall l=1,\dots ,k$, yielding to $\breve{T}$. The finite element method is used to solve the forward problem Equation (1(1) $$\begin{array}{c}\hfill \left\{\begin{array}{ccc}-\mathrm{\Delta }T=0\hfill & & (x_1,x_2)\in \mathcal{D}=]0,1[\times ]0,1[\hfill \\ T=0\hfill & & x_1=0\hfill \\ \mathrm{\nabla }T·\mathbf{n}=0\hfill & & x_2=0\text{and}{x}_2=1\hfill \\ -\mathit{\lambda }\mathrm{\nabla }T·\mathbf{n}=\mathit{\phi }\hfill & & x_1=1\hfill \end{array}\right.\end{array}$$(1) ) based on a regular mesh of the bounded domain $\mathcal{D}$ and a discretization of the temperature $T$ with Lagrange ${\mathcal{P}}_1$ elements. The regular grid associated to $\mathcal{D}$ is chosen sufficiently fine to ensure that errors due to the approximation method are negligible when compared to measurement errors. The basis functions ${\left({\mathrm{\Theta }}_l\right)}_{l=1}^{\mathrm{\Xi }}$ used in the parameterization of the unknown flux $\mathit{\phi }$ are also continuous first-order Lagrange functions, i.e. linear functions per element satisfying ${\mathrm{\Theta }}_l({x_2}_p)=1$ if and only if $p=l$.

Table 1 presents the quasi-optimal Tikhonov parameter ${\mathit{\vartheta }}_{\text{dp}}^{\ast }$ for several uniform Lagrange parameterizations with $\mathrm{\Xi }$ ranging from 7 to 25, and several variances of noise in the data, from ${\mathit{ϵ}}_l^2={10}^{-4}$ to ${\mathit{ϵ}}_l^2={10}^{-1}$. It is seen that for a given level of noise, the Tikhonov parameter ${\mathit{\vartheta }}_{\text{dp}}^{\ast }$ depends only very slightly on the flux discretization. The small fluctuations that remain may come from all numerical approximations: finite element computations to build the state matrix $A$, the singular value decomposition $W\mathrm{\Lambda }{V}^t=A$ and the numerical optimization when solving the nonlinear problem Equation (6(6) $$\begin{array}{c}\hfill R({\mathit{\vartheta }}_{\text{dp}}^{\ast })=\sum _{i=1}^k{\left(\frac{{\mathit{\vartheta }}_{\text{dp}}^{\ast }{\breve{\mathit{\xi }}}_i}{{\mathit{\eta }}_i^2+{\mathit{\vartheta }}_{\text{dp}}^{\ast }}\right)}^2-{\mathit{ϵ}}^2=0\end{array}$$(6) ), ${\mathit{\vartheta }}_{\text{dp}}^{\ast }=argminR({\mathit{\vartheta }}_{\text{dp}})$. Moreover, it is worth noting the linear dependency of ${\mathit{\vartheta }}_{\text{dp}}^{\ast }$ with the noise variance ${\mathit{ϵ}}_l^2$ (Table 1).

Figure 1 presents the distance from the actual solution to the expected target distribution, $E(\mathit{\vartheta })=\frac{\Vert {\mathit{\phi }}_{\mathit{\vartheta }}-\overline{\mathit{\phi }}\Vert }{\Vert \overline{\mathit{\phi }}\Vert }$, as a function of the Tikhonov parameter $\mathit{\vartheta }$, for the variance noise ${\mathit{ϵ}}_l={10}^{-3}$, $\forall l$. The norm was chosen to be defined as $\Vert \mathit{\phi }\Vert ={\left({\int }_{x_1=1}{\mathit{\phi }}^2\mathrm{d}{x}_2\right)}^{\frac{1}{2}}$. Results obtained for other noise variances gave similar curves to the one given in Figure 1 and are thus not presented here. Figure 1 shows that for low Tikhonov parameters $\mathit{\vartheta }$, the distance from the solution to the target decreases when the control space dimension $\mathrm{\Xi }$ decreases. On the contrary, for large Tikhonov parameters, the distance from the solution to the target is independent of the control space dimension. In between, there is a plateau, and the minimum point is found to be independent of $\mathrm{\Xi }$.

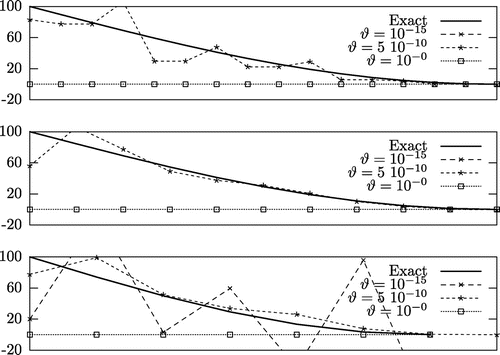
In order to illustrate the effect of regularization, different reconstructions are presented in Figure 2. This figure shows how parameterization influences the reconstructions.[5, 6] It is also observed from Figure 2 that despite the very limited number of steady-state measurements (a study on the optimal number and location of inner pointwise measurements is out of the scope of this paper), the space-dependent heat flux could be retrieved for appropriate Tikhonov regularization combined with appropriate control space parameterization.

Table 1. Value of the Tikhonov parameter ${\mathit{\vartheta }}_{\text{dp}}^{\ast }$ solution of (6(6) $$\begin{array}{c}\hfill R({\mathit{\vartheta }}_{\text{dp}}^{\ast })=\sum _{i=1}^k{\left(\frac{{\mathit{\vartheta }}_{\text{dp}}^{\ast }{\breve{\mathit{\xi }}}_i}{{\mathit{\eta }}_i^2+{\mathit{\vartheta }}_{\text{dp}}^{\ast }}\right)}^2-{\mathit{ϵ}}^2=0\end{array}$$(6) ) for different discretizations and different noise magnitudes.

$\mathrm{\Xi }$$\backslash$${\mathit{ϵ}}_l^2$	${10}^{-4}$	${10}^{-3}$	${10}^{-2}$	${10}^{-1}$
$7$	$4.189\times {10}^{-11}$	$4.198\times {10}^{-10}$	$4.297\times {10}^{-9}$	$5.493\times {10}^{-8}$
$10$	$5.246\times {10}^{-11}$	$5.257\times {10}^{-10}$	$5.374\times {10}^{-9}$	$6.622\times {10}^{-8}$
$15$	$4.240\times {10}^{-11}$	$4.248\times {10}^{-10}$	$4.330\times {10}^{-9}$	$5.151\times {10}^{-8}$
$20$	$4.042\times {10}^{-11}$	$4.049\times {10}^{-10}$	$4.113\times {10}^{-9}$	$4.683\times {10}^{-8}$

Figure 2. Reconstructions ${\mathit{\phi }}_{\mathit{\vartheta }}(x_2)$ for $\mathrm{\Xi }=15$ (top), $\mathrm{\Xi }=10$ (middle) and $\mathrm{\Xi }=7$ (bottom) for under-regularization ($\mathit{\vartheta }={10}^{-15}$), over-regularization ($\mathit{\vartheta }=1$) and appropriate regularization ($\mathit{\vartheta }=5{10}^{-10}\approx {\mathit{\vartheta }}^{\ast }$). Note that points for $\mathrm{\Xi }=15$ and $\mathrm{\Xi }=10$ (over-parameterization) with $\mathit{\vartheta }={10}^{-15}$ (under-regularization) are not presented because of divergence. The noise variance ${\mathit{ϵ}}_l^2=0.001$ was used after generating the synthetic data.

3. Optical tomography

3.1. Forward model and inversion setting

Solving the optical tomography inverse problem is usually based on the minimization of a cost function which depends on the discrepancy between some measurements and the related predictions, the latter being a solution of the forward model which is, in the present case, based on the 2D diffuse approximation. The complex photon density, $\mathit{\phi }:\mathcal{D}\mapsto \mathbb{C}$, is mathematically described by the diffuse approximation model expressed in the frequency domain [1]:(7) $$\begin{array}{cc}\hfill -\mathrm{\nabla }·\left({\left[2\left(\mathit{\kappa }+\mathit{\sigma }\right)\right]}^{-1}\mathrm{\nabla }\mathit{\phi }\right)+\left(\mathit{\kappa }+\frac{2\mathit{\pi }i\mathit{\nu }}{c}\right)\mathit{\phi }& =0in\mathcal{D}\hfill \end{array}$$(7) (8) $$\begin{array}{cc}\hfill \mathit{\phi }+\frac{A}{2{\mathit{\pi }}^{-1}}{\left[2(\mathit{\kappa }+\mathit{\sigma })\right]}^{-1}\mathrm{\nabla }\mathit{\phi }·\mathbf{n}& =\frac{I}{{\mathit{\pi }}^{-1}}{1}_{\left[\mathit{\zeta }\in \mathit{\partial }{\mathcal{D}}_s\right]}on\mathit{\partial }\mathcal{D}\hfill \end{array}$$(8)

where $\mathit{\kappa }$ and $\mathit{\sigma }$ are the absorption and reduced scattering coefficients, respectively, $c$ is the speed of light in the medium, $\mathbf{n}$ is the unit outward normal vector, $I$ is the total inward flux of the amplitude-modulated diffuse source at the frequency $\mathit{\nu }$, $1_{[·]}$ denotes the indicator function, $\mathit{\partial }{\mathcal{D}}_s$ depicts the light source location, $i$ is the imaginary unit and $A$ is the parameter which characterizes the reflection at the boundary and can be derived from Fresnel’s law if specular reflection is considered [18] or from experimental set-ups.[32]

The forward problem consists in solving Equations (7(7) $$\begin{array}{cc}\hfill -\mathrm{\nabla }·\left({\left[2\left(\mathit{\kappa }+\mathit{\sigma }\right)\right]}^{-1}\mathrm{\nabla }\mathit{\phi }\right)+\left(\mathit{\kappa }+\frac{2\mathit{\pi }i\mathit{\nu }}{c}\right)\mathit{\phi }& =0in\mathcal{D}\hfill \end{array}$$(7) )–(8(8) $$\begin{array}{cc}\hfill \mathit{\phi }+\frac{A}{2{\mathit{\pi }}^{-1}}{\left[2(\mathit{\kappa }+\mathit{\sigma })\right]}^{-1}\mathrm{\nabla }\mathit{\phi }·\mathbf{n}& =\frac{I}{{\mathit{\pi }}^{-1}}{1}_{\left[\mathit{\zeta }\in \mathit{\partial }{\mathcal{D}}_s\right]}on\mathit{\partial }\mathcal{D}\hfill \end{array}$$(8) ) for the photon density $\mathit{\phi }$ assuming the absorption coefficient $\mathit{\kappa }$, the reduced scattering coefficient $\mathit{\sigma }$, the location of the light source $\mathit{\partial }{\mathcal{D}}_s$ and values of $\mathit{\nu }$, $c$, $A$ and $I$ are known. In contrast, the inverse problem consists in estimating the space-dependent radiative properties $\mathit{\kappa }$ and $\mathit{\sigma }$ on the basis of photon density measurements $\breve{\mathit{\phi }}$ on $\mathit{\partial }\mathcal{D}$, under the assumption that the location of the light source $\mathit{\partial }{\mathcal{D}}_s$ and values of $\mathit{\nu }$, $c$, $A$ and $I$ are known.

More specifically, the forward model leads to compute the state $\mathit{\phi }$ that depends on radiative properties $\mathit{\gamma }=(\mathit{\kappa },\mathit{\sigma })$. The difference (in the least squares sense) between this density and the measured one is integrated to the cost function to be minimized $j(\mathit{\gamma })=\mathcal{J}(\mathit{\phi })$:(9) $$\begin{array}{c}\hfill \mathcal{J}(\mathit{\phi })=\frac{1}{2}\sum _{k=1}^K\sum _{d=1}^D{\left|\frac{{\mathit{\phi }}_{(k;d)}-{\breve{\mathit{\phi }}}_{(k;d)}}{{\breve{\mathit{\phi }}}_{(k;d)}}\right|}^2\end{array}$$(9)

where the index $k$ defines the source (test) number and the index $d$ defines the detection number. The solution of the inverse problem requires an optimization problem formulation of the kind: ‘Find the functions ${\mathit{\kappa }}^{\ast }(\mathbf{x})$ and ${\mathit{\sigma }}^{\ast }(\mathbf{x})$ such that $j({\mathit{\kappa }}^{\ast },{\mathit{\sigma }}^{\ast })=minj(\mathit{\kappa },\mathit{\sigma })$’.

3.2. Cost function derivative

In order to derive the Gauss–Newton algorithm, one first needs to recall basic definitions of directional derivatives. Following,[33] let us denote the point $(\mathit{\kappa },\mathit{\sigma })=\mathit{\gamma }\in {\mathrm{\Lambda }}^2\subset {[L_2(\mathcal{D})]}^2$ and directions $\mathit{\eta }$ and $\mathit{\zeta }$$\in \mathrm{\Lambda }$. The directional derivative of the state $\mathit{\phi }$ at point $\mathit{\gamma }$ towards $\mathit{\eta }$ is(10) $$\begin{array}{c}\hfill {\mathit{\phi }}^{\prime }(\mathit{\gamma };\mathit{\eta }):=\underset{\mathit{\epsilon }\to 0^{+}}{lim}\frac{\mathit{\phi }(\mathit{\gamma }+\mathit{\epsilon }\mathit{\eta })-\mathit{\phi }(\mathit{\gamma })}{\mathit{\epsilon }}\end{array}$$(10)

An analogous definition can be stated for the directional derivative of the cost function along with its second-order directional derivative such that:(11) $$\begin{array}{c}\hfill j^{″}(\mathit{\gamma };\mathit{\eta },\mathit{\zeta }):=\underset{\mathit{\epsilon }\to 0^{+}}{lim}\frac{j^{\prime }(\mathit{\gamma }+\mathit{\epsilon }\mathit{\zeta };\mathit{\eta })-j^{\prime }(\mathit{\gamma };\mathit{\eta })}{\mathit{\epsilon }}\end{array}$$(11)

Next, the operators involved in Newton’s method are extracted through the following equations:(12) $$\begin{array}{cc}& j^{\prime }(\mathit{\gamma };\mathit{\eta })={\left(\mathrm{\nabla }j(\mathit{\gamma }),\mathit{\eta }\right)}_{L_2(\mathcal{D})}\hfill \end{array}$$(12) (13) $$\begin{array}{cc}& j^{″}(\mathit{\gamma };\mathit{\eta },\mathit{\zeta })={\left({\mathrm{\nabla }}^{2}j(\mathit{\gamma })\mathit{\eta },\mathit{\zeta }\right)}_{L_2(\mathcal{D})}\hfill \end{array}$$(13)

with the inner product is defined as ${\left(\mathit{\gamma },\mathit{\eta }\right)}_{L_2(\mathcal{D})}={\int }_{\mathcal{D}}\mathit{\gamma }\mathit{\eta }\mathrm{d}\mathbf{x}$.

3.3. Parameterization

The solution of the optimization problem relies on iterative minimization algorithms for which control and state spaces must be finite in practice. To do so, let the functions to be determined $\mathit{\alpha }=\mathit{\kappa }$, $\mathit{\sigma }$ and $\mathit{\phi }$ be approximated using finite element basis functions ${\left({\mathit{\psi }}_{\mathit{\xi }}\right)}_{\mathit{\xi }=1}^{{\mathrm{\Xi }}_{\mathit{\alpha }}}$ and ${\left({\mathrm{\Theta }}_{\mathit{\xi }}\right)}_{\mathit{\xi }=1}^{{\mathrm{\Xi }}_{\mathit{\phi }}}$, respectively:(14) $$\begin{array}{cc}\hfill \mathit{\phi }(\mathbf{x})& =\sum _{\mathit{\xi }=1}^{{\mathrm{\Xi }}_{\mathit{\phi }}}{\mathrm{\Theta }}_{\mathit{\xi }}(\mathbf{x})\mathit{\phi }({\mathbf{x}}_{\mathit{\xi }})\hfill \end{array}$$(14) (15) $$\begin{array}{cc}\hfill \mathit{\alpha }(\mathbf{x})& ={\mathit{\alpha }}_{ap}\sum _{\mathit{\xi }=1}^{{\mathrm{\Xi }}_{\mathit{\alpha }}}{\mathit{\psi }}_{\mathit{\xi }}(\mathbf{x})\tilde{\mathit{\alpha }}({\mathbf{x}}_{\mathit{\xi }}),\mathit{\alpha }=\mathit{\kappa },\mathit{\sigma }\hfill \end{array}$$(15)

where it should be noted that the dimension of the control space ${\mathrm{\Xi }}_{\mathit{\alpha }}$ is chosen less or equal to that of the state space ${\mathrm{\Xi }}_{\mathit{\phi }}$. As a consequence, projections of functions of the expression (15(15) $$\begin{array}{cc}\hfill \mathit{\alpha }(\mathbf{x})& ={\mathit{\alpha }}_{ap}\sum _{\mathit{\xi }=1}^{{\mathrm{\Xi }}_{\mathit{\alpha }}}{\mathit{\psi }}_{\mathit{\xi }}(\mathbf{x})\tilde{\mathit{\alpha }}({\mathbf{x}}_{\mathit{\xi }}),\mathit{\alpha }=\mathit{\kappa },\mathit{\sigma }\hfill \end{array}$$(15) ) into the state functional space must be used to make the solution of the system (7(7) $$\begin{array}{cc}\hfill -\mathrm{\nabla }·\left({\left[2\left(\mathit{\kappa }+\mathit{\sigma }\right)\right]}^{-1}\mathrm{\nabla }\mathit{\phi }\right)+\left(\mathit{\kappa }+\frac{2\mathit{\pi }i\mathit{\nu }}{c}\right)\mathit{\phi }& =0in\mathcal{D}\hfill \end{array}$$(7) ) and (8(8) $$\begin{array}{cc}\hfill \mathit{\phi }+\frac{A}{2{\mathit{\pi }}^{-1}}{\left[2(\mathit{\kappa }+\mathit{\sigma })\right]}^{-1}\mathrm{\nabla }\mathit{\phi }·\mathbf{n}& =\frac{I}{{\mathit{\pi }}^{-1}}{1}_{\left[\mathit{\zeta }\in \mathit{\partial }{\mathcal{D}}_s\right]}on\mathit{\partial }\mathcal{D}\hfill \end{array}$$(8) ) possible. Moreover, parameters are adimensionalized with a priori properties ${\mathit{\alpha }}_{ap}={\mathit{\kappa }}_{ap},{\mathit{\sigma }}_{ap}$ such that $\mathit{\alpha }={\mathit{\alpha }}_{ap}\tilde{\mathit{\alpha }}$, in order to make both functions $\tilde{\mathit{\alpha }}=\varkappa (\mathbf{x}),\mathit{\varsigma }(\mathbf{x})$ to be searched about unity.

Let us note $\tilde{\mathit{\gamma }}=(\varkappa ,\mathit{\varsigma })$. Parameterization of radiative property map functions allows the construction of the Gauss–Newton matrix system which is written as:(16) $$\begin{array}{c}\hfill {\tilde{\mathrm{\nabla }}}^{2}j(\tilde{\mathit{\gamma }})\mathit{\delta }\tilde{\mathit{\gamma }}=-\tilde{\mathrm{\nabla }}j(\tilde{\mathit{\gamma }})\end{array}$$(16)

with state second-order derivatives assumed to be negligible when compared to first-order state derivatives and where vector $\tilde{\mathrm{\nabla }}j$ and matrix ${\tilde{\mathrm{\nabla }}}^{2}j$ represent continuous gradient $\mathrm{\nabla }j$ and approached Hessian matrix ${\mathrm{\nabla }}^{2}j$ of (12(12) $$\begin{array}{cc}& j^{\prime }(\mathit{\gamma };\mathit{\eta })={\left(\mathrm{\nabla }j(\mathit{\gamma }),\mathit{\eta }\right)}_{L_2(\mathcal{D})}\hfill \end{array}$$(12) ) and (13(13) $$\begin{array}{cc}& j^{″}(\mathit{\gamma };\mathit{\eta },\mathit{\zeta })={\left({\mathrm{\nabla }}^{2}j(\mathit{\gamma })\mathit{\eta },\mathit{\zeta }\right)}_{L_2(\mathcal{D})}\hfill \end{array}$$(13) ) decomposed on finite element basis functions ${\left({\mathit{\psi }}_{\mathit{\xi }}\right)}_{\mathit{\xi }=1}^{{\mathrm{\Xi }}_{\mathit{\alpha }}}$. Finally, the Gauss–Newton matrix system to be solved in order to update radiative properties at each iteration is expressed as:(17) $$\begin{array}{c}\hfill \mathfrak{R}\left({\mathcal{S}}^{\top }\overline{\mathcal{S}}\right)\mathit{\delta }\tilde{\mathit{\gamma }}=-\mathfrak{R}\left({\mathcal{S}}^{\top }\overline{\mathcal{R}}\right)\end{array}$$(17)

where ${\mathcal{S}}^{\top }$ and $\overline{\mathcal{S}}$ are the transposed and the conjugate of $\mathcal{S}$, respectively, and $\mathfrak{R}(·)$ denotes the real part of the imaginary vector or matrix. The forward model behaving nonlinearly with respect to properties $\tilde{\mathit{\gamma }}=(\varkappa ,\mathit{\varsigma })$, the increment $\mathit{\delta }{\tilde{\mathit{\gamma }}}^l={\tilde{\mathit{\gamma }}}^l-{\tilde{\mathit{\gamma }}}^{l-1}$ given by the solution of the Gauss–Newton Equation (17(17) $$\begin{array}{c}\hfill \mathfrak{R}\left({\mathcal{S}}^{\top }\overline{\mathcal{S}}\right)\mathit{\delta }\tilde{\mathit{\gamma }}=-\mathfrak{R}\left({\mathcal{S}}^{\top }\overline{\mathcal{R}}\right)\end{array}$$(17) ) is solved several times until convergence is attained. With the nomenclature defined earlier, the expressions for $\mathcal{S}$ and $\mathcal{R}$ are obtained such that:(18) $$\begin{array}{cc}\hfill \mathcal{S}& ={\left(\frac{{\left({\mathit{\phi }}_{\varkappa }^{\prime }\right)}_{(k;d)}^{\mathit{\xi }}}{\left|{\breve{\mathit{\phi }}}_{(k;d)}\right|},\frac{{\left({\mathit{\phi }}_{\mathit{\varsigma }}^{\prime }\right)}_{(k;d)}^{\mathit{\xi }}}{\left|{\breve{\mathit{\phi }}}_{(k;d)}\right|}\right)}_{(k;d)=(1,\dots ,K;1,\dots ,D)}^{\mathit{\xi }=1,\dots ,{\mathrm{\Xi }}_{\mathit{\alpha }}}\hfill \end{array}$$(18) (19) $$\begin{array}{cc}\hfill \mathcal{R}& ={\left(\frac{{\mathit{\phi }}_{(k;d)}-{\breve{\mathit{\phi }}}_{(k;d)}}{\left|{\breve{\mathit{\phi }}}_{(k;d)}\right|}\right)}_{(k;d)=(1,\dots ,K;1,\dots ,D)}\hfill \end{array}$$(19)

where $K$ and $D$ are the number of sources and sensors, respectively.

$\mathcal{S}\in {\mathbb{C}}^{(K\times D)\times 2{\mathrm{\Xi }}_{\mathit{\alpha }}}$, $\mathcal{R}\in {\mathbb{C}}^{(K\times D)}$, and derivative functions ${\mathit{\phi }}_{\varkappa }^{\prime }$ and ${\mathit{\phi }}_{\mathit{\varsigma }}^{\prime }$ can be obtained directly by differentiating the forward model (7(7) $$\begin{array}{cc}\hfill -\mathrm{\nabla }·\left({\left[2\left(\mathit{\kappa }+\mathit{\sigma }\right)\right]}^{-1}\mathrm{\nabla }\mathit{\phi }\right)+\left(\mathit{\kappa }+\frac{2\mathit{\pi }i\mathit{\nu }}{c}\right)\mathit{\phi }& =0in\mathcal{D}\hfill \end{array}$$(7) ) and (8(8) $$\begin{array}{cc}\hfill \mathit{\phi }+\frac{A}{2{\mathit{\pi }}^{-1}}{\left[2(\mathit{\kappa }+\mathit{\sigma })\right]}^{-1}\mathrm{\nabla }\mathit{\phi }·\mathbf{n}& =\frac{I}{{\mathit{\pi }}^{-1}}{1}_{\left[\mathit{\zeta }\in \mathit{\partial }{\mathcal{D}}_s\right]}on\mathit{\partial }\mathcal{D}\hfill \end{array}$$(8) ) with respect to the adimensionalized radiative properties $\varkappa$ and $\mathit{\varsigma }$, respectively. ${\mathit{\phi }}_{\varkappa }^{\prime }$ and ${\mathit{\phi }}_{\mathit{\varsigma }}^{\prime }$ are solutions of the following partial differential equations:(20) $$\begin{array}{cc}\hfill -\mathrm{\nabla }·\left({[2(\mathit{\kappa }+\mathit{\sigma })]}^{-1}\mathrm{\nabla }{\mathit{\phi }}_{\varkappa }^{\prime }\right)+\left(\mathit{\kappa }+\frac{2\mathit{\pi }i\mathit{\nu }}{c}\right){\mathit{\phi }}_{\varkappa }^{\prime }& =-{\mathit{\kappa }}_{ap}{\varkappa }^{\prime }\mathit{\phi }-{\mathit{\kappa }}_{ap}\mathrm{\nabla }·\left(\frac{{\varkappa }^{\prime }\mathrm{\nabla }\mathit{\phi }}{2{(\mathit{\kappa }+\mathit{\sigma })}^2}\right)in\mathcal{D}\hfill \end{array}$$(20) (21) $$\begin{array}{cc}\hfill {\mathit{\phi }}_{\varkappa }^{\prime }+\frac{A}{2{\mathit{\pi }}^{-1}}{[2(\mathit{\kappa }+\mathit{\sigma })]}^{-1}\mathrm{\nabla }{\mathit{\phi }}_{\varkappa }^{\prime }·\mathbf{n}& ={\mathit{\kappa }}_{ap}\frac{A}{2{\mathit{\pi }}^{-1}}\frac{{\varkappa }^{\prime }\mathrm{\nabla }\mathit{\phi }}{2{(\mathit{\kappa }+\mathit{\sigma })}^2}\mathrm{\nabla }\mathit{\phi }·\mathbf{n}on\mathit{\partial }\mathcal{D}\hfill \end{array}$$(21)

and(22) $$\begin{array}{cc}\hfill -\mathrm{\nabla }·\left({[2(\mathit{\kappa }+\mathit{\sigma })]}^{-1}\mathrm{\nabla }{\mathit{\phi }}_{\mathit{\varsigma }}^{\prime }\right)+\left(\mathit{\kappa }+\frac{2\mathit{\pi }i\mathit{\nu }}{c}\right){\mathit{\phi }}_{\mathit{\varsigma }}^{\prime }& =-{\mathit{\sigma }}_{ap}\mathrm{\nabla }·\left(\frac{{\mathit{\varsigma }}^{\prime }\mathrm{\nabla }\mathit{\phi }}{2{(\mathit{\kappa }+\mathit{\sigma })}^2}\right)in\mathcal{D}\hfill \end{array}$$(22) (23) $$\begin{array}{cc}\hfill {\mathit{\phi }}_{\mathit{\varsigma }}^{\prime }+\frac{A}{2{\mathit{\pi }}^{-1}}{[2(\mathit{\kappa }+\mathit{\sigma })]}^{-1}\mathrm{\nabla }{\mathit{\phi }}_{\mathit{\varsigma }}^{\prime }·\mathbf{n}& ={\mathit{\sigma }}_{ap}\frac{A}{2{\mathit{\pi }}^{-1}}\frac{{\mathit{\varsigma }}^{\prime }\mathrm{\nabla }\mathit{\phi }}{2{(\mathit{\kappa }+\mathit{\sigma })}^2}\mathrm{\nabla }\mathit{\phi }·\mathbf{n}on\mathit{\partial }\mathcal{D}\hfill \end{array}$$(23)

where ${\varkappa }^{\prime }$, ${\mathit{\varsigma }}^{\prime }$ denote the perturbations. Algorithm 1 gives some explanations about the construction of vector $\mathcal{R}$ and matrix $\mathcal{S}$ involved in (17(17) $$\begin{array}{c}\hfill \mathfrak{R}\left({\mathcal{S}}^{\top }\overline{\mathcal{S}}\right)\mathit{\delta }\tilde{\mathit{\gamma }}=-\mathfrak{R}\left({\mathcal{S}}^{\top }\overline{\mathcal{R}}\right)\end{array}$$(17) ).

3.4. Tikhonov regularization

The Tikhonov regularization method consists in adding a penalization term $\mathit{\vartheta }{\mathcal{J}}^{+}$ which is based on priors to the cost to be minimized (9(9) $$\begin{array}{c}\hfill \mathcal{J}(\mathit{\phi })=\frac{1}{2}\sum _{k=1}^K\sum _{d=1}^D{\left|\frac{{\mathit{\phi }}_{(k;d)}-{\breve{\mathit{\phi }}}_{(k;d)}}{{\breve{\mathit{\phi }}}_{(k;d)}}\right|}^2\end{array}$$(9) ):(24) $$\begin{array}{c}\hfill {\mathcal{J}}^{+}(\varkappa ,\mathit{\varsigma })=\frac{1}{2}\sum _{\tilde{\mathit{\alpha }}=\varkappa ,\mathit{\varsigma }}{\int }_{\mathcal{D}}{\left(\tilde{\mathit{\alpha }}-{\tilde{\mathit{\alpha }}}_{\text{ap}}\right)}^2\mathrm{d}\mathbf{x}\end{array}$$(24) $\mathit{\vartheta }$ being the Tikhonov parameter, and ${\tilde{\mathit{\alpha }}}_{\text{ap}}$ being equal to 1 as explained above. This has been successfully used in the optical tomography area, e.g. by [14–19] when using the Gauss–Newton optimizer. Doing so, the optimization problem becomes ‘Find the functions ${\varkappa }_{\mathit{\vartheta }}^{\ast }(\mathbf{x})$ and ${\mathit{\varsigma }}_{\mathit{\vartheta }}^{\ast }(\mathbf{x})$ such that $j_{\mathit{\vartheta }}({\varkappa }_{\mathit{\vartheta }}^{\ast },{\mathit{\varsigma }}_{\mathit{\vartheta }}^{\ast })=min{j}_{\mathit{\vartheta }}(\varkappa ,\mathit{\varsigma })$’ with $j_{\mathit{\vartheta }}=\mathcal{J}+\mathit{\vartheta }{\mathcal{J}}^{+}$.

The simultaneous use of several regularizations together has been studied in [5, 6], among which the reduction of the control space dimension [4] with Tikhonov regularization. It is shown here that the control space reduction modifies only slightly the optimal Tikhonov parameter.

The control space mesh is assumed to be chosen sufficiently fine to ensure that the spatial fluctuations of the radiative properties are well taken into account. Thus, the projections from the control functional space to the state functional space are such that the state is almost independent of the number of degrees of freedom ${\mathrm{\Xi }}_{\mathit{\alpha }}$, and thus the cost function $\mathcal{J}$ is also almost independent of ${\mathrm{\Xi }}_{\mathit{\alpha }}$. Next, to simplify the presentation, let us consider only one parameter, say $\varkappa$.

Proposition 3.1

Under the following assumptions:

(H1)	${\mathit{\psi }}_{\mathit{\xi }}$ are basis functions constant per element on a regular mesh, i.e. Lagrange ${\mathcal{P}}_0$ elements are used for the discretization of the function $\varkappa$,
(H2)	$\varkappa \sim \mathcal{N}\left(1,{\mathit{\sigma }}_{\varkappa }^2\right)$,

then the optimal Tikhonov parameter is asymptotically independent of the dimension ${\mathrm{\Xi }}_{\mathit{\alpha }}$.

Proof

Let ${\varkappa }_{\mathit{\vartheta }}^{\ast }$ be a solution of the optimization problem(25) $$\begin{array}{c}\hfill {\varkappa }_{\mathit{\vartheta }}^{\ast }=arg\underset{\varkappa }{min}\left(\mathcal{J}(\mathit{\phi })+\mathit{\vartheta }{\mathcal{J}}^{+}(\varkappa )\right)\end{array}$$(25)

with $\mathit{\vartheta }$ representing the best compromise between both costs $\mathcal{J}(\mathit{\phi })$ and ${\mathcal{J}}^{+}(\varkappa )$. Then, showing ${\mathcal{J}}^{+}$ does not depend on the parameterization yields $\mathit{\vartheta }$ independent of ${\mathrm{\Xi }}_{\mathit{\alpha }}$. Let $\tilde{\mathit{\vartheta }}={\mathit{\sigma }}_{\varkappa }^2\mathit{\vartheta }$ and $\mathrm{\Delta }x=|\mathcal{D}|/{\mathrm{\Xi }}_{\mathit{\alpha }}$ be the area of one element of the regular mesh. With H1), we have $\mathit{\vartheta }{\mathcal{J}}^{+}(\varkappa )=\frac{\tilde{\mathit{\vartheta }}|\mathcal{D}|}{2}\frac{1}{{\mathrm{\Xi }}_{\mathit{\alpha }}}{\sum }_{i=1}^{{\mathrm{\Xi }}_{\mathit{\alpha }}}{\left(\frac{{\varkappa }_i-1}{{\mathit{\sigma }}_{\varkappa }}\right)}^2$. With H2), $\frac{{\varkappa }_i-1}{{\mathit{\sigma }}_{\varkappa }}\sim \mathcal{N}\left(0,1\right)$$\forall i$, thus $\mathrm{{\rm Y}}={\sum }_{i=1}^{{\mathrm{\Xi }}_{\mathit{\alpha }}}{\left(\frac{{\varkappa }_i-1}{{\mathit{\sigma }}_{\varkappa }}\right)}^2\sim {\mathit{\chi }}_{{\mathrm{\Xi }}_{\mathit{\alpha }}}^2$. Then, using the fact that $\mathbf{E}\left(\mathrm{{\rm Y}}\right)={\mathrm{\Xi }}_{\mathit{\alpha }}$, we have $\mathbf{E}\left({\mathcal{J}}^{+}\right)=\frac{{\mathit{\sigma }}_{\varkappa }^2|\mathcal{D}|}{2}$ which is independent of ${\mathrm{\Xi }}_{\mathit{\alpha }}$. This completes the proof. $\square$

Remark 3.2

This demonstration can be easily extended to several parameters, say with a function of the type of (24(24) $$\begin{array}{c}\hfill {\mathcal{J}}^{+}(\varkappa ,\mathit{\varsigma })=\frac{1}{2}\sum _{\tilde{\mathit{\alpha }}=\varkappa ,\mathit{\varsigma }}{\int }_{\mathcal{D}}{\left(\tilde{\mathit{\alpha }}-{\tilde{\mathit{\alpha }}}_{\text{ap}}\right)}^2\mathrm{d}\mathbf{x}\end{array}$$(24) ) assuming that ${\mathit{\sigma }}_{\mathit{\varsigma }}\approx {\mathit{\sigma }}_{\varkappa }$.

Remark 3.3

It could also be extended to other finite element parameterizations, but with much heavier calculations.

3.5. Numerical validation

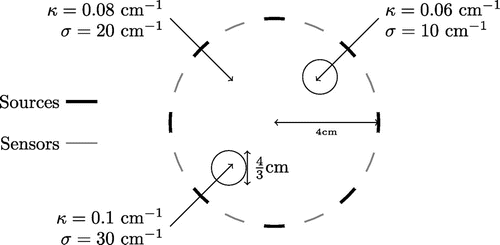
The ability to determine on a coarse mesh a reasonable parameter for the Tikhonov regularization is illustrated on a circular test medium. The rationale behind this choice is to reduce computational time required for getting a Tikhonov parameter so that the solution is close enough to the true solution, at least from an engineering point of view.

Synthetic data and predicted values are collected with the help of eight equally distributed sources and sensors about the disk perimeter $(K=8)$. Sources and sensors are alternatively distributed as schematically depicted in Figure 3. Each sensor contains seven pointwise photon density measurements $(D=56)$. Radiative property maps to be recovered are also given in Figure 3. The areas to be detected are located at about 2.5 cm in opposite locations at ${45}^{\circ }$  and ${225}^{\circ }$, respectively. The defects are $4/3$ cm in diameters, while the whole medium has a 4 cm radius. Each probe is 0.8 cm in length. The other physical parameters involved in (7(7) $$\begin{array}{cc}\hfill -\mathrm{\nabla }·\left({\left[2\left(\mathit{\kappa }+\mathit{\sigma }\right)\right]}^{-1}\mathrm{\nabla }\mathit{\phi }\right)+\left(\mathit{\kappa }+\frac{2\mathit{\pi }i\mathit{\nu }}{c}\right)\mathit{\phi }& =0in\mathcal{D}\hfill \end{array}$$(7) ) and (8(8) $$\begin{array}{cc}\hfill \mathit{\phi }+\frac{A}{2{\mathit{\pi }}^{-1}}{\left[2(\mathit{\kappa }+\mathit{\sigma })\right]}^{-1}\mathrm{\nabla }\mathit{\phi }·\mathbf{n}& =\frac{I}{{\mathit{\pi }}^{-1}}{1}_{\left[\mathit{\zeta }\in \mathit{\partial }{\mathcal{D}}_s\right]}on\mathit{\partial }\mathcal{D}\hfill \end{array}$$(8) ) are fixed to: $n=1.4$, $\mathit{\nu }=1\times {10}^8$ s${}^{-1}$, $c=c_0/n$ with $c_0=3\times {10}^{10}$ cm s${}^{-1}$, $I=0.1$ W cm${}^{-2}$ and $A$ is derived from Fresnel’s law (see [18]).

Figure 3. Test medium geometry representation. Eight sources are located on the boundary. For each source (which constitutes a test), the emerging radiation is measured on all sensors.

The radiative parameters are initialized to the radiative properties of the background considered as priors: ${\mathit{\kappa }}^0={\mathit{\kappa }}_{ap}=0.8{\mathrm{cm}}^{-1}$ and ${\mathit{\sigma }}^0={\mathit{\sigma }}_{ap}=20{\mathrm{cm}}^{-1}$ all over the medium $\mathcal{D}$. Thus, initial control variables ${\varkappa }^0={\mathit{\kappa }}^0/{\mathit{\kappa }}_{ap}$ and ${\mathit{\varsigma }}^0={\mathit{\sigma }}^0/{\mathit{\sigma }}_{ap}$ are initialized to 1. Synthetic data $\breve{\mathit{\phi }}$ and initial adimensionalized radiative properties $\varkappa$ and $\mathit{\varsigma }$ are inputs of the inverse problem. The way in which synthetic data are generated is given hereafter.

Within the inverse procedure, the forward model (7(7) $$\begin{array}{cc}\hfill -\mathrm{\nabla }·\left({\left[2\left(\mathit{\kappa }+\mathit{\sigma }\right)\right]}^{-1}\mathrm{\nabla }\mathit{\phi }\right)+\left(\mathit{\kappa }+\frac{2\mathit{\pi }i\mathit{\nu }}{c}\right)\mathit{\phi }& =0in\mathcal{D}\hfill \end{array}$$(7) ) and (8(8) $$\begin{array}{cc}\hfill \mathit{\phi }+\frac{A}{2{\mathit{\pi }}^{-1}}{\left[2(\mathit{\kappa }+\mathit{\sigma })\right]}^{-1}\mathrm{\nabla }\mathit{\phi }·\mathbf{n}& =\frac{I}{{\mathit{\pi }}^{-1}}{1}_{\left[\mathit{\zeta }\in \mathit{\partial }{\mathcal{D}}_s\right]}on\mathit{\partial }\mathcal{D}\hfill \end{array}$$(8) ) is solved by a finite element method with Lagrange ${\mathcal{P}}_1$ elements, that is, with $\mathit{\phi }\in {\mathcal{V}}_h^{\mathit{\phi }}=\mathcal{V}\left({\mathcal{M}}_h^{\mathit{\phi }},{\mathcal{P}}_1\right)$. The state mesh ${\mathcal{M}}_h^{\mathit{\phi }}$ is chosen fine enough to ensure that numerical predictions can fit the synthetic data. Synthetic data $\breve{\mathit{\phi }}$ are also generated with the finite element method with Lagrange ${\mathcal{P}}_1$ elements but using a much finer mesh ${\mathcal{M}}_h^{\breve{\mathit{\phi }}}$ in order to avoid the inverse crime.[34] After projecting the synthetic data in the functional space ${\mathcal{V}}_h^{\mathit{\phi }}$, $\breve{\mathit{\phi }}$ are corrupted with a multiplicative white Gaussian noise of signal-to-noise ratio $SNR=30$ dB: ${\breve{\mathit{\phi }}}_{noisy}=\breve{\mathit{\phi }}\left(1+{10}^{-SNR/10}\times \mathit{\epsilon }\right)$ where $\mathit{\epsilon }\sim \mathcal{N}(0,1)$.

Next, the control space ${\mathcal{V}}_h^{\mathit{\alpha }}=\mathcal{V}\left({\mathcal{M}}_h^{\mathit{\alpha }},{\mathcal{P}}_1\right)$ for $\mathit{\alpha }=\mathit{\kappa },\mathit{\sigma }$ relies on a more or less coarse mesh ${\mathcal{M}}_h^{\mathit{\alpha }}$ according to cases (see Table 2). The FreeFem++ environment has been used to perform all computations.[35]

Table 2. Dimensions of finite element spaces for $\mathit{\phi }$, $\breve{\mathit{\phi }}$ and $\mathit{\alpha }$.

	${\mathrm{\Xi }}_{\mathit{\alpha }}=dim{\mathcal{V}}_h^{\mathit{\alpha }}$	$dim{\mathcal{V}}_h^{\mathit{\phi }}$	$dim{\mathcal{V}}_h^{\breve{\mathit{\phi }}}$
Case 1	2924
Case 2	1382	2924	5336
Case 3	384

Table 3. CPU time comparisons for the generation of the error curves $E(\mathit{\vartheta })$.

	Case 1	Case 2	Case 3
CPU time	1	0.38	0.09

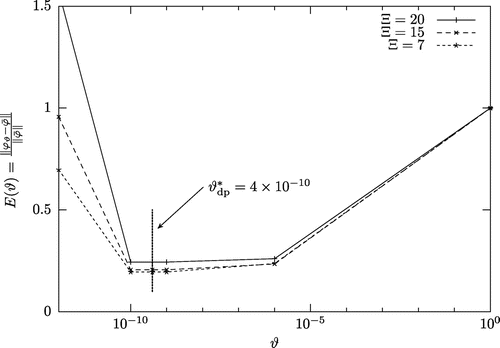
The error curves $E(\mathit{\vartheta })$ are built at the 20th iteration for the three cases described in Table 2: a fine mesh for the state ($dim{\mathcal{V}}_h^{\mathit{\phi }}=2924$), and successively a fine mesh, a medium mesh and a coarse mesh with respectively $dim{\mathcal{V}}_h^{\mathit{\alpha }}$ equal to 2924, 1382 and 384 nodes for the parameters. The three error curves are presented all together in Figure 4. Figure 4 first shows that for $\mathit{\vartheta }>0.4$, the calculated errors are independent of the mesh coarseness. Otherwise, for $\mathit{\vartheta }<0.3$, it is seen that the reduction of the control space reduces dramatically the errors. Such reduction of control space thus regularizes the inverse problem preconditioning the optimization.[4] In between, Figure 4 shows that the optimal Tikhonov parameters are found to be quasi-independent of the number of degrees of freedom of the finite control space. Within the range $[{10}^{-2},{10}^{+2}]$, the optimal Tikhonov parameter ${\mathit{\vartheta }}^{\ast }$ is found to be equal to $0.3$ for ${\mathrm{\Xi }}_{\mathit{\alpha }}=384$ and $0.4$ for ${\mathrm{\Xi }}_{\mathit{\alpha }}=1382$ and $2924$. This means that the minimal residual is indeed quasi-independent of the mesh coarsening, i.e. of $dim{\mathcal{V}}_h^{\mathit{\alpha }}$. This is what has been shown in Proposition 3.1.

Table 3 also provides the relative CPU time needed to build such curves for cases 1, 2 and 3 described in Table 2: the construction of this error curve with the coarsest mesh needs, in this case, roughly the 17th of the initial CPU time related to the construction with the finest mesh. This can be easily understood by examining the construction scheme of the Gauss–Newton matrix system presented above (see Algorithm 1).

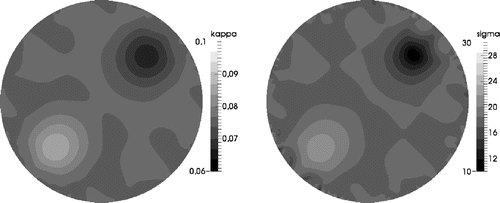
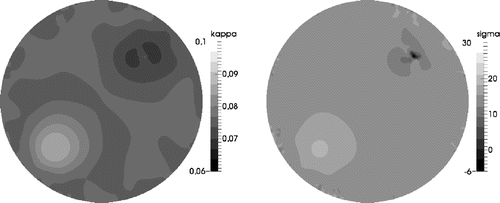
Figures 5 and 6 present the reconstructions of both $\mathit{\kappa }$ and $\mathit{\sigma }$ obtained with the Gauss–Newton optimizer at the 20th iteration, with ${\mathrm{\Xi }}_{\mathit{\alpha }}=2924$, and with the Tikhonov weight equal to 0.2 and 0.4, respectively. Figure 5 shows the divergence of the reconstruction with negative values for $\mathit{\sigma }$ due to under-regularization: the weight parameter $\mathit{\vartheta }$ is too low. Figure 6 presents the same reconstruction but with the Tikhonov parameter $\mathit{\vartheta }$ chosen at the minimum of the error curve. Reconstructions are good even in the presence of a 30 dB noise.

Figure 4. Distance from the solution to the target $E(\mathit{\vartheta })$ as a function of the Tikhonov parameter $\mathit{\vartheta }$, for $\left({\mathit{\kappa }}_{ap},{\mathit{\sigma }}_{ap}\right)=\left(0.08,20\right)c{m}^{-1}$ and three control space dimensions ${\mathrm{\Xi }}_{\mathit{\alpha }}$ equal to $384$, $1382$ and $2924$. It is seen that ${\mathit{\vartheta }}^{\ast }=argminE(\mathit{\vartheta })$ is quasi-independent of $\mathrm{\Xi }$.

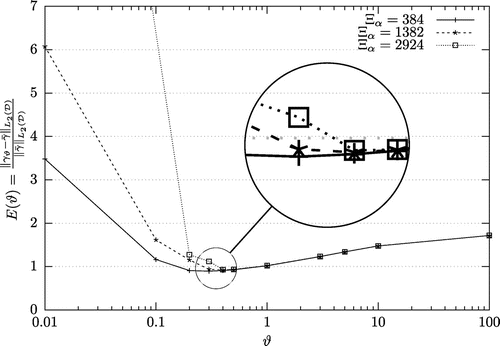
Figure 5. Reconstruction of $\mathit{\kappa }$ (left) and $\mathit{\sigma }$ (right) with $\mathit{\vartheta }=0.2$, $\left({\mathit{\kappa }}_{ap},{\mathit{\sigma }}_{ap}\right)=\left(0.08,20\right){\mathrm{cm}}^{-1}$ and ${\mathrm{\Xi }}_{\mathit{\alpha }}=2924$. It should be noted the divergence for the reduced diffusion coefficient.

Figure 6. Reconstruction of $\mathit{\kappa }$ (left) and $\mathit{\sigma }$ (right) with $\mathit{\vartheta }=0.4$, $\left({\mathit{\kappa }}_{ap},{\mathit{\sigma }}_{ap}\right)=\left(0.08,20\right){\mathrm{cm}}^{-1}$ and ${\mathrm{\Xi }}_{\mathit{\alpha }}=2924$.

Figure 7. Reconstruction of $\mathit{\kappa }$ (left) and $\mathit{\sigma }$ (right) with $\mathit{\vartheta }=1.4$, $\left({\mathit{\kappa }}_{ap},{\mathit{\sigma }}_{ap}\right)=\left(0.088,24\right){\mathrm{cm}}^{-1}$ and ${\mathrm{\Xi }}_{\mathit{\alpha }}=2924$.

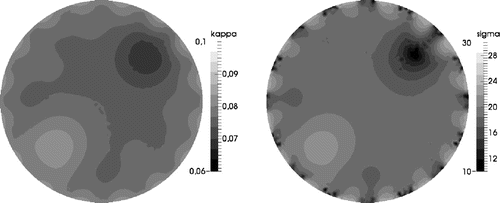
Two supplementary numerical tests are considered in order to investigate the behaviour of the inverse method with respect to the initial guess. As previously, initial control variables ${\varkappa }^0$ and ${\mathit{\varsigma }}^0$ are initialized to 1, so that the initial radiative properties are equal to the a priori properties ${\mathit{\kappa }}_{ap}$ and ${\mathit{\sigma }}_{ap}$. For the first test, a priori properties are fixed to $\left({\mathit{\kappa }}_{ap},{\mathit{\sigma }}_{ap}\right)=\left(0.088,24\right){\mathrm{cm}}^{-1}$ (10 and 20However, it should be noted that, as for the previous case where a priori properties equal the radiative properties of the background, the optimal Tikhonov parameter is found to be slightly smaller for ${\mathrm{\Xi }}_{\mathit{\alpha }}=384$ ($1382$) than for ${\mathrm{\Xi }}_{\mathit{\alpha }}=1382$ ($2924$). This can be explained by the fact that the reduction of the control space dimension acts as a regularization method so that the smaller the control space dimension ${\mathrm{\Xi }}_{\mathit{\alpha }}$, the smaller the optimal Tikhonov parameter ${\mathit{\vartheta }}^{\ast }$. As a result, the optimal Tikhonov parameter provided by a strongly reduced control space should not be considered as such for the original control space, but has to be interpreted as a very good indicator: the optimal Tikhonov parameter for the original control space will be slightly larger. Figure 7 presents the reconstructions of both $\mathit{\kappa }$ and $\mathit{\sigma }$ obtained with the Gauss–Newton optimizer at the 20th iteration, with ${\mathit{\vartheta }}^{\ast }=1.4$ and ${\mathrm{\Xi }}_{\mathit{\alpha }}=2924$. It is observed that the reconstructions are less accurate than those obtained when a priori properties equal the radiative properties of the background, but the inclusions can still be distinguished.

Finally, for the second test, the a priori properties are fixed to $\left({\mathit{\kappa }}_{\text{ap}},{\mathit{\sigma }}_{\text{ap}}\right)=\left(0.096,28\right){\mathrm{cm}}^{-1}$ (20 and 40% larger than radiative properties of the background medium for the absorption and reduced scattering coefficients, respectively). It was observed that the error curves associated to this initial guess are very irregular, so that it is difficult to find an optimal Tikhonov parameter. In fact, the results show that the Gauss–Newton optimizer fails to reconstruct the target properties whatever the value of the Tikhonov parameter. The initial guess is too far from the target so that the descent direction of the Gauss–Newton algorithm is never pointed towards the minimum and leads inevitably to very inaccurate reconstructions whatever the Tikhonov weight. Thus, for such choice of the initial guess, the use of more sophisticated methods, such as the globally convergent ones developed in [21–26], becomes necessary.

4. Conclusion

This paper has demonstrated that the optimal Tikhonov parameter, defined as that which minimizes the distance between the actual solution and the noise-free solution, is almost independent of the control space parameterization. This has first been verified on a standard linear inverse heat conduction problem in which, in phase one, the Tikhonov parameter has been approximated with the singular value decomposition and the maximum discrepancy principle and then, in a second phase, in the sense of the optimal Tikhonov parameter previously defined. Next, this validation has been extended to the nonlinear inverse problem of diffuse optical tomography. The error curves with respect to the Tikhonov parameter showed that their minimum is quasi-independent of the control space parameterization. This may result in CPU time reduction when searching for the optimal Tikhonov parameter, whatever the method used to find it. Of course, this is highly recommended for large size (three-dimensional) objects when the Gauss–Newton optimizer is chosen. Finally, note that the two inverse problems dealt with in this paper were under-determined, as it is the case in most space-dependent function estimation problems. Consequently, the theory has been numerically validated only on these two specific inverse problems. This may be viewed as a limitation, but the need of control space dimension reduction is much less useful for over-determined inverse problems than for space-dependent ones which are usually under-determined.

Acknowledgements

The authors would like to thank Pr. Hecht for providing the very efficient finite element tool FreeFem++.[35] The authors would also like to thank the Levis’s town, the Regional Conference of Elected Representatives of Chaudière-Appalaches, Énergie Valero Inc. and Ecosystem for their financial support to the industrial research chair t3e. The authors also thank the Centre Régional de Calcul Intensif des Pays de la Loire (CCIPL), financed by the French Research Ministry, the Région Pays de la Loire and the University of Nantes, allowing computations on their supercomputers. Finally, the authors would like to sincerely thank the reviewers for their constructive and relevant comments formulated on the first version that significantly enhanced the quality of this paper.

Notes

No potential conflict of interest was reported by the authors.